कम से कम औसत वर्ग फ़िल्टर

कम से कम औसत वर्ग (एलएमएस) एल्गोरिदम अनुकूली फ़िल्टर का वर्ग है जो फ़िल्टर गुणांक खोजकर वांछित फ़िल्टर की प्रतिलिपि करने के लिए उपयोग किया जाता है जो त्रुटि संकेत (वांछित और वास्तविक संकेत के बीच अंतर) के कम से कम औसत वर्ग का उत्पादन करने से संबंधित है। यह स्टोकास्टिक ग्रेडियेंट डिसेंट विधि है जिसमें फ़िल्टर केवल वर्तमान समय में त्रुटि के आधार पर अनुकूलित किया जाता है। इसका आविष्कार 1960 में स्टैनफोर्ड विश्वविद्यालय के प्रोफेसर बर्नार्ड विड्रो और उनके पहले पीएच.डी. छात्र, टेड हॉफ द्वारा किया गया था।

समस्या निर्माण

विनीज़ फ़िल्टर से संबंध

सिग्नल प्रोसेसिंग डोमेन को छोड़कर कारण वीनर फ़िल्टर की प्राप्ति कम से कम वर्गों के अनुमान के समाधान की तरह दिखती है। इनपुट आव्यूह के लिए कम से कम वर्ग समाधान $\mathbf {X}$ और आउटपुट सदिश ${\boldsymbol {y}}$ है

${\boldsymbol {\hat {\beta }}}=(\mathbf {X} ^{\mathbf {T} }\mathbf {X} )^{-1}\mathbf {X} ^{\mathbf {T} }{\boldsymbol {y}}.$

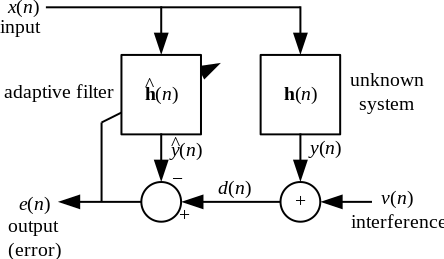
एफआईआर न्यूनतम माध्य वर्ग फ़िल्टर वीनर फ़िल्टर से संबंधित है, किंतु पूर्व के त्रुटि मानदंड को न्यूनतम करना क्रॉस-सहसंबंध या ऑटो-सहसंबंध पर निर्भर नहीं करता है। इसका समाधान वीनर फ़िल्टर समाधान में परिवर्तित हो जाता है। अधिकांश रैखिक अनुकूली फ़िल्टरिंग समस्याओं को उपरोक्त ब्लॉक आरेख का उपयोग करके तैयार किया जा सकता है। अर्थात्, एक अज्ञात प्रणाली $\mathbf {h} (n)$ की पहचान की जानी है और अनुकूली फ़िल्टर ${\hat {\mathbf {h} }}(n)$ को यथासंभव $\mathbf {h} (n)$ के समीप बनाने के लिए इसे अनुकूलित करने का प्रयास करता है। केवल अवलोकन योग्य संकेतों $x(n)$, $d(n)$ और $e(n)$ का उपयोग करते समय; किंतु $y(n)$, $v(n)$और $h(n)$सीधे देखने योग्य नहीं हैं। इसका समाधान वीनर फ़िल्टर से निकटता से संबंधित है।

प्रतीकों की परिभाषा

$n$ वर्तमान इनपुट नमूने की संख्या है

$p$ फिल्टर टेप्स की संख्या है

$\{\cdot \}^{H}$ (हर्मिटियन ट्रांसपोज़ या संयुग्मी स्थानान्तरण )

$\mathbf {x} (n)=\left[x(n),x(n-1),\dots ,x(n-p-1)\right]^{T}$ :$\mathbf {h} (n)=\left[h_{0}(n),h_{1}(n),\dots ,h_{p-1}(n)\right]^{T},\quad \mathbf {h} (n)\in \mathbb {C} ^{p}$

$y(n)=\mathbf {h} ^{H}(n)\cdot \mathbf {x} (n)$

$d(n)=y(n)+\nu (n)$ :${\hat {\mathbf {h} }}(n)$ अनुमानित फ़िल्टर; n नमूनों के बाद फ़िल्टर गुणांक के अनुमान के रूप में व्याख्या करें

$e(n)=d(n)-{\hat {y}}(n)=d(n)-{\hat {\mathbf {h} }}^{H}(n)\cdot \mathbf {x} (n)$

विचार

एलएमएस फिल्टर के पीछे मूल विचार इष्टतम फिल्टर वजन $(R^{-1}P)$ तक पहुंचना है, फिल्टर वजन को इष्टतम फिल्टर वजन में परिवर्तित करने के विधि से अपडेट करके यह ग्रेडिएंट डिसेंट एल्गोरिदम पर आधारित है। एल्गोरिथ्म छोटे वजन (अधिकत्तर स्थिति में शून्य) मानकर प्रारंभ होता है और, प्रत्येक चरण पर, माध्य वर्ग त्रुटि के ग्रेडिएंट को खोजकर वजन अपडेट किया जाता है। अर्थात्, यदि एमएसई-ग्रेडिएंट सकारात्मक है, तो इसका अर्थ है कि यदि उसी वजन का उपयोग आगे की पुनरावृत्तियों के लिए किया जाता है, तो त्रुटि सकारात्मक रूप से बढ़ती रहेगी, जिसका अर्थ है कि हमें वजन कम करने की आवश्यकता है। उसी तरह, यदि ग्रेडिएंट नकारात्मक है, तो हमें वज़न बढ़ाने की ज़रूरत है। वजन अद्यतन समीकरण है

$W_{n+1}=W_{n}-\mu \nabla \varepsilon [n],$

जहाँ $\varepsilon$ माध्य-वर्ग त्रुटि का प्रतिनिधित्व करता है और $\mu$ अभिसरण गुणांक है।

ऋणात्मक चिह्न दर्शाता है कि हम फ़िल्टर भार $W_{i}$ को खोजने के लिए त्रुटि $\varepsilon$ के ढलान से नीचे जाते हैं, जो त्रुटि को कम करता है।

फिल्टर भार के कार्य के रूप में माध्य-स्क्वायर त्रुटि द्विघात कार्य है जिसका अर्थ है कि इसका केवल चरम है, जो औसत-वर्ग त्रुटि को कम करता है, जो कि इष्टतम वजन है। एलएमएस इस प्रकार, माध्य-स्क्वायर-त्रुटि या फ़िल्टर भार वक्र के आरोही/अवरोही द्वारा इस इष्टतम भार की ओर पहुंचता है।

व्युत्पत्ति

एलएमएस फिल्टर के पीछे का विचार फ़िल्टर वजन ${\hat {\mathbf {h} }}(n)$ खोजने के लिए सबसे तेज गिरावट का उपयोग करना है जो हानि कार्य को कम करता है। हम व्यय फलन को इस रूप में परिभाषित करते हुए प्रारंभ करते हैं

$C(n)=E\left\{|e(n)|^{2}\right\}$

जहां $e(n)$ वर्तमान नमूने n में त्रुटि है और $E\{\cdot \}$अपेक्षित मान को दर्शाता है।

यह व्यय फलन ($C(n)$) माध्य वर्ग त्रुटि है, और इसे एलएमएस द्वारा न्यूनतम किया जाता है। यहीं पर एलएमएस को इसका नाम मिला जिसे स्टीपेस्ट डिसेंट को प्रयुक्त करने का अर्थ फ़िल्टर गुणांक (वजन) सदिश की व्यक्तिगत प्रविष्टियों के संबंध में आंशिक डेरिवेटिव लेना है

$\nabla _{{\hat {\mathbf {h} }}^{H}}C(n)=\nabla _{{\hat {\mathbf {h} }}^{H}}E\left\{e(n)\,e^{*}(n)\right\}=2E\left\{\nabla _{{\hat {\mathbf {h} }}^{H}}(e(n))\,e^{*}(n)\right\}$

जहाँ $\nabla$ ग्रेडियेंट ऑपरेटर है

$\nabla _{{\hat {\mathbf {h} }}^{H}}(e(n))=\nabla _{{\hat {\mathbf {h} }}^{H}}\left(d(n)-{\hat {\mathbf {h} }}^{H}\cdot \mathbf {x} (n)\right)=-\mathbf {x} (n)$

$\nabla C(n)=-2E\left\{\mathbf {x} (n)\,e^{*}(n)\right\}$

अब $\nabla C(n)$ एक वेक्टर है जो व्यय फलन की सबसे तीव्र चढ़ाई की ओर संकेत करता है। न्यूनतम व्यय फलन ज्ञात करने के लिए हमें $\nabla C(n)$ की विपरीत दिशा में एक कदम उठाना होगा। उसे गणितीय शब्दों में व्यक्त करना अहि

${\hat {\mathbf {h} }}(n+1)={\hat {\mathbf {h} }}(n)-{\frac {\mu }{2}}\nabla C(n)={\hat {\mathbf {h} }}(n)+\mu \,E\left\{\mathbf {x} (n)\,e^{*}(n)\right\}$

जहां ${\frac {\mu }{2}}$चरण आकार (अनुकूलन स्थिरांक) है। इसका अर्थ है कि हमें एक अनुक्रमिक अद्यतन एल्गोरिदम मिला है जो व्यय फलन को कम करता है। दुर्भाग्य से, यह एल्गोरिथम तब तक साकार नहीं हो सकता जब तक हम $E\left\{\mathbf {x} (n)\,e^{*}(n)\right\}$ नहीं जानते है ।

सामान्यतः ऊपर की अपेक्षा की गणना नहीं की जाती है। इसके अतिरिक्त, एलएमएस को ऑनलाइन (प्रत्येक नए नमूने के प्राप्त होने के पश्चात् अद्यतन करना) वातावरण में चलाने के लिए, हम उस अपेक्षा के तात्कालिक अनुमान का उपयोग करते हैं। नीचे देखें।

सरलीकरण

अधिकांश प्रणालियों के लिए अपेक्षा कार्य ${E}\left\{\mathbf {x} (n)\,e^{*}(n)\right\}$ अनुमानित होना चाहिए। यह निम्नलिखित निष्पक्ष अनुमानक के साथ किया जा सकता है

${\hat {E}}\left\{\mathbf {x} (n)\,e^{*}(n)\right\}={\frac {1}{N}}\sum _{i=0}^{N-1}\mathbf {x} (n-i)\,e^{*}(n-i)$

जहाँ $N$ उस अनुमान के लिए हमारे द्वारा उपयोग किए जाने वाले नमूनों की संख्या को इंगित करता है। सबसे सरल स्थिति $N=1$ है

${\hat {E}}\left\{\mathbf {x} (n)\,e^{*}(n)\right\}=\mathbf {x} (n)\,e^{*}(n)$

उस साधारण स्थिति के लिए अद्यतन एल्गोरिथ्म इस प्रकार है

${\hat {\mathbf {h} }}(n+1)={\hat {\mathbf {h} }}(n)+\mu \mathbf {x} (n)\,e^{*}(n)$

वास्तव में यह एलएमएस फिल्टर के लिए अद्यतन एल्गोरिथ्म का गठन करता है।

एलएमएस एल्गोरिथम सारांश

$p$वें आदेश फ़िल्टर के लिए एलएमएस एल्गोरिदम को संक्षेप में प्रस्तुत किया जा सकता है

Parameters:	$p=$ filter order
	$\mu =$ step size
Initialisation:	${\hat {\mathbf {h} }}(0)=\operatorname {zeros} (p)$
Computation:	For $n=0,1,2,...$
	$\mathbf {x} (n)=\left[x(n),x(n-1),\dots ,x(n-p+1)\right]^{T}$
	$e(n)=d(n)-{\hat {\mathbf {h} }}^{H}(n)\mathbf {x} (n)$
	${\hat {\mathbf {h} }}(n+1)={\hat {\mathbf {h} }}(n)+\mu \,e^{*}(n)\mathbf {x} (n)$

माध्य में अभिसरण और स्थिरता

चूंकि एलएमएस एल्गोरिथ्म अपेक्षाओं के सटीक मूल्यों का उपयोग नहीं करता है, वजन कभी भी पूर्ण अर्थ में इष्टतम वजन तक नहीं पहुंचेगा, किंतु माध्य में एक अभिसरण संभव है। अर्थात् वजन थोड़ी मात्रा में बदल सकता है, यह इष्टतम वजन के बारे में बदलता है। चूँकि यदि भिन्नता जिसके साथ वजन बदलता है, बड़ा है, तो माध्य में अभिसरण अस्पष्ट होगा यदि चरण-आकार $\mu$ का मान ठीक से नहीं चुना गया है तो यह समस्या उत्पन्न हो सकती है।

यदि $\mu$ को बड़ा चुना जाता है, तो भार में परिवर्तन की मात्रा ग्रेडिएंट अनुमान पर बहुत अधिक निर्भर करती है, और इसलिए वज़न बड़े मान से बदल सकता है जिससे ग्रेडिएंट जो पहले पल में नकारात्मक था वह अब सकारात्मक हो सकता है। और दूसरे क्षण में, नकारात्मक ढाल के कारण वजन विपरीत दिशा में बड़ी मात्रा में बदल सकता है और इस प्रकार इष्टतम वजन के बारे में एक बड़े बदलाव के साथ दोलन करता रहेगा। दूसरी ओर यदि $\mu$ को बहुत छोटा चुना जाता है, तो इष्टतम वजन तक पहुंचने का समय बहुत बड़ा होगा।

इस प्रकार, ऊपरी सीमा पर $\mu$ की आवश्यकता होती है जो दिया जाता है

$0<\mu <{\frac {2}{\lambda _{\mathrm {max} }}}$

जहाँ $\lambda _{\max }$ स्वतःसंबंध आव्यूह का सबसे बड़ा आइगेनवैल्यू है ${\mathbf {R} }=E\{{\mathbf {x} }(n){\mathbf {x} ^{H}}(n)\}$. यदि यह स्थिति पूरी नहीं होती है, तो एल्गोरिथम अस्थिर हो जाता है और ${\hat {h}}(n)$ विचलन।

अधिकतम अभिसरण गति तब प्राप्त होती है जब

$\mu ={\frac {2}{\lambda _{\mathrm {max} }+\lambda _{\mathrm {min} }}},$

जहां $\lambda _{\min }$, ${\mathbf {R} }$ का सबसे छोटा आइगेनवैल्यू है। यह देखते हुए कि $\mu$ इस इष्टतम से कम या इसके समान है अभिसरण गति $\lambda _{\min }$ द्वारा निर्धारित की जाती है बड़े मूल्य के साथ तेजी से अभिसरण प्राप्त होता है। इसका अर्थ यह है कि तेजी से अभिसरण तब प्राप्त किया जा सकता है जब $\lambda _{\max }$ , $\lambda _{\min }$ के समीप हो, जिससे , अधिकतम प्राप्त करने योग्य अभिसरण गति ${\mathbf {R} }$ के आइगेनवैल्यू प्रसार पर निर्भर करती है।

एक सफेद ध्वनि सिग्नल में ऑटोसहसंबंध आव्यूह होता है ${\mathbf {R} }=\sigma ^{2}{\mathbf {I} }$ जहां $\sigma ^{2}$ सिग्नल का विचरण होता है। इस मामले में सभी आइगेनवैल्यू ​​समान हैं, और सभी संभावित आव्यूहों पर आइगेनवैल्यू का प्रसार न्यूनतम है। इस परिणाम की सामान्य व्याख्या यह है कि एलएमएस सफेद इनपुट संकेतों के लिए तेजी से और रंगीन इनपुट संकेतों के लिए धीरे-धीरे परिवर्तित होता है, जैसे कम-पास या उच्च-पास विशेषताओं वाली प्रक्रियाएं है ।

यह ध्यान रखना महत्वपूर्ण है कि उपरोक्त ऊपरी सीमा पर $\mu$ केवल माध्य में स्थिरता को प्रयुक्त करता है, किंतु के गुणांक ${\hat {h}}(n)$ अभी भी असीम रूप से बड़ा हो सकता है, अथार्त गुणांकों का विचलन अभी भी संभव है। अधिक व्यावहारिक सीमा है

$0<\mu <{\frac {2}{\mathrm {tr} \left[{\mathbf {R} }\right]}},$

जहां $\mathrm {tr} [{\mathbf {R} }]$ , ${\mathbf {R} }$ के ट्रेस को दर्शाता है। यह सीमा आश्वासन देती है कि ${\hat {h}}(n)$ के गुणांक अलग-अलग नहीं होते हैं (व्यवहार में,$\mu$ का मान इस ऊपरी सीमा के समीप नहीं चुना जाना चाहिए, क्योंकि इसमें किए गए अनुमानों और धारणाओं के कारण यह कुछ सीमा तक आशावादी है। बाउंड की व्युत्पत्ति)।

सामान्यीकृत कम से कम वर्ग फ़िल्टर (एनएलएमएस)

"शुद्ध" एलएमएस एल्गोरिदम का मुख्य दोष यह है कि यह अपने इनपुट $x(n)$ की स्केलिंग के प्रति संवेदनशील है। इससे सीखने की दर $\mu$ चुनना बहुत कठिन (यदि असंभव नहीं) हो जाता है जो एल्गोरिदम की स्थिरता की आश्वासन देता है (हेकिन 2002)। सामान्यीकृत न्यूनतम माध्य वर्ग फ़िल्टर (एनएलएमएस) एलएमएस एल्गोरिथ्म का एक प्रकार है जो इनपुट की शक्ति के साथ सामान्यीकरण करके इस समस्या को हल करता है। एनएलएमएस एल्गोरिदम को संक्षेप में प्रस्तुत किया जा सकता है:

Parameters:	$p=$ filter order
	$\mu =$ step size
Initialization:	${\hat {\mathbf {h} }}(0)=\operatorname {zeros} (p)$
Computation:	For $n=0,1,2,...$
	$\mathbf {x} (n)=\left[x(n),x(n-1),\dots ,x(n-p+1)\right]^{T}$
	$e(n)=d(n)-{\hat {\mathbf {h} }}^{H}(n)\mathbf {x} (n)$
	${\hat {\mathbf {h} }}(n+1)={\hat {\mathbf {h} }}(n)+{\frac {\mu \,e^{*}(n)\mathbf {x} (n)}{\mathbf {x} ^{H}(n)\mathbf {x} (n)}}$

इष्टतम सीखने की दर

यह दिखाया जा सकता है कि यदि कोई हस्तक्षेप नहीं है ($v(n)=0$), तो एनएलएमएस एल्गोरिथम के लिए इष्टतम सीखने की दर है

$\mu _{opt}=1$

और इनपुट $x(n)$ और वास्तविक (अज्ञात) आवेग प्रतिक्रिया $\mathbf {h} (n)$ से स्वतंत्र है। सामान्य स्थिति में हस्तक्षेप $v(n)\neq 0$ के साथ सीखने की इष्टतम दर है

$\mu _{opt}={\frac {E\left[\left|y(n)-{\hat {y}}(n)\right|^{2}\right]}{E\left[|e(n)|^{2}\right]}}$

ऊपर दिए गए परिणाम मानते हैं कि सिग्नल $v(n)$ और $x(n)$ दूसरे से असंबद्ध हैं, जो सामान्यतः व्यवहार में होता है।

प्रमाण

मान लीजिए कि फ़िल्टर गलत संरेखण को $\Lambda (n)=\left|\mathbf {h} (n)-{\hat {\mathbf {h} }}(n)\right|^{2}$के रूप में परिभाषित किया गया है हम अगले नमूने के लिए अपेक्षित मिसलिग्न्मेंट इस प्रकार प्राप्त कर सकते हैं:

$E\left[\Lambda (n+1)\right]=E\left[\left|{\hat {\mathbf {h} }}(n)+{\frac {\mu \,e^{*}(n)\mathbf {x} (n)}{\mathbf {x} ^{H}(n)\mathbf {x} (n)}}-\mathbf {h} (n)\right|^{2}\right]$

$E\left[\Lambda (n+1)\right]=E\left[\left|{\hat {\mathbf {h} }}(n)+{\frac {\mu \,\left(v^{*}(n)+y^{*}(n)-{\hat {y}}^{*}(n)\right)\mathbf {x} (n)}{\mathbf {x} ^{H}(n)\mathbf {x} (n)}}-\mathbf {h} (n)\right|^{2}\right]$

होने देना $\mathbf {\delta } ={\hat {\mathbf {h} }}(n)-\mathbf {h} (n)$ और $r(n)={\hat {y}}(n)-y(n)$

$E\left[\Lambda (n+1)\right]=E\left[\left|\mathbf {\delta } (n)-{\frac {\mu \,\left(v(n)+r(n)\right)\mathbf {x} (n)}{\mathbf {x} ^{H}(n)\mathbf {x} (n)}}\right|^{2}\right]$

$E\left[\Lambda (n+1)\right]=E\left[\left(\mathbf {\delta } (n)-{\frac {\mu \,\left(v(n)+r(n)\right)\mathbf {x} (n)}{\mathbf {x} ^{H}(n)\mathbf {x} (n)}}\right)^{H}\left(\mathbf {\delta } (n)-{\frac {\mu \,\left(v(n)+r(n)\right)\mathbf {x} (n)}{\mathbf {x} ^{H}(n)\mathbf {x} (n)}}\right)\right]$

स्वतंत्रता मानकर, हमारे पास:

$E\left[\Lambda (n+1)\right]=\Lambda (n)+E\left[\left({\frac {\mu \,\left(v(n)+r(n)\right)\mathbf {x} (n)}{\mathbf {x} ^{H}(n)\mathbf {x} (n)}}\right)^{H}\left({\frac {\mu \,\left(v(n)+r(n)\right)\mathbf {x} (n)}{\mathbf {x} ^{H}(n)\mathbf {x} (n)}}\right)\right]-2E\left[{\frac {\mu |r(n)|^{2}}{\mathbf {x} ^{H}(n)\mathbf {x} (n)}}\right]$

$E\left[\Lambda (n+1)\right]=\Lambda (n)+{\frac {\mu ^{2}E\left[|e(n)|^{2}\right]}{\mathbf {x} ^{H}(n)\mathbf {x} (n)}}-{\frac {2\mu E\left[|r(n)|^{2}\right]}{\mathbf {x} ^{H}(n)\mathbf {x} (n)}}$

इष्टतम सीखने की दर पाई जाती है ${\frac {dE\left[\Lambda (n+1)\right]}{d\mu }}=0$, जिससे होता है:

$2\mu E\left[|e(n)|^{2}\right]-2E\left[|r(n)|^{2}\right]=0$

$\mu ={\frac {E\left[|r(n)|^{2}\right]}{E\left[|e(n)|^{2}\right]}}$

यह भी देखें

• रिकर्सिव कम से कम वर्ग
• एलएमएस फ़िल्टर से संबंधित सांख्यिकीय तकनीकों के लिए कम से कम वर्ग देखें।
• वीनर और एलएमएस के बीच समानताएं
• बहुविलंब ब्लॉक आवृत्ति डोमेन अनुकूली फ़िल्टर
• शून्य-बल तुल्यकारक
• कर्नेल अनुकूली फ़िल्टर
• मिलान फ़िल्टर
• वीनर फिल्टर

संदर्भ

• Monson H. Hayes: Statistical Digital Signal Processing and Modeling, Wiley, 1996, ISBN 0-471-59431-8
• Simon Haykin: Adaptive Filter Theory, Prentice Hall, 2002, ISBN 0-13-048434-2
• Simon S. Haykin, Bernard Widrow (Editor): Least-Mean-Square Adaptive Filters, Wiley, 2003, ISBN 0-471-21570-8
• Bernard Widrow, Samuel D. Stearns: Adaptive Signal Processing, Prentice Hall, 1985, ISBN 0-13-004029-0
• Weifeng Liu, Jose Principe and Simon Haykin: Kernel Adaptive Filtering: A Comprehensive Introduction, John Wiley, 2010, ISBN 0-470-44753-2
• Paulo S.R. Diniz: Adaptive Filtering: Algorithms and Practical Implementation, Kluwer Academic Publishers, 1997, ISBN 0-7923-9912-9

बाहरी संबंध

• एलएमएस Algorithm in Adaptive Antenna Arrays www.antenna-theory.com
• एलएमएस Noise cancellation demo www.advsolned.com