अकर्मण्यता: Difference between revisions
m (6 revisions imported from alpha:अकर्मण्यता) |
No edit summary |
||
| Line 102: | Line 102: | ||
* {{cite journal|doi = 10.1007/s11518-014-5245-x|title = Complexity and intransitivity in technological development|journal = Journal of Systems Science and Systems Engineering|volume = 23|issue = 2|pages = 128–152|year = 2014|last1 = Klimenko|first1 = Alexander Y.|s2cid = 59390606|url = http://staff.mechmining.uq.edu.au/klimenko/pub/pdf/JSSSE_2014_p.pdf}} | * {{cite journal|doi = 10.1007/s11518-014-5245-x|title = Complexity and intransitivity in technological development|journal = Journal of Systems Science and Systems Engineering|volume = 23|issue = 2|pages = 128–152|year = 2014|last1 = Klimenko|first1 = Alexander Y.|s2cid = 59390606|url = http://staff.mechmining.uq.edu.au/klimenko/pub/pdf/JSSSE_2014_p.pdf}} | ||
* {{cite journal|doi = 10.3390/e17064364|title = Intransitivity in Theory and in the Real World|journal = Entropy|volume = 17|issue = 12|pages = 4364–4412|year = 2015|last1 = Klimenko|first1 = Alexander|bibcode = 2015Entrp..17.4364K|arxiv = 1507.03169|doi-access = free}} | * {{cite journal|doi = 10.3390/e17064364|title = Intransitivity in Theory and in the Real World|journal = Entropy|volume = 17|issue = 12|pages = 4364–4412|year = 2015|last1 = Klimenko|first1 = Alexander|bibcode = 2015Entrp..17.4364K|arxiv = 1507.03169|doi-access = free}} | ||
[[Category:Articles with hatnote templates targeting a nonexistent page]] | |||
[[Category: | |||
[[Category:Created On 30/06/2023]] | [[Category:Created On 30/06/2023]] | ||
[[Category:Vigyan Ready]] | [[Category:Machine Translated Page]] | ||
[[Category:Pages with script errors]] | |||
[[Category:Templates Vigyan Ready]] | |||
[[Category:द्विआधारी संबंध]] | |||
Latest revision as of 10:43, 13 July 2023
गणित में, अकर्मण्यता (कभी-कभी गैर-संक्रमणीयता कहा जाता है) द्विआधारी संबंध की प्रोपर्टी है जो संक्रमणीय संबंध नहीं हैं। इसमें कोई भी ऐसा संबंध सम्मिलित हो सकता है जो सकर्मक नहीं है, या गणितीय शब्दजाल प्रतिपरिवर्तनशीलता से अधिक सशक्त है, जो ऐसे संबंध का वर्णन करता है जो कभी भी सकर्मक नहीं होता है।
अकर्मण्यता
कोई संबंध सकर्मक होता है यदि, जब भी वह किसी A को किसी B से, और उस B को किसी C से जोड़ता है, जिससे वह उस A को उस C से भी जोड़ता है। कुछ लेखक संबंध कहते हैं अकर्मक यदि यह सकर्मक नहीं है, अर्थात, (यदि प्रश्न में संबंध का नाम दिया गया है)
एक अन्य उदाहरण के रूप में, खाद्य श्रृंखला में, भेड़िये हिरण को खाते हैं, और इस प्रकार हिरण घास को खाते हैं, किन्तु भेड़िये घास को नहीं खाते हैं।[1] इस प्रकार खिलाना इस अर्थ में, जीवन रूपों के बीच संबंध अकर्मक है।
एक अन्य उदाहरण जिसमें प्राथमिकता लूप सम्मिलित नहीं है, फ़्रीमासोंरी में उत्पन्न होता है: कुछ उदाहरणों में लॉज ए लॉज बी को पहचानता है, और लॉज बी लॉज सी को पहचानता है, किन्तु लॉज ए लॉज सी को नहीं पहचानता है। इस प्रकार मेसोनिक लॉज के बीच मान्यता संबंध अकर्मक है।
एंटीट्रांसिटिविटी
अधिकांशतः शब्द अकर्मक का उपयोग एंटीट्रांसिटिविटी के गणितीय शब्दजाल सशक्त को संदर्भित करने के लिए किया जाता है।
उपरोक्त उदाहरण में, खिलाना संबंध सकर्मक नहीं है, किन्तु इसमें अभी भी कुछ सकर्मकता सम्मिलित है: उदाहरण के लिए, मनुष्य खरगोशों को खाते हैं, खरगोश गाजर को खाते हैं, और मनुष्य भी गाजर को खाते हैं।
यदि ऐसा कभी नहीं होता है तो कोई संबंध प्रतिसंक्रमणीय होता है अर्थात
प्रतिसंक्रमणीय संबंध का दूसरा उदाहरण: नॉकआउट टूर्नामेंट में पराजित संबंध यदि खिलाड़ी A ने खिलाड़ी B को हराया है और खिलाड़ी B ने खिलाड़ी C को हराया है, तो A कभी भी C से नहीं खेल सकता है, और इसलिए, A ने C को नहीं हराया है।
स्थानान्तरण (तर्क) द्वारा, निम्नलिखित में से प्रत्येक सूत्र आर की एंटीट्रांसिटिविटी के सामान्य है:
गुण
- एक प्रतिसंक्रमणीय संबंध सदैव अकर्मक संबंध होता है।
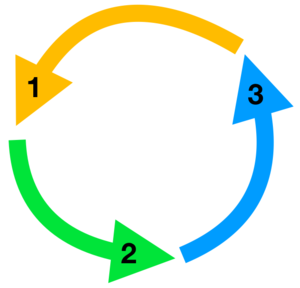
- ≥4 तत्वों के समुच्चय पर एंटीट्रांसिटिव संबंध कभी भी कॉन्नेक्स संबंध नहीं होता है। 3-तत्व समुच्चय पर, चित्रित चक्र में दोनों गुण हैं।
- एक अकर्मक और वाम-अनूठा संबंध या बाएं- (या दायां-अद्वितीय संबंध या दाएं) अद्वितीय संबंध सदैव संक्रमण-विरोधी होता है।[4] इस प्रकार पूर्व का उदाहरण माँ का सम्बन्ध है। यदि A, B की माँ है और B, C की माँ है, तो A, C की माँ नहीं हो सकती है।
- यदि कोई संबंध R प्रतिसंक्रमणीय है, तो R का प्रत्येक उपसमुच्चय भी प्रतिसंक्रमणीय है।
चक्र
शब्द अकर्मण्यता का उपयोग अधिकांशतः उन परिदृश्यों के बारे में बात करते समय किया जाता है जिसमें संबंध विकल्पों के जोड़े के बीच सापेक्ष प्राथमिकताओं का वर्णन करता है, और कई विकल्पों का वजन करने से वरीयता का लूप उत्पन्न होता है:
- A को B से अधिक प्राथमिकता दी जाती है
- B को C से अधिक प्राथमिकता दी जाती है
- C को A से अधिक प्राथमिकता दी जाती है
रॉक कागज कैंची; अकर्मक पासा; और पेनी का खेल इसके उदाहरण हैं। प्रतिस्पर्धी प्रजातियों के वास्तविक जुझारू संबंध,[5] व्यक्तिगत जानवरों की रणनीतियाँ,[6] और बैटलबॉट्स शो में रिमोट-नियंत्रित वाहनों की लड़ाई (रोबोट डार्विनवाद)[7] चक्रीय भी हो सकता है.
यह मानते हुए कि किसी भी विकल्प को प्राथमिकता नहीं दी गई है अर्थात संबंध अपरिवर्तनीय है, लूप के साथ वरीयता संबंध सकर्मक नहीं है। यदि ऐसा है, तो लूप में प्रत्येक विकल्प को प्रत्येक विकल्प के लिए प्राथमिकता दी जाती है, जिसमें स्वयं भी सम्मिलित है। इसे ए, बी और सी के बीच लूप के इस उदाहरण के लिए चित्रित किया जा सकता है। मान लें कि संबंध सकर्मक है। फिर, चूँकि A को B से प्राथमिकता दी जाती है और B को C से प्राथमिकता दी जाती है, इसलिए A को भी C से प्राथमिकता दी जाती है। किन्तु फिर, चूँकि C को A से प्राथमिकता दी जाती है, इसलिए A को भी A से प्राथमिकता दी जाती है।
इसलिए ऐसी वरीयता पाश (या चक्र) को अकर्मण्यता के रूप में जाना जाता है .
ध्यान दें कि किसी द्विआधारी संबंध के सकर्मक न होने के लिए चक्र न तो आवश्यक है और न ही पर्याप्त है। उदाहरण के लिए, तुल्यता संबंध में चक्र होते हैं किन्तु यह परिवर्तनशील होता है। अब, मान लीजिए कि सम्बन्ध दुश्मन है और मान लीजिए कि यह सम्बन्ध सममित है और इस नियम को पूरा करता है कि किसी भी देश के लिए, देश के दुश्मन का कोई भी दुश्मन खुद देश का दुश्मन नहीं है। यह प्रतिसंक्रमणीय संबंध का उदाहरण है जिसका कोई चक्र नहीं है। विशेषकर, प्रतिसंक्रमणीय होने के कारण संबंध सकर्मक नहीं है।
चट्टान, कागज, कैंची का खेल इसका उदाहरण है। चट्टान, कागज और कैंची का संबंध हार है, और खेल के मानक नियम ऐसे हैं कि चट्टान कैंची को हरा देती है, इस प्रकार कैंची कागज को हरा देती है, और कागज चट्टान को हरा देता है। इसके अलावा, यह भी सच है कि कैंची चट्टान को नहीं हराती, कागज कैंची को नहीं हराता, और चट्टान कागज को नहीं हराती। अंतत: यह भी सत्य है कि कोई भी विकल्प स्वयं को पराजित नहीं करता। इस जानकारी को तालिका में दर्शाया जा सकता है:
| रॉक | कैंची | पेपर | |
|---|---|---|---|
| रॉक | 0 | 1 | 0 |
| कैंची | 0 | 0 | 1 |
| पेपर | 1 | 0 | 0 |
संबंध का पहला तर्क पंक्ति है और दूसरा स्तंभ है। इंगित करता है कि संबंध है, शून्य इंगित करता है कि यह कायम नहीं है। अब, ध्यान दें कि समुच्चय {रॉक, कैंची, पेपर} से (प्रतिस्थापन के साथ) निकाले गए तत्वों x और y की किसी भी जोड़ी के लिए निम्नलिखित कथन सत्य है: यदि x, y को हराता है, और y, z को हराता है, तो x, z को नहीं हराता है। अत: संबंध प्रतिसंक्रमणीय है।
इस प्रकार, द्विआधारी संबंध के प्रतिसंक्रमणीय होने के लिए चक्र न तो आवश्यक है और न ही पर्याप्त है।
प्राथमिकताओं में घटित होना
- खेल सिद्धांत के संभाव्य परिणामों में, और कोंडोरसेट मतदान पद्धति में बहुमत नियम के अनुसार अकर्मण्यता हो सकती है, इस प्रकार जिसमें वजन की तुलना करने पर कई उम्मीदवारों की रैंकिंग वरीयता का लूप उत्पन्न कर सकती है (वोटिंग विरोधाभास देखें)।
- अकर्मक पासा यह दर्शाता है कि संबंध डाई X, पासे Y की तुलना में अधिक संख्या में रोल करता है, आधे से अधिक समय के लिए संक्रमणीय होने की आवश्यकता नहीं है।
- मनोविज्ञान में, किसी व्यक्ति की मूल्य प्रणाली (या प्राथमिकताएं, या स्वाद (समाजशास्त्र)) में अधिकांशतः अकर्मण्यता होती है, जो संभावित रूप से अनसुलझे संघर्षों का कारण बनती है।
- अनुरूप रूप से, अर्थशास्त्र में उपभोक्ता की प्राथमिकता (अर्थशास्त्र) में अकर्मण्यता हो सकती है। इससे उपभोक्ता का व्यवहार ऐसा हो सकता है जो सही तर्कसंगतता अर्थशास्त्र के अनुरूप नहीं है। अर्थशास्त्रियों और दार्शनिकों ने सवाल किया है कि क्या परिवर्तनशीलता का उल्लंघन अनिवार्य रूप से 'तर्कहीन व्यवहार' को जन्म देगा (देखें आनंद (1993))।
संभावना
यह सुझाव दिया गया है कि जब बड़ी संख्या में मतदाता भाग लेते हैं तो कॉन्डोर्सेट विधि अकर्मक लूप को समाप्त कर देती है क्योंकि मतदाताओं के लिए समग्र मूल्यांकन मानदंड संतुलित हो जाते हैं। उदाहरण के लिए, मतदाता माप की कई अलग-अलग इकाइयों पर उम्मीदवारों को पसंद कर सकते हैं जैसे कि सामाजिक चेतना के क्रम में या सबसे अधिक वित्तीय रूप से रूढ़िवादी के आधार पर चयन किया जाता है ।
ऐसे स्थितियों में अकर्मण्यता उम्मीदवारों के आकलन में लोगों की संख्या और उनकी माप की इकाइयों के वजन के व्यापक समीकरण तक कम हो जाती है।
जैसे कि:
- 30% सामाजिक चेतना और राजकोषीय रूढ़िवाद के बीच 60/40 के महत्व के पक्ष में हैं
- 50% सामाजिक चेतना और राजकोषीय रूढ़िवाद के बीच 50/50 का अंतर रखने के पक्ष में हैं
- 20% सामाजिक चेतना और राजकोषीय रूढ़िवाद के बीच 40/60 का अंतर रखने के पक्ष में हैं
चूँकि प्रत्येक मतदाता माप की इकाइयों का समान रूप से आकलन नहीं कर सकता है, फिर प्रवृत्ति एकल संभाव्यता वेक्टर बन जाती है जिस पर सामान्य सहमति उम्मीदवार मानदंडों का पसंदीदा संतुलन है।
संदर्भ
- ↑ Wolves do in fact eat grass – see Engel, Cindy (2003). Wild Health: Lessons in Natural Wellness from the Animal Kingdom (paperback ed.). Houghton Mifflin. p. 141. ISBN 0-618-34068-8..
- ↑ "Guide to Logic, Relations II". Archived from the original on 2008-09-16. Retrieved 2006-07-13.
- ↑ "IntransitiveRelation". Archived from the original on 2016-03-03. Retrieved 2006-07-13.
- ↑ If aRb, bRc, and aRc would hold for some a, b, c, then a = b by left uniqueness, contradicting aRb by irreflexivity.
- ↑ Kerr, Benjamin; Riley, Margaret A.; Feldman, Marcus W.; Bohannan, Brendan J. M. (2002). "Local dispersal promotes biodiversity in a real-life game of rock–paper–scissors". Nature. 418 (6894): 171–174. Bibcode:2002Natur.418..171K. doi:10.1038/nature00823. PMID 12110887. S2CID 4348391.
- ↑ Leutwyler, K. (2000). Mating Lizards Play a Game of Rock-Paper-Scissors. Scientific American.
- ↑ Atherton, K. D. (2013). A brief history of the demise of battle bots.
अग्रिम पठन
- Anand, P (1993). Foundations of Rational Choice Under Risk. Oxford: Oxford University Press..
- Bar-Hillel, M., & Margalit, A. (1988). How vicious are cycles of intransitive choice? Theory and Decision, 24(2), 119-145.
- Klimenko, Alexander Y. (2014). "Complexity and intransitivity in technological development" (PDF). Journal of Systems Science and Systems Engineering. 23 (2): 128–152. doi:10.1007/s11518-014-5245-x. S2CID 59390606.
- Klimenko, Alexander (2015). "Intransitivity in Theory and in the Real World". Entropy. 17 (12): 4364–4412. arXiv:1507.03169. Bibcode:2015Entrp..17.4364K. doi:10.3390/e17064364.