फ्यूज़न ट्री: Difference between revisions
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
[[कंप्यूटर विज्ञान|संगणक विज्ञान]] में, | |||
[[कंप्यूटर विज्ञान|संगणक विज्ञान]] में, '''फ्यूजन ट्री''' एक प्रकार की ट्री डेटा संरचना है जो एक विस्तृत यूनिवर्स पर w-बिट पूर्णांकों पर एक सहयोगी संख्या को लागू करती है, जहां प्रत्येक इनपुट पूर्णांक का आकार 2w से न्यूनतम होता है और अवांछित होता है. n की-मान तथा-मान जोड़ी के संग्रह पर आपरेशन करने पर, यह {{math|''O''(''n'')}} अंतरिक्ष का उपयोग करती है और खोजों को {{math|''O''(log<sub>''w''</sub> ''n'')}} समय में पूरा करती है, जो पारंपरिक आपस्तित्व वाले [[स्व-संतुलन द्विआधारी खोज वृक्ष]] से असंतुलित होता है, और {{mvar|w}} के बड़े मानों के लिए [[वैन एम्डे बोस कदम|वैन m्डे बोस]] ट्री से भी बेहतर होता है. यह तेज़ी इसलिए प्राप्त करता है क्योंकि इसमें [[मशीन शब्द]] पर कुछ स्थायी समय आपरेशन का उपयोग किया जा सकता है. फ्यूजन ट्री की खोज में {{math|''O''(log<sub>''w''</sub> ''n'')}} समय के कारण, यह 1990 में [[माइकल फ्रेडमैन]] और [[डैन विलार्ड]] द्वारा आविष्कृत की गई थी।<ref>{{citation | |||
| last1 = Fredman | first1 = M. L. | author1-link = Michael Fredman | | last1 = Fredman | first1 = M. L. | author1-link = Michael Fredman | ||
| last2 = Willard | first2 = D. E. | author2-link = Dan Willard | | last2 = Willard | first2 = D. E. | author2-link = Dan Willard | ||
| Line 12: | Line 14: | ||
}}.</ref> | }}.</ref> | ||
फ्रेडमैन और विलार्ड के मूल 1990 पेपर के उपरांत से कई प्रगति हुई है।<ref name="AMT1999">{{citation | |||
फ्रेडमैन और विलार्ड के मूल 1990 पेपर के | |||
| last1 = Andersson | first1 = Arne | | last1 = Andersson | first1 = Arne | ||
| last2 = Miltersen | first2 = Peter Bro | | last2 = Miltersen | first2 = Peter Bro | ||
| Line 26: | Line 26: | ||
| volume = 215 | | volume = 215 | ||
| year = 1999| doi-access = free | | year = 1999| doi-access = free | ||
}}.</ref> यह | }}.</ref> 1999 में यह दर्शाया गया कि गणना के एक मॉडल के तहत फ़्यूज़न पेड़ों को कैसे कार्यान्वित किया जाए जिसमें एल्गोरिदम के सभी अंतर्निहित संचालन AC<sup>0</sup> से संबंधित हों, [[सर्किट जटिलता]] का एक मॉडल जो जोड़ और बिटवाइज़ बूलियन संचालन की अनुमति देता है परंतु मूल फ़्यूज़न ट्री एल्गोरिदम में उपयोग किए जाने वाले गुणन संचालन की अनुमति नहीं देता है। हैश तालिकाओं का उपयोग करके फ़्यूज़न पेड़ों का एक गतिशील संस्करण 1996 में प्रस्तावित किया गया था<ref>{{citation | ||
| last = Raman | first = Rajeev | | last = Raman | first = Rajeev | ||
| contribution = Priority queues: small, monotone and trans-dichotomous | | contribution = Priority queues: small, monotone and trans-dichotomous | ||
| Line 36: | Line 36: | ||
| title = Fourth Annual European Symposium on Algorithms (ESA '96), Barcelona, Spain, September 25–27, 1996 | | title = Fourth Annual European Symposium on Algorithms (ESA '96), Barcelona, Spain, September 25–27, 1996 | ||
| volume = 1136 | | volume = 1136 | ||
| year = 1996}}.</ref> जो मूल संरचना | | year = 1996}}.</ref> जो मूल संरचना के {{math|''O''(log<sub>''w''</sub> ''n'')}} रनटाइम के अपेक्षानुसार मेल खाता था। [[ घातीय वृक्ष | घातीय वृक्ष]] का उपयोग करने वाला एक और गतिशील संस्करण 2007 में प्रस्तावित किया गया था<ref>{{citation | ||
| last1 = Andersson | first1 = Arne | | last1 = Andersson | first1 = Arne | ||
| last2 = Thorup | first2 = Mikkel | author2-link = Mikkel Thorup | | last2 = Thorup | first2 = Mikkel | author2-link = Mikkel Thorup | ||
| Line 47: | Line 47: | ||
| volume = 54 | | volume = 54 | ||
| year = 2007| arxiv = cs/0210006| s2cid = 8175703 | | year = 2007| arxiv = cs/0210006| s2cid = 8175703 | ||
}}.</ref> जो | }}.</ref> जो प्रत्येक आपरेशन के लिए {{math|''O''(log<sub>''w''</sub> ''n'' + log log ''n'')}} के खराब तरह का रनटाइम प्रदान करता है। अंतिम रूप में, दर्शाया गया कि गतिशील फ्यूजन ट्री संज्ञानात्मक ढंग से प्रत्येक आपरेशन को {{math|''O''(log<sub>''w''</sub> ''n'')}} समय में कर सकता है।<ref>{{cite journal |last1=Patrascu |first1=Mihai |last2=Thorup |first2=Mikkel |title=इष्टतम रैंक, चयन और पूर्ववर्ती खोज के साथ गतिशील पूर्णांक सेट|journal=55th IEEE Annual Symposium on Foundations of Computer Science, FOCS 2014 |date=2014 |page=166-175 |doi=10.1109/FOCS.2014.26 |url=https://doi.org/10.1109/FOCS.2014.26}}</ref> | ||
यह डेटा संरचना | यह डेटा संरचना एक दिए गए कुंजी के लिए कुंजी जोड़ें, कुंजी हटाएं, कुंजी खोजें, और पूर्ववर्ती (अगले छोटे मान) और उत्तरवर्ती खोज आपरेशन को लागू करती है। संख्या के सबसे महत्वपूर्ण बिट लोकेटर के आंशिक परिणाम ने अगले अध्ययन में भी सहायता की है। फ्यूजन ट्री मशीन शब्द में संगठित कुछ छोटे पूर्णांकों पर समय समय पर गणना करने के लिए शब्द-स्तरीय संयोजन का उपयोग करती है, जिससे कुल आपरेशनों की संख्या को न्यूनतम किया जा सकता है। | ||
== यह कैसे | == यह कैसे कार्य करता है == | ||
फ्यूजन ट्री मूल रूप से {{math|''w''<sup>1/5</sup>}} शाखा कारक वाली [[बी-वृक्ष|b-वृक्ष]] होती है, जिससे इसकी ऊचाई {{math|''O''(log<sub>''w''</sub> ''n'')}} होती है। अद्यतन और पूछताछ के लिए वांछित रनटाइम प्राप्त करने के लिए, फ्यूजन ट्री को एक बार में {{math|''w''<sup>1/5</sup>}} कुंजीयों को खोजने की क्षमता होनी चाहिए। इसका कारण है कि कुंजीयों को "स्केच" करके ऐसा संपीड़ित किया जाता है कि सभी एक मशीन शब्द में समायोजित हो सकें, जिससे पुनर्मिलन संघों को पैरालेल में करने में सक्षमता होती है। इसलिए, स्केचिंग, पैरालेल तुलना और सबसे महत्वपूर्ण बिट सूचक स्थानक के आधार पर की जाने वाली गणनाओं का एक श्रृंखला, उचित समाधान तक पहुंचने में सहायता करती है। | |||
===स्केचिंग=== | ===स्केचिंग=== | ||
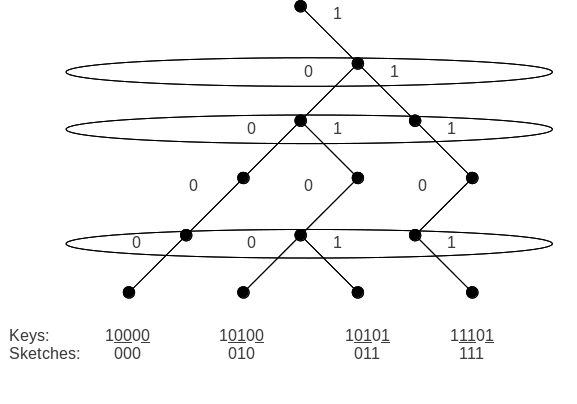
स्केचिंग वह विधि है जिसके द्वारा प्रत्येक {{mvar|w}}-बिट कुंजी एक नोड पर युक्त {{mvar|k}} कुंजियाँ केवल | स्केचिंग वह विधि है जिसके द्वारा प्रत्येक {{mvar|w}}-बिट कुंजी एक नोड पर युक्त {{mvar|k}} कुंजियाँ केवल {{math|''k'' − 1}} बिट्स में संपीड़ित होती हैं।. प्रत्येक कुंजी {{mvar|x}} को {{mvar|w}} ऊंचाई के पूर्ण बाइनरी ट्री में एक पथ के रूप में सोचा जा सकता है जो {{mvar|x}} जड़ से प्रारंभ होकर पत्ती पर समाप्त होता है। यह पथ सामान्यतः इस प्रकार प्रसंस्करण किया जा सकता है कि, सभी बिट स्कैन किए जाने तक, iवें बिट 0 है तो वाम बच्चे की खोज की जाएगी, और iवें बिट 1 है तो दायीं बच्चे की खोज की जाएगी। दो पथों को पृथक करने के लिए, उनके शाखा बिंदु को देखना पर्याप्त है।क्योंकि अधिकतम k कुंजियाँ होती हैं, इसलिए k-1 से अधिक शाखा बिंदु नहीं होंगे, जिसका अर्थ है कि किसी कुंजी की पहचान करने के लिए k-1 बिट्स से अधिक की आवश्यकता नहीं है। और इसलिए, किसी भी स्केच में k-1 बिट्स से अधिक नहीं होगा। | ||
[[File:FusionTreeSketch.gif|center|स्केच फ़ंक्शन का विज़ुअलाइज़ेशन।]]स्केच फ़ंक्शन का एक महत्वपूर्ण गुण यह है कि यह कुंजियों के क्रम को संरक्षित करता है। वह है, {{math|sketch(''x'') < sketch(''y'')}} किन्हीं दो कुंजियों के लिए {{math|''x'' < ''y''}}. तो, चाबियों की पूरी श्रृंखला के लिए, स्केच(x<sub>0</sub>)<स्केच(x<sub>1</sub>)<...<स्केच(x<sub>k-1</sub>) क्योंकि यदि बाइनरी ट्री जैसे पथ का अनुसरण किया जाता है तो नोड्स को इस तरह से ऑर्डर किया जाएगा कि x<sub>0</sub><x<sub>1</sub><...<x<sub>k-1</sub>. | [[File:FusionTreeSketch.gif|center|स्केच फ़ंक्शन का विज़ुअलाइज़ेशन।]]स्केच फ़ंक्शन का एक महत्वपूर्ण गुण यह है कि यह कुंजियों के क्रम को संरक्षित करता है। वह है, {{math|sketch(''x'') < sketch(''y'')}} किन्हीं दो कुंजियों के लिए {{math|''x'' < ''y''}}. तो, चाबियों की पूरी श्रृंखला के लिए, स्केच(x<sub>0</sub>)<स्केच(x<sub>1</sub>)<...<स्केच(x<sub>k-1</sub>) क्योंकि यदि बाइनरी ट्री जैसे पथ का अनुसरण किया जाता है तो नोड्स को इस तरह से ऑर्डर किया जाएगा कि x<sub>0</sub><x<sub>1</sub><...<x<sub>k-1</sub>. | ||
स्केच फ़ंक्शन की एक महत्वपूर्ण गुणधर्म है कि यह कुंजीयों का क्रमबद्धता को संरक्षित रखता है। अर्थात, किसी भी दो कुंजीयों x < y के लिए sketch(x) < sketch(y) होगा। इसलिए, पूरे कुंजी दायरे के लिए, sketch(x0) < sketch(x1) < ... < sketch(xk-1) होगा, क्योंकि यदि बाइनरी ट्री के समान पथ का पालन किया जाता है, तो नोड ऐसी व्यवस्था में क्रमबद्ध x0 < x1 < ... < xk-1 होंगे। | |||
===स्केच का अनुमान लगाना=== | ===स्केच का अनुमान लगाना=== | ||
यदि स्केच | यदि स्केच बिटों की स्थानों को b1 < b2 < ··· < br माना जाता है, तो कुंजी xw-1···x1x0 का स्केच r-बिट पूर्णांक होता है। | ||
<math>x_{b_r}x_{b_{r-1}}\cdots x_{b_1}</math>. | |||
केवल मानक शब्द संचालन, जैसे कि , के साथ, निरंतर समय में किसी कुंजी के सही स्केच की सीधे गणना करना मुश्किल है। इसके अतिरिक्त, स्केच बिट्स को अधिकतम r आकार की श्रेणी में पैक किया जा सकता है, बिटवाइज़ AND और गुणन का उपयोग करते हुए, अनुमानित स्केच कहा जाता है, जिसमें सभी महत्वपूर्ण बिट्स होते हैं परंतु कुछ अतिरिक्त बेकार बिट्स भी एक पूर्वानुमानित पैटर्न में विस्तृत होते हैं। बिटवाइज़ AND ऑपरेशन इन सभी गैर-स्केच बिट्स को कुंजी से हटाने के लिए एक मास्क के रूप में कार्य करता है, जबकि गुणन स्केच बिट्स को एक छोटी सीमा में स्थानांतरित करता है। पूर्ण स्केच की तरह, अनुमानित स्केच भी कुंजियों के क्रम को सुरक्षित रखता है और इसका मतलब है कि स्केच(x<sub>0</sub>)<स्केच(x<sub>1</sub>)<...<स्केच(x<sub>k-1</sub>). | |||
केवल [[सी प्रोग्रामिंग भाषा]] के जैसे मानक शब्द आपरेशन का उपयोग करके, एक कुंजी का पूर्ण स्केच सीधे समय में निर्धारित करना कठिन होता है। इसके अतिरिक्त, स्केच बिट्स को बिटवाइज़ AND और गुणाकार का उपयोग करके, अधिकतम r<sup>4</sup> आकार के रेंज में पैक किया जा सकता है, जिसे अनुमानित स्केच कहा जाता है, जिसमें सभी महत्वपूर्ण बिट होते हैं परंतु इसके साथ कुछ अतिरिक्त बेकार बिट भी होते हैं जो एक पूर्वानुमानित पैटर्न में विस्तृत होते हैं। बिटवाइज़ AND आपरेशन गैर-स्केच बिट्स को कुंजी से हटाने के लिए मास्क के रूप में कार्य करता है, जबकि गुणाकार स्केच बिट्स को एक छोटी सीमा में स्थानांतरित करता है। "पूर्ण" स्केच की तरह, अनुमानित स्केच भी कुंजीयों का क्रमबद्धता संरक्षित करता है और इसका अर्थ है कि sketch(x0) < sketch(x1) < ... < sketch(xk-1) होता है। | |||
सही गुणन स्थिरांक निर्धारित करने के लिए कुछ पूर्वप्रक्रिया की आवश्यकता होती है। जहा स्थान b<sub>''i''</sub> में प्रत्येक स्केच बिट में b<sub>''i''</sub> + m<sub>''i''</sub> m = से गुणा करके <math>\textstyle\sum_{i=1}^r</math> 2<sup>m<sub>''i.''</sub> स्थानांतरित हो जायेंगे वहा अनुमानित स्केच को कार्यान्वित करने के लिए, निम्नलिखित तीन गुण होने चाहिए: | |||
# b<sub>''i''</sub> + m<sub>''j''</sub> सभी जोड़ियों (i, j) के लिए पृथक-पृथक होते हैं। इससे यह सुनिश्चित हो जाएगा कि स्केच बिट्स गुणन द्वारा दूषित नहीं हैं। | |||
# b<sub>''i''</sub> + m<sub>''i''</sub> i का सख्ती से बढ़ता हुआ फलन है। अर्थात्, स्केच बिट्स का क्रम x'.m में भी संरक्षित रहता है। | |||
# (b<sub>''r''</sub> + m<sub>''r''</sub>) - (b<sub>1</sub> + m<sub>1</sub>) ≤ r<sup>4</sup>. अर्थात्, स्केच बिट्स को अधिकतम r<sup>4</sup> आकार की श्रेणी में पैक किया जाता है, जहां r ≤ O(w<sup>1/5</sup>).होता हैं। | |||
एक आगमनात्मक तर्क दिखाता है कि कैसे m<sub>''i''</sub> निर्माण किया जा सकता है. m<sub>1</sub> = w − b<sub>1</sub>. मान लीजिए कि 1 < t ≤ r और वह m<sub>1</sub>, m<sub>2</sub>... m<sub>''t-1''</sub> पहले ही चुना जा चुका है. पुनः सबसे छोटा पूर्णांक m चुनें<sub>''t''</sub> इस प्रकार कि दोनों गुण (1) और (2) संतुष्ट हैं। संपत्ति (1) के लिए आवश्यक है कि m<sub>''t''</sub> ≠ b<sub>''i''</sub> − b<sub>''j''</sub> + m<sub>''l''</sub> सभी 1 ≤ i, j ≤ r और 1 ≤ l ≤ t-1 के लिए। इस प्रकार, tr से न्यूनतम हैं<sup>2</sup> ≤ r<sup>3</sup>मूल्य जो म<sub>''t''</sub> बचना चाहिए. चूंकि m<sub>''t''</sub> न्यूनतम होना चुना गया है, (b<sub>''t''</sub> + m<sub>''t''</sub>) ≤ (b<sub>''t''-1</sub> + m<sub>''t''-1</sub>) + r<sup>3</sup>. इसका तात्पर्य संपत्ति (3) से है। | |||
एक | एक आनुवंशिक तर्क दिखाता है कि कैसे m<sub>''i''</sub> का निर्माण किया जा सकता है। तो m1 = w − b1 चुनें। मान लीजिए कि 1 < t ≤ r है और m1, m2... mt-1 पहले से ही चुन लिए गए हैं। पुनः ऐसा सबसे छोटा पूर्णांक mt चुनें, जिसके लिए प्रोपर्टी (1) और (2) दोनों संतुष्ट होती हैं। प्रोपर्टी (1) यह मांगती है कि mt ≠ bi − bj + ml हर 1 ≤ i, j ≤ r और 1 ≤ l ≤ t-1 के लिए। इसलिए, mt को एक कम से कम r3 मानों को बचना चाहिए। क्योंकि mt को न्यूनतम चुना गया है, (bt + mt) ≤ (bt-1 + mt-1) + r3 होता है। इससे प्रोपर्टी (2) प्राप्त होती है। | ||
इस प्रकार अनुमानित रेखाचित्र की गणना इस प्रकार की जाती है: | इस प्रकार अनुमानित रेखाचित्र की गणना इस प्रकार की जाती है: | ||
# स्केच बिट्स को छोड़कर बाकी सभी को x और के | # स्केच बिट्स को छोड़कर बाकी सभी को x और के bच बिटवाइज़ से मास्क करें <math>\sum_{i=0}^{r-1} 2^{b_i}</math>. | ||
# ऊपर की गणना के अनुसार कुंजी को पूर्व निर्धारित स्थिरांक m से गुणा करें। इस ऑपरेशन के लिए वास्तव में दो मशीनी शब्दों की आवश्यकता होती है, | # ऊपर की गणना के अनुसार कुंजी को पूर्व निर्धारित स्थिरांक m से गुणा करें। इस ऑपरेशन के लिए वास्तव में दो मशीनी शब्दों की आवश्यकता होती है, परंतु यह अभी भी निरंतर समय में किया जा सकता है। | ||
# स्थानांतरित स्केच बिट्स को छोड़कर सभी को मास्क करें। ये अब अधिकतम r के सन्निहित ब्लॉक में समाहित हैं<sup>4</sup> <w<sup>4/5</sup>बिट्स. | # स्थानांतरित स्केच बिट्स को छोड़कर सभी को मास्क करें। ये अब अधिकतम r के सन्निहित ब्लॉक में समाहित हैं<sup>4</sup> <w<sup>4/5</sup>बिट्स. | ||
| Line 82: | Line 90: | ||
:1<code>sketch</code>(एक्स<sub>1</sub>)1<code>sketch</code>(एक्स<sub>2</sub>)...1<code>sketch</code>(एक्स<sub>''k''</sub>) | :1<code>sketch</code>(एक्स<sub>1</sub>)1<code>sketch</code>(एक्स<sub>2</sub>)...1<code>sketch</code>(एक्स<sub>''k''</sub>) | ||
यहां, सभी स्केच शब्दों को उनमें से प्रत्येक के लिए एक सेट बिट जोड़कर एक स्ट्रिंग में एक साथ जोड़ा गया है। हम मान सकते हैं कि स्केच फ़ंक्शन बिल्कुल b ≤ r का उपयोग करता है<sup>4</sup>बिट्स. | यहां, सभी स्केच शब्दों को उनमें से प्रत्येक के लिए एक सेट बिट जोड़कर एक स्ट्रिंग में एक साथ जोड़ा गया है। हम मान सकते हैं कि स्केच फ़ंक्शन बिल्कुल b ≤ r का उपयोग करता है<sup>4</sup>बिट्स. पुनः प्रत्येक ब्लॉक 1 + b ≤ w का उपयोग करता है<sup>4/5</sup>बिट्स, और चूँकि k ≤ w<sup>1/5</sup>, नोड स्केच में बिट्स की कुल संख्या अधिकतम w है। | ||
एक संक्षिप्त नोटेशनल एक तरफ: एक बिट स्ट्रिंग एस और गैर-नकारात्मक पूर्णांक | एक संक्षिप्त नोटेशनल एक तरफ: एक बिट स्ट्रिंग एस और गैर-नकारात्मक पूर्णांक m के लिए, चलो एस<sup>m</sup>s के स्वयं के साथ m बार संयोजन को दर्शाता है। यदि t एक बिट स्ट्रिंग st भी है, तो t से s के संयोजन को दर्शाता है। | ||
नोड स्केच किसी भी | नोड स्केच किसी भी b-बिट पूर्णांक y के लिए कुंजी खोजना संभव बनाता है। मान लीजिए z = (0y)<sup>k</sup>, जिसकी गणना स्थिर समय में की जा सकती है (y को स्थिरांक (0) से गुणा करें)।<sup>ख</sup>1)<sup>k</sup>), इसे नोड स्केच जितना लंबा बनाने के लिए, ताकि नोड स्केच में प्रत्येक शब्द की तुलना एक ऑपरेशन में क्वेरी पूर्णांक y के साथ की जा सके, जो शब्द-स्तरीय समानता का प्रदर्शन करता है। यदि y 5 बिट लंबा होता, तो स्केच(y) प्राप्त करने के लिए इसे 000001....000001 से गुणा किया जाता।<sup>क</sup>. स्केच(x) के bच का अंतर<sub>i</sub>) और 0y के परिणामस्वरूप प्रत्येक ब्लॉक के लिए अग्रणी बिट 1 होता है, यदि और केवल यदि स्केच(y) <math>\leq | ||
</math> स्केच(x<sub>i</sub>). इस प्रकार हम सबसे छोटे सूचकांक i की गणना कर सकते हैं <code>sketch</code>(एक्स<sub>''i''</sub>) ≥ y इस प्रकार है: | </math> स्केच(x<sub>i</sub>). इस प्रकार हम सबसे छोटे सूचकांक i की गणना कर सकते हैं <code>sketch</code>(एक्स<sub>''i''</sub>) ≥ y इस प्रकार है: | ||
| Line 97: | Line 105: | ||
एक मनमानी क्वेरी q के लिए, समानांतर तुलना सूचकांक i की गणना इस प्रकार करती है | एक मनमानी क्वेरी q के लिए, समानांतर तुलना सूचकांक i की गणना इस प्रकार करती है | ||
:<code>sketch</code>(एक्स<sub>''i''-1</sub>) ≤ <code>sketch</code>(क्यू) ≤ <code>sketch</code>(एक्स<sub>''i''</sub>) | :<code>sketch</code>(एक्स<sub>''i''-1</sub>) ≤ <code>sketch</code>(क्यू) ≤ <code>sketch</code>(एक्स<sub>''i''</sub>) | ||
दुर्भाग्य से, यह q का सटीक पूर्ववर्ती या उत्तराधिकारी नहीं देता है, क्योंकि सभी मानों के रेखाचित्रों के | दुर्भाग्य से, यह q का सटीक पूर्ववर्ती या उत्तराधिकारी नहीं देता है, क्योंकि सभी मानों के रेखाचित्रों के bच q के रेखाचित्र का स्थान सभी वास्तविक मानों में q के स्थान के समान नहीं हो सकता है। जो सच है वह यह है कि, सभी कुंजियों में से, या तो x<sub>''i''-1</sub> या एक्स<sub>''i''</sub> q के साथ सबसे लंबा सामान्य उपसर्ग है। ऐसा इसलिए है क्योंकि q के साथ लंबे सामान्य उपसर्ग वाली किसी भी कुंजी y में q के साथ समान रूप से अधिक स्केच बिट्स होंगे, और इस प्रकार <code>sketch</code>(y) के करीब होगा <code>sketch</code>(क्यू) किसी से भी ज्यादा <code>sketch</code>(एक्स<sub>''j''</sub>). | ||
दो डब्ल्यू-बिट पूर्णांक ए और | दो डब्ल्यू-बिट पूर्णांक ए और b के bच लंबाई सबसे लंबे सामान्य उपसर्ग की गणना निरंतर समय में ए और b के bच बिटवाइज एक्सओr के सबसे महत्वपूर्ण बिट को ढूंढकर की जा सकती है। इसके उपरांत इसका उपयोग सबसे लंबे सामान्य उपसर्ग को छोड़कर सभी को छिपाने के लिए किया जा सकता है। | ||
ध्यान दें कि p सटीक रूप से पहचानता है कि कुंजियों के सेट से q शाखाएँ कहाँ निकलती हैं। यदि q का अगला बिट 0 है, तो q का उत्तराधिकारी p1 सबट्री में समाहित है, और यदि q का अगला बिट 1 है, तो q का पूर्ववर्ती p0 सबट्री में समाहित है। यह q का सटीक स्थान निर्धारित करने के लिए निम्नलिखित एल्गोरिदम का सुझाव देता है: | ध्यान दें कि p सटीक रूप से पहचानता है कि कुंजियों के सेट से q शाखाएँ कहाँ निकलती हैं। यदि q का अगला बिट 0 है, तो q का उत्तराधिकारी p1 सबट्री में समाहित है, और यदि q का अगला बिट 1 है, तो q का पूर्ववर्ती p0 सबट्री में समाहित है। यह q का सटीक स्थान निर्धारित करने के लिए निम्नलिखित एल्गोरिदम का सुझाव देता है: | ||
| Line 108: | Line 116: | ||
## यदि q का l-वां बिट 0 है, तो मान लीजिए e = p10 है<sup>w-l</sup>. के उत्तराधिकारी की खोज के लिए समानांतर तुलना का उपयोग करें <code>sketch</code>(इ)। यह q का वास्तविक पूर्ववर्ती है। | ## यदि q का l-वां बिट 0 है, तो मान लीजिए e = p10 है<sup>w-l</sup>. के उत्तराधिकारी की खोज के लिए समानांतर तुलना का उपयोग करें <code>sketch</code>(इ)। यह q का वास्तविक पूर्ववर्ती है। | ||
## यदि q का l-वाँ बिट 1 है, तो मान लीजिए e = p01 है<sup>w-l</sup>. के पूर्ववर्ती की खोज के लिए समानांतर तुलना का उपयोग करें <code>sketch</code>(इ)। यह q का वास्तविक उत्तराधिकारी है। | ## यदि q का l-वाँ बिट 1 है, तो मान लीजिए e = p01 है<sup>w-l</sup>. के पूर्ववर्ती की खोज के लिए समानांतर तुलना का उपयोग करें <code>sketch</code>(इ)। यह q का वास्तविक उत्तराधिकारी है। | ||
# एक बार जब q का पूर्ववर्ती या उत्तराधिकारी मिल जाता है, तो कुंजियों के सेट के | # एक बार जब q का पूर्ववर्ती या उत्तराधिकारी मिल जाता है, तो कुंजियों के सेट के bच q की सटीक स्थिति निर्धारित की जाती है। | ||
==फ्यूजन हैशिंग== | ==फ्यूजन हैशिंग== | ||
[[हैश तालिका]]ओं के लिए फ़्यूज़न ट्री का एक अनुप्रयोग विलार्ड द्वारा दिया गया था, जो हैशिंग के लिए एक डेटा संरचना का वर्णन करता है जिसमें हैश चेनिंग के साथ एक बाहरी स्तर की हैश तालिका को प्रत्येक हैश श्रृंखला का प्रतिनिधित्व करने वाले फ़्यूज़न ट्री के साथ जोड़ा जाता है। | [[हैश तालिका]]ओं के लिए फ़्यूज़न ट्री का एक अनुप्रयोग विलार्ड द्वारा दिया गया था, जो हैशिंग के लिए एक डेटा संरचना का वर्णन करता है जिसमें हैश चेनिंग के साथ एक बाहरी स्तर की हैश तालिका को प्रत्येक हैश श्रृंखला का प्रतिनिधित्व करने वाले फ़्यूज़न ट्री के साथ जोड़ा जाता है। | ||
हैश चेनिंग में, एक स्थिर लोड फैक्टर वाली हैश तालिका में, एक चेन का औसत आकार स्थिर होता है, | हैश चेनिंग में, एक स्थिर लोड फैक्टर वाली हैश तालिका में, एक चेन का औसत आकार स्थिर होता है, परंतु इसके अतिरिक्त उच्च संभावना के साथ सभी चेन का आकार होता है {{math|''O''(log ''n'' / log log ''n'')}}, कहाँ {{mvar|n}} हैश की गई वस्तुओं की संख्या है। | ||
इस श्रृंखला का आकार इतना छोटा है कि एक फ़्यूज़न ट्री प्रति ऑपरेशन निरंतर समय में इसके भीतर खोज और अपडेट को संभाल सकता है। इसलिए, डेटा संरचना में सभी परिचालनों का समय उच्च संभावना के साथ स्थिर है। | इस श्रृंखला का आकार इतना छोटा है कि एक फ़्यूज़न ट्री प्रति ऑपरेशन निरंतर समय में इसके भीतर खोज और अपडेट को संभाल सकता है। इसलिए, डेटा संरचना में सभी परिचालनों का समय उच्च संभावना के साथ स्थिर है। | ||
अधिक सटीक रूप से, इस डेटा संरचना के साथ, प्रत्येक व्युत्क्रम-[[अर्ध-बहुपद समय]] संभावना के लिए {{math|1=''p''(''n'') = exp((log ''n'')<sup>''O''(1)</sup>)}}, एक स्थिरांक है {{mvar|C}} जैसे कि संभावना है कि एक ऑपरेशन मौजूद है जो समय से अधिक है {{mvar|C}} अधिकतम है {{math|''p''(''n'')}}.<ref>{{citation | अधिक सटीक रूप से, इस डेटा संरचना के साथ, प्रत्येक व्युत्क्रम-[[अर्ध-बहुपद समय]] संभावना के लिए {{math|1=''p''(''n'') = exp((log ''n'')<sup>''O''(1)</sup>)}}, एक स्थिरांक है {{mvar|C}} जैसे कि संभावना है कि एक ऑपरेशन मौजूद है जो समय से अधिक है {{mvar|C}} अधिकतम है {{math|''p''(''n'')}}.<ref>{{citation | ||
| Line 126: | Line 134: | ||
== | ==न्यूनतम्प्यूटेशनल मॉडल और आवश्यक धारणाएँ== | ||
फ़्यूज़न ट्री एल्गोरिदम के लिए | फ़्यूज़न ट्री एल्गोरिदम के लिए न्यूनतम्प्यूटेशनल मॉडल एक [[शब्द राम]] है जिसमें एक विशिष्ट निर्देश सेट होता है, जिसमें अंकगणितीय निर्देश शामिल होते हैं - जोड़, घटाव और गुणा (सभी निष्पादित) | ||
सापेक्ष {{math|2<sup>''w''</sup>}}) और बूलियन ऑपरेशन - बिटवाइज और, नहीं आदि। एक डबल-सटीक गुणन निर्देश भी शामिल है। यह | सापेक्ष {{math|2<sup>''w''</sup>}}) और बूलियन ऑपरेशन - बिटवाइज और, नहीं आदि। एक डबल-सटीक गुणन निर्देश भी शामिल है। यह दर्शाया गया है<ref>{{citation | ||
| last1 = Ben-Amram| first1 = Amir M. | | last1 = Ben-Amram| first1 = Amir M. | ||
| last2 = Galil | first2 = Zvi| author2-link = Zvi Galil | | last2 = Galil | first2 = Zvi| author2-link = Zvi Galil | ||
| Line 138: | Line 146: | ||
| volume = 54 | | volume = 54 | ||
| year = 1997| doi-access = free | | year = 1997| doi-access = free | ||
}}.</ref> | }}.</ref> उपरांत वाले निर्देश को हटाने से तेजी से सॉर्ट करना असंभव हो जाता है {{math|''O''(''n'' log ''n'')}}, जब तक कि इसे लगभग मेमोरी स्पेस का उपयोग करने की अनुमति न हो {{math|2<sup>''w''</sup>}} शब्द (फ़्यूज़न ट्रीज़ द्वारा उपयोग किए गए रैखिक स्थान के विपरीत), या इसके अतिरिक्त अन्य निर्देश शामिल करें{{R|AMT1999}}. | ||
== संदर्भ == | == संदर्भ == | ||
Revision as of 08:47, 6 July 2023
संगणक विज्ञान में, फ्यूजन ट्री एक प्रकार की ट्री डेटा संरचना है जो एक विस्तृत यूनिवर्स पर w-बिट पूर्णांकों पर एक सहयोगी संख्या को लागू करती है, जहां प्रत्येक इनपुट पूर्णांक का आकार 2w से न्यूनतम होता है और अवांछित होता है. n की-मान तथा-मान जोड़ी के संग्रह पर आपरेशन करने पर, यह O(n) अंतरिक्ष का उपयोग करती है और खोजों को O(logw n) समय में पूरा करती है, जो पारंपरिक आपस्तित्व वाले स्व-संतुलन द्विआधारी खोज वृक्ष से असंतुलित होता है, और w के बड़े मानों के लिए वैन m्डे बोस ट्री से भी बेहतर होता है. यह तेज़ी इसलिए प्राप्त करता है क्योंकि इसमें मशीन शब्द पर कुछ स्थायी समय आपरेशन का उपयोग किया जा सकता है. फ्यूजन ट्री की खोज में O(logw n) समय के कारण, यह 1990 में माइकल फ्रेडमैन और डैन विलार्ड द्वारा आविष्कृत की गई थी।[1]
फ्रेडमैन और विलार्ड के मूल 1990 पेपर के उपरांत से कई प्रगति हुई है।[2] 1999 में यह दर्शाया गया कि गणना के एक मॉडल के तहत फ़्यूज़न पेड़ों को कैसे कार्यान्वित किया जाए जिसमें एल्गोरिदम के सभी अंतर्निहित संचालन AC0 से संबंधित हों, सर्किट जटिलता का एक मॉडल जो जोड़ और बिटवाइज़ बूलियन संचालन की अनुमति देता है परंतु मूल फ़्यूज़न ट्री एल्गोरिदम में उपयोग किए जाने वाले गुणन संचालन की अनुमति नहीं देता है। हैश तालिकाओं का उपयोग करके फ़्यूज़न पेड़ों का एक गतिशील संस्करण 1996 में प्रस्तावित किया गया था[3] जो मूल संरचना के O(logw n) रनटाइम के अपेक्षानुसार मेल खाता था। घातीय वृक्ष का उपयोग करने वाला एक और गतिशील संस्करण 2007 में प्रस्तावित किया गया था[4] जो प्रत्येक आपरेशन के लिए O(logw n + log log n) के खराब तरह का रनटाइम प्रदान करता है। अंतिम रूप में, दर्शाया गया कि गतिशील फ्यूजन ट्री संज्ञानात्मक ढंग से प्रत्येक आपरेशन को O(logw n) समय में कर सकता है।[5]
यह डेटा संरचना एक दिए गए कुंजी के लिए कुंजी जोड़ें, कुंजी हटाएं, कुंजी खोजें, और पूर्ववर्ती (अगले छोटे मान) और उत्तरवर्ती खोज आपरेशन को लागू करती है। संख्या के सबसे महत्वपूर्ण बिट लोकेटर के आंशिक परिणाम ने अगले अध्ययन में भी सहायता की है। फ्यूजन ट्री मशीन शब्द में संगठित कुछ छोटे पूर्णांकों पर समय समय पर गणना करने के लिए शब्द-स्तरीय संयोजन का उपयोग करती है, जिससे कुल आपरेशनों की संख्या को न्यूनतम किया जा सकता है।
यह कैसे कार्य करता है
फ्यूजन ट्री मूल रूप से w1/5 शाखा कारक वाली b-वृक्ष होती है, जिससे इसकी ऊचाई O(logw n) होती है। अद्यतन और पूछताछ के लिए वांछित रनटाइम प्राप्त करने के लिए, फ्यूजन ट्री को एक बार में w1/5 कुंजीयों को खोजने की क्षमता होनी चाहिए। इसका कारण है कि कुंजीयों को "स्केच" करके ऐसा संपीड़ित किया जाता है कि सभी एक मशीन शब्द में समायोजित हो सकें, जिससे पुनर्मिलन संघों को पैरालेल में करने में सक्षमता होती है। इसलिए, स्केचिंग, पैरालेल तुलना और सबसे महत्वपूर्ण बिट सूचक स्थानक के आधार पर की जाने वाली गणनाओं का एक श्रृंखला, उचित समाधान तक पहुंचने में सहायता करती है।
स्केचिंग
स्केचिंग वह विधि है जिसके द्वारा प्रत्येक w-बिट कुंजी एक नोड पर युक्त k कुंजियाँ केवल k − 1 बिट्स में संपीड़ित होती हैं।. प्रत्येक कुंजी x को w ऊंचाई के पूर्ण बाइनरी ट्री में एक पथ के रूप में सोचा जा सकता है जो x जड़ से प्रारंभ होकर पत्ती पर समाप्त होता है। यह पथ सामान्यतः इस प्रकार प्रसंस्करण किया जा सकता है कि, सभी बिट स्कैन किए जाने तक, iवें बिट 0 है तो वाम बच्चे की खोज की जाएगी, और iवें बिट 1 है तो दायीं बच्चे की खोज की जाएगी। दो पथों को पृथक करने के लिए, उनके शाखा बिंदु को देखना पर्याप्त है।क्योंकि अधिकतम k कुंजियाँ होती हैं, इसलिए k-1 से अधिक शाखा बिंदु नहीं होंगे, जिसका अर्थ है कि किसी कुंजी की पहचान करने के लिए k-1 बिट्स से अधिक की आवश्यकता नहीं है। और इसलिए, किसी भी स्केच में k-1 बिट्स से अधिक नहीं होगा।
स्केच फ़ंक्शन का एक महत्वपूर्ण गुण यह है कि यह कुंजियों के क्रम को संरक्षित करता है। वह है, sketch(x) < sketch(y) किन्हीं दो कुंजियों के लिए x < y. तो, चाबियों की पूरी श्रृंखला के लिए, स्केच(x0)<स्केच(x1)<...<स्केच(xk-1) क्योंकि यदि बाइनरी ट्री जैसे पथ का अनुसरण किया जाता है तो नोड्स को इस तरह से ऑर्डर किया जाएगा कि x0<x1<...<xk-1.
स्केच फ़ंक्शन की एक महत्वपूर्ण गुणधर्म है कि यह कुंजीयों का क्रमबद्धता को संरक्षित रखता है। अर्थात, किसी भी दो कुंजीयों x < y के लिए sketch(x) < sketch(y) होगा। इसलिए, पूरे कुंजी दायरे के लिए, sketch(x0) < sketch(x1) < ... < sketch(xk-1) होगा, क्योंकि यदि बाइनरी ट्री के समान पथ का पालन किया जाता है, तो नोड ऐसी व्यवस्था में क्रमबद्ध x0 < x1 < ... < xk-1 होंगे।
स्केच का अनुमान लगाना
यदि स्केच बिटों की स्थानों को b1 < b2 < ··· < br माना जाता है, तो कुंजी xw-1···x1x0 का स्केच r-बिट पूर्णांक होता है।
.
केवल मानक शब्द संचालन, जैसे कि , के साथ, निरंतर समय में किसी कुंजी के सही स्केच की सीधे गणना करना मुश्किल है। इसके अतिरिक्त, स्केच बिट्स को अधिकतम r आकार की श्रेणी में पैक किया जा सकता है, बिटवाइज़ AND और गुणन का उपयोग करते हुए, अनुमानित स्केच कहा जाता है, जिसमें सभी महत्वपूर्ण बिट्स होते हैं परंतु कुछ अतिरिक्त बेकार बिट्स भी एक पूर्वानुमानित पैटर्न में विस्तृत होते हैं। बिटवाइज़ AND ऑपरेशन इन सभी गैर-स्केच बिट्स को कुंजी से हटाने के लिए एक मास्क के रूप में कार्य करता है, जबकि गुणन स्केच बिट्स को एक छोटी सीमा में स्थानांतरित करता है। पूर्ण स्केच की तरह, अनुमानित स्केच भी कुंजियों के क्रम को सुरक्षित रखता है और इसका मतलब है कि स्केच(x0)<स्केच(x1)<...<स्केच(xk-1).
केवल सी प्रोग्रामिंग भाषा के जैसे मानक शब्द आपरेशन का उपयोग करके, एक कुंजी का पूर्ण स्केच सीधे समय में निर्धारित करना कठिन होता है। इसके अतिरिक्त, स्केच बिट्स को बिटवाइज़ AND और गुणाकार का उपयोग करके, अधिकतम r4 आकार के रेंज में पैक किया जा सकता है, जिसे अनुमानित स्केच कहा जाता है, जिसमें सभी महत्वपूर्ण बिट होते हैं परंतु इसके साथ कुछ अतिरिक्त बेकार बिट भी होते हैं जो एक पूर्वानुमानित पैटर्न में विस्तृत होते हैं। बिटवाइज़ AND आपरेशन गैर-स्केच बिट्स को कुंजी से हटाने के लिए मास्क के रूप में कार्य करता है, जबकि गुणाकार स्केच बिट्स को एक छोटी सीमा में स्थानांतरित करता है। "पूर्ण" स्केच की तरह, अनुमानित स्केच भी कुंजीयों का क्रमबद्धता संरक्षित करता है और इसका अर्थ है कि sketch(x0) < sketch(x1) < ... < sketch(xk-1) होता है।
सही गुणन स्थिरांक निर्धारित करने के लिए कुछ पूर्वप्रक्रिया की आवश्यकता होती है। जहा स्थान bi में प्रत्येक स्केच बिट में bi + mi m = से गुणा करके 2mi. स्थानांतरित हो जायेंगे वहा अनुमानित स्केच को कार्यान्वित करने के लिए, निम्नलिखित तीन गुण होने चाहिए:
- bi + mj सभी जोड़ियों (i, j) के लिए पृथक-पृथक होते हैं। इससे यह सुनिश्चित हो जाएगा कि स्केच बिट्स गुणन द्वारा दूषित नहीं हैं।
- bi + mi i का सख्ती से बढ़ता हुआ फलन है। अर्थात्, स्केच बिट्स का क्रम x'.m में भी संरक्षित रहता है।
- (br + mr) - (b1 + m1) ≤ r4. अर्थात्, स्केच बिट्स को अधिकतम r4 आकार की श्रेणी में पैक किया जाता है, जहां r ≤ O(w1/5).होता हैं।
एक आगमनात्मक तर्क दिखाता है कि कैसे mi निर्माण किया जा सकता है. m1 = w − b1. मान लीजिए कि 1 < t ≤ r और वह m1, m2... mt-1 पहले ही चुना जा चुका है. पुनः सबसे छोटा पूर्णांक m चुनेंt इस प्रकार कि दोनों गुण (1) और (2) संतुष्ट हैं। संपत्ति (1) के लिए आवश्यक है कि mt ≠ bi − bj + ml सभी 1 ≤ i, j ≤ r और 1 ≤ l ≤ t-1 के लिए। इस प्रकार, tr से न्यूनतम हैं2 ≤ r3मूल्य जो मt बचना चाहिए. चूंकि mt न्यूनतम होना चुना गया है, (bt + mt) ≤ (bt-1 + mt-1) + r3. इसका तात्पर्य संपत्ति (3) से है।
एक आनुवंशिक तर्क दिखाता है कि कैसे mi का निर्माण किया जा सकता है। तो m1 = w − b1 चुनें। मान लीजिए कि 1 < t ≤ r है और m1, m2... mt-1 पहले से ही चुन लिए गए हैं। पुनः ऐसा सबसे छोटा पूर्णांक mt चुनें, जिसके लिए प्रोपर्टी (1) और (2) दोनों संतुष्ट होती हैं। प्रोपर्टी (1) यह मांगती है कि mt ≠ bi − bj + ml हर 1 ≤ i, j ≤ r और 1 ≤ l ≤ t-1 के लिए। इसलिए, mt को एक कम से कम r3 मानों को बचना चाहिए। क्योंकि mt को न्यूनतम चुना गया है, (bt + mt) ≤ (bt-1 + mt-1) + r3 होता है। इससे प्रोपर्टी (2) प्राप्त होती है।
इस प्रकार अनुमानित रेखाचित्र की गणना इस प्रकार की जाती है:
- स्केच बिट्स को छोड़कर बाकी सभी को x और के bच बिटवाइज़ से मास्क करें .
- ऊपर की गणना के अनुसार कुंजी को पूर्व निर्धारित स्थिरांक m से गुणा करें। इस ऑपरेशन के लिए वास्तव में दो मशीनी शब्दों की आवश्यकता होती है, परंतु यह अभी भी निरंतर समय में किया जा सकता है।
- स्थानांतरित स्केच बिट्स को छोड़कर सभी को मास्क करें। ये अब अधिकतम r के सन्निहित ब्लॉक में समाहित हैं4 <w4/5बिट्स.
समानांतर तुलना
स्केचिंग द्वारा प्राप्त संपीड़न का उद्देश्य सभी कुंजियों को एक डब्ल्यू-बिट शब्द में संग्रहीत करने की अनुमति देना है। किसी नोड का नोड स्केच बिट स्ट्रिंग होने दें
- 1
sketch(एक्स1)1sketch(एक्स2)...1sketch(एक्सk)
यहां, सभी स्केच शब्दों को उनमें से प्रत्येक के लिए एक सेट बिट जोड़कर एक स्ट्रिंग में एक साथ जोड़ा गया है। हम मान सकते हैं कि स्केच फ़ंक्शन बिल्कुल b ≤ r का उपयोग करता है4बिट्स. पुनः प्रत्येक ब्लॉक 1 + b ≤ w का उपयोग करता है4/5बिट्स, और चूँकि k ≤ w1/5, नोड स्केच में बिट्स की कुल संख्या अधिकतम w है।
एक संक्षिप्त नोटेशनल एक तरफ: एक बिट स्ट्रिंग एस और गैर-नकारात्मक पूर्णांक m के लिए, चलो एसms के स्वयं के साथ m बार संयोजन को दर्शाता है। यदि t एक बिट स्ट्रिंग st भी है, तो t से s के संयोजन को दर्शाता है।
नोड स्केच किसी भी b-बिट पूर्णांक y के लिए कुंजी खोजना संभव बनाता है। मान लीजिए z = (0y)k, जिसकी गणना स्थिर समय में की जा सकती है (y को स्थिरांक (0) से गुणा करें)।ख1)k), इसे नोड स्केच जितना लंबा बनाने के लिए, ताकि नोड स्केच में प्रत्येक शब्द की तुलना एक ऑपरेशन में क्वेरी पूर्णांक y के साथ की जा सके, जो शब्द-स्तरीय समानता का प्रदर्शन करता है। यदि y 5 बिट लंबा होता, तो स्केच(y) प्राप्त करने के लिए इसे 000001....000001 से गुणा किया जाता।क. स्केच(x) के bच का अंतरi) और 0y के परिणामस्वरूप प्रत्येक ब्लॉक के लिए अग्रणी बिट 1 होता है, यदि और केवल यदि स्केच(y) स्केच(xi). इस प्रकार हम सबसे छोटे सूचकांक i की गणना कर सकते हैं sketch(एक्सi) ≥ y इस प्रकार है:
- नोड स्केच से z घटाएँ।
- अंतर और स्थिरांक का बिटवाइज़ AND लें (10ख)क. यह प्रत्येक ब्लॉक के अग्रणी बिट को छोड़कर बाकी सब साफ़ कर देता है।
- क्वेरी स्केच से छोटे स्केच वाले तत्वों से क्वेरी स्केच से बड़े तत्वों में संक्रमण के सटीक सूचकांक की पहचान करने के लिए, परिणाम का सबसे महत्वपूर्ण बिट ढूंढें।
- इस तथ्य का उपयोग करके स्केच की रैंक i की गणना करें कि i-वें ब्लॉक के अग्रणी बिट में इंडेक्स i(b+1) है।
डेस्केचिंग
एक मनमानी क्वेरी q के लिए, समानांतर तुलना सूचकांक i की गणना इस प्रकार करती है
sketch(एक्सi-1) ≤sketch(क्यू) ≤sketch(एक्सi)
दुर्भाग्य से, यह q का सटीक पूर्ववर्ती या उत्तराधिकारी नहीं देता है, क्योंकि सभी मानों के रेखाचित्रों के bच q के रेखाचित्र का स्थान सभी वास्तविक मानों में q के स्थान के समान नहीं हो सकता है। जो सच है वह यह है कि, सभी कुंजियों में से, या तो xi-1 या एक्सi q के साथ सबसे लंबा सामान्य उपसर्ग है। ऐसा इसलिए है क्योंकि q के साथ लंबे सामान्य उपसर्ग वाली किसी भी कुंजी y में q के साथ समान रूप से अधिक स्केच बिट्स होंगे, और इस प्रकार sketch(y) के करीब होगा sketch(क्यू) किसी से भी ज्यादा sketch(एक्सj).
दो डब्ल्यू-बिट पूर्णांक ए और b के bच लंबाई सबसे लंबे सामान्य उपसर्ग की गणना निरंतर समय में ए और b के bच बिटवाइज एक्सओr के सबसे महत्वपूर्ण बिट को ढूंढकर की जा सकती है। इसके उपरांत इसका उपयोग सबसे लंबे सामान्य उपसर्ग को छोड़कर सभी को छिपाने के लिए किया जा सकता है।
ध्यान दें कि p सटीक रूप से पहचानता है कि कुंजियों के सेट से q शाखाएँ कहाँ निकलती हैं। यदि q का अगला बिट 0 है, तो q का उत्तराधिकारी p1 सबट्री में समाहित है, और यदि q का अगला बिट 1 है, तो q का पूर्ववर्ती p0 सबट्री में समाहित है। यह q का सटीक स्थान निर्धारित करने के लिए निम्नलिखित एल्गोरिदम का सुझाव देता है:
- ऐसे सूचकांक को खोजने के लिए समानांतर तुलना का उपयोग करें
sketch(एक्सi-1) ≤sketch(क्यू) ≤sketch(एक्सi). - q और x दोनों में से सबसे लंबे सामान्य उपसर्ग p की गणना करेंi-1 या एक्सi (दोनों में से अधिक समय लेते हुए)।
- मान लीजिए l-1 सबसे लंबे सामान्य उपसर्ग p की लंबाई है।
- यदि q का l-वां बिट 0 है, तो मान लीजिए e = p10 हैw-l. के उत्तराधिकारी की खोज के लिए समानांतर तुलना का उपयोग करें
sketch(इ)। यह q का वास्तविक पूर्ववर्ती है। - यदि q का l-वाँ बिट 1 है, तो मान लीजिए e = p01 हैw-l. के पूर्ववर्ती की खोज के लिए समानांतर तुलना का उपयोग करें
sketch(इ)। यह q का वास्तविक उत्तराधिकारी है।
- यदि q का l-वां बिट 0 है, तो मान लीजिए e = p10 हैw-l. के उत्तराधिकारी की खोज के लिए समानांतर तुलना का उपयोग करें
- एक बार जब q का पूर्ववर्ती या उत्तराधिकारी मिल जाता है, तो कुंजियों के सेट के bच q की सटीक स्थिति निर्धारित की जाती है।
फ्यूजन हैशिंग
हैश तालिकाओं के लिए फ़्यूज़न ट्री का एक अनुप्रयोग विलार्ड द्वारा दिया गया था, जो हैशिंग के लिए एक डेटा संरचना का वर्णन करता है जिसमें हैश चेनिंग के साथ एक बाहरी स्तर की हैश तालिका को प्रत्येक हैश श्रृंखला का प्रतिनिधित्व करने वाले फ़्यूज़न ट्री के साथ जोड़ा जाता है। हैश चेनिंग में, एक स्थिर लोड फैक्टर वाली हैश तालिका में, एक चेन का औसत आकार स्थिर होता है, परंतु इसके अतिरिक्त उच्च संभावना के साथ सभी चेन का आकार होता है O(log n / log log n), कहाँ n हैश की गई वस्तुओं की संख्या है। इस श्रृंखला का आकार इतना छोटा है कि एक फ़्यूज़न ट्री प्रति ऑपरेशन निरंतर समय में इसके भीतर खोज और अपडेट को संभाल सकता है। इसलिए, डेटा संरचना में सभी परिचालनों का समय उच्च संभावना के साथ स्थिर है। अधिक सटीक रूप से, इस डेटा संरचना के साथ, प्रत्येक व्युत्क्रम-अर्ध-बहुपद समय संभावना के लिए p(n) = exp((log n)O(1)), एक स्थिरांक है C जैसे कि संभावना है कि एक ऑपरेशन मौजूद है जो समय से अधिक है C अधिकतम है p(n).[6]
न्यूनतम्प्यूटेशनल मॉडल और आवश्यक धारणाएँ
फ़्यूज़न ट्री एल्गोरिदम के लिए न्यूनतम्प्यूटेशनल मॉडल एक शब्द राम है जिसमें एक विशिष्ट निर्देश सेट होता है, जिसमें अंकगणितीय निर्देश शामिल होते हैं - जोड़, घटाव और गुणा (सभी निष्पादित) सापेक्ष 2w) और बूलियन ऑपरेशन - बिटवाइज और, नहीं आदि। एक डबल-सटीक गुणन निर्देश भी शामिल है। यह दर्शाया गया है[7] उपरांत वाले निर्देश को हटाने से तेजी से सॉर्ट करना असंभव हो जाता है O(n log n), जब तक कि इसे लगभग मेमोरी स्पेस का उपयोग करने की अनुमति न हो 2w शब्द (फ़्यूज़न ट्रीज़ द्वारा उपयोग किए गए रैखिक स्थान के विपरीत), या इसके अतिरिक्त अन्य निर्देश शामिल करें[2].
संदर्भ
- ↑ Fredman, M. L.; Willard, D. E. (1990), "BLASTING Through the Information Theoretic Barrier with FUSION TREES", Proceedings of the Twenty-Second Annual ACM Symposium on Theory of Computing (STOC '90), New York, NY, USA: ACM, pp. 1–7, doi:10.1145/100216.100217, ISBN 0-89791-361-2, S2CID 16367160.
- ↑ 2.0 2.1 Andersson, Arne; Miltersen, Peter Bro; Thorup, Mikkel (1999), "Fusion trees can be implemented with AC0 instructions only", Theoretical Computer Science, 215 (1–2): 337–344, doi:10.1016/S0304-3975(98)00172-8, MR 1678804.
- ↑ Raman, Rajeev (1996), "Priority queues: small, monotone and trans-dichotomous", Fourth Annual European Symposium on Algorithms (ESA '96), Barcelona, Spain, September 25–27, 1996, Lecture Notes in Computer Science, vol. 1136, Berlin: Springer-Verlag, pp. 121–137, doi:10.1007/3-540-61680-2_51, MR 1469229.
- ↑ Andersson, Arne; Thorup, Mikkel (2007), "Dynamic ordered sets with exponential search trees", Journal of the ACM, 54 (3): A13, arXiv:cs/0210006, doi:10.1145/1236457.1236460, MR 2314255, S2CID 8175703.
- ↑ Patrascu, Mihai; Thorup, Mikkel (2014). "इष्टतम रैंक, चयन और पूर्ववर्ती खोज के साथ गतिशील पूर्णांक सेट". 55th IEEE Annual Symposium on Foundations of Computer Science, FOCS 2014: 166-175. doi:10.1109/FOCS.2014.26.
- ↑ Willard, Dan E. (2000), "Examining computational geometry, van Emde Boas trees, and hashing from the perspective of the fusion tree", SIAM Journal on Computing, 29 (3): 1030–1049, doi:10.1137/S0097539797322425, MR 1740562.
- ↑ Ben-Amram, Amir M.; Galil, Zvi (1997), "When Can We Sort in o(n log n) Time?", Journal of Computer and System Sciences, 54 (2): 345–370, doi:10.1006/jcss.1997.1474.
बाहरी संबंध
- MIT CS 6.897: Advanced Data Structures: Lecture 4, Fusion Trees, Prof. Erik Demaine (Spring 2003)
- MIT CS 6.897: Advanced Data Structures: Lecture 5, More fusion trees; self-organizing data structures, move-to-front, static optimality, Prof. Erik Demaine (Spring 2003)
- MIT CS 6.851: Advanced Data Structures: Lecture 13, Fusion Tree notes, Prof. Erik Demaine (Spring 2007)
- MIT CS 6.851: Advanced Data Structures: Lecture 12, Fusion Tree notes, Prof. Erik Demaine (Spring 2012)