काल्पनिक न्यायवाक्य: Difference between revisions
(Created page with "{{Short description|Syllogism with conditional premise(s)}} {{Infobox mathematical statement | name = Hypothetical syllogism | type = Syllogism | field = {{Plainlist| * ...") |
No edit summary |
||
| Line 13: | Line 13: | ||
}} | }} | ||
{{Transformation rules}} | {{Transformation rules}} | ||
[[शास्त्रीय तर्क]] में, एक काल्पनिक न्यायवाक्य एक वैध तर्क रूप है, एक या दोनों परिसरों के लिए एक | [[शास्त्रीय तर्क|मौलिक तर्क]] में, एक काल्पनिक न्यायवाक्य एक वैध तर्क रूप है, एक या दोनों परिसरों के लिए एक नियमानुसार कथन के साथ एक न्यायवाक्य बनाता है। | ||
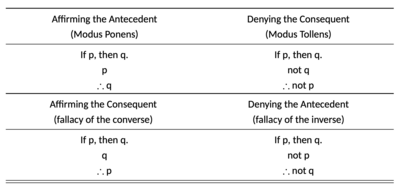
[[File:In Quest of Univeral Logic HypoSyll.png|right|thumbnail|400px|काल्पनिक न्यायवाक्य के चार संभावित रूप हैं, जिनमें से दो वैध हैं, जबकि दो अमान्य हैं। एक बहुत ही सरल उदाहरण पर विचार करने से आपको यह समझने में मदद मिल सकती है कि ये फॉर्म वैध या अमान्य क्यों हैं। यदि p दर्शाता है कि कैंडिरू एक मछली है और q दर्शाता है कि कैंडिरू में गलफड़े हैं, तो उपरोक्त तालिका में इन कथनों को p और q से प्रतिस्थापित करके स्वयं को समझाने का प्रयास करें।<ref name="Quest_Univeral_Logic "></ref>]][[अंग्रेजी भाषा]] में एक उदाहरण: | [[File:In Quest of Univeral Logic HypoSyll.png|right|thumbnail|400px|काल्पनिक न्यायवाक्य के चार संभावित रूप हैं, जिनमें से दो वैध हैं, जबकि दो अमान्य हैं। एक बहुत ही सरल उदाहरण पर विचार करने से आपको यह समझने में मदद मिल सकती है कि ये फॉर्म वैध या अमान्य क्यों हैं। यदि p दर्शाता है कि कैंडिरू एक मछली है और q दर्शाता है कि कैंडिरू में गलफड़े हैं, तो उपरोक्त तालिका में इन कथनों को p और q से प्रतिस्थापित करके स्वयं को समझाने का प्रयास करें।<ref name="Quest_Univeral_Logic "></ref>]][[अंग्रेजी भाषा]] में एक उदाहरण: | ||
: | :यदि मैं नहीं जागा, तो मैं काम पर नहीं जा पाऊंगा. | ||
: | :यदि मैं काम पर नहीं जा सकता तो मुझे वेतन नहीं मिलेगा। | ||
:इसलिए, | :इसलिए, यदि मैं नहीं जागा, तो मुझे भुगतान नहीं मिलेगा। | ||
इस शब्द की उत्पत्ति [[ ठेओफ्रस्तुस ]] से हुई।<ref>[http://www.britannica.com/EBchecked/topic/346217/history-of-logic/65923/Theophrastus-of-Eresus "History of Logic: Theophrastus of Eresus"] in [[Encyclopædia Britannica Online]].</ref> | इस शब्द की उत्पत्ति [[ ठेओफ्रस्तुस ]] से हुई।<ref>[http://www.britannica.com/EBchecked/topic/346217/history-of-logic/65923/Theophrastus-of-Eresus "History of Logic: Theophrastus of Eresus"] in [[Encyclopædia Britannica Online]].</ref> | ||
शुद्ध काल्पनिक न्यायवाक्य वह न्यायवाक्य है जिसमें परिसर और निष्कर्ष दोनों | |||
शुद्ध काल्पनिक न्यायवाक्य वह न्यायवाक्य है जिसमें परिसर और निष्कर्ष दोनों नियमानुसार होते हैं। नियमानुसार वैध होने के लिए एक आधार का पूर्ववृत्त दूसरे के परिणाम से मेल खाना चाहिए। परिणाम स्वरुप नियमानुसार पूर्ववर्ती के रूप में पूर्ववर्ती बने रहे और परिणामी के रूप में परिणामी बने रहे। | |||
:यदि p, तो q. | :यदि p, तो q. | ||
:यदि q, तो r. | :यदि q, तो r. | ||
:∴ यदि p, तो r. | :∴ यदि p, तो r. | ||
एक मिश्रित काल्पनिक न्यायवाक्य में एक | एक मिश्रित काल्पनिक न्यायवाक्य में एक नियमानुसार कथन और एक कथन सम्मिलित होता है जो उस नियमानुसार के पूर्ववृत्त या परिणाम के साथ या तो पुष्टि या खंडन व्यक्त करता है। इसलिए ऐसे मिश्रित काल्पनिक न्यायवाक्य के चार संभावित रूप हैं जिनमें से दो वैध हैं, जबकि अन्य दो अमान्य हैं (तालिका देखें) वैध निष्कर्ष प्राप्त करने का पहला विधि पूर्ववृत्त की पुष्टि करना है। एक वैध काल्पनिक न्यायवाक्य या तो परिणामी (मोडस टोलेंस) को नकारता है या पूर्ववर्ती (मोडस पोनेंस) की पुष्टि करता है।<ref name="Quest_Univeral_Logic "> | ||
{{citation | {{citation | ||
|last1=Kashef |first1=Arman. | |last1=Kashef |first1=Arman. | ||
| Line 34: | Line 35: | ||
</ref> | </ref> | ||
== | ==प्रस्तावित तर्क== | ||
प्रस्तावात्मक तर्क में, काल्पनिक न्यायवाक्य अनुमान के एक वैध नियम का नाम है ( | प्रस्तावात्मक तर्क में, काल्पनिक न्यायवाक्य अनुमान के एक वैध नियम का नाम है (अधिकांशतः संक्षिप्त एचएस और कभी-कभी श्रृंखला तर्क, श्रृंखला नियम, या निहितार्थ की परिवर्तनशीलता का सिद्धांत भी कहा जाता है)। नियम कहा जा सकता है: | ||
:<math>\frac{P \to Q, Q \to R}{\therefore P \to R}</math> | :<math>\frac{P \to Q, Q \to R}{\therefore P \to R}</math> | ||
जहां नियम यह है कि जब भी | जहां नियम यह है कि जब भी "<math>P \to Q</math>", और "<math>Q \to R</math>" के उदाहरण किसी प्रमाण की पंक्तियों पर दिखाई देते हैं, तो "<math>P \to R</math>" को अगली पंक्ति में रखा जा सकता है। | ||
हाइपोथेटिकल सिलोगिज्म निकटता से संबंधित है और [[विच्छेदात्मक न्यायवाक्य]] के समान है, इसमें यह एक प्रकार का सिलोगिज्म भी है, और अनुमान के नियम का नाम भी है। | हाइपोथेटिकल सिलोगिज्म निकटता से संबंधित है और [[विच्छेदात्मक न्यायवाक्य]] के समान है, इसमें यह एक प्रकार का सिलोगिज्म भी है, और अनुमान के नियम का नाम भी है। | ||
== प्रयोज्यता == | == प्रयोज्यता == | ||
काल्पनिक न्यायशास्त्र का नियम | काल्पनिक न्यायशास्त्र का नियम मौलिक तर्क, [[अंतर्ज्ञानवादी तर्क]], प्रासंगिक तर्क की अधिकांश प्रणालियों और तर्क की कई अन्य प्रणालियों में प्रय्युक्त होता है। चूँकि, यह सभी तर्कों पर प्रय्युक्त नहीं होता है, उदाहरण के लिए, [[गैर-मोनोटोनिक तर्क]], [[संभाव्य तर्क]] और [[डिफ़ॉल्ट तर्क]] इसका कारण यह है कि ये तर्क [[अक्षम्य तर्क]] का वर्णन करते हैं, और वास्तविक दुनिया के संदर्भों में दिखाई देने वाली नियमानुसार सामान्यतः अपवादों, डिफ़ॉल्ट मान्यताओं, अन्य सभी समान स्थितियों या बस साधारण अनिश्चितता की अनुमति देती हैं। | ||
अर्नेस्ट डब्ल्यू एडम्स से लिया गया एक उदाहरण, <ref>{{Cite book |last=Adams |first=Ernest W. |title=शर्तों का तर्क|publisher=Dordrecht: Reidel |year=1975 |page=22}}</ref> | अर्नेस्ट डब्ल्यू एडम्स से लिया गया एक उदाहरण, <ref>{{Cite book |last=Adams |first=Ernest W. |title=शर्तों का तर्क|publisher=Dordrecht: Reidel |year=1975 |page=22}}</ref> | ||
| Line 50: | Line 51: | ||
# यदि चुनाव से पहले स्मिथ की मृत्यु हो जाती है, तो चुनाव के बाद स्मिथ सेवानिवृत्त हो जायेंगे. | # यदि चुनाव से पहले स्मिथ की मृत्यु हो जाती है, तो चुनाव के बाद स्मिथ सेवानिवृत्त हो जायेंगे. | ||
स्पष्टतः | स्पष्टतः (3) (1) और (2) से अनुसरण नहीं करता है। (1) डिफ़ॉल्ट रूप से सत्य है, किन्तु स्मिथ की मृत्यु की असाधारण परिस्थितियों में इसे प्रय्युक्त करने में विफल रहता है। वास्तव में, वास्तविक दुनिया की नियमो में सदैव डिफ़ॉल्ट धारणाएं या संदर्भ सम्मिलित होते हैं और उन सभी असाधारण परिस्थितियों को निर्दिष्ट करना असंभव या यहां तक कि असंभव हो सकता है जिनमें वे सत्य होने में विफल हो सकते हैं। समान कारणों से, काल्पनिक न्यायवाक्य का नियम प्रतितथ्यात्मक नियमो पर प्रय्युक्त नहीं होता है। | ||
== औपचारिक संकेतन == | == औपचारिक संकेतन == | ||
| Line 56: | Line 57: | ||
: <math>\frac{P \vdash Q\quad Q \vdash R}{P \vdash R}</math> | : <math>\frac{P \vdash Q\quad Q \vdash R}{P \vdash R}</math> | ||
जहां <math>\vdash</math> एक धातु संबंधी प्रतीक है और <math>A \vdash B</math> का अर्थ है कि <math>B</math> कुछ तार्किक प्रणाली में <math>A</math> का वाक्यात्मक परिणाम है; | |||
और एक सत्य-कार्यात्मक [[टॉटोलॉजी (तर्क)]] या [[प्रस्तावात्मक कलन]] के [[प्रमेय]] के रूप में व्यक्त किया गया: | और एक सत्य-कार्यात्मक [[टॉटोलॉजी (तर्क)]] या [[प्रस्तावात्मक कलन]] के [[प्रमेय]] के रूप में व्यक्त किया गया: | ||
:<math>((P \to Q) \land (Q \to R)) \to (P \to R)</math> | :<math>((P \to Q) \land (Q \to R)) \to (P \to R)</math> | ||
जहाँ <math>P</math>, <math>Q</math>, और <math>R</math> कुछ औपचारिक प्रणाली में व्यक्त किए गए प्रस्ताव हैं। | |||
==प्रमाण == | ==प्रमाण == | ||
{| class="wikitable" | {| class="wikitable" | ||
! '' | ! ''चरण'' | ||
! '' | ! ''प्रस्ताव'' | ||
! '' | ! ''व्युत्पत्ति'' | ||
|- | |- | ||
| 1 || <math>P \to Q</math> || | | 1 || <math>P \to Q</math> || दिया गया | ||
|- | |- | ||
| 2 || <math>Q \to R</math> || | | 2 || <math>Q \to R</math> || दिया गया | ||
|- | |- | ||
| 3 || <math>P</math> || [[Conditional proof| | | 3 || <math>P</math> || [[Conditional proof|नियमित प्रमाण धारणा]] | ||
|- | |- | ||
| 4 || <math>Q</math> || | | 4 || <math>Q</math> || सेटिंग मोड (1,3) | ||
|- | |- | ||
| 5 || <math>R</math> || | | 5 || <math>R</math> || सेटिंग मोड (2,4) | ||
|- | |- | ||
| 6 || <math>P \to R</math> || | | 6 || <math>P \to R</math> || नियमित प्रमाण (3-5) | ||
|} | |} | ||
==वैकल्पिक रूप== | ==वैकल्पिक रूप== | ||
काल्पनिक न्यायवाक्य का एक वैकल्पिक रूप, | काल्पनिक न्यायवाक्य का एक वैकल्पिक रूप, निहितार्थ और निषेध के साथ मौलिक प्रस्तावात्मक कलन प्रणालियों के लिए अधिक उपयोगी (अर्थात संयोजन चिह्न के बिना) निम्नलिखित है: | ||
:(HS1) <math>(Q \to R) \to ((P \to Q) \to (P \to R))</math> | :(HS1) <math>(Q \to R) \to ((P \to Q) \to (P \to R))</math> | ||
| Line 93: | Line 94: | ||
===प्रमाण=== | ===प्रमाण=== | ||
ऐसी प्रणालियों में इन प्रमेयों के प्रमाण का एक उदाहरण नीचे दिया गया है। हम | ऐसी प्रणालियों में इन प्रमेयों के प्रमाण का एक उदाहरण नीचे दिया गया है। हम जान लुकासिविक्ज़ द्वारा वर्णित लोकप्रिय प्रणालियों में से एक में उपयोग किए गए तीन सिद्धांतों में से दो का उपयोग करते हैं। प्रमाण इस प्रणाली के तीन सिद्धांतों में से दो पर निर्भर करते हैं: | ||
प्रमाण इस प्रणाली के तीन सिद्धांतों में से दो पर निर्भर करते हैं: | |||
:(ए1) <math>\phi \to \left( \psi \to \phi \right) </math> | :(ए1) <math>\phi \to \left( \psi \to \phi \right) </math> | ||
:(आआ) <math>\left( \phi \to \left( \psi \rightarrow \xi \right) \right) \to \left( \left( \phi \to \psi \right) \to \left( \phi \to \xi \right) \right)</math> | :(आआ) <math>\left( \phi \to \left( \psi \rightarrow \xi \right) \right) \to \left( \left( \phi \to \psi \right) \to \left( \phi \to \xi \right) \right)</math> | ||
| Line 105: | Line 105: | ||
:(6) <math>(q \to r) \to (p\to(q \to r))</math> ((A1) का उदाहरण) | :(6) <math>(q \to r) \to (p\to(q \to r))</math> ((A1) का उदाहरण) | ||
:(7) <math>(q \to r)\to((p \to q) \to(p \to r))</math> ((5) और (6) से मोडस पोनेन्स द्वारा) | :(7) <math>(q \to r)\to((p \to q) \to(p \to r))</math> ((5) और (6) से मोडस पोनेन्स द्वारा) | ||
:(HS2) का प्रमाण यहां दिया गया है। | |||
(HS2) का प्रमाण हिल्बर्ट_सिस्टम#कुछ_उपयोगी_प्रमेय_और_उनके_प्रमाण दिए गए हैं। | '''(HS2) का प्रमाण हिल्बर्ट_सिस्टम#कुछ_उपयोगी_प्रमेय_और_उनके_प्रमाण दिए गए हैं।''' | ||
===एक मेटाथ्योरम के रूप में=== | ===एक मेटाथ्योरम के रूप में=== | ||
जब भी हमारे पास | जब भी हमारे पास <math>T_1 = (Q \to R)</math> और <math>T_2 = (P \to Q)</math> के रूप में दो प्रमेय हों, तो हम साबित कर सकते हैं <math>(P \to R)</math> निम्नलिखित चरणों द्वारा: | ||
:(1) <math> (Q \to R) \to ((P \to Q) \to (P \to R))) </math> (ऊपर सिद्ध प्रमेय का उदाहरण) | :(1) <math> (Q \to R) \to ((P \to Q) \to (P \to R))) </math> (ऊपर सिद्ध प्रमेय का उदाहरण) | ||
:(2) <math> Q \to R</math> ((T1 का उदाहरण)) | :(2) <math> Q \to R</math> ((T1 का उदाहरण)) | ||
| Line 117: | Line 118: | ||
==यह भी देखें== | ==यह भी देखें== | ||
* | * मोडस पोनेन्स | ||
* | *मोडस टोलेंस | ||
* | *परिणाम की पुष्टि | ||
* | *पूर्ववृत्त को नकारना | ||
* | *संक्रमणीय संबंध | ||
==संदर्भ== | ==संदर्भ== | ||
Revision as of 21:13, 5 July 2023
| Type | Syllogism |
|---|---|
| Field |
|
| Statement | Whenever instances of , and appear on lines of a proof, can be placed on a subsequent line. |
| Symbolic statement |
मौलिक तर्क में, एक काल्पनिक न्यायवाक्य एक वैध तर्क रूप है, एक या दोनों परिसरों के लिए एक नियमानुसार कथन के साथ एक न्यायवाक्य बनाता है।
अंग्रेजी भाषा में एक उदाहरण:
- यदि मैं नहीं जागा, तो मैं काम पर नहीं जा पाऊंगा.
- यदि मैं काम पर नहीं जा सकता तो मुझे वेतन नहीं मिलेगा।
- इसलिए, यदि मैं नहीं जागा, तो मुझे भुगतान नहीं मिलेगा।
इस शब्द की उत्पत्ति ठेओफ्रस्तुस से हुई।[2]
शुद्ध काल्पनिक न्यायवाक्य वह न्यायवाक्य है जिसमें परिसर और निष्कर्ष दोनों नियमानुसार होते हैं। नियमानुसार वैध होने के लिए एक आधार का पूर्ववृत्त दूसरे के परिणाम से मेल खाना चाहिए। परिणाम स्वरुप नियमानुसार पूर्ववर्ती के रूप में पूर्ववर्ती बने रहे और परिणामी के रूप में परिणामी बने रहे।
- यदि p, तो q.
- यदि q, तो r.
- ∴ यदि p, तो r.
एक मिश्रित काल्पनिक न्यायवाक्य में एक नियमानुसार कथन और एक कथन सम्मिलित होता है जो उस नियमानुसार के पूर्ववृत्त या परिणाम के साथ या तो पुष्टि या खंडन व्यक्त करता है। इसलिए ऐसे मिश्रित काल्पनिक न्यायवाक्य के चार संभावित रूप हैं जिनमें से दो वैध हैं, जबकि अन्य दो अमान्य हैं (तालिका देखें) वैध निष्कर्ष प्राप्त करने का पहला विधि पूर्ववृत्त की पुष्टि करना है। एक वैध काल्पनिक न्यायवाक्य या तो परिणामी (मोडस टोलेंस) को नकारता है या पूर्ववर्ती (मोडस पोनेंस) की पुष्टि करता है।[1]
प्रस्तावित तर्क
प्रस्तावात्मक तर्क में, काल्पनिक न्यायवाक्य अनुमान के एक वैध नियम का नाम है (अधिकांशतः संक्षिप्त एचएस और कभी-कभी श्रृंखला तर्क, श्रृंखला नियम, या निहितार्थ की परिवर्तनशीलता का सिद्धांत भी कहा जाता है)। नियम कहा जा सकता है:
जहां नियम यह है कि जब भी "", और "" के उदाहरण किसी प्रमाण की पंक्तियों पर दिखाई देते हैं, तो "" को अगली पंक्ति में रखा जा सकता है।
हाइपोथेटिकल सिलोगिज्म निकटता से संबंधित है और विच्छेदात्मक न्यायवाक्य के समान है, इसमें यह एक प्रकार का सिलोगिज्म भी है, और अनुमान के नियम का नाम भी है।
प्रयोज्यता
काल्पनिक न्यायशास्त्र का नियम मौलिक तर्क, अंतर्ज्ञानवादी तर्क, प्रासंगिक तर्क की अधिकांश प्रणालियों और तर्क की कई अन्य प्रणालियों में प्रय्युक्त होता है। चूँकि, यह सभी तर्कों पर प्रय्युक्त नहीं होता है, उदाहरण के लिए, गैर-मोनोटोनिक तर्क, संभाव्य तर्क और डिफ़ॉल्ट तर्क इसका कारण यह है कि ये तर्क अक्षम्य तर्क का वर्णन करते हैं, और वास्तविक दुनिया के संदर्भों में दिखाई देने वाली नियमानुसार सामान्यतः अपवादों, डिफ़ॉल्ट मान्यताओं, अन्य सभी समान स्थितियों या बस साधारण अनिश्चितता की अनुमति देती हैं।
अर्नेस्ट डब्ल्यू एडम्स से लिया गया एक उदाहरण, [3]
- यदि जोन्स चुनाव जीतता है, तो स्मिथ चुनाव के बाद सेवानिवृत्त हो जाएगा।
- यदि चुनाव से पहले स्मिथ की मृत्यु हो जाती है, तो जोन्स चुनाव जीत जाएगा।
- यदि चुनाव से पहले स्मिथ की मृत्यु हो जाती है, तो चुनाव के बाद स्मिथ सेवानिवृत्त हो जायेंगे.
स्पष्टतः (3) (1) और (2) से अनुसरण नहीं करता है। (1) डिफ़ॉल्ट रूप से सत्य है, किन्तु स्मिथ की मृत्यु की असाधारण परिस्थितियों में इसे प्रय्युक्त करने में विफल रहता है। वास्तव में, वास्तविक दुनिया की नियमो में सदैव डिफ़ॉल्ट धारणाएं या संदर्भ सम्मिलित होते हैं और उन सभी असाधारण परिस्थितियों को निर्दिष्ट करना असंभव या यहां तक कि असंभव हो सकता है जिनमें वे सत्य होने में विफल हो सकते हैं। समान कारणों से, काल्पनिक न्यायवाक्य का नियम प्रतितथ्यात्मक नियमो पर प्रय्युक्त नहीं होता है।
औपचारिक संकेतन
काल्पनिक न्यायवाक्य अनुमान नियम को अनुक्रमिक संकेतन में लिखा जा सकता है, जो कट नियम की विशेषज्ञता के समान है:
जहां एक धातु संबंधी प्रतीक है और का अर्थ है कि कुछ तार्किक प्रणाली में का वाक्यात्मक परिणाम है;
और एक सत्य-कार्यात्मक टॉटोलॉजी (तर्क) या प्रस्तावात्मक कलन के प्रमेय के रूप में व्यक्त किया गया:
जहाँ , , और कुछ औपचारिक प्रणाली में व्यक्त किए गए प्रस्ताव हैं।
प्रमाण
| चरण | प्रस्ताव | व्युत्पत्ति |
|---|---|---|
| 1 | दिया गया | |
| 2 | दिया गया | |
| 3 | नियमित प्रमाण धारणा | |
| 4 | सेटिंग मोड (1,3) | |
| 5 | सेटिंग मोड (2,4) | |
| 6 | नियमित प्रमाण (3-5) |
वैकल्पिक रूप
काल्पनिक न्यायवाक्य का एक वैकल्पिक रूप, निहितार्थ और निषेध के साथ मौलिक प्रस्तावात्मक कलन प्रणालियों के लिए अधिक उपयोगी (अर्थात संयोजन चिह्न के बिना) निम्नलिखित है:
- (HS1)
फिर भी एक और रूप है:
- (HS2)
प्रमाण
ऐसी प्रणालियों में इन प्रमेयों के प्रमाण का एक उदाहरण नीचे दिया गया है। हम जान लुकासिविक्ज़ द्वारा वर्णित लोकप्रिय प्रणालियों में से एक में उपयोग किए गए तीन सिद्धांतों में से दो का उपयोग करते हैं। प्रमाण इस प्रणाली के तीन सिद्धांतों में से दो पर निर्भर करते हैं:
- (ए1)
- (आआ)
(HS1) का प्रमाण इस प्रकार है:
- (1) ((A1) का उदाहरण)
- (2) ((A2 का उदाहरण))
- (3) (सेटिंग विधि द्वारा (1) और (2) से)
- (4) ((A2 का उदाहरण))
- (5) (सेटिंग विधि द्वारा (3) और (4) से)
- (6) ((A1) का उदाहरण)
- (7) ((5) और (6) से मोडस पोनेन्स द्वारा)
- (HS2) का प्रमाण यहां दिया गया है।
(HS2) का प्रमाण हिल्बर्ट_सिस्टम#कुछ_उपयोगी_प्रमेय_और_उनके_प्रमाण दिए गए हैं।
एक मेटाथ्योरम के रूप में
जब भी हमारे पास और के रूप में दो प्रमेय हों, तो हम साबित कर सकते हैं निम्नलिखित चरणों द्वारा:
- (1) (ऊपर सिद्ध प्रमेय का उदाहरण)
- (2) ((T1 का उदाहरण))
- (3) (सेटिंग विधि द्वारा (1) और (2) से)
- (4) ((T2 का उदाहरण))
- (5) (सेटिंग विधि द्वारा (3) और (4) से)
यह भी देखें
- मोडस पोनेन्स
- मोडस टोलेंस
- परिणाम की पुष्टि
- पूर्ववृत्त को नकारना
- संक्रमणीय संबंध
संदर्भ
- ↑ 1.0 1.1 Kashef, Arman. (2023), In Quest of Univeral Logic: A brief overview of formal logic's evolution, doi:10.13140/RG.2.2.24043.82724/1
- ↑ "History of Logic: Theophrastus of Eresus" in Encyclopædia Britannica Online.
- ↑ Adams, Ernest W. (1975). शर्तों का तर्क. Dordrecht: Reidel. p. 22.