काल्पनिक न्यायवाक्य: Difference between revisions
No edit summary |
No edit summary |
||
| Line 2: | Line 2: | ||
{{Infobox mathematical statement | {{Infobox mathematical statement | ||
| name = Hypothetical syllogism | | name = Hypothetical syllogism | ||
| type = [[ | | type = [[न्यायवाक्य]] | ||
| field = {{ | | field = {{सादा सूची| | ||
* [[ | * [[प्रस्तावात्मक कलन]] | ||
* [[ | * [[शास्त्रीय तर्क]] | ||
* [[ | * [[अंतर्ज्ञानवादी तर्क]] | ||
* | * [[प्रासंगिकता तर्क]] की अधिकांश प्रणालियाँ | ||
}} | }} | ||
| statement = | | statement = जब भी के उदाहरण<math>P \to Q</math>, and <math>Q \to R</math> की तर्ज पर दिखाई देते हैं [[formal proof|proof]], <math>P \to R</math> अगली पंक्ति में रखा जा सकता है. | ||
| symbolic statement = <math>\frac{P \to Q, Q \to R}{\therefore P \to R}</math> | | symbolic statement = <math>\frac{P \to Q, Q \to R}{\therefore P \to R}</math> | ||
}} | }} | ||
| Line 19: | Line 19: | ||
:इसलिए, यदि मैं नहीं जागा, तो मुझे भुगतान नहीं मिलेगा। | :इसलिए, यदि मैं नहीं जागा, तो मुझे भुगतान नहीं मिलेगा। | ||
इस शब्द की उत्पत्ति [[ ठेओफ्रस्तुस ]] से हुई।<ref>[http://www.britannica.com/EBchecked/topic/346217/history-of-logic/65923/Theophrastus-of-Eresus "History of Logic: Theophrastus of Eresus"] in [[Encyclopædia Britannica Online]].</ref> | इस शब्द की उत्पत्ति [[ ठेओफ्रस्तुस |ठेओफ्रस्तुस]] से हुई।<ref>[http://www.britannica.com/EBchecked/topic/346217/history-of-logic/65923/Theophrastus-of-Eresus "History of Logic: Theophrastus of Eresus"] in [[Encyclopædia Britannica Online]].</ref> | ||
शुद्ध काल्पनिक न्यायवाक्य वह न्यायवाक्य है जिसमें परिसर और निष्कर्ष दोनों नियमानुसार होते हैं। नियमानुसार वैध होने के लिए एक आधार का पूर्ववृत्त दूसरे के परिणाम से मेल खाना चाहिए। परिणाम स्वरुप नियमानुसार पूर्ववर्ती के रूप में पूर्ववर्ती बने रहे और परिणामी के रूप में परिणामी बने रहे। | शुद्ध काल्पनिक न्यायवाक्य वह न्यायवाक्य है जिसमें परिसर और निष्कर्ष दोनों नियमानुसार होते हैं। नियमानुसार वैध होने के लिए एक आधार का पूर्ववृत्त दूसरे के परिणाम से मेल खाना चाहिए। परिणाम स्वरुप नियमानुसार पूर्ववर्ती के रूप में पूर्ववर्ती बने रहे और परिणामी के रूप में परिणामी बने रहे। | ||
| Line 106: | Line 106: | ||
:(7) <math>(q \to r)\to((p \to q) \to(p \to r))</math> ((5) और (6) से मोडस पोनेन्स द्वारा) | :(7) <math>(q \to r)\to((p \to q) \to(p \to r))</math> ((5) और (6) से मोडस पोनेन्स द्वारा) | ||
:(HS2) का प्रमाण यहां दिया गया है। | :(HS2) का प्रमाण यहां दिया गया है। | ||
===एक मेटाथ्योरम के रूप में=== | ===एक मेटाथ्योरम के रूप में=== | ||
Revision as of 21:18, 5 July 2023
| Type | न्यायवाक्य |
|---|---|
| Field | Template:सादा सूची |
| Statement | जब भी के उदाहरण, and की तर्ज पर दिखाई देते हैं proof, अगली पंक्ति में रखा जा सकता है. |
| Symbolic statement |
मौलिक तर्क में, एक काल्पनिक न्यायवाक्य एक वैध तर्क रूप है, एक या दोनों परिसरों के लिए एक नियमानुसार कथन के साथ एक न्यायवाक्य बनाता है।
अंग्रेजी भाषा में एक उदाहरण:
- यदि मैं नहीं जागा, तो मैं काम पर नहीं जा पाऊंगा.
- यदि मैं काम पर नहीं जा सकता तो मुझे वेतन नहीं मिलेगा।
- इसलिए, यदि मैं नहीं जागा, तो मुझे भुगतान नहीं मिलेगा।
इस शब्द की उत्पत्ति ठेओफ्रस्तुस से हुई।[2]
शुद्ध काल्पनिक न्यायवाक्य वह न्यायवाक्य है जिसमें परिसर और निष्कर्ष दोनों नियमानुसार होते हैं। नियमानुसार वैध होने के लिए एक आधार का पूर्ववृत्त दूसरे के परिणाम से मेल खाना चाहिए। परिणाम स्वरुप नियमानुसार पूर्ववर्ती के रूप में पूर्ववर्ती बने रहे और परिणामी के रूप में परिणामी बने रहे।
- यदि p, तो q.
- यदि q, तो r.
- ∴ यदि p, तो r.
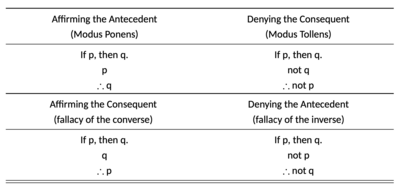
एक मिश्रित काल्पनिक न्यायवाक्य में एक नियमानुसार कथन और एक कथन सम्मिलित होता है जो उस नियमानुसार के पूर्ववृत्त या परिणाम के साथ या तो पुष्टि या खंडन व्यक्त करता है। इसलिए ऐसे मिश्रित काल्पनिक न्यायवाक्य के चार संभावित रूप हैं जिनमें से दो वैध हैं, जबकि अन्य दो अमान्य हैं (तालिका देखें) वैध निष्कर्ष प्राप्त करने का पहला विधि पूर्ववृत्त की पुष्टि करना है। एक वैध काल्पनिक न्यायवाक्य या तो परिणामी (मोडस टोलेंस) को नकारता है या पूर्ववर्ती (मोडस पोनेंस) की पुष्टि करता है।[1]
प्रस्तावित तर्क
प्रस्तावात्मक तर्क में, काल्पनिक न्यायवाक्य अनुमान के एक वैध नियम का नाम है (अधिकांशतः संक्षिप्त एचएस और कभी-कभी श्रृंखला तर्क, श्रृंखला नियम, या निहितार्थ की परिवर्तनशीलता का सिद्धांत भी कहा जाता है)। नियम कहा जा सकता है:
जहां नियम यह है कि जब भी "", और "" के उदाहरण किसी प्रमाण की पंक्तियों पर दिखाई देते हैं, तो "" को अगली पंक्ति में रखा जा सकता है।
हाइपोथेटिकल सिलोगिज्म निकटता से संबंधित है और विच्छेदात्मक न्यायवाक्य के समान है, इसमें यह एक प्रकार का सिलोगिज्म भी है, और अनुमान के नियम का नाम भी है।
प्रयोज्यता
काल्पनिक न्यायशास्त्र का नियम मौलिक तर्क, अंतर्ज्ञानवादी तर्क, प्रासंगिक तर्क की अधिकांश प्रणालियों और तर्क की कई अन्य प्रणालियों में प्रय्युक्त होता है। चूँकि, यह सभी तर्कों पर प्रय्युक्त नहीं होता है, उदाहरण के लिए, गैर-मोनोटोनिक तर्क, संभाव्य तर्क और डिफ़ॉल्ट तर्क इसका कारण यह है कि ये तर्क अक्षम्य तर्क का वर्णन करते हैं, और वास्तविक दुनिया के संदर्भों में दिखाई देने वाली नियमानुसार सामान्यतः अपवादों, डिफ़ॉल्ट मान्यताओं, अन्य सभी समान स्थितियों या बस साधारण अनिश्चितता की अनुमति देती हैं।
अर्नेस्ट डब्ल्यू एडम्स से लिया गया एक उदाहरण, [3]
- यदि जोन्स चुनाव जीतता है, तो स्मिथ चुनाव के बाद सेवानिवृत्त हो जाएगा।
- यदि चुनाव से पहले स्मिथ की मृत्यु हो जाती है, तो जोन्स चुनाव जीत जाएगा।
- यदि चुनाव से पहले स्मिथ की मृत्यु हो जाती है, तो चुनाव के बाद स्मिथ सेवानिवृत्त हो जायेंगे.
स्पष्टतः (3) (1) और (2) से अनुसरण नहीं करता है। (1) डिफ़ॉल्ट रूप से सत्य है, किन्तु स्मिथ की मृत्यु की असाधारण परिस्थितियों में इसे प्रय्युक्त करने में विफल रहता है। वास्तव में, वास्तविक दुनिया की नियमो में सदैव डिफ़ॉल्ट धारणाएं या संदर्भ सम्मिलित होते हैं और उन सभी असाधारण परिस्थितियों को निर्दिष्ट करना असंभव या यहां तक कि असंभव हो सकता है जिनमें वे सत्य होने में विफल हो सकते हैं। समान कारणों से, काल्पनिक न्यायवाक्य का नियम प्रतितथ्यात्मक नियमो पर प्रय्युक्त नहीं होता है।
औपचारिक संकेतन
काल्पनिक न्यायवाक्य अनुमान नियम को अनुक्रमिक संकेतन में लिखा जा सकता है, जो कट नियम की विशेषज्ञता के समान है:
जहां एक धातु संबंधी प्रतीक है और का अर्थ है कि कुछ तार्किक प्रणाली में का वाक्यात्मक परिणाम है;
और एक सत्य-कार्यात्मक टॉटोलॉजी (तर्क) या प्रस्तावात्मक कलन के प्रमेय के रूप में व्यक्त किया गया:
जहाँ , , और कुछ औपचारिक प्रणाली में व्यक्त किए गए प्रस्ताव हैं।
प्रमाण
| चरण | प्रस्ताव | व्युत्पत्ति |
|---|---|---|
| 1 | दिया गया | |
| 2 | दिया गया | |
| 3 | नियमित प्रमाण धारणा | |
| 4 | सेटिंग मोड (1,3) | |
| 5 | सेटिंग मोड (2,4) | |
| 6 | नियमित प्रमाण (3-5) |
वैकल्पिक रूप
काल्पनिक न्यायवाक्य का एक वैकल्पिक रूप, निहितार्थ और निषेध के साथ मौलिक प्रस्तावात्मक कलन प्रणालियों के लिए अधिक उपयोगी (अर्थात संयोजन चिह्न के बिना) निम्नलिखित है:
- (HS1)
फिर भी एक और रूप है:
- (HS2)
प्रमाण
ऐसी प्रणालियों में इन प्रमेयों के प्रमाण का एक उदाहरण नीचे दिया गया है। हम जान लुकासिविक्ज़ द्वारा वर्णित लोकप्रिय प्रणालियों में से एक में उपयोग किए गए तीन सिद्धांतों में से दो का उपयोग करते हैं। प्रमाण इस प्रणाली के तीन सिद्धांतों में से दो पर निर्भर करते हैं:
- (ए1)
- (आआ)
(HS1) का प्रमाण इस प्रकार है:
- (1) ((A1) का उदाहरण)
- (2) ((A2 का उदाहरण))
- (3) (सेटिंग विधि द्वारा (1) और (2) से)
- (4) ((A2 का उदाहरण))
- (5) (सेटिंग विधि द्वारा (3) और (4) से)
- (6) ((A1) का उदाहरण)
- (7) ((5) और (6) से मोडस पोनेन्स द्वारा)
- (HS2) का प्रमाण यहां दिया गया है।
एक मेटाथ्योरम के रूप में
जब भी हमारे पास और के रूप में दो प्रमेय हों, तो हम साबित कर सकते हैं निम्नलिखित चरणों द्वारा:
- (1) (ऊपर सिद्ध प्रमेय का उदाहरण)
- (2) ((T1 का उदाहरण))
- (3) (सेटिंग विधि द्वारा (1) और (2) से)
- (4) ((T2 का उदाहरण))
- (5) (सेटिंग विधि द्वारा (3) और (4) से)
यह भी देखें
- मोडस पोनेन्स
- मोडस टोलेंस
- परिणाम की पुष्टि
- पूर्ववृत्त को नकारना
- संक्रमणीय संबंध
संदर्भ
- ↑ 1.0 1.1 Kashef, Arman. (2023), In Quest of Univeral Logic: A brief overview of formal logic's evolution, doi:10.13140/RG.2.2.24043.82724/1
- ↑ "History of Logic: Theophrastus of Eresus" in Encyclopædia Britannica Online.
- ↑ Adams, Ernest W. (1975). शर्तों का तर्क. Dordrecht: Reidel. p. 22.