एराटोस्थनीज़ की छलनी: Difference between revisions
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
{{short description|Ancient algorithm for generating prime numbers}} | {{short description|Ancient algorithm for generating prime numbers}} | ||
[[File:Animation Sieve of Eratosth.gif|right|frame|एराटोस्थनीज़ की छलनी: 121 से नीचे अभाज्य संख्याओं के लिए कलन विधि चरण (अभाज्य वर्ग से प्रारम्भ | [[File:Animation Sieve of Eratosth.gif|right|frame|एराटोस्थनीज़ की छलनी: 121 से नीचे अभाज्य संख्याओं के लिए कलन विधि चरण (अभाज्य वर्ग से प्रारम्भ करने के अनुकूलन सहित)।]]गणित में, '''एराटोस्थनीज की छलनी''' (सीव) किसी भी सीमा तक प्रत्येक [[अभाज्य संख्या]]ओं के अन्वेषण के लिए एक प्राचीन [[कलन विधि]] होती है। | ||
यह प्रत्येक अभाज्य के गुणजों को मिश्रित संख्या (अर्थात अभाज्य नहीं) के रूप में चिह्नित करके, पहले अभाज्य संख्या 2 से प्रारम्भ करके करता है। किसी दिए गए अभाज्य के गुणज अंकगणित के साथ, उस अभाज्य से प्रारम्भ होने वाली संख्याओं के अनुक्रम के रूप में उत्पन्न होते हैं। उनके मध्य वह उस अभाज्य के बराबर होती है।<ref name="horsley">Horsley, Rev. Samuel, F. R. S., "''{{lang|el|Κόσκινον Ερατοσθένους}}'' or, The Sieve of Eratosthenes. Being an account of his method of finding all the Prime Numbers," [https://www.jstor.org/stable/106053 ''Philosophical Transactions'' (1683–1775), Vol. 62. (1772), pp. 327–347].</ref> प्रत्येक अभाज्य द्वारा विभाज्यता के लिए प्रत्येक उम्मीदवार संख्या का क्रमिक रूप से परीक्षण करने के लिए [[परीक्षण प्रभाग]] का उपयोग करने से यह छलनी का मुख्य | यह प्रत्येक अभाज्य के गुणजों को मिश्रित संख्या (अर्थात अभाज्य नहीं) के रूप में चिह्नित करके, पहले अभाज्य संख्या 2 से प्रारम्भ करके करता है। किसी दिए गए अभाज्य के गुणज अंकगणित के साथ, उस अभाज्य से प्रारम्भ होने वाली संख्याओं के अनुक्रम के रूप में उत्पन्न होते हैं। उनके मध्य वह उस अभाज्य के बराबर होती है।<ref name="horsley">Horsley, Rev. Samuel, F. R. S., "''{{lang|el|Κόσκινον Ερατοσθένους}}'' or, The Sieve of Eratosthenes. Being an account of his method of finding all the Prime Numbers," [https://www.jstor.org/stable/106053 ''Philosophical Transactions'' (1683–1775), Vol. 62. (1772), pp. 327–347].</ref> प्रत्येक अभाज्य द्वारा विभाज्यता के लिए प्रत्येक उम्मीदवार संख्या का क्रमिक रूप से परीक्षण करने के लिए [[परीक्षण प्रभाग]] का उपयोग करने से यह छलनी का मुख्य भिन्नता प्राप्त होती है।<ref name="ONeill" />एक बार जब प्रत्येक अन्वेषण किये गए अभाज्य के प्रत्येक गुणजों को समग्र के रूप में चिह्नित किया जाता है, तो शेष अचिह्नित संख्याएँ अभाज्य प्राप्त होती हैं। | ||
छलनी का सबसे पहला ज्ञात संदर्भ ({{lang-grc|κόσκινον Ἐρατοσθένους}}, कोस्किनन एराटोस्थेनस) गेरासा के अंकगणित के परिचय के [[निकोमैचस]] में प्रारंभिक 2 शताब्दी में देखने को मिलता है।<ref name=nicomachus>{{citation|editor-first=Richard|editor-last=Hoche|editor-link=Richard Hoche|title=Nicomachi Geraseni Pythagorei Introductionis arithmeticae libri II, chapter XIII, 3|year=1866|location= Leipzig|publisher= B.G. Teubner|page=30|url=https://archive.org/stream/nicomachigerasen00nicouoft#page/30/mode/2up}}</ref> | छलनी का सबसे पहला ज्ञात संदर्भ ({{lang-grc|κόσκινον Ἐρατοσθένους}}, कोस्किनन एराटोस्थेनस) गेरासा के अंकगणित के परिचय के [[निकोमैचस]] में प्रारंभिक 2 शताब्दी में देखने को मिलता है।<ref name=nicomachus>{{citation|editor-first=Richard|editor-last=Hoche|editor-link=Richard Hoche|title=Nicomachi Geraseni Pythagorei Introductionis arithmeticae libri II, chapter XIII, 3|year=1866|location= Leipzig|publisher= B.G. Teubner|page=30|url=https://archive.org/stream/nicomachigerasen00nicouoft#page/30/mode/2up}}</ref> सीई पुस्तक जो इसका श्रेय साइरीन के एराटोस्थनीज़ को देती है, जो कि तीसरी शताब्दी का था। ईसा पूर्व यूनानी गणितज्ञ, यद्यपि अभाज्य संख्याओं के अतिरिक्त विषम संख्याओं द्वारा छनाई का वर्णन करते थे।<ref name=nicomachus1926>{{citation|author=Nicomachus of Gerasa|title=Introduction to Arithmetic; translated into English by Martin Luther D'Ooge ; with studies in Greek arithmetic by Frank Egleston Robbins and Louis Charles Karpinski, chapter XIII, 3|year=1926|location=New York|publisher=The Macmillan Company|page=204}}</ref> | ||
कई अभाज्य संख्याओं की छलनी में | कई अभाज्य संख्याओं की छलनी में प्रत्येक छोटे अभाज्य संख्याओं को अन्वेषण के सबसे प्रभावी विधियों में से एक होता है। इसका उपयोग अंकगणितीय प्रगति में अभाज्य संख्या ज्ञात करने के लिए किया जा सकता है।<ref>J. C. Morehead, "Extension of the Sieve of Eratosthenes to arithmetical progressions and applications", [https://www.jstor.org/stable/1967477 ''Annals of Mathematics, Second Series'' '''10''':2 (1909), pp. 88–104].</ref> | ||
== अवलोकन == | == अवलोकन == | ||
{{quote box|fontsize = 105%| | {{quote box|fontsize = 105%|दो को छान लें और तीन को छान लें: | ||
एराटोस्थनीज की छलनी। | |||
जब गुणज उदात्त, | |||
जो संख्याएँ बची हैं वे अभाज्य होती हैं। | |||
|quoted=1|salign=center|source=अज्ञात <ref>Clocksin, William F., Christopher S. Mellish, ''Programming in Prolog'', 1984, p. 170. {{isbn|3-540-11046-1}}.</ref>}} | |||
अभाज्य संख्या एक [[प्राकृतिक संख्या]] होती है जिसमें दो अलग-अलग प्राकृतिक संख्या वि[[भाजक]] होते हैं: संख्या [[1]]और स्वयं। | अभाज्य संख्या एक [[प्राकृतिक संख्या]] होती है जिसमें दो अलग-अलग प्राकृतिक संख्या वि[[भाजक]] होते हैं: संख्या [[1]]और स्वयं। | ||
| Line 16: | Line 20: | ||
# 2 से लेकर लगातार पूर्णांकों की एक सूची बनाएं {{mvar|n}}: {{math|(2, 3, 4, ..., ''n'')}}। | # 2 से लेकर लगातार पूर्णांकों की एक सूची बनाएं {{mvar|n}}: {{math|(2, 3, 4, ..., ''n'')}}। | ||
# प्रारंभ में, मान लीजिए कि p सबसे छोटी अभाज्य संख्या जो | # प्रारंभ में, मान लीजिए कि p सबसे छोटी अभाज्य संख्या जो 2 के बराबर है। | ||
# 2p से n तक p की वृद्धि में गिनकर p के गुणजों की गणना करें, और उन्हें सूची में चिह्नित करें (ये 2p, 3p, 4p, ... होंगे; p को स्वयं चिह्नित नहीं किया जाना चाहिए)। | # 2p से n तक p की वृद्धि में गिनकर p के गुणजों की गणना करें, और उन्हें सूची में चिह्नित करें (ये 2p, 3p, 4p, ... होंगे; p को स्वयं चिह्नित नहीं किया जाना चाहिए)। | ||
# सूची में p से बड़ी वह सबसे छोटी संख्या ज्ञात कीजिए जो अंकित नहीं है। अगर ऐसा कोई नंबर नहीं था तो रुकें. अन्यथा, मान लीजिए p अब इस नई संख्या (जो अगला अभाज्य है) के बराबर है, और चरण 3 से दोहराएँ। | # सूची में p से बड़ी वह सबसे छोटी संख्या ज्ञात कीजिए जो अंकित नहीं है। अगर ऐसा कोई नंबर नहीं था तो रुकें. अन्यथा, मान लीजिए p अब इस नई संख्या (जो अगला अभाज्य है) के बराबर है, और चरण 3 से दोहराएँ। | ||
| Line 23: | Line 27: | ||
यहां मुख्य विचार यह है कि {{mvar|p}} को दिया गया प्रत्येक मान अभाज्य होगा, क्योंकि यदि यह समग्र होता तो इसे किसी अन्य, छोटे अभाज्य के गुणज के रूप में चिह्नित किया जाता। ध्यान दें कि कुछ संख्याओं को एक से अधिक बार चिह्नित किया जा सकता है (उदाहरण के लिए, 3 और 5 दोनों के लिए 15 को चिह्नित किया जाएगा)। | यहां मुख्य विचार यह है कि {{mvar|p}} को दिया गया प्रत्येक मान अभाज्य होगा, क्योंकि यदि यह समग्र होता तो इसे किसी अन्य, छोटे अभाज्य के गुणज के रूप में चिह्नित किया जाता। ध्यान दें कि कुछ संख्याओं को एक से अधिक बार चिह्नित किया जा सकता है (उदाहरण के लिए, 3 और 5 दोनों के लिए 15 को चिह्नित किया जाएगा)। | ||
परिशोधन के रूप में, चरण 3 में | परिशोधन के रूप में, चरण 3 में {{math|''p''<sup>2</sup>}} से प्रारम्भ करके संख्याओं को चिह्नित करना पर्याप्त होता है, के प्रत्येक छोटे गुणजों के रूप में {{mvar|p}} उस बिंदु पर पहले ही चिह्नित किया जा चुका होता है। इसका अर्थ यह है कि कलन विधि को चरण 4 में समाप्त करने की अनुमति है जब {{math|''p''<sup>2</sup>}} {{mvar|n}} से बड़ा होता है।<ref name="horsley" /> | ||
एक और परिशोधन यह है कि प्रारंभ में मात्र | एक और परिशोधन यह है कि प्रारंभ में मात्र विषम संख्याओं को सूचीबद्ध किया जाए, {{math|(3, 5, ..., ''n'')}}, और चरण 3 में {{math|2''p''}} की वृद्धि में गिनती की जाए, इस प्रकार मात्र {{mvar|p}} विषम गुणजों को चिह्नित किया जाता है। यह वास्तव में मूल कलन विधि में दिखाई देता है।<ref name="horsley" /><ref name="nicomachus1926" /> इसे चक्रीय गुणनखंडन के साथ सामान्यीकृत किया जा सकता है, प्रारंभिक सूची मात्र पहले कुछ अभाज्य संख्याओं के साथ सहअभाज्य संख्याओं से बनाई जाती है, न कि मात्र बाधाओं से (अर्थात्, 2 के साथ सहअभाज्य संख्याएं), और तदनुसार समायोजित वेतन वृद्धि में गिनती की जाती है जिससें मात्र {{mvar|p}} के ऐसे गुणज उत्पन्न होते हैं जो सर्वप्रथम उन छोटे अभाज्यों के साथ सहअभाज्य होते हैं।<ref name="Runciman">{{Cite journal | doi = 10.1017/S0956796897002670| title = Functional Pearl: Lazy wheel sieves and spirals of primes| journal = Journal of Functional Programming| volume = 7| issue = 2| pages = 219–225| year = 1997| last1 = Runciman | first1 = Colin| s2cid = 2422563| url = http://eprints.whiterose.ac.uk/3784/1/runcimanc1.pdf}}</ref> | ||
=== उदाहरण === | === उदाहरण === | ||
| Line 38: | Line 42: | ||
2 3 {{gray|<s> 4 </s>}} 5 {{gray|<s> 6 </s>}} 7 {{gray|<s> 8 </s>}} 9 {{gray|<s>10</s>}} 11 {{gray|<s>12</s>}} 13 {{gray|<s>14</s>}} 15 {{gray|<s>16</s>}} 17 {{gray|<s>18</s>}} 19 {{gray|<s>20</s>}} 21 {{gray|<s>22</s>}} 23 {{gray|<s>24</s>}} 25 {{gray|<s>26</s>}} 27 {{gray|<s>28</s>}} 29 {{gray|<s>30</s>}} | 2 3 {{gray|<s> 4 </s>}} 5 {{gray|<s> 6 </s>}} 7 {{gray|<s> 8 </s>}} 9 {{gray|<s>10</s>}} 11 {{gray|<s>12</s>}} 13 {{gray|<s>14</s>}} 15 {{gray|<s>16</s>}} 17 {{gray|<s>18</s>}} 19 {{gray|<s>20</s>}} 21 {{gray|<s>22</s>}} 23 {{gray|<s>24</s>}} 25 {{gray|<s>26</s>}} 27 {{gray|<s>28</s>}} 29 {{gray|<s>30</s>}} | ||
सूची में 2 के बाद अगला नंबर 3 है; 3 के बाद सूची में प्रत्येक तीसरे नंबर को 3 की वृद्धि में 3 से गिनकर हटा | सूची में 2 के बाद अगला नंबर 3 है; 3 के बाद सूची में प्रत्येक तीसरे नंबर को 3 की वृद्धि में 3 से गिनकर हटा दें (ये सूची में 3 के प्रत्येक गुणज होंगे): | ||
2 3 {{gray|<s> 4 </s>}} 5 {{gray|<s> 6 </s>}} 7 {{gray|<s> 8 </s>}}{{gray|<s> 9 </s>}}{{gray|<s>10</s>}} 11 {{gray|<s>12</s>}} 13 {{gray|<s>14 </s>}}{{gray|<s>15 </s>}}{{gray|<s>16</s>}} 17 {{gray|<s>18</s>}} 19 {{gray|<s>20 </s>}}{{gray|<s>21 </s>}}{{gray|<s>22</s>}} 23 {{gray|<s>24</s>}} 25 {{gray|<s>26 </s>}}{{gray|<s>27 </s>}}{{gray|<s>28</s>}} 29 {{gray|<s>30</s>}} | 2 3 {{gray|<s> 4 </s>}} 5 {{gray|<s> 6 </s>}} 7 {{gray|<s> 8 </s>}}{{gray|<s> 9 </s>}}{{gray|<s>10</s>}} 11 {{gray|<s>12</s>}} 13 {{gray|<s>14 </s>}}{{gray|<s>15 </s>}}{{gray|<s>16</s>}} 17 {{gray|<s>18</s>}} 19 {{gray|<s>20 </s>}}{{gray|<s>21 </s>}}{{gray|<s>22</s>}} 23 {{gray|<s>24</s>}} 25 {{gray|<s>26 </s>}}{{gray|<s>27 </s>}}{{gray|<s>28</s>}} 29 {{gray|<s>30</s>}} | ||
3 के बाद सूची में अभी तक नहीं हटाया | 3 के बाद सूची में अभी तक नहीं हटाया गया अगला नंबर 5 है; 5 के बाद सूची में प्रत्येक 5वीं संख्या को 5 की वृद्धि में 5 से गिनकर हटा दें (अर्थात् 5 के प्रत्येक गुणज होंगे): | ||
2 3 {{gray|<s> 4 </s>}} 5 {{gray|<s> 6 </s>}} 7 {{gray|<s> 8 </s>}}{{gray|<s> 9 </s>}}{{gray|<s>10</s>}} 11 {{gray|<s>12</s>}} 13 {{gray|<s>14 </s>}}{{gray|<s>15 </s>}}{{gray|<s>16</s>}} 17 {{gray|<s>18</s>}} 19 {{gray|<s>20 </s>}}{{gray|<s>21 </s>}}{{gray|<s>22</s>}} 23 {{gray|<s>24 </s>}}{{gray|<s>25 </s>}}{{gray|<s>26 </s>}}{{gray|<s>27 </s>}}{{gray|<s>28</s>}} 29 {{gray|<s>30</s>}} | 2 3 {{gray|<s> 4 </s>}} 5 {{gray|<s> 6 </s>}} 7 {{gray|<s> 8 </s>}}{{gray|<s> 9 </s>}}{{gray|<s>10</s>}} 11 {{gray|<s>12</s>}} 13 {{gray|<s>14 </s>}}{{gray|<s>15 </s>}}{{gray|<s>16</s>}} 17 {{gray|<s>18</s>}} 19 {{gray|<s>20 </s>}}{{gray|<s>21 </s>}}{{gray|<s>22</s>}} 23 {{gray|<s>24 </s>}}{{gray|<s>25 </s>}}{{gray|<s>26 </s>}}{{gray|<s>27 </s>}}{{gray|<s>28</s>}} 29 {{gray|<s>30</s>}} | ||
5 के बाद सूची में अभी तक नहीं हटाया गया अगला नंबर 7 है; अगला कदम 7 के बाद सूची में प्रत्येक 7वीं संख्या को हटाना होगा, परन्तु | 5 के बाद सूची में अभी तक नहीं हटाया गया अगला नंबर 7 है; अगला कदम 7 के बाद सूची में प्रत्येक 7वीं संख्या को हटाना होगा, परन्तु वे प्रत्येक इस बिंदु पर पहले ही हटा दी गए हैं, क्योंकि ये संख्याएं (14, 21, 28) भी छोटी अभाज्य संख्याओं के गुणज हैं क्योंकि 7 × 7 से बड़ा और 30 से अधिक होता है। सूची में इस बिंदु पर जिन संख्याओं को नहीं हटाया गया है वे 30 से नीचे की प्रत्येक अभाज्य संख्याएँ हैं: | ||
2 3 5 7 11 13 17 19 23 29 | 2 3 5 7 11 13 17 19 23 29 | ||
| Line 52: | Line 56: | ||
==कलन विधि और प्रकार== | ==कलन विधि और प्रकार== | ||
===[[छद्मकोड]]=== | ===[[छद्मकोड|स्यूडोकोड]]=== | ||
एराटोस्थनीज की छलनी को | एराटोस्थनीज की छलनी को स्यूडोकोड में इस प्रकार व्यक्त किया जा सकता है:<ref name="sedgewick">{{cite book | ||
|last1=Sedgewick |first1=Robert |title=Algorithms in C++ | |last1=Sedgewick |first1=Robert |title=Algorithms in C++ | ||
|publisher=Addison-Wesley |year=1992 |isbn=978-0-201-51059-1 | |publisher=Addison-Wesley |year=1992 |isbn=978-0-201-51059-1 | ||
}}, p. 16.</ref><ref name="intro">[http://research.cs.wisc.edu/techreports/1990/TR909.pdf Jonathan Sorenson, ''An Introduction to Prime Number Sieves''], Computer Sciences Technical Report #909, Department of Computer Sciences University of Wisconsin-Madison, January 2, 1990 (the use of optimization of starting from squares, and thus using only the numbers whose square is below the upper limit, is shown).</ref> | }}, p. 16.</ref><ref name="intro">[http://research.cs.wisc.edu/techreports/1990/TR909.pdf Jonathan Sorenson, ''An Introduction to Prime Number Sieves''], Computer Sciences Technical Report #909, Department of Computer Sciences University of Wisconsin-Madison, January 2, 1990 (the use of optimization of starting from squares, and thus using only the numbers whose square is below the upper limit, is shown).</ref> | ||
एराटोस्थनीज की कलन विधि छलनी है | |||
इनपुट: एक पूर्णांक n > 1. | |||
आउटपुट: 2 से n तक की प्रत्येक अभाज्य संख्याएँ। | |||
मान लीजिए A [[बूलियन डेटा प्रकार]] की एक सरणी है, जो पूर्णांक 2 से n द्वारा अनुक्रमित है, | |||
प्रारंभ में प्रत्येक समूह पर सत्य होती हैं। | |||
i = 2, 3, 4, ... के लिए, √n से अधिक नहीं होती है | |||
यदि A[i] सत्य होताहै | |||
''j'' = ''i''<sup>2</sup>, ''i''<sup>2</sup>+''i'', ''i''<sup>2</sup>+2''i'', ''i''<sup>2</sup>+3''i'', ..., के लिए, n से अधिक नहीं होता है | |||
समूह ''A''[''j''] := असत्य | |||
प्रत्येक i को ऐसे लौटाएँ कि A[i] सत्य हो। | |||
यह कलन विधि | यह कलन विधि प्रत्येक अभाज्य संख्याएँ उत्पन्न करता है जो {{mvar|n}} से बड़ी नहीं होती हैं। इसमें एक सामान्य अनुकूलन सम्मलित होता है, जिसमें {{math|''i''<sup>2</sup>}} प्रत्येक अभाज्य {{mvar|i}} के गुणजों की गणना प्रारम्भ करना सम्मलित होता है। इस कलन विधि की समय सम्मिश्र {{math|''O''(''n'' log log ''n'')}} है,{{r|intro}} परन्तु सरणी अद्यतन एक {{math|''O''(1)}} ऑपरेशन हो, जैसा कि सामान्यतः होता है। | ||
=== | ===विच्छिन्न छलनी=== | ||
जैसा कि सोरेनसन ने वर्णित किया है, एराटोस्थनीज की छलनी के साथ समस्या इसके द्वारा किए जाने वाले ऑपरेशनों की संख्या नहीं है, किन्तु इसकी मेमोरी आवश्यकताएं हैं।{{r|intro}} बड़े के लिए {{mvar|n}}, अभाज्य संख्याओं की सीमा स्मृति में स्थित नहीं हो सकती है; इससे भी व्यर्थ, मध्यम {{mvar|n}} के लिए भी , इसका [[सीपीयू कैश]] उपयोग अत्यधिक श्रेष्ट नहीं होता | जैसा कि सोरेनसन ने वर्णित किया है, एराटोस्थनीज की छलनी के साथ समस्या इसके द्वारा किए जाने वाले ऑपरेशनों की संख्या नहीं है, किन्तु इसकी मेमोरी आवश्यकताएं हैं।{{r|intro}} बड़े के लिए {{mvar|n}}, अभाज्य संख्याओं की सीमा स्मृति में स्थित नहीं हो सकती है; इससे भी व्यर्थ, मध्यम {{mvar|n}} के लिए भी , इसका [[सीपीयू कैश]] उपयोग अत्यधिक श्रेष्ट नहीं होता है। कलन विधि संपूर्ण सरणी {{mvar|A}} से चलता है, संदर्भ का न्यूनाधिक कोई स्थानीयता प्रदर्शित नहीं करता। | ||
इन समस्याओं का समाधान खंडित छलनी द्वारा प्रस्तुत किया जाता है, जहां एक समय में मात्र | इन समस्याओं का समाधान खंडित छलनी द्वारा प्रस्तुत किया जाता है, जहां एक समय में मात्र सीमा के कुछ भागों को ही छलनी किया जाता है।<ref>Crandall & Pomerance, ''Prime Numbers: A Computational Perspective'', second edition, Springer: 2005, pp. 121–24.</ref> इन्हें 1970 के समय से जाना जाता है और ये इस प्रकार काम करते हैं:{{r|intro}}<ref>{{Cite journal | last1 = Bays | first1 = Carter | last2 = Hudson | first2 = Richard H. | year = 1977 | title = The segmented sieve of Eratosthenes and primes in arithmetic progressions to 10<sup>12</sup> | journal = BIT | volume = 17 | issue = 2 | pages = 121–127 | doi = 10.1007/BF01932283 | s2cid = 122592488 }}</ref> | ||
# रेंज | # रेंज 2 से {{mvar|n}} को कुछ आकार के खंडों{{math|Δ ≤ {{sqrt|''n''}}}} में विभाजित करें। | ||
# नियमित छलनी का उपयोग करके, पहले (अर्थात् सबसे निचले) खंड में अभाज्य अन्वेषण करे। | # नियमित छलनी का उपयोग करके, पहले (अर्थात् सबसे निचले) खंड में अभाज्य अन्वेषण करे। | ||
# निम्नलिखित प्रत्येक खंड के लिए, बढ़ते क्रम में, साथ {{mvar|m}} खंड का सर्वोच्च मान होने के कारण, इसमें अभाज्य संख्याएँ इस प्रकार ज्ञात करें: | # निम्नलिखित प्रत्येक खंड के लिए, बढ़ते क्रम में, साथ {{mvar|m}} खंड का सर्वोच्च मान होने के कारण, इसमें अभाज्य संख्याएँ इस प्रकार ज्ञात करें: | ||
## आकार {{math|Δ}} की एक बूलियन सरणी वर्णित करें। | ## आकार {{math|Δ}} की एक बूलियन सरणी वर्णित करें। | ||
## अब तक पाए गए प्रत्येक अभाज्य {{math|''p'' ≤ {{sqrt|''m''}}}} | ## अब तक पाए गए प्रत्येक अभाज्य {{math|''p'' ≤ {{sqrt|''m''}}}} के गुणजों के अनुरूप सरणी में पदों को गैर-अभाज्य के रूप में चिह्नित करें, {{math|{{mvar|m}} - Δ}} और {{mvar|m}} के मध्य {{math|''p''}} के निम्नतम गुणज से प्रारंभ करना करके {{math|''p''}} के चरणों में इसके गुणजों की गणना करके। | ||
## सरणी में शेष गैर-चिह्नित स्थिति खंड में अभाज्य संख्याओं के अनुरूप हैं। इन अभाज्य अभाज्य संख्याओं के किसी भी गुणज को चिह्नित करना आवश्यक नहीं है, क्योंकि ये प्रत्येक अभाज्य संख्याएँ {{math|{{sqrt|''m''}}}} से बड़े है,जैसे की | ## सरणी में शेष गैर-चिह्नित स्थिति खंड में अभाज्य संख्याओं के अनुरूप हैं। इन अभाज्य अभाज्य संख्याओं के किसी भी गुणज को चिह्नित करना आवश्यक नहीं है, क्योंकि ये प्रत्येक अभाज्य संख्याएँ {{math|{{sqrt|''m''}}}} से बड़े है,जैसे की {{math|''k'' ≥ 1}}के लिए, किसी के पास <math>(k\Delta + 1)^2 > (k+1)\Delta</math>होता है। | ||
यदि {{math|Δ}} को {{math|{{sqrt|''n''}}}} चुना जाता है , कलन विधि की | यदि {{math|Δ}} को {{math|{{sqrt|''n''}}}} चुना जाता है, कलन विधि की स्थान सम्मिश्र {{math|''O''({{sqrt|''n''}})}} होती है, जबकि समय सम्मिश्र नियमित छलनी के समान ही होती है।{{r|intro}} | ||
ऊपरी सीमा वाली श्रेणियों के लिए {{math|''n''}} इतना बड़ा कि छानने का काम नीचे हो जाता है {{math|{{sqrt|''n''}}}} जैसा कि पृष्ठ की आवश्यकता के अनुसार एराटोस्थनीज की खंडित छलनी मेमोरी में स्थित नहीं हो सकती है, इसके स्थान पर [[सोरेनसन की छलनी]] जैसी धीमी परन्तु | ऊपरी सीमा वाली श्रेणियों के लिए {{math|''n''}} इतना बड़ा कि छानने का काम नीचे हो जाता है {{math|{{sqrt|''n''}}}} जैसा कि पृष्ठ की आवश्यकता के अनुसार एराटोस्थनीज की खंडित छलनी मेमोरी में स्थित नहीं हो सकती है, इसके स्थान पर [[सोरेनसन की छलनी]] जैसी धीमी परन्तु अधिक स्थान-कुशल छलनी का उपयोग किया जा सकता है।<ref>J. Sorenson, [http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.94.1737 "The pseudosquares prime sieve"], ''Proceedings of the 7th International Symposium on Algorithmic Number Theory''. (ANTS-VII, 2006).</ref> | ||
== वृद्धिशील छलनी == | == वृद्धिशील छलनी == | ||
छलनी का एक वृद्धिशील सूत्रीकरण<ref name="ONeill">O'Neill, Melissa E., [http://www.cs.hmc.edu/~oneill/papers/Sieve-JFP.pdf "The Genuine Sieve of Eratosthenes"], ''Journal of Functional Programming'', published online by Cambridge University Press 9 October 2008 {{doi|10.1017/S0956796808007004}}, pp. 10, 11 (contains two incremental sieves in Haskell: a priority-queue–based one by O'Neill and a list–based, by Richard Bird).</ref> अभाज्यों की पीढ़ी को उनके गुणजों की पीढ़ी के साथ जोड़कर अनिश्चित काल तक (अर्थात्, ऊपरी सीमा के बिना) अभाज्य संख्याओं को उत्पन्न करता है (जिससें अभाज्यों को गुणजों के | छलनी का एक वृद्धिशील सूत्रीकरण<ref name="ONeill">O'Neill, Melissa E., [http://www.cs.hmc.edu/~oneill/papers/Sieve-JFP.pdf "The Genuine Sieve of Eratosthenes"], ''Journal of Functional Programming'', published online by Cambridge University Press 9 October 2008 {{doi|10.1017/S0956796808007004}}, pp. 10, 11 (contains two incremental sieves in Haskell: a priority-queue–based one by O'Neill and a list–based, by Richard Bird).</ref> अभाज्यों की पीढ़ी को उनके गुणजों की पीढ़ी के साथ जोड़कर अनिश्चित काल तक (अर्थात्, ऊपरी सीमा के बिना) अभाज्य संख्याओं को उत्पन्न करता है (जिससें अभाज्यों को गुणजों के मध्य अंतराल में पाया जा सके), जहां प्रत्येक अभाज्य {{mvar|p}} के गुणज की वृद्धि में अभाज्य के वर्ग {{mvar|p}} से गिनती करके सीधे (या {{math|2''p''}} विषम अभाज्य संख्याओं के लिए) उत्पन्न होते हैं। दक्षता पर प्रतिकूल प्रभाव से बचने के लिए, उत्पादन तभी प्रारम्भ किया जाना चाहिए जब अभाज्य वर्ग पहुंच जाए। इसे [[डेटाफ्लो प्रोग्रामिंग]] प्रतिमान के तहत प्रतीकात्मक रूप से व्यक्त किया जा सकता है | ||
अभाज्य संख्याएँ = [2, 3, ...] \ p², p²+p, ...] अभाज्य संख्याओं में p के लिए], | अभाज्य संख्याएँ = [2, 3, ...] \ p², p²+p, ...] अभाज्य संख्याओं में p के लिए], | ||
[[ | संख्याओं की [[अंकगणितीय प्रगति]] का सापेक्ष <code>\</code> पूरक को निरूपित करते हुए [[सूची समझ|सूची ज्ञान]] संकेतन का उपयोग करना। | ||
एक समय में एक अभाज्य, अनुक्रमिक अभाज्य द्वारा | एक समय में एक अभाज्य, अनुक्रमिक अभाज्य द्वारा विभाज्यता परीक्षण के माध्यम से कंपोजिट को पुनरावृत्त रूप से छानकर भी अभाज्य का उत्पादन किया जा सकता है। यह एराटोस्थनीज़ की छलनी नहीं है, परन्तु अधिकांशतः इसके साथ भ्रमित किया जाता है, तथापि एराटोस्थनीज़ की छलनी उनके परीक्षण के अतिरिक्त सीधे समग्र उत्पन्न करती है। परीक्षण प्रभाग में अभाज्य संख्याओं की श्रृंखला उत्पन्न करने में एराटोस्थनीज की छलनी की तुलना में कलन विधि का अत्यधिक व्यर्थ सैद्धांतिक विश्लेषण होता है।<ref name="ONeill"/> | ||
प्रत्येक अभाज्य का परीक्षण करते समय, | प्रत्येक अभाज्य का परीक्षण करते समय, सर्वश्रेष्ठ परीक्षण विभाजन कलन विधि प्रत्येक अभाज्य संख्याओं का उपयोग करता है जो उसके वर्गमूल से अधिक नहीं होती हैं, जबकि एराटोस्थनीज की छलनी प्रत्येक संमिश्र को मात्र उसके अभाज्य कारकों से उत्पन्न करती है, और समग्र के मध्य अभाज्य संख्याओं को मुफ्त में प्राप्त करती है। [[डेविड टर्नर (कंप्यूटर वैज्ञानिक)]] द्वारा व्यापक रूप से ज्ञात 1975 [[कार्यात्मक प्रोग्रामिंग]] छलनी कोड<ref>Turner, David A. SASL language manual. Tech. rept. CS/75/1. Department of Computational Science, University of St. Andrews 1975. (<syntaxhighlight lang="haskell" inline>primes = sieve [2..]; sieve (p:nos) = p:sieve (remove (multsof p) nos); remove m = filter (not . m); multsof p n = rem n p==0</syntaxhighlight>). But see also [http://dl.acm.org/citation.cfm?id=811543&dl=ACM&coll=DL&CFID=663592028&CFTOKEN=36641676 Peter Henderson, Morris, James Jr., A Lazy Evaluator, 1976], where we [http://www.seas.gwu.edu/~rhyspj/cs3221/lab8/henderson.pdf find the following], attributed to P. Quarendon: <syntaxhighlight lang="python" inline>primeswrt[x;l] = if car[l] mod x=0 then primeswrt[x;cdr[l]] else cons[car[l];primeswrt[x;cdr[l]]] ; primes[l] = cons[car[l];primes[primeswrt[car[l];cdr[l]]]] ; primes[integers[2]]</syntaxhighlight>; the priority is unclear.</ref> इसे अधिकांशतः एराटोस्थनीज़ की छलनी के उदाहरण के रूप में प्रस्तुत किया जाता है<ref name="Runciman"/>परन्तु वास्तव में यह एक उप-सर्वोत्तम परीक्षण प्रभाग छलनी होती है।<ref name="ONeill"/> | ||
== कलन विधििक | == कलन विधििक सम्मिश्र == | ||
एराटोस्थनीज की छलनी कंप्यूटर के प्रदर्शन को | एराटोस्थनीज की छलनी कंप्यूटर के प्रदर्शन को मानदंड करने का एक लोकप्रिय विधि होती है।<ref name="peng1985fall">{{cite news | url=https://archive.org/stream/byte-magazine-1985-11/1985_11_BYTE_10-11_Inside_the_IBM_PCs#page/n245/mode/2up | title=छलनी के माध्यम से एक मिलियन प्राइम्स| work=BYTE | date=Fall 1985 | access-date=19 March 2016 | author=Peng, T. A. | pages=243–244}}</ref> [[रैंडम एक्सेस मशीन|रैंडम एक्सेस]] मॉडल में {{mvar|n}} से नीचे के सभी अभाज्य संख्याओं की गणना करने की समय जटिलता {{math|''O''(''n'' log log ''n'')}} संचालन होता है, इस तथ्य का प्रत्यक्ष परिणाम है कि [[प्राइम हार्मोनिक श्रृंखला|अभाज्य हार्मोनिक श्रृंखला]] स्पर्शोन्मुख रूप {{math|log log ''n''}} से तक पहुंचती है। यघपि, इसमें इनपुट आकार के संबंध में एक घातीय समय सम्मिश्र होता है, जो इसे एक छद्म-बहुपद समय कलन विधि बनाती है। आधारभूत कलन विधि को मेमोरी के {{math|''O''(''n'')}} की आवश्यकता होती है। कलन विधि की [[बिट जटिलता|बिट सम्मिश्र]] {{math|''O''<big>(</big>''n'' (log ''n'') (log log ''n'')<big>)</big>}} {{math|''O''(''n'')}} की मेमोरी आवश्यकता के साथ बिट संचालन है।<ref>Pritchard, Paul, "Linear prime-number sieves: a family tree," ''Sci. Comput. Programming'' '''9''':1 (1987), pp. 17–35.</ref> | ||
सामान्य रूप से कार्यान्वित पृष्ठ खंडित संस्करण की परिचालन सम्मिश्र {{math|''O''(''n'' log log ''n'')}} समान होती है गैर-खंडित संस्करण के रूप में, परन्तु खंड पृष्ठ के न्यूनतम आकार के {{math|''O''<big><big>(</big></big>{{sfrac|{{sqrt|''n''}}|log ''n''}}<big><big>)</big></big>}} साथ-साथ आकार के क्रमिक पृष्ठ खंडों से मिश्रण को निकालने के लिए उपयोग की जाने वाली सीमा के वर्गमूल से कम बेस अभाज्य को संग्रहीत करने के लिए आवश्यक मेमोरी के लिए स्थान आवश्यकताओं को कम कर देता है। | |||
सामान्य रूप से कार्यान्वित पृष्ठ खंडित संस्करण की परिचालन | |||
आधारभूत अनुकूलन के साथ एराटोस्थनीज की छलनी का एक विशेष (संभवतः ही कभी, प्रयुक्त किया गया) खंडित संस्करण, {{math|''O''(''n'')}} संचालन और {{math|''O''<big><big>(</big></big>{{sqrt|''n''}}{{sfrac|log log ''n''|log ''n''}}<big><big>)</big></big>}} मेमोरी के बिट्सड़े का उपयोग करता है।<ref name="Pritchard1">Paul Pritchard, "A sublinear additive sieve for finding prime numbers", ''Communications of the ACM'' 24 (1981), 18–23. {{MR|600730}}</ref><ref name="Pritchard2">Paul Pritchard, Explaining the wheel sieve, Acta Informatica 17 (1982), 477–485. {{MR|685983}}</ref><ref name="Pritchard3">Paul Pritchard, "Fast compact prime number sieves" (among others), ''Journal of Algorithms'' 4 | |||
(1983), 332–344. {{MR|729229}}</ref> | (1983), 332–344. {{MR|729229}}</ref> | ||
बड़े O नोटेशन का उपयोग निरंतर कारकों और ऑफसेट को | |||
बड़े O नोटेशन का उपयोग निरंतर कारकों और ऑफसेट को अप्रत्यक्ष करता है जो व्यावहारिक श्रेणियों के लिए बहुत महत्वपूर्ण हो सकते हैं: एराटोस्थनीज भिन्नता की छलनी जिसे प्रिचर्ड व्हील छलनी के रूप में जाना जाता है<ref name="Pritchard1" /><ref name="Pritchard2" /><ref name="Pritchard3" />एक {{math|''O''(''n'')}} प्रदर्शन होता है, परन्तु इसके मूल कार्यान्वयन के लिए या तो एक बड़े सरणी कलन विधि की आवश्यकता होती है जो इसकी प्रयोग करने योग्य सीमा को उपलब्ध मेमोरी की मात्रा तक सीमित करता है अन्यथा मेमोरी उपयोग को कम करने के लिए इसे पृष्ठ खंडित करने की आवश्यकता होती है। जब स्मृति को बचाने के लिए पृष्ठ विभाजन के साथ कार्यान्वित किया जाता है, तब भी मूल कलन विधि {{math|''O''<big><big>(</big></big>{{sfrac|''n''|log ''n''}}<big><big>)</big></big>}} मेमोरी के बिट्स (एराटोस्थनीज के मूल पृष्ठ खंडित छलनी की आवश्यकता से कहीं अधिक) {{math|''O''<big><big>(</big></big>{{sfrac|{{sqrt|''n''}}|log ''n''}}<big><big>)</big></big>}}स्मृति के बिट्स होते है) आवश्यकता होती है। प्रिचर्ड के काम ने एक बड़े स्थिर कारक की कीमत पर मेमोरी की आवश्यकता को कम कर दिया। यद्यपि परिणामी चक्र छलनी होता है {{math|''O''(''n'')}} प्रदर्शन और एक स्वीकार्य मेमोरी की आवश्यकता होती है, यह व्यावहारिक सिविंग रेंज के लिए एराटोस्थनीज की उचित व्हील फैक्टराइज्ड बेसिक छलनी से उच्च नहीं होता है। | |||
==यूलर की छलनी== | ==यूलर की छलनी== | ||
रीमैन ज़ेटा | रीमैन ज़ेटा फलन के लिए यूलर उत्पाद सूत्र का यूलर का प्रमाण यूलर उत्पाद सूत्र के प्रमाण में एराटोस्थनीज की छलनी का एक संस्करण सम्मलित होता है जिसमें प्रत्येक मिश्रित संख्या को ठीक एक बार हटा दिया जाता है।<ref name="intro" />उसी छलनी को फिर से अन्वेषण किया गया और {{harvtxt|ग्रिज़ | मिश्रा|1978}} द्वारा [[रैखिक समय]] लेने के लिए उसका अवलोकन किया गया।<ref>{{citation | ||
| last1 = Gries | first1 = David | author1-link = David Gries | | last1 = Gries | first1 = David | author1-link = David Gries | ||
| last2 = Misra | first2 = Jayadev | | last2 = Misra | first2 = Jayadev | ||
| Line 121: | Line 125: | ||
| volume = 21| hdl = 1813/6407 | s2cid = 11990373 | url = https://ecommons.cornell.edu/bitstream/1813/6407/1/77-313.pdf | | volume = 21| hdl = 1813/6407 | s2cid = 11990373 | url = https://ecommons.cornell.edu/bitstream/1813/6407/1/77-313.pdf | ||
| hdl-access = free | | hdl-access = free | ||
}}.</ref> यह भी 2 से | }}.</ref> यह भी क्रम 2 से {{mvar|n}} तक की संख्याओं की [[सूची (कंप्यूटिंग)]] से प्रारम्भ होता है। प्रत्येक चरण पर पहले तत्व को अगले अभाज्य के रूप में पहचाना जाता है, सूची के प्रत्येक तत्व के साथ गुणा किया जाता है (इस प्रकार स्वयं से प्रारम्भ होता है), और परिणाम को बाद में हटाने के लिए सूची में चिह्नित किया जाता है। फिर प्रारंभिक तत्व और चिह्नित तत्वों को कार्य क्रम से हटा दिया जाता है, और प्रक्रिया दोहराई जाती है: | ||
<div शैली=फ़ॉन्ट-आकार:85%; > | <div शैली=फ़ॉन्ट-आकार:85%; > | ||
[2] (3) 5 7 <u>9</u> 11 13 <u>15</u> 17 19 <u>21</u> 23 25 <u>27</u> 29 31 <u >33</u> 35 37 <u>39</u> 41 43 <u>45</u> 47 49 <u>51</u> 53 55 <u>57</u> 59 61 <u >63</u> 65 67 <u>69</u> 71 73 <u>75</u> 77 79 ... | [2] (3) 5 7 <u>9</u> 11 13 <u>15</u> 17 19 <u>21</u> 23 25 <u>27</u> 29 31 <u >33</u> 35 37 <u>39</u> 41 43 <u>45</u> 47 49 <u>51</u> 53 55 <u>57</u> 59 61 <u >63</u> 65 67 <u>69</u> 71 73 <u>75</u> 77 79 ... | ||
| Line 130: | Line 134: | ||
</div> | </div> | ||
यहां उदाहरण को कलन विधि के पहले चरण के बाद बाधाओं से प्रारम्भ | यहां उदाहरण को कलन विधि के पहले चरण के बाद बाधाओं से प्रारम्भ करते हुए दिखाया गया है। इस प्रकार, पर {{mvar|k}} वें चरण के शेष प्रत्येक गुणज {{mvar|k}}वें के सभी शेष गुणकों को सूची से हटा दिया जाता है, जिसमें उसके बाद मात्र पहले के {{mvar|k}} अभाज्य (cf. व्हील फ़ैक्टराइज़ेशन) के साथ सहअभाज्य संख्याएँ सम्मलित होंगी, जिससें सूची अगले अभाज्य से प्रारम्भ होगी, और इसके पहले तत्व के वर्ग के नीचे की प्रत्येक संख्याएँ भीअभाज्य होंगी। | ||
इस प्रकार, अभाज्य संख्याओं का एक बंधा हुआ क्रम बनाते समय, जब अगला पहचाना गया अभाज्य ऊपरी सीमा के वर्गमूल से अधिक हो जाता है, तो सूची में शेष प्रत्येक संख्याएँ अभाज्य होती हैं।<ref name="intro" />ऊपर दिए गए उदाहरण में, 11 को अगले अभाज्य के रूप में पहचानने पर यह प्राप्त होता है, जिससे 80 से कम या उसके बराबर प्रत्येक अभाज्य अभाज्यों की एक सूची मिलती है। | इस प्रकार, अभाज्य संख्याओं का एक बंधा हुआ क्रम बनाते समय, जब अगला पहचाना गया अभाज्य ऊपरी सीमा के वर्गमूल से अधिक हो जाता है, तो सूची में शेष प्रत्येक संख्याएँ अभाज्य होती हैं।<ref name="intro" />ऊपर दिए गए उदाहरण में, 11 को अगले अभाज्य के रूप में पहचानने पर यह प्राप्त होता है, जिससे 80 से कम या उसके बराबर प्रत्येक अभाज्य अभाज्यों की एक सूची मिलती है। | ||
ध्यान दें कि जो संख्याएँ किसी चरण द्वारा हटा दी जाएंगी, वे अभी भी उस चरण में गुणजों को चिह्नित करते समय उपयोग की जाती हैं, उदाहरण के लिए, 3 के गुणजों के लिए यह है {{nowrap|1=3 × 3 = 9}}, {{nowrap|1=3 × 5 = 15}}, {{nowrap|1=3 × 7 = 21}}, {{nowrap|1=3 × '''''9''''' = 27}}, ..., {{nowrap|1=3 × '''''15''''' = 45}}, ..., इसलिए इससे | ध्यान दें कि जो संख्याएँ किसी चरण द्वारा हटा दी जाएंगी, वे अभी भी उस चरण में गुणजों को चिह्नित करते समय उपयोग की जाती हैं, उदाहरण के लिए, 3 के गुणजों के लिए यह है {{nowrap|1=3 × 3 = 9}}, {{nowrap|1=3 × 5 = 15}}, {{nowrap|1=3 × 7 = 21}}, {{nowrap|1=3 × '''''9''''' = 27}}, ..., {{nowrap|1=3 × '''''15''''' = 45}}, ..., इसलिए इससे सुलझाने में सावधानी बरतनी चाहिए।<ref name="intro" /> | ||
== यह भी देखें == | == यह भी देखें == | ||
Revision as of 11:10, 11 July 2023
गणित में, एराटोस्थनीज की छलनी (सीव) किसी भी सीमा तक प्रत्येक अभाज्य संख्याओं के अन्वेषण के लिए एक प्राचीन कलन विधि होती है।
यह प्रत्येक अभाज्य के गुणजों को मिश्रित संख्या (अर्थात अभाज्य नहीं) के रूप में चिह्नित करके, पहले अभाज्य संख्या 2 से प्रारम्भ करके करता है। किसी दिए गए अभाज्य के गुणज अंकगणित के साथ, उस अभाज्य से प्रारम्भ होने वाली संख्याओं के अनुक्रम के रूप में उत्पन्न होते हैं। उनके मध्य वह उस अभाज्य के बराबर होती है।[1] प्रत्येक अभाज्य द्वारा विभाज्यता के लिए प्रत्येक उम्मीदवार संख्या का क्रमिक रूप से परीक्षण करने के लिए परीक्षण प्रभाग का उपयोग करने से यह छलनी का मुख्य भिन्नता प्राप्त होती है।[2]एक बार जब प्रत्येक अन्वेषण किये गए अभाज्य के प्रत्येक गुणजों को समग्र के रूप में चिह्नित किया जाता है, तो शेष अचिह्नित संख्याएँ अभाज्य प्राप्त होती हैं।
छलनी का सबसे पहला ज्ञात संदर्भ (Ancient Greek: κόσκινον Ἐρατοσθένους, कोस्किनन एराटोस्थेनस) गेरासा के अंकगणित के परिचय के निकोमैचस में प्रारंभिक 2 शताब्दी में देखने को मिलता है।[3] सीई पुस्तक जो इसका श्रेय साइरीन के एराटोस्थनीज़ को देती है, जो कि तीसरी शताब्दी का था। ईसा पूर्व यूनानी गणितज्ञ, यद्यपि अभाज्य संख्याओं के अतिरिक्त विषम संख्याओं द्वारा छनाई का वर्णन करते थे।[4]
कई अभाज्य संख्याओं की छलनी में प्रत्येक छोटे अभाज्य संख्याओं को अन्वेषण के सबसे प्रभावी विधियों में से एक होता है। इसका उपयोग अंकगणितीय प्रगति में अभाज्य संख्या ज्ञात करने के लिए किया जा सकता है।[5]
अवलोकन
दो को छान लें और तीन को छान लें: एराटोस्थनीज की छलनी। जब गुणज उदात्त, जो संख्याएँ बची हैं वे अभाज्य होती हैं।
अज्ञात [6]
अभाज्य संख्या एक प्राकृतिक संख्या होती है जिसमें दो अलग-अलग प्राकृतिक संख्या विभाजक होते हैं: संख्या 1और स्वयं।
किसी दिए गए पूर्णांक से छोटी या उसके बराबर प्रत्येक अभाज्य संख्याएँ ज्ञात करना n एराटोस्थनीज़ की विधि द्वारा:
- 2 से लेकर लगातार पूर्णांकों की एक सूची बनाएं n: (2, 3, 4, ..., n)।
- प्रारंभ में, मान लीजिए कि p सबसे छोटी अभाज्य संख्या जो 2 के बराबर है।
- 2p से n तक p की वृद्धि में गिनकर p के गुणजों की गणना करें, और उन्हें सूची में चिह्नित करें (ये 2p, 3p, 4p, ... होंगे; p को स्वयं चिह्नित नहीं किया जाना चाहिए)।
- सूची में p से बड़ी वह सबसे छोटी संख्या ज्ञात कीजिए जो अंकित नहीं है। अगर ऐसा कोई नंबर नहीं था तो रुकें. अन्यथा, मान लीजिए p अब इस नई संख्या (जो अगला अभाज्य है) के बराबर है, और चरण 3 से दोहराएँ।
- जब कलन विधि समाप्त हो जाती है, तो सूची में अंकित नहीं की गई शेष संख्याएं n के नीचे दी गई प्रत्येक अभाज्य संख्याएं होती हैं।
यहां मुख्य विचार यह है कि p को दिया गया प्रत्येक मान अभाज्य होगा, क्योंकि यदि यह समग्र होता तो इसे किसी अन्य, छोटे अभाज्य के गुणज के रूप में चिह्नित किया जाता। ध्यान दें कि कुछ संख्याओं को एक से अधिक बार चिह्नित किया जा सकता है (उदाहरण के लिए, 3 और 5 दोनों के लिए 15 को चिह्नित किया जाएगा)।
परिशोधन के रूप में, चरण 3 में p2 से प्रारम्भ करके संख्याओं को चिह्नित करना पर्याप्त होता है, के प्रत्येक छोटे गुणजों के रूप में p उस बिंदु पर पहले ही चिह्नित किया जा चुका होता है। इसका अर्थ यह है कि कलन विधि को चरण 4 में समाप्त करने की अनुमति है जब p2 n से बड़ा होता है।[1]
एक और परिशोधन यह है कि प्रारंभ में मात्र विषम संख्याओं को सूचीबद्ध किया जाए, (3, 5, ..., n), और चरण 3 में 2p की वृद्धि में गिनती की जाए, इस प्रकार मात्र p विषम गुणजों को चिह्नित किया जाता है। यह वास्तव में मूल कलन विधि में दिखाई देता है।[1][4] इसे चक्रीय गुणनखंडन के साथ सामान्यीकृत किया जा सकता है, प्रारंभिक सूची मात्र पहले कुछ अभाज्य संख्याओं के साथ सहअभाज्य संख्याओं से बनाई जाती है, न कि मात्र बाधाओं से (अर्थात्, 2 के साथ सहअभाज्य संख्याएं), और तदनुसार समायोजित वेतन वृद्धि में गिनती की जाती है जिससें मात्र p के ऐसे गुणज उत्पन्न होते हैं जो सर्वप्रथम उन छोटे अभाज्यों के साथ सहअभाज्य होते हैं।[7]
उदाहरण
30 से कम या उसके बराबर प्रत्येक अभाज्य संख्याएँ ज्ञात करने के लिए, निम्नानुसार आगे बढ़ें।
सबसे पहले, 2 से 30 तक पूर्णांकों की एक सूची तैयार करें:
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
सूची में पहला नंबर 2 है; 2 के बाद सूची में प्रत्येक दूसरे नंबर को 2 से 2 की वृद्धि में गिनकर हटा दें (ये सूची में 2 के प्रत्येक गुणज होंगे):
2 3456789101112131415161718192021222324252627282930
सूची में 2 के बाद अगला नंबर 3 है; 3 के बाद सूची में प्रत्येक तीसरे नंबर को 3 की वृद्धि में 3 से गिनकर हटा दें (ये सूची में 3 के प्रत्येक गुणज होंगे):
2 3456789101112131415161718192021222324252627282930
3 के बाद सूची में अभी तक नहीं हटाया गया अगला नंबर 5 है; 5 के बाद सूची में प्रत्येक 5वीं संख्या को 5 की वृद्धि में 5 से गिनकर हटा दें (अर्थात् 5 के प्रत्येक गुणज होंगे):
2 3456789101112131415161718192021222324252627282930
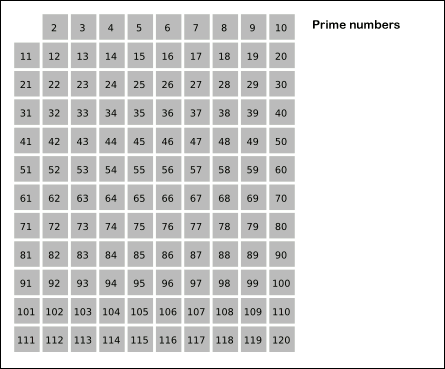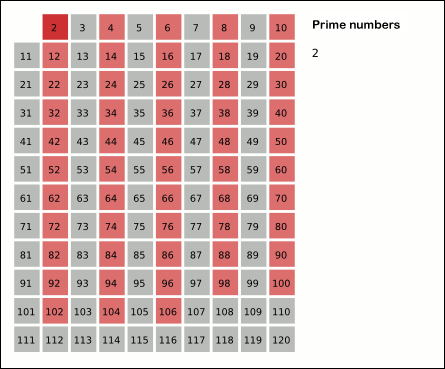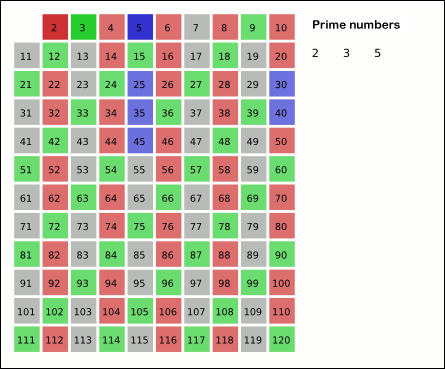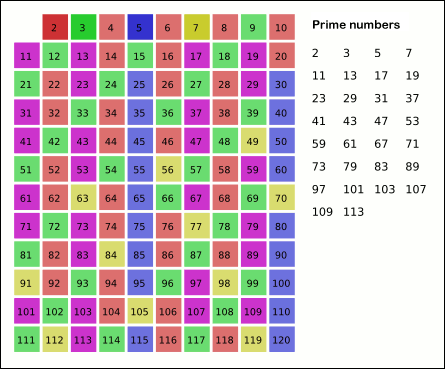
5 के बाद सूची में अभी तक नहीं हटाया गया अगला नंबर 7 है; अगला कदम 7 के बाद सूची में प्रत्येक 7वीं संख्या को हटाना होगा, परन्तु वे प्रत्येक इस बिंदु पर पहले ही हटा दी गए हैं, क्योंकि ये संख्याएं (14, 21, 28) भी छोटी अभाज्य संख्याओं के गुणज हैं क्योंकि 7 × 7 से बड़ा और 30 से अधिक होता है। सूची में इस बिंदु पर जिन संख्याओं को नहीं हटाया गया है वे 30 से नीचे की प्रत्येक अभाज्य संख्याएँ हैं:
2 3 5 7 11 13 17 19 23 29
कलन विधि और प्रकार
स्यूडोकोड
एराटोस्थनीज की छलनी को स्यूडोकोड में इस प्रकार व्यक्त किया जा सकता है:[8][9]
एराटोस्थनीज की कलन विधि छलनी है इनपुट: एक पूर्णांक n > 1. आउटपुट: 2 से n तक की प्रत्येक अभाज्य संख्याएँ। मान लीजिए A बूलियन डेटा प्रकार की एक सरणी है, जो पूर्णांक 2 से n द्वारा अनुक्रमित है, प्रारंभ में प्रत्येक समूह पर सत्य होती हैं। i = 2, 3, 4, ... के लिए, √n से अधिक नहीं होती है यदि A[i] सत्य होताहै j = i2, i2+i, i2+2i, i2+3i, ..., के लिए, n से अधिक नहीं होता है समूह A[j] := असत्य प्रत्येक i को ऐसे लौटाएँ कि A[i] सत्य हो।
यह कलन विधि प्रत्येक अभाज्य संख्याएँ उत्पन्न करता है जो n से बड़ी नहीं होती हैं। इसमें एक सामान्य अनुकूलन सम्मलित होता है, जिसमें i2 प्रत्येक अभाज्य i के गुणजों की गणना प्रारम्भ करना सम्मलित होता है। इस कलन विधि की समय सम्मिश्र O(n log log n) है,[9] परन्तु सरणी अद्यतन एक O(1) ऑपरेशन हो, जैसा कि सामान्यतः होता है।
विच्छिन्न छलनी
जैसा कि सोरेनसन ने वर्णित किया है, एराटोस्थनीज की छलनी के साथ समस्या इसके द्वारा किए जाने वाले ऑपरेशनों की संख्या नहीं है, किन्तु इसकी मेमोरी आवश्यकताएं हैं।[9] बड़े के लिए n, अभाज्य संख्याओं की सीमा स्मृति में स्थित नहीं हो सकती है; इससे भी व्यर्थ, मध्यम n के लिए भी , इसका सीपीयू कैश उपयोग अत्यधिक श्रेष्ट नहीं होता है। कलन विधि संपूर्ण सरणी A से चलता है, संदर्भ का न्यूनाधिक कोई स्थानीयता प्रदर्शित नहीं करता।
इन समस्याओं का समाधान खंडित छलनी द्वारा प्रस्तुत किया जाता है, जहां एक समय में मात्र सीमा के कुछ भागों को ही छलनी किया जाता है।[10] इन्हें 1970 के समय से जाना जाता है और ये इस प्रकार काम करते हैं:[9][11]
- रेंज 2 से n को कुछ आकार के खंडोंΔ ≤ √n में विभाजित करें।
- नियमित छलनी का उपयोग करके, पहले (अर्थात् सबसे निचले) खंड में अभाज्य अन्वेषण करे।
- निम्नलिखित प्रत्येक खंड के लिए, बढ़ते क्रम में, साथ m खंड का सर्वोच्च मान होने के कारण, इसमें अभाज्य संख्याएँ इस प्रकार ज्ञात करें:
- आकार Δ की एक बूलियन सरणी वर्णित करें।
- अब तक पाए गए प्रत्येक अभाज्य p ≤ √m के गुणजों के अनुरूप सरणी में पदों को गैर-अभाज्य के रूप में चिह्नित करें, m - Δ और m के मध्य p के निम्नतम गुणज से प्रारंभ करना करके p के चरणों में इसके गुणजों की गणना करके।
- सरणी में शेष गैर-चिह्नित स्थिति खंड में अभाज्य संख्याओं के अनुरूप हैं। इन अभाज्य अभाज्य संख्याओं के किसी भी गुणज को चिह्नित करना आवश्यक नहीं है, क्योंकि ये प्रत्येक अभाज्य संख्याएँ √m से बड़े है,जैसे की k ≥ 1के लिए, किसी के पास होता है।
यदि Δ को √n चुना जाता है, कलन विधि की स्थान सम्मिश्र O(√n) होती है, जबकि समय सम्मिश्र नियमित छलनी के समान ही होती है।[9]
ऊपरी सीमा वाली श्रेणियों के लिए n इतना बड़ा कि छानने का काम नीचे हो जाता है √n जैसा कि पृष्ठ की आवश्यकता के अनुसार एराटोस्थनीज की खंडित छलनी मेमोरी में स्थित नहीं हो सकती है, इसके स्थान पर सोरेनसन की छलनी जैसी धीमी परन्तु अधिक स्थान-कुशल छलनी का उपयोग किया जा सकता है।[12]
वृद्धिशील छलनी
छलनी का एक वृद्धिशील सूत्रीकरण[2] अभाज्यों की पीढ़ी को उनके गुणजों की पीढ़ी के साथ जोड़कर अनिश्चित काल तक (अर्थात्, ऊपरी सीमा के बिना) अभाज्य संख्याओं को उत्पन्न करता है (जिससें अभाज्यों को गुणजों के मध्य अंतराल में पाया जा सके), जहां प्रत्येक अभाज्य p के गुणज की वृद्धि में अभाज्य के वर्ग p से गिनती करके सीधे (या 2p विषम अभाज्य संख्याओं के लिए) उत्पन्न होते हैं। दक्षता पर प्रतिकूल प्रभाव से बचने के लिए, उत्पादन तभी प्रारम्भ किया जाना चाहिए जब अभाज्य वर्ग पहुंच जाए। इसे डेटाफ्लो प्रोग्रामिंग प्रतिमान के तहत प्रतीकात्मक रूप से व्यक्त किया जा सकता है
अभाज्य संख्याएँ = [2, 3, ...] \ p², p²+p, ...] अभाज्य संख्याओं में p के लिए],
संख्याओं की अंकगणितीय प्रगति का सापेक्ष \ पूरक को निरूपित करते हुए सूची ज्ञान संकेतन का उपयोग करना।
एक समय में एक अभाज्य, अनुक्रमिक अभाज्य द्वारा विभाज्यता परीक्षण के माध्यम से कंपोजिट को पुनरावृत्त रूप से छानकर भी अभाज्य का उत्पादन किया जा सकता है। यह एराटोस्थनीज़ की छलनी नहीं है, परन्तु अधिकांशतः इसके साथ भ्रमित किया जाता है, तथापि एराटोस्थनीज़ की छलनी उनके परीक्षण के अतिरिक्त सीधे समग्र उत्पन्न करती है। परीक्षण प्रभाग में अभाज्य संख्याओं की श्रृंखला उत्पन्न करने में एराटोस्थनीज की छलनी की तुलना में कलन विधि का अत्यधिक व्यर्थ सैद्धांतिक विश्लेषण होता है।[2]
प्रत्येक अभाज्य का परीक्षण करते समय, सर्वश्रेष्ठ परीक्षण विभाजन कलन विधि प्रत्येक अभाज्य संख्याओं का उपयोग करता है जो उसके वर्गमूल से अधिक नहीं होती हैं, जबकि एराटोस्थनीज की छलनी प्रत्येक संमिश्र को मात्र उसके अभाज्य कारकों से उत्पन्न करती है, और समग्र के मध्य अभाज्य संख्याओं को मुफ्त में प्राप्त करती है। डेविड टर्नर (कंप्यूटर वैज्ञानिक) द्वारा व्यापक रूप से ज्ञात 1975 कार्यात्मक प्रोग्रामिंग छलनी कोड[13] इसे अधिकांशतः एराटोस्थनीज़ की छलनी के उदाहरण के रूप में प्रस्तुत किया जाता है[7]परन्तु वास्तव में यह एक उप-सर्वोत्तम परीक्षण प्रभाग छलनी होती है।[2]
कलन विधििक सम्मिश्र
एराटोस्थनीज की छलनी कंप्यूटर के प्रदर्शन को मानदंड करने का एक लोकप्रिय विधि होती है।[14] रैंडम एक्सेस मॉडल में n से नीचे के सभी अभाज्य संख्याओं की गणना करने की समय जटिलता O(n log log n) संचालन होता है, इस तथ्य का प्रत्यक्ष परिणाम है कि अभाज्य हार्मोनिक श्रृंखला स्पर्शोन्मुख रूप log log n से तक पहुंचती है। यघपि, इसमें इनपुट आकार के संबंध में एक घातीय समय सम्मिश्र होता है, जो इसे एक छद्म-बहुपद समय कलन विधि बनाती है। आधारभूत कलन विधि को मेमोरी के O(n) की आवश्यकता होती है। कलन विधि की बिट सम्मिश्र O(n (log n) (log log n)) O(n) की मेमोरी आवश्यकता के साथ बिट संचालन है।[15]
सामान्य रूप से कार्यान्वित पृष्ठ खंडित संस्करण की परिचालन सम्मिश्र O(n log log n) समान होती है गैर-खंडित संस्करण के रूप में, परन्तु खंड पृष्ठ के न्यूनतम आकार के O(√n/log n) साथ-साथ आकार के क्रमिक पृष्ठ खंडों से मिश्रण को निकालने के लिए उपयोग की जाने वाली सीमा के वर्गमूल से कम बेस अभाज्य को संग्रहीत करने के लिए आवश्यक मेमोरी के लिए स्थान आवश्यकताओं को कम कर देता है।
आधारभूत अनुकूलन के साथ एराटोस्थनीज की छलनी का एक विशेष (संभवतः ही कभी, प्रयुक्त किया गया) खंडित संस्करण, O(n) संचालन और O(√nlog log n/log n) मेमोरी के बिट्सड़े का उपयोग करता है।[16][17][18]
बड़े O नोटेशन का उपयोग निरंतर कारकों और ऑफसेट को अप्रत्यक्ष करता है जो व्यावहारिक श्रेणियों के लिए बहुत महत्वपूर्ण हो सकते हैं: एराटोस्थनीज भिन्नता की छलनी जिसे प्रिचर्ड व्हील छलनी के रूप में जाना जाता है[16][17][18]एक O(n) प्रदर्शन होता है, परन्तु इसके मूल कार्यान्वयन के लिए या तो एक बड़े सरणी कलन विधि की आवश्यकता होती है जो इसकी प्रयोग करने योग्य सीमा को उपलब्ध मेमोरी की मात्रा तक सीमित करता है अन्यथा मेमोरी उपयोग को कम करने के लिए इसे पृष्ठ खंडित करने की आवश्यकता होती है। जब स्मृति को बचाने के लिए पृष्ठ विभाजन के साथ कार्यान्वित किया जाता है, तब भी मूल कलन विधि O(n/log n) मेमोरी के बिट्स (एराटोस्थनीज के मूल पृष्ठ खंडित छलनी की आवश्यकता से कहीं अधिक) O(√n/log n)स्मृति के बिट्स होते है) आवश्यकता होती है। प्रिचर्ड के काम ने एक बड़े स्थिर कारक की कीमत पर मेमोरी की आवश्यकता को कम कर दिया। यद्यपि परिणामी चक्र छलनी होता है O(n) प्रदर्शन और एक स्वीकार्य मेमोरी की आवश्यकता होती है, यह व्यावहारिक सिविंग रेंज के लिए एराटोस्थनीज की उचित व्हील फैक्टराइज्ड बेसिक छलनी से उच्च नहीं होता है।
यूलर की छलनी
रीमैन ज़ेटा फलन के लिए यूलर उत्पाद सूत्र का यूलर का प्रमाण यूलर उत्पाद सूत्र के प्रमाण में एराटोस्थनीज की छलनी का एक संस्करण सम्मलित होता है जिसमें प्रत्येक मिश्रित संख्या को ठीक एक बार हटा दिया जाता है।[9]उसी छलनी को फिर से अन्वेषण किया गया और ग्रिज़ & मिश्रा (1978) द्वारा रैखिक समय लेने के लिए उसका अवलोकन किया गया।[19] यह भी क्रम 2 से n तक की संख्याओं की सूची (कंप्यूटिंग) से प्रारम्भ होता है। प्रत्येक चरण पर पहले तत्व को अगले अभाज्य के रूप में पहचाना जाता है, सूची के प्रत्येक तत्व के साथ गुणा किया जाता है (इस प्रकार स्वयं से प्रारम्भ होता है), और परिणाम को बाद में हटाने के लिए सूची में चिह्नित किया जाता है। फिर प्रारंभिक तत्व और चिह्नित तत्वों को कार्य क्रम से हटा दिया जाता है, और प्रक्रिया दोहराई जाती है:
[2] (3) 5 7 9 11 13 15 17 19 21 23 25 27 29 31 33 35 37 39 41 43 45 47 49 51 53 55 57 59 61 63 65 67 69 71 73 75 77 79 ...
[3] (5) 7 11 13 17 19 23 25 29 31 35 37 41 43 47 49 53 55 59 61 65 67 71 73 77 79 ... [4] (7) 11 13 17 19 23 29 31 37 41 43 47 49 53 59 61 67 71 73 77 79... [5] (11) 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 ... [...]
यहां उदाहरण को कलन विधि के पहले चरण के बाद बाधाओं से प्रारम्भ करते हुए दिखाया गया है। इस प्रकार, पर k वें चरण के शेष प्रत्येक गुणज kवें के सभी शेष गुणकों को सूची से हटा दिया जाता है, जिसमें उसके बाद मात्र पहले के k अभाज्य (cf. व्हील फ़ैक्टराइज़ेशन) के साथ सहअभाज्य संख्याएँ सम्मलित होंगी, जिससें सूची अगले अभाज्य से प्रारम्भ होगी, और इसके पहले तत्व के वर्ग के नीचे की प्रत्येक संख्याएँ भीअभाज्य होंगी।
इस प्रकार, अभाज्य संख्याओं का एक बंधा हुआ क्रम बनाते समय, जब अगला पहचाना गया अभाज्य ऊपरी सीमा के वर्गमूल से अधिक हो जाता है, तो सूची में शेष प्रत्येक संख्याएँ अभाज्य होती हैं।[9]ऊपर दिए गए उदाहरण में, 11 को अगले अभाज्य के रूप में पहचानने पर यह प्राप्त होता है, जिससे 80 से कम या उसके बराबर प्रत्येक अभाज्य अभाज्यों की एक सूची मिलती है।
ध्यान दें कि जो संख्याएँ किसी चरण द्वारा हटा दी जाएंगी, वे अभी भी उस चरण में गुणजों को चिह्नित करते समय उपयोग की जाती हैं, उदाहरण के लिए, 3 के गुणजों के लिए यह है 3 × 3 = 9, 3 × 5 = 15, 3 × 7 = 21, 3 × 9 = 27, ..., 3 × 15 = 45, ..., इसलिए इससे सुलझाने में सावधानी बरतनी चाहिए।[9]
यह भी देखें
- प्रिचर्ड की छलनी
- एटकिन की छलनी
- सुन्दरम् की छलनी
- छलनी सिद्धांत
संदर्भ
- ↑ 1.0 1.1 1.2 Horsley, Rev. Samuel, F. R. S., "Κόσκινον Ερατοσθένους or, The Sieve of Eratosthenes. Being an account of his method of finding all the Prime Numbers," Philosophical Transactions (1683–1775), Vol. 62. (1772), pp. 327–347.
- ↑ 2.0 2.1 2.2 2.3 O'Neill, Melissa E., "The Genuine Sieve of Eratosthenes", Journal of Functional Programming, published online by Cambridge University Press 9 October 2008 doi:10.1017/S0956796808007004, pp. 10, 11 (contains two incremental sieves in Haskell: a priority-queue–based one by O'Neill and a list–based, by Richard Bird).
- ↑ Hoche, Richard, ed. (1866), Nicomachi Geraseni Pythagorei Introductionis arithmeticae libri II, chapter XIII, 3, Leipzig: B.G. Teubner, p. 30
- ↑ 4.0 4.1 Nicomachus of Gerasa (1926), Introduction to Arithmetic; translated into English by Martin Luther D'Ooge ; with studies in Greek arithmetic by Frank Egleston Robbins and Louis Charles Karpinski, chapter XIII, 3, New York: The Macmillan Company, p. 204
- ↑ J. C. Morehead, "Extension of the Sieve of Eratosthenes to arithmetical progressions and applications", Annals of Mathematics, Second Series 10:2 (1909), pp. 88–104.
- ↑ Clocksin, William F., Christopher S. Mellish, Programming in Prolog, 1984, p. 170. ISBN 3-540-11046-1.
- ↑ 7.0 7.1 Runciman, Colin (1997). "Functional Pearl: Lazy wheel sieves and spirals of primes" (PDF). Journal of Functional Programming. 7 (2): 219–225. doi:10.1017/S0956796897002670. S2CID 2422563.
- ↑ Sedgewick, Robert (1992). Algorithms in C++. Addison-Wesley. ISBN 978-0-201-51059-1., p. 16.
- ↑ 9.0 9.1 9.2 9.3 9.4 9.5 9.6 9.7 Jonathan Sorenson, An Introduction to Prime Number Sieves, Computer Sciences Technical Report #909, Department of Computer Sciences University of Wisconsin-Madison, January 2, 1990 (the use of optimization of starting from squares, and thus using only the numbers whose square is below the upper limit, is shown).
- ↑ Crandall & Pomerance, Prime Numbers: A Computational Perspective, second edition, Springer: 2005, pp. 121–24.
- ↑ Bays, Carter; Hudson, Richard H. (1977). "The segmented sieve of Eratosthenes and primes in arithmetic progressions to 1012". BIT. 17 (2): 121–127. doi:10.1007/BF01932283. S2CID 122592488.
- ↑ J. Sorenson, "The pseudosquares prime sieve", Proceedings of the 7th International Symposium on Algorithmic Number Theory. (ANTS-VII, 2006).
- ↑ Turner, David A. SASL language manual. Tech. rept. CS/75/1. Department of Computational Science, University of St. Andrews 1975. (
primes = sieve [2..]; sieve (p:nos) = p:sieve (remove (multsof p) nos); remove m = filter (not . m); multsof p n = rem n p==0). But see also Peter Henderson, Morris, James Jr., A Lazy Evaluator, 1976, where we find the following, attributed to P. Quarendon:primeswrt[x;l] = if car[l] mod x=0 then primeswrt[x;cdr[l]] else cons[car[l];primeswrt[x;cdr[l]]] ; primes[l] = cons[car[l];primes[primeswrt[car[l];cdr[l]]]] ; primes[integers[2]]; the priority is unclear. - ↑ Peng, T. A. (Fall 1985). "छलनी के माध्यम से एक मिलियन प्राइम्स". BYTE. pp. 243–244. Retrieved 19 March 2016.
- ↑ Pritchard, Paul, "Linear prime-number sieves: a family tree," Sci. Comput. Programming 9:1 (1987), pp. 17–35.
- ↑ 16.0 16.1 Paul Pritchard, "A sublinear additive sieve for finding prime numbers", Communications of the ACM 24 (1981), 18–23. MR600730
- ↑ 17.0 17.1 Paul Pritchard, Explaining the wheel sieve, Acta Informatica 17 (1982), 477–485. MR685983
- ↑ 18.0 18.1 Paul Pritchard, "Fast compact prime number sieves" (among others), Journal of Algorithms 4 (1983), 332–344. MR729229
- ↑ Gries, David; Misra, Jayadev (December 1978), "A linear sieve algorithm for finding prime numbers" (PDF), Communications of the ACM, 21 (12): 999–1003, doi:10.1145/359657.359660, hdl:1813/6407, S2CID 11990373.
बाहरी संबंध
- primesieve – Very fast highly optimized C/C++ segmented Sieve of Eratosthenes
- Eratosthenes, sieve of at Encyclopaedia of Mathematics
- Interactive JavaScript Page
- Sieve of Eratosthenes by George Beck, Wolfram Demonstrations Project.
- Sieve of Eratosthenes in Haskell
- Sieve of Eratosthenes algorithm illustrated and explained. Java and C++ implementations.
- A related sieve written in x86 assembly language
- Fast optimized highly parallel CUDA segmented Sieve of Eratosthenes in C
- SieveOfEratosthenesInManyProgrammingLanguages c2 wiki page
- The Art of Prime Sieving Sieve of Eratosthenes in C from 1998 with nice features and algorithmic tricks explained.