त्रिकोणीय वितरण: Difference between revisions
(text) |
m (added Category:Vigyan Ready using HotCat) |
||
| Line 164: | Line 164: | ||
[[Category: Machine Translated Page]] | [[Category: Machine Translated Page]] | ||
[[Category:Created On 06/07/2023]] | [[Category:Created On 06/07/2023]] | ||
[[Category:Vigyan Ready]] | |||
Revision as of 17:16, 14 July 2023
|
Probability density function  | |||
|
Cumulative distribution function 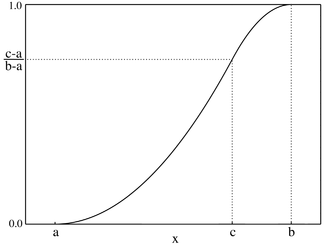 | |||
| Parameters |
| ||
|---|---|---|---|
| Support | |||
| CDF | |||
| Mean | |||
| Median | |||
| Mode | |||
| Variance | |||
| Skewness | |||
| Ex. kurtosis | |||
| Entropy | |||
| MGF | |||
| CF | |||
संभाव्यता सिद्धांत और आंकड़ों में, त्रिकोणीय वितरण निचली सीमा a, ऊपरी सीमा b और प्रणाली c के साथ एक सतत संभाव्यता वितरण है, जहां a < b और a ≤ c ≤ b।
विशेष स्तिथि
सीमा पर प्रणाली
जब c = a या c = b होता है तो वितरण सरल हो जाता है। उदाहरण के लिए, यदि a = 0, b = 1 और c = 1, तो संभाव्यता घनत्व फलन और संचयी वितरण फलन बन जाते हैं:
दो मानक समान चरों के पूर्ण अंतर का वितरण
a = 0, b = 1 और c = 0 के लिए यह वितरण X = |X1 - X2| का वितरण है, जहां X1, X2 मानक समान वितरण के साथ दो स्वतंत्र यादृच्छिक चर हैं।
सममित त्रिकोणीय वितरण
सममित स्थिति तब उत्पन्न होती है जब c = (a + b) / 2 होता है। इस स्तिथि में, वितरण फलन का एक वैकल्पिक रूप है:
दो मानक समान चरों के माध्य का वितरण
a = 0, b = 1 और c = 0.5 के लिए यह वितरण - प्रणाली (यानी, शिखर) अंतराल के ठीक बीच में है - दो मानक समान चर के माध्य के वितरण से मेल खाता है, अर्थात वितरण X = (X1 + X2) / 2, जहां X1, X2 [0,1] में मानक समान वितरण (निरंतर) के साथ दो स्वतंत्र यादृच्छिक चर हैं। [1] यह दो चरों के लिए बेट्स वितरण की स्तिथि है।
त्रिकोणीय-वितरित यादृच्छिक चर उत्पन्न करना
अंतराल (0,1) में समान वितरण (निरंतर) से निकाला गया एक यादृच्छिक चर U दिया गया है, तो चर
जहाँ , मापदंडों के साथ एक त्रिकोणीय वितरण और है। इसे संचयी वितरण फलन से प्राप्त किया जा सकता है।
वितरण का उपयोग
त्रिकोणीय वितरण का उपयोग सामान्यतः जनसंख्या के व्यक्तिपरक विवरण के रूप में किया जाता है जिसके लिए केवल सीमित प्रतिरूप डेटा होता है, और विशेष रूप से ऐसी स्तिथि में जहां चर के बीच संबंध ज्ञात होता है लेकिन डेटा दुर्लभ होता है (संभवतः संग्रह की उच्च लागत के कारण)।
यह न्यूनतम और अधिकतम के ज्ञान और एक प्रेरित अनुमान पर प्रणालील मान के संबंध में आधारित है। [3] इन्हीं कारणों से त्रिकोण वितरण को ज्ञान वितरण का अभाव कहा गया है।
व्यावसायिक अनुकरण
इसलिए त्रिकोणीय वितरण का उपयोग प्रायः विशेषकर अनुकरण में व्यावसायिक निर्णय लेने में किया जाता है। सामान्यतः, जब किसी परिणाम के संभाव्यता वितरण (जैसे, केवल इसके सबसे छोटे और सबसे बड़े मान) के बारे में बहुत कुछ ज्ञात नहीं होता है, तो समान वितरण (निरंतर) का उपयोग करना संभव है। लेकिन यदि सबसे संभावित परिणाम भी ज्ञात है, तो परिणाम को त्रिकोणीय वितरण द्वारा अनुकरण किया जा सकता है। उदाहरण के लिए कॉर्पोरेट वित्त के अंतर्गत देखें।
परियोजना प्रबंधन
त्रिकोणीय वितरण, पीईआरटी वितरण के साथ, न्यूनतम और अधिकतम मूल्य द्वारा परिभाषित अंतराल के भीतर होने वाली घटनाओं को प्रतिरूप करने के लिए परियोजना प्रबंधन (पीईआरटी में निविष्ट और इसलिए महत्वपूर्ण पथ विधि (सीपीएम) के रूप में) में भी व्यापक रूप से उपयोग किया जाता है।
श्रव्य डिथरिंग
सममित त्रिकोणीय वितरण सामान्यतः डिथर में उपयोग किया जाता है, जहां इसे टीपीडीएफ (त्रिकोणीय संभाव्यता घनत्व फलन) कहा जाता है।
धरणी निर्माण
त्रिकोणीय वितरण का अनुप्रयोग धरणी निर्माण और प्रतिरूप संश्लेषण में होता है। [4][5]
यह भी देखें
- समलंबी वितरण
- थॉमस सिम्पसन
- तीन-बिंदु अनुमान
- पांच-संख्या सारांश
- सात-संख्या सारांश
- त्रिकोणीय कार्य
- केंद्रीय सीमा प्रमेय - त्रिकोण वितरण प्रायः दो समान यादृच्छिक चर को एक साथ जोड़ने के परिणामस्वरूप होता है। दूसरे शब्दों में, त्रिकोण वितरण प्रायः (हमेशा नहीं) केंद्रीय सीमा प्रमेय योग प्रक्रिया के पहले पुनरावृत्ति का परिणाम होता है (यानी) )। इस अर्थ में, त्रिभुज वितरण कभी-कभी स्वाभाविक रूप से हो सकता है। यदि अधिक यादृच्छिक चरों को एक साथ जोड़ने की यह प्रक्रिया जारी रहती है (अर्थात ), तो वितरण तेजी से घंटी के आकार का हो जाएगा।
- इरविन-हॉल वितरण - इरविन-हॉल वितरण का उपयोग करना त्रिकोण वितरण उत्पन्न करने का एक आसान तरीका है।
- बेट्स वितरण - इरविन-हॉल वितरण के समान, लेकिन मानों को 0 से 1 की सीमा में वापस लाया गया। एक त्रिभुज वितरण की गणना के लिए उपयोगी जिसे बाद में 0 से 1 सीमा के बाहर अन्य त्रिभुज वितरण बनाने के लिए पुन: मापक्रम और स्थानांतरित किया जा सकता है।
संदर्भ
- ↑ Beyond Beta: Other Continuous Families of Distributions with Bounded Support and Applications. Samuel Kotz and Johan René van Dorp. https://books.google.com/books?id=JO7ICgAAQBAJ&dq=chapter%201%20dig%20out%20suitable%20substitutes%20of%20the%20beta%20distribution%20one%20of%20our%20goals&pg=PA3
- ↑ "संग्रहीत प्रति" (PDF). www.asianscientist.com. Archived from the original (PDF) on 7 April 2014. Retrieved 12 January 2022.
- ↑ "संग्रहीत प्रति" (PDF). Archived from the original (PDF) on 2006-09-23. Retrieved 2006-09-23.
- ↑ Ma, Nam Nicholas; Buchanan, Kristopher; Jensen, Jeffrey; Huff, Gregory (2015). "Distributed beamforming from triangular planar random antenna arrays". MILCOM 2015 - 2015 IEEE Military Communications Conference. pp. 553–558. doi:10.1109/MILCOM.2015.7357501. ISBN 978-1-5090-0073-9. S2CID 3027268.
- ↑ K. Buchanan, C. Flores-Molina, S. Wheeland, D. Overturf and T. Adeyemi, "Babinet's Principle Applied to Distributed Arrays," 2020 International Applied Computational Electromagnetics Society Symposium (ACES), 2020, pp. 1-2, doi: 10.23919/ACES49320.2020.9196157.
बाहरी संबंध
- Weisstein, Eric W. वितरण.html "त्रिकोणीय वितरण". MathWorld.
{{cite web}}: Check|url=value (help) - त्रिकोणीय वितरण, decisionsciences.org
- त्रिकोणीय वितरण, brighton-webs.co.uk
- त्रिकोणीय वितरण के विचरण के लिए प्रमाण, math.stackexchange.com