एल्गोरिथम अनुमान: Difference between revisions
No edit summary |
No edit summary |
||
| Line 5: | Line 5: | ||
== क्लासिक समाधान == | == क्लासिक समाधान == | ||
फिशर ने बेयस के [[पश्च वितरण]], रचनात्मक संभाव्यता और नेमैन के आत्मविश्वास अंतराल जैसी समान धारणाओं की तुलना में पैरामीटर वितरण की | फिशर ने बेयस के [[पश्च वितरण]], रचनात्मक संभाव्यता और नेमैन के आत्मविश्वास अंतराल जैसी समान धारणाओं की तुलना में पैरामीटर वितरण की धारणा के अंतर और श्रेष्ठता की रक्षा के लिए जटिल संघर्ष किया। अर्ध दशक तक, नेमैन के [[विश्वास अंतराल|आत्मविश्वास]] के अंतराल ने सभी व्यावहारिक उद्देश्यों के लिए विजय प्राप्त की, जिसका श्रेय संभाव्यता की घटनात्मक प्रकृति को दिया गया। इस परिप्रेक्ष्य के साथ, जब आप गाऊसी चर का निवारण करते हैं, तो इसका माध्य μ द्वारा देखी जा रही घटना की भौतिक विशेषताओं द्वारा तय किया जाता है, जहां अवलोकन यादृच्छिक संचालन होते हैं, इसलिए देखे गए मान यादृच्छिक प्रारूप के विनिर्देश होते हैं। उनकी यादृच्छिकता के कारण, निश्चित μ वाले प्रारूप विशिष्ट अंतरालों से निश्चित संभावना के साथ गणना कर सकते हैं कि आप आत्मविश्वास को दर्शाते हैं। | ||
=== उदाहरण === | === उदाहरण === | ||
| Line 29: | Line 29: | ||
प्रारूप के द्वारा से पूर्ण विवाद मुर्गी-अंडे की अनिश्चय के जैसे दिखता है: या तो पूर्व डेटा द्वारा निश्चित डेटा और परिणाम के रूप में उनके गुणों का संभाव्यता वितरण, या पूर्व द्वारा निश्चित गुण और परिणाम के रूप में देखे गए डेटा का संभाव्यता वितरण है। क्लासिक समाधान में गुण और अवगुण है। पूर्व की सराहना विशेष रूप से तब की गई जब लोग अभी भी शीट और पेंसिल से गणना करते थे। वास्तव में, निश्चित पैरामीटर θ के लिए नेमैन विश्वास अंतराल की गणना करने का कार्य कठिन है: आप θ नहीं जानते हैं, किंतु आप इसके चारों ओर अंतराल का निवारण करना चाहते हैं जिसमें विफलता की संभवतः अधिक कम संभावना है। अधिक सीमित संख्या में सैद्धांतिक स्थितियों के लिए विश्लेषणात्मक समाधान की अनुमति है। इसके विपरीत, गाऊसी वितरण के निकट विश्वास अंतराल के संदर्भ में [[केंद्रीय सीमा प्रमेय]] के माध्यम से बड़ी संख्या में उदाहरणों को अनुमानित विधिपूर्वक शीघ्रता से समाधान किया जा सकता है- यही लाभ है। दोष यह है कि केंद्रीय सीमा प्रमेय तब प्रारंभ होता है जब प्रारूप आकार पर्याप्त रूप से बड़ा होता है। इसलिए, यह आधुनिक अनुमान उदाहरणों में सम्मिलित प्रारूप के साथ कम और कम प्रारंभ होता है। त्रुटिपूर्ण अपनी ओर से प्रारूप आकार में नहीं है अन्यथा, अनुमान समस्या की [[जटिलता]] के कारण यह आकार पर्याप्त रूप से बड़ा नहीं है। | प्रारूप के द्वारा से पूर्ण विवाद मुर्गी-अंडे की अनिश्चय के जैसे दिखता है: या तो पूर्व डेटा द्वारा निश्चित डेटा और परिणाम के रूप में उनके गुणों का संभाव्यता वितरण, या पूर्व द्वारा निश्चित गुण और परिणाम के रूप में देखे गए डेटा का संभाव्यता वितरण है। क्लासिक समाधान में गुण और अवगुण है। पूर्व की सराहना विशेष रूप से तब की गई जब लोग अभी भी शीट और पेंसिल से गणना करते थे। वास्तव में, निश्चित पैरामीटर θ के लिए नेमैन विश्वास अंतराल की गणना करने का कार्य कठिन है: आप θ नहीं जानते हैं, किंतु आप इसके चारों ओर अंतराल का निवारण करना चाहते हैं जिसमें विफलता की संभवतः अधिक कम संभावना है। अधिक सीमित संख्या में सैद्धांतिक स्थितियों के लिए विश्लेषणात्मक समाधान की अनुमति है। इसके विपरीत, गाऊसी वितरण के निकट विश्वास अंतराल के संदर्भ में [[केंद्रीय सीमा प्रमेय]] के माध्यम से बड़ी संख्या में उदाहरणों को अनुमानित विधिपूर्वक शीघ्रता से समाधान किया जा सकता है- यही लाभ है। दोष यह है कि केंद्रीय सीमा प्रमेय तब प्रारंभ होता है जब प्रारूप आकार पर्याप्त रूप से बड़ा होता है। इसलिए, यह आधुनिक अनुमान उदाहरणों में सम्मिलित प्रारूप के साथ कम और कम प्रारंभ होता है। त्रुटिपूर्ण अपनी ओर से प्रारूप आकार में नहीं है अन्यथा, अनुमान समस्या की [[जटिलता]] के कारण यह आकार पर्याप्त रूप से बड़ा नहीं है। | ||
बड़ी कंप्यूटिंग सुविधाओं की उपलब्धता के साथ, वैज्ञानिकों ने पृथक पैरामीटर के अनुमान से जटिल कार्यों के अनुमान पर फिर से ध्यान केंद्रित किया, अर्थात कार्यों की पहचान करने वाले अत्यधिक नेस्टेड पैरामीटर के समुच्चय इन स्थितियों में अत्यधिक जानकारीपूर्ण प्रारूपों के आधार पर कार्यों को सीखने ([[प्रतिगमन विश्लेषण]], [[न्यूरो फजी]] प्रणाली या कम्प्यूटेशनल सीखने सिद्धांत के संदर्भ में) के बारे में विचार करते हैं। डेटा को जोड़ने वाली जटिल संरचना होने का प्रथम प्रभाव स्वप्रणालीता की प्रारूप डिग्री (सांख्यिकी) की संख्या में कमी है, अर्थात प्रारूप बिंदुओं के भाग का जलना, जिससे केंद्रीय सीमा प्रमेय में विचार किया जाने वाला प्रभावी प्रारूप आकार अधिक छोटा हो। किसी दिए गए [[आत्मविश्वास स्तर]] के साथ सीमित सीखने की त्रुटि सुनिश्चित करने वाले प्रारूप आकार पर ध्यान केंद्रित करने का परिणाम यह होता है कि इस आकार की निचली सीमा [[जटिलता सूचकांक]] जैसे कि [[वीसी आयाम]] या उस वर्ग के विवरण के साथ बढ़ती है, जिससे हम जिस | बड़ी कंप्यूटिंग सुविधाओं की उपलब्धता के साथ, वैज्ञानिकों ने पृथक पैरामीटर के अनुमान से जटिल कार्यों के अनुमान पर फिर से ध्यान केंद्रित किया, अर्थात कार्यों की पहचान करने वाले अत्यधिक नेस्टेड पैरामीटर के समुच्चय इन स्थितियों में अत्यधिक जानकारीपूर्ण प्रारूपों के आधार पर कार्यों को सीखने ([[प्रतिगमन विश्लेषण]], [[न्यूरो फजी]] प्रणाली या कम्प्यूटेशनल सीखने सिद्धांत के संदर्भ में) के बारे में विचार करते हैं। डेटा को जोड़ने वाली जटिल संरचना होने का प्रथम प्रभाव स्वप्रणालीता की प्रारूप डिग्री (सांख्यिकी) की संख्या में कमी है, अर्थात प्रारूप बिंदुओं के भाग का जलना, जिससे केंद्रीय सीमा प्रमेय में विचार किया जाने वाला प्रभावी प्रारूप आकार अधिक छोटा हो। किसी दिए गए [[आत्मविश्वास स्तर]] के साथ सीमित सीखने की त्रुटि सुनिश्चित करने वाले प्रारूप आकार पर ध्यान केंद्रित करने का परिणाम यह होता है कि इस आकार की निचली सीमा [[जटिलता सूचकांक]] जैसे कि [[वीसी आयाम]] या उस वर्ग के विवरण के साथ बढ़ती है, जिससे हम जिस कार्य को सीखना चाहते हैं वह संबंधित है। | ||
=== उदाहरण === | === उदाहरण === | ||
1,000 स्वप्रणाली बिट्स का प्रारूप कम से कम 0.99 के विश्वास के साथ अंतर्निहित बर्नौली चर के पैरामीटर p के अनुमान पर अधिकतम 0.081 की पूर्ण त्रुटि सुनिश्चित करने के लिए पर्याप्त है। समान आकार 0.99 के समान आत्मविश्वास के साथ 0.088 से कम की सीमा | 1,000 स्वप्रणाली बिट्स का प्रारूप कम से कम 0.99 के विश्वास के साथ अंतर्निहित बर्नौली चर के पैरामीटर p के अनुमान पर अधिकतम 0.081 की पूर्ण त्रुटि सुनिश्चित करने के लिए पर्याप्त है। समान आकार 0.99 के समान आत्मविश्वास के साथ 0.088 से कम की सीमा का आश्वासन नहीं दे सकता है, जब त्रुटि की पहचान इस संभावना के साथ की जाती है कि न्यूयॉर्क में रहने वाला 20 वर्षीय व्यक्ति 1,000 बड़ी देखी गई ऊंचाई, भार और कमर की सीमा में फिट नहीं बैठता है। एप्पल निवासी त्रुटिहीनता की कमी इसलिए होती है क्योंकि वीसी आयाम और समानांतर चतुर्भुज के वर्ग का विवरण, जिनमें से 1,000 निवासियों की श्रेणियों में से देखा गया है, दोनों 6 के समान हैं। | ||
== फिशर प्रश्न का समाधान करने वाली सामान्य व्युत्क्रम समस्या == | == फिशर प्रश्न का समाधान करने वाली सामान्य व्युत्क्रम समस्या == | ||
अपर्याप्त रूप से बड़े प्रारूपों के साथ, दृष्टिकोण: निश्चित प्रारूप - यादृच्छिक गुण तीन चरणों में अनुमान प्रक्रियाओं का विचार देते हैं: | अपर्याप्त रूप से बड़े प्रारूपों के साथ, दृष्टिकोण: निश्चित प्रारूप - यादृच्छिक गुण तीन चरणों में अनुमान प्रक्रियाओं का विचार देते हैं: | ||
| Line 54: | Line 54: | ||
:<math>s= \rho(\boldsymbol\theta;z_1,\ldots,z_m)</math>. | :<math>s= \rho(\boldsymbol\theta;z_1,\ldots,z_m)</math>. | ||
इन संबंधों के साथ हम उन पैरामीटर के मानों का निरीक्षण कर सकते हैं जो प्रारूप के सीड का प्रतिनिधित्व करने वाले सीड की विशेष | इन संबंधों के साथ हम उन पैरामीटर के मानों का निरीक्षण कर सकते हैं जो प्रारूप के सीड का प्रतिनिधित्व करने वाले सीड की विशेष समुच्चय से देखे गए सांख्यिकी के साथ प्रारूप उत्पन्न कर सकते थे। इसलिए, प्रारूप सीड की जनसंख्या पैरामीटर की जनसंख्या से संग्युमित होती है। इस जनसंख्या के स्वच्छ गुणों को सुनिश्चित करने के लिए, सीड मानों को यादृच्छिक रूप से निकालना और या तो [[पर्याप्त आँकड़े|पर्याप्त सांख्यिकी]] या, उत्तम आँकड़े सम्मिलित करना पर्याप्त है। मास्टर समीकरणों में पैरामीटर है। | ||
उदाहरण के लिए, | उदाहरण के लिए, सांख्यिकी <math>s_1=\sum_{i=1}^m \log x_i</math> और <math>s_2=\min_{i=1,\ldots,m} \{x_i\}</math> पेरेटो यादृच्छिक चर X के पैरामीटर a और k के लिए पर्याप्त सिद्ध होता है। | ||
प्रारूपकरण प्रणाली (के समतुल्य रूप) के लिए <math>g_{(a,k)}</math> हम उन्हें इस प्रकार पढ़ सकते हैं: | प्रारूपकरण प्रणाली (के समतुल्य रूप) के लिए <math>g_{(a,k)}</math> हम उन्हें इस प्रकार पढ़ सकते हैं: | ||
| Line 72: | Line 72: | ||
:<math> k=\mathrm e^{\frac{ a s_1-\sum\log u_i}{m a}}</math> | :<math> k=\mathrm e^{\frac{ a s_1-\sum\log u_i}{m a}}</math> | ||
जहाँ <math>s_1</math> और <math>s_2</math> देखे गए | जहाँ <math>s_1</math> और <math>s_2</math> देखे गए सांख्यिकी हैं और <math>u_1,\ldots,u_m</math> एकसमान सीड का समुच्चय सीड को प्रभावित करने वाली संभाव्यता (घनत्व) को पैरामीटर में स्थानांतरित करके, स्वयं द्वारा देखे गए सांख्यिकी के साथ संगत यादृच्छिक पैरामीटर ''A'' और ''K'' का वितरण नियम प्राप्त किया जा सकता है। | ||
|} | |} | ||
अनुकूलता संगत आपश्चाती के पैरामीटर को दर्शाती है, अर्थात ऐसी आपश्चाती जो देखे गए सांख्यिकी को उत्पन्न करते हुए प्रारूप उत्पन्न कर सकती थी। इस धारणा को इस प्रकार औपचारिक रूप दे सकते हैं: | अनुकूलता संगत आपश्चाती के पैरामीटर को दर्शाती है, अर्थात ऐसी आपश्चाती जो देखे गए सांख्यिकी को उत्पन्न करते हुए प्रारूप उत्पन्न कर सकती थी। इस धारणा को इस प्रकार औपचारिक रूप दे सकते हैं: | ||
| Line 78: | Line 78: | ||
===परिभाषा=== | ===परिभाषा=== | ||
यादृच्छिक चर और उससे निकाले गए प्रारूप के लिए संगत वितरण समान प्रारूप प्रणाली वाला वितरण <math>\mathcal M_X=(Z,g_{\boldsymbol\theta})</math> है मान के साथ X का <math>\boldsymbol\theta</math> यादृच्छिक पैरामीटर का <math>\mathbf\Theta</math> उत्तम व्यवहार वाले सांख्यिकी पर मास्टर समीकरण | यादृच्छिक चर और उससे निकाले गए प्रारूप के लिए संगत वितरण समान प्रारूप प्रणाली वाला वितरण <math>\mathcal M_X=(Z,g_{\boldsymbol\theta})</math> है मान के साथ X का <math>\boldsymbol\theta</math> यादृच्छिक पैरामीटर का <math>\mathbf\Theta</math> उत्तम व्यवहार वाले सांख्यिकी पर मास्टर समीकरण के आधार से प्राप्त किया गया। | ||
=== उदाहरण === | === उदाहरण === | ||
[[Image:Parecdf.png|frame|left|पैरामीटर का संयुक्त अनुभवजन्य संचयी वितरण | [[Image:Parecdf.png|frame|left|पैरामीटर का संयुक्त अनुभवजन्य संचयी वितरण फलन <math>(A,K)</math> पेरेटो यादृच्छिक चर है।]][[Image:Mucdf.png|frame|right|गाऊसी यादृच्छिक चर के माध्य M का संचयी वितरण फलन]]आप जनसंख्या बूटस्ट्रैप विधि के कार्यान्वयन उदाहरण के रूप में पेरेटो पैरामीटर A और K के वितरण नियम बाईं ओर के चित्र में पा सकते हैं। | ||
ट्विस्टिंग तर्क विधि को प्रारंभ करने से, वितरण नियम <math>F_M(\mu)</math> प्राप्त होता है सांख्यिकी के आधार पर गाऊसी चर X के माध्य M का <math>s_M=\sum_{i=1}^m x_i</math> जब <math>\Sigma^2</math> के समान माना जाता है <math>\sigma^2</math> {{harv|अपोलोनी|मालचिओडी|गैटो|2006}} इसकी अभिव्यक्ति है: | ट्विस्टिंग तर्क विधि को प्रारंभ करने से, वितरण नियम <math>F_M(\mu)</math> प्राप्त होता है सांख्यिकी के आधार पर गाऊसी चर X के माध्य M का <math>s_M=\sum_{i=1}^m x_i</math> जब <math>\Sigma^2</math> के समान माना जाता है <math>\sigma^2</math> {{harv|अपोलोनी|मालचिओडी|गैटो|2006}} इसकी अभिव्यक्ति है: | ||
| Line 88: | Line 88: | ||
दाहिनी ओर चित्र में दिखाया गया है, जहाँ <math>\Phi</math> [[मानक सामान्य वितरण]] का संचयी वितरण फलन है। | दाहिनी ओर चित्र में दिखाया गया है, जहाँ <math>\Phi</math> [[मानक सामान्य वितरण]] का संचयी वितरण फलन है। | ||
[[Image:Muconfint.png|frame|left|निश्चित के लिए गॉसियन यादृच्छिक चर के माध्य | [[Image:Muconfint.png|frame|left|निश्चित के लिए गॉसियन यादृच्छिक चर के माध्य M के 90% विश्वास अंतराल के ऊपरी (बैंगनी वक्र) और निचले (नीले वक्र) शीर्ष <math>\sigma</math> और सांख्यिकी ''s<sub>m</sub>'' के विभिन्न मान है ]]इसके वितरण फलन को देखते हुए M के लिए [[विश्वास अंतराल]] की गणना करना सरल है: हमें केवल दो मात्राओं का परिक्षण करना आवश्यक है (उदाहरण के लिए) <math>\delta/2</math> और <math>1-\delta/2</math> मात्राएँ (यदि हम टेल की संभावनाओं में सममित स्तर δ के विश्वास अंतराल में रुचि रखते हैं) जैसा कि सांख्यिकी में बाईं ओर दर्शाया गया है, जो सांख्यिकी S<sub>''m''</sub> के विभिन्न मानों के लिए दो सीमाओं के व्यवहार को दर्शाता है। | ||
फिशर के दृष्टिकोण की अकिलीज़ हील से अधिक पैरामीटर के संयुक्त वितरण में निहित है, जैसे कि गाऊसी वितरण का माध्य और विचरण है। इसके विपरीत, अंतिम दृष्टिकोण (और उपर्युक्त विधियों: जनसंख्या बूटस्ट्रैप और ट्विस्टिंग तर्क) के साथ हम कई पैरामीटर का संयुक्त वितरण सीख सकते हैं। उदाहरण के लिए, दो या कई अधिक पैरामीटर के वितरण पर ध्यान केंद्रित करते हुए, नीचे दिए गए सांख्यिकी में हम दो आत्मविश्वास क्षेत्रों की रिपोर्ट करते हैं जहां सीखा जाने वाला कार्य 90% के आत्मविश्वास के साथ आता है। पूर्व उस संभावना से संबंधित है जिसके साथ विस्तारित [[समर्थन वेक्टर यंत्र|समर्थन वेक्टर मशीन]] बाइनरी लेबल 1 को बिंदुओं पर प्रदर्शित करती है <math>(x,y)</math> समतल दो सतहों को विशिष्ट वितरण नियम के अनुसार लेबल किए गए प्रारूप बिंदुओं के समुच्चय के आधार पर तैयार किया जाता है {{harv|अपोलोनी|बैसिस|मालचिओडी |विटोल्ड|2008}} से गणना की गई स्तन कैंसर की पुनरावृत्ति संकट दर के विश्वास क्षेत्र से संबंधित है। {{harv|अपोलोनी|मालचिओडी|गेटो|2006}} | फिशर के दृष्टिकोण की अकिलीज़ हील से अधिक पैरामीटर के संयुक्त वितरण में निहित है, जैसे कि गाऊसी वितरण का माध्य और विचरण है। इसके विपरीत, अंतिम दृष्टिकोण (और उपर्युक्त विधियों: जनसंख्या बूटस्ट्रैप और ट्विस्टिंग तर्क) के साथ हम कई पैरामीटर का संयुक्त वितरण सीख सकते हैं। उदाहरण के लिए, दो या कई अधिक पैरामीटर के वितरण पर ध्यान केंद्रित करते हुए, नीचे दिए गए सांख्यिकी में हम दो आत्मविश्वास क्षेत्रों की रिपोर्ट करते हैं जहां सीखा जाने वाला कार्य 90% के आत्मविश्वास के साथ आता है। पूर्व उस संभावना से संबंधित है जिसके साथ विस्तारित [[समर्थन वेक्टर यंत्र|समर्थन वेक्टर मशीन]] बाइनरी लेबल 1 को बिंदुओं पर प्रदर्शित करती है <math>(x,y)</math> समतल दो सतहों को विशिष्ट वितरण नियम के अनुसार लेबल किए गए प्रारूप बिंदुओं के समुच्चय के आधार पर तैयार किया जाता है {{harv|अपोलोनी|बैसिस|मालचिओडी |विटोल्ड|2008}} से गणना की गई स्तन कैंसर की पुनरावृत्ति संकट दर के विश्वास क्षेत्र से संबंधित है। {{harv|अपोलोनी|मालचिओडी|गेटो|2006}} | ||
{| | {| | ||
| [[Image:Svmconf.png|frame|90% | | [[Image:Svmconf.png|frame|समर्थन वेक्टर मशीनों के सदस्यता के लिए 90% आत्मविश्वास क्षेत्र हाइपरबोलिक स्पर्शरेखा प्रोफ़ाइल फलन से संपन्न है]] | ||
| [[Image:Hazardconf.png|frame|90% | | [[Image:Hazardconf.png|frame|सेंसर किए गए प्रारूप से स्तन कैंसर की पुनरावृत्ति के संकट के फलन के लिए 90% विश्वास क्षेत्र की गणना की गई<math>t=(9, 13, > 13, 18, 12, 23, 31, 34, > 45, 48, > 161),\, </math>>''t'' के साथ सेंसर किए गए समय को दर्शाता है]] | ||
|} | |} | ||
Revision as of 19:11, 13 July 2023
एल्गोरिथम अनुमान किसी भी डेटा विश्लेषक के लिए व्यापक रूप से उपलब्ध बलपूर्वक कंप्यूटिंग उपकरणों द्वारा संभव बनाए गए सांख्यिकीय अनुमान विधियों में नए विकास को एकत्र करता है। इस क्षेत्र में आधारशिला कम्प्यूटेशनल शिक्षण सिद्धांत, ग्रैन्युलर कंप्यूटिंग, जैव सूचना विज्ञान, और अधिक पूर्व, संरचनात्मक संभाव्यता (फ्रेजर 1966) हैं। मुख्य फोकस एल्गोरिदम पर है जो यादृच्छिक घटना के अध्ययन को आधार बनाने वाले सांख्यिकी की गणना करता है, साथ ही विश्वसनीय परिणाम देने के लिए उन्हें डेटा की मात्रा भी देनी होती है। यह गणितज्ञों की रुचि को संभाव्यता वितरण के अध्ययन से सांख्यिकी के कार्यात्मक गुणों में स्थानांतरित कर देता है, और कंप्यूटर वैज्ञानिकों की रुचि डेटा को संसाधित करने के लिए एल्गोरिदम से उनके द्वारा संसाधित की जाने वाली जानकारी की ओर स्थानांतरित कर देता है।
फिशर पैरामीट्रिक अनुमान समस्या
वितरण नियम के पैरामीटर की पहचान के संबंध में, परिपक्व पाठक 20वीं दशक के मध्य में प्रत्ययी वितरण (फिशर 1956) संरचनात्मक संभावनाएँ (फ्रेजर 1966), पूर्व/पश्च (रैमसे 1925), के संदर्भ में उनकी परिवर्तनशीलता की व्याख्या के बारे में लंबे अध्ययनो को याद कर सकते हैं। ज्ञानमीमांसीय दृष्टिकोण से, इसमें संभाव्यता की प्रकृति के संबंध में साथी विवाद सम्मिलित है: क्या यह घटना की भौतिक विशेषता है जिसे यादृच्छिक चर के माध्यम से वर्णित किया जाना है या किसी घटना के बारे में डेटा को संश्लेषित करने की विधि है? पश्चात वाले का चयन करते हुए, फिशर किसी दिए गए यादृच्छिक चर के पैरामीटर के प्रत्ययी वितरण नियम को परिभाषित करता है जिसे वह इसके विनिर्देशों के प्रारूपों से प्राप्त करते है। इस नियम के साथ वह गणना करता है, उदाहरण के लिए "संभावना है कि μ (गाऊसी चर का तात्पर्य- ओमूर नोट) किसी निर्दिष्ट मान से कम है, या संभावना है कि यह किसी निर्दिष्ट मान के मध्य स्थित है, या, संक्षेप में, इसकी संभावना वितरण, देखे गए प्रारूप के आलोक में" है।
क्लासिक समाधान
फिशर ने बेयस के पश्च वितरण, रचनात्मक संभाव्यता और नेमैन के आत्मविश्वास अंतराल जैसी समान धारणाओं की तुलना में पैरामीटर वितरण की धारणा के अंतर और श्रेष्ठता की रक्षा के लिए जटिल संघर्ष किया। अर्ध दशक तक, नेमैन के आत्मविश्वास के अंतराल ने सभी व्यावहारिक उद्देश्यों के लिए विजय प्राप्त की, जिसका श्रेय संभाव्यता की घटनात्मक प्रकृति को दिया गया। इस परिप्रेक्ष्य के साथ, जब आप गाऊसी चर का निवारण करते हैं, तो इसका माध्य μ द्वारा देखी जा रही घटना की भौतिक विशेषताओं द्वारा तय किया जाता है, जहां अवलोकन यादृच्छिक संचालन होते हैं, इसलिए देखे गए मान यादृच्छिक प्रारूप के विनिर्देश होते हैं। उनकी यादृच्छिकता के कारण, निश्चित μ वाले प्रारूप विशिष्ट अंतरालों से निश्चित संभावना के साथ गणना कर सकते हैं कि आप आत्मविश्वास को दर्शाते हैं।
उदाहरण
मान लीजिए कि X गाऊसी चर है[1] पैरामीटर के साथ , और इसका प्रारूप प्राप्त किया गया। सांख्यिकी के साथ फलन इस प्रकार है:
और
प्रारूप माध्य है, हम इसे पहचानते हैं
पैरामीटर (स्वप्रणालीता की डिग्री) m − 1 के साथ छात्र का t वितरण (विल्क्स 1962) का अनुसरण करता है, जिससे
दो मात्राओं के मध्य T का मापन करना और उसकी अभिव्यक्ति को फलन के रूप में विपरीत के लिए विश्वास अंतराल प्राप्त करते हैं।
प्रारूप विशिष्टता के साथ है:
आकार m = 10 होने पर, सांख्यिकी की गणना की जाती है और , और इसके लिए 0.90 विश्वास अंतराल प्राप्त करने के लिए शीर्ष सीमा (3.03, 5.65) है।
कंप्यूटर की सहायता से कार्यों का अनुमान लगाना
प्रारूप के द्वारा से पूर्ण विवाद मुर्गी-अंडे की अनिश्चय के जैसे दिखता है: या तो पूर्व डेटा द्वारा निश्चित डेटा और परिणाम के रूप में उनके गुणों का संभाव्यता वितरण, या पूर्व द्वारा निश्चित गुण और परिणाम के रूप में देखे गए डेटा का संभाव्यता वितरण है। क्लासिक समाधान में गुण और अवगुण है। पूर्व की सराहना विशेष रूप से तब की गई जब लोग अभी भी शीट और पेंसिल से गणना करते थे। वास्तव में, निश्चित पैरामीटर θ के लिए नेमैन विश्वास अंतराल की गणना करने का कार्य कठिन है: आप θ नहीं जानते हैं, किंतु आप इसके चारों ओर अंतराल का निवारण करना चाहते हैं जिसमें विफलता की संभवतः अधिक कम संभावना है। अधिक सीमित संख्या में सैद्धांतिक स्थितियों के लिए विश्लेषणात्मक समाधान की अनुमति है। इसके विपरीत, गाऊसी वितरण के निकट विश्वास अंतराल के संदर्भ में केंद्रीय सीमा प्रमेय के माध्यम से बड़ी संख्या में उदाहरणों को अनुमानित विधिपूर्वक शीघ्रता से समाधान किया जा सकता है- यही लाभ है। दोष यह है कि केंद्रीय सीमा प्रमेय तब प्रारंभ होता है जब प्रारूप आकार पर्याप्त रूप से बड़ा होता है। इसलिए, यह आधुनिक अनुमान उदाहरणों में सम्मिलित प्रारूप के साथ कम और कम प्रारंभ होता है। त्रुटिपूर्ण अपनी ओर से प्रारूप आकार में नहीं है अन्यथा, अनुमान समस्या की जटिलता के कारण यह आकार पर्याप्त रूप से बड़ा नहीं है।
बड़ी कंप्यूटिंग सुविधाओं की उपलब्धता के साथ, वैज्ञानिकों ने पृथक पैरामीटर के अनुमान से जटिल कार्यों के अनुमान पर फिर से ध्यान केंद्रित किया, अर्थात कार्यों की पहचान करने वाले अत्यधिक नेस्टेड पैरामीटर के समुच्चय इन स्थितियों में अत्यधिक जानकारीपूर्ण प्रारूपों के आधार पर कार्यों को सीखने (प्रतिगमन विश्लेषण, न्यूरो फजी प्रणाली या कम्प्यूटेशनल सीखने सिद्धांत के संदर्भ में) के बारे में विचार करते हैं। डेटा को जोड़ने वाली जटिल संरचना होने का प्रथम प्रभाव स्वप्रणालीता की प्रारूप डिग्री (सांख्यिकी) की संख्या में कमी है, अर्थात प्रारूप बिंदुओं के भाग का जलना, जिससे केंद्रीय सीमा प्रमेय में विचार किया जाने वाला प्रभावी प्रारूप आकार अधिक छोटा हो। किसी दिए गए आत्मविश्वास स्तर के साथ सीमित सीखने की त्रुटि सुनिश्चित करने वाले प्रारूप आकार पर ध्यान केंद्रित करने का परिणाम यह होता है कि इस आकार की निचली सीमा जटिलता सूचकांक जैसे कि वीसी आयाम या उस वर्ग के विवरण के साथ बढ़ती है, जिससे हम जिस कार्य को सीखना चाहते हैं वह संबंधित है।
उदाहरण
1,000 स्वप्रणाली बिट्स का प्रारूप कम से कम 0.99 के विश्वास के साथ अंतर्निहित बर्नौली चर के पैरामीटर p के अनुमान पर अधिकतम 0.081 की पूर्ण त्रुटि सुनिश्चित करने के लिए पर्याप्त है। समान आकार 0.99 के समान आत्मविश्वास के साथ 0.088 से कम की सीमा का आश्वासन नहीं दे सकता है, जब त्रुटि की पहचान इस संभावना के साथ की जाती है कि न्यूयॉर्क में रहने वाला 20 वर्षीय व्यक्ति 1,000 बड़ी देखी गई ऊंचाई, भार और कमर की सीमा में फिट नहीं बैठता है। एप्पल निवासी त्रुटिहीनता की कमी इसलिए होती है क्योंकि वीसी आयाम और समानांतर चतुर्भुज के वर्ग का विवरण, जिनमें से 1,000 निवासियों की श्रेणियों में से देखा गया है, दोनों 6 के समान हैं।
फिशर प्रश्न का समाधान करने वाली सामान्य व्युत्क्रम समस्या
अपर्याप्त रूप से बड़े प्रारूपों के साथ, दृष्टिकोण: निश्चित प्रारूप - यादृच्छिक गुण तीन चरणों में अनुमान प्रक्रियाओं का विचार देते हैं:
| 1. | प्रारूपकरण प्रणाली: इसमें एक जोड़ी होती है, जहां सीड Z अज्ञात पैरामीटर के बिना यादृच्छिक चर है, जबकि स्पष्टीकरण फलन यह Z के प्रारूपों से यादृच्छिक चर X प्रारूपों की मानचित्रण का फलन है, जिसमें हम रुचि रखते हैं। पैरामीटर सदिश यादृच्छिक पैरामीटर का विनिर्देश है, इसके घटक X वितरण प्रणाली के पैरामीटर हैं। इंटीग्रल ट्रांसफॉर्म प्रमेय प्रत्येक (स्केलर या वेक्टर) X के लिए ऐसी प्रणाली के अस्तित्व को सुनिश्चित करता है जब सीड यादृच्छिक चर U के साथ समान रूप से वितरित होता है।
| ||
| 2. | मास्टर समीकरण: प्रारूप और देखे गए डेटा के मध्य वास्तविक संबंध को डेटा पर सांख्यिकी और अज्ञात पैरामीटर के मध्य संबंधों के समुच्चय के संदर्भ में उपयोग किया जाता है जो प्रारूप प्रणाली के परिणाम के रूप में आते हैं। हम इन संबंधों को मास्टर समीकरण कहते हैं। सांख्यिकी का मार्गदर्शन , मास्टर समीकरण का सामान्य रूप है:
इन संबंधों के साथ हम उन पैरामीटर के मानों का निरीक्षण कर सकते हैं जो प्रारूप के सीड का प्रतिनिधित्व करने वाले सीड की विशेष समुच्चय से देखे गए सांख्यिकी के साथ प्रारूप उत्पन्न कर सकते थे। इसलिए, प्रारूप सीड की जनसंख्या पैरामीटर की जनसंख्या से संग्युमित होती है। इस जनसंख्या के स्वच्छ गुणों को सुनिश्चित करने के लिए, सीड मानों को यादृच्छिक रूप से निकालना और या तो पर्याप्त सांख्यिकी या, उत्तम आँकड़े सम्मिलित करना पर्याप्त है। मास्टर समीकरणों में पैरामीटर है। उदाहरण के लिए, सांख्यिकी और पेरेटो यादृच्छिक चर X के पैरामीटर a और k के लिए पर्याप्त सिद्ध होता है। प्रारूपकरण प्रणाली (के समतुल्य रूप) के लिए हम उन्हें इस प्रकार पढ़ सकते हैं: क्रमश: | ||
| 3. | पैरामीटर जनसंख्या: मास्टर समीकरणों का समुच्चय तय करने के पश्चात, प्रारूप सीड को बूटस्ट्रैपिंग आपश्चाती के माध्यम से संख्यात्मक रूप से, या ट्विस्टिंग तर्क के माध्यम से विश्लेषणात्मक रूप से उपयोग कर सकते हैं। इसलिए सीड की जनसंख्या से पैरामीटर की जनसंख्या प्राप्त होती है।
अनुकूलता संगत आपश्चाती के पैरामीटर को दर्शाती है, अर्थात ऐसी आपश्चाती जो देखे गए सांख्यिकी को उत्पन्न करते हुए प्रारूप उत्पन्न कर सकती थी। इस धारणा को इस प्रकार औपचारिक रूप दे सकते हैं: |
परिभाषा
यादृच्छिक चर और उससे निकाले गए प्रारूप के लिए संगत वितरण समान प्रारूप प्रणाली वाला वितरण है मान के साथ X का यादृच्छिक पैरामीटर का उत्तम व्यवहार वाले सांख्यिकी पर मास्टर समीकरण के आधार से प्राप्त किया गया।
उदाहरण
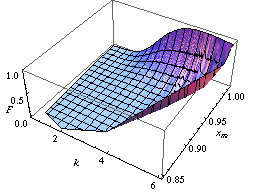
आप जनसंख्या बूटस्ट्रैप विधि के कार्यान्वयन उदाहरण के रूप में पेरेटो पैरामीटर A और K के वितरण नियम बाईं ओर के चित्र में पा सकते हैं।
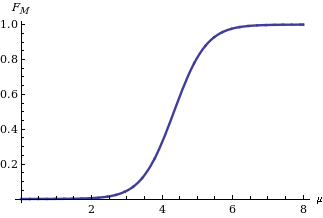
ट्विस्टिंग तर्क विधि को प्रारंभ करने से, वितरण नियम प्राप्त होता है सांख्यिकी के आधार पर गाऊसी चर X के माध्य M का जब के समान माना जाता है (अपोलोनी, मालचिओडी & गैटो 2006) इसकी अभिव्यक्ति है:
दाहिनी ओर चित्र में दिखाया गया है, जहाँ मानक सामान्य वितरण का संचयी वितरण फलन है।
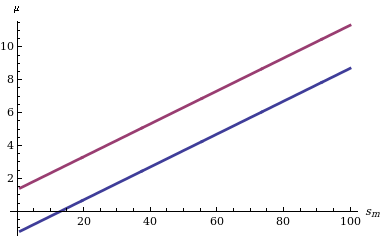
इसके वितरण फलन को देखते हुए M के लिए विश्वास अंतराल की गणना करना सरल है: हमें केवल दो मात्राओं का परिक्षण करना आवश्यक है (उदाहरण के लिए) और मात्राएँ (यदि हम टेल की संभावनाओं में सममित स्तर δ के विश्वास अंतराल में रुचि रखते हैं) जैसा कि सांख्यिकी में बाईं ओर दर्शाया गया है, जो सांख्यिकी Sm के विभिन्न मानों के लिए दो सीमाओं के व्यवहार को दर्शाता है।
फिशर के दृष्टिकोण की अकिलीज़ हील से अधिक पैरामीटर के संयुक्त वितरण में निहित है, जैसे कि गाऊसी वितरण का माध्य और विचरण है। इसके विपरीत, अंतिम दृष्टिकोण (और उपर्युक्त विधियों: जनसंख्या बूटस्ट्रैप और ट्विस्टिंग तर्क) के साथ हम कई पैरामीटर का संयुक्त वितरण सीख सकते हैं। उदाहरण के लिए, दो या कई अधिक पैरामीटर के वितरण पर ध्यान केंद्रित करते हुए, नीचे दिए गए सांख्यिकी में हम दो आत्मविश्वास क्षेत्रों की रिपोर्ट करते हैं जहां सीखा जाने वाला कार्य 90% के आत्मविश्वास के साथ आता है। पूर्व उस संभावना से संबंधित है जिसके साथ विस्तारित समर्थन वेक्टर मशीन बाइनरी लेबल 1 को बिंदुओं पर प्रदर्शित करती है समतल दो सतहों को विशिष्ट वितरण नियम के अनुसार लेबल किए गए प्रारूप बिंदुओं के समुच्चय के आधार पर तैयार किया जाता है (अपोलोनी et al. 2008) से गणना की गई स्तन कैंसर की पुनरावृत्ति संकट दर के विश्वास क्षेत्र से संबंधित है। (अपोलोनी, मालचिओडी & गेटो 2006)
टिप्पणियाँ
- ↑ By default, capital letters (such as U, X) will denote random variables and small letters (u, x) their corresponding specifications.
संदर्भ
- Fraser, D. A. S. (1966), "Structural probability and generalization", Biometrika, 53 (1/2): 1–9, doi:10.2307/2334048, JSTOR 2334048.
- Fisher, M. A. (1956), Statistical Methods and Scientific Inference, Edinburgh and London: Oliver and Boyd
- Apolloni, B.; Malchiodi, D.; Gaito, S. (2006), Algorithmic Inference in Machine Learning, International Series on Advanced Intelligence, vol. 5 (2nd ed.), Adelaide: Magill,
Advanced Knowledge International
- Apolloni, B.; Bassis, S.; Malchiodi, D.; Witold, P. (2008), The Puzzle of Granular Computing, Studies in Computational Intelligence, vol. 138, Berlin: Springer, ISBN 9783540798637
- Ramsey, F. P. (1925), "The Foundations of Mathematics", Proceedings of the London Mathematical Society: 338–384, doi:10.1112/plms/s2-25.1.338.
- Wilks, S.S. (1962), Mathematical Statistics, Wiley Publications in Statistics, New York: John Wiley