अवकलनीय मैनिफोल्ड: Difference between revisions

Revision as of 00:12, 12 July 2023

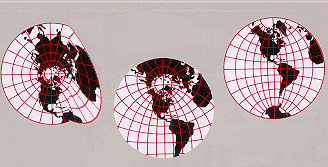
विश्व के लिए चार्ट का अविभाज्य एटलस। यदि एटलस अलग-अलग नहीं है तो कैलकुलस के परिणाम चार्ट के बीच संगत नहीं हो सकते हैं। केंद्र और दाएँ चार्ट में, कर्क रेखा चिकना वक्र है, जबकि बाएँ चार्ट में इसका तीखा कोना है। भिन्न-भिन्न मैनिफोल्ड की धारणा चार्ट के बीच रूपांतरित होने वाले कार्यों को भिन्न-भिन्न करने की आवश्यकता के द्वारा मैनिफोल्ड को परिष्कृत करती है।

गणित में, अवकलनीय मैनिफोल्ड (विभेदक मैनिफोल्ड भी) एक प्रकार का कई गुना है जो स्थानीय रूप से सदिश स्थल के समान होता है जिससे कोई कैलकुलस प्रयुक्त कर सकता है। किसी भी विविधता का वर्णन चार्ट (एटलस (टोपोलॉजी)) के संग्रह द्वारा किया जा सकता है। व्यक्तिगत चार्ट के अंदर काम करते समय कोई भी कैलकुलस के विचारों को प्रयुक्त कर सकता है, क्योंकि प्रत्येक चार्ट एक सदिश स्पेस के अंदर होता है, जिस पर कैलकुलस के सामान्य नियम प्रयुक्त होते हैं। यदि चार्ट उपयुक्त रूप से संगत हैं (अर्थात्, एक चार्ट से दूसरे चार्ट में संक्रमण भिन्न फलन है), तो चार्ट में की गई गणना किसी अन्य भिन्न चार्ट में मान्य हैं।

औपचारिक शब्दों में, विभेदक मैनिफोल्ड विश्व स्तर पर परिभाषित अंतर संरचना के साथ टोपोलॉजिकल मैनिफ़ोल्ड है। किसी भी टोपोलॉजिकल मैनिफोल्ड को उसके एटलस में होमियोमोर्फिज्म और सदिश स्पेस पर मानक अंतर संरचना का उपयोग करके स्थानीय रूप से विभेदक संरचना दी जा सकती है। होमोमोर्फिज्म से प्रेरित स्थानीय समन्वय प्रणालियों पर वैश्विक अंतर संरचना को प्रेरित करने के लिए, एटलस में चार्ट इंटरैक्शन पर उनकी फलन संरचना संबंधित सदिश स्थान पर भिन्न फलन होनी चाहिए। दूसरे शब्दों में, जहां चार्ट के डोमेन ओवरलैप होते हैं, प्रत्येक चार्ट द्वारा परिभाषित निर्देशांक को एटलस में प्रत्येक चार्ट द्वारा परिभाषित निर्देशांक के संबंध में भिन्न होना आवश्यक है। वे मानचित्र जो विभिन्न चार्टों द्वारा परिभाषित निर्देशांकों को एक-दूसरे से जोड़ते हैं, संक्रमण मानचित्र कहलाते हैं।

अमूर्त स्थान पर ऐसी स्थानीय अंतर संरचना को परिभाषित करने की क्षमता किसी को वैश्विक समन्वय प्रणालियों के बिना रिक्त स्थान तक भिन्नता की परिभाषा का विस्तार करने की अनुमति देती है। स्थानीय रूप से विभेदक संरचना किसी को विश्व स्तर पर भिन्न स्पर्शरेखा स्थान, भिन्न कार्यों और भिन्न टेंसर फ़ील्ड और सदिश फ़ील्ड को परिभाषित करने की अनुमति देती है।

भौतिकी में विभेदक मैनिफोल्ड बहुत महत्वपूर्ण हैं। विशेष प्रकार के विभेदक मैनिफोल्ड शास्त्रीय यांत्रिकी, सामान्य सापेक्षता और यांग-मिल्स सिद्धांत जैसे भौतिक सिद्धांतों का आधार बनते हैं। भिन्न-भिन्न मैनिफोल्ड्स के लिए कलन विकसित करना संभव है। यह बाहरी व्युत्पन्न|बाहरी कलन जैसी गणितीय मशीनरी की ओर ले जाता है। अवकलनशील मैनिफोल्ड्स पर कैलकुलस के अध्ययन को डिफरेंशियल ज्योमेट्री और टोपोलॉजी|डिफरेंशियल ज्योमेट्री के रूप में जाना जाता है।

मैनिफ़ोल्ड की भिन्नता को कई अर्थ दिए गए हैं, जिनमें निरंतर भिन्न, k-बार भिन्न, सुचारू फलन (जिसके स्वयं कई अर्थ हैं), और विश्लेषणात्मक फ़लन सम्मिलित हैं।

इतिहास

विशिष्ट अनुशासन के रूप में विभेदक ज्यामिति के उद्भव का श्रेय सामान्यतः कार्ल फ्रेडरिक गॉस और बर्नहार्ड रीमैन को दिया जाता है। रीमैन ने पहली बार गोटिंगेन विश्वविद्यालय में संकाय के समक्ष अपने प्रसिद्ध आवास व्याख्यान में कई गुनाओं का वर्णन किया।^[1] उन्होंने किसी दिए गए ऑब्जेक्ट को नई दिशा में बदलने की सहज प्रक्रिया द्वारा मैनिफोल्ड के विचार को प्रेरित किया, और बाद के औपचारिक विकास में समन्वय प्रणालियों और चार्ट की भूमिका का वर्णन किया:

एन आयामों की विविधता की धारणा का निर्माण करने के बाद, और पाया कि इसका वास्तविक चरित्र इस संपत्ति में निहित है कि इसमें स्थिति का निर्धारण परिमाण के एन निर्धारण तक कम हो सकता है, ... - बी रीमैन

जेम्स क्लर्क मैक्सवेल जैसे भौतिकविदों के फलन,^[2] और गणितज्ञ ग्रेगोरियो रिक्की-कर्बस्ट्रो और टुल्लियो लेवी-सिविटा^[3] टेंसर विश्लेषण के विकास और सामान्य सहप्रसरण की धारणा को जन्म दिया, जो आंतरिक ज्यामितीय संपत्ति की पहचान करता है जो समन्वय परिवर्तन के संबंध में अपरिवर्तनीय है। इन विचारों को अल्बर्ट आइंस्टीन के सामान्य सापेक्षता के सिद्धांत और इसके अंतर्निहित तुल्यता सिद्धांत में महत्वपूर्ण अनुप्रयोग मिला। 2-आयामी मैनिफोल्ड की आधुनिक परिभाषा हरमन वेइल ने अपनी 1913 की रीमैन सतह पर पुस्तक में दी थी।^[4] एटलस (गणित) के संदर्भ में मैनिफोल्ड की व्यापक रूप से स्वीकृत सामान्य परिभाषा हस्लर व्हिटनी के कारण है।^[5]

परिभाषा

एटलस

माना $M$ टोपोलॉजिकल स्पेस बनें हैं। चार्ट $(U, φ)$ पर $M$ में विवृत उपसमुच्चय $U$ का $M$ होता है, और होमियोमोर्फिज्म $φ$ से $U$ कुछ यूक्लिडियन स्थान के विवृत उपसमुच्चय $R n$ के लिए, कुछ सीमा तक अनौपचारिक रूप से, कोई चार्ट का उल्लेख $φ : U \to R n$ कर सकता है, जिसका अर्थ है कि की छवि $φ$ का विवृत उपसमुच्चय $R n$ है, ओर $φ$ इसकी छवि पर समरूपता है; कुछ लेखकों के उपयोग में, इसका अर्थ यह $φ : U \to R n$ हो सकता है, जो स्वयं होमियोमोर्फिज्म है।

चार्ट की उपस्थिति से विभेदक गणना करने की संभावना $M$ का पता चलता है; उदाहरण के लिए, यदि कोई फ़लन $u : M \to R$ दिया गया है और चार्ट $(U, φ)$ पर $M$ , कोई रचना $u \circ φ -1$ पर विचार कर सकता है, जो वास्तविक-मूल्यवान फ़लन है जिसका डोमेन यूक्लिडियन स्पेस का विवृत उपसमुच्चय है; इस प्रकार, यदि यह अवकलनीय होता है, तो कोई इसके आंशिक व्युत्पन्न पर विचार कर सकता है।

यह स्थिति निम्नलिखित कारणों से पूर्णतः संतोषजनक नहीं है। दूसरे चार्ट पर $(V, ψ)$ पर $M$ विचार करें, और मान लीजिये $U$ और $V$ इसमें कुछ बिंदु समान हैं। दो संगत फलन $u \circ φ -1$ और $u \circ ψ -1$ इस अर्थ में जुड़े हुए हैं कि उन्हें एक-दूसरे में पुनर्परिभाषित किया जा सकता है:

u\circ \varphi ^{-1}={\big (}u\circ \psi ^{-1}{\big )}\circ {\big (}\psi \circ \varphi ^{-1}{\big )},

दाहिनी ओर का प्राकृतिक डोमेन

φ (U \cap V)

तब से

φ

और

ψ

होमोमोर्फिज्म हैं, यह उसका अनुसरण करता है;

ψ \circ φ -1

से एक

φ (U \cap V)

को

ψ (U \cap V)

होमोमोर्फिज्म है। परिणामस्वरूप, तथापि दोनों फलन

u \circ φ -1

और

u \circ ψ -1

अवकलनीय हैं, इसलिए उनके विभेदक गुण

ψ \circ φ -1

आवश्यक रूप से एक दूसरे से मजबूती से जुड़े नहीं होंगे, श्रृंखला नियम प्रयुक्त होने के लिए आवश्यक रूप से पर्याप्त रूप से भिन्न नहीं है। यदि कोई इसके अतिरिक्त कार्यों पर विचार करता है तो वही समस्या

c : R \to M

पाई जाती है; एक को पुनर्परिवर्तन सूत्र की ओर ले जाया जाता है

\varphi \circ c={\big (}\varphi \circ \psi ^{-1}{\big )}\circ {\big (}\psi \circ c{\big )},

जिस बिंदु पर कोई पहले जैसा ही अवलोकन कर सकता है।

इसका समाधान चार्ट के एक अलग-अलग एटलस की प्रारंभ से किया जाता है, जो चार्ट के संग्रह को निर्दिष्ट करता है $M$ जिसके लिए संक्रमण मानचित्र $ψ \circ φ -1$ सभी भिन्न हैं। इससे स्थिति अत्यधिक सीमा तक साफ हो जाती है: यदि $u \circ φ -1$ अवकलनीय है, फिर पुनरामितीकरण सूत्र के कारण, मानचित्र $u \circ ψ -1$ क्षेत्र पर भी भिन्न है $ψ (U \cap V)$ . इसके अतिरिक्त, इन दोनों मानचित्रों के व्युत्पन्न श्रृंखला नियम द्वारा एक दूसरे से जुड़े हुए हैं। दिए गए एटलस के सापेक्ष, यह अलग-अलग मैपिंग की धारणा को सुविधाजनक बनाता है जिसका डोमेन या रेंज $M$ है, साथ ही ऐसे मानचित्रों की व्युत्पत्ति की धारणा भी सुविधाजनक है।

औपचारिक रूप से, डिफरेंशियल शब्द कुछ सीमा तक अस्पष्ट है, क्योंकि अलग-अलग लेखकों द्वारा इसका अलग-अलग अर्थ लिया जाता है; कभी-कभी इसका अर्थ पहले डेरिवेटिव का अस्तित्व होता है, कभी-कभी निरंतर पहले डेरिवेटिव का अस्तित्व होता है, और कभी-कभी असीमित कई डेरिवेटिव का अस्तित्व होता है। निम्नलिखित विभेदक एटलस के विभिन्न (अस्पष्ट) अर्थों की औपचारिक परिभाषा देता है। सामान्यतः, विभेदीकरण का उपयोग इन सभी संभावनाओं सहित कैच-ऑल शब्द के रूप में किया जाएगा, बिना किसी नियम $k \geq 1$ के अतिरिक्त किया जायेगा।

टोपोलॉजिकल स्पेस $M$ ... दिया गया
$C k$ एटलस	चार्ट का संग्रह है	${φ α : U α \to R n} α \in A$	ऐसा कि ${U α} α \in A$ $M$ को कवर करता है, और ऐसा कि $A$ में सभी $α$ और $β$ के लिए, संक्रमण मानचित्र $φ α \circ φ -1 β$ है	$C k$ मानचित्र
चिकना या $C \infty$ एटलस		${φ α : U α \to R n} α \in A$		चिकना मानचित्र
विश्लेषणात्मक या $C ω$ एटलस		${φ α : U α \to R n} α \in A$		वास्तविक-विश्लेषणात्मक मानचित्र
होलोमार्फिक एटलस		${φ α : U α \to C n} α \in A$		होलोमार्फिक मानचित्र

M

U_{\alpha }

U_{\beta }

\phi _{\alpha }

\phi _{\beta }

\phi _{\beta \alpha }

\phi _{\alpha \beta }

\mathbf {R} ^{n}

\mathbf {R} ^{n}

The transition map of two charts.

\phi _{\alpha \beta }

denotes

\phi _{\alpha }\circ \phi _{\beta }^{-1}

and

\phi _{\beta \alpha }

denotes

\phi _{\beta }\circ \phi _{\alpha }^{-1}

.

चूँकि प्रत्येक वास्तविक-विश्लेषणात्मक मानचित्र सहज है, और प्रत्येक सहज मानचित्र $C k$ है, किसी के लिए $k$ , कोई यह देख सकता है कि किसी भी विश्लेषणात्मक एटलस को सहज एटलस के रूप में भी देखा जा सकता है, और प्रत्येक सहज एटलस को $C k$ सहज एटलस के रूप में भी देखा जा सकता है। इस श्रृंखला को होलोमोर्फिक एटलस को सम्मिलित करने के लिए बढ़ाया जा सकता है, इस समझ के साथ कि विवृत उपसमुच्चय के बीच कोई भी होलोमोर्फिक मानचित्र $C n$ को विवृत उपसमूहों के बीच वास्तविक-विश्लेषणात्मक मानचित्र $R 2 n$ के रूप में देखा जा सकता है।

टोपोलॉजिकल स्पेस पर अलग-अलग एटलस को देखते हुए, कोई कहता है कि चार्ट एटलस के साथ अलग-अलग संगत है, या दिए गए एटलस के सापेक्ष अलग-अलग है, यदि दिए गए अलग-अलग एटलस वाले चार्ट के संग्रह में चार्ट को सम्मिलित करने से अलग-अलग एटलस बनता है, भिन्न एटलस अधिकतम भिन्न एटलस निर्धारित करता है, जिसमें सभी चार्ट सम्मिलित होते हैं जो दिए गए एटलस के साथ भिन्न रूप से संगत होते हैं। अधिकतम एटलस हमेशा बहुत बड़ा होता है। उदाहरण के लिए, अधिकतम एटलस में किसी भी चार्ट को देखते हुए, उसके डोमेन के इच्छानुसार विवृत उपसमुच्चय पर उसका प्रतिबंध भी अधिकतम एटलस में समाहित होगा। अधिकतम चिकने एटलस को चिकनी संरचना के रूप में भी जाना जाता है; मैक्सिमम होलोमोर्फिक एटलस को जटिल अनेक गुना के रूप में भी जाना जाता है।

वैकल्पिक लेकिन समतुल्य परिभाषा, अधिकतम एटलस के प्रत्यक्ष उपयोग से बचते हुए, विभेदक एटलस के समतुल्य वर्गों पर विचार करना है, जिसमें दो भिन्न एटलस को समतुल्य माना जाता है यदि एटलस का प्रत्येक चार्ट दूसरे एटलस के साथ भिन्न रूप से संगत है। अनौपचारिक रूप से, इसका अर्थ यह है कि सहज मैनिफोल्ड से निपटने में, कोई एकल विभेदक एटलस के साथ काम कर सकता है, जिसमें केवल कुछ चार्ट सम्मिलित हैं, इस अंतर्निहित समझ के साथ कि कई अन्य चार्ट और विभेदक एटलस समान रूप से वैध हैं।

डोमेन के अपरिवर्तनीयता के अनुसार, टोपोलॉजिकल स्पेस के प्रत्येक जुड़े घटक जिसमें एक अलग एटलस होता है, $n$ का अच्छी तरह से परिभाषित आयाम होता है, यह होलोमोर्फिक एटलस के मामले में थोड़ी अस्पष्टता का कारण बनता है, क्योंकि विश्लेषणात्मक, सुचारू, या के रूप में विचार किए जाने पर संबंधित आयाम $C k$ एटलस के आयाम के मूल्य का आधा होगा। इस कारण से, होलोमोर्फिक एटलस के साथ टोपोलॉजिकल स्पेस के वास्तविक और जटिल आयाम को अलग से संदर्भित किया जाता है।

अनेक गुना

A भिन्न मैनिफोल्ड एक हॉसडॉर्फ़ स्थान और दूसरा गणनीय टोपोलॉजिकल स्पेस $M$ है, एक साथ अधिकतम भिन्नात्मक एटलस $M$ के साथ है। अधिकांश मूलभूत सिद्धांत हॉसडॉर्फ और दूसरी गणनीयता स्थितियों की आवश्यकता के बिना विकसित किए जा सकते हैं, चूंकि वे अधिकांश उन्नत सिद्धांत के लिए महत्वपूर्ण हैं। वे अनिवार्य रूप से बुम्प फलन और एकता के विभाजन के सामान्य अस्तित्व के बराबर हैं, दोनों का उपयोग सर्वव्यापी रूप से किया जाता है।

A की धारणा $C 0$ मैनिफोल्ड टोपोलॉजिकल मैनिफोल्ड के समान है। चूँकि, इसमें उल्लेखनीय अंतर किया जाना शेष है। टोपोलॉजिकल स्पेस को देखते हुए, यह पूछना सार्थक है कि क्या यह टोपोलॉजिकल मैनिफोल्ड है या नहीं। इसके विपरीत, यह पूछना सार्थक नहीं है कि क्या दिया गया टोपोलॉजिकल स्पेस (उदाहरण के लिए) एक स्मूथ मैनिफोल्ड है या नहीं, क्योंकि स्मूथ मैनिफोल्ड की धारणा के लिए एक स्मूथ एटलस के विनिर्देशन की आवश्यकता होती है, जो अतिरिक्त संरचना है। चूँकि, यह कहना सार्थक हो सकता है कि एक निश्चित टोपोलॉजिकल स्पेस को एक सहज मैनिफोल्ड की संरचना नहीं दी जा सकती है। परिभाषाओं को दोबारा तैयार करना संभव है ताकि इस प्रकार का असंतुलन उपस्थित न हो; कोई एक सेट $M$ से प्रारंभ कर सकता है (टोपोलॉजिकल स्पेस $M$ के अतिरिक्त), टोपोलॉजिकल स्पेस की संरचना को परिभाषित करने के लिए इस सेटिंग में चिकने एटलस के प्राकृतिक एनालॉग $M$ का उपयोग करना।

मैनिफोल्ड बनाने के लिए यूक्लिडियन टुकड़ों को एक साथ जोड़ना

मैनिफोल्ड्स के निर्माण पर परिप्रेक्ष्य प्राप्त करने के लिए उपरोक्त परिभाषाओं को रिवर्स-इंजीनियरिंग किया जा सकता है। विचार यह है कि चार्ट और संक्रमण मानचित्रों की छवियों के साथ प्रारंभ की जाए और इस डेटा से पूरी तरह से मैनिफोल्ड का निर्माण किया जाए। जैसा कि उपरोक्त चर्चा में है, हम सहज संदर्भ का उपयोग करते हैं लेकिन अन्य सेटिंग्स में भी सब कुछ उतना ही अच्छा काम करता है।

अनुक्रमण सेट $A$ दिया गया है, माना $V_{\alpha }$ के विवृत उपसमूहों का संग्रह $\mathbb {R} ^{n}$ और प्रत्येक के लिए $\alpha ,\beta \in A$ , माना $V_{\alpha \beta }$ का विवृत (संभवतः खाली) उपसमुच्चय $V_{\beta }$ और जाने $\phi _{\alpha \beta }:V_{\alpha \beta }\to V_{\beta \alpha }$ सहज मानचित्र है।लगता है कि $\phi _{\alpha \alpha }$ पहचान मानचित्र है, वह $\phi _{\alpha \beta }\circ \phi _{\beta \alpha }$ पहचान मानचित्र है, और वह $\phi _{\alpha \beta }\circ \phi _{\beta \gamma }\circ \phi _{\gamma \alpha }$ पहचान मानचित्र है। फिर असंयुक्त संघ पर तुल्यता संबंध परिभाषित करें ${\textstyle \bigsqcup _{\alpha \in A}V_{\alpha }}$ घोषणा करके $p\in V_{\alpha \beta }$ के बराबर होना $\phi _{\alpha \beta }(p)\in V_{\beta \alpha }.$ । कुछ तकनीकी कार्यों के साथ, कोई यह दिखा सकता है कि तुल्यता वर्गों के सेट को स्वाभाविक रूप से टोपोलॉजिकल संरचना दी जा सकती है, और ऐसा करने में उपयोग किए जाने वाले चार्ट एक सहज एटलस बनाते हैं। विश्लेषणात्मक संरचनाओं (उपसमुच्चय) को एक साथ जोड़ने के लिए, विश्लेषणात्मक किस्में देखें।

अवकलनीय फलन

एन-डायमेंशनल डिफरेंशियल मैनिफोल्ड M पर वास्तविक मूल्यवान फ़लन एफ को बिंदु पर 'डिफरेंशियल' p ∈ M कहा जाता है। यदि यह p के आसपास परिभाषित किसी भी समन्वय चार्ट में भिन्न है। अधिक स्पष्ट शब्दों में, यदि $(U,\phi )$ जहां भिन्न चार्ट $U$ और विवृत सेट $M$ है, युक्त P तथा $\phi :U\to {\mathbf {R} }^{n}$ चार्ट को परिभाषित करने वाला मानचित्र है, तो f, p पर अवकलनीय है यदि और केवल यदि

f\circ \phi ^{-1}\colon \phi (U)\subset {\mathbf {R} }^{n}\to {\mathbf {R} }

\phi (p)

पर भिन्न है, वह

f\circ \phi ^{-1}

विवृत सेट से भिन्न फलन

\phi (U)

है,

{\mathbf {R} }^{n}

का एक उपसमुच्चय को

\mathbf {R}

माना जाता है, सामान्य तौर पर, कई उपलब्ध चार्ट होंगे; चूँकि, भिन्नता की परिभाषा p पर चार्ट की पसंद पर निर्भर नहीं करती है। यह एक चार्ट और दूसरे चार्ट के बीच संक्रमण कार्यों पर प्रयुक्त श्रृंखला नियम का पालन करता है कि यदि p पर किसी विशेष चार्ट में एफ अलग-अलग है, तो यह p पर सभी चार्ट में अलग-अलग है। C^k फ़लन, सुचारू फ़लन और विश्लेषणात्मक फ़लन को परिभाषित करने के लिए अनुरूप विचार प्रयुक्त होते हैं।

कार्यों का विभेदन

किसी फ़लन के व्युत्पन्न को भिन्न मैनिफोल्ड पर परिभाषित करने के कई विधियाँ हैं, जिनमें से सबसे मौलिक दिशात्मक व्युत्पन्न है। दिशात्मक व्युत्पन्न की परिभाषा इस तथ्य से जटिल है कि मैनिफोल्ड में एक उपयुक्त एफ़िन स्पेस संरचना का अभाव होगा जिसके साथ सदिश (ज्यामितीय) को परिभाषित किया जा सके। इसलिए, दिशात्मक व्युत्पन्न वैक्टर के अतिरिक्त मैनिफोल्ड में वक्रों को देखता है।

दिशात्मक विभेदन

एन आयामी विभेदक मैनिफोल्ड M पर एक वास्तविक मूल्यवान फ़लन एफ को देखते हुए, M में एक बिंदु p पर एफ के दिशात्मक व्युत्पन्न को निम्नानुसार परिभाषित किया गया है। मान लीजिए कि γ(t) M में एक वक्र है γ(0) = p, जो इस अर्थ में भिन्न है कि किसी भी चार्ट के साथ इसकी संरचना 'Rⁿ' में एक भिन्न वक्र है, फिर γ के अनुदिश p पर f का 'दिशात्मक अवकलज' है

\left.{\frac {d}{dt}}f(\gamma (t))\right|_{t=0}.

यदि C₁ और γ₂ दो वक्र ऐसे हैं γ₁(0) = γ₂(0) = p, और किसी भी समन्वय चार्ट में

\phi

,

\left.{\frac {d}{dt}}\phi \circ \gamma _{1}(t)\right|_{t=0}=\left.{\frac {d}{dt}}\phi \circ \gamma _{2}(t)\right|_{t=0}

फिर, श्रृंखला नियम के अनुसार, f के पास γ के साथ p पर समान दिशात्मक व्युत्पन्न है₁ C के साथ के रूप में₂. इसका अर्थ यह है कि दिशात्मक व्युत्पन्न केवल p पर वक्र के स्पर्शरेखा सदिश पर निर्भर करता है। इस प्रकार, अलग-अलग कई गुना के मामले में अनुकूलित दिशात्मक भेदभाव की अधिक अमूर्त परिभाषा अंततः एक संबद्ध स्थान में दिशात्मक भेदभाव की सहज विशेषताओं को पकड़ लेती है।

स्पर्शरेखा सदिश और अंतर

पर एक स्पर्शरेखा सदिश p ∈ M अवकलनीय वक्रों का एक तुल्यता वर्ग है γ साथ में γ(0) = p, मॉड्यूलो वक्रों के बीच प्रथम-क्रम संपर्क (गणित) का तुल्यता संबंध है। इसलिए,

\gamma _{1}\equiv \gamma _{2}\iff \left.{\frac {d}{dt}}\phi \circ \gamma _{1}(t)\right|_{t=0}=\left.{\frac {d}{dt}}\phi \circ \gamma _{2}(t)\right|_{t=0}

प्रत्येक समन्वय चार्ट मे

\phi

इसलिए, समतुल्य वर्ग p पर एक निर्धारित वेग सदिश के साथ p के माध्यम से वक्र हैं। p पर सभी स्पर्शरेखा सदिशों का संग्रह एक सदिश समष्टि बनाता है: p पर M की स्पर्शरेखा समष्टि, T_pM द्वारा निरूपित है।

यदि X, p पर एक स्पर्शरेखा सदिश है और f, p के पास परिभाषित एक भिन्न फलन है, तो X को परिभाषित करने वाले समतुल्य वर्ग में किसी भी वक्र के साथ f को विभेदित करने से X के साथ एक अच्छी तरह से परिभाषित दिशात्मक व्युत्पन्न मिलता है:

Xf(p):=\left.{\frac {d}{dt}}f(\gamma (t))\right|_{t=0}.

एक बार फिर, श्रृंखला नियम स्थापित करता है कि यह समतुल्य वर्ग से γ का चयन करने की स्वतंत्रता से स्वतंत्र है, क्योंकि समान प्रथम क्रम संपर्क वाला कोई भी वक्र समान दिशात्मक व्युत्पन्न प्राप्त करेगा।

यदि फ़लन f निश्चित है, तो मैपिंग

X\mapsto Xf(p)

स्पर्शरेखा स्थान पर एक रैखिक कार्यात्मक है। इस रैखिक कार्यात्मकता को अधिकांशतः df(p) द्वारा निरूपित किया जाता है और इसे p पर f का 'अंतर' कहा जाता है:

df(p)\colon T_{p}M\to {\mathbf {R} }.

स्पर्शरेखा स्थान की परिभाषा और स्थानीय निर्देशांक में विभेदन

मान लीजिये $M$ सुचारु एटलस $\{(U_{\alpha },\phi _{\alpha })\}_{\alpha \in A}$ के साथ टोपोलॉजिकल $n$ -मैनिफोल्ड है। $p\in M$ दिया गया है, माना $A_{p}$ $\{\alpha \in A:p\in U_{\alpha }\}$ निरूपित है। $p\in M$ पर एक स्पर्शरेखा सदिश एक मैपिंग $v:A_{p}\to \mathbb {R} ^{n}$ है, यहाँ $\alpha \mapsto v_{\alpha }$ दर्शाया गया है, ऐसा है कि

v_{\alpha }=D{\Big |}_{\phi _{\beta }(p)}(\phi _{\alpha }\circ \phi _{\beta }^{-1})(v_{\beta })

सभी

\alpha ,\beta \in A_{p}

के लिए। आइए स्पर्शरेखा सदिशों

T_{p}M

का संग्रह कर

p

द्वारा निरूपित किया जाए, एक सुचारु फलन

f:M\to \mathbb {R}

दिया गया,

df_{p}:T_{p}M\to \mathbb {R}

एक स्पर्शरेखा सदिश भेजकर

v:A_{p}\to \mathbb {R} ^{n}

द्वारा दिए गए नंबर पर परिभाषित करना

D{\Big |}_{\phi _{\alpha }(p)}(f\circ \phi _{\alpha }^{-1})(v_{\alpha }),

जो श्रृंखला नियम और स्पर्शरेखा सदिश की परिभाषा में बाधा के कारण की पसंद

\alpha \in A_{p}

पर निर्भर नहीं करता है।

कोई भी इसकी जांच कर सकता है, स्वाभाविक रूप से एक की संरचना $T_{p}M$ है। $n$ -आयामी वास्तविक सदिश स्थान, और वह इस संरचना के साथ, $df_{p}$ एक रेखीय मानचित्र है। मुख्य अवलोकन यह है कि, स्पर्शरेखा सदिश की परिभाषा में दिखाई देने वाली बाधा के कारण, का मान $v_{\beta }$ एक ही तत्व के लिए $\beta$ का $A_{p}$ स्वचालित रूप से सभी के लिए $\alpha \in A$ , $v_{\alpha }$ निर्धारित करता है,

उपरोक्त औपचारिक परिभाषाएँ स्पष्ट रूप से एक अधिक अनौपचारिक संकेतन से मेल खाती हैं जो विशेष रूप से पाठ्यपुस्तकों में अधिकांशतः दिखाई देती है

v^{i}={\widetilde {v}}^{j}{\frac {\partial x^{i}}{\partial {\widetilde {x}}^{j}}}

और

df_{p}(v)={\frac {\partial f}{\partial x^{i}}}v^{i}.

औपचारिक परिभाषाओं के विचार को समझने के साथ, अधिकांश उद्देश्यों के लिए, इस शॉर्टहैंड नोटेशन के साथ काम करना बहुत सरल है।

एकता का विभाजन

विभेदक मैनिफोल्ड पर विभेदक कार्यों के शीफ की टोपोलॉजिकल विशेषताओं में से एक यह है कि यह एकता के विभाजन को स्वीकार करता है। यह विभेदक संरचना को मजबूत संरचनाओं (जैसे विश्लेषणात्मक और होलोमोर्फिक संरचनाओं) से कई गुना अलग करता है जो सामान्यतः एकता के विभाजन में विफल होते हैं।

मान लीजिए कि M वर्ग C^k का मैनिफोल्ड है, जहाँ 0 ≤ k ≤ ∞ है। मान लीजिए कि {U_α} M का एक विवृत आवरण है। फिर आवरण {U_α} के अधीन एकता का एक विभाजन निम्नलिखित नियमों को पूरा करने वाले M पर वास्तविक-मूल्य वाले C^k फलन φ_i का संग्रह है:

φ_i के समर्थन कॉम्पैक्ट और स्थानीय रूप से सीमित हैं;
कुछ α के लिए φ_i का समर्थन पूरी तरह से U_α में निहित है;
M के प्रत्येक बिंदु पर φ_i का योग 1 होता है: $\sum _{i}\phi _{i}(x)=1.$

(ध्यान दें कि यह अंतिम स्थिति वास्तव में φ के समर्थन की स्थानीय परिमितता के कारण प्रत्येक बिंदु पर एक सीमित योग है_i.)

C^k मैनिफोल्ड M के प्रत्येक खुले आवरण में एकता का C^k विभाजन होता है। यह Rⁿ पर C^k फलन की टोपोलॉजी से कुछ निर्माणों को अलग-अलग मैनिफोल्ड्स की श्रेणी में ले जाने की अनुमति देता है। विशेष रूप से, एक विशेष समन्वय एटलस के अधीनस्थ एकता के विभाजन को चुनकर और Rⁿ के प्रत्येक चार्ट में एकीकरण को अंजाम देकर एकीकरण पर चर्चा करना संभव है। इसलिए एकता के विभाजन कुछ अन्य प्रकार के फलन स्पेस पर विचार करने की अनुमति देते हैं: उदाहरण के लिए L^p स्पेस, सोबोलेव स्पेस और अन्य प्रकार के स्पेस जिन्हें एकीकरण की आवश्यकता होती है।

मैनिफोल्ड्स के बीच मैपिंग की भिन्नता

मान लीजिए कि M और N क्रमशः आयाम M और N के साथ दो अलग-अलग मैनिफोल्ड हैं, और f M से N तक एक फ़लन है। चूंकि अलग-अलग मैनिफोल्ड टोपोलॉजिकल स्पेस हैं, इसलिए हम जानते हैं कि f के निरंतर होने का क्या अर्थ है। लेकिन f क्या करता है C^k(M, N) के लिए अर्थ k ≥ 1? हम जानते हैं कि इसका क्या अर्थ है जब एफ यूक्लिडियन स्पेस के बीच एक फ़लन है, इसलिए यदि हम M के चार्ट और n के चार्ट के साथ f की रचना करते हैं, तो हमें एक मानचित्र मिलता है जो यूक्लिडियन स्पेस से M से N से यूक्लिडियन स्पेस तक जाता है, हम जानते हैं कि क्या इसका अर्थ C^k(R^m, Rⁿ) उस मानचित्र के लिए है। हम f को C^k(M, N) परिभाषित करते हैं, इसका अर्थ यह है कि चार्ट के साथ f की ऐसी सभी C^k(R^m, Rⁿ) रचनाएँ हैं। एक बार फिर, श्रृंखला नियम यह गारंटी देता है कि भिन्नता का विचार इस बात पर निर्भर नहीं करता है कि M और N पर एटलस के कौन से चार्ट चुने गए हैं। चूँकि, व्युत्पन्न को परिभाषित करना स्वयं अधिक सूक्ष्म है। यदि M या N स्वयं पहले से ही एक यूक्लिडियन स्थान है, तो हमें इसे एक में मैप करने के लिए चार्ट की आवश्यकता नहीं है।

बंडल

स्पर्शरेखा बंडल

किसी बिंदु के स्पर्शरेखा स्थान में उस बिंदु पर संभावित दिशात्मक व्युत्पन्न होते हैं, और इसका आयाम n के समान होता है जैसा कि मैनिफोल्ड का होता है। (गैर-एकवचन) के एक सेट के लिए बिंदु पर x_k स्थानीय निर्देशांक, निर्देशांक व्युत्पन्न $\partial _{k}={\frac {\partial }{\partial x_{k}}}$ स्पर्शरेखा स्थान के होलोनोमिक आधार को परिभाषित करें। सभी बिंदुओं पर स्पर्शरेखा स्थानों का संग्रह बदले में एक मैनिफोल्ड, स्पर्शरेखा बंडल में बनाया जा सकता है, जिसका आयाम 2n है। स्पर्शरेखा बंडल वह जगह है जहां सदिश फ़ील्ड स्थित हैं, और यह स्वयं एक अलग-अलग कई गुना है। लैग्रेंजियन प्रणाली स्पर्शरेखा बंडल पर एक फ़लन है। स्पर्शरेखा बंडल को 'R' (वास्तविक रेखा) से M तक 1-जेट (गणित) के बंडल के रूप में भी परिभाषित किया जा सकता है।

कोई व्यक्ति स्पर्शरेखा बंडल के लिए एक एटलस का निर्माण कर सकता है जिसमें चार्ट U_α × Rⁿ सम्मिलित हों, जहां U_α M के लिए एटलस में एक चार्ट को दर्शाता है। इन नए चार्टों में से प्रत्येक चार्ट U के लिए स्पर्शरेखा बंडल है, इस एटलस पर संक्रमण मानचित्रों को मूल मैनिफोल्ड पर संक्रमण मानचित्रों से परिभाषित किया गया है, और मूल भिन्नता वर्ग को बरकरार रखा गया है।

कोटैंजेंट बंडल

सदिश समष्टि का दोहरा समष्टि सदिश समष्टि पर वास्तविक मूल्यवान रैखिक फलनों का समुच्चय है। किसी बिंदु पर कोटैंजेंट स्थान उस बिंदु पर स्पर्शरेखा स्पेस का दोहरा है और तत्वों को कोटैंजेंट वैक्टर के रूप में जाना जाता है; कोटैंजेंट बंडल प्राकृतिक विभेदक मैनिफोल्ड संरचना के साथ-साथ सभी कोटैंजेंट वैक्टर का संग्रह है।

स्पर्शरेखा बंडल की तरह, कोटैंजेंट बंडल फिर से एक अलग-अलग प्रकार का है। हैमिल्टनियन यांत्रिकी कोटैंजेंट बंडल पर एक अदिश राशि है। कोटैंजेंट बंडल के कुल स्थान में एक सिंपलेक्टिक मैनिफ़ोल्ड की संरचना होती है। कोटैंजेंट वैक्टर को कभी-कभी कोवेक्टर भी कहा जाता है। कोटैंजेंट बंडल को M से 'R' तक के कार्यों के 1-जेट (गणित) के बंडल के रूप में भी परिभाषित किया जा सकता है।

कोटैंजेंट स्पेस के तत्वों को अनंतिम विस्थापन के रूप में माना जा सकता है: यदि f एक अलग फलन है तो हम प्रत्येक बिंदु p पर एक कोटैंजेंट वेक्टर df_p को परिभाषित कर सकते हैं, जो X_p से जुड़े f के व्युत्पन्न के लिए एक स्पर्शरेखा वेक्टर X_p भेजता है। चूँकि, प्रत्येक कोवेक्टर फ़ील्ड को इस तरह व्यक्त नहीं किया जा सकता है। जिन्हें स्पष्ट अंतर कहा जा सकता है। स्थानीय निर्देशांक x^k के दिए गए सेट के लिए, अंतर dx^k p पर कोटैंजेंट स्पेस का आधार बनाते हैं।

टेंसर बंडल

टेंसर बंडल स्पर्शरेखा बंडल और कोटैंजेंट बंडल के सभी टेंसर उत्पादों के सदिश बंडलों का प्रत्यक्ष योग है। बंडल का प्रत्येक तत्व एक टेंसर फ़ील्ड है, जो सदिश फ़ील्ड या अन्य टेंसर फ़ील्ड पर बहुरेखीय ऑपरेटर के रूप में फलन कर सकता है।

टेंसर बंडल पारंपरिक अर्थों में एक विभेदित मैनिफोल्ड नहीं है, क्योंकि यह अनंत आयामी है। चूँकि यह अदिश कार्यों के वलय पर एक बीजगणित (रिंग सिद्धांत) है। प्रत्येक टेंसर की विशेषता उसके रैंकों से होती है, जो इंगित करता है कि इसमें कितने स्पर्शरेखा और कोटैंजेंट कारक हैं। कभी-कभी इन रैंकों को सहप्रसरण और सहप्रसरण और वैक्टर रैंकों के विरोधाभास के रूप में संदर्भित किया जाता है, जो क्रमशः स्पर्शरेखा और कोटैंजेंट रैंक को दर्शाता है।

फ़्रेम बंडल

एक फ्रेम (या, अधिक स्पष्ट शब्दों में, एक स्पर्शरेखा फ्रेम), विशेष स्पर्शरेखा स्थान का एक क्रमबद्ध आधार है। इसी प्रकार, एक स्पर्शरेखा फ़्रेम R का एक रैखिक समरूपता हैⁿइस स्पर्शरेखा स्थान पर। एक गतिशील स्पर्शरेखा फ़्रेम सदिश फ़ील्ड की एक क्रमबद्ध सूची है जो उनके डोमेन के प्रत्येक बिंदु पर एक आधार देती है। कोई गतिशील फ़्रेम को फ़्रेम बंडल F(M), एक सामान्य रैखिक समूह| के एक भाग के रूप में भी मान सकता है GL(n, R) प्रमुख बंडल M पर सभी फ़्रेमों के सेट से बना है। फ़्रेम बंडल उपयोगी है क्योंकि M पर टेंसर फ़ील्ड को एफ (एम) पर समतुल्य सदिश-मूल्य वाले फ़लन के रूप में माना जा सकता है।

जेट बंडल

ऐसे मैनिफोल्ड पर जो पर्याप्त रूप से चिकना हो, विभिन्न प्रकार के जेट बंडलों पर भी विचार किया जा सकता है। मैनिफोल्ड का (प्रथम-क्रम) स्पर्शरेखा बंडल, प्रथम-क्रम संपर्क (गणित) के समतुल्य संबंध के मैनिफोल्ड मॉड्यूलो में वक्रों का संग्रह है। सादृश्य द्वारा, k-वें क्रम स्पर्शरेखा बंडल, k-वें क्रम संपर्क के संबंध में वक्रों का संग्रह है। इसी तरह, कोटैंजेंट बंडल मैनिफोल्ड पर फ़लन के 1-जेट्स का बंडल है: k-जेट बंडल उनके के-जेट्स का बंडल है। जेट बंडलों के सामान्य विचार के ये और अन्य उदाहरण मैनिफोल्ड्स पर अंतर ऑपरेटरों के अध्ययन में महत्वपूर्ण भूमिका निभाते हैं।

फ़्रेम की धारणा उच्च-क्रम वाले जेट की स्थिति में भी सामान्यीकृत होती है। K-वें क्रम के फ्रेम को Rⁿ से M तक भिन्नता के k-जेट के रूप में परिभाषित करें।^[6] सभी k-वें क्रम फ़्रेमों का संग्रह, F^k(M), M के ऊपर एक प्रमुख G^k बंडल है, जहां G^k, k-जेट्स का समूह है; अर्थात्, Rⁿ की भिन्नता के के-जेट्स से बना समूह जो मूल को ठीक करता है। ध्यान दें कि GL(n, R) स्वाभाविक रूप से G¹ के लिए आइसोमोर्फिक है, और प्रत्येक G^k, k ≥ 2 का एक उपसमूह है। विशेष रूप से, F²(M) का एक खंड M पर कनेक्शन के फ्रेम घटकों को देता है। इस प्रकार, भागफल बंडल F²(M) / GL(n, R) M के ऊपर सममित रैखिक कनेक्शन का बंडल है।

मैनिफोल्ड्स पर कैलकुलस

बहुभिन्नरूपी कलन की कई तकनीकें, यथोचित परिवर्तनों के साथ, भिन्न-भिन्न मैनिफोल्ड्स पर भी प्रयुक्त होती हैं। उदाहरण के लिए, एक स्पर्शरेखा सदिश के साथ एक भिन्न फ़लन के दिशात्मक व्युत्पन्न को परिभाषित किया जा सकता है, और इससे किसी फ़लन के कुल व्युत्पन्न को सामान्य बनाने का एक साधन प्राप्त होता है: अंतर। कैलकुलस के परिप्रेक्ष्य से, मैनिफोल्ड पर किसी फ़लन का व्युत्पन्न यूक्लिडियन स्पेस पर परिभाषित फ़लन के सामान्य व्युत्पन्न के समान ही व्यवहार करता है, कम से कम स्थानीय संपत्ति। उदाहरण के लिए, ऐसे कार्यों के लिए अंतर्निहित फ़लन और व्युत्क्रम फ़लन प्रमेयों के संस्करण हैं।

चूँकि, सदिश फ़ील्ड (और सामान्य रूप से टेंसर फ़ील्ड) की गणना में महत्वपूर्ण अंतर हैं। संक्षेप में, एक सदिश क्षेत्र का दिशात्मक व्युत्पन्न अच्छी तरह से परिभाषित नहीं है, या कम से कम सीधे विधि से परिभाषित नहीं है। एक सदिश क्षेत्र (या टेंसर क्षेत्र) के व्युत्पन्न के कई सामान्यीकरण उपस्थित हैं, और यूक्लिडियन स्थानों में भेदभाव की कुछ औपचारिक विशेषताओं को पकड़ते हैं। इनमें से प्रमुख हैं:

लाई व्युत्पन्न, जिसे विभेदक संरचना द्वारा विशिष्ट रूप से परिभाषित किया गया है, लेकिन दिशात्मक विभेदन की कुछ सामान्य विशेषताओं को संतुष्ट करने में विफल रहता है।
एक एफ़िन कनेक्शन, जो विशिष्ट रूप से परिभाषित नहीं है, लेकिन सामान्य दिशात्मक भेदभाव की विशेषताओं को अधिक संपूर्ण विधि से सामान्यीकृत करता है। क्योंकि एफ़िन कनेक्शन अद्वितीय नहीं है, यह डेटा का एक अतिरिक्त टुकड़ा है जिसे मैनिफोल्ड पर निर्दिष्ट किया जाना चाहिए।

समाकलन गणित के विचार भी डिफरेंशियल मैनिफोल्ड्स तक ले जाते हैं। ये बाह्य कलन और विभेदक रूप की भाषा में स्वाभाविक रूप से व्यक्त होते हैं। कई चरों में इंटीग्रल कैलकुलस के मौलिक प्रमेय - अर्थात् ग्रीन का प्रमेय, विचलन प्रमेय, और स्टोक्स का प्रमेय - एक प्रमेय (जिसे स्टोक्स का प्रमेय भी कहा जाता है) को सामान्यीकृत करते हैं, जो बाहरी व्युत्पन्न और सबमैनिफोल्ड पर एकीकरण से संबंधित होता है।

कार्यों की विभेदक गणना

सबमैनिफोल्ड्स और अन्य संबंधित अवधारणाओं की उपयुक्त धारणाएं तैयार करने के लिए दो मैनिफोल्ड्स के बीच विभेदक कार्यों की आवश्यकता होती है। अगर f : M → N आयाम m के एक भिन्न मैनिफोल्ड M से आयाम n के दूसरे भिन्न मैनिफोल्ड N के लिए एक भिन्न फलन है, फिर f का पुशफॉरवर्ड (अंतर) एक मैपिंग है df : TM → TN. इसे Tf द्वारा भी निरूपित किया जाता है और इसे 'स्पर्शरेखा मानचित्र' कहा जाता है। M के प्रत्येक बिंदु पर, यह एक स्पर्शरेखा स्थान से दूसरे स्पर्शरेखा स्थान में एक रैखिक परिवर्तन है:

df(p)\colon T_{p}M\to T_{f(p)}N.

p पर f की रैंक इस रैखिक परिवर्तन के मैट्रिक्स की रैंक है।

सामान्यतः किसी फ़लन की रैंक एक बिंदुवार संपत्ति होती है। चूँकि, यदि फ़लन की रैंक अधिकतम है, तो रैंक एक बिंदु के पड़ोस में स्थिर रहेगी। सार्ड के प्रमेय द्वारा दिए गए स्पष्ट अर्थ में, एक भिन्न फ़लन में सामान्यतः अधिकतम रैंक होती है। किसी बिंदु पर अधिकतम रैंक के कार्यों को [[विसर्जन (गणित)]] और विसर्जन (गणित) कहा जाता है:

अगर m ≤ n, और f : M → N की रैंक M है p ∈ M, तो f को p पर 'विसर्जन' कहा जाता है। यदि f, M के सभी बिंदुओं पर एक विसर्जन है और इसकी छवि पर एक समरूपता है, तो f एक 'एम्बेडिंग' है। एंबेडिंग M की धारणा को औपचारिक रूप देती है कि यह एन का सबमैनिफोल्ड है। सामान्य तौर पर, एक एम्बेडिंग स्व-प्रतिच्छेदन और अन्य प्रकार की गैर-स्थानीय टोपोलॉजिकल अनियमितताओं के बिना एक विसर्जन है।
यदि m ≥ n, और f : M → N की रैंक p ∈ M पर है, तो f को p पर निमज्जन कहा जाता है। अंतर्निहित फलन प्रमेय में कहा गया है कि यदि f, p पर एक जलमग्नता है, तो M स्थानीय रूप से N और R^m−n का p के पास गुणन है। औपचारिक शब्दों में, N में f(p) के पड़ोस में निर्देशांक (y₁, ..., y_n) उपस्थित हैं, और M में p के पड़ोस में m - n फलन x₁, ..., x_m_−n परिभाषित हैं। वह $(y_{1}\circ f,\dotsc ,y_{n}\circ f,x_{1},\dotsc ,x_{m-n})$ p के पड़ोस में M के स्थानीय निर्देशांक की एक प्रणाली है। विसर्जन तंतु और फाइबर बंडल के सिद्धांत की नींव बनाते हैं।

लाइ व्युत्पन्न

एक लाई व्युत्पन्न, जिसका नाम सोफस लाइ के नाम पर रखा गया है, एक मैनिफोल्ड M पर टेंसर फ़ील्ड के क्षेत्र पर बीजगणित पर एक व्युत्पत्ति (अमूर्त बीजगणित) है। M पर सभी लाई व्युत्पन्नों का सदिश स्थान लाई के संबंध में एक अनंत आयामी लाई बीजगणित बनाता है। द्वारा परिभाषित सदिश फ़ील्ड का ब्रैकेट

[A,B]:={\mathcal {L}}_{A}B=-{\mathcal {L}}_{B}A.

लाई डेरिवेटिव्स को सदिश फ़ील्ड्स द्वारा दर्शाया जाता है, जैसे कि लाई समूह M पर प्रवाह के लाई समूहों (सक्रिय परिवर्तन भिन्नता) से संबंधित लाई बीजगणित। इसे दूसरी विधि से देखते हुए, M के भिन्नता के समूह (गणित) में है लाई डेरिवेटिव की संबद्ध लाई बीजगणित संरचना, एक तरह से लाई समूह सिद्धांत के सीधे अनुरूप है।

बाहरी गणना

बाहरी कैलकुलस ग्रेडियेंट , विचलन और कर्ल (गणित) ऑपरेटरों के सामान्यीकरण की अनुमति देता है।

प्रत्येक बिंदु पर विभेदक रूपों के बंडल में, उस बिंदु पर स्पर्शरेखा स्थान पर सभी पूरी तरह से एंटीसिमेट्रिक टेंसर बहुरेखीय मानचित्र मानचित्र सम्मिलित होते हैं। यह स्वाभाविक रूप से मैनिफोल्ड के आयाम के बराबर प्रत्येक एन के लिए एन-रूपों में विभाजित है; एन-फॉर्म एक एन-वेरिएबल फॉर्म है, जिसे डिग्री एन का फॉर्म भी कहा जाता है। 1-रूप कोटैंजेंट सदिश हैं, जबकि 0-रूप केवल अदिश फलन हैं। सामान्य तौर पर, एक एन-फॉर्म कोटैंजेंट रैंक एन और टैंजेंट रैंक 0 वाला एक टेंसर होता है। लेकिन ऐसा हर टेंसर एक फॉर्म नहीं होता है, क्योंकि एक फॉर्म को एंटीसिमेट्रिक होना चाहिए।

बाहरी व्युत्पन्न

बाहरी व्युत्पन्न एक चिकनी मैनिफोल्ड पर सभी चिकनी अंतर रूपों के वर्गीकृत सदिश स्थान पर एक रैखिक ऑपरेटर $M$ है. इसे सामान्यतः $d$ द्वारा दर्शाया जाता है. अधिक स्पष्ट रूप से, यदि $n=\dim(M)$ , के लिए $0\leq k\leq n$ परिचालक $d$ अंतरिक्ष का मानचित्रण $\Omega ^{k}(M)$ करता है, $M$ का $k$ -पर प्रपत्र अंतरिक्ष में $\Omega ^{k+1}(M)$ का $(k+1)$ -फॉर्म करता है (यदि $k>n$ कोई गैर-शून्य नहीं हैं, $k$ -पर प्रपत्र $M$ तो मानचित्र $d$ समान $n$ -रूप से शून्य है)।

उदाहरण के लिए, एक सुचारु फलन का बाहरी अंतर $f$ स्थानीय निर्देशांक $x_{1},\ldots ,x_{n}$ में दिया गया है, संबद्ध स्थानीय सह-फ़्रेम के साथ $dx_{1},\ldots ,dx_{n}$ सूत्र द्वारा:

df=\sum _{i=1}^{n}{\frac {\partial f}{\partial x_{i}}}dx_{i}.

बाहरी अंतर फॉर्म के वेज गुणन के संबंध में गुणन नियम के समान, निम्नलिखित पहचान को संतुष्ट करता है:

d(\omega \wedge \eta )=d\omega \wedge \eta +(-1)^{\deg \omega }\omega \wedge d\eta .

बाहरी व्युत्पन्न भी पहचान

d\circ d=0

को संतुष्ट करता है। अर्थात यदि

\omega

एक

k

-रूप है, तो

(k+2)

-प्रपत्र

d(df)

समान रूप से लुप्त हो रहा है. एक प्रपत्र

\omega

ऐसा है कि

d\omega =0

बंद कहा जाता है, जबकि एक प्रपत्र

\omega

ऐसा है कि

\omega =d\eta

किसी अन्य रूप के लिए

\eta

स्पष्ट कहा जाता है। पहचान

d\circ d=0

का एक और सूत्रीकरण क्या यह एक स्पष्ट प्रपत्र बंद है। यह किसी को मैनिफोल्ड के डॉ कहलमज कोहोमोलॉजी को

M

परिभाषित करने की अनुमति देता है, जहां

k

वां कोहोमोलोजी समूह बंद रूपों का भागफल समूह

M

है, जिसे

M

पर स्पष्ट रूपों द्वारा अनुमति दिया जाता है।

विभेदक मैनिफोल्ड्स की टोपोलॉजी

टोपोलॉजिकल मैनिफोल्ड्स के साथ संबंध

मान लीजिए कि $M$ टोपोलॉजिकल $n$ -मैनिफोल्ड है।

यदि कोई सहज एटलस $\{(U_{\alpha },\phi _{\alpha })\}_{\alpha \in A}$ दिया जाए, एक चिकनी एटलस ढूंढना सरल है जो एक अलग चिकनी कई गुना संरचना को $M;$ परिभाषित करता है; एक होमियोमोर्फिज्म $\Phi :M\to M$ पर विचार करें, जो दिए गए एटलस के सापेक्ष सहज नहीं है; उदाहरण के लिए, कोई पहचान मानचित्र स्थानीयकृत गैर-चिकनी बुम्प को संशोधित कर सकता है। फिर नये एटलस $\{(\Phi ^{-1}(U_{\alpha }),\phi _{\alpha }\circ \Phi )\}_{\alpha \in A},$ पर विचार करें; जिसे सहज एटलस के रूप में आसानी से सत्यापित किया जा सकता है। चूँकि, नए एटलस के चार्ट पुराने एटलस के चार्ट के साथ आसानी से संगत नहीं हैं, क्योंकि इसके लिए $\phi _{\alpha }\circ \Phi \circ \phi _{\beta }^{-1}$ इसकी आवश्यकता होगी और $\phi _{\alpha }\circ \Phi ^{-1}\circ \phi _{\beta }^{-1}$ किसी के लिए भी सहज हैं $\alpha$ और $\beta ,$ इन नियमों के साथ बिल्कुल वही परिभाषा है, जो दोनों $\Phi$ और $\Phi ^{-1}$ सहज हैं, कैसे के विपरीत $\Phi$ चुना गया।

प्रेरणा के रूप में इस अवलोकन के साथ, कोई भी चिकनी एटलस के स्थान पर एक तुल्यता संबंध को परिभाषित कर सकता है $M$ उस चिकनी एटलस की घोषणा करके $\{(U_{\alpha },\phi _{\alpha })\}_{\alpha \in A}$ और $\{(V_{\beta },\psi _{\beta })\}_{\beta \in B}$ यदि समरूपता है तो समतुल्य हैं $\Phi :M\to M$ ऐसा है कि $\{(\Phi ^{-1}(U_{\alpha }),\phi _{\alpha }\circ \Phi )\}_{\alpha \in A}$ के साथ सहजता से संगत है $\{(V_{\beta },\psi _{\beta })\}_{\beta \in B},$ और ऐसा कि $\{(\Phi (V_{\beta }),\psi _{\beta }\circ \Phi ^{-1})\}_{\beta \in B}$ के साथ $\{(U_{\alpha },\phi _{\alpha })\}_{\alpha \in A}$ सहजता से संगत है।

अधिक संक्षेप में, कोई यह कह सकता है कि यदि कोई भिन्नता उपस्थित है तो दो चिकने एटलस समतुल्य $M\to M,$ हैं, जिसमें एक स्मूथ एटलस डोमेन के लिए लिया जाता है और दूसरा स्मूथ एटलस रेंज के लिए लिया जाता है।

ध्यान दें कि यह समतुल्य संबंध समतुल्य संबंध का परिशोधन है जो एक चिकनी कई गुना संरचना को परिभाषित करता है, क्योंकि कोई भी दो सुचारू रूप से संगत एटलस वर्तमान अर्थ में भी संगत हैं; कोई भी $\Phi$ पहचान मानचित्र ले सकता है।

यदि $M$ का आयाम 1, 2, या 3 है, तो उस पर एक चिकनी संरचना $M$ उपस्थित है, और सभी विशिष्ट चिकनी संरचनाएं उपरोक्त अर्थ में समतुल्य हैं। उच्च आयामों में स्थिति अधिक जटिल है, चूँकि इसे पूरी तरह से समझा नहीं गया है।

कुछ टोपोलॉजिकल मैनिफोल्ड्स में कोई चिकनी संरचना नहीं होती है, जैसा कि मूल रूप से कर्वैयर मैनिफोल्ड के साथ दिखाया गया था। दस-आयामी उदाहरण केरवैरे (1960). माइकल फ्रीडमैन के परिणामों के साथ संयोजन में, साइमन डोनाल्डसन के कारण अंतर ज्यामिति में आंशिक अंतर समीकरणों के डोनाल्डसन के प्रमेय से पता चलता है कि कई सरल रूप से जुड़े कॉम्पैक्ट टोपोलॉजिकल 4-मैनिफोल्ड चिकनी संरचनाओं को स्वीकार नहीं करते हैं। एक सुविख्यात विशेष उदाहरण E₈ मैनिफोल्ड अनेक गुना है।
कुछ टोपोलॉजिकल मैनिफोल्ड कई चिकनी संरचनाओं को स्वीकार करते हैं जो ऊपर दिए गए अर्थ में समकक्ष नहीं हैं। इसकी खोज मूलतः जॉन मिल्नोर ने विदेशी क्षेत्र|विदेशी 7-गोले के रूप में की थी।^[7]

वर्गीकरण

प्रत्येक एक-आयामी जुड़ा हुआ स्मूथ मैनिफोल्ड किसी एक से $\mathbb {R}$ या $S^{1}$ भिन्न होता है, प्रत्येक अपनी मानक चिकनी संरचनाओं के साथ।

स्मूथ 2-मैनिफोल्ड्स के वर्गीकरण के लिए, सतह (टोपोलॉजी) देखें। एक विशेष परिणाम यह है कि प्रत्येक द्वि-आयामी कनेक्टेड कॉम्पैक्ट स्मूथ मैनिफोल्ड निम्नलिखित में से किसी एक $S^{2},$ या $(S^{1}\times S^{1})\sharp \cdots \sharp (S^{1}\times S^{1}),$ या $\mathbb {RP} ^{2}\sharp \cdots \sharp \mathbb {RP} ^{2}$ से भिन्न होता है। यदि कोई चिकनी संरचना के अतिरिक्त जटिल-भिन्न संरचना पर विचार करता है तो स्थिति टेइचमुलर स्थान जैसी है।

तीन आयामों में स्थिति अत्यधिक जटिल है, और ज्ञात परिणाम अधिक अप्रत्यक्ष हैं। एक उल्लेखनीय परिणाम, जिसे 2002 में आंशिक अंतर समीकरणों की विधियों से प्रमाणित किया गया था, थर्स्टन का ज्यामितीयकरण अनुमान है, जिसमें कहा गया है कि किसी भी कॉम्पैक्ट चिकनी 3-मैनिफोल्ड को अलग-अलग हिस्सों में विभाजित किया जा सकता है, जिनमें से प्रत्येक रीमानियन मेट्रिक्स को स्वीकार करता है जिसमें कई समरूपताएं होती हैं। जियोमेट्रिजेबल 3-मैनिफोल्ड्स के लिए विभिन्न मान्यता परिणाम भी हैं, जैसे मोस्टो कठोरता और हाइपरबोलिक समूहों के लिए आइसोमोर्फिज्म समस्या के लिए सेला का एल्गोरिदम है।^[8]

तीन से अधिक n के लिए n-मैनिफोल्ड्स का वर्गीकरण असंभव माना जाता है, यहाँ तक कि समरूप समतुल्यता तक भी। किसी समूह समूह की किसी भी अंतिम प्रस्तुति को देखते हुए, कोई उस समूह को मौलिक समूह के रूप में रखते हुए एक बंद 4-मैनिफोल्ड का निर्माण कर सकता है। चूंकि सीमित रूप से प्रस्तुत समूहों के लिए समरूपता समस्या का निर्णय लेने के लिए कोई एल्गोरिदम नहीं है, इसलिए यह तय करने के लिए कोई एल्गोरिदम नहीं है कि क्या दो 4-मैनिफोल्ड में एक ही मौलिक समूह है। चूंकि पहले वर्णित निर्माण के परिणामस्वरूप 4-मैनिफोल्ड्स का एक वर्ग बनता है जो होमोमोर्फिक हैं यदि और केवल यदि उनके समूह आइसोमोर्फिक हैं, तो 4-मैनिफोल्ड्स के लिए होमोमोर्फिज्म समस्या निर्णय समस्या है। इसके अतिरिक्त, चूंकि तुच्छ समूह को पहचानना भी अनिर्णीत है, सामान्य तौर पर यह तय करना भी संभव नहीं है कि क्या मैनिफोल्ड में तुच्छ मौलिक समूह है, अर्थात बस जुड़ा हुआ है।

माइकल फ्रीडमैन द्वारा प्रतिच्छेदन सिद्धांत और किर्बी-सीबेनमैन इनवेरिएंट का उपयोग करके सरल रूप से जुड़े 4-कई गुना को होमोमोर्फिज्म तक वर्गीकृत किया गया है। स्मूथ 4-मैनिफोल्ड सिद्धांत को अधिक जटिल माना जाता है, जैसे कि R पर विदेशी R4s⁴ प्रदर्शन करना।

चूँकि, आयाम ≥ 5 के आसानी से जुड़े हुए चिकने मैनिफ़ोल्ड के लिए स्थिति अधिक सुव्यवस्थित हो जाती है, जहाँ एच-कोबॉर्डिज़्म प्रमेय का उपयोग वर्गीकरण को होमोटॉपी समकक्ष तक कम करने के लिए किया जा सकता है, और सर्जरी सिद्धांत को प्रयुक्त किया जा सकता है।^[9] यह डेनिस बार्डन द्वारा सरल रूप से जुड़े 5-कई गुना का स्पष्ट वर्गीकरण प्रदान करने के लिए किया गया है।

चिकनी मैनिफ़ोल्ड पर संरचनाएँ

(छद्म-)रीमैनियन मैनिफोल्ड

रीमैनियन मैनिफोल्ड में प्रत्येक व्यक्तिगत स्पर्शरेखा स्थान पर एक सकारात्मक-निश्चित आंतरिक गुणन स्थान के साथ एक चिकनी मैनिफोल्ड होता है। आंतरिक उत्पादों के इस संग्रह को रीमैनियन मीट्रिक कहा जाता है, और यह स्वाभाविक रूप से एक सममित 2-टेंसर क्षेत्र है। यह मीट्रिक एक प्राकृतिक सदिश अंतरिक्ष समरूपता की पहचान $T_{p}M\to T_{p}^{\ast }M$ करता है। प्रत्येक $p\in M$ के लिए रीमैनियन मैनिफ़ोल्ड पर कोई लंबाई, आयतन और कोण की धारणाओं को परिभाषित कर सकता है। किसी भी स्मूथ मैनिफोल्ड को कई अलग-अलग रीमैनियन मेट्रिक्स दिए जा सकते हैं।

एक छद्म-रीमैनियन मैनिफोल्ड, रीमैनियन मैनिफोल्ड की धारणा का एक सामान्यीकरण है जहां आंतरिक उत्पादों को निश्चित बिलिनियर फॉर्म | सकारात्मक-निश्चित होने के विपरीत, मीट्रिक हस्ताक्षर की अनुमति दी जाती है; उन्हें अभी भी गैर-पतित होने की आवश्यकता है। प्रत्येक चिकनी छद्म-रीमैनियन और रीमैनियन मैनिफोल्ड कई संबंधित टेंसर क्षेत्रों को परिभाषित करता है, जैसे कि रीमैन वक्रता टेंसर। छद्म-रिमानियन हस्ताक्षर के कई गुना (3, 1) सामान्य सापेक्षता में मौलिक हैं। प्रत्येक चिकने मैनिफोल्ड को (गैर-रीमानियन) छद्म-रीमैनियन संरचना नहीं दी जा सकती; ऐसा करने पर टोपोलॉजिकल प्रतिबंध हैं।

फिन्सलर मैनिफोल्ड रीमैनियन मैनिफोल्ड का एक अलग सामान्यीकरण है, जिसमें आंतरिक गुणन को सदिश मानदंड से बदल दिया जाता है; इस प्रकार, यह लंबाई की परिभाषा की अनुमति देता है, लेकिन कोण की नहीं।

सिंपलेक्टिक मैनिफोल्ड्स

एक सिंपलेक्टिक मैनिफोल्ड एक बंद फॉर्म (कैलकुलस), नॉनडिजेनरेट फॉर्म 2-प्रपत्र से सुसज्जित मैनिफोल्ड है। यह स्थिति सिम्प्लेक्टिक मैनिफ़ोल्ड को सम-आयामी होने के लिए बाध्य करती है, इस तथ्य के कारण कि तिरछा-सममित $(2n+1)\times (2n+1)$ सभी मैट्रिक्स में शून्य निर्धारक होता है। दो मूलभूत उदाहरण हैं:

कोटैंजेंट बंडल, जो हैमिल्टनियन यांत्रिकी में चरण रिक्त स्थान के रूप में उत्पन्न होते हैं, एक प्रेरक उदाहरण हैं, क्योंकि वे एक टॉटोलॉजिकल एक-रूप को स्वीकार करते हैं।
सभी उन्मुख द्वि-आयामी रीमैनियन मैनिफोल्ड्स $(M,g)$ रूप को परिभाषित करके, स्वाभाविक रूप से, सहानुभूतिपूर्ण हैं $\omega (u,v)=g(u,J(v))$ जहाँ, किसी के लिए $v\in T_{p}M,$ $J(v)$ सदिश को इस प्रकार $v,J(v)$ निरूपित करता है एक उन्मुख $g_{p}$ -अर्थसामान्य आधार का $T_{p}M$ है।

लाइ समूह

एक लाइ समूह में एक C^∞ होता है, कई गुना $G$ एक साथ एक समूह (गणित) संरचना पर $G$ जैसे कि गुणन और व्युत्क्रम मानचित्र $m:G\times G\to G$ और $i:G\to G$ कई गुना के मानचित्रों की तरह चिकने हैं। ये वस्तुएं अधिकांशतः (निरंतर) समरूपता का वर्णन करते समय स्वाभाविक रूप से उत्पन्न होती हैं, और वे चिकनी विविधता के उदाहरणों का एक महत्वपूर्ण स्रोत बनाती हैं।

चूँकि, स्मूथ मैनिफोल्ड्स के कई अन्यथा परिचित उदाहरणों को एक लाई समूह संरचना नहीं दी जा सकती है, क्योंकि एक लाई समूह दिया गया है $G$ और कोई भी $g\in G$ , कोई मानचित्र पर विचार कर सकता है $m(g,\cdot ):G\to G$ जो पहचान तत्व भेजता है $e$ को $g$ और इसलिए, अंतर पर विचार करके $T_{e}G\to T_{g}G,$ लाइ समूह के किन्हीं दो स्पर्शरेखा स्थानों के बीच एक प्राकृतिक पहचान देता है। विशेष रूप से, एक इच्छानुसार गैर-शून्य सदिश पर विचार करके $T_{e}G,$ कोई इन पहचानों का उपयोग सुचारू गैर-लुप्त होने वाले सदिश फ़ील्ड को देने के लिए कर सकता है $G.$ उदाहरण के लिए, इससे पता चलता है कि कोई भी हेयरी बॉल प्रमेय|सम-आयामी क्षेत्र लाई समूह संरचना का समर्थन नहीं कर सकता है। यही तर्क सामान्यतः दिखाता है कि प्रत्येक लाइ समूह को कई गुना समानांतर होना चाहिए।

वैकल्पिक परिभाषाएँ

छद्म समूह

छद्मसमूह की धारणा^[10] विभिन्न संरचनाओं को एक समान विधि से मैनिफोल्ड्स पर परिभाषित करने की अनुमति देने के लिए एटलस का एक लचीला सामान्यीकरण प्रदान करता है। एक छद्म समूह में एक टोपोलॉजिकल स्पेस एस और एक संग्रह Γ होता है जिसमें एस के विवृत उपसमुच्चय से लेकर एस के अन्य विवृत उपसमुच्चय तक होमोमोर्फिज्म सम्मिलित होते हैं जैसे कि

अगर f ∈ Γ, और U, f के डोमेन का एक विवृत उपसमुच्चय है, तो प्रतिबंध f|_U Γ में भी है.
यदि f, S के विवृत उपसमुच्चय के मिलन से एक समरूपता $\cup _{i}\,U_{i}$ है, तो S के एक विवृत उपसमुच्चय के लिए f ∈ Γ बशर्ते $f|_{U_{i}}\in \Gamma$ प्रत्येक i के लिए
हर विवृत के लिए U ⊂ S, U का पहचान परिवर्तन Γ में है।
अगर f ∈ Γ, तब f⁻¹ ∈ Γ.
Γ के दो तत्वों की संरचना Γ में है.

ये अंतिम तीन स्थितियाँ एक समूह (गणित) की परिभाषा के अनुरूप हैं। ध्यान दें कि Γ को एक समूह होने की आवश्यकता नहीं है, चूंकि फ़लन S पर विश्व स्तर पर परिभाषित नहीं हैं। उदाहरण के लिए, सभी स्थानीय C^k का संग्रह 'R' पर भिन्नताⁿएक छद्म समूह बनाएं। 'C' में विवृत सेटों के बीच सभी बिहोलोमोर्फिज्म एक छद्म समूह बनाएं। अधिक उदाहरणों में सम्मिलित हैं: 'R' के मानचित्रों को संरक्षित करने वाला अभिविन्यास, लक्षणरूपता, मोबियस परिवर्तन, एफ़िन परिवर्तन, इत्यादि। इस प्रकार, विभिन्न प्रकार के फ़लन वर्ग छद्मसमूह निर्धारित करते हैं।

एक एटलस (U_i, φ_i) होमोमोर्फिज्म का φ_i से U_i ⊂ M टोपोलॉजिकल स्पेस के सबसेट को खोलने के लिए एस को एक छद्म समूह के साथ संगत माना जाता है Γ बशर्ते कि संक्रमण फलन φ_j ∘ φ_i⁻¹ : φ_i(U_i ∩ U_j) → φ_j(U_i ∩ U_j) सभी Γ में हैं।

एक विभेदक मैनिफोल्ड तब C के छद्म समूह के साथ संगत एक एटलस है 'R' पर फलन करता है. एक कॉम्प्लेक्स मैनिफोल्ड एक एटलस है जो 'C' में विवृत सेट पर बिहोलोमोर्फिक फ़लनो के साथ संगत है। इस प्रकार, छद्म समूह एक एकल ढांचा प्रदान करते हैं जिसमें अंतर ज्यामिति और टोपोलॉजी के लिए कई गुना महत्वपूर्ण संरचनाओं का वर्णन किया जा सकता है।

संरचना शीफ़

कभी-कभी, मैनिफोल्ड को C प्रदान करने के लिए वैकल्पिक दृष्टिकोण का उपयोग करना उपयोगी हो सकता है-संरचना. यहां वास्तविक विश्लेषणात्मक मैनिफोल्ड के लिए k = 1, 2, ..., ∞, या ω है। समन्वय चार्ट पर विचार करने के अतिरिक्त, मैनिफोल्ड पर परिभाषित कार्यों के साथ प्रारंभ करना संभव है। M^k का शीफ (गणित), 'C' को दर्शाता है, एक प्रकार का ऑपरेटर है जो प्रत्येक विवृत सेट के लिए परिभाषित करता है U ⊂ M, एक बीजगणित C^k(U) सतत कार्यों का U → R. एक संरचना शीफ सी कहा जाता है कि k, M को C की संरचना देता हैकआयाम एन के कई गुना बशर्ते कि, किसी के लिए p ∈ M, p और एन फ़लन का पड़ोस U उपस्थित है x¹, ..., xⁿ ∈ C^k(U) ऐसा कि मानचित्र f = (x¹, ..., xⁿ) : U → Rⁿ R में एक विवृत सेट पर एक होमोमोर्फिज्म है, और ऐसा कि U 'R' पर निरन्तर अलग-अलग कार्यों के के-बार के शीफ का ठहराना है।^[11]

विशेष रूप से, इस बाद वाली स्थिति का अर्थ है कि 'C' में कोई भी फ़लन एचk(V), V के लिए, विशिष्ट रूप से लिखा जा सकता है h(x) = H(x¹(x), ..., xⁿ(x)), जहां H, f(V) पर एक k-गुना भिन्न फ़लन है ('R' में एक विवृत सेट). इस प्रकार, शीफ-सैद्धांतिक दृष्टिकोण यह है कि भिन्न-भिन्न मैनिफोल्ड पर कार्यों को स्थानीय निर्देशांक में 'R' पर भिन्न-भिन्न कार्यों के रूप में व्यक्त किया जा सकता है। n, और एक फोर्टिओरी तर्क यह मैनिफोल्ड पर विभेदक संरचना को चित्रित करने के लिए पर्याप्त है।

स्थानीय छल्लों के ढेर

भिन्न-भिन्न मैनिफोल्ड्स को परिभाषित करने के लिए एक समान, लेकिन अधिक तकनीकी दृष्टिकोण, चक्राकार स्थान की धारणा का उपयोग करके तैयार किया जा सकता है। यह दृष्टिकोण बीजगणितीय ज्यामिति में योजना (गणित) के सिद्धांत से अत्यधिक प्रभावित है, लेकिन अलग-अलग कार्यों के रोगाणु (गणित) के स्थानीय छल्ले का उपयोग करता है। यह जटिल विविधताओं के संदर्भ में विशेष रूप से लोकप्रिय है।

हम 'Rⁿ' पर मूल संरचना शीफ का वर्णन करके प्रारंभ करते हैं। यदि U 'Rⁿ' में एक विवृत समुच्चय है, माना

O(U) = C^k(U, R)

U पर सभी वास्तविक-मूल्य वाले के-बार निरन्तर भिन्न-भिन्न कार्यों से मिलकर बनता है। जैसे-जैसे U बदलता है, यह 'Rⁿ' पर रिंगों का एक समूह निर्धारित करता है। डंठल O_p के लिए p ∈ Rⁿ p के निकट कार्यों के रोगाणु (गणित) से युक्त है, और 'R' पर एक बीजगणित है। विशेष रूप से, यह एक स्थानीय वलय है जिसके अद्वितीय अधिकतम आदर्श में वे फलन सम्मिलित होते हैं जो p पर लुप्त हो जाते हैं। जोड़ी (Rⁿ, O) स्थानीय रूप से वलयित स्थान का एक उदाहरण है: यह एक टोपोलॉजिकल स्थान है जो एक शीफ़ से सुसज्जित है जिसके डंठल प्रत्येक स्थानीय वलय हैं।

एक अवकलनीय मैनिफोल्ड (कक्षा C^k का)) में एक जोड़ा (M, O_M) होता है, जहां M दूसरा गणनीय हॉसडॉर्फ स्थान है, और 'O'_M M पर परिभाषित स्थानीय आर-बीजगणित का एक समूह है, जैसे कि स्थानीय रूप से चक्राकार स्थान (M, O_M) स्थानीय रूप (Rⁿ, O) से समरूपी है। इस तरह, अलग-अलग मैनिफोल्ड्स को R में योजना (गणित) मॉडल के रूप में सोचा जा सकता है, इस का अर्थ है कि ^[12] प्रत्येक बिंदु के लिए p ∈ M, p का पड़ोसी U और कार्यों की एक जोड़ी (f, f^#) है, जहाँ

f : U → f(U) ⊂ Rⁿ Rⁿ में एक विवृत सेट पर एक होमोमोर्फिज्म है।
f^#: O|_f(U) → f_∗ (O_M|_U) शीव्स की समरूपता है।
f^# का स्थानीयकरण स्थानीय वलयों की एक समरूपता है

f^#_f(p) : O_f(p) → O_M,p.

इस अमूर्त ढांचे के अंदर भिन्न-भिन्न विविधताओं का अध्ययन करने के लिए कई महत्वपूर्ण प्रेरणाएँ हैं। सबसे पहले, कोई प्राथमिक कारण नहीं है कि मॉडल स्थान को 'R' होना चाहिएⁿ. उदाहरण के लिए, (विशेष रूप से बीजगणितीय ज्यामिति में), कोई इसे सम्मिश्र संख्या C का स्थान मान सकता हैⁿ होलोमोर्फिक फ़लन के शीफ़ (इस प्रकार जटिल विश्लेषणात्मक ज्यामिति के स्थानों पर पहुंचने), या बहुपदों के शीफ़ (इस प्रकार जटिल बीजगणितीय ज्यामिति में रुचि के स्थानों पर पहुंचने) से सुसज्जित। व्यापक संदर्भ में, इस अवधारणा को किसी योजना की किसी भी उपयुक्त धारणा के लिए अनुकूलित किया जा सकता है (टोपोस देखें)। दूसरा, निर्माण के लिए निर्देशांक अब स्पष्ट रूप से आवश्यक नहीं हैं। एक समन्वय प्रणाली का एनालॉग युग्म (f, f^#) है, लेकिन ये चर्चा के केंद्र में होने के अतिरिक्त केवल स्थानीय समरूपता के विचार को मापते हैं (जैसा कि चार्ट और एटलस के मामले में होता है)। तीसरा, शीफO_M यह स्पष्ट रूप से कार्यों का एक समूह नहीं है। बल्कि, यह निर्माण के परिणामस्वरूप कार्यों के एक समूह के रूप में उभरता है (स्थानीय रिंगों के भागफल के माध्यम से उनके अधिकतम आदर्शों द्वारा)। इसलिए, यह संरचना की अधिक आदिम परिभाषा है ( सिंथेटिक विभेदक ज्यामिति देखें)।

इस दृष्टिकोण का एक अंतिम लाभ यह है कि यह विभेदक ज्यामिति और टोपोलॉजी के अध्ययन की कई मूलभूत वस्तुओं के प्राकृतिक प्रत्यक्ष विवरण की अनुमति देता है।

एक बिंदु पर कोटैंजेंट स्पेस I_p/I_p² है, जहां I_pडंठल O_M,p का अधिकतम आदर्श है।
सामान्य तौर पर, संपूर्ण कोटैंजेंट बंडल संबंधित तकनीक द्वारा प्राप्त किया जा सकता है (विवरण के लिए कोटैंजेंट बंडल देखें)।
टेलर श्रृंखला (और जेट (गणित)) को पूर्णता (बीजगणित) क्रल टोपोलॉजी का उपयोग करके समन्वय-स्वतंत्र विधि से प्राप्त किया जा सकता है।
स्पर्शरेखा बंडल (या अधिक स्पष्ट रूप से इसके अनुभागों का शीफ़) को O_M के आकारिकी के शीफ़ से पहचाना जा सकता है दोहरी संख्याओं के वलय में।

सामान्यीकरण

चिकने नक्शों के साथ स्मूथ मैनिफोल्ड्स के श्रेणी सिद्धांत में कुछ वांछनीय गुणों का अभाव है, और लोगों ने इसे सुधारने के लिए स्मूथ मैनिफोल्ड्स को सामान्य बनाने का प्रयास किया है। डिफियोलॉजिकल स्पेस चार्ट की एक अलग धारणा का उपयोग करते हैं जिसे प्लॉट के रूप में जाना जाता है। फ्रोलिचर स्पेस और कक्षीय अन्य प्रयास हैं।

एक संशोधन योग्य सेट उच्च आयामों के लिए टुकड़े-वार चिकने या संशोधन योग्य वक्र के विचार को सामान्यीकृत करता है; चूँकि, संशोधन योग्य सेट सामान्य मैनिफोल्ड में नहीं होते हैं।

विशेष रूप से बनच मैनिफोल्ड और फ़्रेचेट मैनिफ़ोल्ड्स सुविधाजनक सदिश स्पेस#अनुप्रयोग: परिमित आयामी मैनिफोल्ड्स के बीच मैपिंग के मैनिफोल्ड्स अनंत आयामी विभेदक अनेक गुना हैं।

गैर-क्रमविनिमेय ज्यामिति

C के लिए मैनिफोल्ड M, वास्तविक-मूल्यवान C का सेट (गणित) है। मैनिफ़ोल्ड पर k फ़लनो बिंदुवार जोड़ और गुणा के अनुसार एक फ़ील्ड पर एक बीजगणित बनाता है, जिसे स्केलर फ़ील्ड का बीजगणित या बस स्केलर का बीजगणित कहा जाता है। इस बीजगणित में गुणात्मक पहचान के रूप में निरंतर फ़लन 1 है, और यह बीजगणितीय ज्यामिति में नियमित कार्यों की अंगूठी का एक अलग एनालॉग है।

स्केलर के बीजगणित से मैनिफोल्ड का पुनर्निर्माण करना संभव है, पहले एक सेट के रूप में, लेकिन एक टोपोलॉजिकल स्पेस के रूप में भी - यह बानाच-स्टोन प्रमेय का एक अनुप्रयोग है, और इसे औपचारिक रूप से C*-बीजगणित के स्पेक्ट्रम के रूप में जाना जाता है। सबसे पहले, M के बिंदुओं और बीजगणित समरूपता φ: C^k(M) → R के बीच एक-से-एक पत्राचार है, क्योंकि इस तरह की एक समरूपता φ C^k (M) में एक कोडिमेशन एक आदर्श से मेल खाती है (अर्थात् कर्नेल) φ), जो आवश्यक रूप से एक अधिकतम आदर्श है। इसके विपरीत, इस बीजगणित में प्रत्येक अधिकतम आदर्श एक बिंदु पर लुप्त होने वाले कार्यों का एक आदर्श है, जो दर्शाता है कि C^k(M) का MSpec (मैक्स स्पेक) M को एक बिंदु सेट के रूप में पुनर्प्राप्त करता है, चूंकि वास्तव में यह M को एक टोपोलॉजिकल स्पेस के रूप में पुनर्प्राप्त करता है।

कोई व्यक्ति विभिन्न ज्यामितीय संरचनाओं को स्केलर के बीजगणित के संदर्भ में बीजगणितीय रूप से परिभाषित कर सकता है, और ये परिभाषाएँ अधिकांशतः बीजगणितीय ज्यामिति (ज्यामितीय रूप से रिंगों की व्याख्या करना) और ऑपरेटर सिद्धांत (बैनाच रिक्त स्थान की ज्यामितीय रूप से व्याख्या करना) को सामान्यीकृत करती हैं। उदाहरण के लिए, M के स्पर्शरेखा बंडल को M पर सुचारू कार्यों के बीजगणित की व्युत्पत्ति के रूप में परिभाषित किया जा सकता है।

मैनिफोल्ड का यह बीजगणित (एक ज्यामितीय वस्तु को बीजगणित के साथ प्रतिस्थापित करना) एक C*-बीजगणित की धारणा की ओर ले जाता है - एक क्रमविनिमेय C*-बीजगणित, जो बानाच-स्टोन द्वारा स्पष्ट रूप से मैनिफोल्ड के अदिशों का वलय है, और किसी को इसकी अनुमति देता है गैर-अनुवांशिक सी*-बीजगणित को मैनिफोल्ड्स के गैर-अनुवांशिक सामान्यीकरण के रूप में मानें। यह गैर-अनुवांशिक ज्यामिति के क्षेत्र का आधार है।

यह भी देखें

एफ़िन कनेक्शन
एटलस (टोपोलॉजी)
क्रिस्टोफ़ेल प्रतीक
सामान्य सापेक्षता के गणित का परिचय
रीमैनियन ज्यामिति में सूत्रों की सूची
रीमैनियन ज्यामिति
अंतरिक्ष (गणित)

संदर्भ

↑ B. Riemann (1867).
↑ Maxwell himself worked with quaternions rather than tensors, but his equations for electromagnetism were used as an early example of the tensor formalism; see Dimitrienko, Yuriy I. (2002), Tensor Analysis and Nonlinear Tensor Functions, Springer, p. xi, ISBN 9781402010156.
↑ See G. Ricci (1888), G. Ricci and T. Levi-Civita (1901), T. Levi-Civita (1927).
↑ See H. Weyl (1955).
↑ H. Whitney (1936).
↑ See S. Kobayashi (1972).
↑ J. Milnor (1956).
↑ Z. Sela (1995). However, 3-manifolds are only classified in the sense that there is an (impractical) algorithm for generating a non-redundant list of all compact 3-manifolds.
↑ See A. Ranicki (2002).
↑ Kobayashi and Nomizu (1963), Volume 1.
↑ This definition can be found in MacLane and Moerdijk (1992). For an equivalent, ad hoc definition, see Sternberg (1964) Chapter II.
↑ Hartshorne (1997)

ग्रन्थसूची

Donaldson, Simon (1983). "An application of gauge theory to four-dimensional topology". Journal of Differential Geometry. 18 (2): 279–315. doi:10.4310/jdg/1214437665.
Hartshorne, Robin (1977). Algebraic Geometry. Springer-Verlag. ISBN 0-387-90244-9.
"Differentiable manifold", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
Kervaire, Michel A. (1960). "A manifold which does not admit any differentiable structure". Commentarii Mathematici Helvetici. 34 (1): 257–270. doi:10.1007/BF02565940. S2CID 120977898..
Kobayashi, Shoshichi (1972). Transformation groups in differential geometry. Springer.
Lee, Jeffrey M. (2009), Manifolds and Differential Geometry, Graduate Studies in Mathematics, vol. 107, Providence: American Mathematical Society, ISBN 9780821848159 .
Levi-Civita, Tullio (1927). "The absolute differential calculus (calculus of tensors)". Nature. 120 (3024): 542–543. Bibcode:1927Natur.120..542B. doi:10.1038/120542a0. S2CID 4109613.
Mac Lane, Saunders; Moerdijk, Ieke (1992). Sheaves in Geometry and Logic. Springer. ISBN 0-387-97710-4.
Milnor, John (1956). "On manifolds homeomorphic to the 7-Sphere". Annals of Mathematics. 64 (2): 399–405. doi:10.2307/1969983. JSTOR 1969983.
Ranicki, Andrew (2002). Algebraic and Geometric Surgery. Oxford Mathematical Monographs, Clarendon Press. ISBN 0-19-850924-3.
Ricci-Curbastro, Gregorio; Levi-Civita, Tullio (1901). Die Methoden des absoluten Differentialkalkuls.
Ricci-Curbastro, Gregorio (1888). Delle derivazioni covarianti e controvarianti e del loro uso nella analisi applicata (in italiano).
Riemann, Bernhard (1867). "Ueber die Hypothesen, welche der Geometrie zu Grunde liegen (On the Hypotheses which lie at the Bases of Geometry)". Abhandlungen der Königlichen Gesellschaft der Wissenschaften zu Göttingen. 13.
Sela, Zlil (1995). "The isomorphism problem for hyperbolic groups. I". Annals of Mathematics. 141 (2): 217–283. doi:10.2307/2118520. JSTOR 2118520.
Sternberg, Shlomo (1964). Lectures on Differential Geometry. Prentice-Hall.
Weisstein, Eric W. "Smooth Manifold". Retrieved 2008-03-04.

Weyl, Hermann (1955). Die Idee der Riemannschen Fläche. Teubner.
Whitney, Hassler (1936). "Differentiable manifolds". Annals of Mathematics. 37 (3): 645–680. doi:10.2307/1968482. JSTOR 1968482.

[1] B. Riemann (1867).

[2] Maxwell himself worked with quaternions rather than tensors, but his equations for electromagnetism were used as an early example of the tensor formalism; see Dimitrienko, Yuriy I. (2002), Tensor Analysis and Nonlinear Tensor Functions, Springer, p. xi, ISBN 9781402010156.

[3] See G. Ricci (1888), G. Ricci and T. Levi-Civita (1901), T. Levi-Civita (1927).

[4] See H. Weyl (1955).

[5] H. Whitney (1936).

[6] See S. Kobayashi (1972).

[7] J. Milnor (1956).

[8] Z. Sela (1995). However, 3-manifolds are only classified in the sense that there is an (impractical) algorithm for generating a non-redundant list of all compact 3-manifolds.

[9] See A. Ranicki (2002).

[10] Kobayashi and Nomizu (1963), Volume 1.

[11] This definition can be found in MacLane and Moerdijk (1992). For an equivalent, ad hoc definition, see Sternberg (1964) Chapter II.

[12] Hartshorne (1997)

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

@@ Line 1: / Line 1: @@
 {{Short description|Manifold upon which it is possible to perform calculus}}
-[[File:nondifferentiable atlas.png|right|frame|विश्व के लिए चार्ट का अविभाज्य एटलस। यदि एटलस अलग-अलग नहीं है तो कैलकुलस के परिणाम चार्ट के बीच संगत नहीं हो सकते हैं। केंद्र और दाएँ चार्ट में, [[कर्क रेखा]] चिकना वक्र है, जबकि बाएँ चार्ट में इसका तीखा कोना है। भिन्न-भिन्न मैनिफोल्ड की धारणा चार्ट के बीच रूपांतरित होने वाले कार्यों को भिन्न-भिन्न करने की आवश्यकता के द्वारा मैनिफोल्ड को परिष्कृत करती है।]]गणित में, अवकलनीय मैनिफोल्ड (विभेदक मैनिफोल्ड भी) एक प्रकार का [[ कई गुना |कई गुना]] है जो स्थानीय रूप से [[ सदिश स्थल |सदिश स्थल]] के समान होता है जिससे कोई कैलकुलस प्रयुक्त कर सकता है। किसी भी विविधता का वर्णन चार्ट ([[एटलस (टोपोलॉजी)]]) के संग्रह द्वारा किया जा सकता है। व्यक्तिगत चार्ट के अंदर काम करते समय कोई भी कैलकुलस के विचारों को प्रयुक्त कर सकता है, क्योंकि प्रत्येक चार्ट एक वेक्टर स्पेस के अंदर होता है, जिस पर कैलकुलस के सामान्य नियम प्रयुक्त होते हैं। यदि चार्ट उपयुक्त रूप से संगत हैं (अर्थात्, एक चार्ट से दूसरे चार्ट में संक्रमण भिन्न कार्य है), तो चार्ट में की गई [[गणना]] किसी अन्य भिन्न चार्ट में मान्य हैं।
+[[File:nondifferentiable atlas.png|right|frame|विश्व के लिए चार्ट का अविभाज्य एटलस। यदि एटलस अलग-अलग नहीं है तो कैलकुलस के परिणाम चार्ट के बीच संगत नहीं हो सकते हैं। केंद्र और दाएँ चार्ट में, [[कर्क रेखा]] चिकना वक्र है, जबकि बाएँ चार्ट में इसका तीखा कोना है। भिन्न-भिन्न मैनिफोल्ड की धारणा चार्ट के बीच रूपांतरित होने वाले कार्यों को भिन्न-भिन्न करने की आवश्यकता के द्वारा मैनिफोल्ड को परिष्कृत करती है।]]गणित में, अवकलनीय मैनिफोल्ड (विभेदक मैनिफोल्ड भी) एक प्रकार का [[ कई गुना |कई गुना]] है जो स्थानीय रूप से [[ सदिश स्थल |सदिश स्थल]] के समान होता है जिससे कोई कैलकुलस प्रयुक्त कर सकता है। किसी भी विविधता का वर्णन चार्ट ([[एटलस (टोपोलॉजी)]]) के संग्रह द्वारा किया जा सकता है। व्यक्तिगत चार्ट के अंदर काम करते समय कोई भी कैलकुलस के विचारों को प्रयुक्त कर सकता है, क्योंकि प्रत्येक चार्ट एक सदिश स्पेस के अंदर होता है, जिस पर कैलकुलस के सामान्य नियम प्रयुक्त होते हैं। यदि चार्ट उपयुक्त रूप से संगत हैं (अर्थात्, एक चार्ट से दूसरे चार्ट में संक्रमण भिन्न फलन है), तो चार्ट में की गई [[गणना]] किसी अन्य भिन्न चार्ट में मान्य हैं।
-औपचारिक शब्दों में, विभेदक मैनिफोल्ड विश्व स्तर पर परिभाषित अंतर संरचना के साथ [[ टोपोलॉजिकल मैनिफ़ोल्ड |टोपोलॉजिकल मैनिफ़ोल्ड]] है। किसी भी टोपोलॉजिकल मैनिफोल्ड को उसके एटलस में [[होमियोमोर्फिज्म]] और वेक्टर स्पेस पर मानक अंतर संरचना का उपयोग करके स्थानीय रूप से [[विभेदक संरचना]] दी जा सकती है। होमोमोर्फिज्म से प्रेरित स्थानीय समन्वय प्रणालियों पर वैश्विक अंतर संरचना को प्रेरित करने के लिए, एटलस में चार्ट इंटरैक्शन पर उनकी कार्य संरचना संबंधित वेक्टर स्थान पर भिन्न कार्य होनी चाहिए। दूसरे शब्दों में, जहां चार्ट के डोमेन ओवरलैप होते हैं, प्रत्येक चार्ट द्वारा परिभाषित निर्देशांक को एटलस में प्रत्येक चार्ट द्वारा परिभाषित निर्देशांक के संबंध में भिन्न होना आवश्यक है। वे मानचित्र जो विभिन्न चार्टों द्वारा परिभाषित निर्देशांकों को एक-दूसरे से जोड़ते हैं, ''संक्रमण मानचित्र'' कहलाते हैं।
+औपचारिक शब्दों में, विभेदक मैनिफोल्ड विश्व स्तर पर परिभाषित अंतर संरचना के साथ [[ टोपोलॉजिकल मैनिफ़ोल्ड |टोपोलॉजिकल मैनिफ़ोल्ड]] है। किसी भी टोपोलॉजिकल मैनिफोल्ड को उसके एटलस में [[होमियोमोर्फिज्म]] और सदिश स्पेस पर मानक अंतर संरचना का उपयोग करके स्थानीय रूप से [[विभेदक संरचना]] दी जा सकती है। होमोमोर्फिज्म से प्रेरित स्थानीय समन्वय प्रणालियों पर वैश्विक अंतर संरचना को प्रेरित करने के लिए, एटलस में चार्ट इंटरैक्शन पर उनकी फलन संरचना संबंधित सदिश स्थान पर भिन्न फलन होनी चाहिए। दूसरे शब्दों में, जहां चार्ट के डोमेन ओवरलैप होते हैं, प्रत्येक चार्ट द्वारा परिभाषित निर्देशांक को एटलस में प्रत्येक चार्ट द्वारा परिभाषित निर्देशांक के संबंध में भिन्न होना आवश्यक है। वे मानचित्र जो विभिन्न चार्टों द्वारा परिभाषित निर्देशांकों को एक-दूसरे से जोड़ते हैं, ''संक्रमण मानचित्र'' कहलाते हैं।
-अमूर्त स्थान पर ऐसी स्थानीय अंतर संरचना को परिभाषित करने की क्षमता किसी को वैश्विक समन्वय प्रणालियों के बिना रिक्त स्थान तक भिन्नता की परिभाषा का विस्तार करने की अनुमति देती है। स्थानीय रूप से विभेदक संरचना किसी को विश्व स्तर पर भिन्न [[स्पर्शरेखा स्थान]], भिन्न कार्यों और भिन्न [[टेंसर फ़ील्ड]] और [[वेक्टर फ़ील्ड]] फ़ील्ड को परिभाषित करने की अनुमति देती है।
+अमूर्त स्थान पर ऐसी स्थानीय अंतर संरचना को परिभाषित करने की क्षमता किसी को वैश्विक समन्वय प्रणालियों के बिना रिक्त स्थान तक भिन्नता की परिभाषा का विस्तार करने की अनुमति देती है। स्थानीय रूप से विभेदक संरचना किसी को विश्व स्तर पर भिन्न [[स्पर्शरेखा स्थान]], भिन्न कार्यों और भिन्न [[टेंसर फ़ील्ड]] और [[वेक्टर फ़ील्ड|सदिश फ़ील्ड]] को परिभाषित करने की अनुमति देती है।
 भौतिकी में विभेदक मैनिफोल्ड बहुत महत्वपूर्ण हैं। विशेष प्रकार के विभेदक मैनिफोल्ड [[शास्त्रीय यांत्रिकी]], [[सामान्य सापेक्षता]] और यांग-मिल्स सिद्धांत जैसे भौतिक सिद्धांतों का आधार बनते हैं। भिन्न-भिन्न मैनिफोल्ड्स के लिए कलन विकसित करना संभव है। यह बाहरी व्युत्पन्न|बाहरी कलन जैसी गणितीय मशीनरी की ओर ले जाता है। अवकलनशील मैनिफोल्ड्स पर कैलकुलस के अध्ययन को डिफरेंशियल ज्योमेट्री और टोपोलॉजी|डिफरेंशियल ज्योमेट्री के रूप में जाना जाता है।
- मैनिफ़ोल्ड की भिन्नता को कई अर्थ दिए गए हैं, जिनमें सम्मिलित हैं: निरंतर भिन्न, ''k''-बार भिन्न, [[सुचारू कार्य]] (जिसके स्वयं कई अर्थ हैं), और विश्लेषणात्मक फ़लन।
+मैनिफ़ोल्ड की भिन्नता को कई अर्थ दिए गए हैं, जिनमें निरंतर भिन्न, ''k''-बार भिन्न, [[सुचारू कार्य|सुचारू फलन]] (जिसके स्वयं कई अर्थ हैं), और विश्लेषणात्मक फ़लन सम्मिलित हैं।
 == इतिहास ==
@@ Line 17: / Line 17: @@
 : एन आयामों की विविधता की धारणा का निर्माण करने के बाद, और पाया कि इसका वास्तविक चरित्र इस संपत्ति में निहित है कि इसमें स्थिति का निर्धारण परिमाण के एन निर्धारण तक कम हो सकता है, ... - बी रीमैन
-[[जेम्स क्लर्क मैक्सवेल]] जैसे भौतिकविदों के कार्य,<ref>Maxwell himself worked with [[quaternion]]s rather than tensors, but his equations for electromagnetism were used as an early example of the tensor formalism; see {{citation|title=Tensor Analysis and Nonlinear Tensor Functions|first=Yuriy I.|last=Dimitrienko|publisher=Springer|year=2002|isbn=9781402010156|page=xi|url=https://books.google.com/books?id=7UMYToTiYDsC&pg=PR11}}.</ref> और गणितज्ञ [[ग्रेगोरियो रिक्की-कर्बस्ट्रो]] और [[टुल्लियो लेवी-सिविटा]]<ref>See G. Ricci (1888), G. Ricci and T. Levi-Civita (1901), T. Levi-Civita (1927).</ref> [[टेंसर विश्लेषण]] के विकास और [[सामान्य सहप्रसरण]] की धारणा को जन्म दिया, जो आंतरिक ज्यामितीय संपत्ति की पहचान करता है जो [[समन्वय परिवर्तन]] के संबंध में अपरिवर्तनीय है। इन विचारों को [[अल्बर्ट आइंस्टीन]] के सामान्य सापेक्षता के सिद्धांत और इसके अंतर्निहित [[तुल्यता सिद्धांत]] में महत्वपूर्ण अनुप्रयोग मिला। 2-आयामी मैनिफोल्ड की आधुनिक परिभाषा [[हरमन वेइल]] ने अपनी 1913 की [[ रीमैन सतह |रीमैन सतह]] पर पुस्तक में दी थी।<ref>See H. Weyl (1955).</ref> [[एटलस (गणित)]] के संदर्भ में मैनिफोल्ड की व्यापक रूप से स्वीकृत सामान्य परिभाषा [[हस्लर व्हिटनी]] के कारण है।<ref>H. Whitney (1936).</ref>
+[[जेम्स क्लर्क मैक्सवेल]] जैसे भौतिकविदों के फलन,<ref>Maxwell himself worked with [[quaternion]]s rather than tensors, but his equations for electromagnetism were used as an early example of the tensor formalism; see {{citation|title=Tensor Analysis and Nonlinear Tensor Functions|first=Yuriy I.|last=Dimitrienko|publisher=Springer|year=2002|isbn=9781402010156|page=xi|url=https://books.google.com/books?id=7UMYToTiYDsC&pg=PR11}}.</ref> और गणितज्ञ [[ग्रेगोरियो रिक्की-कर्बस्ट्रो]] और [[टुल्लियो लेवी-सिविटा]]<ref>See G. Ricci (1888), G. Ricci and T. Levi-Civita (1901), T. Levi-Civita (1927).</ref> [[टेंसर विश्लेषण]] के विकास और [[सामान्य सहप्रसरण]] की धारणा को जन्म दिया, जो आंतरिक ज्यामितीय संपत्ति की पहचान करता है जो [[समन्वय परिवर्तन]] के संबंध में अपरिवर्तनीय है। इन विचारों को [[अल्बर्ट आइंस्टीन]] के सामान्य सापेक्षता के सिद्धांत और इसके अंतर्निहित [[तुल्यता सिद्धांत]] में महत्वपूर्ण अनुप्रयोग मिला। 2-आयामी मैनिफोल्ड की आधुनिक परिभाषा [[हरमन वेइल]] ने अपनी 1913 की [[ रीमैन सतह |रीमैन सतह]] पर पुस्तक में दी थी।<ref>See H. Weyl (1955).</ref> [[एटलस (गणित)]] के संदर्भ में मैनिफोल्ड की व्यापक रूप से स्वीकृत सामान्य परिभाषा [[हस्लर व्हिटनी]] के कारण है।<ref>H. Whitney (1936).</ref>
@@ Line 28: / Line 28: @@
 चार्ट की उपस्थिति से विभेदक गणना करने की संभावना {{mvar|M}} का पता चलता है; उदाहरण के लिए, यदि कोई फ़लन {{math|''u'' : ''M'' → '''R'''}} दिया गया है और चार्ट {{math|(''U'', ''φ'')}} पर {{mvar|M}}, कोई रचना {{math|''u'' ∘ ''φ''<sup>−1</sup>}} पर विचार कर सकता है, जो वास्तविक-मूल्यवान फ़लन है जिसका डोमेन यूक्लिडियन स्पेस का विवृत उपसमुच्चय है; इस प्रकार, यदि यह अवकलनीय होता है, तो कोई इसके [[आंशिक व्युत्पन्न]] पर विचार कर सकता है।
-यह स्थिति निम्नलिखित कारणों से पूर्णतः संतोषजनक नहीं है। दूसरे चार्ट पर विचार करें {{math|(''V'', ''ψ'')}} पर {{mvar|M}}, और मान लीजिये {{mvar|U}} और {{mvar|V}} इसमें कुछ बिंदु समान हैं। दो संगत कार्य {{math|''u'' ∘ ''φ''<sup>−1</sup>}} और {{math|''u'' ∘ ''ψ''<sup>−1</sup>}} इस अर्थ में जुड़े हुए हैं कि उन्हें एक-दूसरे में पुनर्परिभाषित किया जा सकता है:
+यह स्थिति निम्नलिखित कारणों से पूर्णतः संतोषजनक नहीं है। दूसरे चार्ट पर {{math|(''V'', ''ψ'')}} पर {{mvar|M}} विचार करें, और मान लीजिये {{mvar|U}} और {{mvar|V}} इसमें कुछ बिंदु समान हैं। दो संगत फलन {{math|''u'' ∘ ''φ''<sup>−1</sup>}} और {{math|''u'' ∘ ''ψ''<sup>−1</sup>}} इस अर्थ में जुड़े हुए हैं कि उन्हें एक-दूसरे में पुनर्परिभाषित किया जा सकता है:
 <math display="block">u\circ\varphi^{-1}=\big(u\circ\psi^{-1}\big)\circ\big(\psi\circ\varphi^{-1}\big),</math>
-दाहिनी ओर का प्राकृतिक डोमेन {{math|''φ''(''U'' ∩ ''V'')}} तब से {{math|φ}} और {{math|''ψ''}} होमोमोर्फिज्म हैं, यह उसका अनुसरण करता है {{math|''ψ'' ∘ ''φ''<sup>−1</sup>}} से एक {{math|''φ''(''U'' ∩ ''V'')}} को {{math|''ψ''(''U'' ∩ ''V'')}} होमोमोर्फिज्म है। परिणामस्वरूप, तथापि दोनों कार्य करें {{math|''u'' ∘ ''φ''<sup>−1</sup>}} और {{math|''u'' ∘ ''ψ''<sup>−1</sup>}} अवकलनीय हैं, इसलिए उनके विभेदक गुण आवश्यक रूप से एक दूसरे से मजबूती से जुड़े नहीं होंगे {{math|''ψ'' ∘ ''φ''<sup>−1</sup>}}[[श्रृंखला नियम]] प्रयुक्त होने के लिए आवश्यक रूप से पर्याप्त रूप से भिन्न नहीं है। यदि कोई इसके अतिरिक्त कार्यों पर विचार करता है तो वही समस्या {{math|''c'' : '''R''' → ''M''}} पाई जाती है; एक को पुनर्परिवर्तन सूत्र की ओर ले जाया जाता है
+दाहिनी ओर का प्राकृतिक डोमेन {{math|''φ''(''U'' ∩ ''V'')}} तब से {{math|φ}} और {{math|''ψ''}} होमोमोर्फिज्म हैं, यह उसका अनुसरण करता है; {{math|''ψ'' ∘ ''φ''<sup>−1</sup>}} से एक {{math|''φ''(''U'' ∩ ''V'')}} को {{math|''ψ''(''U'' ∩ ''V'')}} होमोमोर्फिज्म है। परिणामस्वरूप, तथापि दोनों फलन {{math|''u'' ∘ ''φ''<sup>−1</sup>}} और {{math|''u'' ∘ ''ψ''<sup>−1</sup>}} अवकलनीय हैं, इसलिए उनके विभेदक गुण {{math|''ψ'' ∘ ''φ''<sup>−1</sup>}} आवश्यक रूप से एक दूसरे से मजबूती से जुड़े नहीं होंगे, [[श्रृंखला नियम]] प्रयुक्त होने के लिए आवश्यक रूप से पर्याप्त रूप से भिन्न नहीं है। यदि कोई इसके अतिरिक्त कार्यों पर विचार करता है तो वही समस्या {{math|''c'' : '''R''' → ''M''}} पाई जाती है; एक को पुनर्परिवर्तन सूत्र की ओर ले जाया जाता है
 <math display=block>\varphi\circ c=\big(\varphi\circ\psi^{-1}\big)\circ\big(\psi\circ c\big),</math>
 जिस बिंदु पर कोई पहले जैसा ही अवलोकन कर सकता है।
-इसका समाधान चार्ट के एक अलग-अलग एटलस की प्रारंभ से किया जाता है, जो चार्ट के संग्रह को निर्दिष्ट करता है {{mvar|M}} जिसके लिए [[संक्रमण मानचित्र]] {{math|''ψ'' ∘ ''φ''<sup>−1</sup>}} सभी भिन्न हैं। इससे स्थिति अत्यधिक सीमा तक साफ हो जाती है: यदि {{math|''u'' ∘ ''φ''<sup>−1</sup>}} अवकलनीय है, फिर पुनरामितीकरण सूत्र के कारण, मानचित्र {{math|''u'' ∘ ''ψ''<sup>−1</sup>}} क्षेत्र पर भी भिन्न है {{math|''ψ''(''U'' ∩ ''V'')}}. इसके अतिरिक्त, इन दोनों मानचित्रों के व्युत्पन्न श्रृंखला नियम द्वारा एक दूसरे से जुड़े हुए हैं। दिए गए एटलस के सापेक्ष, यह अलग-अलग मैपिंग की धारणा को सुविधाजनक बनाता है जिसका डोमेन या रेंज है {{mvar|M}}, साथ ही ऐसे मानचित्रों की व्युत्पत्ति की धारणा भी।
+इसका समाधान चार्ट के एक अलग-अलग एटलस की प्रारंभ से किया जाता है, जो चार्ट के संग्रह को निर्दिष्ट करता है {{mvar|M}} जिसके लिए [[संक्रमण मानचित्र]] {{math|''ψ'' ∘ ''φ''<sup>−1</sup>}} सभी भिन्न हैं। इससे स्थिति अत्यधिक सीमा तक साफ हो जाती है: यदि {{math|''u'' ∘ ''φ''<sup>−1</sup>}} अवकलनीय है, फिर पुनरामितीकरण सूत्र के कारण, मानचित्र {{math|''u'' ∘ ''ψ''<sup>−1</sup>}} क्षेत्र पर भी भिन्न है {{math|''ψ''(''U'' ∩ ''V'')}}. इसके अतिरिक्त, इन दोनों मानचित्रों के व्युत्पन्न श्रृंखला नियम द्वारा एक दूसरे से जुड़े हुए हैं। दिए गए एटलस के सापेक्ष, यह अलग-अलग मैपिंग की धारणा को सुविधाजनक बनाता है जिसका डोमेन या रेंज {{mvar|M}} है, साथ ही ऐसे मानचित्रों की व्युत्पत्ति की धारणा भी सुविधाजनक है।
-औपचारिक रूप से, डिफरेंशियल शब्द कुछ सीमा तक अस्पष्ट है, क्योंकि अलग-अलग लेखकों द्वारा इसका अलग-अलग अर्थ लिया जाता है; कभी-कभी इसका अर्थ पहले डेरिवेटिव का अस्तित्व होता है, कभी-कभी निरंतर पहले डेरिवेटिव का अस्तित्व होता है, और कभी-कभी असीमित कई डेरिवेटिव का अस्तित्व होता है। निम्नलिखित विभेदक एटलस के विभिन्न (अस्पष्ट) अर्थों की औपचारिक परिभाषा देता है। सामान्यतः, विभेदीकरण का उपयोग इन सभी संभावनाओं सहित कैच-ऑल शब्द के रूप में किया जाएगा, बशर्ते {{math|''k'' ≥ 1}}.
+औपचारिक रूप से, डिफरेंशियल शब्द कुछ सीमा तक अस्पष्ट है, क्योंकि अलग-अलग लेखकों द्वारा इसका अलग-अलग अर्थ लिया जाता है; कभी-कभी इसका अर्थ पहले डेरिवेटिव का अस्तित्व होता है, कभी-कभी निरंतर पहले डेरिवेटिव का अस्तित्व होता है, और कभी-कभी असीमित कई डेरिवेटिव का अस्तित्व होता है। निम्नलिखित विभेदक एटलस के विभिन्न (अस्पष्ट) अर्थों की औपचारिक परिभाषा देता है। सामान्यतः, विभेदीकरण का उपयोग इन सभी संभावनाओं सहित कैच-ऑल शब्द के रूप में किया जाएगा, बिना किसी नियम {{math|''k'' ≥ 1}} के अतिरिक्त किया जायेगा।
 {| class="wikitable"
@@ Line 81: / Line 81: @@
 वैकल्पिक लेकिन समतुल्य परिभाषा, अधिकतम एटलस के प्रत्यक्ष उपयोग से बचते हुए, विभेदक एटलस के समतुल्य वर्गों पर विचार करना है, जिसमें दो भिन्न एटलस को समतुल्य माना जाता है यदि एटलस का प्रत्येक चार्ट दूसरे एटलस के साथ भिन्न रूप से संगत है। अनौपचारिक रूप से, इसका अर्थ यह है कि सहज मैनिफोल्ड से निपटने में, कोई एकल विभेदक एटलस के साथ काम कर सकता है, जिसमें केवल कुछ चार्ट सम्मिलित हैं, इस अंतर्निहित समझ के साथ कि कई अन्य चार्ट और विभेदक एटलस समान रूप से वैध हैं।
-डोमेन के अपरिवर्तनीयता के अनुसार, टोपोलॉजिकल स्पेस के प्रत्येक जुड़े घटक जिसमें एक अलग एटलस होता है, {{mvar|n}} का अच्छी तरह से परिभाषित आयाम होता है, यह होलोमोर्फिक एटलस के मामले में थोड़ी अस्पष्टता का कारण बनता है, क्योंकि विश्लेषणात्मक, सुचारू, या के रूप में विचार किए जाने पर संबंधित आयाम  {{math|''C''<sup>''k''</sup>}}एटलस के आयाम के मूल्य का आधा होगा। इस कारण से, होलोमोर्फिक एटलस के साथ टोपोलॉजिकल स्पेस के वास्तविक और जटिल आयाम को अलग से संदर्भित किया जाता है।
+डोमेन के अपरिवर्तनीयता के अनुसार, टोपोलॉजिकल स्पेस के प्रत्येक जुड़े घटक जिसमें एक अलग एटलस होता है, {{mvar|n}} का अच्छी तरह से परिभाषित आयाम होता है, यह होलोमोर्फिक एटलस के मामले में थोड़ी अस्पष्टता का कारण बनता है, क्योंकि विश्लेषणात्मक, सुचारू, या के रूप में विचार किए जाने पर संबंधित आयाम {{math|''C''<sup>''k''</sup>}} एटलस के आयाम के मूल्य का आधा होगा। इस कारण से, होलोमोर्फिक एटलस के साथ टोपोलॉजिकल स्पेस के वास्तविक और जटिल आयाम को अलग से संदर्भित किया जाता है।
 === अनेक गुना ===
-A भिन्न मैनिफोल्ड एक [[हॉसडॉर्फ़ स्थान]] और [[दूसरा गणनीय]] टोपोलॉजिकल स्पेस है {{mvar|M}}, एक साथ अधिकतम भिन्नात्मक एटलस के साथ {{mvar|M}}. अधिकांश मूलभूत सिद्धांत हॉसडॉर्फ और दूसरी गणनीयता स्थितियों की आवश्यकता के बिना विकसित किए जा सकते हैं, चूंकि वे अधिकांश उन्नत सिद्धांत के लिए महत्वपूर्ण हैं। वे अनिवार्य रूप से [[टक्कर समारोह|टक्कर फलन]] और एकता के विभाजन के सामान्य अस्तित्व के बराबर हैं, दोनों का उपयोग सर्वव्यापी रूप से किया जाता है।
+A भिन्न मैनिफोल्ड एक [[हॉसडॉर्फ़ स्थान]] और [[दूसरा गणनीय]] टोपोलॉजिकल स्पेस {{mvar|M}} है, एक साथ अधिकतम भिन्नात्मक एटलस {{mvar|M}} के साथ है। अधिकांश मूलभूत सिद्धांत हॉसडॉर्फ और दूसरी गणनीयता स्थितियों की आवश्यकता के बिना विकसित किए जा सकते हैं, चूंकि वे अधिकांश उन्नत सिद्धांत के लिए महत्वपूर्ण हैं। वे अनिवार्य रूप से [[टक्कर समारोह|बुम्प फलन]] और एकता के विभाजन के सामान्य अस्तित्व के बराबर हैं, दोनों का उपयोग सर्वव्यापी रूप से किया जाता है।
-A की धारणा {{math|''C''<sup>0</sup>}} मैनिफोल्ड टोपोलॉजिकल मैनिफोल्ड के समान है। चूँकि, इसमें उल्लेखनीय अंतर किया जाना शेष है। टोपोलॉजिकल स्पेस को देखते हुए, यह पूछना सार्थक है कि क्या यह टोपोलॉजिकल मैनिफोल्ड है या नहीं। इसके विपरीत, यह पूछना सार्थक नहीं है कि क्या दिया गया टोपोलॉजिकल स्पेस (उदाहरण के लिए) एक स्मूथ मैनिफोल्ड है या नहीं, क्योंकि स्मूथ मैनिफोल्ड की धारणा के लिए एक स्मूथ एटलस के विनिर्देशन की आवश्यकता होती है, जो अतिरिक्त संरचना है। चूँकि, यह कहना सार्थक हो सकता है कि एक निश्चित टोपोलॉजिकल स्पेस को एक सहज मैनिफोल्ड की संरचना नहीं दी जा सकती है। परिभाषाओं को दोबारा तैयार करना संभव है ताकि इस प्रकार का असंतुलन उपस्थित न हो; कोई एक सेट {{mvar|M}} से प्रारंभ कर सकता है (टोपोलॉजिकल स्पेस के अतिरिक्त {{mvar|M}}), टोपोलॉजिकल स्पेस की संरचना को परिभाषित करने के लिए इस सेटिंग में चिकने एटलस के प्राकृतिक एनालॉग {{mvar|M}} का उपयोग करना।
+A की धारणा {{math|''C''<sup>0</sup>}} मैनिफोल्ड टोपोलॉजिकल मैनिफोल्ड के समान है। चूँकि, इसमें उल्लेखनीय अंतर किया जाना शेष है। टोपोलॉजिकल स्पेस को देखते हुए, यह पूछना सार्थक है कि क्या यह टोपोलॉजिकल मैनिफोल्ड है या नहीं। इसके विपरीत, यह पूछना सार्थक नहीं है कि क्या दिया गया टोपोलॉजिकल स्पेस (उदाहरण के लिए) एक स्मूथ मैनिफोल्ड है या नहीं, क्योंकि स्मूथ मैनिफोल्ड की धारणा के लिए एक स्मूथ एटलस के विनिर्देशन की आवश्यकता होती है, जो अतिरिक्त संरचना है। चूँकि, यह कहना सार्थक हो सकता है कि एक निश्चित टोपोलॉजिकल स्पेस को एक सहज मैनिफोल्ड की संरचना नहीं दी जा सकती है। परिभाषाओं को दोबारा तैयार करना संभव है ताकि इस प्रकार का असंतुलन उपस्थित न हो; कोई एक सेट {{mvar|M}} से प्रारंभ कर सकता है (टोपोलॉजिकल स्पेस {{mvar|M}} के अतिरिक्त), टोपोलॉजिकल स्पेस की संरचना को परिभाषित करने के लिए इस सेटिंग में चिकने एटलस के प्राकृतिक एनालॉग {{mvar|M}} का उपयोग करना।
 === मैनिफोल्ड बनाने के लिए यूक्लिडियन टुकड़ों को एक साथ जोड़ना ===
@@ Line 97: / Line 97: @@
 == अवकलनीय फलन ==
-एन-डायमेंशनल डिफरेंशियल मैनिफोल्ड M पर वास्तविक मूल्यवान फ़लन एफ को बिंदु पर 'डिफरेंशियल' कहा जाता है {{nowrap|''p'' ∈ ''M''}} यदि यह पी के आसपास परिभाषित किसी भी समन्वय चार्ट में भिन्न है। अधिक स्पष्ट शब्दों में, यदि <math>(U,\phi)</math> जहां भिन्न चार्ट <math>U</math> और विवृत सेट <math>M</math> है, युक्त P तथा <math>\phi : U\to {\mathbf R}^n</math> चार्ट को परिभाषित करने वाला मानचित्र है, तो f, p पर अवकलनीय है यदि और केवल यदि
+एन-डायमेंशनल डिफरेंशियल मैनिफोल्ड M पर वास्तविक मूल्यवान फ़लन एफ को बिंदु पर 'डिफरेंशियल' {{nowrap|''p'' ∈ ''M''}} कहा जाता है। यदि यह p के आसपास परिभाषित किसी भी समन्वय चार्ट में भिन्न है। अधिक स्पष्ट शब्दों में, यदि <math>(U,\phi)</math> जहां भिन्न चार्ट <math>U</math> और विवृत सेट <math>M</math> है, युक्त P तथा <math>\phi : U\to {\mathbf R}^n</math> चार्ट को परिभाषित करने वाला मानचित्र है, तो f, p पर अवकलनीय है यदि और केवल यदि
 <math display=block>f\circ \phi^{-1} \colon \phi(U)\subset {\mathbf R}^n \to {\mathbf R}</math>
-पर भिन्न है <math>\phi(p)</math>, वह है <math>f\circ \phi^{-1}</math> विवृत सेट से भिन्न कार्य <math>\phi(U)</math> है, का एक उपसमुच्चय <math>{\mathbf R}^n</math>को <math>\mathbf R</math> माना जाता है, सामान्य तौर पर, कई उपलब्ध चार्ट होंगे; चूँकि, भिन्नता की परिभाषा पी पर चार्ट की पसंद पर निर्भर नहीं करती है। यह एक चार्ट और दूसरे चार्ट के बीच संक्रमण कार्यों पर प्रयुक्त श्रृंखला नियम का पालन करता है कि यदि पी पर किसी विशेष चार्ट में एफ अलग-अलग है, तो यह पी पर सभी चार्ट में अलग-अलग है। C को परिभाषित करने के लिए अनुरूप विचार प्रयुक्त होते हैं<sup>k</sup> फ़लन, सुचारू फ़लन और विश्लेषणात्मक फ़लन।
+<math>\phi(p)</math> पर भिन्न है, वह <math>f\circ \phi^{-1}</math> विवृत सेट से भिन्न फलन <math>\phi(U)</math> है, <math>{\mathbf R}^n</math> का एक उपसमुच्चय को <math>\mathbf R</math> माना जाता है, सामान्य तौर पर, कई उपलब्ध चार्ट होंगे; चूँकि, भिन्नता की परिभाषा p पर चार्ट की पसंद पर निर्भर नहीं करती है। यह एक चार्ट और दूसरे चार्ट के बीच संक्रमण कार्यों पर प्रयुक्त श्रृंखला नियम का पालन करता है कि यदि p पर किसी विशेष चार्ट में एफ अलग-अलग है, तो यह p पर सभी चार्ट में अलग-अलग है। C<sup>k</sup>  फ़लन, सुचारू फ़लन और विश्लेषणात्मक फ़लन को परिभाषित करने के लिए अनुरूप विचार प्रयुक्त होते हैं।
 ===कार्यों का विभेदन===
-किसी फ़लन के व्युत्पन्न को भिन्न मैनिफोल्ड पर परिभाषित करने के कई विधियाँ हैं, जिनमें से सबसे मौलिक [[दिशात्मक व्युत्पन्न]] है। दिशात्मक व्युत्पन्न की परिभाषा इस तथ्य से जटिल है कि मैनिफोल्ड में एक उपयुक्त [[एफ़िन स्पेस]] संरचना का अभाव होगा जिसके साथ [[वेक्टर (ज्यामितीय)]] को परिभाषित किया जा सके। इसलिए, दिशात्मक व्युत्पन्न वैक्टर के अतिरिक्त मैनिफोल्ड में वक्रों को देखता है।
+किसी फ़लन के व्युत्पन्न को भिन्न मैनिफोल्ड पर परिभाषित करने के कई विधियाँ हैं, जिनमें से सबसे मौलिक [[दिशात्मक व्युत्पन्न]] है। दिशात्मक व्युत्पन्न की परिभाषा इस तथ्य से जटिल है कि मैनिफोल्ड में एक उपयुक्त [[एफ़िन स्पेस]] संरचना का अभाव होगा जिसके साथ [[वेक्टर (ज्यामितीय)|सदिश (ज्यामितीय)]] को परिभाषित किया जा सके। इसलिए, दिशात्मक व्युत्पन्न वैक्टर के अतिरिक्त मैनिफोल्ड में वक्रों को देखता है।
 ==== दिशात्मक विभेदन ====
-एन आयामी विभेदक मैनिफोल्ड M पर एक वास्तविक मूल्यवान फ़लन एफ को देखते हुए, M में एक बिंदु पी पर एफ के दिशात्मक व्युत्पन्न को निम्नानुसार परिभाषित किया गया है। मान लीजिए कि γ(t) M में एक वक्र है {{nowrap|1=''γ''(0) = ''p''}}, जो इस अर्थ में भिन्न है कि किसी भी चार्ट के साथ इसकी संरचना 'R<sup>n</sup>' में एक भिन्न वक्र है, फिर γ के अनुदिश p पर f का 'दिशात्मक अवकलज' है
+एन आयामी विभेदक मैनिफोल्ड M पर एक वास्तविक मूल्यवान फ़लन एफ को देखते हुए, M में एक बिंदु p पर एफ के दिशात्मक व्युत्पन्न को निम्नानुसार परिभाषित किया गया है। मान लीजिए कि γ(t) M में एक वक्र है {{nowrap|1=''γ''(0) = ''p''}}, जो इस अर्थ में भिन्न है कि किसी भी चार्ट के साथ इसकी संरचना 'R<sup>n</sup>' में एक भिन्न वक्र है, फिर γ के अनुदिश p पर f का 'दिशात्मक अवकलज' है
 <math display=block>\left.\frac{d}{dt}f(\gamma(t))\right|_{t=0}.</math>
@@ Line 113: / Line 113: @@
 <math display=block>\left.\frac{d}{dt}\phi\circ\gamma_1(t)\right|_{t=0}=\left.\frac{d}{dt}\phi\circ\gamma_2(t)\right|_{t=0}</math>
-फिर, श्रृंखला नियम के अनुसार, f के पास γ के साथ p पर समान दिशात्मक व्युत्पन्न है<sub>1</sub> C के साथ के रूप में<sub>2</sub>. इसका अर्थ यह है कि दिशात्मक व्युत्पन्न केवल पी पर वक्र के स्पर्शरेखा वेक्टर पर निर्भर करता है। इस प्रकार, अलग-अलग कई गुना के मामले में अनुकूलित दिशात्मक भेदभाव की अधिक अमूर्त परिभाषा अंततः एक संबद्ध स्थान में दिशात्मक भेदभाव की सहज विशेषताओं को पकड़ लेती है।
+फिर, श्रृंखला नियम के अनुसार, f के पास γ के साथ p पर समान दिशात्मक व्युत्पन्न है<sub>1</sub> C के साथ के रूप में<sub>2</sub>. इसका अर्थ यह है कि दिशात्मक व्युत्पन्न केवल p पर वक्र के स्पर्शरेखा सदिश पर निर्भर करता है। इस प्रकार, अलग-अलग कई गुना के मामले में अनुकूलित दिशात्मक भेदभाव की अधिक अमूर्त परिभाषा अंततः एक संबद्ध स्थान में दिशात्मक भेदभाव की सहज विशेषताओं को पकड़ लेती है।
 ==== स्पर्शरेखा सदिश और अंतर ====
-पर एक स्पर्शरेखा सदिश {{nowrap|''p'' ∈ ''M''}} अवकलनीय वक्रों का एक [[तुल्यता वर्ग]] है γ साथ में {{nowrap|1=''γ''(0) = ''p''}}, मॉड्यूलो वक्रों के बीच प्रथम-क्रम संपर्क (गणित) का तुल्यता संबंध। इसलिए,
+पर एक स्पर्शरेखा सदिश {{nowrap|''p'' ∈ ''M''}} अवकलनीय वक्रों का एक [[तुल्यता वर्ग]] है γ साथ में {{nowrap|1=''γ''(0) = ''p''}}, मॉड्यूलो वक्रों के बीच प्रथम-क्रम संपर्क (गणित) का तुल्यता संबंध है। इसलिए,
 <math display=block> \gamma_1\equiv \gamma_2 \iff \left.\frac{d}{dt}\phi\circ\gamma_1(t)\right|_{t=0} = \left.\frac{d}{dt}\phi\circ\gamma_2(t)\right|_{t=0}</math>
-प्रत्येक समन्वय चार्ट में <math>\phi</math>. इसलिए, समतुल्य वर्ग पी पर एक निर्धारित वेग वेक्टर के साथ पी के माध्यम से वक्र हैं। पी पर सभी स्पर्शरेखा सदिशों का संग्रह एक सदिश समष्टि बनाता है: पी पर M की स्पर्शरेखा समष्टि, टी द्वारा निरूपित<sub>''p''</sub>एम।
+प्रत्येक समन्वय चार्ट मे <math>\phi</math> इसलिए, समतुल्य वर्ग p पर एक निर्धारित वेग सदिश के साथ p के माध्यम से वक्र हैं। p पर सभी स्पर्शरेखा सदिशों का संग्रह एक सदिश समष्टि बनाता है: p पर M की स्पर्शरेखा समष्टि, ''T<sub>p</sub>M'' द्वारा निरूपित है।
-यदि
+यदि X, p पर एक स्पर्शरेखा सदिश है और f, p के पास परिभाषित एक भिन्न फलन है, तो X को परिभाषित करने वाले समतुल्य वर्ग में किसी भी वक्र के साथ f को विभेदित करने से X के साथ एक अच्छी तरह से परिभाषित दिशात्मक व्युत्पन्न मिलता है:
 <math display=block>Xf(p) := \left.\frac{d}{dt}f(\gamma(t))\right|_{t=0}.</math>
 एक बार फिर, श्रृंखला नियम स्थापित करता है कि यह समतुल्य वर्ग से γ का चयन करने की स्वतंत्रता से स्वतंत्र है, क्योंकि समान प्रथम क्रम संपर्क वाला कोई भी वक्र समान दिशात्मक व्युत्पन्न प्राप्त करेगा।
@@ Line 134: / Line 134: @@
 ==== स्पर्शरेखा स्थान की परिभाषा और स्थानीय निर्देशांक में विभेदन ====
-होने देना <math>M</math> एक टोपोलॉजिकल बनें <math>n</math>-एक चिकनी एटलस के साथ कई गुना <math>\{(U_\alpha,\phi_\alpha)\}_{\alpha\in A}.</math> दिया गया <math>p\in M</math> होने देना <math>A_p</math> निरूपित <math>\{\alpha\in A:p\in U_\alpha\}.</math> पर एक स्पर्शरेखा सदिश <math>p\in M</math>एक मैपिंग है <math>v:A_p\to\mathbb{R}^n,</math> यहाँ दर्शाया गया है <math>\alpha\mapsto v_\alpha,</math> ऐसा है कि
+मान लीजिये <math>M</math> सुचारु एटलस <math>\{(U_\alpha,\phi_\alpha)\}_{\alpha\in A}</math> के साथ टोपोलॉजिकल <math>n</math>-मैनिफोल्ड है। <math>p\in M</math> दिया गया है, माना <math>A_p</math> <math>\{\alpha\in A:p\in U_\alpha\}</math> निरूपित है। <math>p\in M</math> पर एक स्पर्शरेखा सदिश एक मैपिंग <math>v:A_p\to\mathbb{R}^n</math> है, यहाँ <math>\alpha\mapsto v_\alpha</math> दर्शाया गया है, ऐसा है कि
 <math display=block>v_\alpha=D\Big|_{\phi_\beta(p)}(\phi_\alpha\circ\phi_\beta^{-1})(v_\beta)</math>
-सभी के लिए <math>\alpha,\beta\in A_p.</math> आइए स्पर्शरेखा सदिशों  <math>T_pM</math> का संग्रह करें <math>p</math> द्वारा निरूपित किया जाए, एक सुचारु कार्य <math>f:M\to\mathbb{R}</math> दिया गया, परिभाषित करना <math>df_p:T_pM\to\mathbb{R}</math> एक स्पर्शरेखा सदिश भेजकर <math>v:A_p\to\mathbb{R}^n</math> द्वारा दिए गए नंबर पर
+सभी <math>\alpha,\beta\in A_p</math> के लिए। आइए स्पर्शरेखा सदिशों  <math>T_pM</math> का संग्रह कर <math>p</math> द्वारा निरूपित किया जाए, एक सुचारु फलन <math>f:M\to\mathbb{R}</math> दिया गया, <math>df_p:T_pM\to\mathbb{R}</math> एक स्पर्शरेखा सदिश भेजकर <math>v:A_p\to\mathbb{R}^n</math> द्वारा दिए गए नंबर पर परिभाषित करना
 <math display=block>D\Big|_{\phi_\alpha(p)}(f\circ\phi_\alpha^{-1})(v_\alpha),</math>
-जो श्रृंखला नियम और स्पर्शरेखा वेक्टर की परिभाषा में बाधा के कारण की पसंद <math>\alpha\in A_p</math> पर निर्भर नहीं करता है।
+जो श्रृंखला नियम और स्पर्शरेखा सदिश की परिभाषा में बाधा के कारण की पसंद <math>\alpha\in A_p</math> पर निर्भर नहीं करता है।
-कोई भी इसकी जांच कर सकता है, स्वाभाविक रूप से एक की संरचना <math>T_pM</math> है। <math>n</math>-आयामी वास्तविक वेक्टर स्थान, और वह इस संरचना के साथ, <math>df_p</math> एक रेखीय मानचित्र है. मुख्य अवलोकन यह है कि, स्पर्शरेखा वेक्टर की परिभाषा में दिखाई देने वाली बाधा के कारण, का मान <math>v_\beta</math> एक ही तत्व के लिए <math>\beta</math> का <math>A_p</math> स्वचालित रूप से  सभी के लिए <math>\alpha\in A</math>, <math>v_\alpha</math> निर्धारित करता है,
+कोई भी इसकी जांच कर सकता है, स्वाभाविक रूप से एक की संरचना <math>T_pM</math> है। <math>n</math>-आयामी वास्तविक सदिश स्थान, और वह इस संरचना के साथ, <math>df_p</math> एक रेखीय मानचित्र है। मुख्य अवलोकन यह है कि, स्पर्शरेखा सदिश की परिभाषा में दिखाई देने वाली बाधा के कारण, का मान <math>v_\beta</math> एक ही तत्व के लिए <math>\beta</math> का <math>A_p</math> स्वचालित रूप से  सभी के लिए <math>\alpha\in A</math>, <math>v_\alpha</math> निर्धारित करता है,
 उपरोक्त औपचारिक परिभाषाएँ स्पष्ट रूप से एक अधिक अनौपचारिक संकेतन से मेल खाती हैं जो विशेष रूप से पाठ्यपुस्तकों में अधिकांशतः दिखाई देती है
@@ Line 150: / Line 150: @@
 विभेदक मैनिफोल्ड पर विभेदक कार्यों के शीफ की टोपोलॉजिकल विशेषताओं में से एक यह है कि यह एकता के विभाजन को स्वीकार करता है। यह विभेदक संरचना को मजबूत संरचनाओं (जैसे विश्लेषणात्मक और होलोमोर्फिक संरचनाओं) से कई गुना अलग करता है जो सामान्यतः एकता के विभाजन में विफल होते हैं।
-मान लीजिए कि M, वर्ग C का अनेक गुना है, जहाँ {{nowrap|0 ≤ ''k'' ≤ ∞}}।माना {U<sub>''α''</sub>} M का एक विवृत आवरण हो। फिर आवरण के अधीनस्थ 'एकता का विभाजन' हो} वास्तविक-मूल्यवान C का एक संग्रह है<sup>क</sup>फ़ंक्शंस एफ<sub>''i''</sub> M पर निम्नलिखित नियमों को पूरा करना:
+मान लीजिए कि M वर्ग ''C<sup>k</sup>'' का मैनिफोल्ड है, जहाँ 0 ≤ ''k'' ≤ ∞ है। मान लीजिए कि {''U<sub>α</sub>''} M का एक विवृत आवरण है। फिर आवरण {''U<sub>α</sub>''} के अधीन एकता का एक विभाजन निम्नलिखित नियमों को पूरा करने वाले M पर वास्तविक-मूल्य वाले ''C<sup>k</sup>'' फलन ''φ<sub>i</sub>'' का संग्रह है:
-* φ का [[समर्थन (गणित)]]।<sub>''i''</sub> [[सघन स्थान]] और [[स्थानीय रूप से सीमित संग्रह]] हैं;
+* ''φ<sub>i</sub>'' के [[समर्थन (गणित)|समर्थन]] कॉम्पैक्ट और [[स्थानीय रूप से सीमित संग्रह|स्थानीय रूप से सीमित]] हैं;
-* φ का समर्थन<sub>''i''</sub> U में पूरी तरह समाहित है<sub>''α''</sub> कुछ α के लिए;
+* कुछ α के लिए ''φ<sub>i</sub>'' का समर्थन पूरी तरह से ''U<sub>α</sub>'' में निहित है;
-* φ<sub>''i''</sub> M के प्रत्येक बिंदु पर एक का योग करें: <math display="block">\sum_i \phi_i(x) = 1.</math>
+* M के प्रत्येक बिंदु पर φ<sub>''i''</sub> का योग 1 होता है:<math display="block">\sum_i \phi_i(x) = 1.</math>
 (ध्यान दें कि यह अंतिम स्थिति वास्तव में φ के समर्थन की स्थानीय परिमितता के कारण प्रत्येक बिंदु पर एक सीमित योग है<sub>''i''</sub>.)
-सी का हर विवृत आवरण<sup>k</sup>मैनिफोल्ड M में C है<sup>क</sup>एकता का विभाजन. यह C की टोपोलॉजी से कुछ निर्माणों की अनुमति देता है<sup>k</sup> 'R' पर कार्य करता है<sup>n</sup>विभिन्न विविधों की श्रेणी में ले जाया जाना। विशेष रूप से, एक विशेष समन्वय एटलस के अधीनस्थ एकता के विभाजन को चुनकर और 'R' के प्रत्येक चार्ट में एकीकरण को अंजाम देकर एकीकरण पर चर्चा करना संभव है।<sup>n</sup>. इसलिए एकता के विभाजन कुछ अन्य प्रकार के [[कार्य स्थान]] पर विचार करने की अनुमति देते हैं: उदाहरण के लिए एलपी स्पेस|एल<sup>पी</sup> रिक्त स्थान, सोबोलेव रिक्त स्थान, और अन्य प्रकार के स्थान जिन्हें एकीकरण की आवश्यकता होती है।
+''C<sup>k</sup>'' मैनिफोल्ड M के प्रत्येक खुले आवरण में एकता का ''C<sup>k</sup>'' विभाजन होता है। यह '''R'''<sup>''n''</sup> पर ''C<sup>k</sup>'' फलन की टोपोलॉजी से कुछ निर्माणों को अलग-अलग मैनिफोल्ड्स की श्रेणी में ले जाने की अनुमति देता है। विशेष रूप से, एक विशेष समन्वय एटलस के अधीनस्थ एकता के विभाजन को चुनकर और '''R'''<sup>''n''</sup> के प्रत्येक चार्ट में एकीकरण को अंजाम देकर एकीकरण पर चर्चा करना संभव है। इसलिए एकता के विभाजन कुछ अन्य प्रकार के [[कार्य स्थान|फलन]] स्पेस पर विचार करने की अनुमति देते हैं: उदाहरण के लिए L<sup>''p''</sup> स्पेस, सोबोलेव स्पेस और अन्य प्रकार के स्पेस जिन्हें एकीकरण की आवश्यकता होती है।
 === मैनिफोल्ड्स के बीच मैपिंग की भिन्नता ===
-मान लीजिए कि M और एन क्रमशः आयाम M और एन के साथ दो अलग-अलग मैनिफोल्ड हैं, और एफ M से एन तक एक फ़लन है। चूंकि अलग-अलग मैनिफोल्ड टोपोलॉजिकल स्पेस हैं, इसलिए हम जानते हैं कि एफ के निरंतर होने का क्या अर्थ है। लेकिन एफ क्या करता है {{nowrap|''C<sup>k</sup>''(''M'', ''N'')}} के लिए अर्थ {{nowrap|''k'' ≥ 1}}? हम जानते हैं कि इसका क्या अर्थ है जब एफ यूक्लिडियन स्पेस के बीच एक फ़लन है, इसलिए यदि हम M के चार्ट और एन के चार्ट के साथ एफ की रचना करते हैं, तो हमें एक मानचित्र मिलता है जो यूक्लिडियन स्पेस से M से एन से यूक्लिडियन स्पेस तक जाता है, हम जानते हैं कि क्या इसका अर्थ उस मानचित्र के लिए है {{nowrap|''C<sup>k</sup>''('''R'''<sup>''m''</sup>, '''R'''<sup>''n''</sup>)}}. हम f को परिभाषित करते हैं {{nowrap|''C<sup>k</sup>''(''M'', ''N'')}} इसका अर्थ यह है कि चार्ट के साथ एफ की ऐसी सभी रचनाएँ हैं {{nowrap|''C<sup>k</sup>''('''R'''<sup>''m''</sup>, '''R'''<sup>''n''</sup>)}}. एक बार फिर, श्रृंखला नियम यह गारंटी देता है कि भिन्नता का विचार इस बात पर निर्भर नहीं करता है कि M और एन पर एटलस के कौन से चार्ट चुने गए हैं। चूँकि, व्युत्पन्न को परिभाषित करना स्वयं अधिक सूक्ष्म है। यदि M या एन स्वयं पहले से ही एक यूक्लिडियन स्थान है, तो हमें इसे एक में मैप करने के लिए चार्ट की आवश्यकता नहीं है।
+मान लीजिए कि M और N क्रमशः आयाम M और N के साथ दो अलग-अलग मैनिफोल्ड हैं, और f M से N तक एक फ़लन है। चूंकि अलग-अलग मैनिफोल्ड टोपोलॉजिकल स्पेस हैं, इसलिए हम जानते हैं कि f के निरंतर होने का क्या अर्थ है। लेकिन f क्या करता है {{nowrap|''C<sup>k</sup>''(''M'', ''N'')}} के लिए अर्थ {{nowrap|''k'' ≥ 1}}? हम जानते हैं कि इसका क्या अर्थ है जब एफ यूक्लिडियन स्पेस के बीच एक फ़लन है, इसलिए यदि हम M के चार्ट और n के चार्ट के साथ f की रचना करते हैं, तो हमें एक मानचित्र मिलता है जो यूक्लिडियन स्पेस से M से N से यूक्लिडियन स्पेस तक जाता है, हम जानते हैं कि क्या इसका अर्थ {{nowrap|''C<sup>k</sup>''('''R'''<sup>''m''</sup>, '''R'''<sup>''n''</sup>)}} उस मानचित्र के लिए है। हम f को {{nowrap|''C<sup>k</sup>''(''M'', ''N'')}} परिभाषित करते हैं, इसका अर्थ यह है कि चार्ट के साथ f की ऐसी सभी {{nowrap|''C<sup>k</sup>''('''R'''<sup>''m''</sup>, '''R'''<sup>''n''</sup>)}} रचनाएँ हैं। एक बार फिर, श्रृंखला नियम यह गारंटी देता है कि भिन्नता का विचार इस बात पर निर्भर नहीं करता है कि M और N पर एटलस के कौन से चार्ट चुने गए हैं। चूँकि, व्युत्पन्न को परिभाषित करना स्वयं अधिक सूक्ष्म है। यदि M या N स्वयं पहले से ही एक यूक्लिडियन स्थान है, तो हमें इसे एक में मैप करने के लिए चार्ट की आवश्यकता नहीं है।
 == बंडल ==
@@ Line 168: / Line 168: @@
 {{Further|स्पर्शरेखा बंडल}}
-किसी बिंदु के स्पर्शरेखा स्थान में उस बिंदु पर संभावित दिशात्मक व्युत्पन्न होते हैं, और इसका [[आयाम]] n के समान होता है जैसा कि मैनिफोल्ड का होता है। (गैर-एकवचन) निर्देशांक x के एक सेट के लिए<sub>k</sub>बिंदु पर स्थानीय, निर्देशांक व्युत्पन्न <math>\partial_k=\frac{\partial}{\partial x_k}</math> स्पर्शरेखा स्थान के [[होलोनोमिक आधार]] को परिभाषित करें। सभी बिंदुओं पर स्पर्शरेखा स्थानों का संग्रह बदले में एक मैनिफोल्ड, [[स्पर्शरेखा बंडल]] में बनाया जा सकता है, जिसका आयाम 2n है। स्पर्शरेखा बंडल वह जगह है जहां वेक्टर फ़ील्ड स्थित हैं, और यह स्वयं एक अलग-अलग कई गुना है। [[लैग्रेंजियन प्रणाली]] स्पर्शरेखा बंडल पर एक फ़लन है। स्पर्शरेखा बंडल को 'R' (वास्तविक रेखा) से M तक 1-[[जेट (गणित)]] के बंडल के रूप में भी परिभाषित किया जा सकता है।
+किसी बिंदु के स्पर्शरेखा स्थान में उस बिंदु पर संभावित दिशात्मक व्युत्पन्न होते हैं, और इसका आयाम n के समान होता है जैसा कि मैनिफोल्ड का होता है। (गैर-एकवचन) के एक सेट के लिए बिंदु पर ''x<sub>k</sub>'' स्थानीय निर्देशांक, निर्देशांक व्युत्पन्न <math>\partial_k=\frac{\partial}{\partial x_k}</math> स्पर्शरेखा स्थान के [[होलोनोमिक आधार]] को परिभाषित करें। सभी बिंदुओं पर स्पर्शरेखा स्थानों का संग्रह बदले में एक मैनिफोल्ड, [[स्पर्शरेखा बंडल]] में बनाया जा सकता है, जिसका आयाम 2n है। स्पर्शरेखा बंडल वह जगह है जहां सदिश फ़ील्ड स्थित हैं, और यह स्वयं एक अलग-अलग कई गुना है। [[लैग्रेंजियन प्रणाली]] स्पर्शरेखा बंडल पर एक फ़लन है। स्पर्शरेखा बंडल को 'R' (वास्तविक रेखा) से M तक 1-[[जेट (गणित)]] के बंडल के रूप में भी परिभाषित किया जा सकता है।
-कोई व्यक्ति स्पर्शरेखा बंडल के लिए एक एटलस का निर्माण कर सकता है जिसमें चार्ट सम्मिलित हों {{nowrap|''U''<sub>''α''</sub> × '''R'''<sup>''n''</sup>}}, जहां U<sub>''α''</sub> M के लिए एटलस में एक चार्ट को दर्शाता है। इन नए चार्टों में से प्रत्येक चार्ट U के लिए स्पर्शरेखा बंडल है, इस एटलस पर संक्रमण मानचित्रों को मूल मैनिफोल्ड पर संक्रमण मानचित्रों से परिभाषित किया गया है, और मूल भिन्नता वर्ग को बरकरार रखा गया है।
+कोई व्यक्ति स्पर्शरेखा बंडल के लिए एक एटलस का निर्माण कर सकता है जिसमें चार्ट {{nowrap|''U''<sub>''α''</sub> × '''R'''<sup>''n''</sup>}} सम्मिलित हों, जहां U<sub>''α''</sub> M के लिए एटलस में एक चार्ट को दर्शाता है। इन नए चार्टों में से प्रत्येक चार्ट U के लिए स्पर्शरेखा बंडल है, इस एटलस पर संक्रमण मानचित्रों को मूल मैनिफोल्ड पर संक्रमण मानचित्रों से परिभाषित किया गया है, और मूल भिन्नता वर्ग को बरकरार रखा गया है।
 === कोटैंजेंट बंडल ===
@@ Line 179: / Line 179: @@
 स्पर्शरेखा बंडल की तरह, कोटैंजेंट बंडल फिर से एक अलग-अलग प्रकार का है। [[हैमिल्टनियन यांत्रिकी]] कोटैंजेंट बंडल पर एक अदिश राशि है। कोटैंजेंट बंडल के [[कुल स्थान]] में एक [[सिंपलेक्टिक मैनिफ़ोल्ड]] की संरचना होती है। कोटैंजेंट वैक्टर को कभी-कभी [[कोवेक्टर]] भी कहा जाता है। कोटैंजेंट बंडल को M से 'R' तक के कार्यों के 1-जेट (गणित) के बंडल के रूप में भी परिभाषित किया जा सकता है।
-कोटैंजेंट स्पेस के तत्वों को अनंतिम विस्थापन के रूप में माना जा सकता है: यदि एफ एक अलग कार्य है तो हम प्रत्येक बिंदु पी पर एक कोटैंजेंट वेक्टर डीएफ परिभाषित कर सकते हैं<sub>p</sub>, जो एक स्पर्शरेखा सदिश X भेजता है<sub>p</sub>एक्स से जुड़े एफ के व्युत्पन्न के लिए<sub>p</sub>. चूँकि, प्रत्येक कोवेक्टर फ़ील्ड को इस तरह व्यक्त नहीं किया जा सकता है। जिन्हें [[सटीक अंतर|स्पष्ट अंतर]] कहा जा सकता है। स्थानीय निर्देशांक x के दिए गए सेट के लिए<sup>क</sup>, अंतर dx{{su|p=''k''|b=''p''}} पी पर कोटैंजेंट स्पेस का आधार बनाएं।
+कोटैंजेंट स्पेस के तत्वों को अनंतिम विस्थापन के रूप में माना जा सकता है: यदि f एक अलग फलन है तो हम प्रत्येक बिंदु p पर एक कोटैंजेंट वेक्टर ''df<sub>p</sub>'' को परिभाषित कर सकते हैं, जो ''X<sub>p</sub>'' से जुड़े f के व्युत्पन्न के लिए एक स्पर्शरेखा वेक्टर ''X<sub>p</sub>'' भेजता है। चूँकि, प्रत्येक कोवेक्टर फ़ील्ड को इस तरह व्यक्त नहीं किया जा सकता है। जिन्हें स्पष्ट अंतर कहा जा सकता है। स्थानीय निर्देशांक ''x<sup>k</sup>'' के दिए गए सेट के लिए, अंतर d''x<sup>k</sup>'' p पर कोटैंजेंट स्पेस का आधार बनाते हैं।
 === टेंसर बंडल ===
 {{Further|टेंसर बंडल}}
-टेंसर बंडल स्पर्शरेखा बंडल और कोटैंजेंट बंडल के सभी [[टेंसर उत्पाद]]ों के [[वेक्टर बंडलों का प्रत्यक्ष योग]] है। बंडल का प्रत्येक तत्व एक टेंसर फ़ील्ड है, जो वेक्टर फ़ील्ड या अन्य टेंसर फ़ील्ड पर [[बहुरेखीय ऑपरेटर]] के रूप में कार्य कर सकता है।
+टेंसर बंडल स्पर्शरेखा बंडल और कोटैंजेंट बंडल के सभी [[टेंसर उत्पाद]]ों के [[वेक्टर बंडलों का प्रत्यक्ष योग|सदिश बंडलों का प्रत्यक्ष योग]] है। बंडल का प्रत्येक तत्व एक टेंसर फ़ील्ड है, जो सदिश फ़ील्ड या अन्य टेंसर फ़ील्ड पर [[बहुरेखीय ऑपरेटर]] के रूप में फलन कर सकता है।
 टेंसर बंडल पारंपरिक अर्थों में एक विभेदित मैनिफोल्ड नहीं है, क्योंकि यह अनंत आयामी है। चूँकि यह अदिश कार्यों के वलय पर एक [[बीजगणित (रिंग सिद्धांत)]] है। प्रत्येक टेंसर की विशेषता उसके रैंकों से होती है, जो इंगित करता है कि इसमें कितने स्पर्शरेखा और कोटैंजेंट कारक हैं। कभी-कभी इन रैंकों को [[सहप्रसरण]] और सहप्रसरण और वैक्टर रैंकों के विरोधाभास के रूप में संदर्भित किया जाता है, जो क्रमशः स्पर्शरेखा और कोटैंजेंट रैंक को दर्शाता है।
@@ Line 192: / Line 192: @@
 {{Further|फ़्रेम बंडल}}
-एक फ्रेम (या, अधिक स्पष्ट शब्दों में, एक स्पर्शरेखा फ्रेम), विशेष स्पर्शरेखा स्थान का एक क्रमबद्ध आधार है। इसी प्रकार, एक स्पर्शरेखा फ़्रेम R का एक रैखिक समरूपता है<sup>n</sup>इस स्पर्शरेखा स्थान पर। एक गतिशील स्पर्शरेखा फ़्रेम वेक्टर फ़ील्ड की एक क्रमबद्ध सूची है जो उनके डोमेन के प्रत्येक बिंदु पर एक आधार देती है। कोई गतिशील फ़्रेम को फ़्रेम बंडल F(M), एक सामान्य रैखिक समूह| के एक भाग के रूप में भी मान सकता है {{nowrap|GL(''n'', '''R''')}} [[ प्रमुख बंडल |प्रमुख बंडल]] M पर सभी फ़्रेमों के सेट से बना है। फ़्रेम बंडल उपयोगी है क्योंकि M पर टेंसर फ़ील्ड को एफ (एम) पर [[समतुल्य]] वेक्टर-मूल्य वाले फ़लन के रूप में माना जा सकता है।
+एक फ्रेम (या, अधिक स्पष्ट शब्दों में, एक स्पर्शरेखा फ्रेम), विशेष स्पर्शरेखा स्थान का एक क्रमबद्ध आधार है। इसी प्रकार, एक स्पर्शरेखा फ़्रेम R का एक रैखिक समरूपता है<sup>n</sup>इस स्पर्शरेखा स्थान पर। एक गतिशील स्पर्शरेखा फ़्रेम सदिश फ़ील्ड की एक क्रमबद्ध सूची है जो उनके डोमेन के प्रत्येक बिंदु पर एक आधार देती है। कोई गतिशील फ़्रेम को फ़्रेम बंडल F(M), एक सामान्य रैखिक समूह| के एक भाग के रूप में भी मान सकता है {{nowrap|GL(''n'', '''R''')}} [[ प्रमुख बंडल |प्रमुख बंडल]] M पर सभी फ़्रेमों के सेट से बना है। फ़्रेम बंडल उपयोगी है क्योंकि M पर टेंसर फ़ील्ड को एफ (एम) पर [[समतुल्य]] सदिश-मूल्य वाले फ़लन के रूप में माना जा सकता है।
 === जेट बंडल ===
@@ Line 198: / Line 198: @@
 {{Further|जेट बंडल}}
-ऐसे मैनिफोल्ड पर जो पर्याप्त रूप से चिकना हो, विभिन्न प्रकार के जेट बंडलों पर भी विचार किया जा सकता है। मैनिफोल्ड का (प्रथम-क्रम) स्पर्शरेखा बंडल, प्रथम-क्रम संपर्क (गणित) के समतुल्य संबंध के मैनिफोल्ड मॉड्यूलो में वक्रों का संग्रह है। सादृश्य द्वारा, k-वें क्रम स्पर्शरेखा बंडल, k-वें क्रम संपर्क के संबंध में वक्रों का संग्रह है। इसी तरह, कोटैंजेंट बंडल मैनिफोल्ड पर फ़लन के 1-जेट्स का बंडल है: के-जेट बंडल उनके के-जेट्स का बंडल है। जेट बंडलों के सामान्य विचार के ये और अन्य उदाहरण मैनिफोल्ड्स पर अंतर ऑपरेटरों के अध्ययन में महत्वपूर्ण भूमिका निभाते हैं।
+ऐसे मैनिफोल्ड पर जो पर्याप्त रूप से चिकना हो, विभिन्न प्रकार के जेट बंडलों पर भी विचार किया जा सकता है। मैनिफोल्ड का (प्रथम-क्रम) स्पर्शरेखा बंडल, प्रथम-क्रम संपर्क (गणित) के समतुल्य संबंध के मैनिफोल्ड मॉड्यूलो में वक्रों का संग्रह है। सादृश्य द्वारा, k-वें क्रम स्पर्शरेखा बंडल, k-वें क्रम संपर्क के संबंध में वक्रों का संग्रह है। इसी तरह, कोटैंजेंट बंडल मैनिफोल्ड पर फ़लन के 1-जेट्स का बंडल है: k-जेट बंडल उनके के-जेट्स का बंडल है। जेट बंडलों के सामान्य विचार के ये और अन्य उदाहरण मैनिफोल्ड्स पर अंतर ऑपरेटरों के अध्ययन में महत्वपूर्ण भूमिका निभाते हैं।
-फ़्रेम की धारणा उच्च-क्रम वाले जेट के मामले में भी सामान्यीकृत होती है। एक k-वें क्रम के फ्रेम को 'R' से भिन्नरूपता के k-जेट के रूप में परिभाषित करें<sup>n</sup>से एम.<ref>See S. Kobayashi (1972).</ref> सभी k-वें क्रम फ़्रेमों का संग्रह, F<sup>k</sup>(M), एक प्रमुख G है<sup>क</sup>एम के ऊपर बंडल, जहां जी<sup>k</sup>जेट समूह है|k-जेट्स का समूह; अर्थात, 'R' के भिन्नरूपों के जेट (गणित)|k-जेट्स से बना समूह<sup>n</sup>जो मूल को ठीक करता है। ध्यान दें कि {{nowrap|GL(''n'', '''R''')}} स्वाभाविक रूप से G का समरूपी है<sup>1</sup>, और प्रत्येक G का एक उपसमूह<sup>क</sup>, {{nowrap|''k'' ≥ 2}}. विशेष रूप से, एफ का एक खंड<sup>2</sup>(एम) M पर एक [[कनेक्शन (गणित)]] के फ्रेम घटकों को देता है। इस प्रकार, भागफल बंडल {{nowrap|''F''<sup>2</sup>(''M'') / GL(''n'', '''R''')}} M के ऊपर सममित रैखिक कनेक्शन का बंडल है।
+फ़्रेम की धारणा उच्च-क्रम वाले जेट की स्थिति में भी सामान्यीकृत होती है। K-वें क्रम के फ्रेम को '''R'''<sup>''n''</sup> से M तक भिन्नता के k-जेट के रूप में परिभाषित करें।<ref>See S. Kobayashi (1972).</ref> सभी k-वें क्रम फ़्रेमों का संग्रह, ''F<sup>k</sup>''(''M''), M के ऊपर एक प्रमुख ''G<sup>k</sup>'' बंडल है, जहां ''G<sup>k</sup>'', k-जेट्स का समूह है; अर्थात्, '''R'''<sup>''n''</sup> की भिन्नता के के-जेट्स से बना समूह जो मूल को ठीक करता है। ध्यान दें कि GL(''n'', '''R''') स्वाभाविक रूप से ''G''<sup>1</sup> के लिए आइसोमोर्फिक है, और प्रत्येक ''G<sup>k</sup>'', ''k'' ≥ 2 का एक उपसमूह है। विशेष रूप से, ''F''<sup>2</sup>(''M'') का एक खंड ''M'' पर [[कनेक्शन (गणित)|कनेक्शन]] के फ्रेम घटकों को देता है। इस प्रकार, भागफल बंडल ''F''<sup>2</sup>(''M'') / GL(''n'', '''R''') M के ऊपर सममित रैखिक कनेक्शन का बंडल है।
 == मैनिफोल्ड्स पर कैलकुलस ==
-[[ बहुभिन्नरूपी कलन | बहुभिन्नरूपी कलन]] की कई तकनीकें, यथोचित परिवर्तनों के साथ, भिन्न-भिन्न मैनिफोल्ड्स पर भी प्रयुक्त होती हैं। उदाहरण के लिए, एक स्पर्शरेखा वेक्टर के साथ एक भिन्न फ़लन के दिशात्मक व्युत्पन्न को परिभाषित किया जा सकता है, और इससे किसी फ़लन के [[कुल व्युत्पन्न]] को सामान्य बनाने का एक साधन प्राप्त होता है: अंतर। कैलकुलस के परिप्रेक्ष्य से, मैनिफोल्ड पर किसी फ़लन का व्युत्पन्न यूक्लिडियन स्पेस पर परिभाषित फ़लन के सामान्य व्युत्पन्न के समान ही व्यवहार करता है, कम से कम [[स्थानीय संपत्ति]]। उदाहरण के लिए, ऐसे कार्यों के लिए अंतर्निहित फ़लन और व्युत्क्रम फ़लन प्रमेयों के संस्करण हैं।
+[[ बहुभिन्नरूपी कलन | बहुभिन्नरूपी कलन]] की कई तकनीकें, यथोचित परिवर्तनों के साथ, भिन्न-भिन्न मैनिफोल्ड्स पर भी प्रयुक्त होती हैं। उदाहरण के लिए, एक स्पर्शरेखा सदिश के साथ एक भिन्न फ़लन के दिशात्मक व्युत्पन्न को परिभाषित किया जा सकता है, और इससे किसी फ़लन के [[कुल व्युत्पन्न]] को सामान्य बनाने का एक साधन प्राप्त होता है: अंतर। कैलकुलस के परिप्रेक्ष्य से, मैनिफोल्ड पर किसी फ़लन का व्युत्पन्न यूक्लिडियन स्पेस पर परिभाषित फ़लन के सामान्य व्युत्पन्न के समान ही व्यवहार करता है, कम से कम [[स्थानीय संपत्ति]]। उदाहरण के लिए, ऐसे कार्यों के लिए अंतर्निहित फ़लन और व्युत्क्रम फ़लन प्रमेयों के संस्करण हैं।
-चूँकि, वेक्टर फ़ील्ड (और सामान्य रूप से टेंसर फ़ील्ड) की गणना में महत्वपूर्ण अंतर हैं। संक्षेप में, एक सदिश क्षेत्र का दिशात्मक व्युत्पन्न अच्छी तरह से परिभाषित नहीं है, या कम से कम सीधे विधि से परिभाषित नहीं है। एक सदिश क्षेत्र (या टेंसर क्षेत्र) के व्युत्पन्न के कई सामान्यीकरण उपस्थित हैं, और यूक्लिडियन स्थानों में भेदभाव की कुछ औपचारिक विशेषताओं को पकड़ते हैं। इनमें से प्रमुख हैं:
+चूँकि, सदिश फ़ील्ड (और सामान्य रूप से टेंसर फ़ील्ड) की गणना में महत्वपूर्ण अंतर हैं। संक्षेप में, एक सदिश क्षेत्र का दिशात्मक व्युत्पन्न अच्छी तरह से परिभाषित नहीं है, या कम से कम सीधे विधि से परिभाषित नहीं है। एक सदिश क्षेत्र (या टेंसर क्षेत्र) के व्युत्पन्न के कई सामान्यीकरण उपस्थित हैं, और यूक्लिडियन स्थानों में भेदभाव की कुछ औपचारिक विशेषताओं को पकड़ते हैं। इनमें से प्रमुख हैं:
 * लाई व्युत्पन्न, जिसे विभेदक संरचना द्वारा विशिष्ट रूप से परिभाषित किया गया है, लेकिन दिशात्मक विभेदन की कुछ सामान्य विशेषताओं को संतुष्ट करने में विफल रहता है।
 * एक [[एफ़िन कनेक्शन]], जो विशिष्ट रूप से परिभाषित नहीं है, लेकिन सामान्य दिशात्मक भेदभाव की विशेषताओं को अधिक संपूर्ण विधि से सामान्यीकृत करता है। क्योंकि एफ़िन कनेक्शन अद्वितीय नहीं है, यह डेटा का एक अतिरिक्त टुकड़ा है जिसे मैनिफोल्ड पर निर्दिष्ट किया जाना चाहिए।
-[[ समाकलन गणित | समाकलन गणित]] के विचार भी डिफरेंशियल मैनिफोल्ड्स तक ले जाते हैं। ये बाह्य कलन और [[विभेदक रूप]]ों की भाषा में स्वाभाविक रूप से व्यक्त होते हैं। कई चरों में इंटीग्रल कैलकुलस के मौलिक प्रमेय - अर्थात् ग्रीन का प्रमेय, [[विचलन प्रमेय]], और स्टोक्स का प्रमेय - एक प्रमेय (जिसे स्टोक्स का प्रमेय भी कहा जाता है) को सामान्यीकृत करते हैं, जो [[बाहरी व्युत्पन्न]] और [[सबमैनिफोल्ड]]्स पर एकीकरण से संबंधित होता है।
+[[ समाकलन गणित | समाकलन गणित]] के विचार भी डिफरेंशियल मैनिफोल्ड्स तक ले जाते हैं। ये बाह्य कलन और [[विभेदक रूप]] की भाषा में स्वाभाविक रूप से व्यक्त होते हैं। कई चरों में इंटीग्रल कैलकुलस के मौलिक प्रमेय - अर्थात् ग्रीन का प्रमेय, [[विचलन प्रमेय]], और स्टोक्स का प्रमेय - एक प्रमेय (जिसे स्टोक्स का प्रमेय भी कहा जाता है) को सामान्यीकृत करते हैं, जो [[बाहरी व्युत्पन्न]] और [[सबमैनिफोल्ड]] पर एकीकरण से संबंधित होता है।
 === कार्यों की विभेदक गणना ===
-सबमैनिफोल्ड्स और अन्य संबंधित अवधारणाओं की उपयुक्त धारणाएं तैयार करने के लिए दो मैनिफोल्ड्स के बीच विभेदक कार्यों की आवश्यकता होती है। अगर {{nowrap|''f'' : ''M'' → ''N''}} आयाम m के एक भिन्न मैनिफोल्ड M से आयाम n के दूसरे भिन्न मैनिफोल्ड N के लिए एक भिन्न कार्य है, फिर f का पुशफॉरवर्ड (अंतर) एक मैपिंग है {{nowrap|''df'' : T''M'' → T''N''}}. इसे Tf द्वारा भी निरूपित किया जाता है और इसे 'स्पर्शरेखा मानचित्र' कहा जाता है। M के प्रत्येक बिंदु पर, यह एक स्पर्शरेखा स्थान से दूसरे स्पर्शरेखा स्थान में एक रैखिक परिवर्तन है:
+सबमैनिफोल्ड्स और अन्य संबंधित अवधारणाओं की उपयुक्त धारणाएं तैयार करने के लिए दो मैनिफोल्ड्स के बीच विभेदक कार्यों की आवश्यकता होती है। अगर {{nowrap|''f'' : ''M'' → ''N''}} आयाम m के एक भिन्न मैनिफोल्ड M से आयाम n के दूसरे भिन्न मैनिफोल्ड N के लिए एक भिन्न फलन है, फिर f का पुशफॉरवर्ड (अंतर) एक मैपिंग है {{nowrap|''df'' : T''M'' → T''N''}}. इसे Tf द्वारा भी निरूपित किया जाता है और इसे 'स्पर्शरेखा मानचित्र' कहा जाता है। M के प्रत्येक बिंदु पर, यह एक स्पर्शरेखा स्थान से दूसरे स्पर्शरेखा स्थान में एक रैखिक परिवर्तन है:
 <math display=block>df(p)\colon T_p M \to T_{f(p)} N.</math>
 ''p'' पर ''f'' की रैंक इस रैखिक परिवर्तन के मैट्रिक्स की रैंक है।
@@ Line 221: / Line 221: @@
 * अगर {{nowrap|''m'' ≤ ''n''}}, और {{nowrap|''f'' : ''M'' → ''N''}} की रैंक M है {{nowrap|''p'' ∈ ''M''}}, तो f को p पर 'विसर्जन' कहा जाता है। यदि f, M के सभी बिंदुओं पर एक विसर्जन है और इसकी छवि पर एक समरूपता है, तो f एक '[[एम्बेडिंग]]' है। एंबेडिंग M की धारणा को औपचारिक रूप देती है कि यह एन का सबमैनिफोल्ड है। सामान्य तौर पर, एक एम्बेडिंग स्व-प्रतिच्छेदन और अन्य प्रकार की गैर-स्थानीय टोपोलॉजिकल अनियमितताओं के बिना एक विसर्जन है।
-* अगर {{nowrap|''m'' ≥ ''n''}}, और {{nowrap|''f'' : ''M'' → ''N''}} की रैंक n है {{nowrap|''p'' ∈ ''M''}}, तो f को p पर 'डुबकी' कहा जाता है। निहित फलन प्रमेय बताता है कि यदि f, p पर एक निमज्जन है, तो M स्थानीय रूप से N<sup>m−n</sup> और 'R' का गुणन है। p के निकट। औपचारिक शब्दों में, निर्देशांक उपस्थित हैं {{nowrap|(''y''<sub>1</sub>, ..., ''y<sub>n</sub>'')}} एन में एफ(पी) के पड़ोस में, और {{nowrap|''m'' − ''n''}} फ़लनो x<sub>1</sub>, ..., एक्स<sub>''m''−''n''</sub> M में पी के पड़ोस में परिभाषित किया गया है <math display="block">(y_1\circ f,\dotsc,y_n\circ f, x_1, \dotsc, x_{m-n})</math> पी के पड़ोस में M के स्थानीय निर्देशांक की एक प्रणाली है। विसर्जन तंतु और [[फाइबर बंडल]] के सिद्धांत की नींव बनाते हैं।
+* यदि m ≥ n, और f : M → N की रैंक ''p'' ∈ ''M'' पर है, तो f को p पर निमज्जन कहा जाता है। अंतर्निहित फलन प्रमेय में कहा गया है कि यदि f, p पर एक जलमग्नता है, तो M स्थानीय रूप से N और '''R'''<sup>''m''−''n''</sup> का p के पास गुणन है। औपचारिक शब्दों में, N में ''f(p'') के पड़ोस में निर्देशांक (''y''<sub>1</sub>, ..., ''y<sub>n</sub>'') उपस्थित हैं, और M में p के पड़ोस में m - n फलन ''x''<sub>1</sub>, ..., ''x<sub>m</sub>''<sub>−''n''</sub>  परिभाषित हैं। वह<math display="block">(y_1\circ f,\dotsc,y_n\circ f, x_1, \dotsc, x_{m-n})</math> p के पड़ोस में M के स्थानीय निर्देशांक की एक प्रणाली है। विसर्जन तंतु और [[फाइबर बंडल]] के सिद्धांत की नींव बनाते हैं।
 === लाइ व्युत्पन्न ===
-एक लाई व्युत्पन्न, जिसका नाम [[सोफस झूठ|सोफस लाइ]] के नाम पर रखा गया है, एक मैनिफोल्ड M पर टेंसर फ़ील्ड के क्षेत्र पर बीजगणित पर एक [[व्युत्पत्ति (अमूर्त बीजगणित)]] है। M पर सभी लाई व्युत्पन्नों का वेक्टर स्थान लाई के संबंध में एक अनंत आयामी लाई बीजगणित बनाता है। द्वारा परिभाषित वेक्टर फ़ील्ड का ब्रैकेट
+एक लाई व्युत्पन्न, जिसका नाम [[सोफस झूठ|सोफस लाइ]] के नाम पर रखा गया है, एक मैनिफोल्ड M पर टेंसर फ़ील्ड के क्षेत्र पर बीजगणित पर एक [[व्युत्पत्ति (अमूर्त बीजगणित)]] है। M पर सभी लाई व्युत्पन्नों का सदिश स्थान लाई के संबंध में एक अनंत आयामी लाई बीजगणित बनाता है। द्वारा परिभाषित सदिश फ़ील्ड का ब्रैकेट
 <math display=block> [A,B] := \mathcal{L}_A B  = - \mathcal{L}_B A.</math>
-लाई डेरिवेटिव्स को वेक्टर फ़ील्ड्स द्वारा दर्शाया जाता है, जैसे कि लाई समूह#M पर प्रवाह के लाई समूहों ([[सक्रिय परिवर्तन]] भिन्नता) से संबंधित लाई बीजगणित। इसे दूसरी विधि से देखते हुए, M के भिन्नता के [[समूह (गणित)]] में है लाई डेरिवेटिव की संबद्ध लाई बीजगणित संरचना, एक तरह से लाई समूह सिद्धांत के सीधे अनुरूप है।
+लाई डेरिवेटिव्स को सदिश फ़ील्ड्स द्वारा दर्शाया जाता है, जैसे कि लाई समूह M पर प्रवाह के लाई समूहों ([[सक्रिय परिवर्तन]] भिन्नता) से संबंधित लाई बीजगणित। इसे दूसरी विधि से देखते हुए, M के भिन्नता के [[समूह (गणित)]] में है लाई डेरिवेटिव की संबद्ध लाई बीजगणित संरचना, एक तरह से लाई समूह सिद्धांत के सीधे अनुरूप है।
 === बाहरी गणना ===
@@ Line 241: / Line 241: @@
 {{Main |बाह्य व्युत्पन्न}}
-बाहरी व्युत्पन्न एक चिकनी मैनिफोल्ड पर सभी चिकनी अंतर रूपों के वर्गीकृत वेक्टर स्थान पर एक रैखिक ऑपरेटर है <math>M</math>. इसे सामान्यतः द्वारा दर्शाया जाता है <math>d</math>. अधिक स्पष्ट रूप से, यदि <math>n=\dim(M)</math>, के लिए <math>0 \le k \le n</math> परिचालक <math>d</math> अंतरिक्ष का मानचित्रण करता है <math>\Omega^k(M)</math> का <math>k</math>-पर प्रपत्र <math>M</math> अंतरिक्ष में <math>\Omega^{k+1}(M)</math> का <math>(k+1)</math>-फॉर्म (यदि <math>k > n</math> कोई गैर-शून्य नहीं हैं <math>k</math>-पर प्रपत्र <math>M</math> तो मानचित्र <math>d</math> समान रूप से शून्य है <math>n</math>-रूप)।
+बाहरी व्युत्पन्न एक चिकनी मैनिफोल्ड पर सभी चिकनी अंतर रूपों के वर्गीकृत सदिश स्थान पर एक रैखिक ऑपरेटर <math>M</math> है. इसे सामान्यतः <math>d</math> द्वारा दर्शाया जाता है. अधिक स्पष्ट रूप से, यदि <math>n=\dim(M)</math>, के लिए <math>0 \le k \le n</math> परिचालक <math>d</math> अंतरिक्ष का मानचित्रण <math>\Omega^k(M)</math> करता है, <math>M</math> का <math>k</math>-पर प्रपत्र अंतरिक्ष में <math>\Omega^{k+1}(M)</math> का <math>(k+1)</math>-फॉर्म करता है (यदि <math>k > n</math> कोई गैर-शून्य नहीं हैं, <math>k</math>-पर प्रपत्र <math>M</math> तो मानचित्र <math>d</math> समान <math>n</math>-रूप से शून्य है)।
-उदाहरण के लिए, एक सुचारु कार्य का बाहरी अंतर <math>f</math> स्थानीय निर्देशांक में दिया गया है <math>x_1, \ldots, x_n</math>, संबद्ध स्थानीय सह-फ़्रेम के साथ <math>dx_1, \ldots, dx_n</math> सूत्र द्वारा:
+उदाहरण के लिए, एक सुचारु फलन का बाहरी अंतर <math>f</math> स्थानीय निर्देशांक <math>x_1, \ldots, x_n</math> में दिया गया है, संबद्ध स्थानीय सह-फ़्रेम के साथ <math>dx_1, \ldots, dx_n</math> सूत्र द्वारा:
- <math display=block>df = \sum_{i=1}^n \frac{\partial f}{\partial x_i} dx_i. </math>
+<math display=block>df = \sum_{i=1}^n \frac{\partial f}{\partial x_i} dx_i. </math>
 बाहरी अंतर फॉर्म के वेज गुणन के संबंध में गुणन नियम के समान, निम्नलिखित पहचान को संतुष्ट करता है:
 <math display="block">d(\omega \wedge \eta) = d\omega \wedge \eta+(-1)^{\deg\omega}\omega \wedge d\eta.</math>
-बाहरी व्युत्पन्न भी पहचान को संतुष्ट करता है <math>d \circ d = 0</math>. अर्थात यदि <math>\omega</math> एक है <math>k</math>-रूप तो <math>(k+2)</math>-प्रपत्र <math>d(df)</math> समान रूप से लुप्त हो रहा है. एक प्रपत्र <math>\omega</math> ऐसा है कि <math>d\omega = 0</math> बंद कहा जाता है, जबकि एक प्रपत्र <math>\omega</math> ऐसा है कि <math>\omega = d\eta</math> किसी अन्य रूप के लिए <math>\eta</math> स्पष्ट कहा जाता है. पहचान का एक और सूत्रीकरण <math>d \circ d = 0</math> क्या यह एक स्पष्ट प्रपत्र बंद है. यह किसी को मैनिफोल्ड के [[डॉ कहलमज गर्भाशय]] को परिभाषित करने की अनुमति देता है <math>M</math>, जहां <math>k</math>वां कोहोमोलोजी समूह बंद रूपों का [[भागफल समूह]] है <math>M</math> पर स्पष्ट रूपों द्वारा <math>M</math>.
+बाहरी व्युत्पन्न भी पहचान <math>d \circ d = 0</math> को संतुष्ट करता है। अर्थात यदि <math>\omega</math> एक <math>k</math>-रूप है,  तो <math>(k+2)</math>-प्रपत्र <math>d(df)</math> समान रूप से लुप्त हो रहा है. एक प्रपत्र <math>\omega</math> ऐसा है कि <math>d\omega = 0</math> बंद कहा जाता है, जबकि एक प्रपत्र <math>\omega</math> ऐसा है कि <math>\omega = d\eta</math> किसी अन्य रूप के लिए <math>\eta</math> स्पष्ट कहा जाता है। पहचान <math>d \circ d = 0</math> का एक और सूत्रीकरण  क्या यह एक स्पष्ट प्रपत्र बंद है। यह किसी को मैनिफोल्ड के [[डॉ कहलमज गर्भाशय|डॉ कहलमज कोहोमोलॉजी]] को <math>M</math> परिभाषित करने की अनुमति देता है, जहां <math>k</math>वां कोहोमोलोजी समूह बंद रूपों का [[भागफल समूह]] <math>M</math> है, जिसे <math>M</math> पर स्पष्ट रूपों द्वारा अनुमति दिया जाता है।
 ==विभेदक मैनिफोल्ड्स की टोपोलॉजी ==
@@ Line 253: / Line 253: @@
 === टोपोलॉजिकल मैनिफोल्ड्स के साथ संबंध ===
-लगता है कि <math>M</math> एक टोपोलॉजिकल है <math>n</math>-कई गुना.
+मान लीजिए कि <math>M</math> टोपोलॉजिकल <math>n</math>-मैनिफोल्ड है।
-यदि कोई सहज एटलस दिया जाए <math>\{(U_\alpha,\phi_\alpha)\}_{\alpha\in A}</math>, एक चिकनी एटलस ढूंढना सरल है जो एक अलग चिकनी कई गुना संरचना को परिभाषित करता है <math>M;</math> एक होमियोमोर्फिज्म पर विचार करें <math>\Phi:M\to M</math> जो दिए गए एटलस के सापेक्ष सहज नहीं है; उदाहरण के लिए, कोई पहचान मानचित्र स्थानीयकृत गैर-चिकनी टक्कर को संशोधित कर सकता है। फिर नये एटलस पर विचार करें <math>\{(\Phi^{-1}(U_\alpha),\phi_\alpha\circ\Phi)\}_{\alpha\in A},</math> जिसे सहज एटलस के रूप में आसानी से सत्यापित किया जा सकता है। चूँकि, नए एटलस के चार्ट पुराने एटलस के चार्ट के साथ आसानी से संगत नहीं हैं, क्योंकि इसके लिए इसकी आवश्यकता होगी <math>\phi_\alpha\circ\Phi\circ\phi_\beta^{-1}</math> और <math>\phi_\alpha\circ\Phi^{-1}\circ\phi_\beta^{-1}</math> किसी के लिए भी सहज हैं <math>\alpha</math> और <math>\beta,</math> इन नियमों के साथ बिल्कुल वही परिभाषा है जो दोनों <math>\Phi</math> और <math>\Phi^{-1}</math> सहज हैं, कैसे के विपरीत <math>\Phi</math> चुना गया।
+यदि कोई सहज एटलस <math>\{(U_\alpha,\phi_\alpha)\}_{\alpha\in A}</math> दिया जाए, एक चिकनी एटलस ढूंढना सरल है जो एक अलग चिकनी कई गुना संरचना को <math>M;</math> परिभाषित करता है; एक होमियोमोर्फिज्म <math>\Phi:M\to M</math> पर विचार करें, जो दिए गए एटलस के सापेक्ष सहज नहीं है; उदाहरण के लिए, कोई पहचान मानचित्र स्थानीयकृत गैर-चिकनी बुम्प को संशोधित कर सकता है। फिर नये एटलस <math>\{(\Phi^{-1}(U_\alpha),\phi_\alpha\circ\Phi)\}_{\alpha\in A},</math> पर विचार करें; जिसे सहज एटलस के रूप में आसानी से सत्यापित किया जा सकता है। चूँकि, नए एटलस के चार्ट पुराने एटलस के चार्ट के साथ आसानी से संगत नहीं हैं, क्योंकि इसके लिए <math>\phi_\alpha\circ\Phi\circ\phi_\beta^{-1}</math> इसकी आवश्यकता होगी और <math>\phi_\alpha\circ\Phi^{-1}\circ\phi_\beta^{-1}</math> किसी के लिए भी सहज हैं <math>\alpha</math> और <math>\beta,</math> इन नियमों के साथ बिल्कुल वही परिभाषा है, जो दोनों <math>\Phi</math> और <math>\Phi^{-1}</math> सहज हैं, कैसे के विपरीत <math>\Phi</math> चुना गया।
 प्रेरणा के रूप में इस अवलोकन के साथ, कोई भी चिकनी एटलस के स्थान पर एक तुल्यता संबंध को परिभाषित कर सकता है <math>M</math> उस चिकनी एटलस की घोषणा करके <math>\{(U_\alpha,\phi_\alpha)\}_{\alpha\in A}</math> और <math>\{(V_\beta,\psi_\beta)\}_{\beta\in B}</math> यदि समरूपता है तो समतुल्य हैं <math>\Phi:M\to M</math> ऐसा है कि <math>\{(\Phi^{-1}(U_\alpha),\phi_\alpha\circ\Phi)\}_{\alpha\in A}</math> के साथ सहजता से संगत है <math>\{(V_\beta,\psi_\beta)\}_{\beta\in B},</math> और ऐसा कि <math>\{(\Phi(V_\beta),\psi_\beta\circ\Phi^{-1})\}_{\beta\in B}</math> के साथ <math>\{(U_\alpha,\phi_\alpha)\}_{\alpha\in A}</math> सहजता से संगत है।
@@ Line 286: / Line 286: @@
 === (छद्म-)[[रीमैनियन मैनिफोल्ड]] ===
-रीमैनियन मैनिफोल्ड में प्रत्येक व्यक्तिगत स्पर्शरेखा स्थान पर एक सकारात्मक-निश्चित [[आंतरिक उत्पाद स्थान|आंतरिक गुणन स्थान]] के साथ एक चिकनी मैनिफोल्ड होता है। आंतरिक उत्पादों के इस संग्रह को [[रीमैनियन मीट्रिक]] कहा जाता है, और यह स्वाभाविक रूप से एक सममित 2-टेंसर क्षेत्र है। यह मीट्रिक एक प्राकृतिक वेक्टर अंतरिक्ष समरूपता की पहचान <math>T_pM\to T_p^\ast M</math> करता है। प्रत्येक <math>p\in M</math> के लिए  रीमैनियन मैनिफ़ोल्ड पर कोई लंबाई, आयतन और कोण की धारणाओं को परिभाषित कर सकता है। किसी भी स्मूथ मैनिफोल्ड को कई अलग-अलग रीमैनियन मेट्रिक्स दिए जा सकते हैं।
+रीमैनियन मैनिफोल्ड में प्रत्येक व्यक्तिगत स्पर्शरेखा स्थान पर एक सकारात्मक-निश्चित [[आंतरिक उत्पाद स्थान|आंतरिक गुणन स्थान]] के साथ एक चिकनी मैनिफोल्ड होता है। आंतरिक उत्पादों के इस संग्रह को [[रीमैनियन मीट्रिक]] कहा जाता है, और यह स्वाभाविक रूप से एक सममित 2-टेंसर क्षेत्र है। यह मीट्रिक एक प्राकृतिक सदिश अंतरिक्ष समरूपता की पहचान <math>T_pM\to T_p^\ast M</math> करता है। प्रत्येक <math>p\in M</math> के लिए  रीमैनियन मैनिफ़ोल्ड पर कोई लंबाई, आयतन और कोण की धारणाओं को परिभाषित कर सकता है। किसी भी स्मूथ मैनिफोल्ड को कई अलग-अलग रीमैनियन मेट्रिक्स दिए जा सकते हैं।
 एक [[छद्म-रीमैनियन मैनिफोल्ड]], रीमैनियन मैनिफोल्ड की धारणा का एक सामान्यीकरण है जहां आंतरिक उत्पादों को निश्चित बिलिनियर फॉर्म | सकारात्मक-निश्चित होने के विपरीत, [[मीट्रिक हस्ताक्षर]] की अनुमति दी जाती है; उन्हें अभी भी गैर-पतित होने की आवश्यकता है। प्रत्येक चिकनी छद्म-रीमैनियन और रीमैनियन मैनिफोल्ड कई संबंधित टेंसर क्षेत्रों को परिभाषित करता है, जैसे कि [[रीमैन वक्रता टेंसर]]। छद्म-रिमानियन हस्ताक्षर के कई गुना {{nowrap|(3, 1)}} सामान्य सापेक्षता में मौलिक हैं। प्रत्येक चिकने मैनिफोल्ड को (गैर-रीमानियन) छद्म-रीमैनियन संरचना नहीं दी जा सकती; ऐसा करने पर टोपोलॉजिकल प्रतिबंध हैं।
-[[फिन्सलर मैनिफोल्ड]] रीमैनियन मैनिफोल्ड का एक अलग सामान्यीकरण है, जिसमें आंतरिक गुणन को [[वेक्टर मानदंड]] से बदल दिया जाता है; इस प्रकार, यह लंबाई की परिभाषा की अनुमति देता है, लेकिन कोण की नहीं।
+[[फिन्सलर मैनिफोल्ड]] रीमैनियन मैनिफोल्ड का एक अलग सामान्यीकरण है, जिसमें आंतरिक गुणन को [[वेक्टर मानदंड|सदिश मानदंड]] से बदल दिया जाता है; इस प्रकार, यह लंबाई की परिभाषा की अनुमति देता है, लेकिन कोण की नहीं।
 === सिंपलेक्टिक मैनिफोल्ड्स ===
@@ Line 298: / Line 298: @@
 एक सिंपलेक्टिक मैनिफोल्ड एक बंद फॉर्म (कैलकुलस), नॉनडिजेनरेट फॉर्म [[2-प्रपत्र]] से सुसज्जित मैनिफोल्ड है। यह स्थिति सिम्प्लेक्टिक मैनिफ़ोल्ड को सम-आयामी होने के लिए बाध्य करती है, इस तथ्य के कारण कि तिरछा-सममित <math>(2n+1)\times(2n+1)</math> सभी मैट्रिक्स में शून्य निर्धारक होता है। दो मूलभूत उदाहरण हैं:
 * कोटैंजेंट बंडल, जो हैमिल्टनियन यांत्रिकी में चरण रिक्त स्थान के रूप में उत्पन्न होते हैं, एक प्रेरक उदाहरण हैं, क्योंकि वे एक [[टॉटोलॉजिकल एक-रूप]] को स्वीकार करते हैं।
-* सभी उन्मुख द्वि-आयामी रीमैनियन मैनिफोल्ड्स <math>(M,g)</math> रूप को परिभाषित करके, स्वाभाविक रूप से, सहानुभूतिपूर्ण हैं <math>\omega(u,v)=g(u,J(v))</math> जहाँ, किसी के लिए <math>v \in T_pM,</math> <math>J(v)</math> वेक्टर को इस प्रकार <math>v,J(v)</math> निरूपित करता है  एक उन्मुख <math>g_p</math>-अर्थसामान्य आधार का <math>T_pM</math> है।
+* सभी उन्मुख द्वि-आयामी रीमैनियन मैनिफोल्ड्स <math>(M,g)</math> रूप को परिभाषित करके, स्वाभाविक रूप से, सहानुभूतिपूर्ण हैं <math>\omega(u,v)=g(u,J(v))</math> जहाँ, किसी के लिए <math>v \in T_pM,</math> <math>J(v)</math> सदिश को इस प्रकार <math>v,J(v)</math> निरूपित करता है  एक उन्मुख <math>g_p</math>-अर्थसामान्य आधार का <math>T_pM</math> है।
@@ Line 307: / Line 307: @@
 एक लाइ समूह में एक C<sup>∞</sup> होता है, कई गुना <math>G</math> एक साथ एक समूह (गणित) संरचना पर <math>G</math> जैसे कि गुणन और व्युत्क्रम मानचित्र <math>m:G\times G \to G</math> और <math>i:G\to G</math> कई गुना के मानचित्रों की तरह चिकने हैं। ये वस्तुएं अधिकांशतः (निरंतर) समरूपता का वर्णन करते समय स्वाभाविक रूप से उत्पन्न होती हैं, और वे चिकनी विविधता के उदाहरणों का एक महत्वपूर्ण स्रोत बनाती हैं।
-चूँकि, स्मूथ मैनिफोल्ड्स के कई अन्यथा परिचित उदाहरणों को एक लाई समूह संरचना नहीं दी जा सकती है, क्योंकि एक लाई समूह दिया गया है <math>G</math> और कोई भी <math>g\in G</math>, कोई मानचित्र पर विचार कर सकता है <math>m(g,\cdot):G\to G</math> जो पहचान तत्व भेजता है <math>e</math> को <math>g</math> और इसलिए, अंतर पर विचार करके <math>T_eG\to T_gG,</math> लाइ समूह के किन्हीं दो स्पर्शरेखा स्थानों के बीच एक प्राकृतिक पहचान देता है। विशेष रूप से, एक इच्छानुसार गैर-शून्य वेक्टर पर विचार करके <math>T_eG,</math> कोई इन पहचानों का उपयोग सुचारू गैर-लुप्त होने वाले वेक्टर फ़ील्ड को देने के लिए कर सकता है <math>G.</math> उदाहरण के लिए, इससे पता चलता है कि कोई भी हेयरी बॉल प्रमेय|सम-आयामी क्षेत्र लाई समूह संरचना का समर्थन नहीं कर सकता है। यही तर्क सामान्यतः दिखाता है कि प्रत्येक लाइ समूह को कई गुना समानांतर होना चाहिए।
+चूँकि, स्मूथ मैनिफोल्ड्स के कई अन्यथा परिचित उदाहरणों को एक लाई समूह संरचना नहीं दी जा सकती है, क्योंकि एक लाई समूह दिया गया है <math>G</math> और कोई भी <math>g\in G</math>, कोई मानचित्र पर विचार कर सकता है <math>m(g,\cdot):G\to G</math> जो पहचान तत्व भेजता है <math>e</math> को <math>g</math> और इसलिए, अंतर पर विचार करके <math>T_eG\to T_gG,</math> लाइ समूह के किन्हीं दो स्पर्शरेखा स्थानों के बीच एक प्राकृतिक पहचान देता है। विशेष रूप से, एक इच्छानुसार गैर-शून्य सदिश पर विचार करके <math>T_eG,</math> कोई इन पहचानों का उपयोग सुचारू गैर-लुप्त होने वाले सदिश फ़ील्ड को देने के लिए कर सकता है <math>G.</math> उदाहरण के लिए, इससे पता चलता है कि कोई भी हेयरी बॉल प्रमेय|सम-आयामी क्षेत्र लाई समूह संरचना का समर्थन नहीं कर सकता है। यही तर्क सामान्यतः दिखाता है कि प्रत्येक लाइ समूह को कई गुना समानांतर होना चाहिए।
 == वैकल्पिक परिभाषाएँ ==
@@ Line 315: / Line 315: @@
 [[छद्मसमूह]] की धारणा<ref>Kobayashi and Nomizu (1963), Volume 1.</ref> विभिन्न संरचनाओं को एक समान विधि से मैनिफोल्ड्स पर परिभाषित करने की अनुमति देने के लिए एटलस का एक लचीला सामान्यीकरण प्रदान करता है। एक छद्म समूह में एक टोपोलॉजिकल स्पेस एस और एक संग्रह Γ होता है जिसमें एस के विवृत उपसमुच्चय से लेकर एस के अन्य विवृत उपसमुच्चय तक होमोमोर्फिज्म सम्मिलित होते हैं जैसे कि
 # अगर {{nowrap|''f'' ∈ Γ}}, और U, f के डोमेन का एक विवृत उपसमुच्चय है, तो प्रतिबंध f|<sub>''U''</sub> Γ में भी है.
-# यदि f, S के विवृत उपसमुच्चय के मिलन से एक समरूपता है, <math>\cup_i \, U_i </math>, तो एस के एक विवृत उपसमुच्चय के लिए {{nowrap|''f'' ∈ Γ}} बशर्ते <math> f|_{U_i} \in \Gamma </math> प्रत्येक i के लिए
+# यदि f, S के विवृत उपसमुच्चय के मिलन से एक समरूपता <math>\cup_i \, U_i </math> है, तो S के एक विवृत उपसमुच्चय के लिए {{nowrap|''f'' ∈ Γ}} बशर्ते <math> f|_{U_i} \in \Gamma </math> प्रत्येक i के लिए
 # हर विवृत के लिए {{nowrap|''U'' ⊂ ''S''}}, U का पहचान परिवर्तन Γ में है।
 # अगर {{nowrap|''f'' ∈ Γ}}, तब {{nowrap|''f''<sup>−1</sup> ∈ Γ}}.
 # Γ के दो तत्वों की संरचना Γ में है.
-ये अंतिम तीन स्थितियाँ एक समूह (गणित) की परिभाषा के अनुरूप हैं। ध्यान दें कि Γ को एक समूह होने की आवश्यकता नहीं है, चूंकि फ़लन एस पर विश्व स्तर पर परिभाषित नहीं हैं। उदाहरण के लिए, सभी स्थानीय C<sup>k</sup> का संग्रह 'R' पर [[भिन्नता]]<sup>n</sup>एक छद्म समूह बनाएं। 'C' में विवृत सेटों के बीच सभी [[बिहोलोमोर्फिज्म]] एक छद्म समूह बनाएं। अधिक उदाहरणों में सम्मिलित हैं: 'R' के मानचित्रों को संरक्षित करने वाला अभिविन्यास, [[लक्षणरूपता]], मोबियस परिवर्तन, [[एफ़िन परिवर्तन]], इत्यादि। इस प्रकार, विभिन्न प्रकार के फ़लन वर्ग छद्मसमूह निर्धारित करते हैं।
+ये अंतिम तीन स्थितियाँ एक समूह (गणित) की परिभाषा के अनुरूप हैं। ध्यान दें कि Γ को एक समूह होने की आवश्यकता नहीं है, चूंकि फ़लन S पर विश्व स्तर पर परिभाषित नहीं हैं। उदाहरण के लिए, सभी स्थानीय C<sup>k</sup> का संग्रह 'R' पर [[भिन्नता]]<sup>n</sup>एक छद्म समूह बनाएं। 'C' में विवृत सेटों के बीच सभी [[बिहोलोमोर्फिज्म]] एक छद्म समूह बनाएं। अधिक उदाहरणों में सम्मिलित हैं: 'R' के मानचित्रों को संरक्षित करने वाला अभिविन्यास, [[लक्षणरूपता]], मोबियस परिवर्तन, [[एफ़िन परिवर्तन]], इत्यादि। इस प्रकार, विभिन्न प्रकार के फ़लन वर्ग छद्मसमूह निर्धारित करते हैं।
-एक एटलस (''U<sub>i</sub>'', ''φ<sub>i</sub>'') होमोमोर्फिज्म का φ<sub>''i''</sub> से {{nowrap|''U<sub>i</sub>'' ⊂ ''M''}} टोपोलॉजिकल स्पेस के सबसेट को खोलने के लिए एस को एक छद्म समूह के साथ संगत माना जाता है Γ बशर्ते कि संक्रमण कार्य करता हो {{nowrap|''φ''<sub>''j''</sub> ∘ ''φ''<sub>''i''</sub><sup>−1</sup> : ''φ''<sub>''i''</sub>(''U<sub>i</sub>'' ∩ ''U<sub>j</sub>'') → ''φ''<sub>''j''</sub>(''U<sub>i</sub>'' ∩ ''U<sub>j</sub>'')}} सभी Γ में हैं।
+एक एटलस (''U<sub>i</sub>'', ''φ<sub>i</sub>'') होमोमोर्फिज्म का φ<sub>''i''</sub> से {{nowrap|''U<sub>i</sub>'' ⊂ ''M''}} टोपोलॉजिकल स्पेस के सबसेट को खोलने के लिए एस को एक छद्म समूह के साथ संगत माना जाता है Γ बशर्ते कि संक्रमण फलन {{nowrap|''φ''<sub>''j''</sub> ∘ ''φ''<sub>''i''</sub><sup>−1</sup> : ''φ''<sub>''i''</sub>(''U<sub>i</sub>'' ∩ ''U<sub>j</sub>'') → ''φ''<sub>''j''</sub>(''U<sub>i</sub>'' ∩ ''U<sub>j</sub>'')}} सभी Γ में हैं।
-एक विभेदक मैनिफोल्ड तब C के छद्म समूह के साथ संगत एक एटलस है 'R' पर कार्य करता है. एक कॉम्प्लेक्स मैनिफोल्ड एक एटलस है जो 'C' में विवृत सेट पर बिहोलोमोर्फिक फ़लनो के साथ संगत है। इस प्रकार, छद्म समूह एक एकल ढांचा प्रदान करते हैं जिसमें अंतर ज्यामिति और टोपोलॉजी के लिए कई गुना महत्वपूर्ण संरचनाओं का वर्णन किया जा सकता है।
+एक विभेदक मैनिफोल्ड तब C के छद्म समूह के साथ संगत एक एटलस है 'R' पर फलन करता है. एक कॉम्प्लेक्स मैनिफोल्ड एक एटलस है जो 'C' में विवृत सेट पर बिहोलोमोर्फिक फ़लनो के साथ संगत है। इस प्रकार, छद्म समूह एक एकल ढांचा प्रदान करते हैं जिसमें अंतर ज्यामिति और टोपोलॉजी के लिए कई गुना महत्वपूर्ण संरचनाओं का वर्णन किया जा सकता है।
 === संरचना शीफ़ ===
-कभी-कभी, मैनिफोल्ड को C प्रदान करने के लिए वैकल्पिक दृष्टिकोण का उपयोग करना उपयोगी हो सकता है-संरचना. यहां वास्तविक विश्लेषणात्मक मैनिफोल्ड के लिए k = 1, 2, ..., ∞, या ω है। समन्वय चार्ट पर विचार करने के अतिरिक्त, मैनिफोल्ड पर परिभाषित कार्यों के साथ प्रारंभ करना संभव है। M<sup>k</sup> का शीफ (गणित), 'C' को दर्शाता है, एक प्रकार का [[ऑपरेटर]] है जो प्रत्येक विवृत सेट के लिए परिभाषित करता है {{nowrap|''U'' ⊂ ''M''}}, एक बीजगणित '''C'''<sup>''k''</sup>(''U'') सतत कार्यों का {{nowrap|''U'' →  '''R'''}}. एक संरचना शीफ सी कहा जाता है कि k, M को C की संरचना देता हैकआयाम एन के कई गुना बशर्ते कि, किसी के लिए {{nowrap|''p'' ∈ ''M''}}, पी और एन फ़लन का पड़ोस U उपस्थित है {{nowrap|''x''<sup>1</sup>, ..., ''x''<sup>''n''</sup> ∈ '''C'''<sup>''k''</sup>(''U'')}} ऐसा कि मानचित्र {{nowrap|1=''f'' = (''x''<sup>1</sup>, ..., ''x<sup>n</sup>'') : ''U'' → '''R'''<sup>''n''</sup>}} R में एक विवृत सेट पर एक होमोमोर्फिज्म है, और ऐसा कि U 'R' पर निरन्तर अलग-अलग कार्यों के के-बार के शीफ का ठहराना है।<ref>This definition can be found in MacLane and Moerdijk (1992).  For an equivalent, ''ad hoc'' definition, see Sternberg (1964) Chapter II.</ref>
+कभी-कभी, मैनिफोल्ड को C प्रदान करने के लिए वैकल्पिक दृष्टिकोण का उपयोग करना उपयोगी हो सकता है-संरचना. यहां वास्तविक विश्लेषणात्मक मैनिफोल्ड के लिए k = 1, 2, ..., ∞, या ω है। समन्वय चार्ट पर विचार करने के अतिरिक्त, मैनिफोल्ड पर परिभाषित कार्यों के साथ प्रारंभ करना संभव है। M<sup>k</sup> का शीफ (गणित), 'C' को दर्शाता है, एक प्रकार का [[ऑपरेटर]] है जो प्रत्येक विवृत सेट के लिए परिभाषित करता है {{nowrap|''U'' ⊂ ''M''}}, एक बीजगणित '''C'''<sup>''k''</sup>(''U'') सतत कार्यों का {{nowrap|''U'' →  '''R'''}}. एक संरचना शीफ सी कहा जाता है कि k, M को C की संरचना देता हैकआयाम एन के कई गुना बशर्ते कि, किसी के लिए {{nowrap|''p'' ∈ ''M''}}, p और एन फ़लन का पड़ोस U उपस्थित है {{nowrap|''x''<sup>1</sup>, ..., ''x''<sup>''n''</sup> ∈ '''C'''<sup>''k''</sup>(''U'')}} ऐसा कि मानचित्र {{nowrap|1=''f'' = (''x''<sup>1</sup>, ..., ''x<sup>n</sup>'') : ''U'' → '''R'''<sup>''n''</sup>}} R में एक विवृत सेट पर एक होमोमोर्फिज्म है, और ऐसा कि U 'R' पर निरन्तर अलग-अलग कार्यों के के-बार के शीफ का ठहराना है।<ref>This definition can be found in MacLane and Moerdijk (1992).  For an equivalent, ''ad hoc'' definition, see Sternberg (1964) Chapter II.</ref>
 विशेष रूप से, इस बाद वाली स्थिति का अर्थ है कि 'C' में कोई भी फ़लन एचk(V), V के लिए, विशिष्ट रूप से लिखा जा सकता है {{nowrap|1=''h''(''x'') = ''H''(''x''<sup>1</sup>(''x''), ..., ''x''<sup>''n''</sup>(''x''))}}, जहां H, f(V) पर एक k-गुना भिन्न फ़लन है ('R' में एक विवृत सेट). इस प्रकार, शीफ-सैद्धांतिक दृष्टिकोण यह है कि भिन्न-भिन्न मैनिफोल्ड पर कार्यों को स्थानीय निर्देशांक में 'R' पर भिन्न-भिन्न कार्यों के रूप में व्यक्त किया जा सकता है। n, और एक फोर्टिओरी तर्क यह मैनिफोल्ड पर विभेदक संरचना को चित्रित करने के लिए पर्याप्त है।
@@ Line 335: / Line 335: @@
 भिन्न-भिन्न मैनिफोल्ड्स को परिभाषित करने के लिए एक समान, लेकिन अधिक तकनीकी दृष्टिकोण, [[ चक्राकार स्थान |चक्राकार स्थान]] की धारणा का उपयोग करके तैयार किया जा सकता है। यह दृष्टिकोण [[बीजगणितीय ज्यामिति]] में [[योजना (गणित)]] के सिद्धांत से अत्यधिक प्रभावित है, लेकिन अलग-अलग कार्यों के [[रोगाणु (गणित)]] के स्थानीय छल्ले का उपयोग करता है। यह जटिल विविधताओं के संदर्भ में विशेष रूप से लोकप्रिय है।
-हम 'R' पर मूल संरचना शीफ का वर्णन करके शुरू करते हैं<sup>n</sup>. यदि U 'R' में एक विवृत समुच्चय है<sup>n</sup>, चलो
+हम 'R<sup>n</sup>' पर मूल संरचना शीफ का वर्णन करके प्रारंभ करते हैं। यदि U 'R<sup>n</sup>' में एक विवृत समुच्चय है, माना
 :: '''O'''(''U'') = ''C<sup>k</sup>''(''U'', '''R''')
-U पर सभी वास्तविक-मूल्य वाले के-बार निरन्तर भिन्न-भिन्न कार्यों से मिलकर बनता है। जैसे-जैसे U बदलता है, यह 'R<sup>n</sup>' पर रिंगों का एक समूह निर्धारित करता है। डंठल O<sub>''p''</sub> के लिए {{nowrap|''p'' ∈ '''R'''<sup>''n''</sup>}} p के निकट कार्यों के रोगाणु (गणित) से युक्त है, और 'R' पर एक बीजगणित है। विशेष रूप से, यह एक स्थानीय वलय है जिसके अद्वितीय [[अधिकतम आदर्श]] में वे कार्य सम्मिलित होते हैं जो p पर लुप्त हो जाते हैं। जोड़ी {{nowrap|('''R'''<sup>''n''</sup>, '''O''')}} स्थानीय रूप से वलयित स्थान का एक उदाहरण है: यह एक टोपोलॉजिकल स्थान है जो एक शीफ़ से सुसज्जित है जिसके डंठल प्रत्येक स्थानीय वलय हैं।
+U पर सभी वास्तविक-मूल्य वाले के-बार निरन्तर भिन्न-भिन्न कार्यों से मिलकर बनता है। जैसे-जैसे U बदलता है, यह 'R<sup>n</sup>' पर रिंगों का एक समूह निर्धारित करता है। डंठल O<sub>''p''</sub> के लिए {{nowrap|''p'' ∈ '''R'''<sup>''n''</sup>}} p के निकट कार्यों के रोगाणु (गणित) से युक्त है, और 'R' पर एक बीजगणित है। विशेष रूप से, यह एक स्थानीय वलय है जिसके अद्वितीय [[अधिकतम आदर्श]] में वे फलन सम्मिलित होते हैं जो p पर लुप्त हो जाते हैं। जोड़ी {{nowrap|('''R'''<sup>''n''</sup>, '''O''')}} स्थानीय रूप से वलयित स्थान का एक उदाहरण है: यह एक टोपोलॉजिकल स्थान है जो एक शीफ़ से सुसज्जित है जिसके डंठल प्रत्येक स्थानीय वलय हैं।
-एक अवकलनीय मैनिफोल्ड (कक्षा C<sup>k</sup> का)) में एक जोड़ा होता है {{nowrap|(''M'', '''O'''<sub>''M''</sub>)}} जहां M दूसरा गणनीय हॉसडॉर्फ स्थान है, और 'O'<sub>''M''</sub> M पर परिभाषित स्थानीय आर-बीजगणित का एक समूह है, जैसे कि स्थानीय रूप से चक्राकार स्थान {{nowrap|(''M'', '''O'''<sub>''M''</sub>)}} स्थानीय रूप {{nowrap|('''R'''<sup>''n''</sup>, '''O''')}} से समरूपी है। इस तरह, अलग-अलग मैनिफोल्ड्स को R में योजना (गणित) मॉडल के रूप में सोचा जा सकता है, इस का अर्थ है कि <ref>Hartshorne (1997)</ref> प्रत्येक बिंदु के लिए {{nowrap|''p'' ∈ ''M''}}, p का पड़ोसी U और कार्यों की एक जोड़ी {{nowrap|(''f'', ''f''<sup>#</sup>)}} है, जहाँ
+एक अवकलनीय मैनिफोल्ड (कक्षा C<sup>k</sup> का)) में एक जोड़ा {{nowrap|(''M'', '''O'''<sub>''M''</sub>)}} होता है, जहां M दूसरा गणनीय हॉसडॉर्फ स्थान है, और 'O'<sub>''M''</sub> M पर परिभाषित स्थानीय आर-बीजगणित का एक समूह है, जैसे कि स्थानीय रूप से चक्राकार स्थान {{nowrap|(''M'', '''O'''<sub>''M''</sub>)}} स्थानीय रूप {{nowrap|('''R'''<sup>''n''</sup>, '''O''')}} से समरूपी है। इस तरह, अलग-अलग मैनिफोल्ड्स को R में योजना (गणित) मॉडल के रूप में सोचा जा सकता है, इस का अर्थ है कि <ref>Hartshorne (1997)</ref> प्रत्येक बिंदु के लिए {{nowrap|''p'' ∈ ''M''}}, p का पड़ोसी U और कार्यों की एक जोड़ी {{nowrap|(''f'', ''f''<sup>#</sup>)}} है, जहाँ
 # ''f'' : ''U'' → ''f''(''U'') ⊂ '''R'''<sup>''n''</sup> '''R'''<sup>''n''</sup> में एक विवृत सेट पर एक होमोमोर्फिज्म है।
 # ''f''<sup>#</sup>: '''O'''|<sub>''f''(''U'')</sub> → ''f''<sub>∗</sub> ('''O'''<sub>''M''</sub>|<sub>''U''</sub>) शीव्स की समरूपता है।
@@ Line 360: / Line 360: @@
 विशेष रूप से [[बनच मैनिफोल्ड]] और फ़्रेचेट मैनिफ़ोल्ड्स
-सुविधाजनक वेक्टर स्पेस#अनुप्रयोग: परिमित आयामी मैनिफोल्ड्स के बीच मैपिंग के मैनिफोल्ड्स
+सुविधाजनक सदिश स्पेस#अनुप्रयोग: परिमित आयामी मैनिफोल्ड्स के बीच मैपिंग के मैनिफोल्ड्स
 अनंत आयामी विभेदक अनेक गुना हैं।
@@ Line 366: / Line 366: @@
 C के लिए मैनिफोल्ड M, वास्तविक-मूल्यवान C का [[सेट (गणित)]] है। मैनिफ़ोल्ड पर k फ़लनो बिंदुवार जोड़ और गुणा के अनुसार एक फ़ील्ड पर एक बीजगणित बनाता है, जिसे स्केलर फ़ील्ड का बीजगणित या बस स्केलर का बीजगणित कहा जाता है। इस बीजगणित में गुणात्मक पहचान के रूप में निरंतर फ़लन 1 है, और यह बीजगणितीय ज्यामिति में [[नियमित कार्य]]ों की अंगूठी का एक अलग एनालॉग है।
-स्केलर के बीजगणित से मैनिफोल्ड का पुनर्निर्माण करना संभव है, पहले एक सेट के रूप में, लेकिन एक टोपोलॉजिकल स्पेस के रूप में भी - यह बानाच-स्टोन प्रमेय का एक अनुप्रयोग है, और इसे औपचारिक रूप से सी*-बीजगणित के स्पेक्ट्रम के रूप में जाना जाता है। . सबसे पहले, M के बिंदुओं और बीजगणित समरूपताओं के बीच एक-से-एक पत्राचार {{nowrap|''φ'': ''C<sup>k</sup>''(''M'') → '''R'''}} है, इस तरह एक समरूपता φ C<sup>k</sup> में एक आदर्श कोडिमेशन से मेल खाती है(M) (अर्थात् φ का कर्नेल), जो आवश्यक रूप से एक अधिकतम आदर्श है। इसके विपरीत, इस बीजगणित में प्रत्येक अधिकतम आदर्श एक बिंदु पर लुप्त होने वाले कार्यों का एक आदर्श है, जो दर्शाता है कि C का MSpec (मैक्स स्पेक)<sup>k</sup>(M) M को एक बिंदु सेट के रूप में पुनर्प्राप्त करता है, चूंकि वास्तव में यह M को एक टोपोलॉजिकल स्पेस के रूप में पुनर्प्राप्त करता है।
+स्केलर के बीजगणित से मैनिफोल्ड का पुनर्निर्माण करना संभव है, पहले एक सेट के रूप में, लेकिन एक टोपोलॉजिकल स्पेस के रूप में भी - यह बानाच-स्टोन प्रमेय का एक अनुप्रयोग है, और इसे औपचारिक रूप से C*-बीजगणित के स्पेक्ट्रम के रूप में जाना जाता है। सबसे पहले, ''M'' के बिंदुओं और बीजगणित समरूपता φ: ''C<sup>k</sup>''(''M'') → '''R''' के बीच एक-से-एक पत्राचार है, क्योंकि इस तरह की एक समरूपता φ ''C<sup>k</sup>'' (''M'') में एक कोडिमेशन एक आदर्श से मेल खाती है (अर्थात् कर्नेल) φ), जो आवश्यक रूप से एक अधिकतम आदर्श है। इसके विपरीत, इस बीजगणित में प्रत्येक अधिकतम आदर्श एक बिंदु पर लुप्त होने वाले कार्यों का एक आदर्श है, जो दर्शाता है कि ''C<sup>k</sup>''(''M'') का MSpec (मैक्स स्पेक) ''M'' को एक बिंदु सेट के रूप में पुनर्प्राप्त करता है, चूंकि वास्तव में यह M को एक टोपोलॉजिकल स्पेस के रूप में पुनर्प्राप्त करता है।
 कोई व्यक्ति विभिन्न ज्यामितीय संरचनाओं को स्केलर के बीजगणित के संदर्भ में बीजगणितीय रूप से परिभाषित कर सकता है, और ये परिभाषाएँ अधिकांशतः बीजगणितीय ज्यामिति (ज्यामितीय रूप से रिंगों की व्याख्या करना) और [[ऑपरेटर सिद्धांत]] (बैनाच रिक्त स्थान की ज्यामितीय रूप से व्याख्या करना) को सामान्यीकृत करती हैं। उदाहरण के लिए, M के स्पर्शरेखा बंडल को M पर सुचारू कार्यों के बीजगणित की व्युत्पत्ति के रूप में परिभाषित किया जा सकता है।

Anonymous

Search