संचयी वितरण फलन: Difference between revisions
(→उदाहरण) |
|||
| Line 66: | Line 66: | ||
== उदाहरण == | == उदाहरण == | ||
उदाहरण के तौर पर मान लीजिए <math>X</math> | उदाहरण के तौर पर, मान लीजिए कि <math>X</math> को एकांक अंतराल <math>[0,1]</math> पर एक [[समान वितरण (निरंतर)|समान]] रूप से बंटित किया गया है। | ||
फिर | फिर <math>X</math> का सीडीएफ दिया गया है | ||
<math display="block">F_X(x) = \begin{cases} | <math display="block">F_X(x) = \begin{cases} | ||
0 &:\ x < 0\\ | 0 &:\ x < 0\\ | ||
| Line 74: | Line 74: | ||
1 &:\ x > 1 | 1 &:\ x > 1 | ||
\end{cases}</math> | \end{cases}</math> | ||
इसके बजाय मान लीजिए <math>X</math> समान | इसके बजाय मान लीजिए कि <math>X</math> समान प्रायिकता के साथ केवल विविक्त मान 0 और 1 लेता है। | ||
फिर | फिर <math>X</math> का सीडीएफ दिया गया है | ||
<math display="block">F_X(x) = \begin{cases} | <math display="block">F_X(x) = \begin{cases} | ||
0 &:\ x < 0\\ | 0 &:\ x < 0\\ | ||
| Line 82: | Line 82: | ||
1 &:\ x \ge 1 | 1 &:\ x \ge 1 | ||
\end{cases}</math> | \end{cases}</math> | ||
मान लीजिए कि <math>X</math> घातीय रूप से बंटित है | फिर <math>X</math> का सीडीएफ दिया गया है | |||
<math display="block">F_X(x;\lambda) = \begin{cases} | <math display="block">F_X(x;\lambda) = \begin{cases} | ||
1-e^{-\lambda x} & x \ge 0, \\ | 1-e^{-\lambda x} & x \ge 0, \\ | ||
0 & x < 0. | 0 & x < 0. | ||
\end{cases}</math> | \end{cases}</math> | ||
यहां λ > 0 बंटन का | यहां λ > 0 बंटन का प्राचल है, जिसे अधिकतर दर प्राचल कहा जाता है। | ||
मान लीजिए <math>X</math> [[प्रसामान्य बंटन]] है| फिर <math>X</math> का सीडीएफ दिया गया है | |||
<math display="block">F(x;\mu,\sigma) = \frac{1}{\sigma\sqrt{2\pi}} \int_{-\infty}^x \exp \left( -\frac{(t - \mu)^2}{2\sigma^2} \right)\, dt. </math> | <math display="block">F(x;\mu,\sigma) = \frac{1}{\sigma\sqrt{2\pi}} \int_{-\infty}^x \exp \left( -\frac{(t - \mu)^2}{2\sigma^2} \right)\, dt. </math> | ||
यहाँ | यहाँ प्राचल <math>\mu</math> बंटन का माध्य या प्रत्याशा है; और <math>\sigma</math> इसका मानक विचलन है. | ||
मानक | मानक प्रसामान्य बंटन की सीडीएफ की एक सारणी अधिकतर सांख्यिकीय अनुप्रयोगों में उपयोग की जाती है, जहां इसे [[मानक सामान्य तालिका|मानक सामान्य सारणी]], '''एकांक सामान्य सारणी''' या '''Z सारणी''' का नाम दिया जाता है। | ||
मान लीजिए <math>X</math> द्विपद बंटन है. फिर <math>X</math> का सीडीएफ दिया गया है | |||
<math display="block">F(k;n,p) = \Pr(X\leq k) = \sum _{i=0}^{\lfloor k\rfloor }{n \choose i} p^{i} (1-p)^{n-i}</math> | <math display="block">F(k;n,p) = \Pr(X\leq k) = \sum _{i=0}^{\lfloor k\rfloor }{n \choose i} p^{i} (1-p)^{n-i}</math> | ||
यहाँ <math>p</math> | यहाँ <math>p</math> स'''फलता की प्रायिकता है और फलन <math>n</math> स्वतंत्र प्रयोगों के अनुक्रम में सफलताओं की संख्या के असतत संभाव्यता वितरण को दर्शाता है, और <math>\lfloor k\rfloor</math> नीचे की मंजिल है <math>k</math>, यानी [[सबसे बड़ा पूर्णांक]] से कम या उसके बराबर <math>k</math>.''' | ||
==व्युत्पन्न फलन== | ==व्युत्पन्न फलन== | ||
===पूरक संचयी बंटन फलन ( | ===पूरक संचयी बंटन फलन (पुच्छ बंटन)=== | ||
कभी-कभी, विपरीत प्रश्न का अध्ययन करना और यह पूछना उपयोगी होता है कि यादृच्छिक चर कितनी बार किसी विशेष स्तर से ऊपर होता है। इसे '''पूरक संचयी बंटन फलन (सीसीडीएफ)''' या केवल '''पुच्छ बंटन''' या '''अतिरेक''' कहा जाता है, और इसे इस प्रकार परिभाषित किया गया है | |||
कभी-कभी, विपरीत प्रश्न का अध्ययन करना और यह पूछना उपयोगी होता है कि यादृच्छिक चर कितनी बार किसी विशेष स्तर से ऊपर होता है। इसे ' | |||
<math display="block">\bar F_X(x) = \operatorname{P}(X > x) = 1 - F_X(x).</math> | <math display="block">\bar F_X(x) = \operatorname{P}(X > x) = 1 - F_X(x).</math> | ||
उदाहरण के लिए, सांख्यिकी [[परिकल्पना परीक्षण]] में इसका अनुप्रयोग होता है, क्योंकि | उदाहरण के लिए, [[सांख्यिकी]] [[परिकल्पना परीक्षण]] में इसका अनुप्रयोग होता है, क्योंकि एकपक्षीय [[पी-मूल्य|पी-मान]] एक परीक्षण आँकड़ा देखने की प्रायिकता है जो कम से कम उतना ही चरम है जितना कि देखा गया है। इस प्रकार, बशर्ते कि परीक्षण आँकड़ा, ''T'', का सतत बंटन हो, एकपक्षीय पी-मान केवल सीसीडीएफ द्वारा दिया जाता है: परीक्षण आँकड़े के देखे गए मान ''t'' के लिए | ||
<math display="block">p= \operatorname{P}(T \ge t) = \operatorname{P}(T > t) = 1 - F_T(t).</math> | <math display="block">p= \operatorname{P}(T \ge t) = \operatorname{P}(T > t) = 1 - F_T(t).</math> | ||
[[उत्तरजीविता विश्लेषण]] में, <math>\bar F_X(x)</math> को | [[उत्तरजीविता विश्लेषण|अतिजीविता विश्लेषण]] में, <math>\bar F_X(x)</math> को [[अतिजीविता फलन]] कहा जाता है और <math>S(x)</math> को दर्शाया जाता है, जबकि ''विश्वसनीयता फलन'' शब्द [[ अभियांत्रिकी |अभियांत्रिकी]] में सामान्य है। | ||
;गुण | ;गुण | ||
* एक | * एक प्रत्याशा वाले अऋणात्मक संतत यादृच्छिक चर के लिए, मार्कोव की असमानता बताती है कि<ref name="ZK">{{cite book| last1 = Zwillinger| first1 = Daniel| last2 = Kokoska| first2 = Stephen| title = सीआरसी मानक संभाव्यता और सांख्यिकी तालिकाएँ और सूत्र| year = 2010| publisher = CRC Press| isbn = 978-1-58488-059-2| page = 49 }}</ref> <math display="block">\bar F_X(x) \leq \frac{\operatorname{E}(X)}{x} .</math> | ||
* जैसा <math>x \to \infty, \bar F_X(x) \to 0</math>, और वास्तव में <math>\bar F_X(x) = o(1/x)</math> | * जैसा कि <math>x \to \infty, \bar F_X(x) \to 0</math>, और वास्तव में <math>\bar F_X(x) = o(1/x)</math> बशर्ते कि <math>\operatorname{E}(X)</math> परिमित है. <br/> प्रमाण:{{citation needed|date=April 2012}} <br/> यह मानते हुए कि किसी भी <math>c > 0</math> के लिए ''X'' का घनत्व फलन ''fx'' है <math display="block"> | ||
\operatorname{E}(X) = \int_0^\infty x f_X(x) \, dx \geq \int_0^c x f_X(x) \, dx + c\int_c^\infty f_X(x) \, dx | \operatorname{E}(X) = \int_0^\infty x f_X(x) \, dx \geq \int_0^c x f_X(x) \, dx + c\int_c^\infty f_X(x) \, dx | ||
</math> फिर पहचानने पर <math display="block">\bar F_X(c) = \int_c^\infty f_X(x) \, dx</math> और | </math> फिर पहचानने पर <math display="block">\bar F_X(c) = \int_c^\infty f_X(x) \, dx</math> और पदों को पुनर्व्यवस्थित करना, <math display="block"> | ||
0 \leq c\bar F_X(c) \leq \operatorname{E}(X) - \int_0^c x f_X(x) \, dx \to 0 \text{ as } c \to \infty | 0 \leq c\bar F_X(c) \leq \operatorname{E}(X) - \int_0^c x f_X(x) \, dx \to 0 \text{ as } c \to \infty | ||
</math> जैसा कि दावा किया गया है | </math> जैसा कि दावा किया गया है | | ||
* एक | * एक प्रत्याशा वाले यादृच्छिक चर के लिए, <math display="block">\operatorname{E}(X) = \int_0^\infty \bar F_X(x) \, dx - \int_{-\infty}^0 F_X(x) \, dx</math> और एक अऋणात्मक यादृच्छिक चर के लिए दूसरा पद 0 है। <br/> यदि यादृच्छिक चर केवल अऋणात्मक पूर्णांक मान ले सकता है, तो यह इसके तुल्य है <math display="block">\operatorname{E}(X) = \sum_{n=0}^\infty \bar F_X(n).</math> | ||
Revision as of 23:39, 13 July 2023
This article needs additional citations for verification. (March 2010) (Learn how and when to remove this template message) |
प्रायिकता सिद्धांत और सांख्यिकी में, वास्तविक मानांकन वाले यादृच्छिक चर का संचयी बंटन फलन (सीडीएफ), या केवल का बंटन फलन, पर मूल्यांकन किया गया, प्रायिकता यह है कि से कम या उसके बराबर मान लेता है।[1]
वास्तविक संख्याओं पर समर्थित प्रत्येक प्रायिकता बंटन, विविक्त या "मिश्र" के साथ-साथ संतत, एक लंब-संतत एकदिष्ट वर्धमान फलन (एक कैडलैग फलन) द्वारा और को संतुष्ट करके विशिष्ट रूप से पहचाना जाता है।
एक अदिश सतत बंटन की स्थिति में, यह शून्य से अनंत तक तक प्रायिकता घनत्व फलन के अंतर्गत क्षेत्र देता है। संचयी बंटन फलनों का उपयोग बहुविचर यादृच्छिक चरों के बंटन को निर्दिष्ट करने के लिए भी किया जाता है।
परिभाषा
वास्तविक मानांकन यादृच्छिक चर का संचयी बंटन फलन द्वारा दिया गया फलन है[2]: p. 77
|
(Eq.1) |
जहां दाहिना हाथ इस प्रायिकता को दर्शाता है कि यादृच्छिक चर का मान से कम या उसके बराबर है।
प्रायिकता यह है कि अर्ध संवृत अंतराल में स्थित है, जहां , इसलिए है[2]: p. 84
|
(Eq.2) |
उपरोक्त परिभाषा में, "इससे कम या इसके बराबर" चिह्न, "≤", एक कन्वेंशन है, सार्वभौमिक रूप से उपयोग नहीं किया जाने वाला (उदाहरण के लिए हंगेरियन साहित्य "<" का उपयोग करता है), लेकिन सतत बंटन के लिए यह अंतर महत्वपूर्ण है। द्विपद और प्वासों बंटन की सारणियों का उचित उपयोग इस कन्वेंशन पर निर्भर करता है। इसके अलावा, अभिलक्षण फलन के लिए पॉल लेवी के प्रतिलोमन सूत्र जैसे महत्वपूर्ण सूत्र भी "इससे कम या बराबर" सूत्रीकरण पर निर्भर करते हैं।
यदि अनेक यादृच्छिक चरों X,Y....आदि का उपचारण किया जाए तो संगत अक्षरों का उपयोग पादांकों के रूप में किया जाता है, जबकि, यदि केवल एक का उपचारण किया जाता है, तो पादांक को आमतौर पर छोड़ दिया जाता है। प्रायिकता घनत्व फलन और प्रायिकता द्रव्यमान फलन के लिए उपयोग किए जाने वाले लघु अक्षर के विपरीत, संचयी बंटन फलन के लिए पूंजी का उपयोग करना औपचारिक है। यह सामान्य बंटनों पर परिचर्चा करते समय लागू होता है: कुछ विशिष्ट बंटनों के अपने सम्मत संकेतन होते हैं, उदाहरण के लिए प्रसामान्य बंटन क्रमशः F और f के बजाय और का उपयोग करते है।
एक सतत यादृच्छिक चर के प्रायिकता घनत्व फलन को कलन के मूलभूत प्रमेय का उपयोग करके और अवकलन करके संचयी बंटन फलन से निर्धारित किया जा सकता है;[3] यानी दिया गया,
एक सतत यादृच्छिक चर के सीडीएफ को प्रायिकता घनत्व फलन के समाकल में निम्नानुसार व्यक्त किया जा सकता है:[2]: p. 86
गुण
प्रत्येक संचयी बंटन फलन गैर-ह्रासमान [2]: p. 78 और सम-सतत हैं,[2]: p. 79 जो इसे एक कैडलैग फलन बनाता है। आगे,
यदि एक पूर्ण रुप से विविक्त यादृच्छिक चर है, तब यह प्रायिकता के साथ मान x1,x2,... प्राप्त करता है, और का सीडीएफ बिंदु पर असंतत होगा:
यदि का परिमित L1-नोर्म है, अर्थात की प्रत्याशा परिमित है, तो प्रत्याशा रीमैन-स्टिल्टजेस समाकल द्वारा दी गई है
उदाहरण
उदाहरण के तौर पर, मान लीजिए कि को एकांक अंतराल पर एक समान रूप से बंटित किया गया है।
फिर का सीडीएफ दिया गया है
फिर का सीडीएफ दिया गया है
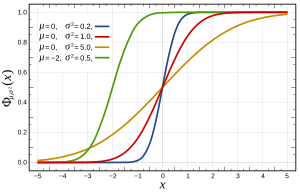
मान लीजिए प्रसामान्य बंटन है| फिर का सीडीएफ दिया गया है
मानक प्रसामान्य बंटन की सीडीएफ की एक सारणी अधिकतर सांख्यिकीय अनुप्रयोगों में उपयोग की जाती है, जहां इसे मानक सामान्य सारणी, एकांक सामान्य सारणी या Z सारणी का नाम दिया जाता है।
मान लीजिए द्विपद बंटन है. फिर का सीडीएफ दिया गया है
व्युत्पन्न फलन
पूरक संचयी बंटन फलन (पुच्छ बंटन)
कभी-कभी, विपरीत प्रश्न का अध्ययन करना और यह पूछना उपयोगी होता है कि यादृच्छिक चर कितनी बार किसी विशेष स्तर से ऊपर होता है। इसे पूरक संचयी बंटन फलन (सीसीडीएफ) या केवल पुच्छ बंटन या अतिरेक कहा जाता है, और इसे इस प्रकार परिभाषित किया गया है
- गुण
- एक प्रत्याशा वाले अऋणात्मक संतत यादृच्छिक चर के लिए, मार्कोव की असमानता बताती है कि[4]
- जैसा कि , और वास्तव में बशर्ते कि परिमित है.
प्रमाण:[citation needed]
यह मानते हुए कि किसी भी के लिए X का घनत्व फलन fx हैफिर पहचानने परऔर पदों को पुनर्व्यवस्थित करना,जैसा कि दावा किया गया है | - एक प्रत्याशा वाले यादृच्छिक चर के लिए, और एक अऋणात्मक यादृच्छिक चर के लिए दूसरा पद 0 है।
यदि यादृच्छिक चर केवल अऋणात्मक पूर्णांक मान ले सकता है, तो यह इसके तुल्य है
मुड़ा हुआ संचयी बंटन

जबकि एक संचयी बंटन की साजिश अक्सर इसका आकार S-जैसा होता है, एक वैकल्पिक चित्रण मुड़ा हुआ संचयी बंटन या पर्वतीय प्लॉट है, जो ग्राफ़ के शीर्ष आधे हिस्से को मोड़ देता है,[5][6] वह है
कहाँ सूचक फलन को दर्शाता है और दूसरा सारांश उत्तरजीवी फलन है, इस प्रकार दो पैमानों का उपयोग किया जाता है, एक ऊपर की ओर और दूसरा नीचे की ओर। चित्रण का यह रूप माध्यिका (सांख्यिकी), फैलाव (सांख्यिकी) (विशेष रूप से, माध्यिका से माध्य निरपेक्ष विचलन) पर जोर देता है[7]) और बंटन या अनुभवजन्य परिणामों की विषमता।
व्युत्क्रम बंटन फलन (मात्राफल फलन)
यदि सीडीएफ एफ सख्ती से बढ़ रहा है और निरंतर है अद्वितीय वास्तविक संख्या है ऐसा है कि . यह व्युत्क्रम बंटन फलन या मात्रात्मक कार्य को परिभाषित करता है।
कुछ बंटनों में कोई अद्वितीय व्युत्क्रम नहीं होता है (उदाहरण के लिए यदि सभी के लिए , कारण स्थिर रहना) इस मामले में, कोई सामान्यीकृत व्युत्क्रम बंटन फलन का उपयोग कर सकता है, जिसे इस प्रकार परिभाषित किया गया है
- उदाहरण 1: माध्यिका है .
- उदाहरण 2: रखो . फिर हम कॉल करते हैं 95वाँ प्रतिशतक.
व्युत्क्रम सीडीएफ के कुछ उपयोगी गुण (जो सामान्यीकृत व्युत्क्रम बंटन फलन की परिभाषा में भी संरक्षित हैं) हैं:
- घट नहीं रहा है
- अगर और केवल अगर
- अगर एक बंटन तो के रूप में वितरित किया जाता है . इसका उपयोग व्युत्क्रम परिवर्तन नमूनाकरण-विधि का उपयोग करके यादृच्छिक संख्या पीढ़ी में किया जाता है।
- अगर स्वतंत्र का एक संग्रह है -वितरित यादृच्छिक चर को एक ही नमूना स्थान पर परिभाषित किया गया है, फिर यादृच्छिक चर मौजूद हैं ऐसा है कि के रूप में वितरित किया जाता है और सभी के लिए प्रायिकता 1 के साथ .[citation needed]
समान बंटन के लिए प्राप्त परिणामों को अन्य बंटनों में अनुवाद करने के लिए सीडीएफ के व्युत्क्रम का उपयोग किया जा सकता है।
अनुभवजन्य बंटन फलन
अनुभवजन्य बंटन फलन संचयी बंटन फलन का एक अनुमान है जो नमूने में अंक उत्पन्न करता है। यह उस अंतर्निहित बंटन में संभाव्यता 1 के साथ अभिसरण करता है। अंतर्निहित संचयी बंटन फलन के लिए अनुभवजन्य बंटन फलन के अभिसरण की दर निर्धारित करने के लिए कई परिणाम मौजूद हैं[citation needed].
बहुभिन्नरूपी मामला
दो यादृच्छिक चर के लिए परिभाषा
एक से अधिक यादृच्छिक चर के साथ एक साथ व्यवहार करते समय संयुक्त संचयी बंटन फलन को भी परिभाषित किया जा सकता है। उदाहरण के लिए, यादृच्छिक चर की एक जोड़ी के लिए , संयुक्त सी.डी.एफ द्वारा दिया गया है[2]: p. 89
|
(Eq.3) |
जहां दाईं ओर यादृच्छिक चर की संभावना का प्रतिनिधित्व करता है से कम या उसके बराबर मान लेता है ओर वो से कम या उसके बराबर मान लेता है .
संयुक्त संचयी बंटन फलन का उदाहरण:
दो सतत चर X और Y के लिए:
| Y = 2 | Y = 4 | Y = 6 | Y = 8 | |
| X = 1 | 0 | 0.1 | 0 | 0.1 |
| X = 3 | 0 | 0 | 0.2 | 0 |
| X = 5 | 0.3 | 0 | 0 | 0.15 |
| X = 7 | 0 | 0 | 0.15 | 0 |
समाधान: X और Y की प्रत्येक संभावित सीमा के लिए संभावनाओं की दी गई तालिका का उपयोग करके, संयुक्त संचयी बंटन फलन का निर्माण सारणीबद्ध रूप में किया जा सकता है:
| Y < 2 | 2 ≤ Y < 4 | 4 ≤ Y < 6 | 6 ≤ Y < 8 | Y ≥ 8 | |
| X < 1 | 0 | 0 | 0 | 0 | 0 |
| 1 ≤ X < 3 | 0 | 0 | 0.1 | 0.1 | 0.2 |
| 3 ≤ X < 5 | 0 | 0 | 0.1 | 0.3 | 0.4 |
| 5 ≤ X < 7 | 0 | 0.3 | 0.4 | 0.6 | 0.85 |
| X ≥ 7 | 0 | 0.3 | 0.4 | 0.75 | 1 |
दो से अधिक यादृच्छिक चरों के लिए परिभाषा
के लिए यादृच्छिक चर , संयुक्त सी.डी.एफ द्वारा दिया गया है
|
(Eq.4) |
की व्याख्या करना एक यादृच्छिक वेक्टर के रूप में यादृच्छिक चर एक छोटा संकेतन उत्पन्न करता है:
गुण
प्रत्येक बहुभिन्नरूपी सीडीएफ है:
- इसके प्रत्येक चर के लिए नीरस रूप से गैर-घटता हुआ,
- इसके प्रत्येक चर में सही-निरंतर,
एकल आयाम मामले के विपरीत, उपरोक्त चार गुणों को संतुष्ट करने वाला प्रत्येक फलन एक बहुभिन्नरूपी सीडीएफ नहीं है। उदाहरण के लिए, चलो के लिए या या और जाने अन्यथा। यह देखना आसान है कि उपरोक्त शर्तें पूरी होती हैं, और फिर भी यदि ऐसा होता तो यह सीडीएफ नहीं है जैसा कि नीचे बताया गया है।
एक बिंदु के हाइपरआयतकोण से संबंधित होने की संभावना 1-आयामी मामले के अनुरूप है:[9]
सम्मिश्र स्थिति
सम्मिश्र यादृच्छिक चर
वास्तविक से सम्मिश्र यादृच्छिक चर में संचयी बंटन फलन का सामान्यीकरण स्पष्ट नहीं है क्योंकि रूप के व्यंजकों कोई अर्थ नहीं है। हालाँकि रूप के व्यंजक समझ में आते हैं। इसलिए, हम एक सम्मिश्र यादृच्छिक चर के संचयी बंटन को उनके वास्तविक और काल्पनिक भागों के संचयी बंटन के माध्यम से परिभाषित करते हैं:
सम्मिश्र यादृच्छिक सदिश
Eq.4 उपज का सामान्यीकरण
सांख्यिकीय विश्लेषण में उपयोग
संचयी बंटन फलन की अवधारणा सांख्यिकीय विश्लेषण में दो (समान) तरीकों से स्पष्ट रूप से प्रकट होती है। संचयी आवृत्ति विश्लेषण एक संदर्भ मान से कम किसी परिघटना के मानों की घटना की आवृत्ति का विश्लेषण है। आनुभविक बंटन फलन संचयी बंटन फलन का एक औपचारिक प्रत्यक्ष आकलन है जिसके लिए सरल सांख्यिकीय गुण प्राप्त किए जा सकते हैं और जो विभिन्न सांख्यिकीय परिकल्पना परीक्षणों का आधार बन सकते हैं | ऐसे परीक्षण यह आकलन कर सकते हैं कि क्या किसी दिए गए बंटन से उत्पन्न डेटा के प्रतिदर्श के सम्मुख प्रमाण है, या एक ही (अज्ञात) समष्टि बंटन से उत्पन्न हुए डेटा के दो प्रतिदर्शों के सम्मुख प्रमाण है।
कोलमोगोरोव-स्मिरनोव और कुइपर के परीक्षण
कोलमोगोरोव-स्मिरनोव परीक्षण संचयी बंटन फलन पर आधारित है और इसका उपयोग यह देखने के लिए किया जा सकता है कि क्या दो आनुभविक बंटन अलग-अलग हैं या क्या एक आनुभविक बंटन एक आदर्श बंटन से अलग है। यदि बंटन का प्रक्षेत्र सप्ताह के दिन के जैसा चक्रीय है तो संवृततः से संबंधित कुइपर का परीक्षण उपयोगी है। उदाहरण के लिए, कुइपर परीक्षण का उपयोग यह देखने के लिए किया जा सकता है कि क्या वर्ष के दौरान टॉर्नेडो की संख्या बदलती रहती है या किसी उत्पाद की बिक्री सप्ताह के दिन या महीने के दिन के अनुसार बदलती रहती है।
यह भी देखें
- वर्णनात्मक सांख्यिकी
- बंटन फिटिंग
- तोरण (सांख्यिकी)
- पीडीएफ के साथ आपरिवर्तित अर्ध-चरघातांकी बंटन[10] के रूप में दिया गया है , जहां फॉक्स-राइट साई फलन को दर्शाता है।
संदर्भ
- ↑ Deisenroth, Marc Peter; Faisal, A. Aldo; Ong, Cheng Soon (2020). मशीन लर्निंग के लिए गणित. Cambridge University Press. p. 181. ISBN 9781108455145.
- ↑ 2.0 2.1 2.2 2.3 2.4 2.5 Park, Kun Il (2018). संचार के अनुप्रयोगों के साथ संभाव्यता और स्टोकेस्टिक प्रक्रियाओं के मूल सिद्धांत. Springer. ISBN 978-3-319-68074-3.
- ↑ Montgomery, Douglas C.; Runger, George C. (2003). इंजीनियरों के लिए अनुप्रयुक्त सांख्यिकी और संभाव्यता (PDF). John Wiley & Sons, Inc. p. 104. ISBN 0-471-20454-4. Archived (PDF) from the original on 2012-07-30.
- ↑ Zwillinger, Daniel; Kokoska, Stephen (2010). सीआरसी मानक संभाव्यता और सांख्यिकी तालिकाएँ और सूत्र. CRC Press. p. 49. ISBN 978-1-58488-059-2.
- ↑ Gentle, J.E. (2009). कम्प्यूटेशनल सांख्यिकी. Springer. ISBN 978-0-387-98145-1. Retrieved 2010-08-06.[page needed]
- ↑ Monti, K. L. (1995). "Folded Empirical Distribution Function Curves (Mountain Plots)". The American Statistician. 49 (4): 342–345. doi:10.2307/2684570. JSTOR 2684570.
- ↑ Xue, J. H.; Titterington, D. M. (2011). "The p-folded cumulative distribution function and the mean absolute deviation from the p-quantile" (PDF). Statistics & Probability Letters. 81 (8): 1179–1182. doi:10.1016/j.spl.2011.03.014.
- ↑ "संयुक्त संचयी वितरण फ़ंक्शन (सीडीएफ)". math.info. Retrieved 2019-12-11.
- ↑ "संग्रहीत प्रति" (PDF). www.math.wustl.edu. Archived from the original (PDF) on 22 February 2016. Retrieved 13 January 2022.
- ↑ Sun, Jingchao; Kong, Maiying; Pal, Subhadip (22 June 2021). "The Modified-Half-Normal distribution: Properties and an efficient sampling scheme". Communications in Statistics - Theory and Methods: 1–23. doi:10.1080/03610926.2021.1934700. ISSN 0361-0926. S2CID 237919587.
बाहरी संबंध
 Media related to Cumulative distribution functions at Wikimedia Commons
Media related to Cumulative distribution functions at Wikimedia Commons




