स्थानीय समतलता: Difference between revisions
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
{{Short description|Property of topological submanifolds}} | {{Short description|Property of topological submanifolds}} | ||
[[टोपोलॉजी|सांस्थितिकी]] में, गणित की एक शाखा, '''स्थानीय समतलता''' निष्कोणता की स्थिति है जिसे सांस्थितिक [[सबमैनिफोल्ड| | [[टोपोलॉजी|सांस्थितिकी]] में, गणित की एक शाखा, '''स्थानीय समतलता''' निष्कोणता की स्थिति है जिसे सांस्थितिक [[सबमैनिफोल्ड|उपबहुरूपताओं]] पर लगाया जा सकता है। सांस्थितिक बहुरूपता की [[श्रेणी (गणित)|श्रेणी]] में, स्थानीय रूप से समतल [[ चिकनी कई गुना |उपबहुरूपताएँ निष्कोण]] बहुरूपताओं की श्रेणी में अंतःस्थापित उपबहुरूपताओं के समान भूमिका निभाती हैं। स्थानीय समतलता का उल्लंघन सामग्री प्रसंस्करण और [[मैकेनिकल इंजीनियरिंग]] के अनुप्रयोगों के साथ रिज नेटवर्क और [[क्रम्प्लिंग|टूटी हुई]] संरचनाओं का वर्णन करता है। | ||
== परिभाषा == | == परिभाषा == | ||
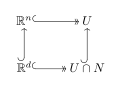
मान लीजिए कि | मान लीजिए कि ''d'' विमीय बहुरूपता ''N'' ''n'' विमीय बहुरूपता ''M'' (जहां ''d'' < ''n'') में अंतः स्थापित है। यदि <math>x \in N,</math> तो हम कहते हैं कि ''N'', ''x'' पर '''स्थानीय रूप से समतल''' है यदि ''x'' का क्षेत्र <math> U \subset M</math> इस प्रकार है कि [[टोपोलॉजिकल जोड़ी|सांस्थितिक युग्म]] <math>(U, U\cap N)</math> <math>\mathbb{R}^d\to\mathbb{R}^n</math> के मानक समावेशन के साथ, युग्म <math>(\mathbb{R}^n,\mathbb{R}^d)</math> के लिए [[होम्योमॉर्फिक|समरूपी]] है। अर्थात्, समरूपता <math>U\to \mathbb{R}^n</math> इस प्रकार उपस्थित है जैसे कि <math>U\cap N</math> का [[छवि (गणित)|चित्र]] [[छवि (गणित)|<math>\mathbb{R}^d</math>]] के साथ मेल खाता है। आरेखीय शब्दों में, निम्नलिखित वर्ग को स्थानांतरित करना होगा- | ||
[[ | |||
=== सीमा | [[File:Locally flat.svg|alt=Commutative diagram: {{math|''U''&cap;''N''}} में एक एकरूपता है {{mvar|U}}, जिनमें से दोनों में समरूपताएं हैं <math>\mathbb{R}^d</math> और <math>\mathbb{R}^n</math> (क्रमशः), और <math>\mathbb{R}^d</math> के लिए एक एकरूपता है <math>\mathbb{R}^n.</math>|केंद्र|फ्रेमरहित|सीधा]] | ||
उपरोक्त परिभाषा मानती है कि, यदि M की | |||
यदि ''N'' प्रत्येक बिंदु पर स्थानीय रूप से समतल है तो हम ''N'' को ''M'' में '''स्थानीय रूप से समतल''' कहते हैं। इसी प्रकार, मानचित्र <math>\chi\colon N\to M</math> को '''स्थानीय रूप से समतल''' कहा जाता है, भले ही यह अंतःस्थापन न हो, यदि ''N'' में प्रत्येक ''x'' का क्षेत्र ''U'' है जिसका चित्र <math>\chi(U)</math> स्थानीय रूप से ''M'' में समतल है। | |||
=== सीमा सहित बहुरूपता में === | |||
उपरोक्त परिभाषा मानती है कि, यदि ''M'' की कोई [[सीमा (टोपोलॉजी)|सीमा]] है, तो ''x'', ''M'' का सीमा बिंदु नहीं है। यदि ''x'', ''M'' की सीमा पर एक बिंदु है तो परिभाषा को निम्नानुसार संशोधित किया गया है। हम कहते हैं कि N, M के सीमा बिंदु x पर '''स्थानीय रूप से समतल''' है यदि ''x'' का क्षेत्र <math>U\subset M</math> इस प्रकार है कि सांस्थितिक युग्म <math>(U, U\cap N)</math> युग्म <math>(\mathbb{R}^n_+,\mathbb{R}^d)</math> के लिए समरूप है, जहां <math>\mathbb{R}^n_+</math> मानक [[अर्ध-स्थान (ज्यामिति)|अर्ध-स्थान]] है और <math>\mathbb{R}^d</math> को इसकी सीमा के मानक उप-अंतराल के रूप में सम्मिलित किया गया है। | |||
== परिणाम == | == परिणाम == | ||
अंतःस्थापन की स्थानीय समतलता का तात्पर्य उन दृढ़ गुणों से है जो सभी अंतःस्थापन द्वारा साझा नहीं किए जाते हैं। ब्राउन (1962) ने सिद्ध किया कि यदि ''d'' = ''n'' − 1, तो ''N'' कॉलर है अर्थात्, इसका क्षेत्र है जो ''N'' × [0,1] के समरूप है, जबकि ''N'' स्वयं ''N'' × 1/2 (यदि ''N'', ''M'' के आंतरिक भाग में है) के अनुरूप है या ''N'' × 0 (यदि ''N'', ''M'' की सीमा में है)। | |||
==यह भी देखें== | ==यह भी देखें== | ||
*[[यूक्लिडियन स्थान]] | *[[यूक्लिडियन स्थान|यूक्लिडियन अंतराल]] | ||
*[[साफ़ सबमैनिफोल्ड]] | *[[साफ़ सबमैनिफोल्ड|अमिश्रित उपबहुरूपता]] | ||
==संदर्भ== | ==संदर्भ== | ||
Revision as of 23:07, 11 July 2023
सांस्थितिकी में, गणित की एक शाखा, स्थानीय समतलता निष्कोणता की स्थिति है जिसे सांस्थितिक उपबहुरूपताओं पर लगाया जा सकता है। सांस्थितिक बहुरूपता की श्रेणी में, स्थानीय रूप से समतल उपबहुरूपताएँ निष्कोण बहुरूपताओं की श्रेणी में अंतःस्थापित उपबहुरूपताओं के समान भूमिका निभाती हैं। स्थानीय समतलता का उल्लंघन सामग्री प्रसंस्करण और मैकेनिकल इंजीनियरिंग के अनुप्रयोगों के साथ रिज नेटवर्क और टूटी हुई संरचनाओं का वर्णन करता है।
परिभाषा
मान लीजिए कि d विमीय बहुरूपता N n विमीय बहुरूपता M (जहां d < n) में अंतः स्थापित है। यदि तो हम कहते हैं कि N, x पर स्थानीय रूप से समतल है यदि x का क्षेत्र इस प्रकार है कि सांस्थितिक युग्म के मानक समावेशन के साथ, युग्म के लिए समरूपी है। अर्थात्, समरूपता इस प्रकार उपस्थित है जैसे कि का चित्र के साथ मेल खाता है। आरेखीय शब्दों में, निम्नलिखित वर्ग को स्थानांतरित करना होगा-
यदि N प्रत्येक बिंदु पर स्थानीय रूप से समतल है तो हम N को M में स्थानीय रूप से समतल कहते हैं। इसी प्रकार, मानचित्र को स्थानीय रूप से समतल कहा जाता है, भले ही यह अंतःस्थापन न हो, यदि N में प्रत्येक x का क्षेत्र U है जिसका चित्र स्थानीय रूप से M में समतल है।
सीमा सहित बहुरूपता में
उपरोक्त परिभाषा मानती है कि, यदि M की कोई सीमा है, तो x, M का सीमा बिंदु नहीं है। यदि x, M की सीमा पर एक बिंदु है तो परिभाषा को निम्नानुसार संशोधित किया गया है। हम कहते हैं कि N, M के सीमा बिंदु x पर स्थानीय रूप से समतल है यदि x का क्षेत्र इस प्रकार है कि सांस्थितिक युग्म युग्म के लिए समरूप है, जहां मानक अर्ध-स्थान है और को इसकी सीमा के मानक उप-अंतराल के रूप में सम्मिलित किया गया है।
परिणाम
अंतःस्थापन की स्थानीय समतलता का तात्पर्य उन दृढ़ गुणों से है जो सभी अंतःस्थापन द्वारा साझा नहीं किए जाते हैं। ब्राउन (1962) ने सिद्ध किया कि यदि d = n − 1, तो N कॉलर है अर्थात्, इसका क्षेत्र है जो N × [0,1] के समरूप है, जबकि N स्वयं N × 1/2 (यदि N, M के आंतरिक भाग में है) के अनुरूप है या N × 0 (यदि N, M की सीमा में है)।
यह भी देखें
संदर्भ
- Brown, Morton (1962), Locally flat imbeddings [sic] of topological manifolds. Annals of Mathematics, Second series, Vol. 75 (1962), pp. 331–341.
- Mazur, Barry. On embeddings of spheres. Bulletin of the American Mathematical Society, Vol. 65 (1959), no. 2, pp. 59–65. http://projecteuclid.org/euclid.bams/1183523034.