बिंदु अनुमान: Difference between revisions

From Vigyanwiki
(Created page with "{{Short description|Parameter estimation via sample statistics}} आंकड़ों में, बिंदु अनुमान में एकल मान की ग...")
 
No edit summary
Line 1: Line 1:
{{Short description|Parameter estimation via sample statistics}}
{{Short description|Parameter estimation via sample statistics}}
आंकड़ों में, बिंदु अनुमान में एकल मान की गणना करने के लिए [[सांख्यिकीय नमूना]] [[आंकड़े]] का उपयोग शामिल होता है (इसे बिंदु अनुमान के रूप में जाना जाता है क्योंकि यह कुछ [[[[पैरामीटर]] स्थान]] में एक [[बिंदु (ज्यामिति)]] की पहचान करता है) जो किसी अज्ञात के सर्वोत्तम अनुमान या सर्वोत्तम अनुमान के रूप में कार्य करता है। जनसंख्या पैरामीटर (उदाहरण के लिए, जनसंख्या माध्य)। अधिक औपचारिक रूप से, यह एक बिंदु अनुमान प्राप्त करने के लिए डेटा पर एक बिंदु अनुमानक का अनुप्रयोग है।


बिंदु अनुमान की तुलना [[अंतराल अनुमान]] से की जा सकती है: ऐसे अंतराल अनुमान आमतौर पर या तो [[विश्वास अंतराल]] होते हैं, बारंबार अनुमान के मामले में, या [[विश्वसनीय अंतराल]], [[बायेसियन अनुमान]] के मामले में। अधिक सामान्यतः, एक बिंदु अनुमानक की तुलना एक निर्धारित अनुमानक से की जा सकती है। उदाहरण कॉन्फिडेंस क्षेत्र या विश्वसनीय अंतराल|विश्वसनीय सेट द्वारा दिए गए हैं। एक बिंदु अनुमानक की तुलना एक वितरण अनुमानक से भी की जा सकती है। उदाहरण आत्म[[विश्वास वितरण]], [[यादृच्छिक निर्णय नियम]] और बायेसियन सांख्यिकी द्वारा दिए गए हैं।
 
आंकड़ों में, '''बिंदु अनुमान''' में एकल मान की गणना करने के लिए नमूना डेटा का उपयोग सम्मिलित होता है (इसे बिंदु अनुमान के रूप में जाना जाता है क्योंकि यह कुछ पैरामीटर स्थान में एक बिंदु की पहचान करता है) जो किसी अज्ञात के "सर्वोत्तम अनुमान" या "सर्वोत्तम अनुमान" के रूप में कार्य करता है। जनसंख्या पैरामीटर (उदाहरण के लिए, जनसंख्या माध्य)। अधिक औपचारिक रूप से, यह एक बिंदु अनुमान प्राप्त करने के लिए डेटा पर एक बिंदु अनुमानक का अनुप्रयोग है।
 
बिंदु अनुमान की तुलना अंतराल अनुमान से की जा सकती है: ऐसे अंतराल अनुमान समान्यता: या तो विश्वास अंतराल होते हैं, बारंबार अनुमान के स्थिति में, या विश्वसनीय अंतराल, बायेसियन अनुमान के स्थिति में अधिक सामान्यतः एक बिंदु अनुमानक की तुलना एक निर्धारित अनुमानक से की जा सकती है। उदाहरण आत्मविश्वास सेट या विश्वसनीय सेट द्वारा दिए गए हैं। एक बिंदु अनुमानक की तुलना एक वितरण अनुमानक से भी की जा सकती है। उदाहरण आत्मविश्वास वितरण यादृच्छिक अनुमानक और बायेसियन पोस्टीरियर द्वारा दिए गए हैं।


==बिंदु अनुमान के गुण ==
==बिंदु अनुमान के गुण ==


=== पक्षपात ===
=== पक्षपात ===
"आकलनकर्ता के पूर्वाग्रह" को अनुमानक के [[अपेक्षित मूल्य]] और अनुमानित जनसंख्या पैरामीटर के वास्तविक मूल्य के बीच अंतर के रूप में परिभाषित किया गया है। इसे यह भी वर्णित किया जा सकता है कि किसी पैरामीटर का अपेक्षित मान मापा पैरामीटर के जितना करीब होगा, पूर्वाग्रह उतना ही कम होगा। जब अनुमानित संख्या और वास्तविक मूल्य बराबर होता है, तो अनुमानक को निष्पक्ष माना जाता है। इसे निष्पक्ष अनुमानक कहा जाता है। यदि अनुमानक में न्यूनतम भिन्नता है तो वह सबसे अच्छा निष्पक्ष अनुमानक बन जाएगा। हालाँकि, छोटे विचरण वाला पक्षपाती अनुमानक बड़े विचरण वाले निष्पक्ष अनुमानक की तुलना में अधिक उपयोगी हो सकता है।<ref name=":0">{{Cite book|title=संभाव्यता और सांख्यिकी का एक आधुनिक परिचय|publisher=F.M. Dekking, C. Kraaikamp, H.P. Lopuhaa, L.E. Meester|year=2005|language=English}}</ref> सबसे महत्वपूर्ण बात यह है कि हम ऐसे बिंदु अनुमानकों को प्राथमिकता देते हैं जिनमें सबसे छोटी माध्य वर्ग त्रुटि|माध्य वर्ग त्रुटियाँ हों।
"आकलनकर्ता के पूर्वाग्रह" को अनुमानक के [[अपेक्षित मूल्य|अपेक्षित]] मान और अनुमानित जनसंख्या पैरामीटर के वास्तविक मान के बीच अंतर के रूप में परिभाषित किया गया है। इसे यह भी वर्णित किया जा सकता है कि किसी पैरामीटर का अपेक्षित मान मापा पैरामीटर के जितना समीप होगा परन्तु पूर्वाग्रह उतना ही कम होगा। जब अनुमानित संख्या और वास्तविक मान समान होता है, तो अनुमानक को निष्पक्ष माना जाता है। इसे निष्पक्ष अनुमानक कहा जाता है। यदि अनुमानक में न्यूनतम भिन्नता है तो वह सबसे अच्छा निष्पक्ष अनुमानक बन जाएगा। चूँकि छोटे विचरण वाला पक्षपाती अनुमानक बड़े विचरण वाले निष्पक्ष अनुमानक की तुलना में अधिक उपयोगी हो सकता है।<ref name=":0">{{Cite book|title=संभाव्यता और सांख्यिकी का एक आधुनिक परिचय|publisher=F.M. Dekking, C. Kraaikamp, H.P. Lopuhaa, L.E. Meester|year=2005|language=English}}</ref> सबसे महत्वपूर्ण बात यह है कि हम ऐसे बिंदु अनुमानकों को प्राथमिकता देते हैं जिनमें सबसे छोटी माध्य वर्ग त्रुटि या माध्य वर्ग त्रुटियाँ हों।


यदि हम T = h(X<sub>1</sub>,एक्स<sub>2</sub>, . . . , एक्स<sub>n</sub>) एक यादृच्छिक नमूना एक्स के आधार पर एक अनुमानक बनें<sub>1</sub>,एक्स<sub>2</sub>, . . . , एक्स<sub>n</sub>, यदि E[T] = θ है, तो अनुमानक T को पैरामीटर θ के लिए निष्पक्ष अनुमानक कहा जाता है, चाहे θ का मान कुछ भी हो।<ref name=":0">{{Cite book|title=संभाव्यता और सांख्यिकी का एक आधुनिक परिचय|publisher=F.M. Dekking, C. Kraaikamp, H.P. Lopuhaa, L.E. Meester|year=2005|language=English}}</ref> उदाहरण के लिए, उसी यादृच्छिक नमूने से हमारे पास E( x̄ ) = µ(माध्य) और E(s) है<sup>2</sup>) = पी<sup>2</sup> (विचरण), फिर x̄ और s<sup>2</sup>µ और σ के लिए निष्पक्ष अनुमानक होंगे<sup>2</sup>. अंतर E[T ] - θ को T का पूर्वाग्रह कहा जाता है; यदि यह अंतर शून्येतर है, तो T को पक्षपाती कहा जाता है।
यदि हम T = h(X1,X2,... , Xn) को एक यादृच्छिक नमूने X<sub>1</sub>,X<sub>2</sub>, . . . , X<sub>n</sub>, के आधार पर एक अनुमानक मानते हैं। अनुमानक T को पैरामीटर θ के लिए एक निष्पक्ष अनुमानक कहा जाता है यदि E[T] = θ, θ के मान पर ध्यान दिए बिना।<ref name=":0">{{Cite book|title=संभाव्यता और सांख्यिकी का एक आधुनिक परिचय|publisher=F.M. Dekking, C. Kraaikamp, H.P. Lopuhaa, L.E. Meester|year=2005|language=English}}</ref> उदाहरण के लिए, उसी यादृच्छिक नमूने से हमारे पास E( x̄ ) = µ(माध्य) और E(s<sup>2</sup>) = σ<sup>2</sup> (विचरण) है, तो x̄ और s<sup>2</sup> µ और σ<sup>2</sup> के लिए निष्पक्ष अनुमानक होंगे। अंतर E[T ] - θ को T का पूर्वाग्रह कहा जाता है; यदि यह अंतर शून्येतर है, तो T को पक्षपाती कहा जाता है।


=== संगति ===
=== संगति ===
संगति इस बारे में है कि जब पैरामीटर अपना आकार बढ़ाता है तो बिंदु अनुमान मूल्य के करीब रहता है या नहीं। नमूना आकार जितना बड़ा होगा, अनुमान उतना ही सटीक होगा। यदि एक बिंदु अनुमानक सुसंगत है, तो इसका अपेक्षित मूल्य और विचरण पैरामीटर के वास्तविक मूल्य के करीब होना चाहिए। एक निष्पक्ष अनुमानक सुसंगत होता है यदि अनुमानक टी के विचरण की सीमा शून्य के बराबर होती है।
संगति इस बारे में है कि जब पैरामीटर अपना आकार बढ़ाता है तो बिंदु अनुमान मान के समीप रहता है या नहीं जो की नमूना आकार जितना बड़ा होगा, अनुमान उतना ही स्पष्ट होगा। यदि एक बिंदु अनुमानक सुसंगत है, तो इसका अपेक्षित मान और विचरण पैरामीटर के वास्तविक मान के समीप होना चाहिए। एक निष्पक्ष अनुमानक सुसंगत होता है यदि अनुमानक t  के विचरण की सीमा शून्य के समान होती है।


=== दक्षता ===
=== दक्षता ===
चलो टी<sub>1</sub> और टी<sub>2</sub> एक ही पैरामीटर θ के लिए दो निष्पक्ष अनुमानक हों। अनुमानक टी<sub>2</sub> अनुमानक टी से अधिक कुशल कहा जाएगा<sub>1</sub> यदि वार(टी<sub>2</sub>) < वार(टी<sub>1</sub>), θ के मान पर ध्यान दिए बिना।<ref name=":0">{{Cite book|title=संभाव्यता और सांख्यिकी का एक आधुनिक परिचय|publisher=F.M. Dekking, C. Kraaikamp, H.P. Lopuhaa, L.E. Meester|year=2005|language=English}}</ref> हम यह भी कह सकते हैं कि सबसे कुशल अनुमानक वे हैं जिनके परिणामों में सबसे कम परिवर्तनशीलता है। इसलिए, यदि अनुमानक के पास नमूने से नमूने के बीच सबसे छोटा अंतर है, तो यह सबसे कुशल और निष्पक्ष दोनों है। हम अनुमानक टी कहकर दक्षता की धारणा का विस्तार करते हैं<sub>2</sub> अनुमानक टी से अधिक कुशल है<sub>1</sub> (रुचि के समान पैरामीटर के लिए), यदि टी का एमएसई (मीन चुकता त्रुटि)।<sub>2</sub> टी के एमएसई से छोटा है<sub>1</sub>.<ref name=":0">{{Cite book|title=संभाव्यता और सांख्यिकी का एक आधुनिक परिचय|publisher=F.M. Dekking, C. Kraaikamp, H.P. Lopuhaa, L.E. Meester|year=2005|language=English}}</ref>
चलो ''T''<sub>1</sub> और ''T''<sub>2</sub> एक ही पैरामीटर θ के लिए दो निष्पक्ष अनुमानक हों। अनुमानक ''T''<sub>2</sub> अनुमानक ''T''<sub>1</sub> की तुलना में अधिक कुशल कहा जाएगा यदि Var(''T''<sub>2</sub>) ''<'' Var(''T''<sub>1</sub>), θ के मान पर ध्यान दिए बिना।<ref name=":0">{{Cite book|title=संभाव्यता और सांख्यिकी का एक आधुनिक परिचय|publisher=F.M. Dekking, C. Kraaikamp, H.P. Lopuhaa, L.E. Meester|year=2005|language=English}}</ref> हम यह भी कह सकते हैं कि सबसे कुशल अनुमानक वे हैं जिनके परिणामों में सबसे कम परिवर्तनशीलता है। इसलिए, यदि अनुमानक के पास नमूने से नमूने के बीच सबसे छोटा अंतर है, तो यह सबसे कुशल और निष्पक्ष दोनों है। हम अनुमानक T<sub>2</sub>  कहकर दक्षता की धारणा का विस्तार करते हैं अनुमानक T<sub>1</sub> से अधिक कुशल है (रुचि के समान पैरामीटर के लिए), यदि T<sub>2</sub>  का एमएसई (मीन चुकता त्रुटि) T<sub>1</sub> के एमएसई से छोटा है.<ref name=":0">{{Cite book|title=संभाव्यता और सांख्यिकी का एक आधुनिक परिचय|publisher=F.M. Dekking, C. Kraaikamp, H.P. Lopuhaa, L.E. Meester|year=2005|language=English}}</ref>
आम तौर पर, हमें अनुमानकर्ताओं की दक्षता निर्धारित करते समय जनसंख्या के वितरण पर विचार करना चाहिए। उदाहरण के लिए, एक [[सामान्य वितरण]] में, माध्य को माध्यिका की तुलना में अधिक कुशल माना जाता है, लेकिन यह बात असममित, या तिरछे वितरण, वितरण में लागू नहीं होती है।
 
समान्यता:  हमें अनुमानकर्ताओं की दक्षता निर्धारित करते समय जनसंख्या के वितरण पर विचार करना चाहिए। उदाहरण के लिए एक [[सामान्य वितरण]] में, माध्य को माध्यिका की तुलना में अधिक कुशल माना जाता है, किंतु यह बात असममित, या विषम  वितरण, वितरण में प्रयुक्त नहीं होती है।


=== पर्याप्तता ===
=== पर्याप्तता ===
सांख्यिकी में, एक सांख्यिकीविद् का काम उन आंकड़ों की व्याख्या करना है जो उन्होंने एकत्र किए हैं और जांच के तहत जनसंख्या के बारे में सांख्यिकीय रूप से वैध निष्कर्ष निकालना है। लेकिन कई मामलों में कच्चा डेटा, जो बहुत अधिक है और भंडारण के लिए बहुत महंगा है, इस उद्देश्य के लिए उपयुक्त नहीं है। इसलिए, सांख्यिकीविद् कुछ आँकड़ों की गणना करके डेटा को संक्षिप्त करना चाहेगा और अपने विश्लेषण को इन आँकड़ों पर आधारित करना चाहेगा ताकि ऐसा करने पर प्रासंगिक जानकारी का कोई नुकसान न हो, अर्थात सांख्यिकीविद् उन आँकड़ों को चुनना चाहेगा जिनके बारे में सारी जानकारी समाप्त हो जाती है पैरामीटर, जो नमूने में निहित है. हम पर्याप्त आँकड़ों को इस प्रकार परिभाषित करते हैं: मान लीजिए X =(<sub>1</sub>, एक्स<sub>2</sub>, ... ,एक्स<sub>n</sub>) एक यादृच्छिक नमूना बनें। एक आँकड़ा T(X) को θ (या वितरण के परिवार के लिए) के लिए पर्याप्त माना जाता है यदि दिए गए T का सशर्त वितरण θ से मुक्त है।<ref name=":1">{{Cite book|title=अनुमान और अनुमानात्मक सांख्यिकी|publisher=Pradip Kumar Sahu, Santi Ranjan Pal, Ajit Kumar Das|year=2015|language=English}}</ref>


सांख्यिकी में, एक सांख्यिकीविद् का काम उन आंकड़ों की व्याख्या करना है जो उन्होंने एकत्र किए हैं और जांच के अनुसार जनसंख्या के बारे में सांख्यिकीय रूप से वैध निष्कर्ष निकालना है। किंतु कई स्थिति में कच्चा डेटा, जो बहुत अधिक है और संचयन के लिए बहुत मूल्यवान `है, इस उद्देश्य के लिए उपयुक्त नहीं है। इसलिए, सांख्यिकीविद् कुछ आँकड़ों की गणना करके डेटा को संक्षिप्त करना चाहेगा और अपने विश्लेषण को इन आँकड़ों पर आधारित करना चाहेगा जिससे ऐसा करने पर प्रासंगिक जानकारी का कोई हानि न हो, अर्थात सांख्यिकीविद् उन आँकड़ों को चुनना चाहेगा जिनके बारे में सारी जानकारी समाप्त हो जाती है पैरामीटर, जो नमूने में निहित है. हम पर्याप्त आँकड़ों को इस प्रकार परिभाषित करते हैं: मान लीजिए X =( X<sub>1</sub>, X<sub>2</sub>, ... ,X<sub>n</sub>) एक यादृच्छिक नमूना है। एक आँकड़ा T(X) को θ (या वितरण के वर्ग के लिए) के लिए पर्याप्त माना जाता है यदि दिए गए T का सशर्त वितरण θ से मुक्त है।<ref name=":1">{{Cite book|title=अनुमान और अनुमानात्मक सांख्यिकी|publisher=Pradip Kumar Sahu, Santi Ranjan Pal, Ajit Kumar Das|year=2015|language=English}}</ref>
== बिंदु अनुमान के प्रकार ==
== बिंदु अनुमान के प्रकार ==


=== बायेसियन बिंदु अनुमान ===
=== बायेसियन बिंदु अनुमान ===
[[बायेसियन अनुमान]] आम तौर पर [[पश्च वितरण]] पर आधारित होता है। कई बायेसियन अनुमान [[केंद्रीय प्रवृत्ति]] के पश्च वितरण के आँकड़े हैं, उदाहरण के लिए, इसका माध्य, माध्य या मोड:
बायेसियन अनुमान समान्यता पश्च वितरण पर आधारित होता है। कई बायेसियन बिंदु अनुमानक केंद्रीय प्रवृत्ति के पश्च वितरण के आँकड़े हैं, उदाहरण के लिए, इसका माध्य माध्यिका या मोड:
* बेयस अनुमानक # पश्च माध्य, जो [[न्यूनतम माध्य वर्ग त्रुटि]] | वर्ग-त्रुटि हानि फ़ंक्शन के लिए (पश्च) जोखिम फ़ंक्शन (अपेक्षित हानि) को कम करता है; बायेसियन अनुमान में, जोखिम को पश्च वितरण के संदर्भ में परिभाषित किया गया है, जैसा कि [[गॉस]] ने देखा है।<ref name="Dodge">{{cite book|title=Statistical data analysis based on the L1-norm and related methods: Papers from the First International Conference held at Neuchâtel, August 31–September 4, 1987|publisher=[[North-Holland Publishing]]|year=1987|editor-last=Dodge|editor-first=Yadolah|editor-link=Yadolah Dodge}}</ref>
 
* बेयस अनुमानक#पश्च माध्यिका और अन्य मात्राएँ, जो पूर्ण-मूल्य हानि फ़ंक्शन के लिए पश्च जोखिम को कम करता है, जैसा कि [[लाप्लास]] द्वारा देखा गया है।<ref name="Dodge" /><ref>{{cite book|last1=Jaynes|first1=E. T.|title=Probability Theory: The logic of science|date=2007|publisher=[[Cambridge University Press]]|isbn=978-0-521-59271-0|edition=5. print.|page=172|author-link=Edwin Thompson Jaynes}}</ref>
* पश्च माध्य, जो वर्ग-त्रुटि हानि फलन के लिए (पश्च) कठिन परिस्थिति (अपेक्षित हानि) को कम करता है; बायेसियन अनुमान में, कठिन परिस्थिति को पश्च वितरण के संदर्भ में परिभाषित किया गया है, जैसा कि गॉस ने देखा है ।<ref name="Dodge">{{cite book|title=Statistical data analysis based on the L1-norm and related methods: Papers from the First International Conference held at Neuchâtel, August 31–September 4, 1987|publisher=[[North-Holland Publishing]]|year=1987|editor-last=Dodge|editor-first=Yadolah|editor-link=Yadolah Dodge}}</ref>
*पश्च माध्यिका, जो पूर्ण-मूल्य हानि फलन के लिए पश्च कठिन परिस्थिति को कम करती है, जैसा कि लाप्लास द्वारा देखा गया है।<ref name="Dodge" /><ref>{{cite book|last1=Jaynes|first1=E. T.|title=Probability Theory: The logic of science|date=2007|publisher=[[Cambridge University Press]]|isbn=978-0-521-59271-0|edition=5. print.|page=172|author-link=Edwin Thompson Jaynes}}</ref>
* अधिकतम एक पोस्टीरियरी (एमएपी), जो अधिकतम पोस्टीरियर वितरण पाता है; एक समान पूर्व संभाव्यता के लिए, एमएपी अनुमानक अधिकतम-संभावना अनुमानक के साथ मेल खाता है;
* अधिकतम एक पोस्टीरियरी (एमएपी), जो अधिकतम पोस्टीरियर वितरण पाता है; एक समान पूर्व संभाव्यता के लिए, एमएपी अनुमानक अधिकतम-संभावना अनुमानक के साथ मेल खाता है;
एमएपी अनुमानक के पास कई कठिन समस्याओं के लिए भी अच्छे स्पर्शोन्मुख गुण हैं, जिन पर अधिकतम संभावना अनुमानक को कठिनाइयाँ होती हैं।
एमएपी अनुमानक के पास कई कठिन समस्याओं के लिए भी अच्छे स्पर्शोन्मुख गुण हैं, जिन पर अधिकतम संभावना अनुमानक को कठिनाइयाँ होती हैं। नियमित समस्याओं के लिए, जहां अधिकतम-संभावना अनुमानक सुसंगत है, अधिकतम-संभावना अनुमानक अंततः एमएपी अनुमानक से सहमत होता है।<ref>{{cite book|last=Ferguson|first=Thomas S.|title=बड़े नमूना सिद्धांत में एक पाठ्यक्रम|publisher=[[Chapman & Hall]]|year=1996|isbn=0-412-04371-8|author-link=Thomas S. Ferguson}}</ref><ref name="LeCam">{{cite book|last=Le Cam|first=Lucien|title=सांख्यिकीय निर्णय सिद्धांत में स्पर्शोन्मुख विधियाँ|publisher=[[Springer-Verlag]]|year=1986|isbn=0-387-96307-3|author-link=Lucien Le Cam}}</ref><ref name="FergJASA">{{cite journal|last=Ferguson|first=Thomas&nbsp;S.|author-link=Thomas S. Ferguson|year=1982|title=एक असंगत अधिकतम संभावना अनुमान|journal=[[Journal of the American Statistical Association]]|volume=77|issue=380|pages=831–834|doi=10.1080/01621459.1982.10477894|jstor=2287314}}</ref> वाल्ड के प्रमेय के अनुसार बायेसियन अनुमानक स्वीकार्य हैं।<ref name="LeCam" /><ref name="LehmannCasella">{{cite book|last1=Lehmann|first1=E. L.|title=बिंदु अनुमान का सिद्धांत|last2=Casella|first2=G.|publisher=Springer|year=1998|isbn=0-387-98502-6|edition=2nd|author-link=Erich Leo Lehmann}}</ref>
नियमित समस्याओं के लिए, जहां अधिकतम-संभावना अनुमानक सुसंगत है, अधिकतम-संभावना अनुमानक अंततः एमएपी अनुमानक से सहमत होता है।<ref>{{cite book|last=Ferguson|first=Thomas S.|title=बड़े नमूना सिद्धांत में एक पाठ्यक्रम|publisher=[[Chapman & Hall]]|year=1996|isbn=0-412-04371-8|author-link=Thomas S. Ferguson}}</ref><ref name="LeCam">{{cite book|last=Le Cam|first=Lucien|title=सांख्यिकीय निर्णय सिद्धांत में स्पर्शोन्मुख विधियाँ|publisher=[[Springer-Verlag]]|year=1986|isbn=0-387-96307-3|author-link=Lucien Le Cam}}</ref><ref name="FergJASA">{{cite journal|last=Ferguson|first=Thomas&nbsp;S.|author-link=Thomas S. Ferguson|year=1982|title=एक असंगत अधिकतम संभावना अनुमान|journal=[[Journal of the American Statistical Association]]|volume=77|issue=380|pages=831–834|doi=10.1080/01621459.1982.10477894|jstor=2287314}}</ref>
वाल्ड के प्रमेय के अनुसार बायेसियन अनुमानक [[स्वीकार्य प्रक्रिया]] हैं।<ref name="LeCam" /><ref name="LehmannCasella">{{cite book|last1=Lehmann|first1=E. L.|title=बिंदु अनुमान का सिद्धांत|last2=Casella|first2=G.|publisher=Springer|year=1998|isbn=0-387-98502-6|edition=2nd|author-link=Erich Leo Lehmann}}</ref>
[[न्यूनतम संदेश लंबाई]] (न्यूनतम संदेश लंबाई) बिंदु अनुमानक बायेसियन [[सूचना सिद्धांत]] पर आधारित है और यह सीधे तौर पर पश्च वितरण से संबंधित नहीं है।


[[बेयस फ़िल्टर]] के विशेष मामले महत्वपूर्ण हैं:
न्यूनतम संदेश लंबाई (एमएमएल) बिंदु अनुमानक बायेसियन सूचना सिद्धांत पर आधारित है और यह सीधे रूप से पश्च वितरण से संबंधित नहीं है।
*[[कलमन फ़िल्टर]]
 
*[[विनीज़ फ़िल्टर]]
[[बेयस फ़िल्टर|बेयस निस्पंदन]] के विशेष स्थिति महत्वपूर्ण हैं:
*[[कलमन फ़िल्टर|कलमन निस्पंदन]]  
*[[विनीज़ फ़िल्टर|विनीज़ निस्पंदन]]  


कम्प्यूटेशनल सांख्यिकी की कई पुनरावृत्तीय पद्धतियों का बायेसियन विश्लेषण के साथ घनिष्ठ संबंध है:
कम्प्यूटेशनल सांख्यिकी की कई पुनरावृत्तीय पद्धतियों का बायेसियन विश्लेषण के साथ घनिष्ठ संबंध है:
*[[कण फिल्टर]]
*[[कण फिल्टर|कण निस्पंदन]]  
*[[मार्कोव श्रृंखला मोंटे कार्लो]] (एमसीएमसी)
*[[मार्कोव श्रृंखला मोंटे कार्लो]] (एमसीएमसी)


==बिंदु अनुमान ज्ञात करने की विधियाँ==
==बिंदु अनुमान ज्ञात करने की विधियाँ==
नीचे अज्ञात मापदंडों का अनुमान लगाने के कुछ सामान्य रूप से उपयोग किए जाने वाले तरीके दिए गए हैं जिनसे अनुमानकर्ताओं को इनमें से कुछ महत्वपूर्ण गुण प्रदान करने की उम्मीद है। सामान्य तौर पर, स्थिति और हमारे अध्ययन के उद्देश्य के आधार पर हम बिंदु अनुमान के तरीकों में से किसी एक तरीके को लागू करते हैं जो उपयुक्त हो सकता है।
नीचे अज्ञात मापदंडों का अनुमान लगाने के कुछ सामान्य रूप से उपयोग किए जाने वाले विधि दिए गए हैं जिनसे अनुमानकर्ताओं को इनमें से कुछ महत्वपूर्ण गुण प्रदान करने की उम्मीद है। सामान्य रूप से  स्थिति और हमारे अध्ययन के उद्देश्य के आधार पर हम बिंदु अनुमान के विधि में से किसी एक विधि को प्रयुक्त करते हैं जो उपयुक्त हो सकता है।


=== अधिकतम संभावना की विधि (एमएलई) ===
=== अधिकतम संभावना की विधि (एमएलई) ===
आर.ए. के कारण [[अधिकतम संभावना अनुमान]] फिशर, अनुमान लगाने की सबसे महत्वपूर्ण सामान्य विधि है। यह अनुमानक विधि अज्ञात मापदंडों को प्राप्त करने का प्रयास करती है जो संभावना फ़ंक्शन को अधिकतम करती है। यह एक ज्ञात मॉडल (उदा. सामान्य वितरण) का उपयोग करता है और मॉडल में पैरामीटर के मानों का उपयोग करता है जो डेटा के लिए सबसे उपयुक्त मिलान खोजने के लिए संभावना फ़ंक्शन को अधिकतम करता है।<ref>{{Cite book|title=श्रेणीबद्ध डेटा विश्लेषण|publisher=Agresti A.|year=1990|location=John Wiley and Sons, New York|pages=}}</ref>
अधिकतम संभावना की विधि, आर.ए. के कारण फिशर, अनुमान लगाने की सबसे महत्वपूर्ण सामान्य विधि है। यह अनुमानक विधि अज्ञात मापदंडों को प्राप्त करने का प्रयास करती है जो संभावना फलन को अधिकतम करती है। यह एक ज्ञात मॉडल (उदा. सामान्य वितरण) का उपयोग करता है और मॉडल में पैरामीटर के मानों का उपयोग करता है जो डेटा के लिए सबसे उपयुक्त मिलान खोजने के लिए संभावना फलन को अधिकतम करता है।<ref>{{Cite book|title=श्रेणीबद्ध डेटा विश्लेषण|publisher=Agresti A.|year=1990|location=John Wiley and Sons, New York|pages=}}</ref>
माना X = (X<sub>1</sub>, एक्स<sub>2</sub>, ... ,एक्स<sub>n</sub>) संयुक्त पी.डी.एफ. या पी.एम.एफ. के साथ एक यादृच्छिक नमूना निरूपित करें। f(x, θ) (θ एक सदिश हो सकता है)। फलन f(x, θ), जिसे θ का फलन माना जाता है, संभाव्यता फलन कहलाता है। इस मामले में, इसे L(θ) द्वारा दर्शाया जाता है। अधिकतम संभावना के सिद्धांत में θ की स्वीकार्य सीमा के भीतर एक अनुमान चुनना शामिल है, जो संभावना को अधिकतम करता है। इस अनुमानक को θ का अधिकतम संभावना अनुमान (एमएलई) कहा जाता है। θ का MLE प्राप्त करने के लिए, हम समीकरण का उपयोग करते हैं
 
मान लीजिए X = (X<sub>1</sub>, X<sub>2</sub>, ... ,X<sub>n</sub>) संयुक्त पीडीएफ या पी.एम.एफ. के साथ एक यादृच्छिक नमूने को दर्शाता है। f(x, θ) (θ एक सदिश हो सकता है)। फलन f(x, θ), जिसे θ का फलन माना जाता है, संभाव्यता फलन कहलाता है। इस स्थिति में, इसे L(θ) द्वारा दर्शाया जाता है। अधिकतम संभावना के सिद्धांत में θ की स्वीकार्य सीमा के अंदर एक अनुमान चुनना सम्मिलित है, जो संभावना को अधिकतम करता है। इस अनुमानक को θ का अधिकतम संभावना अनुमान (एमएलई) कहा जाता है। θ का MLE प्राप्त करने के लिए, हम समीकरण का उपयोग करते हैं
 
''dlog''L(θ)/''d''θ<sub>i</sub>=0, i = 1, 2, …, k.. यदि θ एक सदिश है, तो संभावना समीकरण प्राप्त करने के लिए आंशिक व्युत्पन्न पर विचार किया जाता है।<ref name=":1" />


dlogL(θ)/dθ<sub>i</sub>=0, मैं = 1, 2, …, के. यदि θ एक वेक्टर है, तो संभावना समीकरण प्राप्त करने के लिए आंशिक व्युत्पन्न पर विचार किया जाता है।<ref name=":1" />




=== क्षणों की विधि (MOM) ===
=== क्षणों की विधि (MOM) ===
[[क्षणों की विधि (सांख्यिकी)]] 1887 में के. पियर्सन और पी. चेबीशेव द्वारा शुरू की गई थी, और यह अनुमान लगाने की सबसे पुरानी विधियों में से एक है। यह विधि बड़ी संख्या के कानून पर आधारित है, जो जनसंख्या के बारे में सभी ज्ञात तथ्यों का उपयोग करती है और उन तथ्यों को समीकरण प्राप्त करके जनसंख्या के नमूने पर लागू करती है जो जनसंख्या क्षणों को अज्ञात मापदंडों से जोड़ते हैं। फिर हम जनसंख्या क्षणों के नमूना माध्य से हल कर सकते हैं।<ref>{{Cite book|title=सांख्यिकी का संक्षिप्त विश्वकोश|publisher=Dodge, Y.|year=2008|location=Springer}}</ref> हालाँकि, सरलता के कारण, यह विधि हमेशा सटीक नहीं होती है और आसानी से पक्षपाती हो सकती है।
क्षणों की विधि 1887 में के. पियर्सन और पी. चेबीशेव द्वारा प्रारंभ की गई थी, और यह अनुमान लगाने की सबसे पुरानी विधियों में से एक है। यह विधि बड़ी संख्या के नियम पर आधारित है, जो जनसंख्या के बारे में सभी ज्ञात तथ्यों का उपयोग करती है और उन तथ्यों को समीकरण प्राप्त करके जनसंख्या के नमूने पर प्रयुक्त  करती है जो जनसंख्या क्षणों को अज्ञात मापदंडों से जोड़ते हैं। फिर हम जनसंख्या क्षणों के नमूना माध्य से हल कर सकते हैं।<ref>{{Cite book|title=सांख्यिकी का संक्षिप्त विश्वकोश|publisher=Dodge, Y.|year=2008|location=Springer}}</ref> चूँकि सरलता के कारण यह विधि सदैव स्पष्ट  नहीं होती है और आसानी से पक्षपाती हो सकती है।


चलो (एक्स<sub>1</sub>, एक्स<sub>2</sub>,…एक्स<sub>n</sub>) पी.डी.एफ. वाली जनसंख्या से एक यादृच्छिक नमूना बनें। (या p.m.f) f(x,θ), θ = (θ<sub>1</sub>, मैं<sub>2</sub>, ..., मैं<sub>k</sub>). इसका उद्देश्य पैरामीटर θ का अनुमान लगाना है<sub>1</sub>, मैं<sub>2</sub>, ..., मैं<sub>k</sub>. इसके अलावा, शून्य के बारे में पहले k जनसंख्या क्षणों को θ, यानी μ के स्पष्ट कार्य के रूप में मौजूद होने दें<sub>r</sub> = एम<sub>r</sub>(मैं<sub>1</sub>, मैं<sub>2</sub>,..., मैं<sub>k</sub>), आर = 1, 2, …, के. क्षणों की विधि में, हम k नमूना क्षणों को संबंधित जनसंख्या क्षणों के साथ बराबर करते हैं। आम तौर पर, पहले k क्षण इसलिए लिए जाते हैं क्योंकि नमूने के कारण होने वाली त्रुटियाँ क्षण के क्रम के साथ बढ़ती हैं। इस प्रकार, हमें k समीकरण μ मिलता है<sub>r</sub>(मैं<sub>1</sub>, मैं<sub>2</sub>,..., मैं<sub>k</sub>) = एम<sub>r</sub>, आर = 1, 2, …, के। इन समीकरणों को हल करने पर हमें क्षण अनुमानक (या अनुमान) की विधि प्राप्त होती है
मान लीजिए(X<sub>1</sub>, X<sub>2</sub>,…X<sub>n</sub>) पीडीएफ वाली जनसंख्या से एक यादृच्छिक नमूना है। (या p.m.f) f(x,θ), θ = (θ<sub>1</sub>, θ<sub>2</sub>, …, θ<sub>k</sub>). इसका उद्देश्य पैरामीटर θ<sub>1</sub>, θ<sub>2</sub>, ..., θ<sub>k</sub> का अनुमान लगाना है। इसके अतिरिक्त , शून्य के बारे में पहले k जनसंख्या क्षणों को θ के स्पष्ट कार्य के रूप में उपस्थित  होने दें, अथार्त μ<sub>r</sub> = μ<sub>r</sub>(θ<sub>1</sub>, θ<sub>2</sub>,…, θ<sub>k</sub>), r = 1, 2, …, k क्षणों की विधि में, हम k नमूना क्षणों को संबंधित जनसंख्या क्षणों के साथ समान करते हैं। समान्यता:, पहले k क्षण इसलिए लिए जाते हैं क्योंकि नमूने के कारण होने वाली त्रुटियाँ क्षण के क्रम के साथ बढ़ती हैं। इस प्रकार, हमें k समीकरण μ<sub>r</sub>(θ<sub>1</sub>, θ<sub>2</sub>,…, θ<sub>k</sub>) = m<sub>r</sub>, r = 1, 2, …, k.मिलता है। इन समीकरणों को हल करने पर हमें क्षण अनुमानक (या अनुमान) की विधि प्राप्त होती है


एम<sub>r</sub> = 1/एन ΣX<sub>i</sub><sup>र</sup>.<ref name=":1" />[[क्षणों की सामान्यीकृत विधि]] भी देखें।
m<sub>r</sub> = 1/n ΣX<sub>i</sub><sup>r</sup>.<ref name=":1" />[[क्षणों की सामान्यीकृत विधि]] भी देखें।


=== न्यूनतम वर्ग की विधि ===
=== न्यूनतम वर्ग की विधि ===
न्यूनतम वर्ग की विधि में, हम अपेक्षा के कुछ निर्दिष्ट रूप और अवलोकनों के दूसरे क्षण का उपयोग करके मापदंडों के अनुमान पर विचार करते हैं। के लिए
न्यूनतम वर्ग की विधि में, हम अपेक्षा के कुछ निर्दिष्ट रूप और अवलोकनों के दूसरे क्षण का उपयोग करके मापदंडों के अनुमान पर विचार करते हैं। के लिए


y = f( x, β के रूप का एक वक्र फिट करना<sub>0</sub>, बी<sub>1</sub>, ,,,, बी<sub>p</sub>) डेटा के लिए (x<sub>i</sub>, और<sub>i</sub>), i = 1, 2,…n, हम न्यूनतम वर्ग की विधि का उपयोग कर सकते हैं। इस विधि में न्यूनतम करना शामिल है
फॉर्म  y = f( x, β<sub>0</sub>, β<sub>1</sub>, ,,,, β<sub>p</sub>) के एक वक्र को डेटा (x<sub>i</sub>, y<sub>i</sub>), i = 1, 2,…n, में फिट करते हुए, हम कम से कम वर्गों की विधि का उपयोग कर सकते हैं। इस विधि में न्यूनतम करना सम्मिलित है


वर्गों का योग।
वर्गों का योग।


जब f( x, β<sub>0</sub>, बी<sub>1</sub>, ,,,, बी<sub>p</sub>) पैरामीटरों का एक रैखिक कार्य है और x-मान ज्ञात हैं, न्यूनतम वर्ग अनुमानक [[सर्वोत्तम रैखिक निष्पक्ष अनुमानक]] (नीला) होगा। दोबारा, यदि हम मानते हैं कि न्यूनतम वर्ग अनुमान स्वतंत्र रूप से और समान रूप से सामान्य रूप से वितरित होते हैं, तो एक रैखिक अनुमानक निष्पक्ष अनुमानकों के पूरे वर्ग के लिए [[न्यूनतम-विचरण निष्पक्ष अनुमानक]] (एमवीयूई) होगा। [[न्यूनतम माध्य वर्ग त्रुटि]] (एमएमएसई) भी देखें।<ref name=":1" />
जब f( x, β<sub>0</sub>, β<sub>1</sub>, ,,,, β<sub>p</sub>) पैरामीटरों का एक रैखिक कार्य है और x-मान ज्ञात हैं, न्यूनतम वर्ग अनुमानक [[सर्वोत्तम रैखिक निष्पक्ष अनुमानक]] (नीला) होगा। दोबारा, यदि हम मानते हैं कि न्यूनतम वर्ग अनुमान स्वतंत्र रूप से और समान रूप से सामान्य रूप से वितरित होते हैं, तो एक रैखिक अनुमानक निष्पक्ष अनुमानकों के पूरे वर्ग के लिए [[न्यूनतम-विचरण निष्पक्ष अनुमानक]] (एमवीयूई) होगा। [[न्यूनतम माध्य वर्ग त्रुटि]] (एमएमएसई) भी देखें।<ref name=":1" />
 
 
=== न्यूनतम-विचरण माध्य-निष्पक्ष अनुमानक (एमवीयूई) ===
=== न्यूनतम-विचरण माध्य-निष्पक्ष अनुमानक (एमवीयूई) ===
न्यूनतम-विचरण निष्पक्ष अनुमानक की विधि वर्ग-त्रुटि हानि फ़ंक्शन | हानि-फ़ंक्शन के जोखिम फ़ंक्शन (अपेक्षित हानि) को कम करती है।
न्यूनतम-विचरण निष्पक्ष अनुमानक की विधि वर्ग-त्रुटि हानि-फलन  के कठिन परिस्थिति (अपेक्षित हानि) को कम करती है।


=== माध्यिका निष्पक्ष अनुमानक ===
=== माध्यिका निष्पक्ष अनुमानक ===
[[माध्यिका-निष्पक्ष अनुमानक]] पूर्ण-त्रुटि हानि फ़ंक्शन के जोखिम को कम करता है।
[[माध्यिका-निष्पक्ष अनुमानक]] पूर्ण-त्रुटि हानि फलन के कठिन परिस्थिति को कम करता है।


=== सर्वोत्तम रैखिक निष्पक्ष अनुमानक (नीला) ===
=== सर्वोत्तम रैखिक निष्पक्ष अनुमानक (नीला) ===
सर्वश्रेष्ठ रैखिक निष्पक्ष अनुमानक, जिसे गॉस-मार्कोव प्रमेय के रूप में भी जाना जाता है, बताता है कि साधारण न्यूनतम वर्ग (ओएलएस) अनुमानक में रैखिक निष्पक्ष अनुमानकों के वर्ग के भीतर सबसे कम नमूनाकरण भिन्नता होती है, यदि रैखिक प्रतिगमन मॉडल में त्रुटियां असंबद्ध हैं, तो समान भिन्नताएं होती हैं और उम्मीद का मान शून्य है।<ref>{{Cite book|title=सर्वोत्तम रैखिक निष्पक्ष अनुमान और भविष्यवाणी|publisher=Theil Henri|year=1971|location=New York: John Wiley & Sons}}</ref>
सर्वश्रेष्ठ रैखिक निष्पक्ष अनुमानक, जिसे गॉस-मार्कोव प्रमेय के रूप में भी जाना जाता है, बताता है कि साधारण न्यूनतम वर्ग (ओएलएस) अनुमानक में रैखिक निष्पक्ष अनुमानकों के वर्ग के अंदर सबसे कम नमूनाकरण भिन्नता होती है, यदि रैखिक प्रतिगमन मॉडल में त्रुटियां असंबद्ध हैं, तो समान भिन्नताएं होती हैं और उम्मीद का मान शून्य है।<ref>{{Cite book|title=सर्वोत्तम रैखिक निष्पक्ष अनुमान और भविष्यवाणी|publisher=Theil Henri|year=1971|location=New York: John Wiley & Sons}}</ref>
== बिंदु अनुमान बनाम आत्मविश्वास अंतराल अनुमान ==
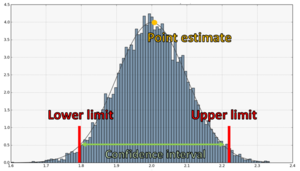
[[File:Point estimation and confidence interval estimation.png|thumb|बिंदु अनुमान और आत्मविश्वास अंतराल अनुमान।]]अनुमान के दो प्रमुख प्रकार हैं: बिंदु अनुमान और अंतराल अनुमान बिंदु अनुमान में हम पैरामीटर स्थान में एक अद्वितीय बिंदु चुनने का प्रयास करते हैं जिसे उचित रूप से पैरामीटर का सही मान माना जा सकता है। दूसरी ओर, पैरामीटर के अनूठे अनुमान के अतिरिक्त  हम सेट के एक वर्ग के निर्माण में रुचि रखते हैं जिसमें एक निर्दिष्ट संभावना के साथ सही (अज्ञात) पैरामीटर मान होता है। सांख्यिकीय अनुमान की कई समस्याओं में हम केवल पैरामीटर का अनुमान लगाने या पैरामीटर से संबंधित कुछ परिकल्पना का परीक्षण करने में रुचि नहीं रखते हैं, हम वास्तविक-मान वाले पैरामीटर के लिए निचली या ऊपरी सीमा या दोनों भी प्राप्त करना चाहते हैं। ऐसा करने के लिए, हमें एक विश्वास अंतराल बनाने की आवश्यकता है।


कॉन्फिडेंस इंटरवल बताता है कि अनुमान कितना विश्वसनीय है। हम देखे गए डेटा से अंतराल की ऊपरी और निचली आत्मविश्वास सीमा की गणना कर सकते हैं। मान लीजिए एक डेटासेट x<sub>1</sub>, . . . , x<sub>n</sub> दिया गया है, जिसे यादृच्छिक चर X<sub>1</sub>, . . . , X<sub>n</sub>. की प्राप्ति के रूप में तैयार किया गया है। मान लीजिए θ रुचि का पैरामीटर है, और γ 0 और 1 के बीच एक संख्या है। यदि नमूना आँकड़े मौजूद हैं  L<sub>n</sub> = g(X<sub>1</sub>, . . . , X<sub>n</sub>) और U<sub>n</sub> = h(X<sub>1</sub>, . . . , X<sub>n</sub>) जैसे कि P(L<sub>n</sub> < θ < U<sub>n</sub>) = γ के प्रत्येक मान के लिए, फिर (l<sub>n</sub>, u<sub>n</sub>), जहां l<sub>n</sub> = g(x<sub>1</sub>, . . . , x<sub>n</sub>) और  u<sub>n</sub> = h(x<sub>1</sub>, . . . , x<sub>n</sub>), है θ के लिए 100γ% विश्वास अंतराल कहा जाता है। संख्या γ को आत्मविश्वास स्तर कहा जाता है।<ref name=":0" /> समान्यता:, सामान्य रूप से वितरित नमूना माध्य के साथ, Ẋ, और मानक विचलन के लिए ज्ञात मान के साथ, σ, सच्चे μ के लिए 100(1-α)% विश्वास अंतराल Ẋ ± e लेकर बनता है, e = z<sub>1-α/2</sub>(σ/n<sup>1/2</sup>),के साथ  जहां z<sub>1-α/2</sub>  मानक सामान्य वक्र का 100(1-α/2)% संचयी मान है, और n उस कॉलम में डेटा मानों की संख्या है। उदाहरण के लिए, 95% आत्मविश्वास के लिए z1-α/2 1.96 के बराबर है।<ref>{{Cite book|title=Experimental Design – With Applications in Management, Engineering, and the Sciences|publisher=Paul D. Berger, Robert E. Maurer, Giovana B. Celli|year=2019|location=Springer}}</ref>


== बिंदु अनुमान बनाम आत्मविश्वास अंतराल अनुमान ==
यहां अवलोकनों के सेट से दो सीमाओं की गणना की जाती है, मान लीजिए l<sub>n</sub> और u<sub>n</sub> और यह कुछ सीमा तक विश्वास के साथ प्रमाणित किया जाता है (संभाव्य शब्दों में मापा जाता है) कि γ का वास्तविक मान (l<sub>n</sub> और u<sub>n</sub> के बीच है। इस प्रकार हमें एक अंतराल (l<sub>n</sub> और u<sub>n</sub> ) मिलता है जिसकी हमें उम्मीद है कि इसमें γ(θ) का वास्तविक मान सम्मिलित होगा। इसलिए इस प्रकार के अनुमान को आत्मविश्वास अंतराल अनुमान कहा जाता है।<ref name=":1" /> यह अनुमान मानों की एक श्रृंखला प्रदान करता है जो पैरामीटर से अपेक्षित है। यह सामान्यतः बिंदु अनुमानों की तुलना में अधिक जानकारी देता है और अनुमान लगाते समय इसे प्राथमिकता दी जाती है। एक तरह से हम कह सकते हैं कि बिंदु अनुमान अंतराल अनुमान के विपरीत है।
[[File:Point estimation and confidence interval estimation.png|thumb|बिंदु अनुमान और आत्मविश्वास अंतराल अनुमान।]]अनुमान के दो प्रमुख प्रकार हैं: बिंदु अनुमान और अंतराल अनुमान। बिंदु अनुमान में हम पैरामीटर स्थान में एक अद्वितीय बिंदु चुनने का प्रयास करते हैं जिसे उचित रूप से पैरामीटर का सही मान माना जा सकता है। दूसरी ओर, पैरामीटर के अनूठे अनुमान के बजाय, हम सेट के एक परिवार के निर्माण में रुचि रखते हैं जिसमें एक निर्दिष्ट संभावना के साथ सही (अज्ञात) पैरामीटर मान होता है। सांख्यिकीय अनुमान की कई समस्याओं में हम केवल पैरामीटर का अनुमान लगाने या पैरामीटर से संबंधित कुछ परिकल्पना का परीक्षण करने में रुचि नहीं रखते हैं, हम वास्तविक-मूल्य वाले पैरामीटर के लिए निचली या ऊपरी सीमा या दोनों भी प्राप्त करना चाहते हैं। ऐसा करने के लिए, हमें एक विश्वास अंतराल बनाने की आवश्यकता है।
 
कॉन्फिडेंस इंटरवल बताता है कि अनुमान कितना विश्वसनीय है। हम देखे गए डेटा से अंतराल की ऊपरी और निचली आत्मविश्वास सीमा की गणना कर सकते हैं। मान लीजिए एक डेटासेट x<sub>1</sub>, . . . , एक्स<sub>n</sub> दिया गया है, जिसे यादृच्छिक चर X की प्राप्ति के रूप में तैयार किया गया है<sub>1</sub>, . . . , एक्स<sub>n</sub>. मान लीजिए θ रुचि का पैरामीटर है, और γ 0 और 1 के बीच की एक संख्या है। यदि नमूना आँकड़े मौजूद हैं तो L<sub>n</sub> = जी(एक्स<sub>1</sub>, . . . , एक्स<sub>n</sub>) और आप<sub>n</sub> = एच(एक्स<sub>1</sub>, . . . , एक्स<sub>n</sub>) ऐसा कि P(L<sub>n</sub> < θ < यू<sub>n</sub>) = θ के प्रत्येक मान के लिए, फिर (l<sub>n</sub>, में<sub>n</sub>), जहां एल<sub>n</sub> = जी(एक्स<sub>1</sub>, . . . , एक्स<sub>n</sub>) और आप<sub>n</sub> = एच(एक्स<sub>1</sub>, . . . , एक्स<sub>n</sub>), को θ के लिए 100γ% विश्वास अंतराल कहा जाता है। संख्या γ को [[आत्मविश्वास स्तर]] कहा जाता है।<ref name=":0" />सामान्य तौर पर, सामान्य रूप से वितरित नमूना माध्य के साथ, Ẋ, और मानक विचलन के लिए ज्ञात मान के साथ, σ, सच्चे μ के लिए 100(1-α)% विश्वास अंतराल Ẋ ± e लेकर बनता है, e = के साथ जेड<sub>1-α/2</sub>(एस/एन<sup>1/2</sup>), जहां z<sub>1-α/2</sub> मानक सामान्य वक्र का 100(1-α/2)% संचयी मान है, और n उस कॉलम में डेटा मानों की संख्या है। उदाहरण के लिए, z<sub>1-α/2</sub> 95% आत्मविश्वास के लिए 1.96 के बराबर है।<ref>{{Cite book|title=Experimental Design – With Applications in Management, Engineering, and the Sciences|publisher=Paul D. Berger, Robert E. Maurer, Giovana B. Celli|year=2019|location=Springer}}</ref>
यहां दो सीमाओं की गणना अवलोकनों के सेट से की गई है, मान लीजिए l<sub>n</sub> और आप<sub>n</sub> और कुछ हद तक विश्वास के साथ यह दावा किया जाता है (संभाव्य शब्दों में मापा गया) कि γ का वास्तविक मान l के बीच है<sub>n</sub> और आप<sub>n</sub>. इस प्रकार हमें एक अंतराल (एल) मिलता है<sub>n</sub> और आप<sub>n</sub>) जिसकी हम अपेक्षा करते हैं उसमें γ(θ) का वास्तविक मान शामिल होगा। तो इस प्रकार के अनुमान को आत्मविश्वास अंतराल अनुमान कहा जाता है।<ref name=":1" />यह अनुमान मानों की एक श्रृंखला प्रदान करता है जो पैरामीटर से अपेक्षित है। यह आम तौर पर बिंदु अनुमानों की तुलना में अधिक जानकारी देता है और अनुमान लगाते समय इसे प्राथमिकता दी जाती है। एक तरह से हम कह सकते हैं कि बिंदु अनुमान अंतराल अनुमान के विपरीत है।


== यह भी देखें ==
== यह भी देखें ==

Revision as of 12:13, 14 July 2023


आंकड़ों में, बिंदु अनुमान में एकल मान की गणना करने के लिए नमूना डेटा का उपयोग सम्मिलित होता है (इसे बिंदु अनुमान के रूप में जाना जाता है क्योंकि यह कुछ पैरामीटर स्थान में एक बिंदु की पहचान करता है) जो किसी अज्ञात के "सर्वोत्तम अनुमान" या "सर्वोत्तम अनुमान" के रूप में कार्य करता है। जनसंख्या पैरामीटर (उदाहरण के लिए, जनसंख्या माध्य)। अधिक औपचारिक रूप से, यह एक बिंदु अनुमान प्राप्त करने के लिए डेटा पर एक बिंदु अनुमानक का अनुप्रयोग है।

बिंदु अनुमान की तुलना अंतराल अनुमान से की जा सकती है: ऐसे अंतराल अनुमान समान्यता: या तो विश्वास अंतराल होते हैं, बारंबार अनुमान के स्थिति में, या विश्वसनीय अंतराल, बायेसियन अनुमान के स्थिति में अधिक सामान्यतः एक बिंदु अनुमानक की तुलना एक निर्धारित अनुमानक से की जा सकती है। उदाहरण आत्मविश्वास सेट या विश्वसनीय सेट द्वारा दिए गए हैं। एक बिंदु अनुमानक की तुलना एक वितरण अनुमानक से भी की जा सकती है। उदाहरण आत्मविश्वास वितरण यादृच्छिक अनुमानक और बायेसियन पोस्टीरियर द्वारा दिए गए हैं।

बिंदु अनुमान के गुण

पक्षपात

"आकलनकर्ता के पूर्वाग्रह" को अनुमानक के अपेक्षित मान और अनुमानित जनसंख्या पैरामीटर के वास्तविक मान के बीच अंतर के रूप में परिभाषित किया गया है। इसे यह भी वर्णित किया जा सकता है कि किसी पैरामीटर का अपेक्षित मान मापा पैरामीटर के जितना समीप होगा परन्तु पूर्वाग्रह उतना ही कम होगा। जब अनुमानित संख्या और वास्तविक मान समान होता है, तो अनुमानक को निष्पक्ष माना जाता है। इसे निष्पक्ष अनुमानक कहा जाता है। यदि अनुमानक में न्यूनतम भिन्नता है तो वह सबसे अच्छा निष्पक्ष अनुमानक बन जाएगा। चूँकि छोटे विचरण वाला पक्षपाती अनुमानक बड़े विचरण वाले निष्पक्ष अनुमानक की तुलना में अधिक उपयोगी हो सकता है।[1] सबसे महत्वपूर्ण बात यह है कि हम ऐसे बिंदु अनुमानकों को प्राथमिकता देते हैं जिनमें सबसे छोटी माध्य वर्ग त्रुटि या माध्य वर्ग त्रुटियाँ हों।

यदि हम T = h(X1,X2,... , Xn) को एक यादृच्छिक नमूने X1,X2, . . . , Xn, के आधार पर एक अनुमानक मानते हैं। अनुमानक T को पैरामीटर θ के लिए एक निष्पक्ष अनुमानक कहा जाता है यदि E[T] = θ, θ के मान पर ध्यान दिए बिना।[1] उदाहरण के लिए, उसी यादृच्छिक नमूने से हमारे पास E( x̄ ) = µ(माध्य) और E(s2) = σ2 (विचरण) है, तो x̄ और s2 µ और σ2 के लिए निष्पक्ष अनुमानक होंगे। अंतर E[T ] - θ को T का पूर्वाग्रह कहा जाता है; यदि यह अंतर शून्येतर है, तो T को पक्षपाती कहा जाता है।

संगति

संगति इस बारे में है कि जब पैरामीटर अपना आकार बढ़ाता है तो बिंदु अनुमान मान के समीप रहता है या नहीं जो की नमूना आकार जितना बड़ा होगा, अनुमान उतना ही स्पष्ट होगा। यदि एक बिंदु अनुमानक सुसंगत है, तो इसका अपेक्षित मान और विचरण पैरामीटर के वास्तविक मान के समीप होना चाहिए। एक निष्पक्ष अनुमानक सुसंगत होता है यदि अनुमानक t के विचरण की सीमा शून्य के समान होती है।

दक्षता

चलो T1 और T2 एक ही पैरामीटर θ के लिए दो निष्पक्ष अनुमानक हों। अनुमानक T2 अनुमानक T1 की तुलना में अधिक कुशल कहा जाएगा यदि Var(T2) < Var(T1), θ के मान पर ध्यान दिए बिना।[1] हम यह भी कह सकते हैं कि सबसे कुशल अनुमानक वे हैं जिनके परिणामों में सबसे कम परिवर्तनशीलता है। इसलिए, यदि अनुमानक के पास नमूने से नमूने के बीच सबसे छोटा अंतर है, तो यह सबसे कुशल और निष्पक्ष दोनों है। हम अनुमानक T2 कहकर दक्षता की धारणा का विस्तार करते हैं अनुमानक T1 से अधिक कुशल है (रुचि के समान पैरामीटर के लिए), यदि T2 का एमएसई (मीन चुकता त्रुटि) T1 के एमएसई से छोटा है.[1]

समान्यता: हमें अनुमानकर्ताओं की दक्षता निर्धारित करते समय जनसंख्या के वितरण पर विचार करना चाहिए। उदाहरण के लिए एक सामान्य वितरण में, माध्य को माध्यिका की तुलना में अधिक कुशल माना जाता है, किंतु यह बात असममित, या विषम वितरण, वितरण में प्रयुक्त नहीं होती है।

पर्याप्तता

सांख्यिकी में, एक सांख्यिकीविद् का काम उन आंकड़ों की व्याख्या करना है जो उन्होंने एकत्र किए हैं और जांच के अनुसार जनसंख्या के बारे में सांख्यिकीय रूप से वैध निष्कर्ष निकालना है। किंतु कई स्थिति में कच्चा डेटा, जो बहुत अधिक है और संचयन के लिए बहुत मूल्यवान `है, इस उद्देश्य के लिए उपयुक्त नहीं है। इसलिए, सांख्यिकीविद् कुछ आँकड़ों की गणना करके डेटा को संक्षिप्त करना चाहेगा और अपने विश्लेषण को इन आँकड़ों पर आधारित करना चाहेगा जिससे ऐसा करने पर प्रासंगिक जानकारी का कोई हानि न हो, अर्थात सांख्यिकीविद् उन आँकड़ों को चुनना चाहेगा जिनके बारे में सारी जानकारी समाप्त हो जाती है पैरामीटर, जो नमूने में निहित है. हम पर्याप्त आँकड़ों को इस प्रकार परिभाषित करते हैं: मान लीजिए X =( X1, X2, ... ,Xn) एक यादृच्छिक नमूना है। एक आँकड़ा T(X) को θ (या वितरण के वर्ग के लिए) के लिए पर्याप्त माना जाता है यदि दिए गए T का सशर्त वितरण θ से मुक्त है।[2]

बिंदु अनुमान के प्रकार

बायेसियन बिंदु अनुमान

बायेसियन अनुमान समान्यता पश्च वितरण पर आधारित होता है। कई बायेसियन बिंदु अनुमानक केंद्रीय प्रवृत्ति के पश्च वितरण के आँकड़े हैं, उदाहरण के लिए, इसका माध्य माध्यिका या मोड:

  • पश्च माध्य, जो वर्ग-त्रुटि हानि फलन के लिए (पश्च) कठिन परिस्थिति (अपेक्षित हानि) को कम करता है; बायेसियन अनुमान में, कठिन परिस्थिति को पश्च वितरण के संदर्भ में परिभाषित किया गया है, जैसा कि गॉस ने देखा है ।[3]
  • पश्च माध्यिका, जो पूर्ण-मूल्य हानि फलन के लिए पश्च कठिन परिस्थिति को कम करती है, जैसा कि लाप्लास द्वारा देखा गया है।[3][4]
  • अधिकतम एक पोस्टीरियरी (एमएपी), जो अधिकतम पोस्टीरियर वितरण पाता है; एक समान पूर्व संभाव्यता के लिए, एमएपी अनुमानक अधिकतम-संभावना अनुमानक के साथ मेल खाता है;

एमएपी अनुमानक के पास कई कठिन समस्याओं के लिए भी अच्छे स्पर्शोन्मुख गुण हैं, जिन पर अधिकतम संभावना अनुमानक को कठिनाइयाँ होती हैं। नियमित समस्याओं के लिए, जहां अधिकतम-संभावना अनुमानक सुसंगत है, अधिकतम-संभावना अनुमानक अंततः एमएपी अनुमानक से सहमत होता है।[5][6][7] वाल्ड के प्रमेय के अनुसार बायेसियन अनुमानक स्वीकार्य हैं।[6][8]

न्यूनतम संदेश लंबाई (एमएमएल) बिंदु अनुमानक बायेसियन सूचना सिद्धांत पर आधारित है और यह सीधे रूप से पश्च वितरण से संबंधित नहीं है।

बेयस निस्पंदन के विशेष स्थिति महत्वपूर्ण हैं:

कम्प्यूटेशनल सांख्यिकी की कई पुनरावृत्तीय पद्धतियों का बायेसियन विश्लेषण के साथ घनिष्ठ संबंध है:

बिंदु अनुमान ज्ञात करने की विधियाँ

नीचे अज्ञात मापदंडों का अनुमान लगाने के कुछ सामान्य रूप से उपयोग किए जाने वाले विधि दिए गए हैं जिनसे अनुमानकर्ताओं को इनमें से कुछ महत्वपूर्ण गुण प्रदान करने की उम्मीद है। सामान्य रूप से स्थिति और हमारे अध्ययन के उद्देश्य के आधार पर हम बिंदु अनुमान के विधि में से किसी एक विधि को प्रयुक्त करते हैं जो उपयुक्त हो सकता है।

अधिकतम संभावना की विधि (एमएलई)

अधिकतम संभावना की विधि, आर.ए. के कारण फिशर, अनुमान लगाने की सबसे महत्वपूर्ण सामान्य विधि है। यह अनुमानक विधि अज्ञात मापदंडों को प्राप्त करने का प्रयास करती है जो संभावना फलन को अधिकतम करती है। यह एक ज्ञात मॉडल (उदा. सामान्य वितरण) का उपयोग करता है और मॉडल में पैरामीटर के मानों का उपयोग करता है जो डेटा के लिए सबसे उपयुक्त मिलान खोजने के लिए संभावना फलन को अधिकतम करता है।[9]

मान लीजिए X = (X1, X2, ... ,Xn) संयुक्त पीडीएफ या पी.एम.एफ. के साथ एक यादृच्छिक नमूने को दर्शाता है। f(x, θ) (θ एक सदिश हो सकता है)। फलन f(x, θ), जिसे θ का फलन माना जाता है, संभाव्यता फलन कहलाता है। इस स्थिति में, इसे L(θ) द्वारा दर्शाया जाता है। अधिकतम संभावना के सिद्धांत में θ की स्वीकार्य सीमा के अंदर एक अनुमान चुनना सम्मिलित है, जो संभावना को अधिकतम करता है। इस अनुमानक को θ का अधिकतम संभावना अनुमान (एमएलई) कहा जाता है। θ का MLE प्राप्त करने के लिए, हम समीकरण का उपयोग करते हैं

dlogL(θ)/dθi=0, i = 1, 2, …, k.. यदि θ एक सदिश है, तो संभावना समीकरण प्राप्त करने के लिए आंशिक व्युत्पन्न पर विचार किया जाता है।[2]


क्षणों की विधि (MOM)

क्षणों की विधि 1887 में के. पियर्सन और पी. चेबीशेव द्वारा प्रारंभ की गई थी, और यह अनुमान लगाने की सबसे पुरानी विधियों में से एक है। यह विधि बड़ी संख्या के नियम पर आधारित है, जो जनसंख्या के बारे में सभी ज्ञात तथ्यों का उपयोग करती है और उन तथ्यों को समीकरण प्राप्त करके जनसंख्या के नमूने पर प्रयुक्त करती है जो जनसंख्या क्षणों को अज्ञात मापदंडों से जोड़ते हैं। फिर हम जनसंख्या क्षणों के नमूना माध्य से हल कर सकते हैं।[10] चूँकि सरलता के कारण यह विधि सदैव स्पष्ट नहीं होती है और आसानी से पक्षपाती हो सकती है।

मान लीजिए(X1, X2,…Xn) पीडीएफ वाली जनसंख्या से एक यादृच्छिक नमूना है। (या p.m.f) f(x,θ), θ = (θ1, θ2, …, θk). इसका उद्देश्य पैरामीटर θ1, θ2, ..., θk का अनुमान लगाना है। इसके अतिरिक्त , शून्य के बारे में पहले k जनसंख्या क्षणों को θ के स्पष्ट कार्य के रूप में उपस्थित होने दें, अथार्त μr = μr(θ1, θ2,…, θk), r = 1, 2, …, k क्षणों की विधि में, हम k नमूना क्षणों को संबंधित जनसंख्या क्षणों के साथ समान करते हैं। समान्यता:, पहले k क्षण इसलिए लिए जाते हैं क्योंकि नमूने के कारण होने वाली त्रुटियाँ क्षण के क्रम के साथ बढ़ती हैं। इस प्रकार, हमें k समीकरण μr(θ1, θ2,…, θk) = mr, r = 1, 2, …, k.मिलता है। इन समीकरणों को हल करने पर हमें क्षण अनुमानक (या अनुमान) की विधि प्राप्त होती है

mr = 1/n ΣXir.[2]क्षणों की सामान्यीकृत विधि भी देखें।

न्यूनतम वर्ग की विधि

न्यूनतम वर्ग की विधि में, हम अपेक्षा के कुछ निर्दिष्ट रूप और अवलोकनों के दूसरे क्षण का उपयोग करके मापदंडों के अनुमान पर विचार करते हैं। के लिए

फॉर्म y = f( x, β0, β1, ,,,, βp) के एक वक्र को डेटा (xi, yi), i = 1, 2,…n, में फिट करते हुए, हम कम से कम वर्गों की विधि का उपयोग कर सकते हैं। इस विधि में न्यूनतम करना सम्मिलित है

वर्गों का योग।

जब f( x, β0, β1, ,,,, βp) पैरामीटरों का एक रैखिक कार्य है और x-मान ज्ञात हैं, न्यूनतम वर्ग अनुमानक सर्वोत्तम रैखिक निष्पक्ष अनुमानक (नीला) होगा। दोबारा, यदि हम मानते हैं कि न्यूनतम वर्ग अनुमान स्वतंत्र रूप से और समान रूप से सामान्य रूप से वितरित होते हैं, तो एक रैखिक अनुमानक निष्पक्ष अनुमानकों के पूरे वर्ग के लिए न्यूनतम-विचरण निष्पक्ष अनुमानक (एमवीयूई) होगा। न्यूनतम माध्य वर्ग त्रुटि (एमएमएसई) भी देखें।[2]

न्यूनतम-विचरण माध्य-निष्पक्ष अनुमानक (एमवीयूई)

न्यूनतम-विचरण निष्पक्ष अनुमानक की विधि वर्ग-त्रुटि हानि-फलन के कठिन परिस्थिति (अपेक्षित हानि) को कम करती है।

माध्यिका निष्पक्ष अनुमानक

माध्यिका-निष्पक्ष अनुमानक पूर्ण-त्रुटि हानि फलन के कठिन परिस्थिति को कम करता है।

सर्वोत्तम रैखिक निष्पक्ष अनुमानक (नीला)

सर्वश्रेष्ठ रैखिक निष्पक्ष अनुमानक, जिसे गॉस-मार्कोव प्रमेय के रूप में भी जाना जाता है, बताता है कि साधारण न्यूनतम वर्ग (ओएलएस) अनुमानक में रैखिक निष्पक्ष अनुमानकों के वर्ग के अंदर सबसे कम नमूनाकरण भिन्नता होती है, यदि रैखिक प्रतिगमन मॉडल में त्रुटियां असंबद्ध हैं, तो समान भिन्नताएं होती हैं और उम्मीद का मान शून्य है।[11]

बिंदु अनुमान बनाम आत्मविश्वास अंतराल अनुमान

बिंदु अनुमान और आत्मविश्वास अंतराल अनुमान।

अनुमान के दो प्रमुख प्रकार हैं: बिंदु अनुमान और अंतराल अनुमान बिंदु अनुमान में हम पैरामीटर स्थान में एक अद्वितीय बिंदु चुनने का प्रयास करते हैं जिसे उचित रूप से पैरामीटर का सही मान माना जा सकता है। दूसरी ओर, पैरामीटर के अनूठे अनुमान के अतिरिक्त हम सेट के एक वर्ग के निर्माण में रुचि रखते हैं जिसमें एक निर्दिष्ट संभावना के साथ सही (अज्ञात) पैरामीटर मान होता है। सांख्यिकीय अनुमान की कई समस्याओं में हम केवल पैरामीटर का अनुमान लगाने या पैरामीटर से संबंधित कुछ परिकल्पना का परीक्षण करने में रुचि नहीं रखते हैं, हम वास्तविक-मान वाले पैरामीटर के लिए निचली या ऊपरी सीमा या दोनों भी प्राप्त करना चाहते हैं। ऐसा करने के लिए, हमें एक विश्वास अंतराल बनाने की आवश्यकता है।

कॉन्फिडेंस इंटरवल बताता है कि अनुमान कितना विश्वसनीय है। हम देखे गए डेटा से अंतराल की ऊपरी और निचली आत्मविश्वास सीमा की गणना कर सकते हैं। मान लीजिए एक डेटासेट x1, . . . , xn दिया गया है, जिसे यादृच्छिक चर X1, . . . , Xn. की प्राप्ति के रूप में तैयार किया गया है। मान लीजिए θ रुचि का पैरामीटर है, और γ 0 और 1 के बीच एक संख्या है। यदि नमूना आँकड़े मौजूद हैं Ln = g(X1, . . . , Xn) और Un = h(X1, . . . , Xn) जैसे कि P(Ln < θ < Un) = γ के प्रत्येक मान के लिए, फिर (ln, un), जहां ln = g(x1, . . . , xn) और un = h(x1, . . . , xn), है θ के लिए 100γ% विश्वास अंतराल कहा जाता है। संख्या γ को आत्मविश्वास स्तर कहा जाता है।[1] समान्यता:, सामान्य रूप से वितरित नमूना माध्य के साथ, Ẋ, और मानक विचलन के लिए ज्ञात मान के साथ, σ, सच्चे μ के लिए 100(1-α)% विश्वास अंतराल Ẋ ± e लेकर बनता है, e = z1-α/2(σ/n1/2),के साथ जहां z1-α/2 मानक सामान्य वक्र का 100(1-α/2)% संचयी मान है, और n उस कॉलम में डेटा मानों की संख्या है। उदाहरण के लिए, 95% आत्मविश्वास के लिए z1-α/2 1.96 के बराबर है।[12]

यहां अवलोकनों के सेट से दो सीमाओं की गणना की जाती है, मान लीजिए ln और un और यह कुछ सीमा तक विश्वास के साथ प्रमाणित किया जाता है (संभाव्य शब्दों में मापा जाता है) कि γ का वास्तविक मान (ln और un के बीच है। इस प्रकार हमें एक अंतराल (ln और un ) मिलता है जिसकी हमें उम्मीद है कि इसमें γ(θ) का वास्तविक मान सम्मिलित होगा। इसलिए इस प्रकार के अनुमान को आत्मविश्वास अंतराल अनुमान कहा जाता है।[2] यह अनुमान मानों की एक श्रृंखला प्रदान करता है जो पैरामीटर से अपेक्षित है। यह सामान्यतः बिंदु अनुमानों की तुलना में अधिक जानकारी देता है और अनुमान लगाते समय इसे प्राथमिकता दी जाती है। एक तरह से हम कह सकते हैं कि बिंदु अनुमान अंतराल अनुमान के विपरीत है।

यह भी देखें

संदर्भ

  1. ↑ 1.0 1.1 1.2 1.3 1.4 संभाव्यता और सांख्यिकी का एक आधुनिक परिचय (in English). F.M. Dekking, C. Kraaikamp, H.P. Lopuhaa, L.E. Meester. 2005.
  2. ↑ 2.0 2.1 2.2 2.3 2.4 अनुमान और अनुमानात्मक सांख्यिकी (in English). Pradip Kumar Sahu, Santi Ranjan Pal, Ajit Kumar Das. 2015.
  3. ↑ 3.0 3.1 Dodge, Yadolah, ed. (1987). Statistical data analysis based on the L1-norm and related methods: Papers from the First International Conference held at Neuchâtel, August 31–September 4, 1987. North-Holland Publishing.
  4. ↑ Jaynes, E. T. (2007). Probability Theory: The logic of science (5. print. ed.). Cambridge University Press. p. 172. ISBN 978-0-521-59271-0.
  5. ↑ Ferguson, Thomas S. (1996). बड़े नमूना सिद्धांत में एक पाठ्यक्रम. Chapman & Hall. ISBN 0-412-04371-8.
  6. ↑ 6.0 6.1 Le Cam, Lucien (1986). सांख्यिकीय निर्णय सिद्धांत में स्पर्शोन्मुख विधियाँ. Springer-Verlag. ISBN 0-387-96307-3.
  7. ↑ Ferguson, Thomas S. (1982). "एक असंगत अधिकतम संभावना अनुमान". Journal of the American Statistical Association. 77 (380): 831–834. doi:10.1080/01621459.1982.10477894. JSTOR 2287314.
  8. ↑ Lehmann, E. L.; Casella, G. (1998). बिंदु अनुमान का सिद्धांत (2nd ed.). Springer. ISBN 0-387-98502-6.
  9. ↑ श्रेणीबद्ध डेटा विश्लेषण. John Wiley and Sons, New York: Agresti A. 1990.
  10. ↑ सांख्यिकी का संक्षिप्त विश्वकोश. Springer: Dodge, Y. 2008.
  11. ↑ सर्वोत्तम रैखिक निष्पक्ष अनुमान और भविष्यवाणी. New York: John Wiley & Sons: Theil Henri. 1971.
  12. ↑ Experimental Design – With Applications in Management, Engineering, and the Sciences. Springer: Paul D. Berger, Robert E. Maurer, Giovana B. Celli. 2019.


अग्रिम पठन

  • Bickel, Peter J. & Doksum, Kjell A. (2001). Mathematical Statistics: Basic and Selected Topics. Vol. I (Second (updated printing 2007) ed.). Pearson Prentice-Hall.
  • Liese, Friedrich & Miescke, Klaus-J. (2008). Statistical Decision Theory: Estimation, Testing, and Selection. Springer.
Retrieved from ‘https://www.vigyanwiki.in/index.php?title=बिंदु_अनुमान&oldid=224235’