बैचर विषम-सम मर्जसॉर्ट: Difference between revisions
(Created page with "{{Infobox Algorithm |class=Sorting algorithm |image=File:Batcher Odd-Even Mergesort for eight inputs.svg|Visualization of the odd–even mergesort network with eight inp...") |
No edit summary |
||
| Line 27: | Line 27: | ||
| doi =10.1145/1468075.1468121 | | doi =10.1145/1468075.1468121 | ||
| series =AFIPS '68 (Spring)}}</ref> | | series =AFIPS '68 (Spring)}}</ref> | ||
आकार O(n (लॉग एन) के नेटवर्क को सॉर्ट करने के लिए [[ क्यों बैच ]] द्वारा तैयार किया गया | आकार O(n (लॉग एन) के नेटवर्क को सॉर्ट करने के लिए [[ क्यों बैच ]] द्वारा तैयार किया गया सामान्य निर्माण है<sup>2</sup>) और गहराई O((लॉग एन)<sup>2</sup>), जहां n क्रमबद्ध किए जाने वाले आइटमों की संख्या है। यद्यपि यह स्पर्शोन्मुख रूप से इष्टतम नहीं है, [[डोनाल्ड नुथ]] ने 1998 में सॉर्टिंग नेटवर्क#ऑप्टिमल सॉर्टिंग नेटवर्क के संबंध में निष्कर्ष निकाला कि बैचर की विधि बहुत बेहतर है, जब तक कि एन पृथ्वी पर सभी कंप्यूटरों की कुल मेमोरी क्षमता से अधिक न हो जाए!<ref>[[Donald Knuth|D.E. Knuth]]. ''[[The Art of Computer Programming]]'', Volume 3: ''Sorting and Searching'', Second Edition. Addison-Wesley, 1998. {{ISBN|0-201-89685-0}}. Section 5.3.4: Networks for Sorting, pp. 219–247.</ref> | ||
इसे दूसरी [[जीपीयू रत्न]] बुक द्वारा लोकप्रिय बनाया गया है,<ref>{{Cite web|url=https://developer.nvidia.com/gpugems/GPUGems2/gpugems2_chapter46.html|title=Chapter 46. Improved GPU Sorting}}</ref> ग्राफ़िक्स-प्रोसेसिंग हार्डवेयर पर यथोचित कुशल सॉर्टिंग करने का | इसे दूसरी [[जीपीयू रत्न]] बुक द्वारा लोकप्रिय बनाया गया है,<ref>{{Cite web|url=https://developer.nvidia.com/gpugems/GPUGems2/gpugems2_chapter46.html|title=Chapter 46. Improved GPU Sorting}}</ref> ग्राफ़िक्स-प्रोसेसिंग हार्डवेयर पर यथोचित कुशल सॉर्टिंग करने का आसान तरीका। | ||
== स्यूडोकोड == | == स्यूडोकोड == | ||
तुलना और क्रमबद्ध किए जाने वाले तत्वों के सूचकांकों की गणना करने के लिए विभिन्न पुनरावर्ती और पुनरावृत्तीय योजनाएं संभव हैं। यह n तत्वों को क्रमबद्ध करने के लिए सूचकांक उत्पन्न करने की | तुलना और क्रमबद्ध किए जाने वाले तत्वों के सूचकांकों की गणना करने के लिए विभिन्न पुनरावर्ती और पुनरावृत्तीय योजनाएं संभव हैं। यह n तत्वों को क्रमबद्ध करने के लिए सूचकांक उत्पन्न करने की पुनरावृत्तीय तकनीक है: | ||
<syntaxhighlight lang="text"> | <syntaxhighlight lang="text"> | ||
# note: the input sequence is indexed from 0 to (n-1) | # note: the input sequence is indexed from 0 to (n-1) | ||
| Line 43: | Line 43: | ||
पार्टनर नोड इंडेक्स की गैर-पुनरावर्ती गणना भी संभव है।<ref>{{cite web|url=https://gist.github.com/Bekbolatov/c8e42f5fcaa36db38402|title=Sorting network from Batcher's Odd-Even merge: partner calculation|publisher=Renat Bekbolatov|accessdate=7 May 2015}}</ref> | पार्टनर नोड इंडेक्स की गैर-पुनरावर्ती गणना भी संभव है।<ref>{{cite web|url=https://gist.github.com/Bekbolatov/c8e42f5fcaa36db38402|title=Sorting network from Batcher's Odd-Even merge: partner calculation|publisher=Renat Bekbolatov|accessdate=7 May 2015}}</ref> | ||
== यह भी देखें == | |||
==यह भी देखें== | |||
* [[बिटोनिक सॉर्टर]] | * [[बिटोनिक सॉर्टर]] | ||
* [[जोड़ीवार छँटाई नेटवर्क]] | * [[जोड़ीवार छँटाई नेटवर्क]] | ||
Revision as of 18:05, 3 August 2023
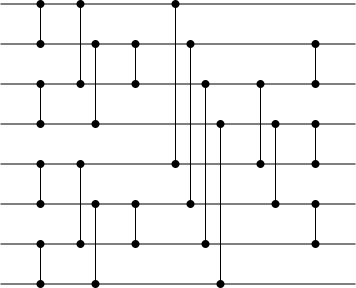 Visualization of the odd–even mergesort network with eight inputs | |
| Class | Sorting algorithm |
|---|---|
| Data structure | Array |
| Worst-case performance | parallel time |
| Best-case performance | parallel time |
| Average performance | parallel time |
| Worst-case space complexity | non-parallel time |
बैचर का सम-विषम मर्ज सॉर्ट[1] आकार O(n (लॉग एन) के नेटवर्क को सॉर्ट करने के लिए क्यों बैच द्वारा तैयार किया गया सामान्य निर्माण है2) और गहराई O((लॉग एन)2), जहां n क्रमबद्ध किए जाने वाले आइटमों की संख्या है। यद्यपि यह स्पर्शोन्मुख रूप से इष्टतम नहीं है, डोनाल्ड नुथ ने 1998 में सॉर्टिंग नेटवर्क#ऑप्टिमल सॉर्टिंग नेटवर्क के संबंध में निष्कर्ष निकाला कि बैचर की विधि बहुत बेहतर है, जब तक कि एन पृथ्वी पर सभी कंप्यूटरों की कुल मेमोरी क्षमता से अधिक न हो जाए![2] इसे दूसरी जीपीयू रत्न बुक द्वारा लोकप्रिय बनाया गया है,[3] ग्राफ़िक्स-प्रोसेसिंग हार्डवेयर पर यथोचित कुशल सॉर्टिंग करने का आसान तरीका।
स्यूडोकोड
तुलना और क्रमबद्ध किए जाने वाले तत्वों के सूचकांकों की गणना करने के लिए विभिन्न पुनरावर्ती और पुनरावृत्तीय योजनाएं संभव हैं। यह n तत्वों को क्रमबद्ध करने के लिए सूचकांक उत्पन्न करने की पुनरावृत्तीय तकनीक है:
# note: the input sequence is indexed from 0 to (n-1)
for p = 1, 2, 4, 8, ... # as long as p < n
for k = p, p/2, p/4, p/8, ... # as long as k >= 1
for j = mod(k,p) to (n-1-k) with a step size of 2k
for i = 0 to min(k-1, n-j-k-1) with a step size of 1
if floor((i+j) / (p*2)) == floor((i+j+k) / (p*2))
compare and sort elements (i+j) and (i+j+k)
पार्टनर नोड इंडेक्स की गैर-पुनरावर्ती गणना भी संभव है।[4]
यह भी देखें
संदर्भ
- ↑ Batcher, Ken (1968), Sorting Networks and their Applications, AFIPS '68 (Spring), Atlantic City, New Jersey: Association for Computing Machinery, pp. 307–314, doi:10.1145/1468075.1468121, archived from the original on 2020-10-24
- ↑ D.E. Knuth. The Art of Computer Programming, Volume 3: Sorting and Searching, Second Edition. Addison-Wesley, 1998. ISBN 0-201-89685-0. Section 5.3.4: Networks for Sorting, pp. 219–247.
- ↑ "Chapter 46. Improved GPU Sorting".
- ↑ "Sorting network from Batcher's Odd-Even merge: partner calculation". Renat Bekbolatov. Retrieved 7 May 2015.
बाहरी संबंध
- Odd–even mergesort at hs-flensburg.de
- Odd-even mergesort network generator Interactive Batcher's Odd-Even merge-based sorting network generator.