सिस्टोलिक ज्यामिति: Difference between revisions

Revision as of 20:22, 11 July 2023

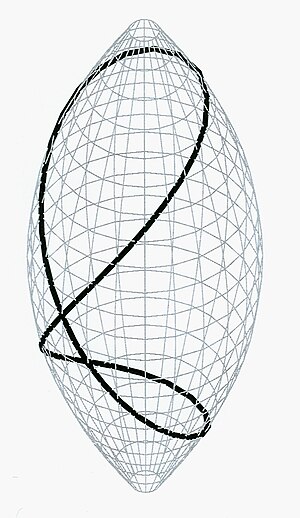
लेमन (ज्यामिति) पर एक जियोडेसिक हाइपरेलिप्टिक मामले में ग्रोमोव के भरने वाले क्षेत्र अनुमान के प्रमाण को दर्शाता है (नीचे सिस्टोलिक ज्यामिति#भरण क्षेत्र अनुमान देखें)।

गणित में, सिस्टोलिक ज्यामिति विविध कार्य और बहुकोणीय आकृति सांस्थितिक के सिस्टोलिक अपरिवर्तनीय का अध्ययन है, जैसा कि शुरू में चार्ल्स लोवेनर के माध्यम से कल्पना की गई थी और मिखाइल ग्रोमोव (गणितज्ञ), माइकल फ्रीडमैन, पीटर इतिहास , मिखाइल काट्ज़, लैरी गुथ और अन्य के माध्यम से इसके अंकगणितीय ऊर्जापंथी और सांस्थितिक अभिव्यक्तियों में विकसित की गई थी। सिस्टोलिक ज्यामिति का अक्रियाशील गति वाला परिचय भी देखें।

सिस्टोल की धारणा

टोरस पर सबसे छोटा चक्र

एक सघन सेट मापीय स्थान X का सिस्टोल, X का एक मापीय अपरिवर्तनीय है, जिसे (यानी एक चक्र जिसे व्यापक स्थान X में किसी बिंदु पर अनुबंधित नहीं किया जा सकता है)। अधिक तकनीकी भाषा में हम X के मौलिक समूह में अ-साधारण संयुग्मी वर्गों का प्रतिनिधित्व करने वाले मुक्त चक्रों पर लंबाई को कम करते हैं। जब एक्स एक लेखाचित्र है जिसे डब्ल्यू. टी. टुट्टे के माध्यम से परिधि पर 1947 के लेख के पश्चात् आमतौर पर अपरिवर्तनीय को परिधि के रूप में संदर्भित किया जाता है।^[1] संभवतः टुट्टे के लेख से प्रेरित होकर लोवेनर ने 1940 के दशक के अंत में सतहों पर सिस्टोलिक प्रश्नों के विषय में विचार करना प्रारंभ किया जिसके परिणामस्वरूप उनके छात्र पाओ मिंग पु के माध्यम से 1950 में अभिधारणा प्रस्तुत की गई। वास्तविक शब्द "सिस्टोल" एक चौथाई सदी पश्चात्त क मार्सेल बर्जर के माध्यम से निर्मित नहीं गया था।

अनुसंधान की इस नेतृत्व को स्पष्ट रूप से आर. अकोला और सी के पत्रों के प्रकाशन के तुरंत बाद 1961-62 शैक्षणिक वर्ष के दौरान स्ट्रासबर्ग विश्वविद्यालय के पुस्तकालय में बर्जर के साथ वार्तालाप में रेने थॉम की एक टिप्पणी से और अधिक प्रोत्साहन मिला। इन सिस्टोलिक असमानताओं से संबंधित थॉम ने कथित रूप से कहा कि यह परिणाम मौलिक महत्व के हैं

इसके पश्चात् बर्जर ने हाल ही में अमेरिकन मैथमैटिकल सोसाइटी के ज्ञापन के मार्च 2008 अंक में लेखों और पुस्तकों की एक श्रृंखला में इस विषय को लोकप्रिय बनाया (नीचे संदर्भ देखें)। सिस्टोलिक ज्यामिति और सांस्थिति के लिए वेबसाइट पर एक ग्रन्थसूची संदर्भिका में वर्तमान में 160 से अधिक लेख शामिल हैं। सिस्टोलिक ज्यामिति एक शीघ्रता से विकसित होने वाला क्षेत्र है, जिसमें प्रमुख पत्रिकाओं में अनेक आधुनिक प्रकाशन शामिल हैं। हाल ही में (नीचे काट्ज़ और रुड्यक का 2006 का प्रपत्र देखें) लस्टर्निक-श्निरेलमैन श्रेणी का संपर्क सामने आया है। ऐसे संपर्क के अस्तित्व को सिस्टोलिक सांस्थिति में एक प्रमेय के रूप में विचार करा जा सकता है।

3-स्थान में एक केंद्रीय सममित बहुफलक का गुण

'आर' में प्रत्येक उत्तल केंद्रीय सममित पॉलीहेड्रॉन पी³ विपरीत (एंटीपोडल) बिंदुओं की एक जोड़ी और उन्हें जोड़ने वाली लंबाई L का एक पथ स्वीकार करता है और P की सीमा ∂P पर स्थित है, जो संतोषजनक है

L^{2}\leq {\frac {\pi }{4}}\mathrm {area} (\partial P).

एक वैकल्पिक सूत्रीकरण इस प्रकार है. सतह क्षेत्र A के किसी भी केंद्रीय सममित उत्तल शरीर को लंबाई के फंदे के माध्यम से दबाया जा सकता है ${\sqrt {\pi A}}$ , एक गोले के माध्यम से प्राप्त सबसे चुस्त फिट के साथ। यह संपत्ति पु की असमानता (नीचे देखें) के एक विशेष मामले के बराबर है, जो शुरुआती सिस्टोलिक असमानताओं में से एक है।

अवधारणाएँ

क्षेत्र के स्वाद का प्रारंभिक अंदाज़ा देने के लिए, कोई निम्नलिखित टिप्पणियाँ कर सकता है। ऊपर उद्धृत बर्जर के प्रति थॉम की टिप्पणी का मुख्य जोर निम्नलिखित प्रतीत होता है। जब भी किसी को ज्यामितीय अपरिवर्तनीयता से संबंधित असमानता का सामना करना पड़ता है, तो ऐसी घटना अपने आप में दिलचस्प होती है; और भी अधिक जब असमानता तीव्र हो (अर्थात, इष्टतम)। शास्त्रीय आइसोपरिमेट्री इसका एक अच्छा उदाहरण है।

एक टोरस

सतहों के बारे में सिस्टोलिक प्रश्नों में, अभिन्न-ज्यामितीय पहचान विशेष रूप से महत्वपूर्ण भूमिका निभाती हैं। मोटे तौर पर कहें तो, एक तरफ एक अभिन्न पहचान संबंधित क्षेत्र है, और दूसरी तरफ चक्र के उपयुक्त परिवार की ऊर्जा का औसत है। कॉची-श्वार्ज़ असमानता के अनुसार, लंबाई वर्ग के लिए ऊर्जा एक ऊपरी सीमा है; इसलिए सिस्टोल के क्षेत्रफल और वर्ग के बीच एक असमानता प्राप्त होती है। ऐसा दृष्टिकोण लोवेनर की टोरस असमानता दोनों के लिए काम करता है

\mathrm {sys} ^{2}\leq {\frac {2}{\sqrt {3}}}\cdot \mathrm {area}

टोरस्र्स के लिए, जहां समानता का मामला फ्लैट टोरस के माध्यम से प्राप्त किया जाता है जिसका डेक परिवर्तन ईसेनस्टीन पूर्णांक की जाली बनाता हैs,

पी का प्रतिनिधित्व करने वाली रोमन सतह का एक एनीमेशन²(आर) आर में³

और पु की असमानता के लिए|वास्तविक प्रक्षेप्य तल पी के लिए पु की असमानता²(आर):

\mathrm {sys} ^{2}\leq {\frac {\pi }{2}}\cdot \mathrm {area}

,

समानता के साथ निरंतर गाऊसी वक्रता की एक मापीय की विशेषता।

विचरण के लिए कम्प्यूटेशनल सूत्र का अनुप्रयोग वास्तव में आइसोसिस्टोलिक दोष के साथ लोवेनर की टोरस असमानता का निम्नलिखित संस्करण उत्पन्न करता है:

\mathrm {area} -{\frac {\sqrt {3}}{2}}\mathrm {sys} ^{2}\geq \mathrm {var} (f),

जहां f अपने अनुरूप वर्ग में एक इकाई क्षेत्र फ्लैट मापीय के संबंध में मापीय का अनुरूप कारक है। इस असमानता को आइसोपेरिमेट्रिक दोष के साथ बोन्सन की असमानता के अनुरूप माना जा सकता है, जो आइसोपेरिमेट्रिक असमानता को मजबूत करता है।

इस प्रकार की अनेक नई असमानताएँ हाल ही में खोजी गई हैं, जिनमें सार्वभौमिक आयतन निचली सीमाएँ भी शामिल हैं। सतहों के सिस्टोल पर अधिक विवरण दिखाई देते हैं।

ग्रोमोव की सिस्टोलिक असमानता

क्षेत्र में सबसे गहरा परिणाम आवश्यक मैनिफोल्ड के लिए ग्रोमोव की सिस्टोलिक असमानता है|एक आवश्यक मैनिफोल्ड के होमोटॉपी 1-सिस्टोल के लिए ग्रोमोव की असमानता|आवश्यक एन-मैनिफोल्ड एम:

\operatorname {sys\pi } _{1}{}^{n}\leq C_{n}\operatorname {vol} (M),

जहां सी_nकेवल एम के आयाम के आधार पर एक सार्वभौमिक स्थिरांक है। यहां होमोटॉपी सिस्टोल sysπ है₁ परिभाषा के अनुसार एम में एक गैर-संविदात्मक चक्र की न्यूनतम लंबाई है। एक मैनिफोल्ड को आवश्यक कहा जाता है यदि इसका मौलिक वर्ग [एम] अपने मौलिक समूह के समरूपता (गणित) में एक गैर-तुच्छ वर्ग का प्रतिनिधित्व करता है। प्रमाण में एक नया अपरिवर्तनीय शामिल है जिसे फिलिंग त्रिज्या कहा जाता है, जिसे ग्रोमोव के माध्यम से पेश किया गया है, जिसे निम्नानुसार परिभाषित किया गया है।

गुणांक वलय 'Z' या 'Z' को A से निरूपित करें₂, यह इस बात पर निर्भर करता है कि एम उन्मुख है या नहीं। फिर एक सघन एन-डायमेंशनल मैनिफोल्ड एम का मूल वर्ग, जिसे [एम] कहा जाता है, एक जनरेटर है $H_{n}(M;A)=A$ . यूक्लिडियन स्पेस ई में एम के समावेश को देखते हुए, हम सेट करते हैं

\mathrm {FillRad} (M\subset E)=\inf \left\{\epsilon >0\left|\;\iota _{\epsilon }([M])=0\in H_{n}(U_{\epsilon }M)\right.\right\},

कहाँ ι_ε इसके ε-पड़ोस यू में एम को शामिल करने से प्रेरित समावेश समरूपता है_ε मेरा।

ऐसी स्थिति में पूर्ण भरने वाले त्रिज्या को परिभाषित करने के लिए जहां एम रीमैनियन मापीय जी से सुसज्जित है, ग्रोमोव निम्नानुसार आगे बढ़ता है। सी. कुराटोस्की के कारण एक व्यक्ति घुसपैठ का फायदा उठाता है। एक ने एम को बानाच स्पेस एल में समाहित कर लिया है^∞(M) M पर बाउंडेड बोरेल फ़ंक्शन करता है, जो सुपर मानदंड से सुसज्जित है $\|\;\|$ . अर्थात्, हम एक बिंदु x ∈ M को फ़ंक्शन f पर मैप करते हैं_x∈ एल^∞(M) सूत्र f के माध्यम से परिभाषित_x(y) = d(x,y) सभी y ∈ M के लिए, जहां d मापीय के माध्यम से परिभाषित दूरी फ़ंक्शन है। हमारे पास त्रिभुज असमानता है $d(x,y)=\|f_{x}-f_{y}\|,$ और इसलिए एम्बेडिंग दृढ़ता से आइसोमेट्रिक है, सटीक अर्थ में कि आंतरिक दूरी और परिवेश दूरी मेल खाती है। यदि व्यापकय स्थान एक हिल्बर्ट स्थान है, तब भी जब एम रीमैनियन सर्कल है (विपरीत बिंदुओं के बीच की दूरी π होनी चाहिए, 2 नहीं!) तो इतनी दृढ़ता से आइसोमेट्रिक इंबेडिंग असंभव है। फिर हमने E = L सेट किया^∞(M) उपरोक्त सूत्र में, और परिभाषित करें

\mathrm {FillRad} (M)=\mathrm {FillRad} \left(M\subset L^{\infty }(M)\right).

अर्थात्, ग्रोमोव ने सिस्टोल और भरने की त्रिज्या से संबंधित एक तीव्र असमानता साबित की,

\mathrm {sys\pi } _{1}\leq 6\;\mathrm {FillRad} (M),

सभी आवश्यक विविध कार्य के लिए मान्य एम; साथ ही एक असमानता भी

\mathrm {FillRad} \leq C_{n}\mathrm {vol} _{n}{}^{1/n}(M),

सभी बंद विविध कार्य के लिए मान्य एम.

एस. वेंगर के माध्यम से ज्यामितीय माप सिद्धांत में हाल के परिणामों के आधार पर, एल. एम्ब्रोसियो और बी. किर्चहैम के पहले के काम पर आधारित एक प्रमाण का सारांश, नीचे संदर्भित सिस्टोलिक ज्यामिति और सांस्थिति पुस्तक की धारा 12.2 में दिखाई देता है। ग्रोमोव की असमानता के प्रमाण के लिए एक पूरी तरह से अलग दृष्टिकोण हाल ही में लैरी गुथ के माध्यम से प्रस्तावित किया गया था।^[2]

ग्रोमोव की स्थिर असमानता

1-सिस्टोलिक अपरिवर्तनीय (चक्र की लंबाई के संदर्भ में परिभाषित) और उच्चतर, के-सिस्टोलिक अपरिवर्तनीय (चक्रों के क्षेत्रों आदि के संदर्भ में परिभाषित) के बीच एक महत्वपूर्ण अंतर को ध्यान में रखा जाना चाहिए। जबकि 1-सिस्टोल को शामिल करते हुए अनेक इष्टतम सिस्टोलिक असमानताएं अब तक प्राप्त की जा चुकी हैं, विशुद्ध रूप से उच्च के-सिस्टोल को शामिल करने वाली एकमात्र इष्टतम असमानता जटिल प्रक्षेप्य स्थान के लिए ग्रोमोव की असमानता है | ग्रोमोव की इष्टतम स्थिर 2-सिस्टोलिक असमानता

\mathrm {stsys} _{2}{}^{n}\leq n!\;\mathrm {vol} _{2n}(\mathbb {CP} ^{n})

जटिल प्रक्षेप्य स्थान के लिए, जहां सममित फ़ुबिनी-स्टडी मापीय के माध्यम से इष्टतम सीमा प्राप्त की जाती है, जो क्वांटम यांत्रिकी के लिंक की ओर इशारा करती है। यहां रीमैनियन मैनिफोल्ड एम के स्थिर 2-सिस्टोल को सेटिंग के माध्यम से परिभाषित किया गया है

\mathrm {stsys} _{2}=\lambda _{1}\left(H_{2}(M,\mathbb {Z} )_{\mathbb {R} },\|\;\|\right),

कहाँ $\|\;\|$ स्थिर मानदंड है, जबकि λ₁ जाली के शून्येतर तत्व का न्यूनतम मान है। ग्रोमोव की स्थिर असमानता कितनी असाधारण है, यह हाल ही में स्पष्ट हुआ। अर्थात्, यह पता चला कि, अपेक्षा के विपरीत, जटिल मामले में 2-सिस्टोल के विपरीत, चतुर्धातुक प्रक्षेप्य तल पर सममित मापीय इसकी सिस्टोलिक रूप से इष्टतम मापीय नहीं है। जबकि इसके सममित मापीय के साथ चतुर्धातुक प्रक्षेप्य तल का मध्य-आयामी स्थिर सिस्टोलिक अनुपात 10/3 है, जटिल प्रक्षेप्य 4-स्पेस के सममित मापीय के लिए अनुरूप अनुपात 6 मान देता है, जबकि इस तरह के लिए सबसे अच्छा उपलब्ध ऊपरी सीमा है इन दोनों स्थानों पर एक मनमाना मापीय का अनुपात 14 है। यह ऊपरी सीमा ली बीजगणित E7 (गणित) के गुणों से संबंधित है। यदि असाधारण स्पिन (7) होलोनॉमी और 4-वें बेट्टी नंबर 1 के साथ 8-मैनिफोल्ड मौजूद है, तो मूल्य 14 वास्तव में इष्टतम है। स्पिन(7)-मैनिफोल्ड|स्पिन(7) होलोनॉमी वाले विविध कार्य का डोमिनिक जॉयस के माध्यम से गहन अध्ययन किया गया है।

2-सिस्टोल के लिए निचली सीमा

इसी तरह, के = 2 के साथ के-सिस्टोल के लिए एकमात्र गैर-तुच्छ निचली सीमा के बारे में, गेज सिद्धांत और स्यूडोहोलोमोर्फिक वक्र | जे-होलोमोर्फिक वक्र में हाल के काम का परिणाम है। जेक सोलोमन के माध्यम से 4-विविध कार्य के अनुरूप 2-सिस्टोल के लिए निचली सीमा के अध्ययन से अवधि मानचित्र की छवि के घनत्व का एक सरलीकृत प्रमाण प्राप्त हुआ है।

शॉट्की समस्या

शायद सिस्टोल के सबसे उल्लेखनीय अनुप्रयोगों में से एक शोट्की समस्या के संदर्भ में है, पी. बसर और पीटर सरनाक|पी के माध्यम से । सरनाक, जिन्होंने मुख्य रूप से ध्रुवीकृत एबेलियन किस्मों के बीच रीमैन सतहों की जैकोबियन किस्मों को प्रतिष्ठित किया, सिस्टोलिक अंकगणित की नींव रखी।

लस्टर्निक-श्निरेलमैन श्रेणी

सिस्टोलिक प्रश्न पूछना अक्सर संबंधित क्षेत्रों में प्रश्नों को प्रेरित करता है। इस प्रकार, मैनिफोल्ड की सिस्टोलिक श्रेणी की धारणा को परिभाषित और जांच की गई है, जो लस्टर्निक-श्निरेलमैन श्रेणी (एलएस श्रेणी) से संबंध प्रदर्शित करती है। ध्यान दें कि सिस्टोलिक श्रेणी (साथ ही एलएस श्रेणी), परिभाषा के अनुसार, एक पूर्णांक है। दोनों श्रेणियों को सतहों और 3-विविध कार्य दोनों के लिए मेल खाते हुए दिखाया गया है। इसके अलावा, ओरिएंटेबल 4-विविध कार्य के लिए, सिस्टोलिक श्रेणी एलएस श्रेणी के लिए निचली सीमा है। एक बार कनेक्शन स्थापित हो जाने पर, प्रभाव परस्पर होता है: एलएस श्रेणी के बारे में ज्ञात परिणाम सिस्टोलिक प्रश्नों को उत्तेजित करते हैं, और इसके विपरीत।

नया अपरिवर्तनीय काट्ज़ और रुड्यक के माध्यम से पेश किया गया था (नीचे देखें)। चूंकि अपरिवर्तनीय लस्टर्निक-श्निरेलमैन श्रेणी (एलएस श्रेणी) से निकटता से संबंधित है, इसलिए इसे सिस्टोलिक श्रेणी कहा जाता था।

मैनिफोल्ड एम की सिस्टोलिक श्रेणी को एम के विभिन्न के-सिस्टोल के संदर्भ में परिभाषित किया गया है। मोटे तौर पर, विचार इस प्रकार है। मैनिफोल्ड एम को देखते हुए, कोई सिस्टोल के सबसे लंबे उत्पाद की तलाश करता है जो एम की कुल मात्रा के लिए वक्रता-मुक्त निचली सीमा देता है (मापीय के निरंतर स्वतंत्र के साथ)। परिभाषा में एम के कवर के सिस्टोलिक अपरिवर्तनीय को भी शामिल करना स्वाभाविक है। इतने लंबे उत्पाद में कारकों की संख्या परिभाषा के अनुसार एम की सिस्टोलिक श्रेणी है।

उदाहरण के लिए, मिखाइल ग्रोमोव (गणितज्ञ) ने दिखाया कि एक आवश्यक एन-मैनिफोल्ड होमोटॉपी 1-सिस्टोल की एन'वीं शक्ति के संदर्भ में कम मात्रा में सीमित मात्रा को स्वीकार करता है (ऊपर अनुभाग देखें)। इससे यह निष्कर्ष निकलता है कि आवश्यक एन-मैनिफोल्ड की सिस्टोलिक श्रेणी बिल्कुल एन है। वास्तव में, बंद एन-विविध कार्य के लिए, एलएस श्रेणी और सिस्टोलिक श्रेणी दोनों का अधिकतम मूल्य एक साथ प्राप्त होता है।

दोनों श्रेणियों के बीच एक दिलचस्प संबंध के अस्तित्व का एक और संकेत अपरिवर्तनीय से संबंध है जिसे कपलेंथ कहा जाता है। इस प्रकार, वास्तविक कप लंबाई दोनों श्रेणियों के लिए निचली सीमा बन जाती है।

अनेक मामलों में सिस्टोलिक श्रेणी एलएस श्रेणी से मेल खाती है, जिसमें आयाम 2 और 3 के मैनिफोल्ड का मामला भी शामिल है। आयाम 4 में, हाल ही में यह दिखाया गया था कि सिस्टोलिक श्रेणी एलएस श्रेणी के लिए निचली सीमा है।

सिस्टोलिक हाइपरबोलिक ज्यामिति

हाइपरबोलिक सतहों के सिस्टोल के बड़े जीनस जी के लिए स्पर्शोन्मुख व्यवहार के अध्ययन से कुछ दिलचस्प स्थिरांक का पता चलता है। इस प्रकार, हर्विट्ज़ सतह Σ है_g (2,3,7) त्रिभुज समूह के प्रमुख सर्वांगसम उपसमूहों के एक टावर के माध्यम से परिभाषित|(2,3,7) अतिशयोक्तिपूर्ण त्रिभुज समूह सीमा को संतुष्ट करता है

\mathrm {sys} \pi _{1}(\Sigma _{g})\geq {\frac {4}{3}}\log g,

और एक समान सीमा अधिक सामान्य अंकगणितीय फ़ुचियन समूहों के लिए है। यह 2007 का परिणाम काट्ज़, शाप्स और विश्ने के माध्यम से दिया गया है^[3] क्यू पर परिभाषित अंकगणितीय समूहों के मामले में जुर्ग पीटर बसर और पीटर सरनाक के परिणामों को उनके मौलिक 1994 पेपर से सामान्यीकृत किया गया है।^[4] अतिशयोक्तिपूर्ण ज्यामिति में सिस्टोल के लिए एक ग्रंथ सूची में वर्तमान में चालीस लेख हैं। दिलचस्प उदाहरण बोल्ज़ा सतह, क्लेन चतुर्थक, मैकबीथ सतह, पहला हर्विट्ज़ ट्रिपलेट के माध्यम से प्रदान किए गए हैं।

हाबिल-जैकोबी मानचित्रों से संबंध

बुरगो और इवानोव की तकनीकों के अनुप्रयोग के रूप में इष्टतम सिस्टोलिक असमानताओं का एक परिवार प्राप्त किया जाता है, जो उपयुक्त एबेल-जैकोबी मानचित्रों का उपयोग करता है, जिसे निम्नानुसार परिभाषित किया गया है।

मान लीजिए M एक मैनिफोल्ड है, π = π₁(एम), इसका मौलिक समूह और एफ: π → π^abइसके आबेलियनाइजेशन मानचित्र बनें। मान लीजिए कि tor π का मरोड़ उपसमूह है^ab. Let g: π^ab → π^ab/tor मरोड़ के माध्यम से भागफल हो। स्पष्टतः, π^{अब</सुप>/तोर= 'ज़'^बी, जहां बी = बी₁ (एम)। मान लीजिए φ: π → 'Z'^बीरचित समरूपता हो।}

<ब्लॉककोट>'परिभाषा:' आवरण ${\bar {M}}$ उपसमूह Ker(φ) ⊂ π के संगत मैनिफोल्ड M को सार्वभौमिक (या अधिकतम) मुक्त एबेलियन आवरण कहा जाता है।

अब मान लें कि एम के पास रीमैनियन मापीय है। मान लीजिए कि E, M पर हार्मोनिक 1-रूपों का स्थान है, जिसमें दोहरे E* को H के साथ प्रामाणिक रूप से पहचाना जाता है₁(श्री')। बेसपॉइंट x से पथों के साथ एक इंटीग्रल हार्मोनिक 1-फॉर्म को एकीकृत करके₀ ∈ एम, हमें वृत्त 'आर'/'जेड' = 'एस' का एक नक्शा मिलता है¹.

इसी प्रकार, मानचित्र को परिभाषित करने के लिए M → H₁(एम,'आर')/एच₁(एम,'जेड')_R सहसंगति के लिए कोई आधार चुने बिना, हम इस प्रकार तर्क देते हैं। माना x सार्वभौमिक आवरण में एक बिंदु है ${\tilde {M}}$ एम का। इस प्रकार X को X से पथ सी के साथ एम के एक बिंदु के माध्यम से दर्शाया गया है₀ इसे. पथ c के साथ एकीकृत करके, हम एक रैखिक रूप प्राप्त करते हैं, $h\to \int _{c}h$ , एक बार। इस प्रकार हमें एक मानचित्र प्राप्त होता है ${\tilde {M}}\to E^{*}=H_{1}(M,\mathbf {R} )$ , जो, इसके अलावा, एक मानचित्र पर उतरता है

{\overline {A}}_{M}:{\overline {M}}\to E^{*},\;\;c\mapsto \left(h\mapsto \int _{c}h\right),

कहाँ ${\overline {M}}$ यूनिवर्सल फ्री एबेलियन कवर है।

<ब्लॉककोट>परिभाषा: एम की जैकोबी किस्म (जैकोबी टोरस) टोरस जे है₁(एम)= एच₁(एम,'आर')/एच₁(एम,'जेड')_R</ब्लॉककोट>

<ब्लॉककोट>परिभाषा: हाबिल-जैकोबी मानचित्र $A_{M}:M\to J_{1}(M),$ उपरोक्त मानचित्र से भागफल को पास करके प्राप्त किया जाता है। एबेल-जैकोबी मानचित्र जैकोबी टोरस के अनुवादों तक अद्वितीय है।

उदाहरण के तौर पर डी. बुरागो, एस. इवानोव और मिखाइल ग्रोमोव (गणितज्ञ)|एम के कारण निम्नलिखित असमानता का हवाला दिया जा सकता है। ग्रोमोव।

मान लीजिए कि M पहले बेट्टी नंबर n के साथ एक n-आयामी रीमैनियन मैनिफोल्ड है, जैसे कि M से इसके जैकोबी टोरस तक के मानचित्र में नॉनज़रो डिग्री (निरंतर मानचित्र) है। तब एम इष्टतम स्थिर सिस्टोलिक असमानता को संतुष्ट करता है

\mathrm {stsys} _{1}{}^{n}\leq \gamma _{n}\mathrm {vol} _{n}(M),

कहाँ $\gamma _{n}$ शास्त्रीय हर्मिट स्थिरांक है।

भरण क्षेत्र अनुमान

ग्रोमोव के भरण क्षेत्र अनुमान को हाइपरलिप्टिक सेटिंग में सिद्ध किया गया है (नीचे बैंगर्ट एट अल के माध्यम से संदर्भ देखें)।

भराव क्षेत्र अनुमान का दावा है कि दृढ़ता से आइसोमेट्रिक संपत्ति के साथ एक सतह के माध्यम से लंबाई 2π के रीमैनियन सर्कल के सभी संभावित भरावों में से, गोल गोलार्ध में सबसे कम क्षेत्र होता है। यहां रीमैनियन सर्कल कुल 1-वॉल्यूम 2π और रीमैनियन व्यास π के अद्वितीय बंद 1-आयामी रीमैनियन मैनिफोल्ड को संदर्भित करता है।

अनुमान को समझाने के लिए, हम इस अवलोकन से शुरू करते हैं कि इकाई 2-गोले का भूमध्यरेखीय वृत्त, एस²⊂ आर³, एक रीमैनियन सर्कल एस है¹लंबाई 2π और व्यास π का।

अधिक सटीक रूप से, एस का रीमैनियन दूरी फ़ंक्शन¹गोले पर व्यापक रीमैनियन दूरी का प्रतिबंध है। यह संपत्ति यूक्लिडियन विमान में यूनिट सर्कल के मानक एम्बेडिंग से संतुष्ट नहीं है, जहां विपरीत बिंदुओं की एक जोड़ी दूरी 2 पर है, π नहीं।

हम 'एस' की सभी फिलिंग्स पर विचार करते हैं¹एक सतह के माध्यम से , जैसे कि सतह की सीमा के रूप में वृत्त को शामिल करने से परिभाषित प्रतिबंधित मापीय 2π लंबाई के एक वृत्त का रीमैनियन मापीय है। वृत्त को सीमा के रूप में शामिल करने को वृत्त का दृढ़तापूर्वक सममितीय अंतर्विरोध कहा जाता है।

1983 में ग्रोमोव ने अनुमान लगाया कि गोल गोलार्ध सभी भरने वाली सतहों के बीच वृत्त को भरने का सबसे अच्छा तरीका देता है।

सरलता से जुड़ी फिलिंग का मामला पु की असमानता के बराबर है। हाल ही में जीनस (गणित)-1 भरने के मामले को भी सकारात्मक रूप से निपटाया गया था (नीचे बैंगर्ट एट अल के माध्यम से संदर्भ देखें)। अर्थात्, यह पता चलता है कि कोई व्यक्ति अभिन्न ज्यामिति से जे. हर्श के आधी सदी पुराने सूत्र का उपयोग कर सकता है। अर्थात्, भूमध्य रेखा पर स्व-प्रतिच्छेदन बिंदु के साथ, फ़ुटबॉल पर चित्र-8 चक्र के परिवार पर विचार करें (लेख की शुरुआत में चित्र देखें)। हर्श का सूत्र फुटबॉल के अनुरूप वर्ग में एक मापीय के क्षेत्र को परिवार से आकृति -8 चक्र की ऊर्जा के औसत के रूप में व्यक्त करता है। रीमैन सतह के हाइपरलिप्टिक भागफल पर हर्श के सूत्र का अनुप्रयोग इस मामले में भरने वाले क्षेत्र अनुमान को साबित करता है।

जीनस 2 में हाइपरलिप्टिक वक्र के अन्य सिस्टोलिक प्रभावों की पहचान की गई है।

सर्वेक्षण

क्षेत्र के सर्वेक्षणों में एम. बर्जर का सर्वेक्षण (1993), ग्रोमोव का सर्वेक्षण (1996), ग्रोमोव की पुस्तक (1999), बर्जर की पैनोरमिक पुस्तक (2003), साथ ही काट्ज़ की पुस्तक (2007) शामिल हैं। ये संदर्भ किसी शुरुआती को इस क्षेत्र में प्रवेश करने में मदद कर सकते हैं। उनमें काम करने के लिए खुली समस्याएं भी होती हैं।

यह भी देखें

भरण क्षेत्र अनुमान
प्रथम हर्विट्ज़ त्रिक
परिधि (कार्यात्मक विश्लेषण)
जटिल प्रक्षेप्य स्थान के लिए ग्रोमोव की असमानता
ग्रोमोव की आवश्यक विविधताओं के लिए सिस्टोलिक असमानता
विभेदक ज्यामिति विषयों की सूची
लोवेनर की टोरस असमानता
पु की असमानता
सतहों का सिस्टोल
सिस्टोलिक स्वतंत्रता

↑ Tutte, William T. (1947). "घनाकार रेखांकन का एक परिवार". Proc. Cambridge Philos. Soc. 43 (4): 459–474. Bibcode:1947PCPS...43..459T. doi:10.1017/S0305004100023720. MR 0021678. S2CID 123505185.
↑ Guth, Larry (2011). "बड़े रीमैनियन मैनिफोल्ड्स में गेंदों की मात्रा". Annals of Mathematics. 173 (1): 51–76. arXiv:math/0610212. doi:10.4007/annals.2011.173.1.2. MR 2753599. S2CID 1392012.
↑ Katz, Mikhail G.; Schaps, Mary; Vishne, Uzi (2007). "Logarithmic growth of systole of arithmetic Riemann surfaces along congruence subgroups". Journal of Differential Geometry. 76 (3): 399–422. arXiv:math.DG/0505007. doi:10.4310/jdg/1180135693.
↑ Buser, P.; Sarnak, P. (1994). "On the period matrix of a Riemann surface of large genus (with an Appendix by J.H. Conway and N.J.A. Sloane)". Inventiones Mathematicae. 117 (1): 27–56. doi:10.1007/BF01232233. ISSN 0020-9910. S2CID 116904696.

संदर्भ

Bangert, V.; Croke, C.; Ivanov, S.; Katz, M. (2005). "Filling area conjecture and ovalless real hyperelliptic surfaces". Geometric and Functional Analysis. 15 (3): 577–597. arXiv:math/0405583. CiteSeerX 10.1.1.240.2242. doi:10.1007/s00039-005-0517-8. S2CID 17100812.
Berger, Marcel (1992–1993). "Systoles et applications selon Gromov" (PDF). Séminaire Bourbaki. 35: 279–310.
Berger, M. (2003). A panoramic view of Riemannian geometry. Springer. ISBN 978-3-642-18245-7.
Berger, M. (2008). "What is... a Systole?" (PDF). Notices of the AMS. 55 (3): 374–6.
Gromov, M. (1983). "Filling Riemannian manifolds". J. Diff. Geom. 18: 1–147. CiteSeerX 10.1.1.400.9154. doi:10.4310/jdg/1214509283.
Gromov, M. (1996). "Systoles and intersystolic inequalities". Actes de la Table Ronde de Géométrie Différentielle (Luminy, 1992). Sémin. Congr. Vol. 1. Soc. Math. France. pp. 291–362. CiteSeerX 10.1.1.539.1365.
Katz, M.; Semmes, S.; Gromov, M. (2007) [2001]. Metric Structures for Riemannian and Non-Riemannian Spaces. Progress in Mathematics. Vol. 152. Birkhäuser. ISBN 978-0-8176-4583-0.
Katz, M. (1983). "The filling radius of two-point homogeneous spaces". Journal of Differential Geometry. 18 (3): 505–511. doi:10.4310/jdg/1214437785.
Katz, M. (2007). Systolic geometry and topology. Mathematical Surveys and Monographs. Vol. 137. American Mathematical Society. ISBN 978-0-8218-4177-8.
Katz, M.; Rudyak, Y. (2006). "Systolic category and Lusternik–Schnirelman category of low-dimensional manifolds". Communications on Pure and Applied Mathematics. 59: 1433–56. arXiv:math/0410456. CiteSeerX 10.1.1.236.3757. doi:10.1002/cpa.20146. S2CID 15470409.
Katz, M.; Sabourau, S. (2005). "Entropy of systolically extremal surfaces and asymptotic bounds". Ergo. Th. Dynam. Sys. 25 (4): 1209–20. arXiv:math/0410312. CiteSeerX 10.1.1.236.5949. doi:10.1017/S0143385704001014. S2CID 11631690.
Pu, P.M. (1952). "Some inequalities in certain nonorientable Riemannian manifolds" (PDF). Pacific J. Math. 2: 55–71. doi:10.2140/pjm.1952.2.55.

बाहरी संबंध

Template:Systolic geometry navbox

[1] Tutte, William T. (1947). "घनाकार रेखांकन का एक परिवार". Proc. Cambridge Philos. Soc. 43 (4): 459–474. Bibcode:1947PCPS...43..459T. doi:10.1017/S0305004100023720. MR 0021678. S2CID 123505185.

[2] Guth, Larry (2011). "बड़े रीमैनियन मैनिफोल्ड्स में गेंदों की मात्रा". Annals of Mathematics. 173 (1): 51–76. arXiv:math/0610212. doi:10.4007/annals.2011.173.1.2. MR 2753599. S2CID 1392012.

[3] Katz, Mikhail G.; Schaps, Mary; Vishne, Uzi (2007). "Logarithmic growth of systole of arithmetic Riemann surfaces along congruence subgroups". Journal of Differential Geometry. 76 (3): 399–422. arXiv:math.DG/0505007. doi:10.4310/jdg/1180135693.

[4] Buser, P.; Sarnak, P. (1994). "On the period matrix of a Riemann surface of large genus (with an Appendix by J.H. Conway and N.J.A. Sloane)". Inventiones Mathematicae. 117 (1): 27–56. doi:10.1007/BF01232233. ISSN 0020-9910. S2CID 116904696.

[1]

[2]

[3]

[4]

@@ Line 1: / Line 1: @@
 {{Short description|Form of differential geometry}}
 {{For introduction}}
-[[Image:Football3c.jpg|right|thumb|लेमन (ज्यामिति) पर एक [[जियोडेसिक]] हाइपरेलिप्टिक मामले में ग्रोमोव के भरने वाले क्षेत्र अनुमान के प्रमाण को दर्शाता है (नीचे सिस्टोलिक ज्यामिति#[[भरण क्षेत्र अनुमान]] देखें)।]]गणित में, सिस्टोलिक ज्यामिति [[ कई गुना ]]्स और पॉलीहेड्रा#टोपोलॉजिकल पॉलीहेड्रा के सिस्टोलिक इनवेरिएंट (गणित) का अध्ययन है, जैसा कि शुरुआत में [[चार्ल्स लोवेनर]] द्वारा कल्पना की गई थी और मिखाइल ग्रोमोव (गणितज्ञ), [[माइकल फ्रीडमैन]], [[ पीटर इतिहास ]], [[मिखाइल काट्ज़]], [[लैरी गुथ]] और द्वारा विकसित की गई थी। अन्य, इसके अंकगणितीय, [[ ergodic ]] और टोपोलॉजिकल अभिव्यक्तियों में। सिस्टोलिक ज्यामिति का धीमी गति वाला परिचय भी देखें।
+[[Image:Football3c.jpg|right|thumb|लेमन (ज्यामिति) पर एक [[जियोडेसिक]] हाइपरेलिप्टिक मामले में ग्रोमोव के भरने वाले क्षेत्र अनुमान के प्रमाण को दर्शाता है (नीचे सिस्टोलिक ज्यामिति#[[भरण क्षेत्र अनुमान]] देखें)।]]गणित में, सिस्टोलिक ज्यामिति [[ कई गुना | विविध कार्य]] और बहुकोणीय आकृति  सांस्थितिक के सिस्टोलिक अपरिवर्तनीय  का अध्ययन है, जैसा कि शुरू में  [[चार्ल्स लोवेनर]]  के माध्यम से  कल्पना की गई थी और मिखाइल ग्रोमोव (गणितज्ञ),  [[माइकल फ्रीडमैन]], [[ पीटर इतिहास ]], [[मिखाइल काट्ज़]], [[लैरी गुथ]] और अन्य के माध्यम से  इसके अंकगणितीय [[ ergodic |ऊर्जापंथी]] और  सांस्थितिक अभिव्यक्तियों में विकसित की गई थी। सिस्टोलिक ज्यामिति का अक्रियाशील  गति वाला परिचय भी देखें।
 ==सिस्टोल की धारणा==
-[[Image:TorusSystoleLoop.png|right|thumb|200px|टोरस पर सबसे छोटा लूप]]एक [[कॉम्पैक्ट सेट]] [[ मीट्रिक स्थान ]] X का सिस्टोल, अधिक तकनीकी भाषा में, हम एक्स के [[मौलिक समूह]] में गैर-तुच्छ संयुग्मी वर्गों का प्रतिनिधित्व करने वाले मुक्त लूपों पर लंबाई को कम करते हैं। जब एक्स एक ग्राफ (अलग गणित) है, तो अपरिवर्तनीय को आमतौर पर 1947 के बाद से परिधि (ग्राफ सिद्धांत) के रूप में जाना जाता है। डब्ल्यू. टी. टुटे द्वारा परिधि पर लेख।<ref>{{cite journal | last=Tutte | first=William T. | title=घनाकार रेखांकन का एक परिवार| mr=0021678 | journal=[[Proc. Cambridge Philos. Soc.]] | volume=43 | issue=4 | year=1947 | pages=459–474 | doi=10.1017/S0305004100023720| bibcode=1947PCPS...43..459T | s2cid=123505185 }}</ref> संभवतः टुट्टे के लेख से प्रेरित होकर, लोवनर ने 1940 के दशक के अंत में सतहों पर सिस्टोलिक प्रश्नों के बारे में सोचना शुरू किया, जिसके परिणामस्वरूप उनके छात्र [[पीए या मिनट जीपीयू]] ने पु की असमानता को जन्म दिया। वास्तविक शब्द सिस्टोल एक चौथाई सदी बाद तक [[मार्सेल बर्जर]] द्वारा गढ़ा नहीं गया था।
+[[Image:TorusSystoleLoop.png|right|thumb|200px|टोरस पर सबसे छोटा चक्र ]]एक  [[कॉम्पैक्ट सेट|सघन  सेट]] [[ मीट्रिक स्थान |मापीय स्थान]] X का सिस्टोल, X का एक मापीय अपरिवर्तनीय है, जिसे (यानी एक चक्र जिसे व्यापक स्थान X में किसी बिंदु पर अनुबंधित नहीं किया जा सकता है)। अधिक तकनीकी भाषा में हम X के [[मौलिक समूह]] में अ-साधारण  संयुग्मी वर्गों का प्रतिनिधित्व करने वाले मुक्त चक्रों पर लंबाई को कम करते हैं।  जब एक्स एक लेखाचित्र है जिसे डब्ल्यू. टी. टुट्टे के माध्यम से  परिधि पर 1947 के लेख के पश्चात्  आमतौर पर अपरिवर्तनीय को परिधि के रूप में संदर्भित किया जाता है।<ref>{{cite journal | last=Tutte | first=William T. | title=घनाकार रेखांकन का एक परिवार| mr=0021678 | journal=[[Proc. Cambridge Philos. Soc.]] | volume=43 | issue=4 | year=1947 | pages=459–474 | doi=10.1017/S0305004100023720| bibcode=1947PCPS...43..459T | s2cid=123505185 }}</ref> संभवतः टुट्टे के लेख से प्रेरित होकर लोवेनर ने 1940 के दशक के अंत में सतहों पर सिस्टोलिक प्रश्नों के विषय में विचार करना  प्रारंभ किया जिसके परिणामस्वरूप उनके छात्र [[पीए या मिनट जीपीयू|पाओ मिंग पु]]  के माध्यम से 1950 में अभिधारणा  प्रस्तुत की गई। वास्तविक शब्द "सिस्टोल" एक चौथाई सदी पश्चात्त क  [[मार्सेल बर्जर]] के माध्यम से निर्मित नहीं गया था।
-अनुसंधान की इस दिशा को, जाहिरा तौर पर, आर. एकोला और सी के पत्रों के प्रकाशन के तुरंत बाद, 1961-62 शैक्षणिक वर्ष के दौरान स्ट्रासबर्ग विश्वविद्यालय के पुस्तकालय में बर्जर के साथ बातचीत में रेने थॉम की एक टिप्पणी से और प्रोत्साहन मिला। ब्लैटर. इन सिस्टोलिक असमानताओं का जिक्र करते हुए, थॉम ने कथित तौर पर कहा: माईस सी'एस्ट फंडामेंटल! [ये परिणाम मौलिक महत्व के हैं!]
+अनुसंधान की इस नेतृत्व को स्पष्ट रूप से आर. अकोला और सी के पत्रों के प्रकाशन के तुरंत बाद 1961-62 शैक्षणिक वर्ष के दौरान स्ट्रासबर्ग विश्वविद्यालय के पुस्तकालय में बर्जर के साथ  वार्तालाप में रेने थॉम की एक टिप्पणी से और अधिक प्रोत्साहन मिला। इन सिस्टोलिक असमानताओं  से संबंधित थॉम ने कथित रूप से  कहा  कि यह परिणाम मौलिक महत्व के हैं
-इसके बाद, बर्जर ने लेखों और पुस्तकों की एक श्रृंखला में इस विषय को लोकप्रिय बनाया, हाल ही में अमेरिकन मैथमैटिकल सोसाइटी के नोटिस के मार्च 2008 अंक में (नीचे संदर्भ देखें)। सिस्टोलिक ज्यामिति और टोपोलॉजी के लिए वेबसाइट पर एक ग्रंथ सूची में वर्तमान में 160 से अधिक लेख शामिल हैं। सिस्टोलिक ज्यामिति एक तेजी से विकसित होने वाला क्षेत्र है, जिसमें प्रमुख पत्रिकाओं में कई हालिया प्रकाशन शामिल हैं। हाल ही में (नीचे काट्ज़ और रुड्यक का 2006 का पेपर देखें), लस्टर्निक-श्निरेलमैन श्रेणी का लिंक सामने आया है। ऐसे लिंक के अस्तित्व को [[सिस्टोलिक श्रेणी]] में एक प्रमेय के रूप में माना जा सकता है।
+इसके पश्चात् बर्जर ने हाल ही में अमेरिकन मैथमैटिकल सोसाइटी के ज्ञापन के मार्च 2008 अंक में लेखों और पुस्तकों की एक श्रृंखला में इस विषय को लोकप्रिय बनाया (नीचे संदर्भ देखें)। सिस्टोलिक ज्यामिति और सांस्थिति के लिए वेबसाइट पर एक  ग्रन्थसूची संदर्भिका में वर्तमान में 160 से अधिक लेख शामिल हैं। सिस्टोलिक ज्यामिति एक शीघ्रता से विकसित होने वाला क्षेत्र है, जिसमें प्रमुख पत्रिकाओं में अनेक  आधुनिक  प्रकाशन शामिल हैं। हाल ही में (नीचे काट्ज़ और रुड्यक का 2006 का प्रपत्र देखें) लस्टर्निक-श्निरेलमैन श्रेणी का संपर्क सामने आया है। ऐसे संपर्क के अस्तित्व को [[सिस्टोलिक श्रेणी|सिस्टोलिक]] सांस्थिति में एक प्रमेय के रूप में विचार करा जा सकता है।
 ==3-स्थान में एक केंद्रीय सममित बहुफलक का गुण==
@@ Line 14: / Line 14: @@
 : <math>L^2 \leq \frac{\pi}{4} \mathrm{area}(\partial P).</math>
-एक वैकल्पिक सूत्रीकरण इस प्रकार है. सतह क्षेत्र A के किसी भी केंद्रीय सममित उत्तल शरीर को लंबाई के फंदे के माध्यम से दबाया जा सकता है <math>\sqrt{\pi A}</math>, एक गोले द्वारा प्राप्त सबसे चुस्त फिट के साथ। यह संपत्ति पु की असमानता (नीचे देखें) के एक विशेष मामले के बराबर है, जो शुरुआती सिस्टोलिक असमानताओं में से एक है।
+एक वैकल्पिक सूत्रीकरण इस प्रकार है. सतह क्षेत्र A के किसी भी केंद्रीय सममित उत्तल शरीर को लंबाई के फंदे के माध्यम से दबाया जा सकता है <math>\sqrt{\pi A}</math>, एक गोले के माध्यम से  प्राप्त सबसे चुस्त फिट के साथ। यह संपत्ति पु की असमानता (नीचे देखें) के एक विशेष मामले के बराबर है, जो शुरुआती सिस्टोलिक असमानताओं में से एक है।
 ==अवधारणाएँ==
 क्षेत्र के स्वाद का प्रारंभिक अंदाज़ा देने के लिए, कोई निम्नलिखित टिप्पणियाँ कर सकता है। ऊपर उद्धृत बर्जर के प्रति थॉम की टिप्पणी का मुख्य जोर निम्नलिखित प्रतीत होता है। जब भी किसी को ज्यामितीय अपरिवर्तनीयता से संबंधित असमानता का सामना करना पड़ता है, तो ऐसी घटना अपने आप में दिलचस्प होती है; और भी अधिक जब असमानता तीव्र हो (अर्थात, इष्टतम)। शास्त्रीय [[आइसोपरिमेट्री]] इसका एक अच्छा उदाहरण है।
-[[Image:Torus.png|right|thumb|250px|एक टोरस]]सतहों के बारे में सिस्टोलिक प्रश्नों में, अभिन्न-ज्यामितीय पहचान विशेष रूप से महत्वपूर्ण भूमिका निभाती हैं। मोटे तौर पर कहें तो, एक तरफ एक अभिन्न पहचान संबंधित क्षेत्र है, और दूसरी तरफ लूप के उपयुक्त परिवार की ऊर्जा का औसत है। कॉची-श्वार्ज़ असमानता के अनुसार, लंबाई वर्ग के लिए ऊर्जा एक ऊपरी सीमा है; इसलिए सिस्टोल के क्षेत्रफल और वर्ग के बीच एक असमानता प्राप्त होती है। ऐसा दृष्टिकोण लोवेनर की टोरस असमानता दोनों के लिए काम करता है
+[[Image:Torus.png|right|thumb|250px|एक टोरस]]सतहों के बारे में सिस्टोलिक प्रश्नों में, अभिन्न-ज्यामितीय पहचान विशेष रूप से महत्वपूर्ण भूमिका निभाती हैं। मोटे तौर पर कहें तो, एक तरफ एक अभिन्न पहचान संबंधित क्षेत्र है, और दूसरी तरफ चक्र  के उपयुक्त परिवार की ऊर्जा का औसत है। कॉची-श्वार्ज़ असमानता के अनुसार, लंबाई वर्ग के लिए ऊर्जा एक ऊपरी सीमा है; इसलिए सिस्टोल के क्षेत्रफल और वर्ग के बीच एक असमानता प्राप्त होती है। ऐसा दृष्टिकोण लोवेनर की टोरस असमानता दोनों के लिए काम करता है
 : <math>\mathrm{sys}^2 \le \frac{2}{\sqrt{3}}\cdot\mathrm{area}</math>
-[[ टोरस्र्स ]] के लिए, जहां समानता का मामला फ्लैट टोरस द्वारा प्राप्त किया जाता है जिसका डेक परिवर्तन ईसेनस्टीन पूर्णांक की जाली बनाता हैs, [[Image:Steiner's Roman Surface.gif|thumb|पी का प्रतिनिधित्व करने वाली [[रोमन सतह]] का एक एनीमेशन<sup>2</sup>(आर) आर में<sup>3</sup>]]और पु की असमानता के लिए|वास्तविक प्रक्षेप्य तल पी के लिए पु की असमानता<sup>2</sup>(आर):
+[[ टोरस्र्स ]] के लिए, जहां समानता का मामला फ्लैट टोरस के माध्यम से  प्राप्त किया जाता है जिसका डेक परिवर्तन ईसेनस्टीन पूर्णांक की जाली बनाता हैs, [[Image:Steiner's Roman Surface.gif|thumb|पी का प्रतिनिधित्व करने वाली [[रोमन सतह]] का एक एनीमेशन<sup>2</sup>(आर) आर में<sup>3</sup>]]और पु की असमानता के लिए|वास्तविक प्रक्षेप्य तल पी के लिए पु की असमानता<sup>2</sup>(आर):
 : <math>\mathrm{sys}^2 \le \frac{\pi}{2}\cdot\mathrm{area}</math>,
-समानता के साथ निरंतर [[गाऊसी वक्रता]] की एक मीट्रिक की विशेषता।
+समानता के साथ निरंतर [[गाऊसी वक्रता]] की एक मापीय की विशेषता।
 विचरण के लिए कम्प्यूटेशनल सूत्र का अनुप्रयोग वास्तव में आइसोसिस्टोलिक दोष के साथ लोवेनर की टोरस असमानता का निम्नलिखित संस्करण उत्पन्न करता है:
 :<math>\mathrm{area}-\frac{\sqrt{3}}{2}\mathrm{sys}^2\geq \mathrm{var}(f),</math>
-जहां f अपने अनुरूप वर्ग में एक इकाई क्षेत्र फ्लैट मीट्रिक के संबंध में मीट्रिक का अनुरूप कारक है। इस असमानता को आइसोपेरिमेट्रिक दोष के साथ बोन्सन की असमानता के अनुरूप माना जा सकता है, जो आइसोपेरिमेट्रिक असमानता को मजबूत करता है।
+जहां f अपने अनुरूप वर्ग में एक इकाई क्षेत्र फ्लैट मापीय के संबंध में मापीय का अनुरूप कारक है। इस असमानता को आइसोपेरिमेट्रिक दोष के साथ बोन्सन की असमानता के अनुरूप माना जा सकता है, जो आइसोपेरिमेट्रिक असमानता को मजबूत करता है।
-इस प्रकार की कई नई असमानताएँ हाल ही में खोजी गई हैं, जिनमें सार्वभौमिक आयतन निचली सीमाएँ भी शामिल हैं। सतहों के सिस्टोल पर अधिक विवरण दिखाई देते हैं।
+इस प्रकार की अनेक  नई असमानताएँ हाल ही में खोजी गई हैं, जिनमें सार्वभौमिक आयतन निचली सीमाएँ भी शामिल हैं। सतहों के सिस्टोल पर अधिक विवरण दिखाई देते हैं।
 ==ग्रोमोव की सिस्टोलिक असमानता==
@@ Line 38: / Line 38: @@
 :<math> \operatorname{sys\pi}_1{}^n \leq C_n \operatorname{vol}(M),</math>
-जहां सी<sub>n</sub>केवल एम के आयाम के आधार पर एक सार्वभौमिक स्थिरांक है। यहां होमोटॉपी सिस्टोल sysπ है<sub>1</sub> परिभाषा के अनुसार एम में एक गैर-संविदात्मक लूप की न्यूनतम लंबाई है। एक मैनिफोल्ड को आवश्यक कहा जाता है यदि इसका मौलिक वर्ग [एम] अपने मौलिक समूह के समरूपता (गणित) में एक गैर-तुच्छ वर्ग का प्रतिनिधित्व करता है। प्रमाण में एक नया अपरिवर्तनीय शामिल है जिसे फिलिंग त्रिज्या कहा जाता है, जिसे ग्रोमोव द्वारा पेश किया गया है, जिसे निम्नानुसार परिभाषित किया गया है।
+जहां सी<sub>n</sub>केवल एम के आयाम के आधार पर एक सार्वभौमिक स्थिरांक है। यहां होमोटॉपी सिस्टोल sysπ है<sub>1</sub> परिभाषा के अनुसार एम में एक गैर-संविदात्मक चक्र  की न्यूनतम लंबाई है। एक मैनिफोल्ड को आवश्यक कहा जाता है यदि इसका मौलिक वर्ग [एम] अपने मौलिक समूह के समरूपता (गणित) में एक गैर-तुच्छ वर्ग का प्रतिनिधित्व करता है। प्रमाण में एक नया अपरिवर्तनीय शामिल है जिसे फिलिंग त्रिज्या कहा जाता है, जिसे ग्रोमोव के माध्यम से  पेश किया गया है, जिसे निम्नानुसार परिभाषित किया गया है।
-गुणांक वलय 'Z' या 'Z' को A से निरूपित करें<sub>2</sub>, यह इस बात पर निर्भर करता है कि एम उन्मुख है या नहीं। फिर एक कॉम्पैक्ट एन-डायमेंशनल मैनिफोल्ड एम का मूल वर्ग, जिसे [एम] कहा जाता है, एक जनरेटर है <math>H_n(M;A)=A</math>. यूक्लिडियन स्पेस ई में एम के समावेश को देखते हुए, हम सेट करते हैं
+गुणांक वलय 'Z' या 'Z' को A से निरूपित करें<sub>2</sub>, यह इस बात पर निर्भर करता है कि एम उन्मुख है या नहीं। फिर एक सघन  एन-डायमेंशनल मैनिफोल्ड एम का मूल वर्ग, जिसे [एम] कहा जाता है, एक जनरेटर है <math>H_n(M;A)=A</math>. यूक्लिडियन स्पेस ई में एम के समावेश को देखते हुए, हम सेट करते हैं
 :<math> \mathrm{FillRad}(M\subset E) = \inf \left\{ \epsilon > 0 \left|\;\iota_\epsilon([M])=0\in H_n(U_\epsilon M) \right. \right\},</math>
 कहाँ ι<sub>ε</sub> इसके ε-पड़ोस यू में एम को शामिल करने से प्रेरित समावेश समरूपता है<sub>ε</sub> मेरा।
-ऐसी स्थिति में पूर्ण भरने वाले त्रिज्या को परिभाषित करने के लिए जहां एम रीमैनियन मीट्रिक जी से सुसज्जित है, ग्रोमोव निम्नानुसार आगे बढ़ता है। सी. कुराटोस्की के कारण एक व्यक्ति घुसपैठ का फायदा उठाता है। एक ने एम को बानाच स्पेस एल में समाहित कर लिया है<sup>∞</sup>(M) M पर बाउंडेड बोरेल फ़ंक्शन करता है, जो सुपर मानदंड से सुसज्जित है <math>\|\;\|</math>. अर्थात्, हम एक बिंदु x ∈ M को फ़ंक्शन f पर मैप करते हैं<sub>x</sub>∈ एल<sup>∞</sup>(M) सूत्र f द्वारा परिभाषित<sub>x</sub>(y) = d(x,y) सभी y ∈ M के लिए, जहां d मीट्रिक द्वारा परिभाषित दूरी फ़ंक्शन है। हमारे पास त्रिभुज असमानता है <math>d(x,y) = \| f_x - f_y \|,</math> और इसलिए एम्बेडिंग दृढ़ता से आइसोमेट्रिक है, सटीक अर्थ में कि आंतरिक दूरी और परिवेश दूरी मेल खाती है। यदि परिवेशीय स्थान एक हिल्बर्ट स्थान है, तब भी जब एम रीमैनियन सर्कल है (विपरीत बिंदुओं के बीच की दूरी π होनी चाहिए, 2 नहीं!) तो इतनी दृढ़ता से आइसोमेट्रिक इंबेडिंग असंभव है। फिर हमने E = L सेट किया<sup>∞</sup>(M) उपरोक्त सूत्र में, और परिभाषित करें
+ऐसी स्थिति में पूर्ण भरने वाले त्रिज्या को परिभाषित करने के लिए जहां एम रीमैनियन मापीय जी से सुसज्जित है, ग्रोमोव निम्नानुसार आगे बढ़ता है। सी. कुराटोस्की के कारण एक व्यक्ति घुसपैठ का फायदा उठाता है। एक ने एम को बानाच स्पेस एल में समाहित कर लिया है<sup>∞</sup>(M) M पर बाउंडेड बोरेल फ़ंक्शन करता है, जो सुपर मानदंड से सुसज्जित है <math>\|\;\|</math>. अर्थात्, हम एक बिंदु x ∈ M को फ़ंक्शन f पर मैप करते हैं<sub>x</sub>∈ एल<sup>∞</sup>(M) सूत्र f के माध्यम से  परिभाषित<sub>x</sub>(y) = d(x,y) सभी y ∈ M के लिए, जहां d मापीय के माध्यम से  परिभाषित दूरी फ़ंक्शन है। हमारे पास त्रिभुज असमानता है <math>d(x,y) = \| f_x - f_y \|,</math> और इसलिए एम्बेडिंग दृढ़ता से आइसोमेट्रिक है, सटीक अर्थ में कि आंतरिक दूरी और परिवेश दूरी मेल खाती है। यदि व्यापकय स्थान एक हिल्बर्ट स्थान है, तब भी जब एम रीमैनियन सर्कल है (विपरीत बिंदुओं के बीच की दूरी π होनी चाहिए, 2 नहीं!) तो इतनी दृढ़ता से आइसोमेट्रिक इंबेडिंग असंभव है। फिर हमने E = L सेट किया<sup>∞</sup>(M) उपरोक्त सूत्र में, और परिभाषित करें
 :<math>\mathrm{FillRad}(M)=\mathrm{FillRad} \left( M\subset L^{\infty}(M) \right).</math>
@@ Line 51: / Line 51: @@
 :<math>\mathrm{sys\pi}_1 \leq 6\; \mathrm{FillRad}(M),</math>
-सभी आवश्यक मैनिफोल्ड्स के लिए मान्य एम; साथ ही एक असमानता भी
+सभी आवश्यक विविध कार्य के लिए मान्य एम; साथ ही एक असमानता भी
 :<math>\mathrm{FillRad} \leq C_n \mathrm{vol}_n{}^{1/n}(M),</math>
-सभी बंद मैनिफोल्ड्स के लिए मान्य एम.
+सभी बंद विविध कार्य के लिए मान्य एम.
-एस. वेंगर द्वारा ज्यामितीय माप सिद्धांत में हाल के परिणामों के आधार पर, एल. एम्ब्रोसियो और बी. किर्चहैम के पहले के काम पर आधारित एक प्रमाण का सारांश, नीचे संदर्भित सिस्टोलिक ज्यामिति और टोपोलॉजी पुस्तक की धारा 12.2 में दिखाई देता है। ग्रोमोव की असमानता के प्रमाण के लिए एक पूरी तरह से अलग दृष्टिकोण हाल ही में लैरी गुथ द्वारा प्रस्तावित किया गया था।<ref>{{cite journal | arxiv=math/0610212 | journal=[[Annals of Mathematics]] | last=Guth | first=Larry | year=2011 | volume=173 | issue=1 | pages=51–76 | mr=2753599 | doi=10.4007/annals.2011.173.1.2 | title=बड़े रीमैनियन मैनिफोल्ड्स में गेंदों की मात्रा| s2cid=1392012 }}</ref>
+एस. वेंगर के माध्यम से  ज्यामितीय माप सिद्धांत में हाल के परिणामों के आधार पर, एल. एम्ब्रोसियो और बी. किर्चहैम के पहले के काम पर आधारित एक प्रमाण का सारांश, नीचे संदर्भित सिस्टोलिक ज्यामिति और सांस्थिति पुस्तक की धारा 12.2 में दिखाई देता है। ग्रोमोव की असमानता के प्रमाण के लिए एक पूरी तरह से अलग दृष्टिकोण हाल ही में लैरी गुथ के माध्यम से  प्रस्तावित किया गया था।<ref>{{cite journal | arxiv=math/0610212 | journal=[[Annals of Mathematics]] | last=Guth | first=Larry | year=2011 | volume=173 | issue=1 | pages=51–76 | mr=2753599 | doi=10.4007/annals.2011.173.1.2 | title=बड़े रीमैनियन मैनिफोल्ड्स में गेंदों की मात्रा| s2cid=1392012 }}</ref>
 ==ग्रोमोव की स्थिर असमानता==
--सिस्टोलिक इनवेरिएंट (लूप की लंबाई के संदर्भ में परिभाषित) और उच्चतर, के-सिस्टोलिक इनवेरिएंट (चक्रों के क्षेत्रों आदि के संदर्भ में परिभाषित) के बीच एक महत्वपूर्ण अंतर को ध्यान में रखा जाना चाहिए। जबकि 1-सिस्टोल को शामिल करते हुए कई इष्टतम सिस्टोलिक असमानताएं अब तक प्राप्त की जा चुकी हैं, विशुद्ध रूप से उच्च के-सिस्टोल को शामिल करने वाली एकमात्र इष्टतम असमानता जटिल प्रक्षेप्य स्थान के लिए ग्रोमोव की असमानता है | ग्रोमोव की इष्टतम स्थिर 2-सिस्टोलिक असमानता
+-सिस्टोलिक अपरिवर्तनीय  (चक्र  की लंबाई के संदर्भ में परिभाषित) और उच्चतर, के-सिस्टोलिक अपरिवर्तनीय  (चक्रों के क्षेत्रों आदि के संदर्भ में परिभाषित) के बीच एक महत्वपूर्ण अंतर को ध्यान में रखा जाना चाहिए। जबकि 1-सिस्टोल को शामिल करते हुए अनेक  इष्टतम सिस्टोलिक असमानताएं अब तक प्राप्त की जा चुकी हैं, विशुद्ध रूप से उच्च के-सिस्टोल को शामिल करने वाली एकमात्र इष्टतम असमानता जटिल प्रक्षेप्य स्थान के लिए ग्रोमोव की असमानता है | ग्रोमोव की इष्टतम स्थिर 2-सिस्टोलिक असमानता
 : <math>\mathrm{stsys}_2{}^n \leq n! \;\mathrm{vol}_{2n}(\mathbb{CP}^n)</math>
-[[जटिल प्रक्षेप्य स्थान]] के लिए, जहां सममित फ़ुबिनी-स्टडी मीट्रिक द्वारा इष्टतम सीमा प्राप्त की जाती है, जो [[क्वांटम यांत्रिकी]] के लिंक की ओर इशारा करती है। यहां रीमैनियन मैनिफोल्ड एम के स्थिर 2-सिस्टोल को सेटिंग द्वारा परिभाषित किया गया है
+[[जटिल प्रक्षेप्य स्थान]] के लिए, जहां सममित फ़ुबिनी-स्टडी मापीय के माध्यम से  इष्टतम सीमा प्राप्त की जाती है, जो [[क्वांटम यांत्रिकी]] के लिंक की ओर इशारा करती है। यहां रीमैनियन मैनिफोल्ड एम के स्थिर 2-सिस्टोल को सेटिंग के माध्यम से  परिभाषित किया गया है
 :<math>\mathrm{stsys}_2 = \lambda_1\left(H_2(M,\mathbb{Z})_{\mathbb{R}}, \|\;\|\right),</math>
-कहाँ <math>\|\;\|</math> स्थिर मानदंड है, जबकि λ<sub>1</sub> जाली के शून्येतर तत्व का न्यूनतम मान है। ग्रोमोव की स्थिर असमानता कितनी असाधारण है, यह हाल ही में स्पष्ट हुआ। अर्थात्, यह पता चला कि, अपेक्षा के विपरीत, जटिल मामले में 2-सिस्टोल के विपरीत, चतुर्धातुक प्रक्षेप्य तल पर सममित मीट्रिक इसकी सिस्टोलिक रूप से इष्टतम मीट्रिक नहीं है। जबकि इसके सममित मीट्रिक के साथ चतुर्धातुक प्रक्षेप्य तल का मध्य-आयामी स्थिर सिस्टोलिक अनुपात 10/3 है, जटिल प्रक्षेप्य 4-स्पेस के सममित मीट्रिक के लिए अनुरूप अनुपात 6 मान देता है, जबकि इस तरह के लिए सबसे अच्छा उपलब्ध ऊपरी सीमा है इन दोनों स्थानों पर एक मनमाना मीट्रिक का अनुपात 14 है। यह ऊपरी सीमा ली बीजगणित [[E7 (गणित)]] के गुणों से संबंधित है। यदि असाधारण स्पिन (7) होलोनॉमी और 4-वें बेट्टी नंबर 1 के साथ 8-मैनिफोल्ड मौजूद है, तो मूल्य 14 वास्तव में इष्टतम है। स्पिन(7)-मैनिफोल्ड|स्पिन(7) होलोनॉमी वाले मैनिफोल्ड्स का [[डोमिनिक जॉयस]] द्वारा गहन अध्ययन किया गया है।
+कहाँ <math>\|\;\|</math> स्थिर मानदंड है, जबकि λ<sub>1</sub> जाली के शून्येतर तत्व का न्यूनतम मान है। ग्रोमोव की स्थिर असमानता कितनी असाधारण है, यह हाल ही में स्पष्ट हुआ। अर्थात्, यह पता चला कि, अपेक्षा के विपरीत, जटिल मामले में 2-सिस्टोल के विपरीत, चतुर्धातुक प्रक्षेप्य तल पर सममित मापीय इसकी सिस्टोलिक रूप से इष्टतम मापीय नहीं है। जबकि इसके सममित मापीय के साथ चतुर्धातुक प्रक्षेप्य तल का मध्य-आयामी स्थिर सिस्टोलिक अनुपात 10/3 है, जटिल प्रक्षेप्य 4-स्पेस के सममित मापीय के लिए अनुरूप अनुपात 6 मान देता है, जबकि इस तरह के लिए सबसे अच्छा उपलब्ध ऊपरी सीमा है इन दोनों स्थानों पर एक मनमाना मापीय का अनुपात 14 है। यह ऊपरी सीमा ली बीजगणित [[E7 (गणित)]] के गुणों से संबंधित है। यदि असाधारण स्पिन (7) होलोनॉमी और 4-वें बेट्टी नंबर 1 के साथ 8-मैनिफोल्ड मौजूद है, तो मूल्य 14 वास्तव में इष्टतम है। स्पिन(7)-मैनिफोल्ड|स्पिन(7) होलोनॉमी वाले विविध कार्य का [[डोमिनिक जॉयस]] के माध्यम से  गहन अध्ययन किया गया है।
 ==2-सिस्टोल के लिए निचली सीमा==
-इसी तरह, के = 2 के साथ के-सिस्टोल के लिए एकमात्र गैर-तुच्छ निचली सीमा के बारे में, [[गेज सिद्धांत]] और [[स्यूडोहोलोमोर्फिक वक्र]] | जे-होलोमोर्फिक वक्र में हाल के काम का परिणाम है। [[जेक सोलोमन]] द्वारा 4-मैनिफोल्ड्स के अनुरूप 2-सिस्टोल के लिए निचली सीमा के अध्ययन से अवधि मानचित्र की छवि के घनत्व का एक सरलीकृत प्रमाण प्राप्त हुआ है।
+इसी तरह, के = 2 के साथ के-सिस्टोल के लिए एकमात्र गैर-तुच्छ निचली सीमा के बारे में, [[गेज सिद्धांत]] और [[स्यूडोहोलोमोर्फिक वक्र]] | जे-होलोमोर्फिक वक्र में हाल के काम का परिणाम है। [[जेक सोलोमन]] के माध्यम से  4-विविध कार्य के अनुरूप 2-सिस्टोल के लिए निचली सीमा के अध्ययन से अवधि मानचित्र की छवि के घनत्व का एक सरलीकृत प्रमाण प्राप्त हुआ है।
 ==शॉट्की समस्या==
-शायद सिस्टोल के सबसे उल्लेखनीय अनुप्रयोगों में से एक [[शोट्की समस्या]] के संदर्भ में है, पी. बसर और पीटर सरनाक|पी द्वारा। सरनाक, जिन्होंने मुख्य रूप से ध्रुवीकृत एबेलियन किस्मों के बीच [[रीमैन सतह]]ों की [[जैकोबियन किस्म]]ों को प्रतिष्ठित किया, सिस्टोलिक अंकगणित की नींव रखी।
+शायद सिस्टोल के सबसे उल्लेखनीय अनुप्रयोगों में से एक [[शोट्की समस्या]] के संदर्भ में है, पी. बसर और पीटर सरनाक|पी के माध्यम से । सरनाक, जिन्होंने मुख्य रूप से ध्रुवीकृत एबेलियन किस्मों के बीच [[रीमैन सतह]]ों की [[जैकोबियन किस्म]]ों को प्रतिष्ठित किया, सिस्टोलिक अंकगणित की नींव रखी।
 ==लस्टर्निक-श्निरेलमैन श्रेणी==
-सिस्टोलिक प्रश्न पूछना अक्सर संबंधित क्षेत्रों में प्रश्नों को प्रेरित करता है। इस प्रकार, मैनिफोल्ड की सिस्टोलिक श्रेणी की धारणा को परिभाषित और जांच की गई है, जो लस्टर्निक-श्निरेलमैन श्रेणी (एलएस श्रेणी) से संबंध प्रदर्शित करती है। ध्यान दें कि सिस्टोलिक श्रेणी (साथ ही एलएस श्रेणी), परिभाषा के अनुसार, एक पूर्णांक है। दोनों श्रेणियों को सतहों और 3-मैनिफोल्ड्स दोनों के लिए मेल खाते हुए दिखाया गया है। इसके अलावा, ओरिएंटेबल 4-मैनिफोल्ड्स के लिए, सिस्टोलिक श्रेणी एलएस श्रेणी के लिए निचली सीमा है। एक बार कनेक्शन स्थापित हो जाने पर, प्रभाव परस्पर होता है: एलएस श्रेणी के बारे में ज्ञात परिणाम सिस्टोलिक प्रश्नों को उत्तेजित करते हैं, और इसके विपरीत।
+सिस्टोलिक प्रश्न पूछना अक्सर संबंधित क्षेत्रों में प्रश्नों को प्रेरित करता है। इस प्रकार, मैनिफोल्ड की सिस्टोलिक श्रेणी की धारणा को परिभाषित और जांच की गई है, जो लस्टर्निक-श्निरेलमैन श्रेणी (एलएस श्रेणी) से संबंध प्रदर्शित करती है। ध्यान दें कि सिस्टोलिक श्रेणी (साथ ही एलएस श्रेणी), परिभाषा के अनुसार, एक पूर्णांक है। दोनों श्रेणियों को सतहों और 3-विविध कार्य दोनों के लिए मेल खाते हुए दिखाया गया है। इसके अलावा, ओरिएंटेबल 4-विविध कार्य के लिए, सिस्टोलिक श्रेणी एलएस श्रेणी के लिए निचली सीमा है। एक बार कनेक्शन स्थापित हो जाने पर, प्रभाव परस्पर होता है: एलएस श्रेणी के बारे में ज्ञात परिणाम सिस्टोलिक प्रश्नों को उत्तेजित करते हैं, और इसके विपरीत।
-नया अपरिवर्तनीय काट्ज़ और रुड्यक द्वारा पेश किया गया था (नीचे देखें)। चूंकि अपरिवर्तनीय लस्टर्निक-श्निरेलमैन श्रेणी (एलएस श्रेणी) से निकटता से संबंधित है, इसलिए इसे सिस्टोलिक श्रेणी कहा जाता था।
+नया अपरिवर्तनीय काट्ज़ और रुड्यक के माध्यम से  पेश किया गया था (नीचे देखें)। चूंकि अपरिवर्तनीय लस्टर्निक-श्निरेलमैन श्रेणी (एलएस श्रेणी) से निकटता से संबंधित है, इसलिए इसे सिस्टोलिक श्रेणी कहा जाता था।
-मैनिफोल्ड एम की सिस्टोलिक श्रेणी को एम के विभिन्न के-सिस्टोल के संदर्भ में परिभाषित किया गया है। मोटे तौर पर, विचार इस प्रकार है। मैनिफोल्ड एम को देखते हुए, कोई सिस्टोल के सबसे लंबे उत्पाद की तलाश करता है जो एम की कुल मात्रा के लिए वक्रता-मुक्त निचली सीमा देता है (मीट्रिक के निरंतर स्वतंत्र के साथ)। परिभाषा में एम के कवर के सिस्टोलिक इनवेरिएंट को भी शामिल करना स्वाभाविक है। इतने लंबे उत्पाद में कारकों की संख्या परिभाषा के अनुसार एम की सिस्टोलिक श्रेणी है।
+मैनिफोल्ड एम की सिस्टोलिक श्रेणी को एम के विभिन्न के-सिस्टोल के संदर्भ में परिभाषित किया गया है। मोटे तौर पर, विचार इस प्रकार है। मैनिफोल्ड एम को देखते हुए, कोई सिस्टोल के सबसे लंबे उत्पाद की तलाश करता है जो एम की कुल मात्रा के लिए वक्रता-मुक्त निचली सीमा देता है (मापीय के निरंतर स्वतंत्र के साथ)। परिभाषा में एम के कवर के सिस्टोलिक अपरिवर्तनीय  को भी शामिल करना स्वाभाविक है। इतने लंबे उत्पाद में कारकों की संख्या परिभाषा के अनुसार एम की सिस्टोलिक श्रेणी है।
-उदाहरण के लिए, मिखाइल ग्रोमोव (गणितज्ञ) ने दिखाया कि एक आवश्यक एन-मैनिफोल्ड होमोटॉपी 1-सिस्टोल की एन'वीं शक्ति के संदर्भ में कम मात्रा में सीमित मात्रा को स्वीकार करता है (ऊपर अनुभाग देखें)। इससे यह निष्कर्ष निकलता है कि आवश्यक एन-मैनिफोल्ड की सिस्टोलिक श्रेणी बिल्कुल एन है। वास्तव में, बंद एन-मैनिफोल्ड्स के लिए, एलएस श्रेणी और सिस्टोलिक श्रेणी दोनों का अधिकतम मूल्य एक साथ प्राप्त होता है।
+उदाहरण के लिए, मिखाइल ग्रोमोव (गणितज्ञ) ने दिखाया कि एक आवश्यक एन-मैनिफोल्ड होमोटॉपी 1-सिस्टोल की एन'वीं शक्ति के संदर्भ में कम मात्रा में सीमित मात्रा को स्वीकार करता है (ऊपर अनुभाग देखें)। इससे यह निष्कर्ष निकलता है कि आवश्यक एन-मैनिफोल्ड की सिस्टोलिक श्रेणी बिल्कुल एन है। वास्तव में, बंद एन-विविध कार्य के लिए, एलएस श्रेणी और सिस्टोलिक श्रेणी दोनों का अधिकतम मूल्य एक साथ प्राप्त होता है।
 दोनों श्रेणियों के बीच एक दिलचस्प संबंध के अस्तित्व का एक और संकेत अपरिवर्तनीय से संबंध है जिसे कपलेंथ कहा जाता है। इस प्रकार, वास्तविक कप लंबाई दोनों श्रेणियों के लिए निचली सीमा बन जाती है।
-कई मामलों में सिस्टोलिक श्रेणी एलएस श्रेणी से मेल खाती है, जिसमें आयाम 2 और 3 के मैनिफोल्ड का मामला भी शामिल है। आयाम 4 में, हाल ही में यह दिखाया गया था कि सिस्टोलिक श्रेणी एलएस श्रेणी के लिए निचली सीमा है।
+अनेक  मामलों में सिस्टोलिक श्रेणी एलएस श्रेणी से मेल खाती है, जिसमें आयाम 2 और 3 के मैनिफोल्ड का मामला भी शामिल है। आयाम 4 में, हाल ही में यह दिखाया गया था कि सिस्टोलिक श्रेणी एलएस श्रेणी के लिए निचली सीमा है।
 ==सिस्टोलिक हाइपरबोलिक ज्यामिति==
-हाइपरबोलिक सतहों के सिस्टोल के बड़े जीनस जी के लिए स्पर्शोन्मुख व्यवहार के अध्ययन से कुछ दिलचस्प स्थिरांक का पता चलता है। इस प्रकार, [[हर्विट्ज़ सतह]] Σ है<sub>''g''</sub> (2,3,7) त्रिभुज समूह के प्रमुख सर्वांगसम उपसमूहों के एक टावर द्वारा परिभाषित|(2,3,7) अतिशयोक्तिपूर्ण त्रिभुज समूह सीमा को संतुष्ट करता है
+हाइपरबोलिक सतहों के सिस्टोल के बड़े जीनस जी के लिए स्पर्शोन्मुख व्यवहार के अध्ययन से कुछ दिलचस्प स्थिरांक का पता चलता है। इस प्रकार, [[हर्विट्ज़ सतह]] Σ है<sub>''g''</sub> (2,3,7) त्रिभुज समूह के प्रमुख सर्वांगसम उपसमूहों के एक टावर के माध्यम से  परिभाषित|(2,3,7) अतिशयोक्तिपूर्ण त्रिभुज समूह सीमा को संतुष्ट करता है
 :<math> \mathrm{sys}\pi_1(\Sigma_g) \geq \frac{4}{3} \log g,</math>
-और एक समान सीमा अधिक सामान्य अंकगणितीय फ़ुचियन समूहों के लिए है। यह 2007 का परिणाम काट्ज़, शाप्स और विश्ने द्वारा दिया गया है<ref>{{cite journal
+और एक समान सीमा अधिक सामान्य अंकगणितीय फ़ुचियन समूहों के लिए है। यह 2007 का परिणाम काट्ज़, शाप्स और विश्ने के माध्यम से  दिया गया है<ref>{{cite journal
 | last1=Katz | first1=Mikhail G. | authorlink1=Mikhail G. Katz
 | last2=Schaps | first2=Mary | authorlink2=Mary Schaps
@@ Line 114: / Line 114: @@
 | doi=10.1007/BF01232233 | doi-access=free
 | s2cid=116904696}}</ref>
-[[अतिशयोक्तिपूर्ण ज्यामिति]] में सिस्टोल के लिए एक ग्रंथ सूची में वर्तमान में चालीस लेख हैं। दिलचस्प उदाहरण [[बोल्ज़ा सतह]], [[क्लेन चतुर्थक]], मैकबीथ सतह, [[पहला हर्विट्ज़ ट्रिपलेट]] द्वारा प्रदान किए गए हैं।
+[[अतिशयोक्तिपूर्ण ज्यामिति]] में सिस्टोल के लिए एक ग्रंथ सूची में वर्तमान में चालीस लेख हैं। दिलचस्प उदाहरण [[बोल्ज़ा सतह]], [[क्लेन चतुर्थक]], मैकबीथ सतह, [[पहला हर्विट्ज़ ट्रिपलेट]] के माध्यम से  प्रदान किए गए हैं।
 ==हाबिल-जैकोबी मानचित्रों से संबंध==
 बुरगो और इवानोव की तकनीकों के अनुप्रयोग के रूप में इष्टतम सिस्टोलिक असमानताओं का एक परिवार प्राप्त किया जाता है, जो उपयुक्त एबेल-जैकोबी मानचित्रों का उपयोग करता है, जिसे निम्नानुसार परिभाषित किया गया है।
-मान लीजिए M एक मैनिफोल्ड है, π = π<sub>1</sub>(एम), इसका मौलिक समूह और एफ: π → π<sup>ab</sup>इसके [[ आबेलियनाइजेशन ]] मानचित्र बनें। मान लीजिए कि tor π का मरोड़ उपसमूह है<sup>ab</sup>. Let g: π<sup>ab</sup> → π<sup>ab</sup>/tor मरोड़ द्वारा भागफल हो। स्पष्टतः, π<sup>अब</सुप>/तोर= 'ज़'<sup>बी</sup>, जहां बी = बी<sub>1</sub> (एम)। मान लीजिए φ: π → 'Z'<sup>बी</sup>रचित समरूपता हो।
+मान लीजिए M एक मैनिफोल्ड है, π = π<sub>1</sub>(एम), इसका मौलिक समूह और एफ: π → π<sup>ab</sup>इसके [[ आबेलियनाइजेशन ]] मानचित्र बनें। मान लीजिए कि tor π का मरोड़ उपसमूह है<sup>ab</sup>. Let g: π<sup>ab</sup> → π<sup>ab</sup>/tor मरोड़ के माध्यम से  भागफल हो। स्पष्टतः, π<sup>अब</सुप>/तोर= 'ज़'<sup>बी</sup>, जहां बी = बी<sub>1</sub> (एम)। मान लीजिए φ: π → 'Z'<sup>बी</sup>रचित समरूपता हो।
 <ब्लॉककोट>'परिभाषा:' आवरण <math>\bar M</math> उपसमूह Ker(φ) ⊂ π के संगत मैनिफोल्ड M को सार्वभौमिक (या अधिकतम) मुक्त एबेलियन आवरण कहा जाता है।</blockquote>
-अब मान लें कि एम के पास [[रीमैनियन मीट्रिक]] है। मान लीजिए कि E, M पर हार्मोनिक 1-रूपों का स्थान है, जिसमें दोहरे E* को H के साथ प्रामाणिक रूप से पहचाना जाता है<sub>1</sub>(श्री')। बेसपॉइंट x से पथों के साथ एक इंटीग्रल हार्मोनिक 1-फॉर्म को एकीकृत करके<sub>0</sub> ∈ एम, हमें वृत्त 'आर'/'जेड' = 'एस' का एक नक्शा मिलता है<sup>1</sup>.
+अब मान लें कि एम के पास [[रीमैनियन मीट्रिक|रीमैनियन मापीय]] है। मान लीजिए कि E, M पर हार्मोनिक 1-रूपों का स्थान है, जिसमें दोहरे E* को H के साथ प्रामाणिक रूप से पहचाना जाता है<sub>1</sub>(श्री')। बेसपॉइंट x से पथों के साथ एक इंटीग्रल हार्मोनिक 1-फॉर्म को एकीकृत करके<sub>0</sub> ∈ एम, हमें वृत्त 'आर'/'जेड' = 'एस' का एक नक्शा मिलता है<sup>1</sup>.
-इसी प्रकार, मानचित्र को परिभाषित करने के लिए M → H<sub>1</sub>(एम,'आर')/एच<sub>1</sub>(एम,'जेड')<sub>'''R'''</sub> सहसंगति के लिए कोई आधार चुने बिना, हम इस प्रकार तर्क देते हैं। माना x [[सार्वभौमिक आवरण]] में एक बिंदु है <math>\tilde{M}</math> एम का। इस प्रकार एक्स को एक्स से पथ सी के साथ एम के एक बिंदु द्वारा दर्शाया गया है<sub>0</sub> इसे. पथ c के साथ एकीकृत करके, हम एक रैखिक रूप प्राप्त करते हैं, <math>h\to \int_c h</math>, एक बार। इस प्रकार हमें एक मानचित्र प्राप्त होता है <math>\tilde{M}\to E^* = H_1(M,\mathbf{R})</math>, जो, इसके अलावा, एक मानचित्र पर उतरता है
+इसी प्रकार, मानचित्र को परिभाषित करने के लिए M → H<sub>1</sub>(एम,'आर')/एच<sub>1</sub>(एम,'जेड')<sub>'''R'''</sub> सहसंगति के लिए कोई आधार चुने बिना, हम इस प्रकार तर्क देते हैं। माना x [[सार्वभौमिक आवरण]] में एक बिंदु है <math>\tilde{M}</math> एम का। इस प्रकार X को X से पथ सी के साथ एम के एक बिंदु के माध्यम से  दर्शाया गया है<sub>0</sub> इसे. पथ c के साथ एकीकृत करके, हम एक रैखिक रूप प्राप्त करते हैं, <math>h\to \int_c h</math>, एक बार। इस प्रकार हमें एक मानचित्र प्राप्त होता है <math>\tilde{M}\to E^* = H_1(M,\mathbf{R})</math>, जो, इसके अलावा, एक मानचित्र पर उतरता है
 :<math> \overline{A}_M: \overline{M}\to E^*,\;\; c\mapsto \left(h\mapsto \int_c h \right),</math>
@@ Line 142: / Line 142: @@
 ==संबंधित फ़ील्ड, [[वॉल्यूम एन्ट्रापी]]==
-बड़े जीनस की सतहों के सिस्टोल के लिए स्पर्शोन्मुख घटनाओं को दिलचस्प एर्गोडिक घटनाओं और [[अंकगणित समूह]]ों के सर्वांगसम उपसमूहों के गुणों से संबंधित दिखाया गया है।
+बड़े जीनस की सतहों के सिस्टोल के लिए स्पर्शोन्मुख घटनाओं को दिलचस्प ऊर्जापंथी घटनाओं और [[अंकगणित समूह]]ों के सर्वांगसम उपसमूहों के गुणों से संबंधित दिखाया गया है।
 होमोटॉपी सिस्टोल के लिए ग्रोमोव की 1983 की असमानता, विशेष रूप से, इसके सिस्टोल के संदर्भ में एक गोलाकार सतह के क्षेत्र के लिए एक समान निचली सीमा का तात्पर्य है। इस तरह की सीमा लोवनर और पु की असमानताओं को सामान्यीकृत करती है, भले ही गैर-इष्टतम फैशन में।
@@ Line 148: / Line 148: @@
 ग्रोमोव के मौलिक 1983 पेपर में सिस्टोल और क्षेत्र से संबंधित एसिम्प्टोटिक सीमाएँ भी शामिल हैं, जो समान सीमा (सभी आयामों में मान्य) में सुधार करती हैं।
-यह हाल ही में खोजा गया था (नीचे काट्ज़ और सबौरौ द्वारा पेपर देखें) कि वॉल्यूम एन्ट्रॉपी एच, एच के लिए ए कटोक की इष्टतम असमानता के साथ, सतहों के सिस्टोलिक अनुपात के लिए एम ग्रोमोव की एसिम्प्टोटिक बाध्यता के पारदर्शी प्रमाण में सही मध्यस्थ है बड़ी जाति.
+यह हाल ही में खोजा गया था (नीचे काट्ज़ और सबौरौ के माध्यम से  पेपर देखें) कि वॉल्यूम एन्ट्रॉपी एच, एच के लिए ए कटोक की इष्टतम असमानता के साथ, सतहों के सिस्टोलिक अनुपात के लिए एम ग्रोमोव की एसिम्प्टोटिक बाध्यता के पारदर्शी प्रमाण में सही मध्यस्थ है बड़ी जाति.
-ए कटोक के शास्त्रीय परिणाम में कहा गया है कि नकारात्मक यूलर विशेषता के साथ एक बंद सतह एम पर प्रत्येक मीट्रिक एन्ट्रापी और क्षेत्र से संबंधित एक इष्टतम असमानता को संतुष्ट करता है।
+ए कटोक के शास्त्रीय परिणाम में कहा गया है कि नकारात्मक यूलर विशेषता के साथ एक बंद सतह एम पर प्रत्येक मापीय एन्ट्रापी और क्षेत्र से संबंधित एक इष्टतम असमानता को संतुष्ट करता है।
 यह पता चला है कि एक बंद सतह की न्यूनतम एन्ट्रापी उसके इष्टतम सिस्टोलिक अनुपात से संबंधित हो सकती है। अर्थात्, सिस्टोलिक रूप से चरम सतह की एन्ट्रापी के लिए उसके सिस्टोल के संदर्भ में एक ऊपरी सीमा होती है। आयतन के संदर्भ में कटोक की इष्टतम निचली सीमा के साथ इस ऊपरी सीमा को जोड़कर, बड़े जीनस की सतहों के इष्टतम सिस्टोलिक अनुपात के लिए ग्रोमोव के एसिम्प्टोटिक अनुमान का एक सरल वैकल्पिक प्रमाण प्राप्त होता है। इसके अलावा, इस तरह का दृष्टिकोण ग्रोमोव के प्रमेय में एक बेहतर गुणक स्थिरांक उत्पन्न करता है।
-एक अनुप्रयोग के रूप में, इस पद्धति का तात्पर्य है कि जीनस की सतह पर प्रत्येक मीट्रिक कम से कम 20 लोवेनर की टोरस असमानता को संतुष्ट करता है। यह 50 के सर्वोत्तम पूर्व अनुमान में सुधार करता है जो ग्रोमोव के अनुमान से लिया गया था।
+एक अनुप्रयोग के रूप में, इस पद्धति का तात्पर्य है कि जीनस की सतह पर प्रत्येक मापीय कम से कम 20 लोवेनर की टोरस असमानता को संतुष्ट करता है। यह 50 के सर्वोत्तम पूर्व अनुमान में सुधार करता है जो ग्रोमोव के अनुमान से लिया गया था।
 ==भरण क्षेत्र अनुमान==
 {{main|भरण क्षेत्र अनुमान}}
-ग्रोमोव के भरण क्षेत्र अनुमान को हाइपरलिप्टिक सेटिंग में सिद्ध किया गया है (नीचे बैंगर्ट एट अल द्वारा संदर्भ देखें)।
+ग्रोमोव के भरण क्षेत्र अनुमान को हाइपरलिप्टिक सेटिंग में सिद्ध किया गया है (नीचे बैंगर्ट एट अल के माध्यम से  संदर्भ देखें)।
-भराव क्षेत्र अनुमान का दावा है कि दृढ़ता से आइसोमेट्रिक संपत्ति के साथ एक सतह द्वारा लंबाई 2π के रीमैनियन सर्कल के सभी संभावित भरावों में से, गोल गोलार्ध में सबसे कम क्षेत्र होता है। यहां रीमैनियन सर्कल कुल 1-वॉल्यूम 2π और रीमैनियन व्यास π के अद्वितीय बंद 1-आयामी रीमैनियन मैनिफोल्ड को संदर्भित करता है।
+भराव क्षेत्र अनुमान का दावा है कि दृढ़ता से आइसोमेट्रिक संपत्ति के साथ एक सतह के माध्यम से  लंबाई 2π के रीमैनियन सर्कल के सभी संभावित भरावों में से, गोल गोलार्ध में सबसे कम क्षेत्र होता है। यहां रीमैनियन सर्कल कुल 1-वॉल्यूम 2π और रीमैनियन व्यास π के अद्वितीय बंद 1-आयामी रीमैनियन मैनिफोल्ड को संदर्भित करता है।
 अनुमान को समझाने के लिए, हम इस अवलोकन से शुरू करते हैं कि इकाई 2-गोले का भूमध्यरेखीय वृत्त, एस<sup>2</sup>⊂ आर<sup>3</sup>, एक रीमैनियन सर्कल एस है<sup>1</sup>लंबाई 2π और व्यास π का।
-अधिक सटीक रूप से, एस का रीमैनियन दूरी फ़ंक्शन<sup>1</sup>गोले पर परिवेशी रीमैनियन दूरी का प्रतिबंध है। यह संपत्ति यूक्लिडियन विमान में यूनिट सर्कल के मानक एम्बेडिंग से संतुष्ट नहीं है, जहां विपरीत बिंदुओं की एक जोड़ी दूरी 2 पर है, π नहीं।
+अधिक सटीक रूप से, एस का रीमैनियन दूरी फ़ंक्शन<sup>1</sup>गोले पर व्यापक रीमैनियन दूरी का प्रतिबंध है। यह संपत्ति यूक्लिडियन विमान में यूनिट सर्कल के मानक एम्बेडिंग से संतुष्ट नहीं है, जहां विपरीत बिंदुओं की एक जोड़ी दूरी 2 पर है, π नहीं।
-हम 'एस' की सभी फिलिंग्स पर विचार करते हैं<sup>1</sup>एक सतह द्वारा, जैसे कि सतह की सीमा के रूप में वृत्त को शामिल करने से परिभाषित प्रतिबंधित मीट्रिक 2π लंबाई के एक वृत्त का रीमैनियन मीट्रिक है। वृत्त को सीमा के रूप में शामिल करने को वृत्त का दृढ़तापूर्वक सममितीय अंतर्विरोध कहा जाता है।
+हम 'एस' की सभी फिलिंग्स पर विचार करते हैं<sup>1</sup>एक सतह के माध्यम से , जैसे कि सतह की सीमा के रूप में वृत्त को शामिल करने से परिभाषित प्रतिबंधित मापीय 2π लंबाई के एक वृत्त का रीमैनियन मापीय है। वृत्त को सीमा के रूप में शामिल करने को वृत्त का दृढ़तापूर्वक सममितीय अंतर्विरोध कहा जाता है।
 में ग्रोमोव ने अनुमान लगाया कि गोल गोलार्ध सभी भरने वाली सतहों के बीच वृत्त को भरने का सबसे अच्छा तरीका देता है।
-सरलता से जुड़ी फिलिंग का मामला पु की असमानता के बराबर है। हाल ही में [[जीनस (गणित)]]-1 भरने के मामले को भी सकारात्मक रूप से निपटाया गया था (नीचे बैंगर्ट एट अल द्वारा संदर्भ देखें)। अर्थात्, यह पता चलता है कि कोई व्यक्ति अभिन्न ज्यामिति से जे. हर्श के आधी सदी पुराने सूत्र का उपयोग कर सकता है। अर्थात्, भूमध्य रेखा पर स्व-प्रतिच्छेदन बिंदु के साथ, फ़ुटबॉल पर चित्र-8 लूप के परिवार पर विचार करें (लेख की शुरुआत में चित्र देखें)। हर्श का सूत्र फुटबॉल के अनुरूप वर्ग में एक मीट्रिक के क्षेत्र को परिवार से आकृति -8 लूप की ऊर्जा के औसत के रूप में व्यक्त करता है। रीमैन सतह के हाइपरलिप्टिक भागफल पर हर्श के सूत्र का अनुप्रयोग इस मामले में भरने वाले क्षेत्र अनुमान को साबित करता है।
+सरलता से जुड़ी फिलिंग का मामला पु की असमानता के बराबर है। हाल ही में [[जीनस (गणित)]]-1 भरने के मामले को भी सकारात्मक रूप से निपटाया गया था (नीचे बैंगर्ट एट अल के माध्यम से  संदर्भ देखें)। अर्थात्, यह पता चलता है कि कोई व्यक्ति अभिन्न ज्यामिति से जे. हर्श के आधी सदी पुराने सूत्र का उपयोग कर सकता है। अर्थात्, भूमध्य रेखा पर स्व-प्रतिच्छेदन बिंदु के साथ, फ़ुटबॉल पर चित्र-8 चक्र  के परिवार पर विचार करें (लेख की शुरुआत में चित्र देखें)। हर्श का सूत्र फुटबॉल के अनुरूप वर्ग में एक मापीय के क्षेत्र को परिवार से आकृति -8 चक्र  की ऊर्जा के औसत के रूप में व्यक्त करता है। रीमैन सतह के हाइपरलिप्टिक भागफल पर हर्श के सूत्र का अनुप्रयोग इस मामले में भरने वाले क्षेत्र अनुमान को साबित करता है।
 जीनस 2 में [[हाइपरलिप्टिक वक्र]] के अन्य सिस्टोलिक प्रभावों की पहचान की गई है।

Anonymous

Search

सिस्टोलिक ज्यामिति: Difference between revisions

Namespaces

More

Page actions

Revision as of 20:22, 11 July 2023

Contents

सिस्टोल की धारणा

3-स्थान में एक केंद्रीय सममित बहुफलक का गुण

अवधारणाएँ

ग्रोमोव की सिस्टोलिक असमानता

ग्रोमोव की स्थिर असमानता

2-सिस्टोल के लिए निचली सीमा

शॉट्की समस्या

लस्टर्निक-श्निरेलमैन श्रेणी

सिस्टोलिक हाइपरबोलिक ज्यामिति

हाबिल-जैकोबी मानचित्रों से संबंध

संबंधित फ़ील्ड, वॉल्यूम एन्ट्रापी

भरण क्षेत्र अनुमान

सर्वेक्षण

यह भी देखें

टिप्पणियाँ

संदर्भ

बाहरी संबंध

Navigation

Navigation

Wiki tools

Wiki tools

Anonymous

Search

सिस्टोलिक ज्यामिति: Difference between revisions

Revision as of 20:22, 11 July 2023

सिस्टोल की धारणा

3-स्थान में एक केंद्रीय सममित बहुफलक का गुण

अवधारणाएँ

ग्रोमोव की सिस्टोलिक असमानता

ग्रोमोव की स्थिर असमानता

2-सिस्टोल के लिए निचली सीमा

शॉट्की समस्या

लस्टर्निक-श्निरेलमैन श्रेणी

सिस्टोलिक हाइपरबोलिक ज्यामिति

हाबिल-जैकोबी मानचित्रों से संबंध

संबंधित फ़ील्ड, वॉल्यूम एन्ट्रापी

भरण क्षेत्र अनुमान

सर्वेक्षण

यह भी देखें

टिप्पणियाँ

संदर्भ

बाहरी संबंध

Navigation

Wiki tools

Page tools

Other projects

Categories