फलन का शून्य

"किसी फलन का रुट" redirects here. For किसी फलन का हाफ ईटीरेट, see फंक्शनल वर्गमूल.

A graph of the function $\cos(x)$ for $x$ in $\left[-2\pi ,2\pi \right]$, with zeros at $-{\tfrac {3\pi }{2}},\;-{\tfrac {\pi }{2}},\;{\tfrac {\pi }{2}}$, and ${\tfrac {3\pi }{2}},$ marked in red.

गणित में, एक वास्तविक संख्या, सम्मिश्र संख्या या सामान्यतः सदिश फलन का मान शून्य होता है, जिसे कभी-कभी रूट भी कहा जाता है और इस प्रकार $f$ के डोमेन का एक सदस्य $x$ के रूप में है, जैसे कि $f$ ऐसा है कि $f(x)$ पर वनिश हो जाता है अर्थात फलन $f$, $x$ पर 0 का मान प्राप्त करता है $x$, या समकक्ष, $x$ समीकरण का $f(x)=0$ सॉलूशन है. इस प्रकार किसी फलन का शून्य एक इनपुट मान होता है, जो 0 का आउटपुट उत्पन्न करता है।

एक बहुपद का रूट संगत बहुपद फलन शून्य होता है। इस प्रकार बीजगणित के फंडामेंटल प्रमेय से पता चलता है कि किसी भी गैर-शून्य बहुपद में बहुपद की घात के बराबर रूट की संख्या होती है और जब कोई सम्मिश्र रूट पर कंसीडर करता है तो रूट की संख्या और घात बराबर होती है और इस प्रकार सामान्यतः बीजगणितीय क्लोज्ड एक्सटेंशन में रुट ें उनकी बहुलता (गणित) के साथ गिनी जाती हैं। उदाहरण के लिए, $f(x)=x^{2}-5x+6$ द्वारा परिभाषित घात दो के बहुपद $f$ के दो रुट जो 2 और 3 के रूप में होते है या शून्य रूप में होते है।

$$f(2)=2^{2}-5\times 2+6=0{\text{ and }}f(3)=3^{2}-5\times 3+6=0.$$

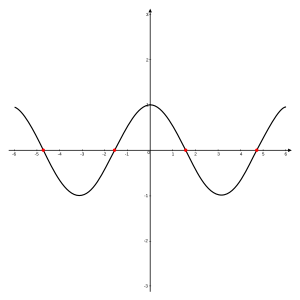
यदि फलन वास्तविक संख्याओं को वास्तविक संख्याओं में मैप करता है, तो इसके शून्य उन बिंदुओं के $x$- निर्देशांक होते हैं, जहां इस फलन का ग्राफ़ x-अक्ष से मिलता है। इस संदर्भ में ऐसे बिंदु $(x,0)$ के लिए एक वैकल्पिक नाम $x$-इंटरसेप्ट के रूप में होता है

समीकरण का सॉलूशन

अज्ञात $x$ में प्रत्येक समीकरण (गणित) को इस प्रकार पुनः लिखा जा सकता है,

$f(x)=0$

बायीं ओर के सभी पदों को पुनः समूहित करते है। इससे निष्कर्ष यह निकलता है कि ऐसे समीकरण के सॉलूशन बिल्कुल फलन $f$ के रूप में शून्य होते हैं और इस प्रकार दूसरे शब्दों में किसी फलन का शून्य वास्तव में फलन को 0 के बराबर करके प्राप्त समीकरण का एक सॉलूशन होता है और फलन के शून्य का अध्ययन बिल्कुल समीकरणों के सॉलूशन के अध्ययन के समान होता है।

बहुपद रुट

Main article: बहुपद रुट के गुण

बहुपद की विषम घात वाले प्रत्येक वास्तविक बहुपद में वास्तविक रुट की एक विषम संख्या होती है और इस प्रकार बहुपद की एक रुट की बहुलता (गणित) बहुलता की काउंटिंग होती है। इसी प्रकार, सम घात वाले वास्तविक बहुपद में वास्तविक रुट की संख्या भी सम होनी चाहिए। फलस्वरूप वास्तविक विषम बहुपदों में कम से कम एक वास्तविक रूट होना चाहिए क्योंकि सबसे छोटी विषम पूर्ण संख्या 1 होती है। जबकि सम बहुपदों में कोई भी नहीं होता है। इस सिद्धांत को मध्यवर्ती मूल्य प्रमेय के संदर्भ से सिद्ध किया जाता है, चूंकि बहुपद फलन सतत फलन के रूप में होते है, इसलिए ऋणात्मक से धनात्मक या इसके विपरीत में बदलने की प्रक्रिया में फलन का मान शून्य को पार करना चाहिए, जो सदैव विषम कार्यों के लिए होता है।

बीजगणित का फंडामेंटल प्रमेय

Main article: बीजगणित का फंडामेंटल प्रमेय

बीजगणित के मौलिक प्रमेय में कहा गया है कि घात $n$ के प्रत्येक बहुपद में $n$ सम्मिश्र रुट के रूप में होती हैं, जिन्हें उनकी बहुलता के साथ गिना जाता है। वास्तविक गुणांक वाले बहुपदों की अवास्तविक रुट सम्मिश्र संयुग्मी युग्मों के रूप में होती है। विएटा के सूत्र एक बहुपद के गुणांकों को उसके रुट के योग और गुणन से जोड़ते हैं।

कंप्यूटिंग रूट

Main articles: रुट फाइंडिंग कलन विधि, वास्तविक रुट आइसोलेशन, and समीकरण हल करना

फलन की रूट कंप्यूटिंग इस प्रकार होती है, उदाहरण के लिए बहुपद फलन के लिए अधिकांशतः विशेष या सन्निकटन प्रोद्योगिकीय के रूप में उपयोग की आवश्यकता होती है। उदाहरण के लिए न्यूटन की विधि आदि। चूंकि, कुछ बहुपद फलन जिनमें 4 से अधिक वाले बहुपद की सभी घातें सम्मलित होती है, उनके सभी रूट उनके गुणांकों के संदर्भ में बीजगणितीय फलन के रूप में व्यक्त किए जाते हैं और अधिक जानकारी के लिए, बीजगणितीय सॉलूशन में दिखाया गया है।

जीरो सेट

"जीरो सेट" redirects here. For म्यूजिकल एल्बम, see जीरो सेट.

गणित के विभिन्न क्षेत्रों में, किसी फलन (गणित) का शून्य सेट उसके सभी शून्यों का सेट होता है और इस प्रकार अधिक सटीक रूप से यदि $f:X\to \mathbb {R}$ एक वास्तविक मूल्य फलन के रूप में होते है और सामान्यतः कुछ एड्डीटीव समूह में मान लेने वाले फलन होते है, इसका शून्य सेट $f^{-1}(0)$, की व्युत्क्रम छवि $\{0\}$ में $X$.के रूप में होती है

फलन के कोडोमेन पर समान परिकल्पना के अनुसार फलन $f$ का एक लेवेल सेट फलन का शून्य सेट होता है $f-c$ के लिए $c$ के कोडोमेन में $f.$होता है

एक रेखीय मानचित्र के शून्य सेट को उसके कर्नेल (बीजगणित) के रूप में भी जाना जाता है।

फलन का कोज़ेरो सेट $f:X\to \mathbb {R}$ के शून्य समुच्चय का पूरक (सेट सिद्धांत) है और इस प्रकार $f$ का उपसमुच्चय $X$ है, जिस पर $f$ शून्येतर रूप में है।

अनुप्रयोग

बीजगणितीय ज्यामिति में, बीजीय विविधता की पसॉलूशन ी परिभाषा शून्य सेट के माध्यम से होती है। विशेष रूप से, एक एफ़िन बीजगणितीय सेट एक बहुपद वलय में कई बहुपदों के शून्य सेटों का सेट प्रतिच्छेदन है $k\left[x_{1},\ldots ,x_{n}\right]$ एक क्षेत्र पर (गणित)। इस संदर्भ में, शून्य सेट को कभी-कभी शून्य लोकस कहा जाता है।

गणितीय विश्लेषण और ज्यामिति में, कोई भी बंद सेट $\mathbb {R} ^{n}$ सभी पर परिभाषित एक सुचारु कार्य का शून्य सेट है $\mathbb {R} ^{n}$. यह पैराकॉम्पैक्टनेस के परिणाम के रूप में किसी भी चिकनी विविधता तक विस्तारित होता है। विभेदक ज्यामिति में, शून्य सेट का उपयोग अक्सर कई गुना ्स को परिभाषित करने के लिए किया जाता है। एक महत्वपूर्ण विशेष मामला यह है कि $f$ से एक सुचारू कार्य है $\mathbb {R} ^{p}$ को $\mathbb {R} ^{n}$. यदि शून्य एक नियमित मान है $f$, फिर शून्य सेट $f$ आयाम का एक सहज अनेक गुना है $m=p-n$ सबमर्शन_(गणित)#स्थानीय_सामान्य_फॉर्म द्वारा।

उदाहरण के लिए, इकाई $m$-गोले में $\mathbb {R} ^{m+1}$ वास्तविक-रुट ्यवान फलन का शून्य सेट है $f(x)=\Vert x\Vert ^{2}-1$.

यह भी देखें

• मार्डन का प्रमेय
• रुट -खोज एल्गोरिथ्म
• सेंडोव का अनुमान
• अनंत पर लुप्त हो जाना
• जीबरा क्रोससिंग
• शून्य और ध्रुव

अग्रिम पठन

• Weisstein, Eric W. "Root". MathWorld.