आर-समता: Difference between revisions

From Vigyanwiki
No edit summary
No edit summary
Line 1: Line 1:
{{Short description|Discrete symmetry in certain supersymmetric models}}
{{Short description|Discrete symmetry in certain supersymmetric models}}
आर-समता [[कण भौतिकी]] में अवधारणा है। [[न्यूनतम सुपरसिमेट्रिक मानक मॉडल]] में, बैरियन संख्या और [[लेप्टान संख्या]] अब सिद्धांत में सभी [[पुनर्सामान्यीकरण]] कपलिंगों द्वारा संरक्षित नहीं हैं। चूंकि बैरियन संख्या और लेप्टान संख्या संरक्षण का बहुत त्रुटिहीन परीक्षण किया गया है, इसलिए प्रयोगात्मक डेटा के साथ टकराव न होने के लिए इन युग्मों को बहुत छोटा होना आवश्यक है। आर-समता है <math>\mathbb{Z}_2</math> मिनिमल सुपरसिमेट्रिक स्टैंडर्ड मॉडल (एमएसएसएम) फ़ील्ड पर अभिनय करने वाली समरूपता जो इन कपलिंगों को रोकती है और इसे इस प्रकार परिभाषित किया जा सकता है<ref>
'''आर-समता''' [[कण भौतिकी]] में अवधारणा है। [[न्यूनतम सुपरसिमेट्रिक मानक मॉडल]] में, बैरियन संख्या और [[लेप्टान संख्या]] अब सिद्धांत में सभी [[पुनर्सामान्यीकरण]] योग्य कपलिंगों द्वारा संरक्षित नहीं हैं। चूंकि बैरियन संख्या और लेप्टान संख्या संरक्षण का बहुत त्रुटिहीन परीक्षण किया गया है, इसलिए प्रयोगात्मक डेटा के साथ टकराव न होने के लिए इन युग्मों को बहुत छोटा होना आवश्यक है। आर-समता <math>\mathbb{Z}_2</math> है मिनिमल सुपरसिमेट्रिक स्टैंडर्ड मॉडल (एमएसएसएम) फ़ील्ड पर अभिनय करने वाली समरूपता जो इन कपलिंगों को रोकती है और इसे इस प्रकार परिभाषित किया जा सकता है<ref>
{{cite journal
{{cite journal
  |last=Martin |first=S. P.
  |last=Martin |first=S. P.
Line 12: Line 12:
  |isbn=978-981-02-3553-6
  |isbn=978-981-02-3553-6
  |s2cid=118973381
  |s2cid=118973381
}}</ref> :<math>P_\mathrm{R} = (-1)^{3B+L+2s},</math>
}}</ref>
 
<math>P_\mathrm{R} = (-1)^{3B+L+2s},</math>
 
या, समकक्ष, जैसे
या, समकक्ष, जैसे
:<math>P_\mathrm{R} = (-1)^{3(B-L)+2s},</math>
:<math>P_\mathrm{R} = (-1)^{3(B-L)+2s},</math>
कहाँ {{mvar|s}} [[स्पिन (भौतिकी)]] है, {{mvar|B}} बेरिऑन संख्या है, और {{mvar|L}} लेप्टान संख्या है. सभी मानक मॉडल कणों में R-समता +1 होती है चूँकि सुपरसिमेट्रिक कणों में R-समता -1 होती है।
जहां {{mvar|s}} [[स्पिन (भौतिकी)]] है, {{mvar|B}} बैरियन संख्या है, और {{mvar|L}} लेप्टान संख्या है। सभी मानक मॉडल कणों में R-समता +1 होती है चूँकि सुपरसिमेट्रिक कणों में R-समता -1 होती है।


ध्यान दें कि विभिन्न प्रभावों और सिद्धांतों के साथ समता के विभिन्न रूप हैं, किसी को इस समता को [[समता (भौतिकी)]] के साथ भ्रमित नहीं करना चाहिए।
ध्यान दें कि विभिन्न प्रभावों और सिद्धांतों के साथ समता के विभिन्न रूप हैं, किसी को इस समता को [[समता (भौतिकी)]] के साथ भ्रमित नहीं करना चाहिए।


==[[ गहरे द्रव्य | गहरे द्रव्य]] उम्मीदवार==
==[[ गहरे द्रव्य | गहरे द्रव्य]] उम्मीदवार==
आर-समता संरक्षित होने से, [[सबसे हल्का सुपरसिमेट्रिक कण]] (लाइटेस्ट सुपरसिमेट्रिक पार्टिकल) क्षय नहीं हो सकता है। इसलिए यह सबसे हल्का कण (यदि यह अस्तित्व में है) ब्रह्मांड के देखे गए गायब द्रव्यमान का कारण हो सकता है जिसे आम तौर पर डार्क मैटर कहा जाता है।<ref>
आर-समता संरक्षित होने से, [[सबसे हल्का सुपरसिमेट्रिक कण]] (लाइटेस्ट सुपरसिमेट्रिक पार्टिकल) क्षय नहीं हो सकता है। इसलिए यह सबसे हल्का कण (यदि यह अस्तित्व में है) ब्रह्मांड के देखे गए गायब द्रव्यमान का कारण हो सकता है जिसे सामान्यतः डार्क मैटर कहा जाता है।<ref>
{{cite journal
{{cite journal
  |last1=Jungman |first1=G.
  |last1=Jungman |first1=G.
Line 33: Line 36:
  |bibcode=1996PhR...267..195J
  |bibcode=1996PhR...267..195J
  |s2cid=119067698
  |s2cid=119067698
}}</ref> अवलोकनों को फिट करने के लिए, यह माना जाता है कि इस कण का द्रव्यमान है {{val|100|ul=GeV/c2}} को {{val|1|ul=TeV/c2}}, तटस्थ है और केवल [[कमजोर अंतःक्रिया]]ओं और गुरुत्वाकर्षण के माध्यम से अंतःक्रिया करता है। इसे अक्सर कमजोर रूप से अंतःक्रिया करने वाला विशाल कण या WIMP कहा जाता है।
}}</ref> अवलोकनों को फिट करने के लिए, यह माना जाता है कि इस कण का द्रव्यमान है {{val|100|ul=GeV/c2}} को {{val|1|ul=TeV/c2}}, तटस्थ है और केवल [[कमजोर अंतःक्रिया]]ओं और गुरुत्वाकर्षण के माध्यम से अंतःक्रिया करता है। इसे अधिकांशतः कमजोर रूप से अंतःक्रिया करने वाला विशाल कण या डब्ल्यूआईएमपी कहा जाता है।


आमतौर पर एमएसएसएम का डार्क मैटर उम्मीदवार इलेक्ट्रोवीक [[गौगिनो]] और [[हिग्सिनो]] का मिश्रण होता है और इसे [[न्यूट्रलिनो]] कहा जाता है। एमएसएसएम के विस्तार में यह संभव है कि [[न्युट्रीनो]] डार्क मैटर का उम्मीदवार हो। अन्य संभावना [[आकर्षण-शक्ति]] है, जो केवल गुरुत्वाकर्षण के माध्यम से संपर्क करता है और इसके लिए सख्त आर-समता की आवश्यकता नहीं होती है।
सामान्यतः एमएसएसएम का डार्क मैटर उम्मीदवार इलेक्ट्रोवीक [[गौगिनो]] और [[हिग्सिनो]] का मिश्रण होता है और इसे [[न्यूट्रलिनो]] कहा जाता है। एमएसएसएम के विस्तार में यह संभव है कि [[न्युट्रीनो]] डार्क मैटर का उम्मीदवार हो। अन्य संभावना [[आकर्षण-शक्ति]] है, जो केवल गुरुत्वाकर्षण के माध्यम से संपर्क करता है और इसके लिए सख्त आर-समता की आवश्यकता नहीं होती है।


==आर-समता एमएसएसएम के कपलिंग का उल्लंघन कर रही है==
==आर-समता एमएसएसएम के कपलिंग का उल्लंघन कर रही है==
एमएसएसएम के पुनर्सामान्यीकरण योग्य आर-समता उल्लंघन कपलिंग हैं
एमएसएसएम के पुनर्सामान्यीकरण योग्य आर-समता उल्लंघन कपलिंग हैं
* <math> \int d^2\theta\; \lambda_1\; U^c D^c D^c </math> का उल्लंघन करती है {{mvar|B}} 1 इकाई से
* <math> \int d^2\theta\; \lambda_1\; U^c D^c D^c </math> का उल्लंघन करती है {{mvar|B}} 1 इकाई से
अकेले इस युग्मन से जुड़ी सबसे मजबूत बाधा एंटीन्यूट्रॉन | न्यूट्रॉन-एंटीन्यूट्रॉन दोलनों के गैर-अवलोकन से है।
अकेले इस युग्मन से जुड़ी सबसे मजबूत बाधा एंटीन्यूट्रॉन दोलनों के गैर-अवलोकन से है।


* <math>\int d^2 \theta\; \lambda_2\; Q D^c L </math> का उल्लंघन करती है {{mvar|L}} 1 इकाई से
* <math>\int d^2 \theta\; \lambda_2\; Q D^c L </math> का उल्लंघन करती है {{mvar|L}} 1 इकाई से
अकेले इस युग्मन से जुड़ी सबसे मजबूत बाधा [[फर्मी युग्मन स्थिरांक]] की सार्वभौमिकता का उल्लंघन है <math>G_F</math> क्वार्क और लेप्टोनिक आवेशित धारा क्षय में।
अकेले इस युग्मन से जुड़ी सबसे मजबूत बाधा [[फर्मी युग्मन स्थिरांक]] की सार्वभौमिकता क्वार्क और लेप्टोनिक आवेशित धारा क्षय में <math>G_F</math> का उल्लंघन है।


* <math>\int d^2 \theta\; \lambda_3\; L E^cL </math> का उल्लंघन करती है {{mvar|L}} 1 इकाई से
* <math>\int d^2 \theta\; \lambda_3\; L E^cL </math> का 1 इकाई से उल्लंघन करता है
अकेले इस युग्मन से जुड़ी सबसे मजबूत बाधा लेप्टोनिक चार्ज किए गए वर्तमान क्षय में फर्मी स्थिरांक की सार्वभौमिकता का उल्लंघन है।
अकेले इस युग्मन से जुड़ी सबसे मजबूत बाधा लेप्टोनिक चार्ज किए गए वर्तमान क्षय में फर्मी स्थिरांक की सार्वभौमिकता का उल्लंघन है।


* <math>\int d^2 \theta\; \kappa\; L H_u</math> का उल्लंघन करती है {{mvar|L}} 1 इकाई से
* <math>\int d^2 \theta\; \kappa\; L H_u</math> का 1 इकाई से उल्लंघन करता है
अकेले इस युग्मन से जुड़ी सबसे मजबूत बाधा यह है कि यह बड़े न्यूट्रिनो द्रव्यमान की ओर ले जाता है।
अकेले इस युग्मन से जुड़ी सबसे मजबूत बाधा यह है कि यह बड़े न्यूट्रिनो द्रव्यमान की ओर ले जाता है।


चूँकि एकल कपलिंग पर बाधाएं काफी मजबूत हैं, यदि कई कपलिंग को साथ जोड़ दिया जाता है, तो वे प्रोटॉन क्षय का कारण बनते हैं। इस प्रकार प्रोटॉन क्षय दर पर अधिकतम सीमा से युग्मन के मूल्यों पर और अधिक अधिकतम सीमा होती है।
चूँकि एकल कपलिंग पर बाधाएं अत्यधिक मजबूत हैं, यदि कई कपलिंग को साथ जोड़ दिया जाता है, तो वे प्रोटॉन क्षय का कारण बनते हैं। इस प्रकार प्रोटॉन क्षय दर पर अधिकतम सीमा से युग्मन के मूल्यों पर और अधिक अधिकतम सीमा होती है।


==प्रोटॉन क्षय==
==प्रोटॉन क्षय==
Line 59: Line 62:


==आर-समता की संभावित उत्पत्ति==
==आर-समता की संभावित उत्पत्ति==
आर-समता को प्रेरित करने का बहुत ही आकर्षक विधि है, {{nowrap|{{mvar|B − L}}}} सतत गेज समरूपता है जो वर्तमान प्रयोगशालाओं के लिए पहुंच नहीं होने वाले स्तर पर स्वतंत्र रूप से टूट जाती है। सतत <math>U(1)_{B-L}</math> वे संविदानशील शर्तें निष्क्रिय करती है जो B और L का उल्लंघन करने वाले रेनॉर्मेनटबल शर्तों को मना करती हैं।<ref>
आर-समता को प्रेरित करने का बहुत ही आकर्षक विधि है, {{nowrap|{{mvar|B − L}}}} सतत गेज समरूपता है जो वर्तमान प्रयोगशालाओं के लिए पहुंच नहीं होने वाले स्तर पर स्वतंत्र रूप से टूट जाती है। सतत <math>U(1)_{B-L}</math> वे संविदानशील शर्तें निष्क्रिय करती है जो B और L का उल्लंघन करने वाले रेनॉर्मेनटबल शर्तों को मना करती हैं।<ref>
{{cite journal
{{cite journal
  |last=Mohapatra |first=R.N.
  |last=Mohapatra |first=R.N.
Line 106: Line 109:
  |pmid=10020912
  |pmid=10020912
  |s2cid=5751474
  |s2cid=5751474
}}</ref> यदि <math>U(1)_{B-L}</math> को केवल स्केलर वैक्यूम अपेक्षा मूल्यों (या अन्य क्रम पैरामीटर) द्वारा टूटा जाता है जो {{nowrap|3({{mvar|B − L}})}}, के सममिति मूल्यों को लेकर समर्थ हैं, तो एक ऐसा बिल्कुल संरक्षित विच्छेदित उपसमूह होता है जिसमें आवश्यक गुण होते हैं।<ref>
}}</ref> यदि <math>U(1)_{B-L}</math> को केवल स्केलर वैक्यूम अपेक्षा मूल्यों (या अन्य क्रम पैरामीटर) द्वारा टूटा जाता है जो {{nowrap|3({{mvar|B − L}})}}, के सममिति मूल्यों को लेकर समर्थ हैं, तो ऐसा बिल्कुल संरक्षित विच्छेदित उपसमूह होता है जिसमें आवश्यक गुण होते हैं।<ref>
{{cite journal
{{cite journal
  |last1=Fayet |first1=P.
  |last1=Fayet |first1=P.
Line 155: Line 158:
  |bibcode=1978PhLB...76..575F
  |bibcode=1978PhLB...76..575F
  |doi=10.1016/0370-2693(78)90858-4
  |doi=10.1016/0370-2693(78)90858-4
}}</ref> यहां महत्वपूर्ण मुद्दा यह है कि स्न्यूट्रीनो (न्यूट्रीनो का सुपरसिमेट्रिक साथी), जो R-पैरिटी के तहत विषम है, क्या एक वैक्यूम इक्षेप्टेशन मूल्य विकसित करता है या नहीं, यह निर्धारित करना है। दर्शाता जा सकता है, दृष्टांतिक प्रमाणों के आधार पर, कि यह किसी भी सिद्धांत में संभव नहीं है जहां <math>U(1)_{B-L}</math> [[ विद्युत |विद्युत]] से काफी ऊपर के पैमाने पर टूटा हुआ है। बड़े पैमाने पर सीसॉ तंत्र पर आधारित किसी भी सिद्धांत में यह सच है।<ref>
}}</ref> यहां महत्वपूर्ण मुद्दा यह है कि स्न्यूट्रीनो (न्यूट्रीनो का सुपरसिमेट्रिक साथी), जो R-पैरिटी के अनुसार विषम है, क्या एक वैक्यूम इक्षेप्टेशन मूल्य विकसित करता है या नहीं, यह निर्धारित करना है। दर्शाता जा सकता है, दृष्टांतिक प्रमाणों के आधार पर, कि यह किसी भी सिद्धांत में संभव नहीं है जहां <math>U(1)_{B-L}</math> [[ विद्युत |विद्युत]] से अत्यधिक ऊपर के पैमाने पर टूटा हुआ है। बड़े पैमाने पर सीसॉ तंत्र पर आधारित किसी भी सिद्धांत में यह सच है।<ref>
{{cite journal
{{cite journal
  |last1=Aulakh |first1=C.S.
  |last1=Aulakh |first1=C.S.

Revision as of 21:44, 30 November 2023

आर-समता कण भौतिकी में अवधारणा है। न्यूनतम सुपरसिमेट्रिक मानक मॉडल में, बैरियन संख्या और लेप्टान संख्या अब सिद्धांत में सभी पुनर्सामान्यीकरण योग्य कपलिंगों द्वारा संरक्षित नहीं हैं। चूंकि बैरियन संख्या और लेप्टान संख्या संरक्षण का बहुत त्रुटिहीन परीक्षण किया गया है, इसलिए प्रयोगात्मक डेटा के साथ टकराव न होने के लिए इन युग्मों को बहुत छोटा होना आवश्यक है। आर-समता है मिनिमल सुपरसिमेट्रिक स्टैंडर्ड मॉडल (एमएसएसएम) फ़ील्ड पर अभिनय करने वाली समरूपता जो इन कपलिंगों को रोकती है और इसे इस प्रकार परिभाषित किया जा सकता है[1]

या, समकक्ष, जैसे

जहां s स्पिन (भौतिकी) है, B बैरियन संख्या है, और L लेप्टान संख्या है। सभी मानक मॉडल कणों में R-समता +1 होती है चूँकि सुपरसिमेट्रिक कणों में R-समता -1 होती है।

ध्यान दें कि विभिन्न प्रभावों और सिद्धांतों के साथ समता के विभिन्न रूप हैं, किसी को इस समता को समता (भौतिकी) के साथ भ्रमित नहीं करना चाहिए।

गहरे द्रव्य उम्मीदवार

आर-समता संरक्षित होने से, सबसे हल्का सुपरसिमेट्रिक कण (लाइटेस्ट सुपरसिमेट्रिक पार्टिकल) क्षय नहीं हो सकता है। इसलिए यह सबसे हल्का कण (यदि यह अस्तित्व में है) ब्रह्मांड के देखे गए गायब द्रव्यमान का कारण हो सकता है जिसे सामान्यतः डार्क मैटर कहा जाता है।[2] अवलोकनों को फिट करने के लिए, यह माना जाता है कि इस कण का द्रव्यमान है 100 GeV/c2 को 1 TeV/c2, तटस्थ है और केवल कमजोर अंतःक्रियाओं और गुरुत्वाकर्षण के माध्यम से अंतःक्रिया करता है। इसे अधिकांशतः कमजोर रूप से अंतःक्रिया करने वाला विशाल कण या डब्ल्यूआईएमपी कहा जाता है।

सामान्यतः एमएसएसएम का डार्क मैटर उम्मीदवार इलेक्ट्रोवीक गौगिनो और हिग्सिनो का मिश्रण होता है और इसे न्यूट्रलिनो कहा जाता है। एमएसएसएम के विस्तार में यह संभव है कि न्युट्रीनो डार्क मैटर का उम्मीदवार हो। अन्य संभावना आकर्षण-शक्ति है, जो केवल गुरुत्वाकर्षण के माध्यम से संपर्क करता है और इसके लिए सख्त आर-समता की आवश्यकता नहीं होती है।

आर-समता एमएसएसएम के कपलिंग का उल्लंघन कर रही है

एमएसएसएम के पुनर्सामान्यीकरण योग्य आर-समता उल्लंघन कपलिंग हैं

  • का उल्लंघन करती है B 1 इकाई से

अकेले इस युग्मन से जुड़ी सबसे मजबूत बाधा एंटीन्यूट्रॉन दोलनों के गैर-अवलोकन से है।

  • का उल्लंघन करती है L 1 इकाई से

अकेले इस युग्मन से जुड़ी सबसे मजबूत बाधा फर्मी युग्मन स्थिरांक की सार्वभौमिकता क्वार्क और लेप्टोनिक आवेशित धारा क्षय में का उल्लंघन है।

  • का 1 इकाई से उल्लंघन करता है

अकेले इस युग्मन से जुड़ी सबसे मजबूत बाधा लेप्टोनिक चार्ज किए गए वर्तमान क्षय में फर्मी स्थिरांक की सार्वभौमिकता का उल्लंघन है।

  • का 1 इकाई से उल्लंघन करता है

अकेले इस युग्मन से जुड़ी सबसे मजबूत बाधा यह है कि यह बड़े न्यूट्रिनो द्रव्यमान की ओर ले जाता है।

चूँकि एकल कपलिंग पर बाधाएं अत्यधिक मजबूत हैं, यदि कई कपलिंग को साथ जोड़ दिया जाता है, तो वे प्रोटॉन क्षय का कारण बनते हैं। इस प्रकार प्रोटॉन क्षय दर पर अधिकतम सीमा से युग्मन के मूल्यों पर और अधिक अधिकतम सीमा होती है।

प्रोटॉन क्षय

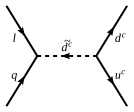
R-parity violating decay.svg

जब बैरियन और लेप्टान संख्या को संरक्षित नहीं हैं और बिग ओ नोटेशन कप्लिंग्स को आर-समता का उल्लंघन करने वाले कपलिंग के लिए लिया जाता है, तो प्रोटॉन का विघटन लगभग 10−2 सेकंड में क्षय हो सकता है यदि न्यूनतम स्वाद उल्लंघन मान लिया जाए तो प्रोटॉन का जीवनकाल 1 वर्ष तक बढ़ाया जा सकता है। चूंकि प्रोटॉन का जीवनकाल 1033 से 1034 वर्ष से अधिक होने का पर्याय (त्रुटिहीन क्षय चैनल के आधार पर), यह मॉडल को को अधिक अप्रिय होता है। आर-समता युग्मन का उल्लंघन करने वाले सभी पुनर्सामान्यीकरण योग्य बैरियन और लेप्टान संख्या को शून्य पर समुच्चय करती है और प्रोटॉन पुनर्सामान्यीकरण योग्य स्तर पर स्थिर होता है और प्रोटॉन का जीवनकाल 1032 वर्ष तक बढ़ जाता है और लगभग वर्तमान अवलोकन आंकड़ों के अनुरूप है।

क्योंकि प्रोटॉन क्षय में लेप्टान और बैरियन संख्या दोनों का साथ उल्लंघन होता है, युग्मन का उल्लंघन करने वाला कोई भी पुनर्सामान्यीकरण योग्य आर-समता प्रोटॉन क्षय की ओर नहीं ले जाता है। इसने आर-समता उल्लंघन के अध्ययन को प्रेरित किया है जहां आर-समता का उल्लंघन करने वाले कपलिंग का केवल समुच्चय गैर-शून्य है जिसे कभी-कभी एकल युग्मन प्रभुत्व परिकल्पना कहा जाता है।

आर-समता की संभावित उत्पत्ति

आर-समता को प्रेरित करने का बहुत ही आकर्षक विधि है, B − L सतत गेज समरूपता है जो वर्तमान प्रयोगशालाओं के लिए पहुंच नहीं होने वाले स्तर पर स्वतंत्र रूप से टूट जाती है। सतत वे संविदानशील शर्तें निष्क्रिय करती है जो B और L का उल्लंघन करने वाले रेनॉर्मेनटबल शर्तों को मना करती हैं।[3][4][5][6] यदि को केवल स्केलर वैक्यूम अपेक्षा मूल्यों (या अन्य क्रम पैरामीटर) द्वारा टूटा जाता है जो 3(B − L), के सममिति मूल्यों को लेकर समर्थ हैं, तो ऐसा बिल्कुल संरक्षित विच्छेदित उपसमूह होता है जिसमें आवश्यक गुण होते हैं।[7][8][9][10][11] यहां महत्वपूर्ण मुद्दा यह है कि स्न्यूट्रीनो (न्यूट्रीनो का सुपरसिमेट्रिक साथी), जो R-पैरिटी के अनुसार विषम है, क्या एक वैक्यूम इक्षेप्टेशन मूल्य विकसित करता है या नहीं, यह निर्धारित करना है। दर्शाता जा सकता है, दृष्टांतिक प्रमाणों के आधार पर, कि यह किसी भी सिद्धांत में संभव नहीं है जहां विद्युत से अत्यधिक ऊपर के पैमाने पर टूटा हुआ है। बड़े पैमाने पर सीसॉ तंत्र पर आधारित किसी भी सिद्धांत में यह सच है।[12] परिणामस्वरूप, ऐसे सिद्धांतों में आर-समता सभी ऊर्जाओं पर त्रुटिहीन रहती है।

यह प्रक्रिया एसओ(10) भव्य एकीकृत सिद्धांत में स्वचालित समरूपता के रूप में उत्पन्न हो सकती है। इस आर-समता के स्वाभाविक होने का कारण है कि एसओ(10) में मानक मॉडल फ़र्मियन को 16 आयामी स्पिनर प्रतिनिधित्व से उत्पन्न किया जाता हैं, चूँकि हिग्स को 10 आयामी सदिश प्रतिनिधित्व से उत्पन्न होते हैं। एसओ(10) अपरिवर्तनीय युग्मन बनाने के लिए, किसी के पास सम संख्या में स्पिनर फ़ील्ड होने चाहिए (अर्थात स्पिनर समता होनी चाहिए)। जीयूटी समरूपता टूटने के बाद, यह स्पिनर समता आर-समता में उतर जाती है, जब तक कि जीयूटी समरूपता को तोड़ने के लिए किसी स्पिनर फ़ील्ड का उपयोग नहीं किया जाता है। ऐसे SO(10) सिद्धांतों के स्पष्ट उदाहरण तैयार किए गए हैं।[13][14]

यह भी देखें

संदर्भ

  1. ↑ Martin, S. P. (6 Sep 2011). "A Supersymmetry Primer". Advanced Series on Directions in High Energy Physics. 18: 1–98. arXiv:hep-ph/9709356. doi:10.1142/9789812839657_0001. ISBN 978-981-02-3553-6. S2CID 118973381.
  2. ↑ Jungman, G.; Kamionkowski, M.; Griest, K. (1996). "Supersymmetric dark matter". Physics Reports. 267 (5–6): 195–373. arXiv:hep-ph/9506380. Bibcode:1996PhR...267..195J. doi:10.1016/0370-1573(95)00058-5. S2CID 119067698.
  3. ↑ Mohapatra, R.N. (1986). "New contributions to neutrinoless double-beta decay in supersymmetric theories". Physical Review D. 34 (11): 3457–3461. Bibcode:1986PhRvD..34.3457M. doi:10.1103/PhysRevD.34.3457. PMID 9957083.
  4. ↑ Font, A.; Ibáñez, L.E.; Quevedo, F. (1989). "Does proton stability imply the existence of an extra Z0?" (PDF). Physics Letters B. 228 (1): 79–88. Bibcode:1989PhLB..228...79F. doi:10.1016/0370-2693(89)90529-7.
  5. ↑ Martin, S.P. (1992). "Some simple criteria for gauged R parity". Physical Review D. 46 (7): R2769–R2772. arXiv:hep-ph/9207218. Bibcode:1992PhRvD..46.2769M. doi:10.1103/PhysRevD.46.R2769. PMID 10015267. S2CID 14821065.
  6. ↑ Martin, S.P. (1996). "Implications of supersymmetric models with natural R-parity conservation". Physical Review D. 54 (3): 2340–2348. arXiv:hep-ph/9602349. Bibcode:1996PhRvD..54.2340M. doi:10.1103/PhysRevD.54.2340. PMID 10020912. S2CID 5751474.
  7. ↑ Fayet, P. (1975). "Supergauge invariant extension of the Higgs mechanism and a model for the electron and its neutrino". Nuclear Physics B. 90: 104–124. Bibcode:1975NuPhB..90..104F. doi:10.1016/0550-3213(75)90636-7.
  8. ↑ Salam, A.; Strathdee, J. (1975). "Supersymmetry and fermion-number conservation". Nuclear Physics B. 87 (1): 85–92. Bibcode:1975NuPhB..87...85S. doi:10.1016/0550-3213(75)90253-9.
  9. ↑ Farrar, G.R.; Weinberg, S. (1983). "Supersymmetry at ordinary energies. II. R invariance, Goldstone bosons, and gauge-fermion masses". Physical Review D. 27 (11): 2732. Bibcode:1983PhRvD..27.2732F. doi:10.1103/PhysRevD.27.2732.
  10. ↑ Fayet, P. (1977). "Spontaneously broken supersymmetric theories of weak, electromagnetic and strong interactions". Physics Letters B. 69 (4): 489–494. Bibcode:1977PhLB...69..489F. doi:10.1016/0370-2693(77)90852-8.
  11. ↑ Farrar, G.R.; Fayet, P. (1978). "Phenomenology of the production, decay, and detection of new hadronic states associated with supersymmetry". Physics Letters B. 76 (5): 575. Bibcode:1978PhLB...76..575F. doi:10.1016/0370-2693(78)90858-4.
  12. ↑ Aulakh, C.S.; Melfo, A.; Rašin, A.; Senjanović, G. (1998). "Supersymmetry and large scale left-right symmetry". Physical Review D. 58 (11): 115007. arXiv:hep-ph/9712551. Bibcode:1998PhRvD..58k5007A. doi:10.1103/PhysRevD.58.115007. S2CID 43296921.
  13. ↑ Aulakh, C.S.; Bajc, B.; Melfo, A.; Rašin, A.; Senjanović, G. (2001). "SO(10) theory of R-parity and neutrino mass". Nuclear Physics B. 597 (1–3): 89–109. arXiv:hep-ph/0004031. Bibcode:2001NuPhB.597...89A. doi:10.1016/S0550-3213(00)00721-5. S2CID 119100803.
  14. ↑ Aulakh, C.S.; Bajc, B.; Melfo, A.; Senjanović, G.; Vissani, F. (2004). "The minimal supersymmetric grand unified theory". Physics Letters B. 588 (3–4): 196–202. arXiv:hep-ph/0306242. Bibcode:2004PhLB..588..196A. doi:10.1016/j.physletb.2004.03.031. S2CID 119401374.

बाहरी संबंध

Retrieved from ‘https://www.vigyanwiki.in/index.php?title=आर-समता&oldid=277156’