आवृत्ति-समाधान प्रकाशीय गेटिंग: Difference between revisions
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
''' | '''आवृत्ति-समाधान प्रकाशीय गेटिंग''' (एफआरओजी) [[अल्ट्राशॉर्ट पल्स|अति लघु पल्स]] के वर्णक्रमीय चरण को मापने के लिए सामान्य विधि है, जिसकी लंबाई [[गुजरने|निकलने]] से लेकर लगभग [[नैनोसेकंड]] तक होती है। 1991 में रिक ट्रेबिनो और डैनियल जे. केन द्वारा आविष्कार किया गया, फ्रॉग इस समस्या को हल करने वाली पहली तकनीक थी, जो कठिन है क्योंकि, सामान्यतः, किसी घटना को समय में मापने के लिए, इसे मापने के लिए छोटी घटना की आवश्यकता होती है। उदाहरण के लिए, साबुन के बुलबुले फूटने की क्रिया को मापने के लिए कम अवधि वाले स्ट्रोब लाइट की आवश्यकता होती है। चूँकि अति लघु लेज़र पल्स अब तक की सबसे छोटी घटनाएँ हैं, एफआरओजी से पहले, यह अनेक लोगों द्वारा विचार किया गया था कि समय में उनका पूरा माप संभव नहीं था। चूँकि, एफआरओजी ने पल्स के ऑटो-स्पेक्ट्रोग्राम को मापकर समस्या का समाधान किया, जिसमें पल्स स्वयं को [[अरैखिक ऑप्टिकल माध्यम|अरैखिक प्रकाशीय माध्यम]] में गेट करता है। अरेखीय-प्रकाशीय माध्यम और पल्स के परिणामी गेटेड टुकड़े को दो स्पंदनों के बीच विलंब फिर फलन के रूप में वर्णक्रमीय रूप से हल किया जाता है। इसके एफआरओजी ट्रेस से पल्स की पुनर्प्राप्ति द्वि-आयामी चरण-पुनर्प्राप्ति एल्गोरिथ्म का उपयोग करके पूरी की जाती है। | ||
एफआरओजी वर्तमान में अति लघु लेजर पल्स को मापने के लिए मानक तकनीक है, और यह लोकप्रिय भी है, इसने [[ऑप्टिकल ऑटोसहसंबंध]] नामक पुरानी विधि का स्थान ले लिया है, जो केवल पल्स लंबाई के लिए मोटा अनुमान देती थी। एफआरओजी बस वर्णक्रमीय रूप से हल किया गया ऑटोसहसंबंध है, जो स्पष्ट पल्स तीव्रता और चरण बनाम समय को पुनः प्राप्त करने के लिए चरण-पुनर्प्राप्ति एल्गोरिदम के उपयोग की अनुमति देता है। यह अधिक सरल और अधिक सम्मिश्र | एफआरओजी वर्तमान में अति लघु लेजर पल्स को मापने के लिए मानक तकनीक है, और यह लोकप्रिय भी है, इसने [[ऑप्टिकल ऑटोसहसंबंध|प्रकाशीय ऑटोसहसंबंध]] नामक पुरानी विधि का स्थान ले लिया है, जो केवल पल्स लंबाई के लिए मोटा अनुमान देती थी। एफआरओजी बस वर्णक्रमीय रूप से हल किया गया ऑटोसहसंबंध है, जो स्पष्ट पल्स तीव्रता और चरण बनाम समय को पुनः प्राप्त करने के लिए चरण-पुनर्प्राप्ति एल्गोरिदम के उपयोग की अनुमति देता है। यह अधिक सरल और अधिक सम्मिश्र अति लघु लेजर पल्स दोनों को माप सकता है, और इसने संदर्भ पल्स के उपयोग के बिना अब तक मापी गई सबसे सम्मिश्र पल्स को मापा है। इस प्रकार से एफआरओजी के सरल संस्करण उपस्तिथ हैं (संक्षिप्त रूप में, [[GRENOUILLE|ग्रेनोइल]], एफआरओजी के लिए फ्रांसीसी शब्द), केवल कुछ सरलता से संरेखित प्रकाशीय घटकों का उपयोग करते हुए। फ्रॉग और ग्रेनोइल दोनों संसार के अनुसंधान और औद्योगिक प्रयोगशालाओं में समान उपयोग में हैं। | ||
==सिद्धांत== | ==सिद्धांत== | ||
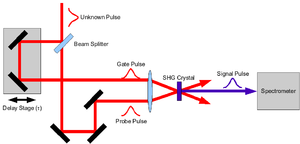
[[Image:SHG FROG.png|thumb|right|300px|एक विशिष्ट प्रयोगात्मक, मल्टीशॉट एसएचजी फ्रॉग स्थापना का योजनाबद्ध विवरण।]]एफआरओजी और ऑटोसहसंबंध गैर-रेखीय माध्यम में पल्स को अपने साथ संयोजित करने के विचार को साझा करते हैं। चूंकि गैर-रेखीय माध्यम केवल तभी वांछित संकेत उत्पन्न करेगा जब दोनों पल्स ही समय में उपस्तिथ हों (अर्थात " | [[Image:SHG FROG.png|thumb|right|300px|एक विशिष्ट प्रयोगात्मक, मल्टीशॉट एसएचजी फ्रॉग स्थापना का योजनाबद्ध विवरण।]]एफआरओजी और ऑटोसहसंबंध गैर-रेखीय माध्यम में पल्स को अपने साथ संयोजित करने के विचार को साझा करते हैं। चूंकि गैर-रेखीय माध्यम केवल तभी वांछित संकेत उत्पन्न करेगा जब दोनों पल्स ही समय में उपस्तिथ हों (अर्थात "प्रकाशीय गेटिंग"), पल्स प्रतियों के बीच विलंब को अलग-अलग करना और प्रत्येक विलंब पर संकेत को मापने से पल्स की लंबाई का अस्पष्ट अनुमान मिलता है। ऑटोकोरेलेटर्स अरेखीय संकेत क्षेत्र की तीव्रता को मापकर पल्स को मापते हैं। इस प्रकार से पल्स लंबाई का अनुमान लगाने के लिए पल्स आकार मानने की आवश्यकता होती है, और पल्स विद्युत क्षेत्र के चरण को पूर्णतः भी नहीं मापा जा सकता है। एफआरओजी केवल तीव्रता के अतिरिक्त प्रत्येक विलंब (इसलिए "आवृत्ति-समाधान") पर संकेत के विस्तार को मापकर इस विचार का विस्तार करता है। यह माप पल्स का [[ spectrogram |स्पेक्ट्रोग्राम]] बनाता है, जिसका उपयोग समय या आवृत्ति के फलन के रूप में सम्मिश्र विद्युत क्षेत्र को निर्धारित करने के लिए किया जा सकता है जब तक कि माध्यम की गैर-रैखिकता ज्ञात हो। | ||
फ्रॉग स्पेक्ट्रोग्राम (सामान्यतः फ्रॉग ट्रेस कहा जाता है) आवृत्ति <math>\omega</math> और विलंब <math>\tau</math> के फलन के रूप में तीव्रता का ग्राफ है, चूँकि, अरेखीय अंतःक्रिया से | फ्रॉग स्पेक्ट्रोग्राम (सामान्यतः फ्रॉग ट्रेस कहा जाता है) आवृत्ति <math>\omega</math> और विलंब <math>\tau</math> के फलन के रूप में तीव्रता का ग्राफ है, चूँकि, अरेखीय अंतःक्रिया से संकेत क्षेत्र को समय डोमेन में व्यक्त करना सरल है, इसलिए एफआरओजी ट्रेस के लिए विशिष्ट अभिव्यक्ति में [[फूरियर रूपांतरण]] सम्मिलित है। | ||
: <math>I_\text{FROG}(\omega,\tau) = \left| E_\text{sig}(\omega,\tau) \right|^2 = \left| FT[ E_\text{sig}(t,\tau)] \right|^2 = \left| \int_{-\infty}^\infty E_{sig}(t,\tau) e^{-i \omega t} \,dt \right|^2.</math> | : <math>I_\text{FROG}(\omega,\tau) = \left| E_\text{sig}(\omega,\tau) \right|^2 = \left| FT[ E_\text{sig}(t,\tau)] \right|^2 = \left| \int_{-\infty}^\infty E_{sig}(t,\tau) e^{-i \omega t} \,dt \right|^2.</math> | ||
अरेखीय संकेत क्षेत्र <math>E_\text{sig}(t,\tau)</math> मूल पल्स <math>E(t)</math>, पर निर्भर करता है, और गैर-रेखीय प्रक्रिया का उपयोग किया जाता है, जिसे लगभग | अरेखीय संकेत क्षेत्र <math>E_\text{sig}(t,\tau)</math> मूल पल्स <math>E(t)</math>, पर निर्भर करता है, और गैर-रेखीय प्रक्रिया का उपयोग किया जाता है, जिसे लगभग सदैव <math>E_\text{gate}(t - \tau)</math> के रूप में व्यक्त किया जा सकता है , जैसे कि <math>E_\text{sig}(t,\tau) = E(t)E_\text{gate}(t - \tau)</math>. सबसे सामान्य गैर-रैखिकता [[दूसरी हार्मोनिक पीढ़ी]] है, जहां <math>E_\text{gate}(t - \tau) = E(t - \tau)</math>. पल्स क्षेत्र के संदर्भ में ट्रेस के लिए अभिव्यक्ति तब है: | ||
:<math>I_\text{SHG FROG}(\omega,\tau) = \left| \int_{-\infty}^\infty E(t) E(t - \tau) e^{-i \omega t} \,dt \right|^2.</math> | :<math>I_\text{SHG FROG}(\omega,\tau) = \left| \int_{-\infty}^\infty E(t) E(t - \tau) e^{-i \omega t} \,dt \right|^2.</math> | ||
| Line 17: | Line 17: | ||
==प्रयोग== | ==प्रयोग== | ||
एक विशिष्ट | एक विशिष्ट बहु-शॉट फ्रॉग स्थापना में, अज्ञात पल्स को किरण विभाजक के साथ दो प्रतियों में विभाजित किया जाता है। एक प्रति में दूसरी की तुलना में ज्ञात मात्रा से विलंब होती है। दोनों पल्सेस को गैर-रेखीय माध्यम में ही बिंदु पर केंद्रित किया जाता है, और गैर-रेखीय संकेत के विस्तार को वर्णक्रममापी से मापा जाता है। यह प्रक्रिया अनेक विलंब बिंदुओं के लिए दोहराई जाती है। | ||
कुछ सामान्य समायोजनों के साथ ही शॉट में फ्रॉग मापन किया जा सकता है। दो पल्स प्रतियों को कोण पर पार किया जाता है और बिंदु के अतिरिक्त रेखा पर केंद्रित किया जाता है। यह लाइन फोकस के साथ दो पल्स के बीच अलग-अलग विलंब उत्पन्न करता है। इस आकृति में, माप को अधिकृत करने के लिए घर-निर्मित वर्णक्रममापी का उपयोग करना सामान्य है, जिसमें विवर्तन झंझरी और कैमरा सम्मिलित होता है। | कुछ सामान्य समायोजनों के साथ ही शॉट में फ्रॉग मापन किया जा सकता है। दो पल्स प्रतियों को कोण पर पार किया जाता है और बिंदु के अतिरिक्त रेखा पर केंद्रित किया जाता है। यह लाइन फोकस के साथ दो पल्स के बीच अलग-अलग विलंब उत्पन्न करता है। इस आकृति में, माप को अधिकृत करने के लिए घर-निर्मित वर्णक्रममापी का उपयोग करना सामान्य है, जिसमें विवर्तन झंझरी और कैमरा सम्मिलित होता है। | ||
| Line 24: | Line 24: | ||
यद्यपि यह सैद्धांतिक रूप से कुछ सीमा तक सम्मिश्र है, सामान्यीकृत अनुमानों की विधि एफआरओजी चिन्हों से पल्सेस को पुनः प्राप्त करने के लिए अत्यंत विश्वसनीय विधि प्रमाणित हुई है। दुर्भाग्यवश, इसका परिष्कार प्रकाशिकी समुदाय के वैज्ञानिकों के कुछ भ्रम और अविश्वास का स्रोत है।इसलिए, यह खंड विधि के विस्तृत कार्यकलाप नहीं तो उसके मूल दर्शन और कार्यान्वयन के बारे में कुछ जानकारी देने का प्रयास करेगा। | यद्यपि यह सैद्धांतिक रूप से कुछ सीमा तक सम्मिश्र है, सामान्यीकृत अनुमानों की विधि एफआरओजी चिन्हों से पल्सेस को पुनः प्राप्त करने के लिए अत्यंत विश्वसनीय विधि प्रमाणित हुई है। दुर्भाग्यवश, इसका परिष्कार प्रकाशिकी समुदाय के वैज्ञानिकों के कुछ भ्रम और अविश्वास का स्रोत है।इसलिए, यह खंड विधि के विस्तृत कार्यकलाप नहीं तो उसके मूल दर्शन और कार्यान्वयन के बारे में कुछ जानकारी देने का प्रयास करेगा। | ||
सर्वप्रथम, ऐसे स्थान की कल्पना करें जिसमें सभी संभावित | सर्वप्रथम, ऐसे स्थान की कल्पना करें जिसमें सभी संभावित संकेत विद्युत क्षेत्र हों'''।''' किसी दिए गए माप के लिए, इन क्षेत्रों का सम्मुचय है जो मापे गए फ्रॉग ट्रेस को संतुष्ट करेगा। हम इन क्षेत्रों को डेटा प्रतिबंध को संतुष्ट करने वाले के रूप में संदर्भित करते हैं। एक और सम्मुचय है जिसमें संकेत क्षेत्र सम्मिलित हैं जिन्हें माप में उपयोग किए जाने वाले अरेखीय अंतःक्रिया के लिए फॉर्म का उपयोग करके व्यक्त किया जा सकता है। [[दूसरी-हार्मोनिक पीढ़ी]] (एसएचजी) के लिए, यह क्षेत्र का सम्मुचय है जिसे फॉर्म <math>E_\text{sig}(t,\tau) = E(t) E(t - \tau)</math> में व्यक्त किया जा सकता है. इसे गणितीय रूप प्रतिबंध को संतुष्ट करने के रूप में जाना जाता है। | ||
ये दोनों सम्मुचय पूर्णतः बिंदु पर प्रतिच्छेद करते हैं। केवल एक ही संभावित | ये दोनों सम्मुचय पूर्णतः बिंदु पर प्रतिच्छेद करते हैं। केवल एक ही संभावित संकेत क्षेत्र है जिसमें डेटा ट्रेस से मेल खाने के लिए दोनों की सही तीव्रता है और अरेखीय अंतःक्रिया द्वारा निर्धारित गणितीय रूप में फिट बैठता है। उस बिंदु को खोजने के लिए, जो वह पल्स देगा जिसे हम मापने की प्रयास कर रहे हैं, सामान्यीकृत अनुमानों का उपयोग किया जाता है। सामान्यीकृत प्रक्षेपण एल्गोरिथ्म इस विद्युत क्षेत्र स्थान में संचालित होता है। प्रत्येक चरण में, हम वर्तमान अनुमान बिंदु के निकटतम बिंदु को खोजते हैं जो दूसरे सम्मुचय के लिए प्रतिबंध को संतुष्ट करेगा। अर्थात्, वर्तमान अनुमान दूसरे सम्मुचय पर "प्रक्षेपित" है। यह निकटतम बिंदु नया वर्तमान अनुमान बन जाता है, और पहले सम्मुचय पर निकटतम बिंदु पाया जाता है। गणितीय प्रतिबंध सम्मुचय पर प्रोजेक्ट करने और डेटा प्रतिबंध सेट पर प्रोजेक्ट करने के बीच बारी-बारी से, हम अंततः समाधान पर पहुँचते हैं। | ||
डेटा | डेटा प्रतिबंध सेट पर प्रोजेक्ट करना सरल है। उस सम्मुचय में होने के लिए, संकेत क्षेत्र के वर्ग परिमाण को ट्रेस द्वारा मापी गई तीव्रता से मेल खाना होगा। संकेत क्षेत्र <math>E_\text{sig}(t,\tau)</math> को फूरियर-रूपांतरित है <math>E_\text{sig}(\omega,\tau)</math>. डेटा प्रतिबंध सेट में निकटतम बिंदु <math>E_\text{sig}(\omega,\tau)</math> के परिमाण को डेटा के परिमाण से को प्रतिस्थापित करके पाया जाता है, जिससे <math>E_\text{sig}(\omega,\tau)</math> का चरण अखंड रहता है। | ||
गणितीय | गणितीय प्रतिबंध सम्मुचय पर प्रोजेक्ट करना सरल नहीं है। डेटा प्रतिबंध के विपरीत, यह बताने का कोई सरल विधि नहीं है कि गणितीय प्रतिबंध सम्मुचय में कौन सा बिंदु निकटतम है। गणितीय प्रतिबंध सम्मुचय में वर्तमान बिंदु और किसी भी बिंदु के बीच की दूरी के लिए सामान्य अभिव्यक्ति बनाई जाती है, और फिर उस अभिव्यक्ति को वर्तमान क्षेत्र अनुमान के संबंध में उस दूरी की ढाल लेकर कम से कम किया जाता है। इस प्रक्रिया पर [http://frog.gatech.edu/Pubs/DeLong-GenProj-OptLett19-1994.pdf इस पेपर] में अधिक विस्तार से चर्चा की गई है। | ||
यह चक्र तब तक दोहराया जाता है जब तक कि | यह चक्र तब तक दोहराया जाता है जब तक कि संकेत अनुमान और डेटा प्रतिबंध (गणितीय प्रतिबंध प्रयुक्त करने के बाद) के बीच त्रुटि कुछ लक्ष्य न्यूनतम मूल्य तक नहीं पहुंच जाती। <math>E(t)</math> को केवल विलंब <math>\tau</math> के संबंध में <math>E_\text{sig}(t,\tau)</math> को एकीकृत करके पाया जा सकता है. दूसरा फ्रॉग ट्रेस सामान्यतः समाधान से गणितीय रूप से बनाया जाता है और मूल माप के साथ तुलना की जाती है। | ||
==माप पुष्टि== | ==माप पुष्टि== | ||
फ्रॉग माप की महत्वपूर्ण विशेषता यह है कि पल्स विद्युत क्षेत्र को खोजने के लिए आवश्यक से कहीं अधिक डेटा बिंदु एकत्र किए जाते हैं। उदाहरण के लिए, मान लें कि मापे गए ट्रेस में विलंब दिशा में 128 बिंदु और आवृत्ति दिशा में 128 बिंदु सम्मिलित हैं। ट्रेस में कुल 128×128 अंक हैं। इन बिंदुओं का उपयोग करके, विद्युत क्षेत्र प्राप्त किया जाता है जिसमें 2×128 बिंदु होते हैं (परिमाण के लिए 128 और चरण के लिए अन्य 128)। यह व्यापक रूप से [[अतिनिर्धारित प्रणाली]] है, जिसका अर्थ है कि समीकरणों की संख्या अज्ञात की संख्या से बहुत बड़ी है। इस प्रकार प्रत्येक व्यक्तिगत डेटा बिंदु के पूर्णतः सही होने का महत्व बहुत कम हो जाता है। यह वास्तविक संसार के मापों के लिए बहुत उपयोगी है जो संसूचक ध्वनि और व्यवस्थित त्रुटियों से प्रभावित हो सकते हैं। ध्वनि द्वारा मापे गए मानचित्र को इस तरह से प्रभावित करने की अत्यधिक संभावना नहीं है कि इसे पल्स में भौतिक घटना के साथ भ्रमित किया जा सके। उपलब्ध अतिरिक्त जानकारी की मात्रा और समाधान खोजने में गणितीय रूप की | फ्रॉग माप की महत्वपूर्ण विशेषता यह है कि पल्स विद्युत क्षेत्र को खोजने के लिए आवश्यक से कहीं अधिक डेटा बिंदु एकत्र किए जाते हैं। उदाहरण के लिए, मान लें कि मापे गए ट्रेस में विलंब दिशा में 128 बिंदु और आवृत्ति दिशा में 128 बिंदु सम्मिलित हैं। ट्रेस में कुल 128×128 अंक हैं। इन बिंदुओं का उपयोग करके, विद्युत क्षेत्र प्राप्त किया जाता है जिसमें 2×128 बिंदु होते हैं (परिमाण के लिए 128 और चरण के लिए अन्य 128)। यह व्यापक रूप से [[अतिनिर्धारित प्रणाली]] है, जिसका अर्थ है कि समीकरणों की संख्या अज्ञात की संख्या से बहुत बड़ी है। इस प्रकार प्रत्येक व्यक्तिगत डेटा बिंदु के पूर्णतः सही होने का महत्व बहुत कम हो जाता है। यह वास्तविक संसार के मापों के लिए बहुत उपयोगी है जो संसूचक ध्वनि और व्यवस्थित त्रुटियों से प्रभावित हो सकते हैं। ध्वनि द्वारा मापे गए मानचित्र को इस तरह से प्रभावित करने की अत्यधिक संभावना नहीं है कि इसे पल्स में भौतिक घटना के साथ भ्रमित किया जा सके। उपलब्ध अतिरिक्त जानकारी की मात्रा और समाधान खोजने में गणितीय रूप की प्रतिबंध के उपयोग के कारण एफआरओजी एल्गोरिदम इन प्रभावों को "देखने" की प्रवृत्ति रखता है। इसका अर्थ यह है कि प्रायोगिक एफआरओजी ट्रेस और पुनर्प्राप्त एफआरओजी ट्रेस के बीच त्रुटि कदाचित ही कभी शून्य होती है, चूंकि व्यवस्थित त्रुटियों के बिना ट्रेस के लिए यह अधिक छोटी होनी चाहिए। | ||
परिणामस्वरूप, मापे गए और पुनर्प्राप्त किए गए फ्रॉग चिन्हों के बीच महत्वपूर्ण अंतर की जांच की जानी चाहिए। प्रयोगात्मक स्थापना असत्य संरेखित हो सकता है, या पल्स में महत्वपूर्ण स्थानिक-अस्थायी विकृतियाँ हो सकती हैं। यदि माप का औसत अनेक या अनेक पल्सेस पर है, तो वे पल्स दूसरे से अधिक भिन्न हो सकती हैं। | परिणामस्वरूप, मापे गए और पुनर्प्राप्त किए गए फ्रॉग चिन्हों के बीच महत्वपूर्ण अंतर की जांच की जानी चाहिए। प्रयोगात्मक स्थापना असत्य संरेखित हो सकता है, या पल्स में महत्वपूर्ण स्थानिक-अस्थायी विकृतियाँ हो सकती हैं। यदि माप का औसत अनेक या अनेक पल्सेस पर है, तो वे पल्स दूसरे से अधिक भिन्न हो सकती हैं। | ||
| Line 48: | Line 48: | ||
===प्रतिस्पर्धी तकनीक=== | ===प्रतिस्पर्धी तकनीक=== | ||
* | * प्रकाशीय ऑटोसहसंबंध, इसकी तीव्रता या फ्रिंज-एफआरईएजी (इंटरफेरोमेट्रिक) संस्करण में | ||
* प्रत्यक्ष विद्युत-क्षेत्र पुनर्निर्माण (स्पाइडर) के लिए वर्णक्रमीय चरण व्यतिकरणमिति | * प्रत्यक्ष विद्युत-क्षेत्र पुनर्निर्माण (स्पाइडर) के लिए वर्णक्रमीय चरण व्यतिकरणमिति | ||
* [[मल्टीफोटोन इंट्रापल्स इंटरफेरेंस चरण स्कैन|बहुफोटॉन अंतःस्पंदन व्यवधान चरण स्कैन]] (एमआईआईपीएस), अति लघु पल्स को चिह्नित करने और परिवर्तन करने की विधि। | * [[मल्टीफोटोन इंट्रापल्स इंटरफेरेंस चरण स्कैन|बहुफोटॉन अंतःस्पंदन व्यवधान चरण स्कैन]] (एमआईआईपीएस), अति लघु पल्स को चिह्नित करने और परिवर्तन करने की विधि। | ||
Revision as of 14:32, 3 December 2023
आवृत्ति-समाधान प्रकाशीय गेटिंग (एफआरओजी) अति लघु पल्स के वर्णक्रमीय चरण को मापने के लिए सामान्य विधि है, जिसकी लंबाई निकलने से लेकर लगभग नैनोसेकंड तक होती है। 1991 में रिक ट्रेबिनो और डैनियल जे. केन द्वारा आविष्कार किया गया, फ्रॉग इस समस्या को हल करने वाली पहली तकनीक थी, जो कठिन है क्योंकि, सामान्यतः, किसी घटना को समय में मापने के लिए, इसे मापने के लिए छोटी घटना की आवश्यकता होती है। उदाहरण के लिए, साबुन के बुलबुले फूटने की क्रिया को मापने के लिए कम अवधि वाले स्ट्रोब लाइट की आवश्यकता होती है। चूँकि अति लघु लेज़र पल्स अब तक की सबसे छोटी घटनाएँ हैं, एफआरओजी से पहले, यह अनेक लोगों द्वारा विचार किया गया था कि समय में उनका पूरा माप संभव नहीं था। चूँकि, एफआरओजी ने पल्स के ऑटो-स्पेक्ट्रोग्राम को मापकर समस्या का समाधान किया, जिसमें पल्स स्वयं को अरैखिक प्रकाशीय माध्यम में गेट करता है। अरेखीय-प्रकाशीय माध्यम और पल्स के परिणामी गेटेड टुकड़े को दो स्पंदनों के बीच विलंब फिर फलन के रूप में वर्णक्रमीय रूप से हल किया जाता है। इसके एफआरओजी ट्रेस से पल्स की पुनर्प्राप्ति द्वि-आयामी चरण-पुनर्प्राप्ति एल्गोरिथ्म का उपयोग करके पूरी की जाती है।
एफआरओजी वर्तमान में अति लघु लेजर पल्स को मापने के लिए मानक तकनीक है, और यह लोकप्रिय भी है, इसने प्रकाशीय ऑटोसहसंबंध नामक पुरानी विधि का स्थान ले लिया है, जो केवल पल्स लंबाई के लिए मोटा अनुमान देती थी। एफआरओजी बस वर्णक्रमीय रूप से हल किया गया ऑटोसहसंबंध है, जो स्पष्ट पल्स तीव्रता और चरण बनाम समय को पुनः प्राप्त करने के लिए चरण-पुनर्प्राप्ति एल्गोरिदम के उपयोग की अनुमति देता है। यह अधिक सरल और अधिक सम्मिश्र अति लघु लेजर पल्स दोनों को माप सकता है, और इसने संदर्भ पल्स के उपयोग के बिना अब तक मापी गई सबसे सम्मिश्र पल्स को मापा है। इस प्रकार से एफआरओजी के सरल संस्करण उपस्तिथ हैं (संक्षिप्त रूप में, ग्रेनोइल, एफआरओजी के लिए फ्रांसीसी शब्द), केवल कुछ सरलता से संरेखित प्रकाशीय घटकों का उपयोग करते हुए। फ्रॉग और ग्रेनोइल दोनों संसार के अनुसंधान और औद्योगिक प्रयोगशालाओं में समान उपयोग में हैं।
सिद्धांत
एफआरओजी और ऑटोसहसंबंध गैर-रेखीय माध्यम में पल्स को अपने साथ संयोजित करने के विचार को साझा करते हैं। चूंकि गैर-रेखीय माध्यम केवल तभी वांछित संकेत उत्पन्न करेगा जब दोनों पल्स ही समय में उपस्तिथ हों (अर्थात "प्रकाशीय गेटिंग"), पल्स प्रतियों के बीच विलंब को अलग-अलग करना और प्रत्येक विलंब पर संकेत को मापने से पल्स की लंबाई का अस्पष्ट अनुमान मिलता है। ऑटोकोरेलेटर्स अरेखीय संकेत क्षेत्र की तीव्रता को मापकर पल्स को मापते हैं। इस प्रकार से पल्स लंबाई का अनुमान लगाने के लिए पल्स आकार मानने की आवश्यकता होती है, और पल्स विद्युत क्षेत्र के चरण को पूर्णतः भी नहीं मापा जा सकता है। एफआरओजी केवल तीव्रता के अतिरिक्त प्रत्येक विलंब (इसलिए "आवृत्ति-समाधान") पर संकेत के विस्तार को मापकर इस विचार का विस्तार करता है। यह माप पल्स का स्पेक्ट्रोग्राम बनाता है, जिसका उपयोग समय या आवृत्ति के फलन के रूप में सम्मिश्र विद्युत क्षेत्र को निर्धारित करने के लिए किया जा सकता है जब तक कि माध्यम की गैर-रैखिकता ज्ञात हो।
फ्रॉग स्पेक्ट्रोग्राम (सामान्यतः फ्रॉग ट्रेस कहा जाता है) आवृत्ति और विलंब के फलन के रूप में तीव्रता का ग्राफ है, चूँकि, अरेखीय अंतःक्रिया से संकेत क्षेत्र को समय डोमेन में व्यक्त करना सरल है, इसलिए एफआरओजी ट्रेस के लिए विशिष्ट अभिव्यक्ति में फूरियर रूपांतरण सम्मिलित है।
अरेखीय संकेत क्षेत्र मूल पल्स , पर निर्भर करता है, और गैर-रेखीय प्रक्रिया का उपयोग किया जाता है, जिसे लगभग सदैव के रूप में व्यक्त किया जा सकता है , जैसे कि . सबसे सामान्य गैर-रैखिकता दूसरी हार्मोनिक पीढ़ी है, जहां . पल्स क्षेत्र के संदर्भ में ट्रेस के लिए अभिव्यक्ति तब है:
इस मूलभूत स्थापना में अनेक संभावित विविधताएँ हैं। यदि प्रसिद्ध संदर्भ पल्स उपलब्ध है, तो इसे अज्ञात पल्स की प्रतिलिपि के अतिरिक्त गेटिंग पल्स के रूप में उपयोग किया जा सकता है। इसे क्रॉस-सहसंबंध एफआरओजी या एक्सएफआरओजी के रूप में जाना जाता है। इसके अतिरिक्त, दूसरी हार्मोनिक पीढ़ी के अतिरिक्त अन्य गैर-रैखिक प्रभावों का उपयोग किया जा सकता है, जैसे तृतीय हार्मोनिक पीढ़ी (टीएचजी) या ध्रुवीकरण गेटिंग (पीजी) है। ये परिवर्तन अभिव्यक्ति को प्रभावित करेंगे।
प्रयोग
एक विशिष्ट बहु-शॉट फ्रॉग स्थापना में, अज्ञात पल्स को किरण विभाजक के साथ दो प्रतियों में विभाजित किया जाता है। एक प्रति में दूसरी की तुलना में ज्ञात मात्रा से विलंब होती है। दोनों पल्सेस को गैर-रेखीय माध्यम में ही बिंदु पर केंद्रित किया जाता है, और गैर-रेखीय संकेत के विस्तार को वर्णक्रममापी से मापा जाता है। यह प्रक्रिया अनेक विलंब बिंदुओं के लिए दोहराई जाती है।
कुछ सामान्य समायोजनों के साथ ही शॉट में फ्रॉग मापन किया जा सकता है। दो पल्स प्रतियों को कोण पर पार किया जाता है और बिंदु के अतिरिक्त रेखा पर केंद्रित किया जाता है। यह लाइन फोकस के साथ दो पल्स के बीच अलग-अलग विलंब उत्पन्न करता है। इस आकृति में, माप को अधिकृत करने के लिए घर-निर्मित वर्णक्रममापी का उपयोग करना सामान्य है, जिसमें विवर्तन झंझरी और कैमरा सम्मिलित होता है।
पुनर्प्राप्ति एल्गोरिथ्म
यद्यपि यह सैद्धांतिक रूप से कुछ सीमा तक सम्मिश्र है, सामान्यीकृत अनुमानों की विधि एफआरओजी चिन्हों से पल्सेस को पुनः प्राप्त करने के लिए अत्यंत विश्वसनीय विधि प्रमाणित हुई है। दुर्भाग्यवश, इसका परिष्कार प्रकाशिकी समुदाय के वैज्ञानिकों के कुछ भ्रम और अविश्वास का स्रोत है।इसलिए, यह खंड विधि के विस्तृत कार्यकलाप नहीं तो उसके मूल दर्शन और कार्यान्वयन के बारे में कुछ जानकारी देने का प्रयास करेगा।
सर्वप्रथम, ऐसे स्थान की कल्पना करें जिसमें सभी संभावित संकेत विद्युत क्षेत्र हों। किसी दिए गए माप के लिए, इन क्षेत्रों का सम्मुचय है जो मापे गए फ्रॉग ट्रेस को संतुष्ट करेगा। हम इन क्षेत्रों को डेटा प्रतिबंध को संतुष्ट करने वाले के रूप में संदर्भित करते हैं। एक और सम्मुचय है जिसमें संकेत क्षेत्र सम्मिलित हैं जिन्हें माप में उपयोग किए जाने वाले अरेखीय अंतःक्रिया के लिए फॉर्म का उपयोग करके व्यक्त किया जा सकता है। दूसरी-हार्मोनिक पीढ़ी (एसएचजी) के लिए, यह क्षेत्र का सम्मुचय है जिसे फॉर्म में व्यक्त किया जा सकता है. इसे गणितीय रूप प्रतिबंध को संतुष्ट करने के रूप में जाना जाता है।
ये दोनों सम्मुचय पूर्णतः बिंदु पर प्रतिच्छेद करते हैं। केवल एक ही संभावित संकेत क्षेत्र है जिसमें डेटा ट्रेस से मेल खाने के लिए दोनों की सही तीव्रता है और अरेखीय अंतःक्रिया द्वारा निर्धारित गणितीय रूप में फिट बैठता है। उस बिंदु को खोजने के लिए, जो वह पल्स देगा जिसे हम मापने की प्रयास कर रहे हैं, सामान्यीकृत अनुमानों का उपयोग किया जाता है। सामान्यीकृत प्रक्षेपण एल्गोरिथ्म इस विद्युत क्षेत्र स्थान में संचालित होता है। प्रत्येक चरण में, हम वर्तमान अनुमान बिंदु के निकटतम बिंदु को खोजते हैं जो दूसरे सम्मुचय के लिए प्रतिबंध को संतुष्ट करेगा। अर्थात्, वर्तमान अनुमान दूसरे सम्मुचय पर "प्रक्षेपित" है। यह निकटतम बिंदु नया वर्तमान अनुमान बन जाता है, और पहले सम्मुचय पर निकटतम बिंदु पाया जाता है। गणितीय प्रतिबंध सम्मुचय पर प्रोजेक्ट करने और डेटा प्रतिबंध सेट पर प्रोजेक्ट करने के बीच बारी-बारी से, हम अंततः समाधान पर पहुँचते हैं।
डेटा प्रतिबंध सेट पर प्रोजेक्ट करना सरल है। उस सम्मुचय में होने के लिए, संकेत क्षेत्र के वर्ग परिमाण को ट्रेस द्वारा मापी गई तीव्रता से मेल खाना होगा। संकेत क्षेत्र को फूरियर-रूपांतरित है . डेटा प्रतिबंध सेट में निकटतम बिंदु के परिमाण को डेटा के परिमाण से को प्रतिस्थापित करके पाया जाता है, जिससे का चरण अखंड रहता है।
गणितीय प्रतिबंध सम्मुचय पर प्रोजेक्ट करना सरल नहीं है। डेटा प्रतिबंध के विपरीत, यह बताने का कोई सरल विधि नहीं है कि गणितीय प्रतिबंध सम्मुचय में कौन सा बिंदु निकटतम है। गणितीय प्रतिबंध सम्मुचय में वर्तमान बिंदु और किसी भी बिंदु के बीच की दूरी के लिए सामान्य अभिव्यक्ति बनाई जाती है, और फिर उस अभिव्यक्ति को वर्तमान क्षेत्र अनुमान के संबंध में उस दूरी की ढाल लेकर कम से कम किया जाता है। इस प्रक्रिया पर इस पेपर में अधिक विस्तार से चर्चा की गई है।
यह चक्र तब तक दोहराया जाता है जब तक कि संकेत अनुमान और डेटा प्रतिबंध (गणितीय प्रतिबंध प्रयुक्त करने के बाद) के बीच त्रुटि कुछ लक्ष्य न्यूनतम मूल्य तक नहीं पहुंच जाती। को केवल विलंब के संबंध में को एकीकृत करके पाया जा सकता है. दूसरा फ्रॉग ट्रेस सामान्यतः समाधान से गणितीय रूप से बनाया जाता है और मूल माप के साथ तुलना की जाती है।
माप पुष्टि
फ्रॉग माप की महत्वपूर्ण विशेषता यह है कि पल्स विद्युत क्षेत्र को खोजने के लिए आवश्यक से कहीं अधिक डेटा बिंदु एकत्र किए जाते हैं। उदाहरण के लिए, मान लें कि मापे गए ट्रेस में विलंब दिशा में 128 बिंदु और आवृत्ति दिशा में 128 बिंदु सम्मिलित हैं। ट्रेस में कुल 128×128 अंक हैं। इन बिंदुओं का उपयोग करके, विद्युत क्षेत्र प्राप्त किया जाता है जिसमें 2×128 बिंदु होते हैं (परिमाण के लिए 128 और चरण के लिए अन्य 128)। यह व्यापक रूप से अतिनिर्धारित प्रणाली है, जिसका अर्थ है कि समीकरणों की संख्या अज्ञात की संख्या से बहुत बड़ी है। इस प्रकार प्रत्येक व्यक्तिगत डेटा बिंदु के पूर्णतः सही होने का महत्व बहुत कम हो जाता है। यह वास्तविक संसार के मापों के लिए बहुत उपयोगी है जो संसूचक ध्वनि और व्यवस्थित त्रुटियों से प्रभावित हो सकते हैं। ध्वनि द्वारा मापे गए मानचित्र को इस तरह से प्रभावित करने की अत्यधिक संभावना नहीं है कि इसे पल्स में भौतिक घटना के साथ भ्रमित किया जा सके। उपलब्ध अतिरिक्त जानकारी की मात्रा और समाधान खोजने में गणितीय रूप की प्रतिबंध के उपयोग के कारण एफआरओजी एल्गोरिदम इन प्रभावों को "देखने" की प्रवृत्ति रखता है। इसका अर्थ यह है कि प्रायोगिक एफआरओजी ट्रेस और पुनर्प्राप्त एफआरओजी ट्रेस के बीच त्रुटि कदाचित ही कभी शून्य होती है, चूंकि व्यवस्थित त्रुटियों के बिना ट्रेस के लिए यह अधिक छोटी होनी चाहिए।
परिणामस्वरूप, मापे गए और पुनर्प्राप्त किए गए फ्रॉग चिन्हों के बीच महत्वपूर्ण अंतर की जांच की जानी चाहिए। प्रयोगात्मक स्थापना असत्य संरेखित हो सकता है, या पल्स में महत्वपूर्ण स्थानिक-अस्थायी विकृतियाँ हो सकती हैं। यदि माप का औसत अनेक या अनेक पल्सेस पर है, तो वे पल्स दूसरे से अधिक भिन्न हो सकती हैं।
यह भी देखें
फ्रॉग तकनीक
- अति तीव्र घटना लेजर लाइट ई-फील्ड्स (ग्रेनोइल) का ग्रेटिंग-उन्मूलन रहित अवलोकन, फ्रॉग का सरलीकृत संस्करण
- डबल-ब्लाइंड फ्रॉग ,एक साथ दो पल्स मापने के लिए
प्रतिस्पर्धी तकनीक
- प्रकाशीय ऑटोसहसंबंध, इसकी तीव्रता या फ्रिंज-एफआरईएजी (इंटरफेरोमेट्रिक) संस्करण में
- प्रत्यक्ष विद्युत-क्षेत्र पुनर्निर्माण (स्पाइडर) के लिए वर्णक्रमीय चरण व्यतिकरणमिति
- बहुफोटॉन अंतःस्पंदन व्यवधान चरण स्कैन (एमआईआईपीएस), अति लघु पल्स को चिह्नित करने और परिवर्तन करने की विधि।
- फ़्रिक्वेंसी-रिज़ॉल्यूशन इलेक्ट्रो-अवशोषण गेटिंग (एफआरईएजी)
संदर्भ
- Rick Trebino (2002). Frequency-Resolved Optical Gating: The Measurement of Ultrashort Laser Pulses. Springer. ISBN 1-4020-7066-7.
- R. Trebino, K. W. DeLong, D. N. Fittinghoff, J. N. Sweetser, M. A. Krumbügel, and D. J. Kane, "Measuring Ultrashort Laser Pulses in the Time-Frequency Domain Using Frequency-Resolved Optical Gating," Review of Scientific Instruments 68, 3277-3295 (1997).
बाहरी संबंध
- एफआरओजी Page by Rick Trebino (co-inventor of एफआरओजी)