क्रमपरिवर्तन परीक्षण

क्रमपरिवर्तन परीक्षण (जिसे पुन: यादृच्छिकीकरण परीक्षण या शफ़ल परीक्षण भी कहा जाता है) विरोधाभास द्वारा प्रमाण का उपयोग करने वाला एक सटीक सांख्यिकीय परिकल्पना परीक्षण है। एक क्रमपरिवर्तन परीक्षण में दो या अधिक नमूने शामिल होते हैं। अशक्त परिकल्पना यह है कि सभी नमूने एक ही वितरण $H_{0}:F=G$ से आते हैं। अशक्त परिकल्पना के तहत, परीक्षण आँकड़ों का वितरण प्रेक्षित डेटा के संभावित पुनर्व्यवस्था के तहत परीक्षण आँकड़ों के सभी संभावित मूल्यों की गणना करके प्राप्त किया जाता है। इसलिए, क्रमपरिवर्तन परीक्षण पुनः नमूनाकरण का एक रूप हैं।

क्रमपरिवर्तन परीक्षणों को सरोगेट डेटा परीक्षण के रूप में समझा जा सकता है जहां अशक्त परिकल्पना के तहत सरोगेट डेटा मूल डेटा के क्रमपरिवर्तन के माध्यम से प्राप्त किया जाता है।

दूसरे शब्दों में, वह विधि जिसके द्वारा प्रयोगात्मक डिजाइन में विषयों को उपचार आवंटित किया जाता है, उस डिजाइन के विश्लेषण में प्रतिबिंबित होता है। यदि लेबल अशक्त परिकल्पना के तहत विनिमेय हैं, तो परिणामी परीक्षण सटीक महत्व स्तर प्राप्त करते हैं; विनिमयशीलता भी देखें. फिर परीक्षणों से आत्मविश्वास अंतराल प्राप्त किया जा सकता है। यह सिद्धांत 1930 के दशक में रोनाल्ड फिशर और ई.जे.जी. पिटमैन के कार्यों से विकसित हुआ है।

क्रमपरिवर्तन परीक्षण को यादृच्छिक परीक्षण के साथ भ्रमित नहीं किया जाना चाहिए।

विधि

4 और 5 यादृच्छिक मानों के सेट पर गणना किए जा रहे क्रमपरिवर्तन परीक्षण का एनीमेशन। लाल रंग में 4 मान एक वितरण से और नीले रंग में 5 मान दूसरे वितरण से लिए गए हैं; हम परीक्षण करना चाहेंगे कि क्या दोनों वितरणों के माध्य मान भिन्न हैं। परिकल्पना यह है कि पहले वितरण का माध्य दूसरे के माध्य से अधिक है; शून्य परिकल्पना यह है कि नमूनों के दोनों समूह एक ही वितरण से लिए गए हैं। 4 मानों को एक समूह में और 5 को दूसरे समूह में रखने के 126 अलग-अलग तरीके हैं (9-चुनें-4 या 9-चुनें-5)। इनमें से एक मूल लेबलिंग के अनुसार है, और अन्य 125 क्रमपरिवर्तन हैं जो माध्य अंतर का हिस्टोग्राम उत्पन्न करते हैं ${\hat {\mu }}_{1}-{\hat {\mu }}_{2}$ दिखाया गया. परिकल्पना के पी-मूल्य का अनुमान उन क्रमपरिवर्तनों के अनुपात के रूप में लगाया जाता है जो मूल नमूनों के साधनों के अंतर से बड़ा या बड़ा अंतर देते हैं। इस उदाहरण में, शून्य परिकल्पना को अस्वीकार नहीं किया जा सकता है p = 5% स्तर।

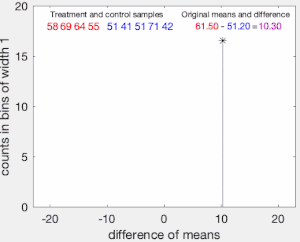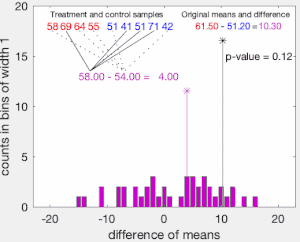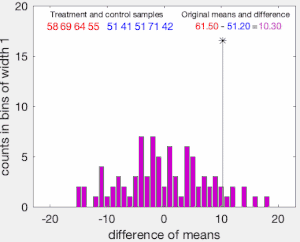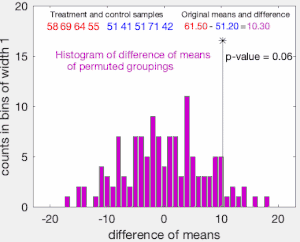
क्रमपरिवर्तन परीक्षण के मूल विचार को स्पष्ट करने के लिए, मान लीजिए कि हम दो समूहों $X_{A}$ और $X_{B}$ से प्रत्येक व्यक्ति के लिए यादृच्छिक चर $A$ और $B$ एकत्र करते हैं, जिनका नमूना माध्य ${\bar {x}}_{A}$और ${\bar {x}}_{B}$ है, और वह हम जानना चाहते हैं कि क्या $X_{A}$और $X_{B}$ एक ही वितरण से आते हैं। मान लीजिए $n_{A}$और $n_{B}$ प्रत्येक समूह से एकत्रित नमूना आकार हैं। क्रमपरिवर्तन परीक्षण यह निर्धारित करने के लिए डिज़ाइन किया गया है कि क्या नमूना साधनों के बीच मनाया गया अंतर कुछ महत्व स्तर पर, शून्य परिकल्पना H$_{0}$ को अस्वीकार करने के लिए पर्याप्त है कि $A$ से लिया गया डेटा उसी वितरण से है जैसा कि $B$ से लिया गया डेटा है।

परीक्षण इस प्रकार आगे बढ़ता है. सबसे पहले, दो नमूनों के बीच के अंतर की गणना की जाती है: यह परीक्षण सांख्यिकीय, $T_{\text{obs}}$ का मनाया गया मूल्य है।

इसके बाद, समूह $A$ और $B$ के अवलोकनों को पूल किया जाता है, और नमूना साधनों में अंतर की गणना की जाती है और पूल किए गए मानों को आकार के दो समूहों $n_{A}$और $n_{B}$ में विभाजित करने के हर संभव तरीके के लिए रिकॉर्ड किया जाता है (यानी, समूह लेबल ए और बी के प्रत्येक क्रमपरिवर्तन के लिए)। इन गणना किए गए अंतरों का सेट अशक्त परिकल्पना के तहत संभावित अंतरों (इस नमूने के लिए) का सटीक वितरण है कि समूह लेबल विनिमेय हैं (यानी, यादृच्छिक रूप से निर्दिष्ट हैं)।

परीक्षण के एक तरफा पी-वैल्यू की गणना नमूना क्रमपरिवर्तन के अनुपात के रूप में की जाती है जहां साधनों में अंतर $T_{\text{obs}}$ से अधिक था। परीक्षण के दो-तरफा पी-मान की गणना नमूना क्रमपरिवर्तन के अनुपात के रूप में की जाती है जहां पूर्ण अंतर $|T_{\text{obs}}|$ से अधिक था। क्रमपरिवर्तन परीक्षणों के कई कार्यान्वयन के लिए आवश्यक है कि देखे गए डेटा को स्वयं क्रमपरिवर्तन में से एक के रूप में गिना जाए ताकि क्रमपरिवर्तन पी-मान कभी भी शून्य न हो।

वैकल्पिक रूप से, यदि परीक्षण का एकमात्र उद्देश्य शून्य परिकल्पना को अस्वीकार करना या अस्वीकार करना है, तो कोई रिकॉर्ड किए गए मतभेदों को हल कर सकता है, और फिर देखें कि क्या $T_{\text{obs}}$ कुछ महत्व स्तर के लिए उनमें से मध्य $\alpha$ $(1-\alpha )\times 100$ के भीतर समाहित है। यदि ऐसा नहीं है, तो हम $\alpha \times 100\%$ महत्व स्तर पर समान संभाव्यता वक्रों की परिकल्पना को अस्वीकार कर देते हैं।

युग्मित नमूनों के लिए युग्मित क्रमपरिवर्तन परीक्षण लागू करने की आवश्यकता है।

पैरामीट्रिक परीक्षणों से संबंध

क्रमपरिवर्तन परीक्षण गैर-पैरामीट्रिक आँकड़ों का एक उपसमूह हैं। यह मानते हुए कि हमारा प्रयोगात्मक डेटा दो उपचार समूहों से मापा गया डेटा से आता है, विधि केवल इस धारणा के तहत औसत अंतर का वितरण उत्पन्न करती है कि दोनों समूह मापा चर के संदर्भ में अलग नहीं हैं। इससे, कोई प्रेक्षित आँकड़े का उपयोग कर सकता है ($T_{\text{obs}}$ ऊपर) यह देखने के लिए कि यह सांख्यिकीय किस हद तक विशेष है, यानी, यदि उपचार के बाद उपचार लेबल को यादृच्छिक रूप से यादृच्छिक किया गया था, तो ऐसे मूल्य (या बड़े) के परिमाण को देखने की संभावना।

क्रमपरिवर्तन परीक्षणों के विपरीत, कई लोकप्रिय शास्त्रीय आँकड़ों में अंतर्निहित वितरण| शास्त्रीय सांख्यिकीय परीक्षण, जैसे कि टी-टेस्ट|टी-टेस्ट, एफ-टेस्ट|एफ-टेस्ट, जेड-टेस्ट|जेड-टेस्ट, और ची-स्क्वेर्ड टेस्ट|χ²परीक्षण, सैद्धांतिक संभाव्यता वितरण से प्राप्त किए जाते हैं। फिशर का सटीक परीक्षण दो द्विभाजित चरों के बीच संबंध का मूल्यांकन करने के लिए आमतौर पर इस्तेमाल किए जाने वाले क्रमपरिवर्तन परीक्षण का एक उदाहरण है। जब नमूना आकार बहुत बड़ा होता है, तो पियर्सन का ची-स्क्वायर परीक्षण सटीक परिणाम देगा। छोटे नमूनों के लिए, ची-स्क्वायर संदर्भ वितरण को परीक्षण आंकड़ों के संभाव्यता वितरण का सही विवरण देने के लिए नहीं माना जा सकता है, और इस स्थिति में फिशर के सटीक परीक्षण का उपयोग अधिक उपयुक्त हो जाता है।

क्रमपरिवर्तन परीक्षण कई स्थितियों में मौजूद होते हैं जहां पैरामीट्रिक परीक्षण नहीं होते हैं (उदाहरण के लिए, जब एक इष्टतम परीक्षण प्राप्त होता है जब नुकसान उसके वर्ग के बजाय त्रुटि के आकार के समानुपाती होता है)। सभी सरल और कई अपेक्षाकृत जटिल पैरामीट्रिक परीक्षणों में एक समान क्रमपरिवर्तन परीक्षण संस्करण होता है जिसे पैरामीट्रिक परीक्षण के समान परीक्षण आंकड़ों का उपयोग करके परिभाषित किया जाता है, लेकिन सैद्धांतिक के बजाय उस आंकड़े के नमूना-विशिष्ट क्रमपरिवर्तन वितरण से पी-मान प्राप्त होता है पैरामीट्रिक धारणा से प्राप्त वितरण। उदाहरण के लिए, क्रमपरिवर्तन t-परीक्षण|t-परीक्षण, क्रमपरिवर्तन ची-वर्ग परीक्षण| का निर्माण इस प्रकार संभव है।${\textstyle \chi ^{2}}$ एसोसिएशन का परीक्षण, भिन्नताओं की तुलना करने के लिए एली के परीक्षण का क्रमपरिवर्तन संस्करण इत्यादि।

क्रमपरिवर्तन परीक्षणों की प्रमुख कमियाँ यह हैं कि वे

• कम्प्यूटेशनल रूप से गहन हो सकता है और गणना करने में कठिन आँकड़ों के लिए कस्टम कोड की आवश्यकता हो सकती है। इसे हर मामले के लिए फिर से लिखा जाना चाहिए।
• मुख्य रूप से पी-वैल्यू प्रदान करने के लिए उपयोग किया जाता है। आत्मविश्वास क्षेत्र/अंतराल प्राप्त करने के लिए परीक्षण के व्युत्क्रमण के लिए और भी अधिक गणना की आवश्यकता होती है।

फायदे

किसी भी परीक्षण आँकड़े के लिए क्रमपरिवर्तन परीक्षण मौजूद हैं, भले ही उसका वितरण ज्ञात हो या नहीं। इस प्रकार व्यक्ति हमेशा उस आंकड़े को चुनने के लिए स्वतंत्र होता है जो परिकल्पना और विकल्प के बीच सबसे अच्छा भेदभाव करता है और जो नुकसान को कम करता है।

असंतुलित डिज़ाइनों के विश्लेषण के लिए क्रमपरिवर्तन परीक्षणों का उपयोग किया जा सकता है और श्रेणीबद्ध, क्रमिक और मीट्रिक डेटा के मिश्रण पर निर्भर परीक्षणों के संयोजन के लिए (पेसारिन, 2001). उनका उपयोग गुणात्मक डेटा का विश्लेषण करने के लिए भी किया जा सकता है जिसे परिमाणित किया गया है (यानी, संख्याओं में बदल दिया गया है)। क्रमपरिवर्तन परीक्षण परिमाणित डेटा का विश्लेषण करने के लिए आदर्श हो सकते हैं जो पारंपरिक पैरामीट्रिक परीक्षणों (उदाहरण के लिए, टी-परीक्षण, एनोवा) में अंतर्निहित सांख्यिकीय मान्यताओं को संतुष्ट नहीं करते हैं। पर्मानोवा देखें।

1980 के दशक से पहले, छोटे नमूना आकार वाले डेटा सेट को छोड़कर संदर्भ वितरण बनाने का बोझ बहुत अधिक था।

1980 के दशक के बाद से, अपेक्षाकृत सस्ते तेज़ कंप्यूटरों के संगम और विशेष परिस्थितियों में लागू नए परिष्कृत पथ एल्गोरिदम के विकास ने समस्याओं की एक विस्तृत श्रृंखला के लिए क्रमपरिवर्तन परीक्षण विधियों के अनुप्रयोग को व्यावहारिक बना दिया है। इसने मुख्य सांख्यिकीय सॉफ़्टवेयर पैकेजों में सटीक-परीक्षण विकल्पों को जोड़ने और यूनी- और बहु-परिवर्तनीय सटीक परीक्षणों की एक विस्तृत श्रृंखला और परीक्षण-आधारित सटीक आत्मविश्वास अंतराल की गणना करने के लिए विशेष सॉफ़्टवेयर की उपस्थिति की भी शुरुआत की।

सीमाएँ

क्रमपरिवर्तन परीक्षण के पीछे एक महत्वपूर्ण धारणा यह है कि अवलोकन शून्य परिकल्पना के तहत विनिमय योग्य हैं। इस धारणा का एक महत्वपूर्ण परिणाम यह है कि स्थान में अंतर के परीक्षण (क्रमपरिवर्तन टी-परीक्षण की तरह) को सामान्यता धारणा के तहत समान भिन्नता की आवश्यकता होती है। इस संबंध में, क्रमपरिवर्तन टी-परीक्षण शास्त्रीय छात्र के टी-परीक्षण (बेहरेंस-फिशर समस्या) के समान ही कमजोरी साझा करता है। इस स्थिति में तीसरा विकल्प बूटस्ट्रैप-आधारित परीक्षण का उपयोग करना है। सांख्यिकीविद् फिलिप गुड क्रमपरिवर्तन परीक्षणों और बूटस्ट्रैप परीक्षणों के बीच अंतर को निम्नलिखित तरीके से समझाते हैं: क्रमपरिवर्तन वितरण से संबंधित परिकल्पनाओं का परीक्षण करते हैं; बूटस्ट्रैप्स मापदंडों से संबंधित परिकल्पनाओं का परीक्षण करते हैं। परिणामस्वरूप, बूटस्ट्रैप में कम कठोर धारणाएँ शामिल होती हैं। बूटस्ट्रैप परीक्षण सटीक नहीं हैं. कुछ मामलों में, उचित रूप से छात्रीकृत आँकड़ों पर आधारित एक क्रमपरिवर्तन परीक्षण विनिमयशीलता धारणा का उल्लंघन होने पर भी स्पर्शोन्मुख रूप से सटीक हो सकता है। बूटस्ट्रैप-आधारित परीक्षण शून्य परिकल्पना के साथ परीक्षण कर सकते हैं $H_{0}:F\neq G$ और, इसलिए, तुल्यता परीक्षण करने के लिए उपयुक्त हैं।

मोंटे कार्लो परीक्षण

जब सुविधाजनक तरीके से पूर्ण गणना की अनुमति देने के लिए डेटा के बहुत अधिक संभावित क्रम हों तो एक असम्बद्ध रूप से समतुल्य क्रमपरिवर्तन परीक्षण बनाया जा सकता है। यह मोंटे कार्लो नमूनाकरण द्वारा संदर्भ वितरण उत्पन्न करके किया जाता है, जो संभावित प्रतिकृति का एक छोटा (क्रमपरिवर्तन की कुल संख्या के सापेक्ष) यादृच्छिक नमूना लेता है। यह एहसास कि इसे किसी भी डेटासेट पर किसी भी क्रमपरिवर्तन परीक्षण पर लागू किया जा सकता है, लागू आंकड़ों के क्षेत्र में एक महत्वपूर्ण सफलता थी। इस दृष्टिकोण के सबसे पहले ज्ञात संदर्भ ईडन और फ्रैंक येट्स (1933) और मेयर डवास (1957) हैं। इस प्रकार के क्रमपरिवर्तन परीक्षण को विभिन्न नामों से जाना जाता है: अनुमानित क्रमपरिवर्तन परीक्षण, मोंटे कार्लो क्रमपरिवर्तन परीक्षण या यादृच्छिक क्रमपरिवर्तन परीक्षण। बाद $N$ यादृच्छिक क्रमपरिवर्तन, द्विपद वितरण के आधार पर पी-मान के लिए विश्वास अंतराल प्राप्त करना संभव है, द्विपद अनुपात विश्वास अंतराल देखें। उदाहरण के लिए, यदि बाद में $N=10000$ यादृच्छिक क्रमपरिवर्तन से पी-मान का अनुमान लगाया जाता है ${\widehat {p}}=0.05$, फिर सत्य के लिए 99% विश्वास अंतराल $p$ (वह जो सभी संभावित क्रमपरिवर्तनों को आज़माने का परिणाम होगा) है $\left[{\hat {p}}-z{\sqrt {\frac {0.05(1-0.05)}{10000}}},{\hat {p}}+z{\sqrt {\frac {0.05(1-0.05)}{10000}}}\right]=[0.045,0.055]$.

दूसरी ओर, पी-वैल्यू का अनुमान लगाने का उद्देश्य अक्सर यह तय करना होता है कि क्या $p\leq \alpha$, कहाँ $\scriptstyle \ \alpha$ वह सीमा है जिस पर शून्य परिकल्पना खारिज कर दी जाएगी (आमतौर पर)। $\alpha =0.05$). उपरोक्त उदाहरण में, आत्मविश्वास अंतराल हमें केवल यह बताता है कि लगभग 50% संभावना है कि पी-वैल्यू 0.05 से कम है, यानी यह पूरी तरह से अस्पष्ट है कि शून्य परिकल्पना को एक स्तर पर खारिज कर दिया जाना चाहिए या नहीं $\alpha =0.05$.

यदि केवल यह जानना महत्वपूर्ण है कि क्या $p\leq \alpha$ किसी प्रदत्त के लिए $\alpha$, कथन तक अनुकरण जारी रखना तर्कसंगत है $p\leq \alpha$ त्रुटि की बहुत कम संभावना के साथ सत्य या असत्य स्थापित किया जा सकता है। एक बंधन दिया गया $\epsilon$ त्रुटि की स्वीकार्य संभावना पर (उसे खोजने की संभावना)। ${\widehat {p}}>\alpha$ जब वास्तव में $p\leq \alpha$ या इसके विपरीत), कितने क्रमपरिवर्तन उत्पन्न करने का प्रश्न इस प्रश्न के रूप में देखा जा सकता है कि अब तक के सिमुलेशन के परिणामों के आधार पर क्रमपरिवर्तन उत्पन्न करना कब बंद करना है, यह गारंटी देने के लिए कि निष्कर्ष (जो या तो है) $p\leq \alpha$ या $p>\alpha$) कम से कम इतनी बड़ी संभावना के साथ सही है $1-\epsilon$. ($\epsilon$ आम तौर पर बेहद छोटा चुना जाएगा, उदा. 1/1000.) इसे प्राप्त करने के लिए रोकथाम नियम विकसित किए गए हैं जिसे न्यूनतम अतिरिक्त कम्प्यूटेशनल लागत के साथ शामिल किया जा सकता है। वास्तव में, वास्तविक अंतर्निहित पी-वैल्यू के आधार पर यह अक्सर पाया जाएगा कि आभासी निश्चितता के साथ किसी निर्णय पर पहुंचने से पहले आवश्यक सिमुलेशन की संख्या उल्लेखनीय रूप से छोटी है (उदाहरण के लिए 5 जितनी कम और अक्सर 100 से बड़ी नहीं)।

उदाहरण परीक्षण

• विचरण का क्रमिक विश्लेषण

साहित्य

मूल संदर्भ:

• आर. ए. फिशर|फिशर, आर.ए. (1935) प्रयोगों का डिज़ाइन, न्यूयॉर्क: हाफनर प्रकाशन
• ई. जे. जी. पिटमैन|पिटमैन, ई. जे. जी. (1937) महत्व परीक्षण जो किसी भी आबादी के नमूनों पर लागू किए जा सकते हैं, रॉयल स्टैटिस्टिकल सोसाइटी सप्लीमेंट, 4: 119-130 और 225-32 (भाग I और II)। JSTOR 2984124 JSTOR 2983647
• Pitman, E. J. G. (1938). "महत्व परीक्षण जो किसी भी जनसंख्या के नमूनों पर लागू किए जा सकते हैं। भाग III. विचरण परीक्षण का विश्लेषण". Biometrika. 29 (3–4): 322–335. doi:10.1093/biomet/29.3-4.322.

आधुनिक संदर्भ:

• Collingridge, D.S. (2013). "परिमाणित डेटा विश्लेषण और क्रमपरिवर्तन परीक्षण पर एक प्राइमर". Journal of Mixed Methods Research. 7 (1): 79–95. doi:10.1177/1558689812454457. S2CID 124618343.
• एजिंगटन, ई.एस., और ओन्घेना, पी. (2007) रैंडमाइजेशन टेस्ट, चौथा संस्करण। न्यूयॉर्क: चैपमैन और हॉल/सीआरसी ISBN 9780367577711
• गुड, फिलिप आई. (2005) परमुटेशन, पैरामीट्रिक और बूटस्ट्रैप टेस्ट ऑफ हाइपोथीसिस, तीसरा संस्करण, स्प्रिंगर साइंस+बिजनेस मीडिया ISBN 0-387-98898-X
• Good, P (2002). "विनिमेयता की अवधारणा का विस्तार और उनके अनुप्रयोग". Journal of Modern Applied Statistical Methods. 1 (2): 243–247. doi:10.22237/jmasm/1036110240.
• लूनबॉर्ग, क्लिफ। (1999) रेज़ैम्पलिंग द्वारा डेटा विश्लेषण, डक्सबरी प्रेस। ISBN 0-534-22110-6.
• पेसारिन, एफ. (2001)। बहुभिन्नरूपी क्रमपरिवर्तन परीक्षण: जैवसांख्यिकी में अनुप्रयोगों के साथ, जॉन विले एंड संस। ISBN 978-0471496700
• Welch, W. J. (1990). "क्रमपरिवर्तन परीक्षणों का निर्माण". Journal of the American Statistical Association. 85 (411): 693–698. doi:10.1080/01621459.1990.10474929.

कम्प्यूटेशनल तरीके:

• Mehta, C. R.; Patel, N. R. (1983). "आरएक्ससी आकस्मिकता तालिकाओं में फिशर का सटीक परीक्षण करने के लिए एक नेटवर्क एल्गोरिदम". Journal of the American Statistical Association. 78 (382): 427–434. doi:10.1080/01621459.1983.10477989.
• Mehta, C. R.; Patel, N. R.; Senchaudhuri, P. (1988). "क्रमपरिवर्तनीय अनुमान में सटीक संभावनाओं का अनुमान लगाने के लिए नमूनाकरण का महत्व". Journal of the American Statistical Association. 83 (404): 999–1005. doi:10.1080/01621459.1988.10478691.
• Gill, P. M. W. (2007). "रैखिक-सांख्यिकीय क्रमपरिवर्तन महत्व परीक्षणों में पी-मानों की कुशल गणना" (PDF). Journal of Statistical Computation and Simulation. 77 (1): 55–61. CiteSeerX 10.1.1.708.1957. doi:10.1080/10629360500108053. S2CID 1813706.

क्रमपरिवर्तन परीक्षणों पर वर्तमान शोध

• अच्छा, पी.आई. (2012) पुन: नमूनाकरण विधियों के लिए प्रैक्टिशनर्स गाइड।
• अच्छा, पी.आई. (2005) परिकल्पनाओं का क्रमपरिवर्तन, पैरामीट्रिक और बूटस्ट्रैप परीक्षण
• हेस्टरबर्ग, टी.सी., डी.एस. मूर, एस. मोनाघन, ए. क्लिपसन, और आर. एपस्टीन (2005): /content/cat_080/pdf/moore14.pdf बूटस्ट्रैप तरीके और क्रमपरिवर्तन परीक्षण, सॉफ्टवेयर।
• मूर, डी.एस., जी. मैककेबे, डब्ल्यू. डकवर्थ, और एस. स्कोलोव (2003): बूटस्ट्रैप तरीके और क्रमपरिवर्तन परीक्षण
• साइमन, जे.एल. (1997): रेज़ैम्पलिंग: द न्यू स्टैटिस्टिक्स।
• यू, चोंग हो (2003): पुन: नमूनाकरण विधियां: अवधारणाएं, अनुप्रयोग और औचित्य। व्यावहारिक मूल्यांकन, अनुसंधान एवं मूल्यांकन, 8(19)। (सांख्यिकीय बूटस्ट्रैपिंग)
• पुन: नमूनाकरण: कंप्यूटर और सांख्यिकी का विवाह (ईआरआईसी डाइजेस्ट)