सूचना में अस्थिरता जटिलता: Difference between revisions
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
इनफार्मेशन में अस्थिरता [[जटिलता|काम्प्लेक्सता]] [[सूचना सिद्धांत|इनफार्मेशन सैद्धांतिक]] मात्रा है जिसे [[एन्ट्रॉपी (सूचना सिद्धांत)|एन्ट्रॉपी (इनफार्मेशन सिद्धांत)]] के बारे में जानकारी के अस्थिरता के रूप में परिभाषित किया गया है। यह गतिशील सिस्टम में व्यवस्था और अराजकता की प्रबलता में अस्थिरता से व्युत्पन्न है और इसका उपयोग कई विविध क्षेत्रों में काम्प्लेक्सता के माप के रूप में किया गया है। इसे बेट्स और शेपर्ड द्वारा 1993 के पेपर में प्रस्तुत किया गया था।<ref name=":0">{{Cite journal|last1=Bates|first1=John E.|last2=Shepard|first2=Harvey K.|date=1993-01-18|title=सूचना के उतार-चढ़ाव का उपयोग करके जटिलता को मापना|journal=Physics Letters A|language=en|volume=172|issue=6|pages=416–425|doi=10.1016/0375-9601(93)90232-O|bibcode=1993PhLA..172..416B|issn=0375-9601}}</ref> | |||
== परिभाषा == | == परिभाषा == | ||
असतत गतिशील | असतत गतिशील सिस्टम की इनफार्मेशन में अस्थिरता की काम्प्लेक्सता स्तिथि की संभाव्यता वितरण का फलन है जब यह यादृच्छिक बाहरी इनपुट डेटा के अधीन होता है। सिस्टम को समृद्ध इनफार्मेशन स्रोत जैसे कि [[यादृच्छिक संख्या पीढ़ी|यादृच्छिक संख्या जनरेटर]] या [[श्वेत रव]] सिग्नल के साथ चलाने का उद्देश्य सिस्टम की आंतरिक गतिशीलता का परीक्षण करना है, जैसे [[ संकेत आगे बढ़ाना |सिग्नल प्रोसेसिंग]] में आवृत्ति-समृद्ध [[आवेग प्रतिक्रिया|आवेग]] का उपयोग किया जाता है। | ||
यदि कोई | यदि कोई सिस्टम <math display="inline">N</math> है संभावित स्थितियाँ <math display="inline">p_i</math>ज्ञात हैं, तो इसकी इनफार्मेशन एन्ट्रापी है: | ||
: <math>\Eta = \sum_{i=1}^N p_i I_i = - \sum_{i=1}^N p_i \log p_i,</math> | : <math>\Eta = \sum_{i=1}^N p_i I_i = - \sum_{i=1}^N p_i \log p_i,</math> | ||
जहाँ <math display="inline">I_i = -\log p_i</math> स्तिथि की | जहाँ <math display="inline">I_i = -\log p_i</math> स्तिथि की इनफार्मेशन सामग्री <math display="inline">i</math> है। | ||
सिस्टम की इनफार्मेशन अस्थिरता काम्प्लेक्सता को मानक विचलन या अस्थिरता के रूप में परिभाषित किया गया है <math display="inline">I</math> माध्य के बारे में <math display="inline">\Eta</math> इस प्रकार है: | |||
: <math>\sigma_I = \sqrt{\sum_{i=1}^N p_i(I_i - \Eta)^2} = \sqrt{\sum_{i=1}^N p_iI_i^2 - \Eta^2}</math> | : <math>\sigma_I = \sqrt{\sum_{i=1}^N p_i(I_i - \Eta)^2} = \sqrt{\sum_{i=1}^N p_iI_i^2 - \Eta^2}</math> | ||
| Line 16: | Line 16: | ||
: <math>\sigma_I = \sqrt{\sum_{i=1}^N p_i \log^2 p_i - \Biggl(\sum_{i=1}^N p_i \log p_i \Biggr)^2}.</math> | : <math>\sigma_I = \sqrt{\sum_{i=1}^N p_i \log^2 p_i - \Biggl(\sum_{i=1}^N p_i \log p_i \Biggr)^2}.</math> | ||
स्तिथि की जानकारी में अस्थिरता <math>\sigma_I | स्तिथि की जानकारी में अस्थिरता <math>\sigma_I | ||
</math> सभी के साथ अधिकतम अव्यवस्थित | </math> सभी के साथ अधिकतम अव्यवस्थित सिस्टम में शून्य है सिस्टम अपने यादृच्छिक इनपुट <math>p_i = 1/N</math> को कॉपी करता है। जब सिस्टम केवल निश्चित स्थिति के साथ सम्पूर्ण रूप से व्यवस्थित होता है, तो <math>\sigma_I | ||
</math> भी शून्य होता है <math>(p_1 = 1)</math>, इनपुट को ध्यान किए बिना <math>\sigma_I | </math> भी शून्य होता है <math>(p_1 = 1)</math>, इनपुट को ध्यान किए बिना <math>\sigma_I | ||
</math> इन दो शीर्ष सीमाओं के मध्य उच्च-संभावना वाली स्तिथि और निम्न-संभावना वाली स्तिथि के मिश्रण के साथ स्थान को संपन्न करने वाला अशून्य है। | </math> इन दो शीर्ष सीमाओं के मध्य उच्च-संभावना वाली स्तिथि और निम्न-संभावना वाली स्तिथि के मिश्रण के साथ स्थान को संपन्न करने वाला अशून्य है। | ||
== | == इनफार्मेशन की अस्थिरता मेमोरी और गणना की अनुमति देता है == | ||
जैसे-जैसे | जैसे-जैसे काम्प्लेक्स गतिशील सिस्टम समय के साथ विकसित होती है, यह स्थितियों के मध्य कैसे परिवर्तन करती है यह अनियमित विधियों से बाहरी उत्तेजनाओं पर निर्भर करता है। कभी-कभी यह बाहरी उत्तेजनाओं के प्रति अधिक संवेदनशील (अस्थिर) हो सकता है और कभी-कभी कम संवेदनशील (स्थिर) हो सकता है। यदि किसी विशेष स्तिथि में कई संभावित स्तिथि हैं, तो बाहरी जानकारी यह निर्धारित करती है कि कौन सा अगला होगा और सिस्टम स्थान में विशेष प्रक्षेपवक्र का पालन करके उस जानकारी को प्राप्त करता है। किंतु यदि कई भिन्न-भिन्न स्थितियां एक ही स्थितियों की ओर ले जाते हैं, तो नेक्स्ट स्तिथि में प्रवेश करने पर सिस्टम यह जानकारी विलुप्त कर देता है कि कौन सी स्तिथि उससे पहले आई थी। इस प्रकार, काम्प्लेक्स सिस्टम समय के साथ विकसित होने पर समय-समय से इनफार्मेशन लाभ और हानि प्रदर्शित करती है। इनफार्मेशन का परिवर्तन या अस्थिरता याद रखने और भूलने के समान है। | ||
स्थितियों के मध्य ट्रांजीशन से जुड़ी जानकारी का लाभ या हानि स्तिथि की जानकारी से संबंधित हो सकती है। स्थितियों से ट्रांजीशन का | स्थितियों के मध्य ट्रांजीशन से जुड़ी जानकारी का लाभ या हानि स्तिथि की जानकारी से संबंधित हो सकती है। स्थितियों से ट्रांजीशन का इनफार्मेशन लाभ <math>i</math>, <math>j</math> स्तिथि छोड़ते समय प्राप्त की गई जानकारी है <math>i</math> स्तिथि में प्रवेश करते समय विलुप्त हुई जानकारी <math>j</math> कम होगी : | ||
: <math>\Gamma_{ij} = -\log p_{i \rightarrow j} + \log p_{i \leftarrow j}.</math> | : <math>\Gamma_{ij} = -\log p_{i \rightarrow j} + \log p_{i \leftarrow j}.</math> | ||
| Line 34: | Line 34: | ||
: <math>\Gamma_{ij} = -\log (p_{ij}/p_i) + \log (p_{ij}/p_j) = \log p_i - \log p_j = I_j - I_i.</math> | : <math>\Gamma_{ij} = -\log (p_{ij}/p_i) + \log (p_{ij}/p_j) = \log p_i - \log p_j = I_j - I_i.</math> | ||
इसलिए ट्रांजीशन के परिणामस्वरूप | इसलिए ट्रांजीशन के परिणामस्वरूप सिस्टम द्वारा प्राप्त शुद्ध जानकारी केवल प्रारंभिक से अंतिम स्थिति तक जानकारी में वृद्धि पर निर्भर करती है। यह दिखाया जा सकता है कि यह निरंतर कई परिवर्तन के लिए भी सत्य है।<ref name=":0" /> | ||
<math>\Gamma = \Delta I</math> बल और संभावित ऊर्जा के मध्य संबंध | <math>\Gamma = \Delta I</math> बल और संभावित ऊर्जा के मध्य संबंध है किसी क्षमता <math>I</math> से व्युत्पन्न <math>\Phi</math> और <math>\Gamma</math> बल के जैसे है <math>\mathbf{F}</math> में <math>\mathbf{F}={\nabla \Phi}</math> बाहरी जानकारी मेमोरी स्टोरेज को पूर्ण करने के लिए सिस्टम को उच्च इनफार्मेशन क्षमता की स्थिति में "ऊपर की ओर" पुश करती है, ठीक उसी प्रकार जैसे किसी द्रव्यमान को उच्च गुरुत्वाकर्षण क्षमता की स्थिति में ऊपर की ओर पुश करना ऊर्जा को संग्रहीत करता है। ऊर्जा स्टोरेज की मात्रा केवल अंतिम ऊंचाई पर निर्भर करती है, पहाड़ी के मार्ग पर नहीं पर निर्भर करती है। इसी प्रकार, इनफार्मेशन स्टोरेज की मात्रा स्थिति स्थान में दो स्थिति के मध्य ट्रांजीशन पथ पर निर्भर नहीं करती है। जब कोई सिस्टम उच्च इनफार्मेशन क्षमता वाली दुर्लभ स्थिति में पहुंच जाता है, तो यह पहले से संग्रहीत जानकारी विलुप्त करके अधिक सामान्य स्थिति में आ सकता है। | ||
मानक विचलन | मानक विचलन असतत यादृच्छिक चर की गणना करना उपयोगी हो सकता है, इसके माध्य <math>\Gamma</math> के बारे में (जो शून्य है), अर्थात् शुद्ध इनफार्मेशन लाभ की अस्थिरता <math>\sigma_\Gamma</math>,<ref name=":0" />किंतु <math>\sigma_I</math> स्थिति स्थान में बहु-ट्रांजीशन मेमोरी लूप को ध्यान में रखता है और इसलिए यह सिस्टम की कम्प्यूटेशनल शक्ति का उत्तम संकेतक होना चाहिए। इसके अतिरिक्त, <math>\sigma_I</math> गणना करना सरल है क्योंकि स्थितियों की तुलना में कई अधिक ट्रांजीशन हो सकते हैं। | ||
== | == कैओस और व्यवस्था == | ||
गतिशील प्रणाली जो बाहरी जानकारी के प्रति संवेदनशील है (अस्थिर) कैओस सिद्धांत व्यवहार प्रदर्शित करती है जबकि | गतिशील प्रणाली जो बाहरी जानकारी के प्रति संवेदनशील है (अस्थिर) कैओस सिद्धांत व्यवहार प्रदर्शित करती है जबकि बाहरी जानकारी के प्रति असंवेदनशील है (स्थिर) व्यवस्थित व्यवहार प्रदर्शित करती है। काम्प्लेक्स सिस्टम दोनों व्यवहार प्रदर्शित करते है, समृद्ध इनफार्मेशन स्रोत के अधीन होने पर गतिशील संतुलन में उनके मध्य अस्थिरता होता है। अस्थिरता की डिग्री की मात्रा निर्धारित की जाती है <math>\sigma_I</math>; समय के साथ विकसित होने पर काम्प्लेक्स सिस्टम में कैओस और व्यवस्था की प्रबलता में परिवर्तन करता है। | ||
== उदाहरण: [[प्राथमिक सेलुलर ऑटोमेटन]] का [[नियम 110]] संस्करण == | == उदाहरण: [[प्राथमिक सेलुलर ऑटोमेटन]] का [[नियम 110]] संस्करण == | ||
प्राथमिक सेलुलर ऑटोमेटन का नियम 110 संस्करण | प्राथमिक सेलुलर ऑटोमेटन का नियम 110 संस्करण सार्वभौमिक गणना में सक्षम सिद्ध हुआ है। प्रमाण ग्लाइडर या स्पेसशिप के रूप में जाने जाने वाले एकजुट और स्वयं-स्थायी सेल पैटर्न के अस्तित्व और इंटरैक्शन पर आधारित है, जो आकस्मिक घटना है, जो ऑटोमेटन सेल्स के ग्रुपों की यह याद रखने की क्षमता का संकेत देता है कि ग्लाइडर उनके मध्य से निकल रहा है। इसलिए यह आशा की जाती है कि इनफार्मेशन लाभ और हानि, अस्थिरता और स्थिरता, अराजकता और व्यवस्था के विकल्पों के परिणामस्वरूप स्तिथि स्थान में मेमोरी लूप होंगे। | ||
आसन्न ऑटोमेटन | आसन्न ऑटोमेटन सेल्स के 3-सेल ग्रुप पर विचार किया जाता है, जो नियम 110 {{inline block|end-center-end}} का पालन करते हैं: सेण्टर सेल की अगली स्थिति स्वयं की वर्तमान स्थिति और नियम द्वारा निर्दिष्ट अंतिम सेल्स पर निर्भर करती है: | ||
{| class="wikitable" style="width: 500px; margin: auto; text-align: center" | {| class="wikitable" style="width: 500px; margin: auto; text-align: center" | ||
|+ | |+प्राथमिक सेलुलर ऑटोमेटन नियम 110 | ||
!3- | !3-सेल ग्रुप | ||
|1-1-1 | |1-1-1 | ||
|1-1-0 | |1-1-0 | ||
| Line 60: | Line 60: | ||
|0-0-0 | |0-0-0 | ||
|- | |- | ||
! | !नेक्स्ट सेण्टर सेल | ||
|0 | |0 | ||
|1 | |1 | ||
| Line 70: | Line 70: | ||
|0 | |0 | ||
|} | |} | ||
इस | इस सिस्टम की इनफार्मेशन अस्थिरता काम्प्लेक्सता की गणना करने के लिए, 3-सेल ग्रुप के प्रत्येक एंड पर ड्राइवर सेल संलग्न किया जाता है, जिससे {{inline block|driver→end-center-end←driver}}यादृच्छिक बाहरी उत्तेजना प्रदान की जा सके, जिससे नियम को दो अंतिम सेल्स पर प्रारम्भ किया जा सके। आगे की सशर्त संभावनाओं को निर्धारित करने के लिए, आगे निर्धारित करें कि प्रत्येक संभावित वर्तमान स्थिति के लिए और ड्राइवर सेल सामग्री के प्रत्येक संभावित संयोजन के लिए अगली स्थिति क्या है। | ||
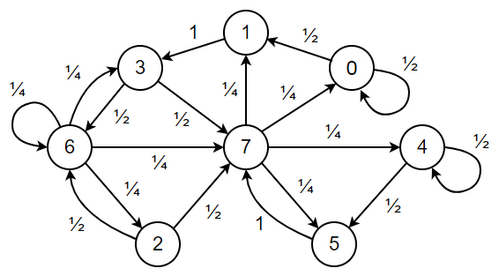
इस | इस सिस्टम का स्तिथि [[राज्य आरेख|आरेख]] नीचे दर्शाया गया है, जिसमें वृत्त स्थितियों का प्रतिनिधित्व करते हैं और एरो स्थितियों के मध्य ट्रांजीशन का प्रतिनिधित्व करते हैं। इस सिस्टम की आठ अवस्थाएँ, {{inline block|1-1-1}} को {{inline block|0-0-0}} को 3-सेल ग्रुप की 3-बिट सामग्री के ऑक्टल समकक्ष के साथ लेबल किया गया है: 7 से 0 ट्रांजीशन एरो को आगे की सशर्त संभावनाओं के साथ लेबल किया गया है। ध्यान दें कि अराजकता और व्यवस्था, संवेदनशीलता और असंवेदनशीलता, ड्राईवर सेल से बाहरी जानकारी के लाभ और हानि में परिवर्तनशीलता के अनुरूप एरो के विचलन और अभिसरण में परिवर्तनशीलता है। | ||
[[File:State diagram for rule 110 with transition probabilities.png|alt=|center|thumb|499x499px|नियम 110 प्राथमिक सेलुलर ऑटोमेटन के लिए 3-सेल | [[File:State diagram for rule 110 with transition probabilities.png|alt=|center|thumb|499x499px|नियम 110 प्राथमिक सेलुलर ऑटोमेटन के लिए 3-सेल स्तिथिआरेख यादृच्छिक उत्तेजना के साथ आगे की सशर्त ट्रांजीशन संभावनाओं को दर्शाता है।]]आगे की सशर्त संभावनाएं संभावित ड्राइवर सेल सामग्री के अनुपात से निर्धारित होती हैं जो विशेष ट्रांजीशन को चलाती हैं। उदाहरण के लिए, दो ड्राइवर सेल सामग्री के चार संभावित संयोजनों के लिए, स्थिति 7 स्थिति 5, 4, 1 और 0 की ओर ले जाती है इसलिए <math>p_{7 \rightarrow 5}</math>, <math>p_{7 \rightarrow 4}</math>, <math>p_{7 \rightarrow 1}</math>, और <math>p_{7 \rightarrow 0}</math> प्रत्येक ¼ या 25% हैं। इसी प्रकार, अवस्था 0 अवस्था 0, 1, 0 और 1 की ओर ले जाती है <math>p_{0 \rightarrow 1}</math>और <math>p_{0 \rightarrow 0}</math> प्रत्येक ½ या 50% हैं। इत्यादि। | ||
अवस्था की संभावनाएँ इससे संबंधित हैं | |||
: <math>p_j = \sum_{i=0}^7 p_i p_{i \rightarrow j}</math> और <math>\sum_{i=0}^7 p_i = 1.</math> | : <math>p_j = \sum_{i=0}^7 p_i p_{i \rightarrow j}</math> और <math>\sum_{i=0}^7 p_i = 1.</math> | ||
इन रैखिक बीजगणितीय समीकरणों को | इन रैखिक बीजगणितीय समीकरणों को अवस्था संभावनाओं के लिए मैन्युअल रूप से या कंप्यूटर प्रोग्राम की सहायता से निम्नलिखित परिणामों के साथ समाधान किया जा सकता है: | ||
{| class="wikitable" style="width: 300px; margin: auto; text-align: center" | {| class="wikitable" style="width: 300px; margin: auto; text-align: center" | ||
|+ | |+नियम 110 यादृच्छिक उत्तेजना के साथ 3-सेल ऑटोमेटन के लिए संभावनाएं बताता है | ||
|p<sub>0</sub> | |p<sub>0</sub> | ||
|p<sub>1</sub> | |p<sub>1</sub> | ||
| Line 100: | Line 100: | ||
|{{sfrac|4|17}} | |{{sfrac|4|17}} | ||
|} | |} | ||
इनफार्मेशन एन्ट्रापी और काम्प्लेक्स की गणना अवस्था संभावनाओं से की जा सकती है: | |||
: <math>\Eta = - \sum_{i=0}^7 p_i \log_2 p_i = 2.86 \text{ bits},</math> | : <math>\Eta = - \sum_{i=0}^7 p_i \log_2 p_i = 2.86 \text{ bits},</math> | ||
: <math>\sigma_I = \sqrt{\sum_{i=0}^7 p_i \log_2^2 p_i - \Eta^2} = 0.56 \text{ bits}.</math> | : <math>\sigma_I = \sqrt{\sum_{i=0}^7 p_i \log_2^2 p_i - \Eta^2} = 0.56 \text{ bits}.</math> | ||
ध्यान दें कि आठ राज्यों के लिए अधिकतम संभव एन्ट्रापी है <math>\log_2 8 = 3 \text{ bits},</math> जो कि स्थिति होगी यदि सभी आठ राज्य ⅛ (यादृच्छिकता) की संभावनाओं के साथ समान रूप से संभावित हों। इस प्रकार नियम 110 में 2.86 बिट्स पर अपेक्षाकृत उच्च एन्ट्रापी या राज्य उपयोग है। किंतु यह एन्ट्रापी के बारे में राज्य की जानकारी में पर्याप्त अस्थिरता और इस प्रकार | ध्यान दें कि आठ राज्यों के लिए अधिकतम संभव एन्ट्रापी है <math>\log_2 8 = 3 \text{ bits},</math> जो कि स्थिति होगी यदि सभी आठ राज्य ⅛ (यादृच्छिकता) की संभावनाओं के साथ समान रूप से संभावित हों। इस प्रकार नियम 110 में 2.86 बिट्स पर अपेक्षाकृत उच्च एन्ट्रापी या राज्य उपयोग है। किंतु यह एन्ट्रापी के बारे में राज्य की जानकारी में पर्याप्त अस्थिरता और इस प्रकार काम्प्लेक्सता के पर्याप्त मूल्य को नहीं रोकता है। जबकि, अधिकतम एन्ट्रापी काम्प्लेक्सता को दूर कर देगी। | ||
जब ऊपर उपयोग की गई विश्लेषणात्मक विधि अव्यवहार्य हो तो राज्य की संभावनाओं को प्राप्त करने के लिए वैकल्पिक विधि का उपयोग किया जा सकता है। बस कई पीढ़ियों के लिए यादृच्छिक स्रोत के साथ | जब ऊपर उपयोग की गई विश्लेषणात्मक विधि अव्यवहार्य हो तो राज्य की संभावनाओं को प्राप्त करने के लिए वैकल्पिक विधि का उपयोग किया जा सकता है। बस कई पीढ़ियों के लिए यादृच्छिक स्रोत के साथ सिस्टम को उसके इनपुट (ड्राइवर सेल) पर चलाएं और अनुभवजन्य रूप से राज्य की संभावनाओं का निरीक्षण करें। जब यह 10 मिलियन पीढ़ियों तक कंप्यूटर सिमुलेशन के माध्यम से किया जाता है तो परिणाम इस प्रकार हैं:<ref>{{Cite web|url=https://www.researchgate.net/publication/340284677|title=Measuring complexity using information fluctuation: a tutorial|last=Bates|first=John E.|date=2020-03-30|website=Research Gate}}</ref> | ||
{| class="wikitable" style="width: 600px; margin: auto; text-align: center" | {| class="wikitable" style="width: 600px; margin: auto; text-align: center" | ||
| Line 162: | Line 162: | ||
|0.10 | |0.10 | ||
|} | |} | ||
चूंकि दोनों <math>\Eta</math> और <math>\sigma_I</math> | चूंकि दोनों <math>\Eta</math> और <math>\sigma_I</math> सिस्टम आकार के साथ उनके आयाम रहित अनुपात में वृद्धि होती है <math>\sigma_I/\Eta</math>, सापेक्ष इनफार्मेशन अस्थिरता काम्प्लेक्सता, विभिन्न आकारों की प्रणालियों की उत्तम तुलना करने के लिए शामिल है। ध्यान दें कि अनुभवजन्य और विश्लेषणात्मक परिणाम 3-सेल ऑटोमेटन के लिए सहमत हैं। | ||
बेट्स और शेपर्ड के पेपर में,<ref name=":0" /> <math>\sigma_I</math> सभी प्राथमिक सेलुलर ऑटोमेटन नियमों के लिए गणना की गई है और यह देखा गया है कि जो धीमी गति से चलने वाले ग्लाइडर और संभवतः स्थिर वस्तुओं को प्रदर्शित करते हैं, जैसा कि नियम 110 करता है, बड़े मूल्यों के साथ अत्यधिक सहसंबद्ध हैं <math>\sigma_I</math>. <math>\sigma_I</math> इसलिए इसे सार्वभौमिक गणना के लिए उम्मीदवार नियमों का चयन करने के लिए फिल्टर के रूप में उपयोग किया जा सकता है, जिसे साबित करना कठिन है। | बेट्स और शेपर्ड के पेपर में,<ref name=":0" /> <math>\sigma_I</math> सभी प्राथमिक सेलुलर ऑटोमेटन नियमों के लिए गणना की गई है और यह देखा गया है कि जो धीमी गति से चलने वाले ग्लाइडर और संभवतः स्थिर वस्तुओं को प्रदर्शित करते हैं, जैसा कि नियम 110 करता है, बड़े मूल्यों के साथ अत्यधिक सहसंबद्ध हैं <math>\sigma_I</math>. <math>\sigma_I</math> इसलिए इसे सार्वभौमिक गणना के लिए उम्मीदवार नियमों का चयन करने के लिए फिल्टर के रूप में उपयोग किया जा सकता है, जिसे साबित करना कठिन है। | ||
== अनुप्रयोग == | == अनुप्रयोग == | ||
यद्यपि | यद्यपि इनफार्मेशन अस्थिरता काम्प्लेक्सता सूत्र की व्युत्पत्ति गतिशील सिस्टम में इनफार्मेशन के अस्थिरता पर आधारित है, सूत्र केवल राज्य संभावनाओं पर निर्भर करता है और इसलिए यह किसी भी संभाव्यता वितरण पर भी प्रारम्भ होता है, जिसमें स्थिर छवियों या पाठ से प्राप्त वितरण भी शामिल है। | ||
वर्षों से मूल पेपर<ref name=":0" />कई विविध क्षेत्रों में शोधकर्ताओं द्वारा [https://scholar.google.com/scholar?cites=18239232465073627536&as_sdt=2005&sciodt=0,5&hl=en संदर्भित] किया गया है: | वर्षों से मूल पेपर<ref name=":0" />कई विविध क्षेत्रों में शोधकर्ताओं द्वारा [https://scholar.google.com/scholar?cites=18239232465073627536&as_sdt=2005&sciodt=0,5&hl=en संदर्भित] किया गया है: काम्प्लेक्सता सिद्धांत,<ref>{{Cite journal|last=Atmanspacher|first=Harald|date=September 1997|title=कार्टेशियन कट, हाइजेनबर्ग कट, और जटिलता की अवधारणा|journal=World Futures|language=en|volume=49|issue=3–4|pages=333–355|doi=10.1080/02604027.1997.9972639|issn=0260-4027}}</ref> काम्प्लेक्स सिस्टम विज्ञान,<ref>{{Citation|last=Shalizi|first=Cosma Rohilla|title=Methods and Techniques of Complex Systems Science: An Overview|date=2006|work=Complex Systems Science in Biomedicine|pages=33–114|editor-last=Deisboeck|editor-first=Thomas S.|series=Topics in Biomedical Engineering International Book Series|publisher=Springer US|language=en|doi=10.1007/978-0-387-33532-2_2|arxiv=nlin/0307015|isbn=978-0-387-33532-2|s2cid=11972113|editor2-last=Kresh|editor2-first=J. Yasha}}</ref> काम्प्लेक्स नेटवर्क,<ref>{{Cite journal |last1=Huang |first1=Min |last2=Sun |first2=Zhongkui |last3=Donner |first3=Reik V. |last4=Zhang |first4=Jie |last5=Gua |first5=Shuguang |last6=Zou |first6=Yong |date=2021-03-09 |title=क्रमिक पैटर्न संक्रमण नेटवर्क के आधार पर सांख्यिकीय जटिलता उपायों द्वारा गतिशील संक्रमण की विशेषता|url=https://pubs.aip.org/aip/cha/article/31/3/033127/342127 |journal=[[Chaos: An Interdisciplinary Journal of Nonlinear Science]] |volume=31 |issue=3 |page=033127 |doi=10.1063/5.0038876|pmid=33810737 |s2cid=232771788 }}</ref> अराजक गतिशीलता,<ref>{{Cite journal|last=Wackerbauer|first=Renate|date=1995-11-01|title=लोरेन्ज़ प्रणाली का शोर-प्रेरित स्थिरीकरण|journal=Physical Review E|volume=52|issue=5|pages=4745–4749|doi=10.1103/PhysRevE.52.4745|pmid=9963970|bibcode=1995PhRvE..52.4745W}}</ref> अनेक-निकाय स्थानीयकरण उलझाव,<ref>{{Cite journal |last1=Hamilton |first1=Gregory A. |last2=Clark |first2=Bryan K. |date=2023-02-14 |title=कई-निकाय स्थानीयकरण के लिए एकात्मक प्रवाह दक्षता और उलझाव की मात्रा निर्धारित करना|url=https://link.aps.org/doi/10.1103/PhysRevB.107.064203 |journal=Physical Review B |volume=107 |issue=6 |pages=064203 |doi=10.1103/PhysRevB.107.064203|arxiv=2110.10148 |s2cid=239024666 }}</ref> पर्यावरणीय इंजीनियरिंग,<ref>{{Cite book|last=Singh|first=Vijay P.|url=https://books.google.com/books?id=A8_-5-VWJiAC&pg=PT9|title=एन्ट्रॉपी सिद्धांत और पर्यावरण और जल इंजीनियरिंग में इसका अनुप्रयोग|date=2013-01-10|publisher=John Wiley & Sons|isbn=978-1-118-42860-3|language=en}}</ref> पारिस्थितिक काम्प्लेक्सता,<ref>{{Cite journal|last=Parrott|first=Lael|date=2010-11-01|title=पारिस्थितिक जटिलता को मापना|url=http://www.sciencedirect.com/science/article/pii/S1470160X10000567|journal=Ecological Indicators|language=en|volume=10|issue=6|pages=1069–1076|doi=10.1016/j.ecolind.2010.03.014|issn=1470-160X}}</ref> पारिस्थितिक समय-श्रृंखला विश्लेषण,<ref>{{Citation|last=Lange|first=Holger|title=Time-series Analysis in Ecology|date=2006|work=eLS|publisher=American Cancer Society|language=en|doi=10.1038/npg.els.0003276|isbn=978-0-470-01590-2}}</ref> पारिस्थितिकी तंत्र स्थिरता,<ref>{{Cite journal|last1=Wang|first1=Chaojun|last2=Zhao|first2=Hongrui|date=2019-04-18|title=Analysis of remote sensing time-series data to foster ecosystem sustainability: use of temporal information entropy|journal=International Journal of Remote Sensing|volume=40|issue=8|pages=2880–2894|doi=10.1080/01431161.2018.1533661|bibcode=2019IJRS...40.2880W|s2cid=135003743|issn=0143-1161}}</ref> वायु<ref>{{Cite journal|last1=Klemm|first1=Otto|last2=Lange|first2=Holger|date=1999-12-01|title=फिचटेलगेबिर्ज पर्वत, बवेरिया में वायु प्रदूषण के रुझान|journal=Environmental Science and Pollution Research|language=en|volume=6|issue=4|pages=193–199|doi=10.1007/BF02987325|pmid=19005662|s2cid=35043|issn=1614-7499}}</ref> और पानी<ref>{{Cite journal|last1=Wang|first1=Kang|last2=Lin|first2=Zhongbing|date=2018|title=विभिन्न स्थानिक पैमानों पर नदी में नॉनपॉइंट स्रोत प्रदूषण का लक्षण वर्णन|journal=Water and Environment Journal|language=en|volume=32|issue=3|pages=453–465|doi=10.1111/wej.12345|s2cid=115667734 |issn=1747-6593}}</ref> प्रदूषण, जलवैज्ञानिक तरंगिका विश्लेषण,<ref>{{Cite journal|last=Labat|first=David|date=2005-11-25|title=Recent advances in wavelet analyses: Part 1. A review of concepts|url=http://www.sciencedirect.com/science/article/pii/S0022169405001769|journal=Journal of Hydrology|language=en|volume=314|issue=1|pages=275–288|doi=10.1016/j.jhydrol.2005.04.003|bibcode=2005JHyd..314..275L|issn=0022-1694}}</ref> मृदा जल प्रवाह,<ref>{{Cite journal|last1=Pachepsky|first1=Yakov|last2=Guber|first2=Andrey|last3=Jacques|first3=Diederik|last4=Simunek|first4=Jiri|last5=Van Genuchten|first5=Marthinus Th.|last6=Nicholson|first6=Thomas|last7=Cady|first7=Ralph|date=2006-10-01|title=सिम्युलेटेड मृदा जल प्रवाह की सूचना सामग्री और जटिलता|url=http://www.sciencedirect.com/science/article/pii/S0016706106000504|journal=Geoderma|series=Fractal Geometry Applied to Soil and Related Hierarchical Systems - Fractals, Complexity and Heterogeneity|language=en|volume=134|issue=3|pages=253–266|doi=10.1016/j.geoderma.2006.03.003|bibcode=2006Geode.134..253P|issn=0016-7061}}</ref> मिट्टी की नमी,<ref>{{Cite journal|last1=Kumar|first1=Sujay V.|last2=Dirmeyer|first2=Paul A.|last3=Peters-Lidard|first3=Christa D.|author-link3=Christa Peters-Lidard|last4=Bindlish|first4=Rajat|last5=Bolten|first5=John|date=2018-01-01|title=उपग्रह मिट्टी की नमी पुनर्प्राप्ति का सूचना सैद्धांतिक मूल्यांकन|url= |journal=Remote Sensing of Environment|language=en|volume=204|pages=392–400|doi=10.1016/j.rse.2017.10.016|pmid=32636571|pmc=7340154|bibcode=2018RSEnv.204..392K|issn=0034-4257|hdl=2060/20180003069|hdl-access=free}}</ref> हेडवाटर अपवाह,<ref>{{Cite journal|last1=Hauhs|first1=Michael|last2=Lange|first2=Holger|date=2008|title=Classification of Runoff in Headwater Catchments: A Physical Problem?|journal=Geography Compass|language=en|volume=2|issue=1|pages=235–254|doi=10.1111/j.1749-8198.2007.00075.x|issn=1749-8198}}</ref> भूजल की गहराई,<ref>{{Cite journal|last1=Liu|first1=Meng|last2=Liu|first2=Dong|last3=Liu|first3=Le|date=2013-09-01|title=Complexity research of regional groundwater depth series based on multiscale entropy: a case study of Jiangsanjiang Branch Bureau in China|journal=Environmental Earth Sciences|language=en|volume=70|issue=1|pages=353–361|doi=10.1007/s12665-012-2132-y|bibcode=2013EES....70..353L |s2cid=128958458|issn=1866-6299}}</ref> हवाई यातायात नियंत्रण,<ref>{{Cite journal|last1=Xing|first1=Jing|last2=Manning|first2=Carol A.|date=April 2005|title=Complexity and Automation Displays of Air Traffic Control: Literature Review and Analysis|url=https://apps.dtic.mil/docs/citations/ADA460107|archive-url=https://web.archive.org/web/20220601070456/https://apps.dtic.mil/docs/citations/ADA460107|url-status=live|archive-date=June 1, 2022|language=en}}</ref> प्रवाह पैटर्न<ref>{{Cite book|last1=Wang|first1=Kang|last2=Li|first2=Li|title=2008 First International Conference on Intelligent Networks and Intelligent Systems |chapter=Characterizing Heterogeneous Flow Patterns Using Information Measurements |date=November 2008|pages=654–657|doi=10.1109/ICINIS.2008.110|s2cid=8867649}}</ref> और बाढ़ की घटनाएँ,<ref>{{Cite journal|last1=Al Sawaf|first1=Mohamad Basel|last2=Kawanisi|first2=Kiyosi|date=2020-11-01|title=सूचना और जटिलता उपायों का उपयोग करके पहाड़ी नदी धारा प्रवाह पैटर्न और बाढ़ की घटनाओं का आकलन|url=https://www.sciencedirect.com/science/article/pii/S0022169420309689|journal=Journal of Hydrology|language=en|volume=590|pages=125508|doi=10.1016/j.jhydrol.2020.125508|bibcode=2020JHyd..59025508A|s2cid=225261677|issn=0022-1694}}</ref> टोपोलॉजी,<ref>{{Citation|last1=Javaheri Javid|first1=Mohammad Ali|title=A Comparative Analysis of Detecting Symmetries in Toroidal Topology|date=2016|work=Intelligent Systems and Applications: Extended and Selected Results from the SAI Intelligent Systems Conference (IntelliSys) 2015|pages=323–344|editor-last=Bi|editor-first=Yaxin|series=Studies in Computational Intelligence|publisher=Springer International Publishing|language=en|doi=10.1007/978-3-319-33386-1_16|isbn=978-3-319-33386-1|last2=Alghamdi|first2=Wajdi|last3=Zimmer|first3=Robert|last4=al-Rifaie|first4=Mohammad Majid|url=https://research.gold.ac.uk/17245/1/2016_Computational_Intelligence_partial_symmetry.pdf|editor2-last=Kapoor|editor2-first=Supriya|editor3-last=Bhatia|editor3-first=Rahul}}</ref> अर्थशास्त्र,<ref>{{Cite journal |last1=Jurado-González |first1=Javier |last2=Gómez-Barroso |first2=José Luis |date=2022-11-28 |title=Economic complexity and Information Society paradigms: a hybrid contribution to explain economic growth |url=https://jau.vgtu.lt/index.php/TEDE/article/view/17104 |journal=Technological and Economic Development of Economy |language=en |volume=28 |issue=6 |pages=1871–1896 |doi=10.3846/tede.2022.17104 |s2cid=254339040 |issn=2029-4921}}</ref> धातु का बाजार पूर्वानुमान<ref>{{Cite journal|last1=He|first1=Kaijian|last2=Lu|first2=Xingjing|last3=Zou|first3=Yingchao|last4=Keung Lai|first4=Kin|date=2015-09-01|title=कर्वलेट आधारित मल्टीस्केल पद्धति के साथ धातु की कीमतों का पूर्वानुमान लगाना|url=http://www.sciencedirect.com/science/article/pii/S0301420715000367|journal=Resources Policy|language=en|volume=45|pages=144–150|doi=10.1016/j.resourpol.2015.03.011|bibcode=2015RePol..45..144H |issn=0301-4207}}</ref> और बिजली<ref>{{Cite journal|last1=He|first1=Kaijian|last2=Xu|first2=Yang|last3=Zou|first3=Yingchao|last4=Tang|first4=Ling|date=2015-05-01|title=कर्वलेट डीनोइज़िंग आधारित दृष्टिकोण का उपयोग करके बिजली की कीमत का पूर्वानुमान|url=http://www.sciencedirect.com/science/article/pii/S037843711500014X|journal=Physica A: Statistical Mechanics and Its Applications|language=en|volume=425|pages=1–9|doi=10.1016/j.physa.2015.01.012|issn=0378-4371}}</ref> कीमतें, स्वास्थ्य इनफार्मेशन विज्ञान,<ref>{{Citation|last=Ahmed|first=Mosabber Uddin|title=Complexity Analysis in Health Informatics|date=2021|url=https://doi.org/10.1007/978-3-030-54932-9_4|work=Signal Processing Techniques for Computational Health Informatics|pages=103–121|editor-last=Ahad|editor-first=Md Atiqur Rahman|series=Intelligent Systems Reference Library|volume=192|place=Cham|publisher=Springer International Publishing|language=en|doi=10.1007/978-3-030-54932-9_4|isbn=978-3-030-54932-9|s2cid=225129992|access-date=2021-02-01|editor2-last=Ahmed|editor2-first=Mosabber Uddin}}</ref> मानव संज्ञान,<ref>{{Cite journal|last1=Shi Xiujian|last2=Sun Zhiqiang|last3=Li Long|last4=Xie Hongwei|title=परिवहन प्रणालियों में मानव संज्ञानात्मक जटिलता विश्लेषण|journal=Logistics|series=Proceedings|year=2009|pages=4361–4368|doi=10.1061/40996(330)637|isbn=9780784409961}}</ref> मानव चाल कीनेमेटिक्स,<ref>{{Cite book|last1=Zhang|first1=Shutao|last2=Qian|first2=Jinwu|last3=Shen|first3=Linyong|last4=Wu|first4=Xi|last5=Hu|first5=Xiaowu|title=2015 International Symposium on Bioelectronics and Bioinformatics (ISBB) |chapter=Gait complexity and frequency content analyses of patients with Parkinson's disease |date=October 2015|pages=87–90|doi=10.1109/ISBB.2015.7344930|isbn=978-1-4673-6609-0|s2cid=2891655}}</ref> तंत्रिका विज्ञान,<ref>{{Cite journal|last1=Wang|first1=Jisung|last2=Noh|first2=Gyu-Jeong|last3=Choi|first3=Byung-Moon|last4=Ku|first4=Seung-Woo|last5=Joo|first5=Pangyu|last6=Jung|first6=Woo-Sung|last7=Kim|first7=Seunghwan|last8=Lee|first8=Heonsoo|date=2017-07-13|title=केटामाइन- और प्रोपोफोल-प्रेरित बेहोशी के दौरान दबी हुई तंत्रिका जटिलता|url=http://www.sciencedirect.com/science/article/pii/S030439401730441X|journal=Neuroscience Letters|language=en|volume=653|pages=320–325|doi=10.1016/j.neulet.2017.05.045|pmid=28572032|s2cid=13767209|issn=0304-3940}}</ref> ईईजी विश्लेषण,<ref>{{Cite journal|last1=Bola|first1=Michał|last2=Orłowski|first2=Paweł|last3=Płomecka|first3=Martyna|last4=Marchewka|first4=Artur|date=2019-01-30|title=EEG signal diversity during propofol sedation: an increase in sedated but responsive, a decrease in sedated and unresponsive subjects|url=https://www.biorxiv.org/content/10.1101/444281v2|journal=bioRxiv|language=en|pages=444281|doi=10.1101/444281|s2cid=214726084}}</ref> शिक्षा,<ref>{{Cite journal|last=Dilger|first=Alexander|date=2012-01-01|title=अंतर्जात जटिलता, विशेषज्ञता और सामान्य शिक्षा|journal=On the Horizon|volume=20|issue=1|pages=49–53|doi=10.1108/10748121211202062|issn=1074-8121}}</ref> निवेश,<ref>{{Cite web|url=https://www.elibrary.ru/item.asp?id=24017528|title=गतिशील रणनीतिक निवेश पोर्टफोलियो प्रबंधन मॉडल|last=Ivanyuk|first=Vera Alekseevna|date=2015|website=elibrary.ru}}</ref> कृत्रिम जीवन<ref>{{Cite journal |last1=Peña |first1=Eric |last2=Sayama |first2=Hiroki |date=2021-05-02 |title=Life Worth Mentioning: Complexity in Life-Like Cellular Automata |url=https://direct.mit.edu/artl/article/27/2/105/107883/Life-Worth-Mentioning-Complexity-in-Life-Like |journal=[[Artificial Life]] |volume=27 |issue=2 |pages=105–112 |doi=10.1162/artl_a_00348|pmid=34727158 |s2cid=240424110 }}</ref> और सौंदर्यशास्त्र.<ref>{{Cite thesis|title=Aesthetic Automata: Synthesis and Simulation of Aesthetic Behaviour in Cellular Automata|url=http://research.gold.ac.uk/27681/|publisher=Goldsmiths, University of London|date=2019-11-30|degree=doctoral|doi=10.25602/gold.00027681|first=Mohammad Ali|last=Javaheri Javid}}</ref> | ||
== संदर्भ == | == संदर्भ == | ||
Revision as of 22:06, 7 December 2023
इनफार्मेशन में अस्थिरता काम्प्लेक्सता इनफार्मेशन सैद्धांतिक मात्रा है जिसे एन्ट्रॉपी (इनफार्मेशन सिद्धांत) के बारे में जानकारी के अस्थिरता के रूप में परिभाषित किया गया है। यह गतिशील सिस्टम में व्यवस्था और अराजकता की प्रबलता में अस्थिरता से व्युत्पन्न है और इसका उपयोग कई विविध क्षेत्रों में काम्प्लेक्सता के माप के रूप में किया गया है। इसे बेट्स और शेपर्ड द्वारा 1993 के पेपर में प्रस्तुत किया गया था।[1]
परिभाषा
असतत गतिशील सिस्टम की इनफार्मेशन में अस्थिरता की काम्प्लेक्सता स्तिथि की संभाव्यता वितरण का फलन है जब यह यादृच्छिक बाहरी इनपुट डेटा के अधीन होता है। सिस्टम को समृद्ध इनफार्मेशन स्रोत जैसे कि यादृच्छिक संख्या जनरेटर या श्वेत रव सिग्नल के साथ चलाने का उद्देश्य सिस्टम की आंतरिक गतिशीलता का परीक्षण करना है, जैसे सिग्नल प्रोसेसिंग में आवृत्ति-समृद्ध आवेग का उपयोग किया जाता है।
यदि कोई सिस्टम है संभावित स्थितियाँ ज्ञात हैं, तो इसकी इनफार्मेशन एन्ट्रापी है:
जहाँ स्तिथि की इनफार्मेशन सामग्री है।
सिस्टम की इनफार्मेशन अस्थिरता काम्प्लेक्सता को मानक विचलन या अस्थिरता के रूप में परिभाषित किया गया है माध्य के बारे में इस प्रकार है:
या
स्तिथि की जानकारी में अस्थिरता सभी के साथ अधिकतम अव्यवस्थित सिस्टम में शून्य है सिस्टम अपने यादृच्छिक इनपुट को कॉपी करता है। जब सिस्टम केवल निश्चित स्थिति के साथ सम्पूर्ण रूप से व्यवस्थित होता है, तो भी शून्य होता है , इनपुट को ध्यान किए बिना इन दो शीर्ष सीमाओं के मध्य उच्च-संभावना वाली स्तिथि और निम्न-संभावना वाली स्तिथि के मिश्रण के साथ स्थान को संपन्न करने वाला अशून्य है।
इनफार्मेशन की अस्थिरता मेमोरी और गणना की अनुमति देता है
जैसे-जैसे काम्प्लेक्स गतिशील सिस्टम समय के साथ विकसित होती है, यह स्थितियों के मध्य कैसे परिवर्तन करती है यह अनियमित विधियों से बाहरी उत्तेजनाओं पर निर्भर करता है। कभी-कभी यह बाहरी उत्तेजनाओं के प्रति अधिक संवेदनशील (अस्थिर) हो सकता है और कभी-कभी कम संवेदनशील (स्थिर) हो सकता है। यदि किसी विशेष स्तिथि में कई संभावित स्तिथि हैं, तो बाहरी जानकारी यह निर्धारित करती है कि कौन सा अगला होगा और सिस्टम स्थान में विशेष प्रक्षेपवक्र का पालन करके उस जानकारी को प्राप्त करता है। किंतु यदि कई भिन्न-भिन्न स्थितियां एक ही स्थितियों की ओर ले जाते हैं, तो नेक्स्ट स्तिथि में प्रवेश करने पर सिस्टम यह जानकारी विलुप्त कर देता है कि कौन सी स्तिथि उससे पहले आई थी। इस प्रकार, काम्प्लेक्स सिस्टम समय के साथ विकसित होने पर समय-समय से इनफार्मेशन लाभ और हानि प्रदर्शित करती है। इनफार्मेशन का परिवर्तन या अस्थिरता याद रखने और भूलने के समान है।
स्थितियों के मध्य ट्रांजीशन से जुड़ी जानकारी का लाभ या हानि स्तिथि की जानकारी से संबंधित हो सकती है। स्थितियों से ट्रांजीशन का इनफार्मेशन लाभ , स्तिथि छोड़ते समय प्राप्त की गई जानकारी है स्तिथि में प्रवेश करते समय विलुप्त हुई जानकारी कम होगी :
यहाँ यदि वर्तमान स्थिति है तो आगे की सशर्त संभावना है फिर अगली स्थिति है विपरीत सशर्त संभावना और है यदि वर्तमान स्थिति है तब पूर्व स्थिति थी, सशर्त संभावनाएँ ट्रांजीशन संभावना से संबंधित हैं , स्थिति संभावना का कहना है कि स्थिति द्वारा ट्रांजीशन होता है:
सशर्त संभावनाओं को समाप्त करना:
इसलिए ट्रांजीशन के परिणामस्वरूप सिस्टम द्वारा प्राप्त शुद्ध जानकारी केवल प्रारंभिक से अंतिम स्थिति तक जानकारी में वृद्धि पर निर्भर करती है। यह दिखाया जा सकता है कि यह निरंतर कई परिवर्तन के लिए भी सत्य है।[1]
बल और संभावित ऊर्जा के मध्य संबंध है किसी क्षमता से व्युत्पन्न और बल के जैसे है में बाहरी जानकारी मेमोरी स्टोरेज को पूर्ण करने के लिए सिस्टम को उच्च इनफार्मेशन क्षमता की स्थिति में "ऊपर की ओर" पुश करती है, ठीक उसी प्रकार जैसे किसी द्रव्यमान को उच्च गुरुत्वाकर्षण क्षमता की स्थिति में ऊपर की ओर पुश करना ऊर्जा को संग्रहीत करता है। ऊर्जा स्टोरेज की मात्रा केवल अंतिम ऊंचाई पर निर्भर करती है, पहाड़ी के मार्ग पर नहीं पर निर्भर करती है। इसी प्रकार, इनफार्मेशन स्टोरेज की मात्रा स्थिति स्थान में दो स्थिति के मध्य ट्रांजीशन पथ पर निर्भर नहीं करती है। जब कोई सिस्टम उच्च इनफार्मेशन क्षमता वाली दुर्लभ स्थिति में पहुंच जाता है, तो यह पहले से संग्रहीत जानकारी विलुप्त करके अधिक सामान्य स्थिति में आ सकता है।
मानक विचलन असतत यादृच्छिक चर की गणना करना उपयोगी हो सकता है, इसके माध्य के बारे में (जो शून्य है), अर्थात् शुद्ध इनफार्मेशन लाभ की अस्थिरता ,[1]किंतु स्थिति स्थान में बहु-ट्रांजीशन मेमोरी लूप को ध्यान में रखता है और इसलिए यह सिस्टम की कम्प्यूटेशनल शक्ति का उत्तम संकेतक होना चाहिए। इसके अतिरिक्त, गणना करना सरल है क्योंकि स्थितियों की तुलना में कई अधिक ट्रांजीशन हो सकते हैं।
कैओस और व्यवस्था
गतिशील प्रणाली जो बाहरी जानकारी के प्रति संवेदनशील है (अस्थिर) कैओस सिद्धांत व्यवहार प्रदर्शित करती है जबकि बाहरी जानकारी के प्रति असंवेदनशील है (स्थिर) व्यवस्थित व्यवहार प्रदर्शित करती है। काम्प्लेक्स सिस्टम दोनों व्यवहार प्रदर्शित करते है, समृद्ध इनफार्मेशन स्रोत के अधीन होने पर गतिशील संतुलन में उनके मध्य अस्थिरता होता है। अस्थिरता की डिग्री की मात्रा निर्धारित की जाती है ; समय के साथ विकसित होने पर काम्प्लेक्स सिस्टम में कैओस और व्यवस्था की प्रबलता में परिवर्तन करता है।
उदाहरण: प्राथमिक सेलुलर ऑटोमेटन का नियम 110 संस्करण
प्राथमिक सेलुलर ऑटोमेटन का नियम 110 संस्करण सार्वभौमिक गणना में सक्षम सिद्ध हुआ है। प्रमाण ग्लाइडर या स्पेसशिप के रूप में जाने जाने वाले एकजुट और स्वयं-स्थायी सेल पैटर्न के अस्तित्व और इंटरैक्शन पर आधारित है, जो आकस्मिक घटना है, जो ऑटोमेटन सेल्स के ग्रुपों की यह याद रखने की क्षमता का संकेत देता है कि ग्लाइडर उनके मध्य से निकल रहा है। इसलिए यह आशा की जाती है कि इनफार्मेशन लाभ और हानि, अस्थिरता और स्थिरता, अराजकता और व्यवस्था के विकल्पों के परिणामस्वरूप स्तिथि स्थान में मेमोरी लूप होंगे।
आसन्न ऑटोमेटन सेल्स के 3-सेल ग्रुप पर विचार किया जाता है, जो नियम 110 end-center-end का पालन करते हैं: सेण्टर सेल की अगली स्थिति स्वयं की वर्तमान स्थिति और नियम द्वारा निर्दिष्ट अंतिम सेल्स पर निर्भर करती है:
| 3-सेल ग्रुप | 1-1-1 | 1-1-0 | 1-0-1 | 1-0-0 | 0-1-1 | 0-1-0 | 0-0-1 | 0-0-0 |
|---|---|---|---|---|---|---|---|---|
| नेक्स्ट सेण्टर सेल | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 |
इस सिस्टम की इनफार्मेशन अस्थिरता काम्प्लेक्सता की गणना करने के लिए, 3-सेल ग्रुप के प्रत्येक एंड पर ड्राइवर सेल संलग्न किया जाता है, जिससे driver→end-center-end←driverयादृच्छिक बाहरी उत्तेजना प्रदान की जा सके, जिससे नियम को दो अंतिम सेल्स पर प्रारम्भ किया जा सके। आगे की सशर्त संभावनाओं को निर्धारित करने के लिए, आगे निर्धारित करें कि प्रत्येक संभावित वर्तमान स्थिति के लिए और ड्राइवर सेल सामग्री के प्रत्येक संभावित संयोजन के लिए अगली स्थिति क्या है।
इस सिस्टम का स्तिथि आरेख नीचे दर्शाया गया है, जिसमें वृत्त स्थितियों का प्रतिनिधित्व करते हैं और एरो स्थितियों के मध्य ट्रांजीशन का प्रतिनिधित्व करते हैं। इस सिस्टम की आठ अवस्थाएँ, 1-1-1 को 0-0-0 को 3-सेल ग्रुप की 3-बिट सामग्री के ऑक्टल समकक्ष के साथ लेबल किया गया है: 7 से 0 ट्रांजीशन एरो को आगे की सशर्त संभावनाओं के साथ लेबल किया गया है। ध्यान दें कि अराजकता और व्यवस्था, संवेदनशीलता और असंवेदनशीलता, ड्राईवर सेल से बाहरी जानकारी के लाभ और हानि में परिवर्तनशीलता के अनुरूप एरो के विचलन और अभिसरण में परिवर्तनशीलता है।
आगे की सशर्त संभावनाएं संभावित ड्राइवर सेल सामग्री के अनुपात से निर्धारित होती हैं जो विशेष ट्रांजीशन को चलाती हैं। उदाहरण के लिए, दो ड्राइवर सेल सामग्री के चार संभावित संयोजनों के लिए, स्थिति 7 स्थिति 5, 4, 1 और 0 की ओर ले जाती है इसलिए , , , और प्रत्येक ¼ या 25% हैं। इसी प्रकार, अवस्था 0 अवस्था 0, 1, 0 और 1 की ओर ले जाती है और प्रत्येक ½ या 50% हैं। इत्यादि।
अवस्था की संभावनाएँ इससे संबंधित हैं
- और
इन रैखिक बीजगणितीय समीकरणों को अवस्था संभावनाओं के लिए मैन्युअल रूप से या कंप्यूटर प्रोग्राम की सहायता से निम्नलिखित परिणामों के साथ समाधान किया जा सकता है:
| p0 | p1 | p2 | p3 | p4 | p5 | p6 | p7 |
| 2/17 | 2/17 | 1/34 | 5/34 | 2/17 | 2/17 | 2/17 | 4/17 |
इनफार्मेशन एन्ट्रापी और काम्प्लेक्स की गणना अवस्था संभावनाओं से की जा सकती है:
ध्यान दें कि आठ राज्यों के लिए अधिकतम संभव एन्ट्रापी है जो कि स्थिति होगी यदि सभी आठ राज्य ⅛ (यादृच्छिकता) की संभावनाओं के साथ समान रूप से संभावित हों। इस प्रकार नियम 110 में 2.86 बिट्स पर अपेक्षाकृत उच्च एन्ट्रापी या राज्य उपयोग है। किंतु यह एन्ट्रापी के बारे में राज्य की जानकारी में पर्याप्त अस्थिरता और इस प्रकार काम्प्लेक्सता के पर्याप्त मूल्य को नहीं रोकता है। जबकि, अधिकतम एन्ट्रापी काम्प्लेक्सता को दूर कर देगी।
जब ऊपर उपयोग की गई विश्लेषणात्मक विधि अव्यवहार्य हो तो राज्य की संभावनाओं को प्राप्त करने के लिए वैकल्पिक विधि का उपयोग किया जा सकता है। बस कई पीढ़ियों के लिए यादृच्छिक स्रोत के साथ सिस्टम को उसके इनपुट (ड्राइवर सेल) पर चलाएं और अनुभवजन्य रूप से राज्य की संभावनाओं का निरीक्षण करें। जब यह 10 मिलियन पीढ़ियों तक कंप्यूटर सिमुलेशन के माध्यम से किया जाता है तो परिणाम इस प्रकार हैं:[2]
| number of cells | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| (bits) | 2.86 | 3.81 | 4.73 | 5.66 | 6.56 | 7.47 | 8.34 | 9.25 | 10.09 | 10.97 | 11.78 |
| (bits) | 0.56 | 0.65 | 0.72 | 0.73 | 0.79 | 0.81 | 0.89 | 0.90 | 1.00 | 1.01 | 1.15 |
| 0.20 | 0.17 | 0.15 | 0.13 | 0.12 | 0.11 | 0.11 | 0.10 | 0.10 | 0.09 | 0.10 |
चूंकि दोनों और सिस्टम आकार के साथ उनके आयाम रहित अनुपात में वृद्धि होती है , सापेक्ष इनफार्मेशन अस्थिरता काम्प्लेक्सता, विभिन्न आकारों की प्रणालियों की उत्तम तुलना करने के लिए शामिल है। ध्यान दें कि अनुभवजन्य और विश्लेषणात्मक परिणाम 3-सेल ऑटोमेटन के लिए सहमत हैं।
बेट्स और शेपर्ड के पेपर में,[1] सभी प्राथमिक सेलुलर ऑटोमेटन नियमों के लिए गणना की गई है और यह देखा गया है कि जो धीमी गति से चलने वाले ग्लाइडर और संभवतः स्थिर वस्तुओं को प्रदर्शित करते हैं, जैसा कि नियम 110 करता है, बड़े मूल्यों के साथ अत्यधिक सहसंबद्ध हैं . इसलिए इसे सार्वभौमिक गणना के लिए उम्मीदवार नियमों का चयन करने के लिए फिल्टर के रूप में उपयोग किया जा सकता है, जिसे साबित करना कठिन है।
अनुप्रयोग
यद्यपि इनफार्मेशन अस्थिरता काम्प्लेक्सता सूत्र की व्युत्पत्ति गतिशील सिस्टम में इनफार्मेशन के अस्थिरता पर आधारित है, सूत्र केवल राज्य संभावनाओं पर निर्भर करता है और इसलिए यह किसी भी संभाव्यता वितरण पर भी प्रारम्भ होता है, जिसमें स्थिर छवियों या पाठ से प्राप्त वितरण भी शामिल है।
वर्षों से मूल पेपर[1]कई विविध क्षेत्रों में शोधकर्ताओं द्वारा संदर्भित किया गया है: काम्प्लेक्सता सिद्धांत,[3] काम्प्लेक्स सिस्टम विज्ञान,[4] काम्प्लेक्स नेटवर्क,[5] अराजक गतिशीलता,[6] अनेक-निकाय स्थानीयकरण उलझाव,[7] पर्यावरणीय इंजीनियरिंग,[8] पारिस्थितिक काम्प्लेक्सता,[9] पारिस्थितिक समय-श्रृंखला विश्लेषण,[10] पारिस्थितिकी तंत्र स्थिरता,[11] वायु[12] और पानी[13] प्रदूषण, जलवैज्ञानिक तरंगिका विश्लेषण,[14] मृदा जल प्रवाह,[15] मिट्टी की नमी,[16] हेडवाटर अपवाह,[17] भूजल की गहराई,[18] हवाई यातायात नियंत्रण,[19] प्रवाह पैटर्न[20] और बाढ़ की घटनाएँ,[21] टोपोलॉजी,[22] अर्थशास्त्र,[23] धातु का बाजार पूर्वानुमान[24] और बिजली[25] कीमतें, स्वास्थ्य इनफार्मेशन विज्ञान,[26] मानव संज्ञान,[27] मानव चाल कीनेमेटिक्स,[28] तंत्रिका विज्ञान,[29] ईईजी विश्लेषण,[30] शिक्षा,[31] निवेश,[32] कृत्रिम जीवन[33] और सौंदर्यशास्त्र.[34]
संदर्भ
- ↑ 1.0 1.1 1.2 1.3 1.4 Bates, John E.; Shepard, Harvey K. (1993-01-18). "सूचना के उतार-चढ़ाव का उपयोग करके जटिलता को मापना". Physics Letters A (in English). 172 (6): 416–425. Bibcode:1993PhLA..172..416B. doi:10.1016/0375-9601(93)90232-O. ISSN 0375-9601.
- ↑ Bates, John E. (2020-03-30). "Measuring complexity using information fluctuation: a tutorial". Research Gate.
- ↑ Atmanspacher, Harald (September 1997). "कार्टेशियन कट, हाइजेनबर्ग कट, और जटिलता की अवधारणा". World Futures (in English). 49 (3–4): 333–355. doi:10.1080/02604027.1997.9972639. ISSN 0260-4027.
- ↑ Shalizi, Cosma Rohilla (2006), Deisboeck, Thomas S.; Kresh, J. Yasha (eds.), "Methods and Techniques of Complex Systems Science: An Overview", Complex Systems Science in Biomedicine, Topics in Biomedical Engineering International Book Series (in English), Springer US, pp. 33–114, arXiv:nlin/0307015, doi:10.1007/978-0-387-33532-2_2, ISBN 978-0-387-33532-2, S2CID 11972113
- ↑ Huang, Min; Sun, Zhongkui; Donner, Reik V.; Zhang, Jie; Gua, Shuguang; Zou, Yong (2021-03-09). "क्रमिक पैटर्न संक्रमण नेटवर्क के आधार पर सांख्यिकीय जटिलता उपायों द्वारा गतिशील संक्रमण की विशेषता". Chaos: An Interdisciplinary Journal of Nonlinear Science. 31 (3): 033127. doi:10.1063/5.0038876. PMID 33810737. S2CID 232771788.
- ↑ Wackerbauer, Renate (1995-11-01). "लोरेन्ज़ प्रणाली का शोर-प्रेरित स्थिरीकरण". Physical Review E. 52 (5): 4745–4749. Bibcode:1995PhRvE..52.4745W. doi:10.1103/PhysRevE.52.4745. PMID 9963970.
- ↑ Hamilton, Gregory A.; Clark, Bryan K. (2023-02-14). "कई-निकाय स्थानीयकरण के लिए एकात्मक प्रवाह दक्षता और उलझाव की मात्रा निर्धारित करना". Physical Review B. 107 (6): 064203. arXiv:2110.10148. doi:10.1103/PhysRevB.107.064203. S2CID 239024666.
- ↑ Singh, Vijay P. (2013-01-10). एन्ट्रॉपी सिद्धांत और पर्यावरण और जल इंजीनियरिंग में इसका अनुप्रयोग (in English). John Wiley & Sons. ISBN 978-1-118-42860-3.
- ↑ Parrott, Lael (2010-11-01). "पारिस्थितिक जटिलता को मापना". Ecological Indicators (in English). 10 (6): 1069–1076. doi:10.1016/j.ecolind.2010.03.014. ISSN 1470-160X.
- ↑ Lange, Holger (2006), "Time-series Analysis in Ecology", eLS (in English), American Cancer Society, doi:10.1038/npg.els.0003276, ISBN 978-0-470-01590-2
- ↑ Wang, Chaojun; Zhao, Hongrui (2019-04-18). "Analysis of remote sensing time-series data to foster ecosystem sustainability: use of temporal information entropy". International Journal of Remote Sensing. 40 (8): 2880–2894. Bibcode:2019IJRS...40.2880W. doi:10.1080/01431161.2018.1533661. ISSN 0143-1161. S2CID 135003743.
- ↑ Klemm, Otto; Lange, Holger (1999-12-01). "फिचटेलगेबिर्ज पर्वत, बवेरिया में वायु प्रदूषण के रुझान". Environmental Science and Pollution Research (in English). 6 (4): 193–199. doi:10.1007/BF02987325. ISSN 1614-7499. PMID 19005662. S2CID 35043.
- ↑ Wang, Kang; Lin, Zhongbing (2018). "विभिन्न स्थानिक पैमानों पर नदी में नॉनपॉइंट स्रोत प्रदूषण का लक्षण वर्णन". Water and Environment Journal (in English). 32 (3): 453–465. doi:10.1111/wej.12345. ISSN 1747-6593. S2CID 115667734.
- ↑ Labat, David (2005-11-25). "Recent advances in wavelet analyses: Part 1. A review of concepts". Journal of Hydrology (in English). 314 (1): 275–288. Bibcode:2005JHyd..314..275L. doi:10.1016/j.jhydrol.2005.04.003. ISSN 0022-1694.
- ↑ Pachepsky, Yakov; Guber, Andrey; Jacques, Diederik; Simunek, Jiri; Van Genuchten, Marthinus Th.; Nicholson, Thomas; Cady, Ralph (2006-10-01). "सिम्युलेटेड मृदा जल प्रवाह की सूचना सामग्री और जटिलता". Geoderma. Fractal Geometry Applied to Soil and Related Hierarchical Systems - Fractals, Complexity and Heterogeneity (in English). 134 (3): 253–266. Bibcode:2006Geode.134..253P. doi:10.1016/j.geoderma.2006.03.003. ISSN 0016-7061.
- ↑ Kumar, Sujay V.; Dirmeyer, Paul A.; Peters-Lidard, Christa D.; Bindlish, Rajat; Bolten, John (2018-01-01). "उपग्रह मिट्टी की नमी पुनर्प्राप्ति का सूचना सैद्धांतिक मूल्यांकन". Remote Sensing of Environment (in English). 204: 392–400. Bibcode:2018RSEnv.204..392K. doi:10.1016/j.rse.2017.10.016. hdl:2060/20180003069. ISSN 0034-4257. PMC 7340154. PMID 32636571.
- ↑ Hauhs, Michael; Lange, Holger (2008). "Classification of Runoff in Headwater Catchments: A Physical Problem?". Geography Compass (in English). 2 (1): 235–254. doi:10.1111/j.1749-8198.2007.00075.x. ISSN 1749-8198.
- ↑ Liu, Meng; Liu, Dong; Liu, Le (2013-09-01). "Complexity research of regional groundwater depth series based on multiscale entropy: a case study of Jiangsanjiang Branch Bureau in China". Environmental Earth Sciences (in English). 70 (1): 353–361. Bibcode:2013EES....70..353L. doi:10.1007/s12665-012-2132-y. ISSN 1866-6299. S2CID 128958458.
- ↑ Xing, Jing; Manning, Carol A. (April 2005). "Complexity and Automation Displays of Air Traffic Control: Literature Review and Analysis" (in English). Archived from the original on June 1, 2022.
{{cite journal}}: Cite journal requires|journal=(help) - ↑ Wang, Kang; Li, Li (November 2008). "Characterizing Heterogeneous Flow Patterns Using Information Measurements". 2008 First International Conference on Intelligent Networks and Intelligent Systems. pp. 654–657. doi:10.1109/ICINIS.2008.110. S2CID 8867649.
- ↑ Al Sawaf, Mohamad Basel; Kawanisi, Kiyosi (2020-11-01). "सूचना और जटिलता उपायों का उपयोग करके पहाड़ी नदी धारा प्रवाह पैटर्न और बाढ़ की घटनाओं का आकलन". Journal of Hydrology (in English). 590: 125508. Bibcode:2020JHyd..59025508A. doi:10.1016/j.jhydrol.2020.125508. ISSN 0022-1694. S2CID 225261677.
- ↑ Javaheri Javid, Mohammad Ali; Alghamdi, Wajdi; Zimmer, Robert; al-Rifaie, Mohammad Majid (2016), Bi, Yaxin; Kapoor, Supriya; Bhatia, Rahul (eds.), "A Comparative Analysis of Detecting Symmetries in Toroidal Topology" (PDF), Intelligent Systems and Applications: Extended and Selected Results from the SAI Intelligent Systems Conference (IntelliSys) 2015, Studies in Computational Intelligence (in English), Springer International Publishing, pp. 323–344, doi:10.1007/978-3-319-33386-1_16, ISBN 978-3-319-33386-1
- ↑ Jurado-González, Javier; Gómez-Barroso, José Luis (2022-11-28). "Economic complexity and Information Society paradigms: a hybrid contribution to explain economic growth". Technological and Economic Development of Economy (in English). 28 (6): 1871–1896. doi:10.3846/tede.2022.17104. ISSN 2029-4921. S2CID 254339040.
- ↑ He, Kaijian; Lu, Xingjing; Zou, Yingchao; Keung Lai, Kin (2015-09-01). "कर्वलेट आधारित मल्टीस्केल पद्धति के साथ धातु की कीमतों का पूर्वानुमान लगाना". Resources Policy (in English). 45: 144–150. Bibcode:2015RePol..45..144H. doi:10.1016/j.resourpol.2015.03.011. ISSN 0301-4207.
- ↑ He, Kaijian; Xu, Yang; Zou, Yingchao; Tang, Ling (2015-05-01). "कर्वलेट डीनोइज़िंग आधारित दृष्टिकोण का उपयोग करके बिजली की कीमत का पूर्वानुमान". Physica A: Statistical Mechanics and Its Applications (in English). 425: 1–9. doi:10.1016/j.physa.2015.01.012. ISSN 0378-4371.
- ↑ Ahmed, Mosabber Uddin (2021), Ahad, Md Atiqur Rahman; Ahmed, Mosabber Uddin (eds.), "Complexity Analysis in Health Informatics", Signal Processing Techniques for Computational Health Informatics, Intelligent Systems Reference Library (in English), Cham: Springer International Publishing, vol. 192, pp. 103–121, doi:10.1007/978-3-030-54932-9_4, ISBN 978-3-030-54932-9, S2CID 225129992, retrieved 2021-02-01
- ↑ Shi Xiujian; Sun Zhiqiang; Li Long; Xie Hongwei (2009). "परिवहन प्रणालियों में मानव संज्ञानात्मक जटिलता विश्लेषण". Logistics. Proceedings: 4361–4368. doi:10.1061/40996(330)637. ISBN 9780784409961.
- ↑ Zhang, Shutao; Qian, Jinwu; Shen, Linyong; Wu, Xi; Hu, Xiaowu (October 2015). "Gait complexity and frequency content analyses of patients with Parkinson's disease". 2015 International Symposium on Bioelectronics and Bioinformatics (ISBB). pp. 87–90. doi:10.1109/ISBB.2015.7344930. ISBN 978-1-4673-6609-0. S2CID 2891655.
- ↑ Wang, Jisung; Noh, Gyu-Jeong; Choi, Byung-Moon; Ku, Seung-Woo; Joo, Pangyu; Jung, Woo-Sung; Kim, Seunghwan; Lee, Heonsoo (2017-07-13). "केटामाइन- और प्रोपोफोल-प्रेरित बेहोशी के दौरान दबी हुई तंत्रिका जटिलता". Neuroscience Letters (in English). 653: 320–325. doi:10.1016/j.neulet.2017.05.045. ISSN 0304-3940. PMID 28572032. S2CID 13767209.
- ↑ Bola, Michał; Orłowski, Paweł; Płomecka, Martyna; Marchewka, Artur (2019-01-30). "EEG signal diversity during propofol sedation: an increase in sedated but responsive, a decrease in sedated and unresponsive subjects". bioRxiv (in English): 444281. doi:10.1101/444281. S2CID 214726084.
- ↑ Dilger, Alexander (2012-01-01). "अंतर्जात जटिलता, विशेषज्ञता और सामान्य शिक्षा". On the Horizon. 20 (1): 49–53. doi:10.1108/10748121211202062. ISSN 1074-8121.
- ↑ Ivanyuk, Vera Alekseevna (2015). "गतिशील रणनीतिक निवेश पोर्टफोलियो प्रबंधन मॉडल". elibrary.ru.
- ↑ Peña, Eric; Sayama, Hiroki (2021-05-02). "Life Worth Mentioning: Complexity in Life-Like Cellular Automata". Artificial Life. 27 (2): 105–112. doi:10.1162/artl_a_00348. PMID 34727158. S2CID 240424110.
- ↑ Javaheri Javid, Mohammad Ali (2019-11-30). Aesthetic Automata: Synthesis and Simulation of Aesthetic Behaviour in Cellular Automata (doctoral thesis). Goldsmiths, University of London. doi:10.25602/gold.00027681.