कारण संकेतन: Difference between revisions
(Created page with "{{Short description|Notation to express cause and effect}} {{SpecialChars}} प्रकृति और मानव समाज में, कई घटनाओं म...") |
No edit summary |
||
| Line 3: | Line 3: | ||
{{SpecialChars}} | {{SpecialChars}} | ||
प्रकृति और मानव समाज में, कई घटनाओं में कारण संबंध होते हैं जहां | प्रकृति और मानव समाज में, कई घटनाओं में कारण संबंध होते हैं जहां घटना ए ( कारण) दूसरी घटना बी ( प्रभाव) को प्रभावित करती है। कारण संबंध स्थापित करना जीव विज्ञान से लेकर विभिन्न क्षेत्रों में कई वैज्ञानिक अध्ययनों का उद्देश्य है<ref name=Marshall1>{{cite journal |last1=Marshall |first1=BarryJ |last2=Warren |first2=J.Robin |title=गैस्ट्राइटिस और पेप्टिक अल्सरेशन वाले रोगियों के पेट में अज्ञात घुमावदार बेसिली|journal=The Lancet |date=June 1984 |volume=323 |issue=8390 |pages=1311–1315 |doi=10.1016/S0140-6736(84)91816-6 |pmid=6145023 |s2cid=10066001 }}</ref> और भौतिकी<ref name=Aspect1>{{cite journal |last1=Aspect |first1=Alain |last2=Grangier |first2=Philippe |last3=Roger |first3=Gérard |title=Experimental Realization of Einstein-Podolsky-Rosen-Bohm Gedankenexperiment : A New Violation of Bell's Inequalities |journal=Physical Review Letters |date=12 July 1982 |volume=49 |issue=2 |pages=91–94 |doi=10.1103/PhysRevLett.49.91 |bibcode=1982PhRvL..49...91A }}</ref> [[सामाजिक विज्ञान]] और [[अर्थशास्त्र]] के लिए.<ref name=Fischer1>{{cite journal |last1=Fischer |first1=Stanley |last2=Easterly |first2=William |title=सरकारी बजट बाधा का अर्थशास्त्र|journal=The World Bank Research Observer |date=1990 |volume=5 |issue=2 |pages=127–142 |doi=10.1093/wbro/5.2.127 }}</ref> यह दुर्घटना विश्लेषण का भी विषय है,<ref>{{cite conference|date= April 1998|series=Spring Symposion|publisher=[[Association for the Advancement of Artificial Intelligence]]|title=डब्ल्यूबी-विश्लेषण का उपयोग करके विमानन दुर्घटनाओं का विश्लेषण - मल्टीमॉडल रीजनिंग का एक अनुप्रयोग|url=https://www.aaai.org/Papers/Symposia/Spring/1998/SS-98-04/SS98-04-031.pdf|first1=Peter|last1=Ladkin|first2=Karsten|last2=Loer|archive-url=https://web.archive.org/web/20221221093954/https://www.aaai.org/Papers/Symposia/Spring/1998/SS-98-04/SS98-04-031.pdf |archive-date=2022-12-21 }}</ref> और इसे प्रभावी नीति निर्माण के लिए शर्त माना जा सकता है। | ||
घटनाओं के बीच कारण संबंधों का वर्णन करने के लिए, गैर-मात्रात्मक दृश्य संकेतन आम हैं, जैसे कि तीर, उदा। [[नाइट्रोजन चक्र]] या कई रसायन विज्ञान में<ref name=":4">{{Cite book|page=44,45 |edition=5th |title=कार्बनिक रसायन विज्ञान|last1=Bruice|first1=Paula Yurkanis|date=2007|publisher=Pearson Prentice Hall Upper Saddle River, NJ|isbn=978-0-13-196316-0|language=en}}</ref><ref name=":5">{{Cite book|pages=573–650 |edition=9th |title=सामान्य रसायन विज्ञान सिद्धांत और आधुनिक अनुप्रयोग|last1=Petrucci|first1=Ralph H.|last2=Harwood|first2=William S.|last3=Herring|first3=F. Geoffrey|last4=Madura|first4=Jeffry D.|date=2007|publisher=Pearson Prentice Hall Upper Saddle River, NJ|isbn=978-0-13-149330-8|language=en}}</ref> और गणित<ref name=":9">{{Cite book|page=20 |edition=11th |title=थॉमस की गणना|last1=B. George|first1=George|date=2007|publisher=Pearson|isbn=978-0-321-18558-7|language=en}}</ref> पाठ्यपुस्तकें। गणितीय सम्मेलनों का भी उपयोग किया जाता है, जैसे क्षैतिज अक्ष पर | घटनाओं के बीच कारण संबंधों का वर्णन करने के लिए, गैर-मात्रात्मक दृश्य संकेतन आम हैं, जैसे कि तीर, उदा। [[नाइट्रोजन चक्र]] या कई रसायन विज्ञान में<ref name=":4">{{Cite book|page=44,45 |edition=5th |title=कार्बनिक रसायन विज्ञान|last1=Bruice|first1=Paula Yurkanis|date=2007|publisher=Pearson Prentice Hall Upper Saddle River, NJ|isbn=978-0-13-196316-0|language=en}}</ref><ref name=":5">{{Cite book|pages=573–650 |edition=9th |title=सामान्य रसायन विज्ञान सिद्धांत और आधुनिक अनुप्रयोग|last1=Petrucci|first1=Ralph H.|last2=Harwood|first2=William S.|last3=Herring|first3=F. Geoffrey|last4=Madura|first4=Jeffry D.|date=2007|publisher=Pearson Prentice Hall Upper Saddle River, NJ|isbn=978-0-13-149330-8|language=en}}</ref> और गणित<ref name=":9">{{Cite book|page=20 |edition=11th |title=थॉमस की गणना|last1=B. George|first1=George|date=2007|publisher=Pearson|isbn=978-0-321-18558-7|language=en}}</ref> पाठ्यपुस्तकें। गणितीय सम्मेलनों का भी उपयोग किया जाता है, जैसे क्षैतिज अक्ष पर स्वतंत्र चर और ऊर्ध्वाधर अक्ष पर आश्रित चर की साजिश रचना,<ref>{{Cite book|page=575 |edition=9th |title=सामान्य रसायन विज्ञान सिद्धांत और आधुनिक अनुप्रयोग|last1=Petrucci|first1=Ralph H.|last2=Harwood|first2=William S.|last3=Herring|first3=F. Geoffrey|last4=Madura|first4=Jeffry D.|date=2007|publisher=Pearson Prentice Hall Upper Saddle River, NJ|isbn=978-0-13-149330-8|language=en}}</ref> या संकेतन <math>y=f(x)</math> उस मात्रा को दर्शाने के लिए<math>y</math> आश्रित चर है जो स्वतंत्र चर का कार्य है<math>x</math>.<ref>{{Cite book|page=19 |edition=11th |title=थॉमस की गणना|last1=B. George|first1=George|date=2007|publisher=Pearson|isbn=978-0-321-18558-7|language=en}}</ref> मात्रात्मक गणितीय अभिव्यक्तियों का उपयोग करके कारण संबंधों का भी वर्णन किया गया है।<ref name=":10">{{Cite book|url={{google books |plainurl=y |id=9H0dDQAAQBAJ}} |title=The Book of Why: The New Science of Cause and Effect|last1=Pearl|first1=Judea|last2=Mackenzie|first2=Dana|date=2018-05-15|publisher=Basic Books|isbn=9780465097616|language=en|author-link=Judea Pearl}}</ref> | ||
निम्नलिखित उदाहरण विभिन्न प्रकार के कारण संबंधों को दर्शाते हैं। इसके बाद कारण संबंधों को दर्शाने के लिए विभिन्न संकेतन का उपयोग किया जाता है। | निम्नलिखित उदाहरण विभिन्न प्रकार के कारण संबंधों को दर्शाते हैं। इसके बाद कारण संबंधों को दर्शाने के लिए विभिन्न संकेतन का उपयोग किया जाता है। | ||
==उदाहरण== | ==उदाहरण== | ||
इसके बाद जो कुछ होता है, वह ''जरूरी नहीं कि'' उस परंपरा को मानता हो <math>y</math> | इसके बाद जो कुछ होता है, वह ''जरूरी नहीं कि'' उस परंपरा को मानता हो <math>y</math> स्वतंत्र चर को दर्शाता है, और | ||
<math>f(y)</math> स्वतंत्र चर के | <math>f(y)</math> स्वतंत्र चर के फ़ंक्शन को दर्शाता है <math>y</math>. बजाय, <math>y</math> और <math>f(y)</math> प्राथमिक अज्ञात कारण संबंध के साथ दो मात्राओं को निरूपित करें, जिसे गणितीय अभिव्यक्ति द्वारा संबंधित किया जा सकता है। | ||
====पारिस्थितिकी तंत्र उदाहरण: कार्य-कारण के बिना सहसंबंध==== | ====पारिस्थितिकी तंत्र उदाहरण: कार्य-कारण के बिना सहसंबंध==== | ||
शून्य डिग्री सेल्सियस से नीचे मौसम के दिनों की संख्या की कल्पना करें, <math>y</math>, झील पर बर्फ बनने का कारण बनता है, <math>f(y)</math>, और इसके कारण भालू शीतनिद्रा में चले जाते हैं <math>g(y)</math>. चाहे <math>g(y)</math> इसके कारण नहीं होता है <math>f(y)</math> और इसके विपरीत, कोई संबंधित समीकरण लिख सकता है <math>g(y)</math> और <math>f(y)</math>. इस समीकरण का उपयोग हाइबरनेटिंग भालुओं की संख्या की सफलतापूर्वक गणना करने के लिए किया जा सकता है <math>g(y)</math>, बर्फ से ढकी झील का सतह क्षेत्र दिया गया है। हालाँकि, झील के | शून्य डिग्री सेल्सियस से नीचे मौसम के दिनों की संख्या की कल्पना करें, <math>y</math>, झील पर बर्फ बनने का कारण बनता है, <math>f(y)</math>, और इसके कारण भालू शीतनिद्रा में चले जाते हैं <math>g(y)</math>. चाहे <math>g(y)</math> इसके कारण नहीं होता है <math>f(y)</math> और इसके विपरीत, कोई संबंधित समीकरण लिख सकता है <math>g(y)</math> और <math>f(y)</math>. इस समीकरण का उपयोग हाइबरनेटिंग भालुओं की संख्या की सफलतापूर्वक गणना करने के लिए किया जा सकता है <math>g(y)</math>, बर्फ से ढकी झील का सतह क्षेत्र दिया गया है। हालाँकि, झील के क्षेत्र में बर्फ पर नमक डालकर उसे पिघलाने से भालू शीतनिद्रा से बाहर नहीं आएँगे। न ही भालुओं को शारीरिक रूप से परेशान करके जगाने से बर्फ पिघलेगी। इस मामले में दो मात्राएँ <math>f(y)</math> और <math>g(y)</math> दोनों कन्फ़ाउंडिंग के कारण होते हैं <math>y</math> (बाहर का तापमान), लेकिन दूसरे से नहीं। <math>f(y)</math> और <math>g(y)</math> बिना किसी कारण के सहसंबंध से संबंधित हैं। | ||
====भौतिकी उदाहरण: | ====भौतिकी उदाहरण: यूनिडायरेक्शनल कारण संबंध==== | ||
मान लीजिए कि | मान लीजिए कि आदर्श सौर-संचालित प्रणाली इस प्रकार बनाई गई है कि यदि धूप है, और सूर्य तीव्रता प्रदान करता है <math>I</math> का <math>100</math> ए पर वाट्स घटना <math>1</math>m<math>^2</math> के लिए सौर पैनल <math>10~</math> सेकंड, विद्युत मोटर उठाती है <math>2</math>किलो पत्थर द्वारा <math>50</math> मीटर, <math>h(I)</math>. अधिक सामान्यतः, हम मानते हैं कि सिस्टम को निम्नलिखित अभिव्यक्ति द्वारा वर्णित किया गया है: | ||
<math>I \times A \times t = m \times g \times h ~</math>, | <math>I \times A \times t = m \times g \times h ~</math>, | ||
| Line 25: | Line 25: | ||
इस उदाहरण में, तथ्य यह है कि यह धूप है <math>I</math> पथरी को ऊपर उठाने का कारण बनता है <math>h(I)</math>, उल्टा नहीं; पत्थर उठाना (बढ़ाना)। <math>h(I)</math>) सौर पैनल को रोशन करने के लिए सूर्य को चालू करने में परिणाम नहीं देगा (वृद्धि)। <math>I</math>). के बीच कारणात्मक संबंध <math>I</math> और <math>h(I)</math> यूनिडायरेक्शनल है. | इस उदाहरण में, तथ्य यह है कि यह धूप है <math>I</math> पथरी को ऊपर उठाने का कारण बनता है <math>h(I)</math>, उल्टा नहीं; पत्थर उठाना (बढ़ाना)। <math>h(I)</math>) सौर पैनल को रोशन करने के लिए सूर्य को चालू करने में परिणाम नहीं देगा (वृद्धि)। <math>I</math>). के बीच कारणात्मक संबंध <math>I</math> और <math>h(I)</math> यूनिडायरेक्शनल है. | ||
====चिकित्सा उदाहरण: | ====चिकित्सा उदाहरण: ही परिणाम के दो कारण==== | ||
धूम्रपान, <math>f(y)</math>, और एस्बेस्टस के संपर्क में, <math>g(y)</math>, दोनों कैंसर के ज्ञात कारण हैं, <math>y</math>. कोई | धूम्रपान, <math>f(y)</math>, और एस्बेस्टस के संपर्क में, <math>g(y)</math>, दोनों कैंसर के ज्ञात कारण हैं, <math>y</math>. कोई समीकरण लिख सकता है <math>f(y) = g(y)</math> व्यक्ति कितनी सिगरेट पीता है, इसके बीच समतुल्य कैंसरजन्यता का वर्णन करना, <math>f(y)</math>, और व्यक्ति कितने ग्राम एस्बेस्टस ग्रहण करता है, <math>g(y)</math>. यहाँ, न ही <math>f(y)</math> कारण <math>g(y)</math> और न <math>g(y)</math> कारण <math>f(y)</math>, लेकिन उन दोनों का परिणाम समान है। | ||
====वस्तु विनिमय उदाहरण: | ====वस्तु विनिमय उदाहरण: द्विदिश कारण संबंध==== | ||
वस्तु विनिमय आधारित अर्थव्यवस्था पर विचार करें जहां गायों की संख्या अधिक हो <math>C</math> किसी के पास मुर्गियों का मूल्य मानक मुद्रा में मापा जाता है, <math>y</math>. इसके अतिरिक्त, तेल के बैरल की संख्या <math>B</math> किसी का अपना मूल्य होता है जिसे मुर्गियों में मापा जा सकता है, <math>y</math>. यदि कोई बाज़ार मौजूद है जहाँ गायों का व्यापार मुर्गियों के लिए किया जा सकता है और बदले में तेल के बैरल के लिए व्यापार किया जा सकता है, तो कोई | वस्तु विनिमय आधारित अर्थव्यवस्था पर विचार करें जहां गायों की संख्या अधिक हो <math>C</math> किसी के पास मुर्गियों का मूल्य मानक मुद्रा में मापा जाता है, <math>y</math>. इसके अतिरिक्त, तेल के बैरल की संख्या <math>B</math> किसी का अपना मूल्य होता है जिसे मुर्गियों में मापा जा सकता है, <math>y</math>. यदि कोई बाज़ार मौजूद है जहाँ गायों का व्यापार मुर्गियों के लिए किया जा सकता है और बदले में तेल के बैरल के लिए व्यापार किया जा सकता है, तो कोई समीकरण लिख सकता है <math>C(y) = B(y)</math> गायों के बीच मूल्य संबंध का वर्णन करने के लिए <math>C</math> और तेल के बैरल <math>B</math>. मान लीजिए कि इस अर्थव्यवस्था में व्यक्ति हमेशा अपने मूल्य का आधा हिस्सा गायों के रूप में और आधा हिस्सा तेल के बैरल के रूप में रखता है। फिर, उनकी गायों की संख्या में वृद्धि हुई <math>C(y)</math> उन्हें 4 गायों की पेशकश करने से अंततः उनके तेल बैरल की संख्या में वृद्धि होगी <math>B(y)</math>, या विपरीत। इस मामले में, गणितीय समानता <math>C(y) = B(y)</math> द्विदिश कारण संबंध का वर्णन करता है। | ||
==नोटेशन== | ==नोटेशन== | ||
| Line 37: | Line 37: | ||
====रासायनिक प्रतिक्रियाएँ==== | ====रासायनिक प्रतिक्रियाएँ==== | ||
रसायन विज्ञान में, कई रासायनिक प्रतिक्रियाएं प्रतिवर्ती होती हैं और समीकरणों का उपयोग करके वर्णित की जाती हैं जो | रसायन विज्ञान में, कई रासायनिक प्रतिक्रियाएं प्रतिवर्ती होती हैं और समीकरणों का उपयोग करके वर्णित की जाती हैं जो गतिशील [[रासायनिक संतुलन]] की ओर प्रवृत्त होती हैं। इन प्रतिक्रियाओं में, [[अभिकर्मक]] या [[उत्पाद (रसायन विज्ञान)]] जोड़ने से प्रतिक्रिया क्रमशः अधिक उत्पाद, या अधिक अभिकारक उत्पन्न करती है। समान चिह्न के स्थान पर "हार्पून-प्रकार" तीर निकालना मानक है, {{eqm}}, प्रतिक्रिया की प्रतिवर्ती प्रकृति और अभिकारकों और उत्पादों के बीच गतिशील कारण संबंध को दर्शाने के लिए।<ref name=":4" /><ref name=":5" /> | ||
'''सांख्यिकी: अंकन करें''' | |||
कारण मॉडल#हस्तक्षेप|डू-कैलकुलस, और विशेष रूप से डू ऑपरेटर, का उपयोग संभाव्यता की भाषा में कारण संबंधों का वर्णन करने के लिए किया जाता है। उदाहरण के लिए, डू-कैलकुलस में प्रयुक्त नोटेशन है: | |||
कारण मॉडल#हस्तक्षेप|डू-कैलकुलस, और विशेष रूप से डू ऑपरेटर, का उपयोग संभाव्यता की भाषा में कारण संबंधों का वर्णन करने के लिए किया जाता है। उदाहरण के लिए, डू-कैलकुलस में प्रयुक्त | |||
:<math>P(Y|do(X)) = P(Y)~</math>, | :<math>P(Y|do(X)) = P(Y)~</math>, | ||
| Line 50: | Line 49: | ||
====कारण रेखाचित्र==== | ====कारण रेखाचित्र==== | ||
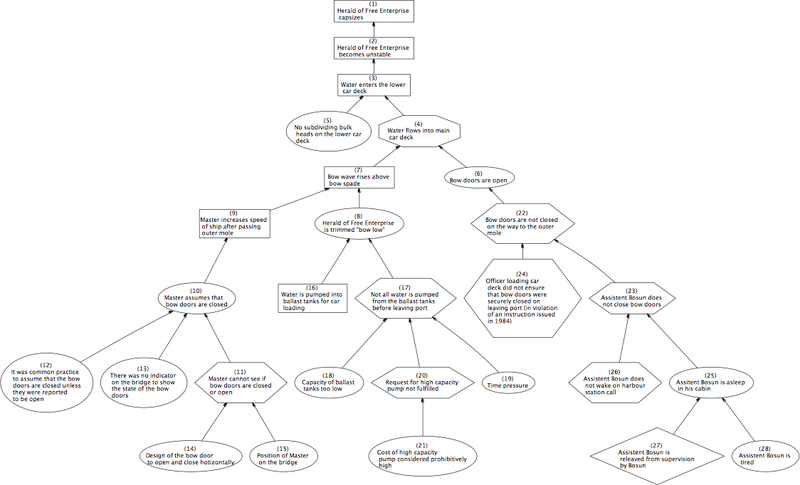
कारण आरेख में नोड्स का | कारण आरेख में नोड्स का सेट होता है जो तीरों द्वारा आपस में जुड़ा हो भी सकता है और नहीं भी। नोड्स के बीच के तीर कारण से प्रभाव की ओर इशारा करते हुए तीर के साथ कारण संबंधों को दर्शाते हैं। कारण आरेखों के कई रूप मौजूद हैं जिनमें [[इशिकावा]] आरेख, [[निर्देशित अचक्रीय ग्राफ]]़, [[कारण लूप आरेख]],<ref name=":10"/>और क्यों-क्योंकि विश्लेषण|क्यों-क्योंकि ग्राफ़ (डब्ल्यूबीजी)। नीचे दी गई छवि आंशिक क्यों-क्योंकि ग्राफ़ दिखाती है जिसका उपयोग हेराल्ड ऑफ़ फ्री एंटरप्राइज़ के कैप्साइज़िंग का विश्लेषण करने के लिए किया जाता है. [[Image:Herald of Free Enterprise WBG.png|thumb|800px|center|आंशिक क्यों-क्योंकि मुक्त उद्यम के हेराल्ड के पलटने का ग्राफ]] | ||
==संदर्भ== | ==संदर्भ== | ||
Revision as of 23:51, 4 August 2023
प्रकृति और मानव समाज में, कई घटनाओं में कारण संबंध होते हैं जहां घटना ए ( कारण) दूसरी घटना बी ( प्रभाव) को प्रभावित करती है। कारण संबंध स्थापित करना जीव विज्ञान से लेकर विभिन्न क्षेत्रों में कई वैज्ञानिक अध्ययनों का उद्देश्य है[1] और भौतिकी[2] सामाजिक विज्ञान और अर्थशास्त्र के लिए.[3] यह दुर्घटना विश्लेषण का भी विषय है,[4] और इसे प्रभावी नीति निर्माण के लिए शर्त माना जा सकता है।
घटनाओं के बीच कारण संबंधों का वर्णन करने के लिए, गैर-मात्रात्मक दृश्य संकेतन आम हैं, जैसे कि तीर, उदा। नाइट्रोजन चक्र या कई रसायन विज्ञान में[5][6] और गणित[7] पाठ्यपुस्तकें। गणितीय सम्मेलनों का भी उपयोग किया जाता है, जैसे क्षैतिज अक्ष पर स्वतंत्र चर और ऊर्ध्वाधर अक्ष पर आश्रित चर की साजिश रचना,[8] या संकेतन उस मात्रा को दर्शाने के लिए आश्रित चर है जो स्वतंत्र चर का कार्य है.[9] मात्रात्मक गणितीय अभिव्यक्तियों का उपयोग करके कारण संबंधों का भी वर्णन किया गया है।[10] निम्नलिखित उदाहरण विभिन्न प्रकार के कारण संबंधों को दर्शाते हैं। इसके बाद कारण संबंधों को दर्शाने के लिए विभिन्न संकेतन का उपयोग किया जाता है।
उदाहरण
इसके बाद जो कुछ होता है, वह जरूरी नहीं कि उस परंपरा को मानता हो स्वतंत्र चर को दर्शाता है, और स्वतंत्र चर के फ़ंक्शन को दर्शाता है . बजाय, और प्राथमिक अज्ञात कारण संबंध के साथ दो मात्राओं को निरूपित करें, जिसे गणितीय अभिव्यक्ति द्वारा संबंधित किया जा सकता है।
पारिस्थितिकी तंत्र उदाहरण: कार्य-कारण के बिना सहसंबंध
शून्य डिग्री सेल्सियस से नीचे मौसम के दिनों की संख्या की कल्पना करें, , झील पर बर्फ बनने का कारण बनता है, , और इसके कारण भालू शीतनिद्रा में चले जाते हैं . चाहे इसके कारण नहीं होता है और इसके विपरीत, कोई संबंधित समीकरण लिख सकता है और . इस समीकरण का उपयोग हाइबरनेटिंग भालुओं की संख्या की सफलतापूर्वक गणना करने के लिए किया जा सकता है , बर्फ से ढकी झील का सतह क्षेत्र दिया गया है। हालाँकि, झील के क्षेत्र में बर्फ पर नमक डालकर उसे पिघलाने से भालू शीतनिद्रा से बाहर नहीं आएँगे। न ही भालुओं को शारीरिक रूप से परेशान करके जगाने से बर्फ पिघलेगी। इस मामले में दो मात्राएँ और दोनों कन्फ़ाउंडिंग के कारण होते हैं (बाहर का तापमान), लेकिन दूसरे से नहीं। और बिना किसी कारण के सहसंबंध से संबंधित हैं।
भौतिकी उदाहरण: यूनिडायरेक्शनल कारण संबंध
मान लीजिए कि आदर्श सौर-संचालित प्रणाली इस प्रकार बनाई गई है कि यदि धूप है, और सूर्य तीव्रता प्रदान करता है का ए पर वाट्स घटना m के लिए सौर पैनल सेकंड, विद्युत मोटर उठाती है किलो पत्थर द्वारा मीटर, . अधिक सामान्यतः, हम मानते हैं कि सिस्टम को निम्नलिखित अभिव्यक्ति द्वारा वर्णित किया गया है:
,
कहाँ सूर्य के प्रकाश की तीव्रता को दर्शाता है (जेsm), सौर पैनल का सतह क्षेत्र है (एम), समय का प्रतिनिधित्व करता है, द्रव्यमान (किग्रा) का प्रतिनिधित्व करता है, पृथ्वी के गुरुत्वाकर्षण के कारण त्वरण का प्रतिनिधित्व करता है ( ms), और चट्टान को उठाए जाने की ऊंचाई (एम) को दर्शाता है।
इस उदाहरण में, तथ्य यह है कि यह धूप है पथरी को ऊपर उठाने का कारण बनता है , उल्टा नहीं; पत्थर उठाना (बढ़ाना)। ) सौर पैनल को रोशन करने के लिए सूर्य को चालू करने में परिणाम नहीं देगा (वृद्धि)। ). के बीच कारणात्मक संबंध और यूनिडायरेक्शनल है.
चिकित्सा उदाहरण: ही परिणाम के दो कारण
धूम्रपान, , और एस्बेस्टस के संपर्क में, , दोनों कैंसर के ज्ञात कारण हैं, . कोई समीकरण लिख सकता है व्यक्ति कितनी सिगरेट पीता है, इसके बीच समतुल्य कैंसरजन्यता का वर्णन करना, , और व्यक्ति कितने ग्राम एस्बेस्टस ग्रहण करता है, . यहाँ, न ही कारण और न कारण , लेकिन उन दोनों का परिणाम समान है।
वस्तु विनिमय उदाहरण: द्विदिश कारण संबंध
वस्तु विनिमय आधारित अर्थव्यवस्था पर विचार करें जहां गायों की संख्या अधिक हो किसी के पास मुर्गियों का मूल्य मानक मुद्रा में मापा जाता है, . इसके अतिरिक्त, तेल के बैरल की संख्या किसी का अपना मूल्य होता है जिसे मुर्गियों में मापा जा सकता है, . यदि कोई बाज़ार मौजूद है जहाँ गायों का व्यापार मुर्गियों के लिए किया जा सकता है और बदले में तेल के बैरल के लिए व्यापार किया जा सकता है, तो कोई समीकरण लिख सकता है गायों के बीच मूल्य संबंध का वर्णन करने के लिए और तेल के बैरल . मान लीजिए कि इस अर्थव्यवस्था में व्यक्ति हमेशा अपने मूल्य का आधा हिस्सा गायों के रूप में और आधा हिस्सा तेल के बैरल के रूप में रखता है। फिर, उनकी गायों की संख्या में वृद्धि हुई उन्हें 4 गायों की पेशकश करने से अंततः उनके तेल बैरल की संख्या में वृद्धि होगी , या विपरीत। इस मामले में, गणितीय समानता द्विदिश कारण संबंध का वर्णन करता है।
नोटेशन
रासायनिक प्रतिक्रियाएँ
रसायन विज्ञान में, कई रासायनिक प्रतिक्रियाएं प्रतिवर्ती होती हैं और समीकरणों का उपयोग करके वर्णित की जाती हैं जो गतिशील रासायनिक संतुलन की ओर प्रवृत्त होती हैं। इन प्रतिक्रियाओं में, अभिकर्मक या उत्पाद (रसायन विज्ञान) जोड़ने से प्रतिक्रिया क्रमशः अधिक उत्पाद, या अधिक अभिकारक उत्पन्न करती है। समान चिह्न के स्थान पर "हार्पून-प्रकार" तीर निकालना मानक है, ⇌, प्रतिक्रिया की प्रतिवर्ती प्रकृति और अभिकारकों और उत्पादों के बीच गतिशील कारण संबंध को दर्शाने के लिए।[5][6]
सांख्यिकी: अंकन करें
कारण मॉडल#हस्तक्षेप|डू-कैलकुलस, और विशेष रूप से डू ऑपरेटर, का उपयोग संभाव्यता की भाषा में कारण संबंधों का वर्णन करने के लिए किया जाता है। उदाहरण के लिए, डू-कैलकुलस में प्रयुक्त नोटेशन है:
- ,
जिसे "की संभावना" के रूप में पढ़ा जा सकता है यह देखते हुए कि आप ऐसा करते हैं ”। उपरोक्त अभिव्यक्ति उस मामले का वर्णन करती है जहां किए गए किसी भी कार्य से स्वतंत्र है .[5]यह निर्दिष्ट करता है कि जहां कोई यूनिडायरेक्शनल कारण संबंध नहीं है कारण .
कारण रेखाचित्र
कारण आरेख में नोड्स का सेट होता है जो तीरों द्वारा आपस में जुड़ा हो भी सकता है और नहीं भी। नोड्स के बीच के तीर कारण से प्रभाव की ओर इशारा करते हुए तीर के साथ कारण संबंधों को दर्शाते हैं। कारण आरेखों के कई रूप मौजूद हैं जिनमें इशिकावा आरेख, निर्देशित अचक्रीय ग्राफ़, कारण लूप आरेख,[10]और क्यों-क्योंकि विश्लेषण|क्यों-क्योंकि ग्राफ़ (डब्ल्यूबीजी)। नीचे दी गई छवि आंशिक क्यों-क्योंकि ग्राफ़ दिखाती है जिसका उपयोग हेराल्ड ऑफ़ फ्री एंटरप्राइज़ के कैप्साइज़िंग का विश्लेषण करने के लिए किया जाता है.
संदर्भ
- ↑ Marshall, BarryJ; Warren, J.Robin (June 1984). "गैस्ट्राइटिस और पेप्टिक अल्सरेशन वाले रोगियों के पेट में अज्ञात घुमावदार बेसिली". The Lancet. 323 (8390): 1311–1315. doi:10.1016/S0140-6736(84)91816-6. PMID 6145023. S2CID 10066001.
- ↑ Aspect, Alain; Grangier, Philippe; Roger, Gérard (12 July 1982). "Experimental Realization of Einstein-Podolsky-Rosen-Bohm Gedankenexperiment : A New Violation of Bell's Inequalities". Physical Review Letters. 49 (2): 91–94. Bibcode:1982PhRvL..49...91A. doi:10.1103/PhysRevLett.49.91.
- ↑ Fischer, Stanley; Easterly, William (1990). "सरकारी बजट बाधा का अर्थशास्त्र". The World Bank Research Observer. 5 (2): 127–142. doi:10.1093/wbro/5.2.127.
- ↑ Ladkin, Peter; Loer, Karsten (April 1998). डब्ल्यूबी-विश्लेषण का उपयोग करके विमानन दुर्घटनाओं का विश्लेषण - मल्टीमॉडल रीजनिंग का एक अनुप्रयोग (PDF). Spring Symposion. Association for the Advancement of Artificial Intelligence. Archived from the original (PDF) on 2022-12-21.
- ↑ 5.0 5.1 5.2 Bruice, Paula Yurkanis (2007). कार्बनिक रसायन विज्ञान (in English) (5th ed.). Pearson Prentice Hall Upper Saddle River, NJ. p. 44,45. ISBN 978-0-13-196316-0.
- ↑ 6.0 6.1 Petrucci, Ralph H.; Harwood, William S.; Herring, F. Geoffrey; Madura, Jeffry D. (2007). सामान्य रसायन विज्ञान सिद्धांत और आधुनिक अनुप्रयोग (in English) (9th ed.). Pearson Prentice Hall Upper Saddle River, NJ. pp. 573–650. ISBN 978-0-13-149330-8.
- ↑ B. George, George (2007). थॉमस की गणना (in English) (11th ed.). Pearson. p. 20. ISBN 978-0-321-18558-7.
- ↑ Petrucci, Ralph H.; Harwood, William S.; Herring, F. Geoffrey; Madura, Jeffry D. (2007). सामान्य रसायन विज्ञान सिद्धांत और आधुनिक अनुप्रयोग (in English) (9th ed.). Pearson Prentice Hall Upper Saddle River, NJ. p. 575. ISBN 978-0-13-149330-8.
- ↑ B. George, George (2007). थॉमस की गणना (in English) (11th ed.). Pearson. p. 19. ISBN 978-0-321-18558-7.
- ↑ 10.0 10.1 Pearl, Judea; Mackenzie, Dana (2018-05-15). The Book of Why: The New Science of Cause and Effect (in English). Basic Books. ISBN 9780465097616.