स्तुईचिओमेटरी: Difference between revisions
No edit summary |
No edit summary |
||
| Line 2: | Line 2: | ||
[[File:Combustion reaction of methane.jpg|thumb|400px|[[ मीथेन ]]की [[ दहन |दहन]] अभिक्रिया का एक स्टोइकियोमेट्रिक आरेख।]]स्टोइकियोमेस्ट्री [[ रासायनिक प्रतिक्रिया |रासायनिक अभिक्रिया]]ओं से पहले, दौरान और बाद में [[ अभिकारक |अभिकारक]] और [[ उत्पाद (रसायन विज्ञान) |उत्पाद(रसायन विज्ञान)]] की मात्रा के बीच संबंध को संदर्भित करता है। | [[File:Combustion reaction of methane.jpg|thumb|400px|[[ मीथेन ]]की [[ दहन |दहन]] अभिक्रिया का एक स्टोइकियोमेट्रिक आरेख।]]स्टोइकियोमेस्ट्री [[ रासायनिक प्रतिक्रिया |रासायनिक अभिक्रिया]]ओं से पहले, दौरान और बाद में [[ अभिकारक |अभिकारक]] और [[ उत्पाद (रसायन विज्ञान) |उत्पाद(रसायन विज्ञान)]] की मात्रा के बीच संबंध को संदर्भित करता है। | ||
स्टोइकियोमेस्ट्री द्रव्यमान के संरक्षण के नियम पर स्थापित किया गया है जहां अभिकारकों का कुल द्रव्यमान उत्पादों के कुल द्रव्यमान के बराबर होता है, जिससे यह अंतर्दृष्टि प्राप्त होती है कि अभिकारकों और उत्पादों की मात्रा के बीच संबंध सामान्यतः सकारात्मक पूर्णांक का अनुपात | स्टोइकियोमेस्ट्री द्रव्यमान के संरक्षण के नियम पर स्थापित किया गया है जहां अभिकारकों का कुल द्रव्यमान उत्पादों के कुल द्रव्यमान के बराबर होता है, जिससे यह अंतर्दृष्टि प्राप्त होती है कि अभिकारकों और उत्पादों की मात्रा के बीच संबंध सामान्यतः सकारात्मक पूर्णांक का अनुपात बकारण हैं। इसका मतलब यह है कि यदि अलग-अलग अभिकारकों की मात्रा ज्ञात हो, तो उत्पाद की मात्रा की गणना की जा सकती है। इसके विपरीत, यदि अभिकारक की मात्रा ज्ञात होती है और उत्पादों की मात्रा को आनुभविक रूप से निर्धारित किया जा सकता है, तो अन्य अभिकारकों की मात्रा की भी गणना की जा सकती है। | ||
यह यहाँ की छवि में दिखाया गया है, जहाँ संतुलित समीकरण है: | यह यहाँ की छवि में दिखाया गया है, जहाँ संतुलित समीकरण है: | ||
| Line 42: | Line 42: | ||
==मोलर अनुपात== | ==मोलर अनुपात== | ||
स्टोइकियोमेस्ट्री | स्टोइकियोमेस्ट्री प्रायः रासायनिक समीकरणों(स्टोइकियोमेस्ट्री अभिक्रिया) को संतुलित करने के लिए प्रयोग किया जाता है। उदाहरण के लिए, दो डायटोमिक अणु गैसें, [[ हाइड्रोजन |हाइड्रोजन]] और ऑक्सीजन, ऊष्माक्षेपी अभिक्रिया में एक तरल, पानी बनाने के लिए सम्मिलित हो सकते हैं, जैसा कि निम्नलिखित समीकरण द्वारा वर्णित है: | ||
:2{{chem|H|2}} + {{chem|O|2}} → 2 {{chem|H|2|O}} | :2{{chem|H|2}} + {{chem|O|2}} → 2 {{chem|H|2|O}} | ||
अभिक्रिया स्टोइकोमेट्री उपरोक्त समीकरण में हाइड्रोजन, ऑक्सीजन और पानी के अणुओं के 2:1:2 अनुपात का वर्णन करती है। | अभिक्रिया स्टोइकोमेट्री उपरोक्त समीकरण में हाइड्रोजन, ऑक्सीजन और पानी के अणुओं के 2:1:2 अनुपात का वर्णन करती है। | ||
| Line 51: | Line 51: | ||
:<math>\left(\frac{0.27 \mbox{ mol }\mathrm{CH_3OH}}{1}\right)\left(\frac{4 \mbox{ mol }\mathrm{H_2O}}{2 \mbox{ mol } \mathrm{CH_3OH}}\right) = 0.54\ \text{mol }\mathrm{H_2O}</math> | :<math>\left(\frac{0.27 \mbox{ mol }\mathrm{CH_3OH}}{1}\right)\left(\frac{4 \mbox{ mol }\mathrm{H_2O}}{2 \mbox{ mol } \mathrm{CH_3OH}}\right) = 0.54\ \text{mol }\mathrm{H_2O}</math> | ||
स्टोइकोमेट्री शब्द का प्रयोग | स्टोइकोमेट्री शब्द का प्रयोग प्रायः स्टोइकियोमेट्रिक यौगिकों(रचना स्टोइकोमेट्री) में तत्वों के मोल(इकाई) अनुपात के लिए भी किया जाता है। उदाहरण के लिए, H . में हाइड्रोजन और ऑक्सीजन की स्टोइकोमेट्री<sub>2</sub>हे 2:1 है। स्टोइकियोमेट्रिक यौगिकों में, ग्राम अणुक अनुपात पूर्णांक होते हैं। | ||
== उत्पाद की मात्रा निर्धारित करना == | == उत्पाद की मात्रा निर्धारित करना == | ||
स्टोइकोमेट्री का उपयोग किसी अभिक्रिया द्वारा प्राप्त उत्पाद की मात्रा को खोजने के लिए भी किया जा सकता है। यदि [[ सिल्वर नाइट्रेट ]] के जलीय घोल में ठोस तांबे(Cu) का एक टुकड़ा मिलाया जाता है | स्टोइकोमेट्री का उपयोग किसी अभिक्रिया द्वारा प्राप्त उत्पाद की मात्रा को खोजने के लिए भी किया जा सकता है। यदि [[ सिल्वर नाइट्रेट |सिल्वर नाइट्रेट]](AgNO<sub>3</sub>) के जलीय घोल में ठोस तांबे(Cu) का एक टुकड़ा मिलाया जाता है, [[ चांदी |चांदी]](Ag) को जलीय कॉपर नाइट्रेट बनाने वाली एकल विस्थापन अभिक्रिया में बदल दिया जाएगा। यदि अतिरिक्त सिल्वर नाइट्रेट के विलयन में 16.00 ग्राम Cu मिला दिया जाए तो कितनी चाँदी उत्पन्न होती है? | ||
निम्नलिखित चरणों का उपयोग किया जाएगा: | निम्नलिखित चरणों का उपयोग किया जाएगा: | ||
# समीकरण लिखें और संतुलित करें | # समीकरण लिखें और संतुलित करें | ||
# द्रव्यमान से मोल: Cu के ग्राम को Cu | # द्रव्यमान से मोल: Cu के ग्राम को Cu के मोल में बदलें | ||
# मोल अनुपात: Cu के मोल को उत्पादित Ag के मोल में बदलें | # मोल अनुपात: Cu के मोल को उत्पादित Ag के मोल में बदलें | ||
# तिल से द्रव्यमान: Ag के मोल को उत्पादित Ag के ग्राम में बदलें | # तिल से द्रव्यमान: Ag के मोल को उत्पादित Ag के ग्राम में बदलें | ||
| Line 64: | Line 64: | ||
पूर्ण संतुलित समीकरण होगा: | पूर्ण संतुलित समीकरण होगा: | ||
:{{chem|Cu}} + 2 {{chem|Ag|NO|3}} → {{chem|Cu|(NO|3|)|2}} + 2 {{chem|Ag}} | :{{chem|Cu}} + 2 {{chem|Ag|NO|3}} → {{chem|Cu|(NO|3|)|2}} + 2 {{chem|Ag}} | ||
द्रव्यमान से मोल चरण के लिए, तांबे के द्रव्यमान(16.00 g) को तांबे के द्रव्यमान को उसके आणविक द्रव्यमान: 63.55 g/ | द्रव्यमान से मोल चरण के लिए, तांबे के द्रव्यमान(16.00 g) को तांबे के द्रव्यमान को उसके आणविक द्रव्यमान: 63.55 g/मोल से विभाजित करके तांबे के मोल में परिवर्तित किया जाएगा। | ||
:<math>\left(\frac{16.00 \mbox{ g Cu}}{1}\right)\left(\frac{1 \mbox{ mol Cu}}{63.55 \mbox{ g Cu}}\right) = 0.2518\ \text{mol Cu}</math> | :<math>\left(\frac{16.00 \mbox{ g Cu}}{1}\right)\left(\frac{1 \mbox{ mol Cu}}{63.55 \mbox{ g Cu}}\right) = 0.2518\ \text{mol Cu}</math> | ||
अब जब मोल में Cu की मात्रा(0.2518) मिल गई है, तो | अब जब मोल में Cu की मात्रा(0.2518) मिल गई है, तो मोल अनुपात सेट कर सकते हैं। यह संतुलित समीकरण में गुणांकों को देखकर पाया जाता है: Cu और Ag 1:2 के अनुपात में हैं। | ||
:<math>\left(\frac{0.2518 \mbox{ mol Cu}}{1}\right)\left(\frac{2 \mbox{ mol Ag}}{1 \mbox{ mol Cu}}\right) = 0.5036\ \text{mol Ag}</math> | :<math>\left(\frac{0.2518 \mbox{ mol Cu}}{1}\right)\left(\frac{2 \mbox{ mol Ag}}{1 \mbox{ mol Cu}}\right) = 0.5036\ \text{mol Ag}</math> | ||
अब जबकि उत्पादित Ag का मोल 0. | अब जबकि उत्पादित Ag का मोल 0.5036 मोल है, तो हम अंतिम उत्तर पर आने के लिए इस मात्रा को उत्पादित Ag के ग्राम में बदल देते हैं: | ||
:<math>\left(\frac{0.5036 \mbox{ mol Ag}}{1}\right)\left(\frac{107.87 \mbox{ g Ag}}{1 \mbox{ mol Ag}}\right) = 54.32 \ \text{g Ag}</math> | :<math>\left(\frac{0.5036 \mbox{ mol Ag}}{1}\right)\left(\frac{107.87 \mbox{ g Ag}}{1 \mbox{ mol Ag}}\right) = 54.32 \ \text{g Ag}</math> | ||
| Line 78: | Line 78: | ||
=== | === अन्य उदाहरण === | ||
[[ प्रोपेन | [[ प्रोपेन | प्रोपेन(C<sub>3</sub>H<sub>8</sub>)]] की ऑक्सीजन(O<sub>2</sub>) के साथ अभिक्रिया के लिए संतुलित रासायनिक समीकरण है: | ||
:{{chem2|C3H8 + 5 O2 -> 3 CO2 + 4 H2O}} | :{{chem2|C3H8 + 5 O2 -> 3 CO2 + 4 H2O}} | ||
पानी का द्रव्यमान यदि 120 ग्राम प्रोपेन(C | पानी का द्रव्यमान यदि 120 ग्राम प्रोपेन(C<sub>3</sub>H<sub>8</sub>) अधिक ऑक्सीजन में जलाया जाता है तो | ||
:<math>m_\mathrm{H_2O} = \left(\frac{120. \mbox{ g }\mathrm{C_3H_8}}{1}\right)\left(\frac{1 \mbox{ mol }\mathrm{C_3H_8}}{44.09 \mbox{ g }\mathrm{C_3H_8}}\right)\left(\frac{4 \mbox{ mol }\mathrm{H_2O}}{1 \mbox{ mol }\mathrm{C_3H_8}}\right)\left(\frac{18.02 \mbox{ g }\mathrm{H_2O}}{1 \mbox{ mol }\mathrm{H_2O}}\right) = 196 \mbox{ g}</math> | :<math>m_\mathrm{H_2O} = \left(\frac{120. \mbox{ g }\mathrm{C_3H_8}}{1}\right)\left(\frac{1 \mbox{ mol }\mathrm{C_3H_8}}{44.09 \mbox{ g }\mathrm{C_3H_8}}\right)\left(\frac{4 \mbox{ mol }\mathrm{H_2O}}{1 \mbox{ mol }\mathrm{C_3H_8}}\right)\left(\frac{18.02 \mbox{ g }\mathrm{H_2O}}{1 \mbox{ mol }\mathrm{H_2O}}\right) = 196 \mbox{ g}</math> | ||
| Line 89: | Line 89: | ||
स्टोइकोमेट्री का उपयोग एक रासायनिक अभिक्रिया में अन्य अभिकारक के साथ पूरी तरह से अभिक्रिया करने के लिए एक अभिकारक की सही मात्रा को खोजने के लिए भी किया जाता है - अर्थात, स्टोइकियोमेट्रिक मात्रा जिसके परिणामस्वरूप अभिक्रिया होने पर कोई बचे हुए अभिकारक नहीं होंगे। थर्माइट अभिक्रिया का उपयोग करते हुए एक उदाहरण नीचे दिखाया गया है, | स्टोइकोमेट्री का उपयोग एक रासायनिक अभिक्रिया में अन्य अभिकारक के साथ पूरी तरह से अभिक्रिया करने के लिए एक अभिकारक की सही मात्रा को खोजने के लिए भी किया जाता है - अर्थात, स्टोइकियोमेट्रिक मात्रा जिसके परिणामस्वरूप अभिक्रिया होने पर कोई बचे हुए अभिकारक नहीं होंगे। थर्माइट अभिक्रिया का उपयोग करते हुए एक उदाहरण नीचे दिखाया गया है, | ||
:{{chem2|Fe2O3 + 2 Al -> Al2O3 + 2 Fe}} | :{{chem2|Fe2O3 + 2 Al -> Al2O3 + 2 Fe}} | ||
यह समीकरण दर्शाता है कि 1 मोल {{nowrap|[[ | यह समीकरण दर्शाता है कि 1 मोल {{nowrap|[[आयरन ऑक्साइड(III)]]}} और 2 मोल [[ अल्युमीनियम |एल्युमिनियम]] से 1 मोल [[Index.php?title=एल्युमिनियम ऑक्साइड|एल्युमिनियम ऑक्साइड]] और 2 मोल आयरन पैदा होगा। तो, 85.0 ग्राम के साथ पूरी तरह से अभिक्रिया करने के लिए आयरन ऑक्साइड(0.532 मोल), 28.7g(1.06 मोल) एल्युमिनियम की आवश्यकता होती है। | ||
:<math>m_\mathrm{Al} = \left(\frac{85.0 \mbox{ g }\mathrm{Fe_2O_3}}{1}\right)\left(\frac{1 \mbox{ mol }\mathrm{Fe_2 O_3}}{159.7 \mbox{ g }\mathrm{Fe_2 O_3}}\right)\left(\frac{2 \mbox{ mol Al}}{1 \mbox{ mol }\mathrm{Fe_2 O_3}}\right)\left(\frac{26.98 \mbox{ g Al}}{1 \mbox{ mol Al}}\right) = 28.7 \mbox{ g}</math> | :<math>m_\mathrm{Al} = \left(\frac{85.0 \mbox{ g }\mathrm{Fe_2O_3}}{1}\right)\left(\frac{1 \mbox{ mol }\mathrm{Fe_2 O_3}}{159.7 \mbox{ g }\mathrm{Fe_2 O_3}}\right)\left(\frac{2 \mbox{ mol Al}}{1 \mbox{ mol }\mathrm{Fe_2 O_3}}\right)\left(\frac{26.98 \mbox{ g Al}}{1 \mbox{ mol Al}}\right) = 28.7 \mbox{ g}</math> | ||
== सीमित अभिकर्मक और प्रतिशत | == सीमित अभिकर्मक और प्रतिशत उत्पाद == | ||
{{Main| | {{Main|सीमित अभिकर्मक|उत्पाद(रसायन विज्ञान)}} | ||
ऑक्सीजन(O | सीमित अभिकर्मक वह अभिकर्मक है जो बनने वाले उत्पाद की मात्रा को सीमित करता है और अभिक्रिया पूरी होने पर पूरी तरह से उपभोग होता है। अतिरिक्त अभिकारक वह अभिकारक है जो एक बार सीमित अभिकारक के समाप्त होने के कारण अभिक्रिया बंद हो जाने के बाद बचा रहता है। | ||
ऑक्सीजन(O<sub>2</sub>) में भर्जित लेड सल्फाइड(PbS) के समीकरण पर विचार करें लेड ऑक्साइड(PbO) और [[ सल्फर डाइऑक्साइड |सल्फर डाइऑक्साइड]](SO<sub>2</sub>) का उत्पादन करने के लिए: | |||
:2 {{chem|PbS}} + 3 {{chem|O|2}} → 2 {{chem|PbO}} + 2 {{chem|SO|2}} | :2 {{chem|PbS}} + 3 {{chem|O|2}} → 2 {{chem|PbO}} + 2 {{chem|SO|2}} | ||
लेड | लेड ऑक्साइड की सैद्धांतिक उत्पादन निर्धारित करने के लिए यदि एक खुले कंटेनर में 200.0 ग्राम लेड सल्फाइड और 200.0 ग्राम ऑक्सीजन गर्म किया जाता है: | ||
:<math>m_\mathrm{PbO} = \left(\frac{200.0 \mbox{ g }\mathrm{PbS}}{1}\right)\left(\frac{1 \mbox{ mol }\mathrm{PbS}}{239.27 \mbox{ g }\mathrm{PbS}}\right)\left(\frac{2 \mbox{ mol }\mathrm{PbO}}{2 \mbox{ mol }\mathrm{PbS}}\right)\left(\frac{223.2 \mbox{ g }\mathrm{PbO}}{1 \mbox{ mol }\mathrm{PbO}}\right) = 186.6 \mbox{ g}</math> | :<math>m_\mathrm{PbO} = \left(\frac{200.0 \mbox{ g }\mathrm{PbS}}{1}\right)\left(\frac{1 \mbox{ mol }\mathrm{PbS}}{239.27 \mbox{ g }\mathrm{PbS}}\right)\left(\frac{2 \mbox{ mol }\mathrm{PbO}}{2 \mbox{ mol }\mathrm{PbS}}\right)\left(\frac{223.2 \mbox{ g }\mathrm{PbO}}{1 \mbox{ mol }\mathrm{PbO}}\right) = 186.6 \mbox{ g}</math> | ||
:<math>m_\mathrm{PbO} = \left(\frac{200.0 \mbox{ g }\mathrm{O_2}}{1}\right)\left(\frac{1 \mbox{ mol }\mathrm{O_2}}{32.00 \mbox{ g }\mathrm{O_2}}\right)\left(\frac{2 \mbox{ mol }\mathrm{PbO}}{3 \mbox{ mol }\mathrm{O_2}}\right)\left(\frac{223.2 \mbox{ g }\mathrm{PbO}}{1 \mbox{ mol }\mathrm{PbO}}\right) = 930.0 \mbox{ g}</math> | :<math>m_\mathrm{PbO} = \left(\frac{200.0 \mbox{ g }\mathrm{O_2}}{1}\right)\left(\frac{1 \mbox{ mol }\mathrm{O_2}}{32.00 \mbox{ g }\mathrm{O_2}}\right)\left(\frac{2 \mbox{ mol }\mathrm{PbO}}{3 \mbox{ mol }\mathrm{O_2}}\right)\left(\frac{223.2 \mbox{ g }\mathrm{PbO}}{1 \mbox{ mol }\mathrm{PbO}}\right) = 930.0 \mbox{ g}</math> | ||
चूंकि | चूंकि PbS के 200.0 ग्राम के लिए PbO की कम मात्रा का उत्पादन होता है, यह स्पष्ट है कि PbS सीमित अभिकर्मक है। | ||
वास्तव में, वास्तविक | वास्तव में, वास्तविक उत्पादन स्टोइकियोमेट्रिक रूप से परिकलित सैद्धांतिक उत्पादन के समान नहीं है। प्रतिशत उत्पादन, तब, निम्नलिखित समीकरण में व्यक्त की जाती है: | ||
:<math>\mbox{percent yield} = \frac{\mbox{actual yield}}{\mbox{theoretical yield}}</math> | :<math>\mbox{percent yield} = \frac{\mbox{actual yield}}{\mbox{theoretical yield}}</math> | ||
यदि 170.0 ग्राम लेड(II) ऑक्साइड प्राप्त होता है, तो प्रतिशत | यदि 170.0 ग्राम लेड(II) ऑक्साइड प्राप्त होता है, तो प्रतिशत उत्पादन की गणना निम्नानुसार की जाएगी: | ||
:<math>\mbox{percent yield} = \frac{\mbox{170.0 g PbO}}{\mbox{186.6 g PbO}} = 91.12\%</math> | :<math>\mbox{percent yield} = \frac{\mbox{170.0 g PbO}}{\mbox{186.6 g PbO}} = 91.12\%</math> | ||
=== उदाहरण === | === उदाहरण === | ||
निम्नलिखित अभिक्रिया पर विचार करें, जिसमें आयरन | निम्नलिखित अभिक्रिया पर विचार करें, जिसमें आयरन क्लोराइड [[ हाइड्रोजन सल्फाइड |हाइड्रोजन सल्फाइड]] के साथ आयरन सल्फाइड और [[ हाईड्रोजन क्लोराईड |हाईड्रोजन क्लोराईड]] का उत्पादन करने के लिए अभिक्रिया करता है: | ||
:{{chem2|2 FeCl3 + 3 H2S -> Fe2S3 + 6 HCl}} | :{{chem2|2 FeCl3 + 3 H2S -> Fe2S3 + 6 HCl}} | ||
इस अभिक्रिया के लिए स्टोइकियोमेट्रिक द्रव्यमान हैं: | इस अभिक्रिया के लिए स्टोइकियोमेट्रिक द्रव्यमान हैं: | ||
:324. | :324.41g FeCl<sub>3</sub>, 102.25g H<sub>2</sub>S, 207.89g Fe<sub>2</sub>S<sub>3</sub>, 218.77g HCl | ||
मान लीजिए 90.0 ग्राम FeCl<sub>3</sub> 52.0 ग्राम H | मान लीजिए 90.0 ग्राम FeCl<sub>3</sub> 52.0 ग्राम H<sub>2</sub>S के साथ अभिक्रिया करता है। सीमित अभिकर्मक और अभिक्रिया द्वारा उत्पादित HCl के द्रव्यमान को खोजने के लिए, हम उपरोक्त मात्रा को 90/324.41 के कारक से बदलते हैं और निम्नलिखित मात्रा प्राप्त करते हैं: | ||
:90. | :90.00g FeCl<sub>3</sub>, 28.37g H<sub>2</sub>S, 57.67g Fe<sub>2</sub>S<sub>3</sub>, 60.69g HCl | ||
सीमित अभिकारक | सीमित अभिकारक या अभिकर्मक FeCl<sub>3</sub> है, चूंकि इसका सभी 90.00 ग्राम उपयोग किया जाता है जबकि केवल 28.37 ग्राम H<sub>2</sub>S का सेवन किया जाता है। इस प्रकार, 52.0 - 28.4 = 23.6g H<sub>2</sub>S अधिक छोड़ दिया जाता है। उत्पादित HCl का द्रव्यमान 60.7 ग्राम है। | ||
नोट: अभिक्रिया के स्टोइकोमेट्री को देखकर, | नोट: अभिक्रिया के स्टोइकोमेट्री को देखकर, FeCl<sub>3</sub> का अनुमान लगाया जा सकता है, सीमित अभिकारक होने के कारण; तीन गुना अधिक FeCl<sub>3</sub> प्रयोग किया जाता है(324 ग्राम/102 ग्राम)। | ||
==प्रतिस्पर्धी अभिक्रियाओं में विभिन्न स्टोइकोमेट्री== | ==प्रतिस्पर्धी अभिक्रियाओं में विभिन्न स्टोइकोमेट्री== | ||
प्रायः, एक ही प्रारंभिक सामग्री को देखते हुए एक से अधिक अभिक्रिया संभव है। अभिक्रियाएं उनके स्टोइकोमेट्री में भिन्न हो सकती हैं। उदाहरण के लिए, [[ बेंजीन ]] का [[ मेथिलिकरण | मेथिलिकरण]](C .)<sub>6</sub>H<sub>6</sub>), एल्यूमीनियम क्लोराइड का उपयोग करके एक फ्राइडल-शिल्प अभिक्रिया के माध्यम से|AlCl<sub>3</sub>उत्प्रेरक के रूप में, एकल मिथाइलेटेड(C .) का उत्पादन कर सकता है<sub>6</sub>H<sub>5</sub>चौधरी<sub>3</sub>), दोगुना मिथाइलेटेड(C .)<sub>6</sub>H<sub>4</sub>(सीएच<sub>3</sub>)<sub>2</sub>), या फिर भी अत्यधिक मिथाइलेटेड(C .)<sub>6</sub>H<sub>6−''n''</sub>(सीएच<sub>3</sub>)<sub>''n''</sub>) उत्पाद, जैसा कि निम्नलिखित उदाहरण में दिखाया गया है, | |||
:सी<sub>6</sub>H<sub>6</sub> + सीएच<sub>3</sub>सीएल → सी<sub>6</sub>H<sub>5</sub>चौधरी<sub>3</sub> + | :सी<sub>6</sub>H<sub>6</sub> + सीएच<sub>3</sub>सीएल → सी<sub>6</sub>H<sub>5</sub>चौधरी<sub>3</sub> + HCl | ||
:सी<sub>6</sub>H<sub>6</sub> + 2 सीएच<sub>3</sub>सीएल → सी<sub>6</sub>H<sub>4</sub>(सीएच<sub>3</sub>)<sub>2</sub> + 2 | :सी<sub>6</sub>H<sub>6</sub> + 2 सीएच<sub>3</sub>सीएल → सी<sub>6</sub>H<sub>4</sub>(सीएच<sub>3</sub>)<sub>2</sub> + 2 HCl | ||
:सी<sub>6</sub>H<sub>6</sub> + एन सीएच<sub>3</sub>सीएल → सी<sub>6</sub>H<sub>6−''n''</sub>(सीएच<sub>3</sub>)<sub>''n''</sub> + एन | :सी<sub>6</sub>H<sub>6</sub> + एन सीएच<sub>3</sub>सीएल → सी<sub>6</sub>H<sub>6−''n''</sub>(सीएच<sub>3</sub>)<sub>''n''</sub> + एन HCl | ||
इस उदाहरण में, कौन सी अभिक्रिया होती है, इसे अभिकारकों की सापेक्ष सांद्रता द्वारा नियंत्रित किया जाता है। | इस उदाहरण में, कौन सी अभिक्रिया होती है, इसे अभिकारकों की सापेक्ष सांद्रता द्वारा नियंत्रित किया जाता है। | ||
| Line 148: | Line 149: | ||
स्टोइकियोमेट्रिक संख्या<math>\nu_i</math> उस डिग्री का प्रतिनिधित्व करता है जिस तक एक रासायनिक प्रजाति अभिक्रिया में भाग लेती है। सम्मेलन अभिकारकों(जो उपभोग किया जाता है) और सकारात्मक वाले उत्पादों को ऋणात्मक संख्या प्रदान करने के लिए है, इस सम्मेलन के अनुरूप है कि अभिक्रिया की सीमा में वृद्धि अभिकारकों से उत्पादों की ओर संरचना को स्थानांतरित करने के अनुरूप होगी। हालांकि, किसी भी अभिक्रिया को विपरीत दिशा में जाने के रूप में देखा जा सकता है, और उस दृष्टिकोण में, सिस्टम की गिब्स मुक्त ऊर्जा को कम करने के लिए नकारात्मक दिशा में बदल जाएगा। अभिक्रिया वास्तव में मनमाने ढंग से चयनित आगे की दिशा में जाएगी या नहीं यह किसी भी समय मौजूद [[ रासायनिक पदार्थ ]] की मात्रा पर निर्भर करता है, जो [[ रासायनिक गतिकी ]] और [[ थर्मोडायनामिक संतुलन ]] को निर्धारित करता है, अर्थात, [[ रासायनिक संतुलन ]] दाईं ओर है या बाईं ओर है प्रारंभिक अवस्था, | स्टोइकियोमेट्रिक संख्या<math>\nu_i</math> उस डिग्री का प्रतिनिधित्व करता है जिस तक एक रासायनिक प्रजाति अभिक्रिया में भाग लेती है। सम्मेलन अभिकारकों(जो उपभोग किया जाता है) और सकारात्मक वाले उत्पादों को ऋणात्मक संख्या प्रदान करने के लिए है, इस सम्मेलन के अनुरूप है कि अभिक्रिया की सीमा में वृद्धि अभिकारकों से उत्पादों की ओर संरचना को स्थानांतरित करने के अनुरूप होगी। हालांकि, किसी भी अभिक्रिया को विपरीत दिशा में जाने के रूप में देखा जा सकता है, और उस दृष्टिकोण में, सिस्टम की गिब्स मुक्त ऊर्जा को कम करने के लिए नकारात्मक दिशा में बदल जाएगा। अभिक्रिया वास्तव में मनमाने ढंग से चयनित आगे की दिशा में जाएगी या नहीं यह किसी भी समय मौजूद [[ रासायनिक पदार्थ ]] की मात्रा पर निर्भर करता है, जो [[ रासायनिक गतिकी ]] और [[ थर्मोडायनामिक संतुलन ]] को निर्धारित करता है, अर्थात, [[ रासायनिक संतुलन ]] दाईं ओर है या बाईं ओर है प्रारंभिक अवस्था, | ||
[[ प्रतिक्रिया तंत्र | अभिक्रिया तंत्र]] में, प्रत्येक चरण के लिए स्टोइकियोमेट्रिक गुणांक हमेशा [[ पूर्णांक ]] होते हैं, क्योंकि प्राथमिक अभिक्रियाओं में हमेशा पूरे अणु सम्मिलित होते हैं। यदि कोई समग्र अभिक्रिया के समग्र प्रतिनिधित्व का उपयोग करता है, तो कुछ तर्कसंगत संख्या [[ अंश (गणित) | अंश(गणित)]] हो सकते हैं। | [[ प्रतिक्रिया तंत्र | अभिक्रिया तंत्र]] में, प्रत्येक चरण के लिए स्टोइकियोमेट्रिक गुणांक हमेशा [[ पूर्णांक ]] होते हैं, क्योंकि प्राथमिक अभिक्रियाओं में हमेशा पूरे अणु सम्मिलित होते हैं। यदि कोई समग्र अभिक्रिया के समग्र प्रतिनिधित्व का उपयोग करता है, तो कुछ तर्कसंगत संख्या [[ अंश (गणित) | अंश(गणित)]] हो सकते हैं। प्रायः रासायनिक प्रजातियां मौजूद होती हैं जो अभिक्रिया में भाग नहीं लेती हैं; इसलिए उनके स्टोइकोमीट्रिक गुणांक शून्य हैं। किसी भी रासायनिक प्रजाति को पुनर्जीवित किया जाता है, जैसे कि [[ उत्प्रेरक ]], में भी शून्य का स्टोइकियोमेट्रिक गुणांक होता है। | ||
सबसे सरल संभव मामला एक [[ आइसोमराइज़ेशन ]] है | सबसे सरल संभव मामला एक [[ आइसोमराइज़ेशन ]] है | ||
| Line 163: | Line 164: | ||
अभिक्रिया के विस्तार संरचनागत परिवर्तन का प्रतिनिधित्व करने का सबसे स्पष्ट और सबसे स्पष्ट तरीका प्रदान करते हैं, हालांकि उनका अभी तक व्यापक रूप से उपयोग नहीं किया गया है। | अभिक्रिया के विस्तार संरचनागत परिवर्तन का प्रतिनिधित्व करने का सबसे स्पष्ट और सबसे स्पष्ट तरीका प्रदान करते हैं, हालांकि उनका अभी तक व्यापक रूप से उपयोग नहीं किया गया है। | ||
जटिल अभिक्रिया प्रणालियों के साथ, मौजूद रसायनों की मात्रा के संदर्भ में अभिक्रिया प्रणाली के प्रतिनिधित्व दोनों पर विचार करना | जटिल अभिक्रिया प्रणालियों के साथ, मौजूद रसायनों की मात्रा के संदर्भ में अभिक्रिया प्रणाली के प्रतिनिधित्व दोनों पर विचार करना प्रायः उपयोगी होता है {{math|1={{mset| ''N<sub>i</sub>'' }}}}(ऊष्मप्रवैगिकी चर), और वास्तविक संरचना के संदर्भ में प्रतिनिधित्व [[ स्वतंत्रता की डिग्री (भौतिकी और रसायन विज्ञान) | स्वतंत्रता की डिग्री(भौतिकी और रसायन विज्ञान)]] , जैसा कि अभिक्रिया के विस्तार द्वारा व्यक्त किया गया है {{math|1={{mset| ''ξ<sub>k</sub>'' }}}}. एक सदिश समष्टि से परिमाणों को व्यक्त करने वाले सदिश में परिवर्तन एक आयताकार [[ मैट्रिक्स (गणित) | मैट्रिक्स(गणित)]] का उपयोग करता है जिसके तत्व स्टोइकोमीट्रिक संख्याएं हैं {{math|1=[ ''ν<sub>i k</sub>'' ]}}. | ||
किसी भी . के लिए [[ चरम मूल्य ]]<sub>k</sub>तब होता है जब अग्र अभिक्रिया के लिए अभिकारकों में से पहला समाप्त हो जाता है; या उत्पादों में से पहला समाप्त हो जाता है यदि अभिक्रिया को विपरीत दिशा में धकेलने के रूप में देखा जाता है। यह रिएक्शन [[ सिंप्लेक्स ]], कंपोजिशन स्पेस में एक [[ हाइपरप्लेन ]], या एन-स्पेस पर विशुद्ध रूप से [[ गतिकी ]] प्रतिबंध है, जिसकी [[ आयाम ]]ीता [[ रैखिक स्वतंत्रता ]] की संख्या के बराबर होती है।रैखिक-स्वतंत्र रासायनिक अभिक्रियाएं। यह आवश्यक रूप से रासायनिक घटकों की संख्या से कम है, क्योंकि प्रत्येक अभिक्रिया कम से कम दो रसायनों के बीच संबंध को प्रकट करती है। हाइपरप्लेन का सुलभ क्षेत्र वास्तव में मौजूद प्रत्येक रासायनिक प्रजाति की मात्रा पर निर्भर करता है, एक आकस्मिक तथ्य। अलग-अलग ऐसी मात्राएँ अलग-अलग हाइपरप्लेन भी उत्पन्न कर सकती हैं, सभी समान बीजीय स्टोइकोमेट्री साझा करते हैं। | किसी भी . के लिए [[ चरम मूल्य ]]<sub>k</sub>तब होता है जब अग्र अभिक्रिया के लिए अभिकारकों में से पहला समाप्त हो जाता है; या उत्पादों में से पहला समाप्त हो जाता है यदि अभिक्रिया को विपरीत दिशा में धकेलने के रूप में देखा जाता है। यह रिएक्शन [[ सिंप्लेक्स ]], कंपोजिशन स्पेस में एक [[ हाइपरप्लेन ]], या एन-स्पेस पर विशुद्ध रूप से [[ गतिकी ]] प्रतिबंध है, जिसकी [[ आयाम ]]ीता [[ रैखिक स्वतंत्रता ]] की संख्या के बराबर होती है।रैखिक-स्वतंत्र रासायनिक अभिक्रियाएं। यह आवश्यक रूप से रासायनिक घटकों की संख्या से कम है, क्योंकि प्रत्येक अभिक्रिया कम से कम दो रसायनों के बीच संबंध को प्रकट करती है। हाइपरप्लेन का सुलभ क्षेत्र वास्तव में मौजूद प्रत्येक रासायनिक प्रजाति की मात्रा पर निर्भर करता है, एक आकस्मिक तथ्य। अलग-अलग ऐसी मात्राएँ अलग-अलग हाइपरप्लेन भी उत्पन्न कर सकती हैं, सभी समान बीजीय स्टोइकोमेट्री साझा करते हैं। | ||
| Line 175: | Line 176: | ||
==स्टोइकोमेट्री मैट्रिक्स== | ==स्टोइकोमेट्री मैट्रिक्स== | ||
{{Main|Chemical reaction network theory}} | {{Main|Chemical reaction network theory}} | ||
जटिल अभिक्रियाओं में, स्टोइकोमेट्री को | जटिल अभिक्रियाओं में, स्टोइकोमेट्री को प्रायः अधिक कॉम्पैक्ट रूप में दर्शाया जाता है जिसे स्टोइकोमेट्री मैट्रिक्स कहा जाता है। स्टोइकोमेट्री मैट्रिक्स को प्रतीक एन द्वारा दर्शाया गया है।<ref>{{cite journal |last1=Ghaderi |first1=Susan |last2=Haraldsdóttir |first2=Hulda S. |last3=Ahookhosh |first3=Masoud |last4=Arreckx |first4=Sylvain |last5=Fleming |first5=Ronan M.T. |title=एक स्टोइकोमेट्रिक मैट्रिक्स का संरचनात्मक संरक्षित आंशिक विभाजन|journal=Journal of Theoretical Biology |date=August 2020 |volume=499 |pages=110276 |doi=10.1016/j.jtbi.2020.110276|pmid=32333975 |bibcode=2020JThBi.49910276G |doi-access=free }}</ref><ref>{{cite journal |last1=Hofmeyr |first1=Jan-hendrik S. |title=संक्षेप में चयापचय नियंत्रण विश्लेषण|journal=In Proceedings of the 2 Nd International Conference on Systems Biology |date=2001 |pages=291–300 |citeseerx=10.1.1.324.922 |url=https://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.324.922&rank=1}}</ref><ref>{{cite journal |last1=Reder |first1=Christine |title=चयापचय नियंत्रण सिद्धांत: एक संरचनात्मक दृष्टिकोण|journal=Journal of Theoretical Biology |date=21 November 1988 |volume=135 |issue=2 |pages=175–201 |doi=10.1016/s0022-5193(88)80073-0|pmid=3267767 |bibcode=1988JThBi.135..175R }}</ref> | ||
यदि किसी अभिक्रिया नेटवर्क में n अभिक्रियाएँ और m भाग लेने वाली आणविक प्रजातियाँ हैं तो स्टोइकोमेट्री मैट्रिक्स में संगत m पंक्तियाँ और n कॉलम होंगे। | यदि किसी अभिक्रिया नेटवर्क में n अभिक्रियाएँ और m भाग लेने वाली आणविक प्रजातियाँ हैं तो स्टोइकोमेट्री मैट्रिक्स में संगत m पंक्तियाँ और n कॉलम होंगे। | ||
| Line 196: | Line 197: | ||
जहाँ पंक्तियाँ S . से मेल खाती हैं<sub>1</sub>, एस<sub>2</sub>, एस<sub>3</sub>, एस<sub>4</sub> और<sub>5</sub>, क्रमश। ध्यान दें कि एक अभिक्रिया योजना को एक स्टोइकोमेट्री मैट्रिक्स में परिवर्तित करने की प्रक्रिया एक हानिकारक परिवर्तन हो सकती है: उदाहरण के लिए, दूसरी अभिक्रिया में स्टोइकोमेट्री मैट्रिक्स में सम्मिलित होने पर सरल हो जाती है। इसका मतलब यह है कि स्टोइकोमेट्री मैट्रिक्स से मूल अभिक्रिया योजना को पुनर्प्राप्त करना हमेशा संभव नहीं होता है। | जहाँ पंक्तियाँ S . से मेल खाती हैं<sub>1</sub>, एस<sub>2</sub>, एस<sub>3</sub>, एस<sub>4</sub> और<sub>5</sub>, क्रमश। ध्यान दें कि एक अभिक्रिया योजना को एक स्टोइकोमेट्री मैट्रिक्स में परिवर्तित करने की प्रक्रिया एक हानिकारक परिवर्तन हो सकती है: उदाहरण के लिए, दूसरी अभिक्रिया में स्टोइकोमेट्री मैट्रिक्स में सम्मिलित होने पर सरल हो जाती है। इसका मतलब यह है कि स्टोइकोमेट्री मैट्रिक्स से मूल अभिक्रिया योजना को पुनर्प्राप्त करना हमेशा संभव नहीं होता है। | ||
आणविक प्रजातियों के परिवर्तन की दरों का वर्णन करते हुए एक कॉम्पैक्ट समीकरण बनाने के लिए | आणविक प्रजातियों के परिवर्तन की दरों का वर्णन करते हुए एक कॉम्पैक्ट समीकरण बनाने के लिए प्रायः स्टोइकोमेट्री मैट्रिक्स को दर वेक्टर, वी, और प्रजाति वेक्टर, एक्स के साथ जोड़ा जाता है: | ||
: <math> | : <math> | ||
| Line 204: | Line 205: | ||
== गैस स्टोइकोमेट्री == | == गैस स्टोइकोमेट्री == | ||
गैस स्टोइकोमेट्री एक रासायनिक अभिक्रिया में अभिकारकों और उत्पादों के बीच [[ मात्रा ]]त्मक संबंध(अनुपात) है जो [[ गैसों ]] का उत्पादन करने वाली अभिक्रियाओं के साथ होता है। गैस स्टोइकोमेट्री तब लागू होती है जब उत्पादित गैसों को आदर्श गैस माना जाता है, और गैसों का तापमान, दबाव और आयतन सभी ज्ञात होते हैं। इन गणनाओं के लिए आदर्श गैस नियम का उपयोग किया जाता है। | गैस स्टोइकोमेट्री एक रासायनिक अभिक्रिया में अभिकारकों और उत्पादों के बीच [[ मात्रा ]]त्मक संबंध(अनुपात) है जो [[ गैसों ]] का उत्पादन करने वाली अभिक्रियाओं के साथ होता है। गैस स्टोइकोमेट्री तब लागू होती है जब उत्पादित गैसों को आदर्श गैस माना जाता है, और गैसों का तापमान, दबाव और आयतन सभी ज्ञात होते हैं। इन गणनाओं के लिए आदर्श गैस नियम का उपयोग किया जाता है। प्रायः, लेकिन हमेशा नहीं, [[ मानक तापमान और दबाव | मानक तापमान और दबाव]](एसटीपी) को 0 डिग्री सेल्सियस और 1 बार के रूप में लिया जाता है और गैस स्टोइकियोमेट्रिक गणना के लिए शर्तों के रूप में उपयोग किया जाता है। | ||
गैस स्टोइकोमेट्री गणना अज्ञात मात्रा या गैसीय उत्पाद या अभिकारक के द्रव्यमान के लिए हल करती है। उदाहरण के लिए, यदि हम गैसीय NO . के आयतन की गणना करना चाहते हैं<sub>2</sub> 100 ग्राम NH . के दहन से उत्पन्न<sub>3</sub>, अभिक्रिया से: | गैस स्टोइकोमेट्री गणना अज्ञात मात्रा या गैसीय उत्पाद या अभिकारक के द्रव्यमान के लिए हल करती है। उदाहरण के लिए, यदि हम गैसीय NO . के आयतन की गणना करना चाहते हैं<sub>2</sub> 100 ग्राम NH . के दहन से उत्पन्न<sub>3</sub>, अभिक्रिया से: | ||
| Line 211: | Line 212: | ||
हम निम्नलिखित गणना करेंगे: | हम निम्नलिखित गणना करेंगे: | ||
:<math>100\, \mathrm{g\, NH_3}\cdot\frac{1\, \mathrm{mol\, NH_3}}{17.034\, \mathrm{g\, NH_3}}=5.871\, \mathrm{mol\, NH_3} </math> | :<math>100\, \mathrm{g\, NH_3}\cdot\frac{1\, \mathrm{mol\, NH_3}}{17.034\, \mathrm{g\, NH_3}}=5.871\, \mathrm{mol\, NH_3} </math> | ||
NH . का 1:1 मोलर अनुपात होता है<sub>3</sub> नहीं करने के लिए<sub>2</sub> उपरोक्त संतुलित दहन अभिक्रिया में, इसलिए NO . का 5. | NH . का 1:1 मोलर अनुपात होता है<sub>3</sub> नहीं करने के लिए<sub>2</sub> उपरोक्त संतुलित दहन अभिक्रिया में, इसलिए NO . का 5.871 मोल<sub>2</sub> गठन किया जाएगा। हम 0°C(273.15 K) और 1 वायुमंडल के आयतन को R = 0.08206 L·atm·K के [[ गैस स्थिरांक ]] का उपयोग करके हल करने के लिए आदर्श गैस नियम का उपयोग करेंगे।<sup>-1</sup> मोल<sup>-1</sup>: | ||
:<math>\begin{align} | :<math>\begin{align} | ||
PV&= nRT\\ | PV&= nRT\\ | ||
| Line 218: | Line 219: | ||
&= 131.597\, \mathrm{L\, NO_2} | &= 131.597\, \mathrm{L\, NO_2} | ||
\end{align}</math> | \end{align}</math> | ||
गैस स्टोइकोमेट्री में | गैस स्टोइकोमेट्री में प्रायः उस गैस के घनत्व को देखते हुए, गैस के ग्राम अणुक द्रव्यमान को जानना सम्मिलित होता है। आदर्श गैस के घनत्व और ग्राम अणुक द्रव्यमान के बीच संबंध प्राप्त करने के लिए आदर्श गैस नियम को फिर से व्यवस्थित किया जा सकता है: | ||
:<math>\rho = \frac{m}{V}</math> तथा <math>n = \frac{m}{M}</math> | :<math>\rho = \frac{m}{V}</math> तथा <math>n = \frac{m}{M}</math> | ||
और इस तरह: | और इस तरह: | ||
| Line 343: | Line 344: | ||
* [https://web.archive.org/web/20070206060439/http://www.tech.plym.ac.uk/sme/ther305-web/Combust1.PDF Engine Combustion primer] from the University of Plymouth | * [https://web.archive.org/web/20070206060439/http://www.tech.plym.ac.uk/sme/ther305-web/Combust1.PDF Engine Combustion primer] from the University of Plymouth | ||
* [http://www.chemcollective.org/tutorials.php Free स्टोइकियोमेस्ट्री Tutorials] from Carnegie Mellon's ChemCollective | * [http://www.chemcollective.org/tutorials.php Free स्टोइकियोमेस्ट्री Tutorials] from Carnegie Mellon's ChemCollective | ||
* [http://chemistry-in-excel.jimdo.com/ स्टोइकियोमेस्ट्री Add-In for Microsoft Excel] for calculation of | * [http://chemistry-in-excel.jimdo.com/ स्टोइकियोमेस्ट्री Add-In for Microsoft Excel] for calculation of मोलecular weights, reaction coëfficients and स्टोइकियोमेस्ट्री. | ||
* [http://www.thermobook.net/stoichiometry/ Reaction स्टोइकियोमेस्ट्री Calculator] a comprehensive free online reaction स्टोइकियोमेस्ट्री calculator. | * [http://www.thermobook.net/stoichiometry/ Reaction स्टोइकियोमेस्ट्री Calculator] a comprehensive free online reaction स्टोइकियोमेस्ट्री calculator. | ||
* [https://play.google.com/store/apps/details?id=net.thermobook.thermostoichiometryplus स्टोइकियोमेस्ट्री Plus] a स्टोइकियोमेस्ट्री calculator and more for Android. | * [https://play.google.com/store/apps/details?id=net.thermobook.thermostoichiometryplus स्टोइकियोमेस्ट्री Plus] a स्टोइकियोमेस्ट्री calculator and more for Android. | ||
Revision as of 11:44, 3 December 2022
स्टोइकियोमेस्ट्री रासायनिक अभिक्रियाओं से पहले, दौरान और बाद में अभिकारक और उत्पाद(रसायन विज्ञान) की मात्रा के बीच संबंध को संदर्भित करता है।
स्टोइकियोमेस्ट्री द्रव्यमान के संरक्षण के नियम पर स्थापित किया गया है जहां अभिकारकों का कुल द्रव्यमान उत्पादों के कुल द्रव्यमान के बराबर होता है, जिससे यह अंतर्दृष्टि प्राप्त होती है कि अभिकारकों और उत्पादों की मात्रा के बीच संबंध सामान्यतः सकारात्मक पूर्णांक का अनुपात बकारण हैं। इसका मतलब यह है कि यदि अलग-अलग अभिकारकों की मात्रा ज्ञात हो, तो उत्पाद की मात्रा की गणना की जा सकती है। इसके विपरीत, यदि अभिकारक की मात्रा ज्ञात होती है और उत्पादों की मात्रा को आनुभविक रूप से निर्धारित किया जा सकता है, तो अन्य अभिकारकों की मात्रा की भी गणना की जा सकती है।
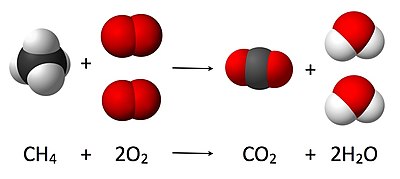
यह यहाँ की छवि में दिखाया गया है, जहाँ संतुलित समीकरण है:
- CH4 + 2 O2 → CO2 + 2 H2O
यहाँ, मीथेन का एक अणु ऑक्सीजन गैस के दो अणुओं के साथ क्रिया करके कार्बन डाइआक्साइड के एक अणु और पानी के गुणों के दो अणु उत्पन्न करता है। यह विशेष रासायनिक समीकरण पूर्ण दहन का एक उदाहरण है। स्टोइकियोमेस्ट्री इन मात्रात्मक संबंधों को मापता है, और इसका उपयोग उत्पादों और अभिकारकों की मात्रा निर्धारित करने के लिए किया जाता है जो किसी दिए गए अभिक्रिया में उत्पादित या आवश्यक होते हैं। रासायनिक अभिक्रियाओं में भाग लेने वाले पदार्थों के बीच मात्रात्मक संबंधों का वर्णन करना अथवा यह अभिक्रिया स्टोइकोमेट्री के रूप में जाना जाता है। उपरोक्त उदाहरण में, अभिक्रिया स्टोइकोमेट्री मीथेन और ऑक्सीजन की मात्रा के बीच संबंध को मापती है जो कार्बन डाइऑक्साइड और पानी बनाने के लिए अभिक्रिया करती है।
मोल(इकाई) के सापेक्ष परमाणु द्रव्यमान के प्रसिद्ध संबंध के कारण, स्टोइकोमेट्री द्वारा आने वाले अनुपातों का उपयोग संतुलित समीकरण द्वारा वर्णित अभिक्रिया में वजन द्वारा मात्रा निर्धारित करने के लिए किया जा सकता है। इसे कंपोजीशन स्टोइकोमेट्री कहते हैं।
गैस स्टोइकोमेट्री गैसों से संबंधित अभिक्रियाओं से संबंधित है, जहां गैसें एक ज्ञात तापमान, दबाव और आयतन पर होती हैं और इसे आदर्श गैस माना जा सकता है। गैसों के लिए, आदर्श गैस नियम के अनुसार आयतन अनुपात आदर्श रूप से समान होता है, लेकिन एकल अभिक्रिया के द्रव्यमान अनुपात की गणना अभिकारकों और उत्पादों के आणविक द्रव्यमान से की जानी चाहिए। व्यवहार में, समस्थानिकों के अस्तित्व के कारण, द्रव्यमान अनुपात की गणना करते समय मोलर द्रव्यमान का उपयोग किया जाता है।
व्युत्पत्ति
स्टोइकोमेट्री शब्द का उपयोग पहली बार यिर्मयाह बेंजामिन रिक्टर द्वारा 1792 में किया गया था जब रिक्टर की स्टोइकोमेट्री या रासायनिक तत्वों को मापने की कला का पहला खंड प्रकाशित हुआ था।[1] यह शब्द प्राचीन यूनानी शब्दों στοιχεῖον स्टोइचियन 'तत्व' और μέτρον मेट्रोन 'उपाय' से लिया गया है। पैट्रिस्टिक ग्रीक में, स्टोइचिओमेट्रिया शब्द का उपयोग नीसफोरस द्वारा कैनोनिकल न्यू टेस्टामेंट और कुछ अपोक्रिफा की लाइन काउंट की संख्या को संदर्भित करने के लिए किया गया था।
परिभाषा
एक स्टोइकियोमेट्रिक राशि[2] या अभिकर्मक का स्टोइकोमीट्रिक अनुपात इष्टतम राशि या अनुपात है, जहां यह मानते हुए कि अभिक्रिया पूर्ण होने के लिए आगे बढ़ती है:
- सभी अभिकर्मक का उपभुक्त किया जाता है
- अभिकर्मक की कोई कमी नहीं है
- अभिकर्मक की अधिकता नहीं है।
स्टोइकियोमेस्ट्री बहुत ही बुनियादी नियमों पर टिकी हुई है जो इसे बेहतर ढंग से समझने में मदद करते हैं, जैसे कि द्रव्यमान के संरक्षण का नियम, निश्चित अनुपात का नियम(अर्थात, निरंतर संरचना का नियम), कई अनुपातों का नियम और पारस्परिक अनुपात का नियम। साधारणतः, रासायनिक अभिक्रियाएं रसायनों के निश्चित अनुपात में संयोजित होती हैं। चूंकि रासायनिक अभिक्रियाएं न तो पदार्थ को बना सकती हैं और न ही नष्ट कर सकती हैं, न ही परमाणु रूपांतरण एक तत्व को दूसरे में बदल सकता है, प्रत्येक तत्व की मात्रा समग्र अभिक्रिया में समान होनी चाहिए। उदाहरण के लिए, अभिकारक पक्ष पर दिए गए तत्व X के परमाणुओं की संख्या उत्पाद पक्ष पर उस तत्व के परमाणुओं की संख्या के बराबर होनी चाहिए, चाहे वे सभी परमाणु वास्तव में अभिक्रिया में सम्मिलित हों या न हो।
रासायनिक अभिक्रियाएं, सूक्ष्मदर्शी इकाई संचालन के रूप में, बहुत बड़ी संख्या में प्राथमिक अभिक्रियाएं होती हैं, जहां एक अणु दूसरे अणु के साथ अभिक्रिया करता है। चूंकि अभिकारक अणु(या अंश) में एक पूर्णांक अनुपात में परमाणुओं का एक निश्चित समूह होता है, एक पूर्ण अभिक्रिया में अभिकारकों के बीच का अनुपात भी पूर्णांक में होता है। एक अभिक्रिया एक से अधिक अणुओं का उपभोग कर सकती है, और स्टोइकियोमेट्रिक संख्या इस संख्या की गणना करती है, जिसे उत्पादों के लिए सकारात्मक(जोड़ा गया) और रिएक्टेंट्स(हटाए गए) के लिए नकारात्मक के रूप में परिभाषित किया गया है।[3] अहस्ताक्षरित गुणांकों को सामान्यतः स्टोइकियोमेट्रिक गुणांक के रूप में संदर्भित किया जाता है।[4] प्रत्येक तत्व का एक परमाणु द्रव्यमान होता है, और अणुओं को परमाणुओं के संग्रह के रूप में देखते हुए, यौगिकों का एक निश्चित ग्राम अणुक द्रव्यमान होता है। परिभाषा के अनुसार, कार्बन-12 का ग्राम अणुक द्रव्यमान 12 ग्राम/मोल है। किसी पदार्थ में प्रति मोल अणुओं की संख्या अवोगाद्रो स्थिरांक द्वारा दी जाती है। इस प्रकार, द्रव्यमान द्वारा स्टोइकोमेट्री की गणना करने के लिए, प्रत्येक अभिकारक के लिए आवश्यक अणुओं की संख्या को मोल में व्यक्त किया जाता है और प्रत्येक ग्राम अणुक द्रव्यमान से गुणा करके प्रत्येक अभिकारक का द्रव्यमान प्रति मोल में दिया जाता है। संपूर्ण अभिक्रिया में प्रत्येक को कुल से विभाजित करके द्रव्यमान अनुपात की गणना की जा सकती है।
तत्व अपनी प्राकृतिक अवस्था में भिन्नात्मक द्रव्यमान के समस्थानिकों के मिश्रण होते हैं; इस प्रकार, परमाणु द्रव्यमान और इस प्रकार ग्राम अणुक द्रव्यमान बिल्कुल पूर्णांक नहीं होते हैं। उदाहरण के लिए, ठीक 14:3 अनुपात के बजाय, 17.04 किलो अमोनिया में 14.01 किलो नाइट्रोजन और 3 × 1.01 किलो हाइड्रोजन होता है, क्योंकि प्राकृतिक नाइट्रोजन में नाइट्रोजन -15 और प्राकृतिक हाइड्रोजन में हाइड्रोजन -2(ड्यूटेरियम) की थोड़ी मात्रा सम्मिलित होती है।
स्टोइकियोमेट्रिक अभिकारक है जो अभिक्रिया में उपभोग होता है, एक उत्प्रेरण के विपरीत, यह समग्र अभिक्रिया में उपभोग नहीं होता है क्योंकि यह एक चरण में अभिक्रिया करता है और दूसरे चरण में पुन: उत्पन्न होता है।
ग्राम को मोल में बदलना
स्टोइकियोमेस्ट्री का उपयोग न केवल रासायनिक समीकरणों को संतुलित करने के लिए किया जाता है, बल्कि रूपांतरणों में भी किया जाता है, अर्थात, ग्राम से मोल्स में रूपांतरण कारक के रूप में, या ग्राम से मिलीलीटर तक घनत्व का उपयोग करके परिवर्तित किया जाता है। उदाहरण के लिए, 2.00 ग्राम में NaCl(सोडियम क्लोराइड) के पदार्थ की मात्रा ज्ञात करने के लिए, कोई निम्नलिखित कार्य करेगा:
उपरोक्त उदाहरण में, जब अंश के रूप में लिखा जाता है, तो ग्राम की इकाइयाँ एक गुणनात्मक पहचान बनाती हैं, जो एक(g/g = 1) के बराबर होती है, जिसके परिणामस्वरूप मोल(इकाई की आवश्यकता होती है) में परिणामी मात्रा होती है, जैसा कि दिखाया गया है निम्नलिखित समीकरण में,
मोलर अनुपात
स्टोइकियोमेस्ट्री प्रायः रासायनिक समीकरणों(स्टोइकियोमेस्ट्री अभिक्रिया) को संतुलित करने के लिए प्रयोग किया जाता है। उदाहरण के लिए, दो डायटोमिक अणु गैसें, हाइड्रोजन और ऑक्सीजन, ऊष्माक्षेपी अभिक्रिया में एक तरल, पानी बनाने के लिए सम्मिलित हो सकते हैं, जैसा कि निम्नलिखित समीकरण द्वारा वर्णित है:
- 2H
2 + O
2 → 2 H
2O
अभिक्रिया स्टोइकोमेट्री उपरोक्त समीकरण में हाइड्रोजन, ऑक्सीजन और पानी के अणुओं के 2:1:2 अनुपात का वर्णन करती है।
ग्राम अणुक अनुपात एक पदार्थ के मोल और दूसरे के मोल के बीच रूपांतरण की अनुमति देता है। उदाहरण के लिए, अभिक्रिया में
- 2CH
3OH + 3 O
2 → 2 CO
2 + 4 H
2O
पानी की मात्रा जो 0.27 मोल . के दहन से उत्पन्न होगी CH
3OH के बीच ग्राम अणुक अनुपात का उपयोग करके प्राप्त किया जाता है CH
3OH तथा H
2O 2 से 4.
स्टोइकोमेट्री शब्द का प्रयोग प्रायः स्टोइकियोमेट्रिक यौगिकों(रचना स्टोइकोमेट्री) में तत्वों के मोल(इकाई) अनुपात के लिए भी किया जाता है। उदाहरण के लिए, H . में हाइड्रोजन और ऑक्सीजन की स्टोइकोमेट्री2हे 2:1 है। स्टोइकियोमेट्रिक यौगिकों में, ग्राम अणुक अनुपात पूर्णांक होते हैं।
उत्पाद की मात्रा निर्धारित करना
स्टोइकोमेट्री का उपयोग किसी अभिक्रिया द्वारा प्राप्त उत्पाद की मात्रा को खोजने के लिए भी किया जा सकता है। यदि सिल्वर नाइट्रेट(AgNO3) के जलीय घोल में ठोस तांबे(Cu) का एक टुकड़ा मिलाया जाता है, चांदी(Ag) को जलीय कॉपर नाइट्रेट बनाने वाली एकल विस्थापन अभिक्रिया में बदल दिया जाएगा। यदि अतिरिक्त सिल्वर नाइट्रेट के विलयन में 16.00 ग्राम Cu मिला दिया जाए तो कितनी चाँदी उत्पन्न होती है?
निम्नलिखित चरणों का उपयोग किया जाएगा:
- समीकरण लिखें और संतुलित करें
- द्रव्यमान से मोल: Cu के ग्राम को Cu के मोल में बदलें
- मोल अनुपात: Cu के मोल को उत्पादित Ag के मोल में बदलें
- तिल से द्रव्यमान: Ag के मोल को उत्पादित Ag के ग्राम में बदलें
पूर्ण संतुलित समीकरण होगा:
- Cu + 2 AgNO
3 → Cu(NO
3)
2 + 2 Ag
द्रव्यमान से मोल चरण के लिए, तांबे के द्रव्यमान(16.00 g) को तांबे के द्रव्यमान को उसके आणविक द्रव्यमान: 63.55 g/मोल से विभाजित करके तांबे के मोल में परिवर्तित किया जाएगा।
अब जब मोल में Cu की मात्रा(0.2518) मिल गई है, तो मोल अनुपात सेट कर सकते हैं। यह संतुलित समीकरण में गुणांकों को देखकर पाया जाता है: Cu और Ag 1:2 के अनुपात में हैं।
अब जबकि उत्पादित Ag का मोल 0.5036 मोल है, तो हम अंतिम उत्तर पर आने के लिए इस मात्रा को उत्पादित Ag के ग्राम में बदल देते हैं:
गणना के इस सेट को आगे एक चरण में संघनित किया जा सकता है:
अन्य उदाहरण
प्रोपेन(C3H8) की ऑक्सीजन(O2) के साथ अभिक्रिया के लिए संतुलित रासायनिक समीकरण है:
- C3H8 + 5 O2 → 3 CO2 + 4 H2O
पानी का द्रव्यमान यदि 120 ग्राम प्रोपेन(C3H8) अधिक ऑक्सीजन में जलाया जाता है तो
स्टोइकियोमेट्रिक अनुपात
स्टोइकोमेट्री का उपयोग एक रासायनिक अभिक्रिया में अन्य अभिकारक के साथ पूरी तरह से अभिक्रिया करने के लिए एक अभिकारक की सही मात्रा को खोजने के लिए भी किया जाता है - अर्थात, स्टोइकियोमेट्रिक मात्रा जिसके परिणामस्वरूप अभिक्रिया होने पर कोई बचे हुए अभिकारक नहीं होंगे। थर्माइट अभिक्रिया का उपयोग करते हुए एक उदाहरण नीचे दिखाया गया है,
- Fe2O3 + 2 Al → Al2O3 + 2 Fe
यह समीकरण दर्शाता है कि 1 मोल आयरन ऑक्साइड(III) और 2 मोल एल्युमिनियम से 1 मोल एल्युमिनियम ऑक्साइड और 2 मोल आयरन पैदा होगा। तो, 85.0 ग्राम के साथ पूरी तरह से अभिक्रिया करने के लिए आयरन ऑक्साइड(0.532 मोल), 28.7g(1.06 मोल) एल्युमिनियम की आवश्यकता होती है।
सीमित अभिकर्मक और प्रतिशत उत्पाद
सीमित अभिकर्मक वह अभिकर्मक है जो बनने वाले उत्पाद की मात्रा को सीमित करता है और अभिक्रिया पूरी होने पर पूरी तरह से उपभोग होता है। अतिरिक्त अभिकारक वह अभिकारक है जो एक बार सीमित अभिकारक के समाप्त होने के कारण अभिक्रिया बंद हो जाने के बाद बचा रहता है।
ऑक्सीजन(O2) में भर्जित लेड सल्फाइड(PbS) के समीकरण पर विचार करें लेड ऑक्साइड(PbO) और सल्फर डाइऑक्साइड(SO2) का उत्पादन करने के लिए:
- 2 PbS + 3 O
2 → 2 PbO + 2 SO
2
लेड ऑक्साइड की सैद्धांतिक उत्पादन निर्धारित करने के लिए यदि एक खुले कंटेनर में 200.0 ग्राम लेड सल्फाइड और 200.0 ग्राम ऑक्सीजन गर्म किया जाता है:
चूंकि PbS के 200.0 ग्राम के लिए PbO की कम मात्रा का उत्पादन होता है, यह स्पष्ट है कि PbS सीमित अभिकर्मक है।
वास्तव में, वास्तविक उत्पादन स्टोइकियोमेट्रिक रूप से परिकलित सैद्धांतिक उत्पादन के समान नहीं है। प्रतिशत उत्पादन, तब, निम्नलिखित समीकरण में व्यक्त की जाती है:
यदि 170.0 ग्राम लेड(II) ऑक्साइड प्राप्त होता है, तो प्रतिशत उत्पादन की गणना निम्नानुसार की जाएगी:
उदाहरण
निम्नलिखित अभिक्रिया पर विचार करें, जिसमें आयरन क्लोराइड हाइड्रोजन सल्फाइड के साथ आयरन सल्फाइड और हाईड्रोजन क्लोराईड का उत्पादन करने के लिए अभिक्रिया करता है:
- 2 FeCl3 + 3 H2S → Fe2S3 + 6 HCl
इस अभिक्रिया के लिए स्टोइकियोमेट्रिक द्रव्यमान हैं:
- 324.41g FeCl3, 102.25g H2S, 207.89g Fe2S3, 218.77g HCl
मान लीजिए 90.0 ग्राम FeCl3 52.0 ग्राम H2S के साथ अभिक्रिया करता है। सीमित अभिकर्मक और अभिक्रिया द्वारा उत्पादित HCl के द्रव्यमान को खोजने के लिए, हम उपरोक्त मात्रा को 90/324.41 के कारक से बदलते हैं और निम्नलिखित मात्रा प्राप्त करते हैं:
- 90.00g FeCl3, 28.37g H2S, 57.67g Fe2S3, 60.69g HCl
सीमित अभिकारक या अभिकर्मक FeCl3 है, चूंकि इसका सभी 90.00 ग्राम उपयोग किया जाता है जबकि केवल 28.37 ग्राम H2S का सेवन किया जाता है। इस प्रकार, 52.0 - 28.4 = 23.6g H2S अधिक छोड़ दिया जाता है। उत्पादित HCl का द्रव्यमान 60.7 ग्राम है।
नोट: अभिक्रिया के स्टोइकोमेट्री को देखकर, FeCl3 का अनुमान लगाया जा सकता है, सीमित अभिकारक होने के कारण; तीन गुना अधिक FeCl3 प्रयोग किया जाता है(324 ग्राम/102 ग्राम)।
प्रतिस्पर्धी अभिक्रियाओं में विभिन्न स्टोइकोमेट्री
प्रायः, एक ही प्रारंभिक सामग्री को देखते हुए एक से अधिक अभिक्रिया संभव है। अभिक्रियाएं उनके स्टोइकोमेट्री में भिन्न हो सकती हैं। उदाहरण के लिए, बेंजीन का मेथिलिकरण(C .)6H6), एल्यूमीनियम क्लोराइड का उपयोग करके एक फ्राइडल-शिल्प अभिक्रिया के माध्यम से|AlCl3उत्प्रेरक के रूप में, एकल मिथाइलेटेड(C .) का उत्पादन कर सकता है6H5चौधरी3), दोगुना मिथाइलेटेड(C .)6H4(सीएच3)2), या फिर भी अत्यधिक मिथाइलेटेड(C .)6H6−n(सीएच3)n) उत्पाद, जैसा कि निम्नलिखित उदाहरण में दिखाया गया है,
- सी6H6 + सीएच3सीएल → सी6H5चौधरी3 + HCl
- सी6H6 + 2 सीएच3सीएल → सी6H4(सीएच3)2 + 2 HCl
- सी6H6 + एन सीएच3सीएल → सी6H6−n(सीएच3)n + एन HCl
इस उदाहरण में, कौन सी अभिक्रिया होती है, इसे अभिकारकों की सापेक्ष सांद्रता द्वारा नियंत्रित किया जाता है।
स्टोइकियोमेट्रिक गुणांक और स्टोइकियोमेट्रिक संख्या
सामान्य शब्दों में, किसी दिए गए घटक का स्टोइकियोमेट्रिक गुणांक अणुओं और/या सूत्र इकाइयों की संख्या है जो लिखित रूप में अभिक्रिया में भाग लेते हैं। एक संबंधित अवधारणा स्टोइकियोमेट्रिक संख्या(आईयूपीएसी नामकरण का उपयोग करके) है, जिसमें स्टोइकियोमेट्रिक गुणांक को सभी उत्पादों के लिए +1 और सभी अभिकारकों के लिए -1 से गुणा किया जाता है।
उदाहरण के लिए, अभिक्रिया में CH4 + 2 O2 → CO2 + 2 H2O, सीएच . की स्टोइकियोमेट्रिक संख्या4 −1 है, O . की स्टोइकोमीट्रिक संख्या2 -2 है, के लिए CO2 यह +1 होगा और H . के लिए2ओ यह +2 है।
अधिक तकनीकी रूप से सटीक शब्दों में, ith घटक की रासायनिक अभिक्रिया प्रणाली में स्टोइकोमीट्रिक संख्या को परिभाषित किया गया है:
या
कहाँ पे i, और . के अणुओं की संख्या है प्रगति चर या अभिक्रिया की सीमा है।[5][6] स्टोइकियोमेट्रिक संख्या उस डिग्री का प्रतिनिधित्व करता है जिस तक एक रासायनिक प्रजाति अभिक्रिया में भाग लेती है। सम्मेलन अभिकारकों(जो उपभोग किया जाता है) और सकारात्मक वाले उत्पादों को ऋणात्मक संख्या प्रदान करने के लिए है, इस सम्मेलन के अनुरूप है कि अभिक्रिया की सीमा में वृद्धि अभिकारकों से उत्पादों की ओर संरचना को स्थानांतरित करने के अनुरूप होगी। हालांकि, किसी भी अभिक्रिया को विपरीत दिशा में जाने के रूप में देखा जा सकता है, और उस दृष्टिकोण में, सिस्टम की गिब्स मुक्त ऊर्जा को कम करने के लिए नकारात्मक दिशा में बदल जाएगा। अभिक्रिया वास्तव में मनमाने ढंग से चयनित आगे की दिशा में जाएगी या नहीं यह किसी भी समय मौजूद रासायनिक पदार्थ की मात्रा पर निर्भर करता है, जो रासायनिक गतिकी और थर्मोडायनामिक संतुलन को निर्धारित करता है, अर्थात, रासायनिक संतुलन दाईं ओर है या बाईं ओर है प्रारंभिक अवस्था,
अभिक्रिया तंत्र में, प्रत्येक चरण के लिए स्टोइकियोमेट्रिक गुणांक हमेशा पूर्णांक होते हैं, क्योंकि प्राथमिक अभिक्रियाओं में हमेशा पूरे अणु सम्मिलित होते हैं। यदि कोई समग्र अभिक्रिया के समग्र प्रतिनिधित्व का उपयोग करता है, तो कुछ तर्कसंगत संख्या अंश(गणित) हो सकते हैं। प्रायः रासायनिक प्रजातियां मौजूद होती हैं जो अभिक्रिया में भाग नहीं लेती हैं; इसलिए उनके स्टोइकोमीट्रिक गुणांक शून्य हैं। किसी भी रासायनिक प्रजाति को पुनर्जीवित किया जाता है, जैसे कि उत्प्रेरक , में भी शून्य का स्टोइकियोमेट्रिक गुणांक होता है।
सबसे सरल संभव मामला एक आइसोमराइज़ेशन है
- ए → बी
जिसमें νB = 1 चूंकि अभिक्रिया होने पर हर बार B का एक अणु उत्पन्न होता है, जबकि νA = −1 चूँकि A का एक अणु आवश्यक रूप से भस्म हो जाता है। किसी भी रासायनिक अभिक्रिया में, न केवल द्रव्यमान का कुल संरक्षण होता है, बल्कि प्रत्येक आवर्त सारणी के परमाणु ओं की संख्या भी संरक्षित होती है, और यह स्टोइकियोमेट्रिक गुणांक के संभावित मूल्यों पर संबंधित बाधाओं को लगाता है।
सामान्यतः किसी भी प्रकृति अभिक्रिया प्रणाली में एक साथ कई अभिक्रियाएं होती हैं, जिसमें जीव विज्ञान भी सम्मिलित है। चूंकि कोई भी रासायनिक घटक एक साथ कई अभिक्रियाओं में भाग ले सकता है, kth अभिक्रिया में ith घटक की स्टोइकियोमेट्रिक संख्या को इस प्रकार परिभाषित किया जाता है
ताकि ith घटक की मात्रा में कुल(अंतर) परिवर्तन हो
अभिक्रिया के विस्तार संरचनागत परिवर्तन का प्रतिनिधित्व करने का सबसे स्पष्ट और सबसे स्पष्ट तरीका प्रदान करते हैं, हालांकि उनका अभी तक व्यापक रूप से उपयोग नहीं किया गया है।
जटिल अभिक्रिया प्रणालियों के साथ, मौजूद रसायनों की मात्रा के संदर्भ में अभिक्रिया प्रणाली के प्रतिनिधित्व दोनों पर विचार करना प्रायः उपयोगी होता है { Ni }(ऊष्मप्रवैगिकी चर), और वास्तविक संरचना के संदर्भ में प्रतिनिधित्व स्वतंत्रता की डिग्री(भौतिकी और रसायन विज्ञान) , जैसा कि अभिक्रिया के विस्तार द्वारा व्यक्त किया गया है { ξk }. एक सदिश समष्टि से परिमाणों को व्यक्त करने वाले सदिश में परिवर्तन एक आयताकार मैट्रिक्स(गणित) का उपयोग करता है जिसके तत्व स्टोइकोमीट्रिक संख्याएं हैं [ νi k ].
किसी भी . के लिए चरम मूल्य kतब होता है जब अग्र अभिक्रिया के लिए अभिकारकों में से पहला समाप्त हो जाता है; या उत्पादों में से पहला समाप्त हो जाता है यदि अभिक्रिया को विपरीत दिशा में धकेलने के रूप में देखा जाता है। यह रिएक्शन सिंप्लेक्स , कंपोजिशन स्पेस में एक हाइपरप्लेन , या एन-स्पेस पर विशुद्ध रूप से गतिकी प्रतिबंध है, जिसकी आयाम ीता रैखिक स्वतंत्रता की संख्या के बराबर होती है।रैखिक-स्वतंत्र रासायनिक अभिक्रियाएं। यह आवश्यक रूप से रासायनिक घटकों की संख्या से कम है, क्योंकि प्रत्येक अभिक्रिया कम से कम दो रसायनों के बीच संबंध को प्रकट करती है। हाइपरप्लेन का सुलभ क्षेत्र वास्तव में मौजूद प्रत्येक रासायनिक प्रजाति की मात्रा पर निर्भर करता है, एक आकस्मिक तथ्य। अलग-अलग ऐसी मात्राएँ अलग-अलग हाइपरप्लेन भी उत्पन्न कर सकती हैं, सभी समान बीजीय स्टोइकोमेट्री साझा करते हैं।
रासायनिक कैनेटीक्स और थर्मोडायनामिक संतुलन के सिद्धांतों के अनुसार, प्रत्येक रासायनिक अभिक्रिया कम से कम कुछ हद तक प्रतिवर्ती होती है, ताकि प्रत्येक संतुलन बिंदु सिम्प्लेक्स का एक आंतरिक(टोपोलॉजी) होना चाहिए। एक परिणाम के रूप में, s के लिए एक्स्ट्रेमा तब तक नहीं होगा जब तक कि कुछ उत्पादों की शून्य प्रारंभिक मात्रा के साथ एक प्रयोगात्मक प्रणाली तैयार नहीं की जाती है।
शारीरिक रूप से स्वतंत्र अभिक्रियाओं की संख्या रासायनिक घटकों की संख्या से भी अधिक हो सकती है, और विभिन्न अभिक्रिया तंत्रों पर निर्भर करती है। उदाहरण के लिए, उपरोक्त समरूपता के लिए दो(या अधिक) अभिक्रिया पथ हो सकते हैं। एक उत्प्रेरक की उपस्थिति में अभिक्रिया अपने आप हो सकती है, लेकिन तेज और विभिन्न मध्यवर्ती के साथ।
(आयाम रहित) इकाइयों को अणु या मोल(इकाई) माना जा सकता है। मोल्स का सबसे अधिक उपयोग किया जाता है, लेकिन यह अणुओं के संदर्भ में वृद्धिशील रासायनिक अभिक्रियाओं को चित्रित करने के लिए अधिक सूचक है। Avogadro स्थिरांक से विभाजित करके Ns और ξs को मोलर इकाइयों में घटाया जाता है। जबकि आयामी द्रव्यमान इकाइयों का उपयोग किया जा सकता है, पूर्णांकों के बारे में टिप्पणियां अब लागू नहीं होती हैं।
स्टोइकोमेट्री मैट्रिक्स
जटिल अभिक्रियाओं में, स्टोइकोमेट्री को प्रायः अधिक कॉम्पैक्ट रूप में दर्शाया जाता है जिसे स्टोइकोमेट्री मैट्रिक्स कहा जाता है। स्टोइकोमेट्री मैट्रिक्स को प्रतीक एन द्वारा दर्शाया गया है।[7][8][9] यदि किसी अभिक्रिया नेटवर्क में n अभिक्रियाएँ और m भाग लेने वाली आणविक प्रजातियाँ हैं तो स्टोइकोमेट्री मैट्रिक्स में संगत m पंक्तियाँ और n कॉलम होंगे।
उदाहरण के लिए, नीचे दिखाए गए अभिक्रियाओं की प्रणाली पर विचार करें:
- एस1 → एस2
- 5 एस3 + एस2 → 4 एस3 + 2 एस2
- एस3 → एस4
- एस4 → एस5
इस प्रणाली में चार अभिक्रियाएं और पांच अलग-अलग आणविक प्रजातियां सम्मिलित हैं। इस प्रणाली के लिए स्टोइकोमेट्री मैट्रिक्स को इस प्रकार लिखा जा सकता है:
जहाँ पंक्तियाँ S . से मेल खाती हैं1, एस2, एस3, एस4 और5, क्रमश। ध्यान दें कि एक अभिक्रिया योजना को एक स्टोइकोमेट्री मैट्रिक्स में परिवर्तित करने की प्रक्रिया एक हानिकारक परिवर्तन हो सकती है: उदाहरण के लिए, दूसरी अभिक्रिया में स्टोइकोमेट्री मैट्रिक्स में सम्मिलित होने पर सरल हो जाती है। इसका मतलब यह है कि स्टोइकोमेट्री मैट्रिक्स से मूल अभिक्रिया योजना को पुनर्प्राप्त करना हमेशा संभव नहीं होता है।
आणविक प्रजातियों के परिवर्तन की दरों का वर्णन करते हुए एक कॉम्पैक्ट समीकरण बनाने के लिए प्रायः स्टोइकोमेट्री मैट्रिक्स को दर वेक्टर, वी, और प्रजाति वेक्टर, एक्स के साथ जोड़ा जाता है:
गैस स्टोइकोमेट्री
गैस स्टोइकोमेट्री एक रासायनिक अभिक्रिया में अभिकारकों और उत्पादों के बीच मात्रा त्मक संबंध(अनुपात) है जो गैसों का उत्पादन करने वाली अभिक्रियाओं के साथ होता है। गैस स्टोइकोमेट्री तब लागू होती है जब उत्पादित गैसों को आदर्श गैस माना जाता है, और गैसों का तापमान, दबाव और आयतन सभी ज्ञात होते हैं। इन गणनाओं के लिए आदर्श गैस नियम का उपयोग किया जाता है। प्रायः, लेकिन हमेशा नहीं, मानक तापमान और दबाव(एसटीपी) को 0 डिग्री सेल्सियस और 1 बार के रूप में लिया जाता है और गैस स्टोइकियोमेट्रिक गणना के लिए शर्तों के रूप में उपयोग किया जाता है।
गैस स्टोइकोमेट्री गणना अज्ञात मात्रा या गैसीय उत्पाद या अभिकारक के द्रव्यमान के लिए हल करती है। उदाहरण के लिए, यदि हम गैसीय NO . के आयतन की गणना करना चाहते हैं2 100 ग्राम NH . के दहन से उत्पन्न3, अभिक्रिया से:
- 4 NH3 (g) + 7 O2 (g) → 4 NO2 (g) + 6 H2O (l)
हम निम्नलिखित गणना करेंगे:
NH . का 1:1 मोलर अनुपात होता है3 नहीं करने के लिए2 उपरोक्त संतुलित दहन अभिक्रिया में, इसलिए NO . का 5.871 मोल2 गठन किया जाएगा। हम 0°C(273.15 K) और 1 वायुमंडल के आयतन को R = 0.08206 L·atm·K के गैस स्थिरांक का उपयोग करके हल करने के लिए आदर्श गैस नियम का उपयोग करेंगे।-1 मोल-1:
गैस स्टोइकोमेट्री में प्रायः उस गैस के घनत्व को देखते हुए, गैस के ग्राम अणुक द्रव्यमान को जानना सम्मिलित होता है। आदर्श गैस के घनत्व और ग्राम अणुक द्रव्यमान के बीच संबंध प्राप्त करने के लिए आदर्श गैस नियम को फिर से व्यवस्थित किया जा सकता है:
- तथा
और इस तरह:
कहाँ पे:
- P = निरपेक्ष गैस दाब
- वी = गैस की मात्रा
- n = राशि(तिल(इकाई) में मापा जाता है)
- R = सार्वभौमिक आदर्श गैस नियम स्थिरांक
- T = पूर्ण गैस तापमान
- ρ = T और P . पर गैस का घनत्व
- m = गैस का द्रव्यमान
- M = गैस का मोलर द्रव्यमान
सामान्य ईंधनों का वायु-से-ईंधन अनुपात स्टोइकोमीट्रिक
दहन अभिक्रिया में, ऑक्सीजन ईंधन के साथ अभिक्रिया करता है, और वह बिंदु जहां वास्तव में सभी ऑक्सीजन की उपभोग होती है और सभी ईंधन को जला दिया जाता है, जिसे स्टोइकियोमेट्रिक बिंदु के रूप में परिभाषित किया जाता है। अधिक ऑक्सीजन(ओवरस्टोइकियोमेट्रिक दहन) के साथ, इसमें से कुछ अप्राप्य रहता है। इसी तरह, यदि पर्याप्त ऑक्सीजन की कमी के कारण दहन अधूरा है, तो ईंधन अप्राप्य रहता है।(अप्रत्यक्ष ईंधन धीमी दहन या ईंधन और ऑक्सीजन के अपर्याप्त मिश्रण के कारण भी रह सकता है - यह स्टोइकोमेट्री के कारण नहीं है)। विभिन्न हाइड्रोकार्बन ईंधन में कार्बन, हाइड्रोजन और अन्य तत्वों की अलग-अलग सामग्री होती है, इस प्रकार उनकी स्टोइकोमेट्री भिन्न होती है।
ध्यान दें कि ऑक्सीजन हवा के आयतन का केवल 20.95% और इसके द्रव्यमान का केवल 23.20% बनाता है।[10] हवा में अक्रिय गैसों के उच्च अनुपात के कारण, नीचे सूचीबद्ध वायु-ईंधन अनुपात बराबर ऑक्सीजन-ईंधन अनुपात से बहुत अधिक है।
| Fuel | Ratio by mass [11] | Ratio by volume [12] | Percent fuel by mass | Main reaction |
|---|---|---|---|---|
| Gasoline | 14.7 : 1 | — | 6.8% | 2 C 8H 18 + 25 O 2 → 16 CO 2 + 18 H 2O |
| Natural gas | 17.2 : 1 | 9.7 : 1 | 5.8% | CH 4 + 2 O 2 → CO 2 + 2 H 2O |
| Propane(LP) | 15.67 : 1 | 23.9 : 1 | 6.45% | C 3H 8 + 5 O 2 → 3 CO 2 + 4 H 2O |
| Ethanol | 9 : 1 | — | 11.1% | C 2H 6O + 3 O 2 → 2 CO 2 + 3 H 2O |
| Methanol | 6.47 : 1 | — | 15.6% | 2 CH 4O + 3 O 2 → 2 CO 2 + 4 H 2O |
| n-Butanol | 11.2 : 1 | — | 8.2% | C 4H 10O + 6 O 2 → 4 CO 2 + 5 H 2O |
| Hydrogen | 34.3 : 1 | 2.39 : 1 | 2.9% | 2 H 2 + O 2 → 2 H 2O |
| Diesel | 14.5 : 1 | — | 6.8% | 2 C 12H 26 + 37 O 2 → 24 CO 2 + 26 H 2O |
| Methane | 17.19 : 1 | 9.52 : 1 | 5.5% | CH 4 + 2 O 2 → CO 2 + 2 H 2O |
| Acetylene | 13.26 : 1 | 11.92 : 1 | 7.0% | 2 C 2H 2 + 5 O 2 → 4 CO 2 + 2 H 2O |
| Ethane | 16.07 : 1 | 16.68 : 1 | 5.9% | 2 C 2H 6 + 7 O 2 → 4 CO 2 + 6 H 2O |
| Butane | 15.44 : 1 | 30.98 : 1 | 6.1% | 2 C 4H 10 + 13 O 2 → 8 CO 2 + 10 H 2O |
| Pentane | 15.31 : 1 | 38.13 : 1 | 6.1% | C 5H 12 + 8 O 2 → 5 CO 2 + 6 H 2O |
गैसोलीन इंजन स्टोइकियोमेट्रिक एयर-टू-फ्यूल अनुपात में चल सकते हैं, क्योंकि गैसोलीन काफी अस्थिर होता है और इग्निशन से पहले हवा के साथ मिश्रित(स्प्रे या कार्बोरेटेड) होता है। डीजल इंजन, इसके विपरीत, सरल स्टोइकोमेट्री की तुलना में अधिक हवा उपलब्ध होने के साथ दुबला चलते हैं। डीजल ईंधन कम अस्थिर होता है और इसे इंजेक्ट करते ही प्रभावी रूप से जला दिया जाता है।[13]
यह भी देखें
संदर्भ
- ↑ Richter, J.B. (1792). स्टोइकोमेट्री के मूल सिद्धांत ... (3 खंड में) [Rudiments of Stoichiometry …] (in Deutsch). Vol. 1. Breslau and Hirschberg, (Germany): Johann Friedrich Korn der Aeltere. p. 121. From p. 121: "Die Stöchyometrie (Stöchyometria) ist die Wissenschaft die quantitativen oder Massenverhältnisse … zu messen, in welchen die chemischen Elemente … gegen einander stehen." (Stoichiometry (stoichiometria) is the science of measuring the quantitative or mass relations in which the chemical "elements" exist in relation to each other.) [Note: On pp. 3–7, Richter explains that an "element" is a pure substance, and that a "chemical element" (chymisches Element (Elementum chymicum)) is a substance that cannot be resolved into dissimilar substances by known physical or chemical means. Thus, for example, aluminium oxide was a "chemical element" because in Richter's time, it couldn't be resolved further into its component elements.]
- ↑ What’s in a Name? Amount of Substance, Chemical Amount, and Stoichiometric Amount Carmen J. Giunta Journal of Chemical Education 2016 93 (4), 583-586 doi:10.1021/acs.jchemed.5b00690
- ↑ IUPAC, Compendium of Chemical Terminology, 2nd ed. (the "Gold Book") (1997). Online corrected version: (2006–) "stoichiometric number, ν". doi:10.1351/goldbook.S06025
- ↑ Nijmeh, Joseph; Tye, Mark (2 October 2013). "Stoichiometry और संतुलन प्रतिक्रियाएं". LibreTexts. Retrieved 5 May 2021.
- ↑ Prigogine & Defay, p. 18; Prigogine, pp. 4–7; Guggenheim, p. 37 & 62
- ↑ IUPAC, Compendium of Chemical Terminology, 2nd ed. (the "Gold Book") (1997). Online corrected version: (2006–) "extent of reaction, ξ". doi:10.1351/goldbook.E02283
- ↑ Ghaderi, Susan; Haraldsdóttir, Hulda S.; Ahookhosh, Masoud; Arreckx, Sylvain; Fleming, Ronan M.T. (August 2020). "एक स्टोइकोमेट्रिक मैट्रिक्स का संरचनात्मक संरक्षित आंशिक विभाजन". Journal of Theoretical Biology. 499: 110276. Bibcode:2020JThBi.49910276G. doi:10.1016/j.jtbi.2020.110276. PMID 32333975.
- ↑ Hofmeyr, Jan-hendrik S. (2001). "संक्षेप में चयापचय नियंत्रण विश्लेषण". In Proceedings of the 2 Nd International Conference on Systems Biology: 291–300. CiteSeerX 10.1.1.324.922.
- ↑ Reder, Christine (21 November 1988). "चयापचय नियंत्रण सिद्धांत: एक संरचनात्मक दृष्टिकोण". Journal of Theoretical Biology. 135 (2): 175–201. Bibcode:1988JThBi.135..175R. doi:10.1016/s0022-5193(88)80073-0. PMID 3267767.
- ↑ "यूनिवर्सल इंडस्ट्रियल गैसेस, इंक: वायु की संरचना - वायु के घटक और गुण - "वायु क्या है?" के उत्तर - "हवा किससे बनी है?" - "वायु उत्पाद क्या हैं और इनका उपयोग किस लिए किया जाता है?"".
- ↑ John B. Heywood: "Internal Combustion Engine Fundamentals page 915", 1988
- ↑ North American Mfg. Co.: "North American Combustion Handbook", 1952
- ↑ "वायु-ईंधन अनुपात, लैम्ब्डा और इंजन प्रदर्शन" (in English). Retrieved 2019-05-31.
- Zumdahl, Steven S. Chemical Principles. Houghton Mifflin, New York, 2005, pp 148–150.
- Internal Combustion Engine Fundamentals, John B. Heywood
बाहरी संबंध
| Library resources about Stoichiometry |
- Engine Combustion primer from the University of Plymouth
- Free स्टोइकियोमेस्ट्री Tutorials from Carnegie Mellon's ChemCollective
- स्टोइकियोमेस्ट्री Add-In for Microsoft Excel for calculation of मोलecular weights, reaction coëfficients and स्टोइकियोमेस्ट्री.
- Reaction स्टोइकियोमेस्ट्री Calculator a comprehensive free online reaction स्टोइकियोमेस्ट्री calculator.
- स्टोइकियोमेस्ट्री Plus a स्टोइकियोमेस्ट्री calculator and more for Android.