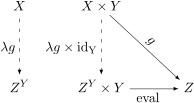घातीय ऑब्जेक्ट: Difference between revisions
No edit summary |
No edit summary |
||
| Line 6: | Line 6: | ||
== परिभाषा == | == परिभाषा == | ||
मान लीजिये <math>\mathbf{C}</math> एक श्रेणी हो, और <math>Z</math> तथा <math>Y</math> <math>\mathbf{C}</math> की वस्तु (श्रेणी सिद्धांत) हो, और <math>\mathbf{C}</math> के पास <math>Y</math> के साथ सभी बाइनरी उत्पाद (श्रेणी सिद्धांत) हैं. एक वस्तु <math display="inline">Z^Y</math> एक साथ एक आकारिकी के साथ <math display="inline">\mathrm{eval}\colon (Z^Y \times Y) \to Z</math> किसी भी वस्तु के लिए एक चरघातीय वस्तु है किसी वस्तु के लिये <math>X</math> और <math display="inline">g \colon X\times Y \to Z</math> एक अद्वितीय आकारिकी <math display="inline">\lambda g\colon X\to Z^Y</math> (का स्थानांतरण कहा जाता है <math>g</math>) है, जैसे कि निम्न आरेख क्रमविनिमेय आरेख में बदलना: | |||
[[File:ExponentialObject-01.svg|center|घातीय वस्तु की सार्वभौमिक संपत्ति]] | [[File:ExponentialObject-01.svg|center|घातीय वस्तु की सार्वभौमिक संपत्ति]]प्रत्येक <math>g</math> के लिए एक अद्वितीय <math>\lambda g</math> का यह कार्य होम-सेट का एक समरूपता (आक्षेप) <math display="inline">\mathrm{Hom}(X\times Y,Z) \cong \mathrm{Hom}(X,Z^Y)</math> को स्थापित करता है | ||
यदि <math display="inline">Z^Y</math>सभी वस्तुओं के लिए | यदि <math display="inline">Z^Y</math>सभी वस्तुओं के लिए उपस्थित है <math>Z, Y</math> में <math>\mathbf{C}</math>, फिर गुणन <math>(-)^Y \colon \mathbf{C}\to \mathbf{C}</math> द्वारा वस्तुओं पर परिभाषित <math>Z \mapsto Z^Y</math> और तीर पर <math>(f\colon X\to Z) \mapsto (f^Y\colon X^Y \to Z^Y)</math>, उत्पाद फ़ंक्टर के लिए एक सही आसन्न है <math>-\times Y</math>. इस कारण से, आकारिकी <math>\lambda g</math> तथा <math>g</math> कभी-कभी एक दूसरे के चरघातांकी संलग्नक कहलाते हैं।<ref name="Goldblatt">{{cite book|title=टोपोई: तर्क का श्रेणीबद्ध विश्लेषण|publisher=[[North-Holland Publishing Company|North-Holland]]|year=1984|isbn=978-0-444-86711-7|edition=Revised|series=Studies in Logic and the Foundations of Mathematics #98|page=72|chapter=Chapter 3: Arrows instead of epsilon|last1=Goldblatt|first1=Robert|author-link=Robert Goldblatt}}</ref> | ||
| Line 14: | Line 14: | ||
वैकल्पिक रूप से, घातीय वस्तु को समीकरणों के माध्यम से परिभाषित किया जा सकता है: | वैकल्पिक रूप से, घातीय वस्तु को समीकरणों के माध्यम से परिभाषित किया जा सकता है: | ||
* | * उपस्थितगी में <math>\lambda g</math> ऑपरेशन के अस्तित्व की गारंटी है <math>\lambda - </math>. | ||
* उपरोक्त आरेखों की क्रमविनिमेयता समानता द्वारा गारंटीकृत है <math>\forall g \colon X \times Y \to Z,\ \mathrm{eval} \circ (\lambda g \times \mathrm{id}_Y) = g</math>. | * उपरोक्त आरेखों की क्रमविनिमेयता समानता द्वारा गारंटीकृत है <math>\forall g \colon X \times Y \to Z,\ \mathrm{eval} \circ (\lambda g \times \mathrm{id}_Y) = g</math>. | ||
* की विशिष्टता <math>\lambda g</math> समानता की गारंटी है <math>\forall h \colon X \to Z^Y, \ \lambda (\mathrm{eval} \circ (h \times \mathrm{id}_Y)) = h</math>. | * की विशिष्टता <math>\lambda g</math> समानता की गारंटी है <math>\forall h \colon X \to Z^Y, \ \lambda (\mathrm{eval} \circ (h \times \mathrm{id}_Y)) = h</math>. | ||
| Line 28: | Line 28: | ||
एक हेटिंग बीजगणित <math>H</math> केवल एक बंधी हुई जाली (क्रम) है जिसमें सभी घातीय वस्तुएँ हैं। हेटिंग निहितार्थ, <math>Y \Rightarrow Z</math>, के लिए एक वैकल्पिक संकेतन है <math>Z^Y</math>. उपरोक्त संयोजन परिणाम निहितार्थ में अनुवाद करते हैं (<math>\Rightarrow : H \times H \to H</math>) शामिल होने और मिलने के ठीक बगल में होना (<math>\wedge : H \times H \to H</math>). इस संयोजन को इस प्रकार लिखा जा सकता है <math>(- \wedge Y) \dashv (Y \Rightarrow -)</math>, या अधिक पूरी तरह से: | एक हेटिंग बीजगणित <math>H</math> केवल एक बंधी हुई जाली (क्रम) है जिसमें सभी घातीय वस्तुएँ हैं। हेटिंग निहितार्थ, <math>Y \Rightarrow Z</math>, के लिए एक वैकल्पिक संकेतन है <math>Z^Y</math>. उपरोक्त संयोजन परिणाम निहितार्थ में अनुवाद करते हैं (<math>\Rightarrow : H \times H \to H</math>) शामिल होने और मिलने के ठीक बगल में होना (<math>\wedge : H \times H \to H</math>). इस संयोजन को इस प्रकार लिखा जा सकता है <math>(- \wedge Y) \dashv (Y \Rightarrow -)</math>, या अधिक पूरी तरह से: | ||
<math display="block">(- \wedge Y): H \stackrel {\longrightarrow} {\underset {\longleftarrow}{\top}} H: (Y \Rightarrow -)</math> | <math display="block">(- \wedge Y): H \stackrel {\longrightarrow} {\underset {\longleftarrow}{\top}} H: (Y \Rightarrow -)</math> | ||
टोपोलॉजिकल स्पेस की श्रेणी में, एक्सपोनेंशियल ऑब्जेक्ट <math>Z^Y</math> | टोपोलॉजिकल स्पेस की श्रेणी में, एक्सपोनेंशियल ऑब्जेक्ट <math>Z^Y</math> उपस्थित है बशर्ते कि <math>Y</math> एक स्थानीय रूप से कॉम्पैक्ट स्पेस हौसडॉर्फ स्पेस है। ऐसे में स्पेस <math>Z^Y</math> से सभी निरंतर कार्य (टोपोलॉजी) का सेट है <math>Y</math> प्रति <math>Z</math> कॉम्पैक्ट-ओपन टोपोलॉजी के साथ। मूल्यांकन मानचित्र सेट की श्रेणी के समान ही है; यह उपरोक्त टोपोलॉजी के साथ निरंतर है।<ref>[[Joseph J. Rotman]], ''An Introduction to Algebraic Topology'' (1988) Springer-Verlag {{ISBN|0-387-96678-1}} ''(See Chapter 11 for proof.)''</ref> यदि <math>Y</math> हॉसडॉर्फ स्थानीय रूप से कॉम्पैक्ट नहीं है, घातीय वस्तु उपस्थित नहीं हो सकती है (space <math>Z^Y</math> अभी भी उपस्थित है, लेकिन यह एक घातीय वस्तु होने में विफल हो सकता है क्योंकि मूल्यांकन कार्य निरंतर नहीं होना चाहिए)। इस कारण से टोपोलॉजिकल रिक्त स्थान की श्रेणी कार्तीय बंद होने में विफल रहती है। | ||
हालाँकि, स्थानीय रूप से कॉम्पैक्ट टोपोलॉजिकल स्पेस की श्रेणी कार्टेशियन बंद नहीं है, क्योंकि <math>Z^Y</math> स्थानीय रूप से कॉम्पैक्ट रिक्त स्थान के लिए स्थानीय रूप से कॉम्पैक्ट होने की आवश्यकता नहीं है <math>Z</math> तथा <math>Y</math>. रिक्त स्थान की एक कार्टेशियन बंद श्रेणी, उदाहरण के लिए, उपश्रेणी#Formal_definition द्वारा दी गई है, जो सघन रूप से उत्पन्न स्थान हौसडॉर्फ रिक्त स्थान द्वारा फैली हुई है। | हालाँकि, स्थानीय रूप से कॉम्पैक्ट टोपोलॉजिकल स्पेस की श्रेणी कार्टेशियन बंद नहीं है, क्योंकि <math>Z^Y</math> स्थानीय रूप से कॉम्पैक्ट रिक्त स्थान के लिए स्थानीय रूप से कॉम्पैक्ट होने की आवश्यकता नहीं है <math>Z</math> तथा <math>Y</math>. रिक्त स्थान की एक कार्टेशियन बंद श्रेणी, उदाहरण के लिए, उपश्रेणी#Formal_definition द्वारा दी गई है, जो सघन रूप से उत्पन्न स्थान हौसडॉर्फ रिक्त स्थान द्वारा फैली हुई है। | ||
Revision as of 18:41, 15 December 2022
गणित में, विशेष रूप से श्रेणी सिद्धांत में, एक घातीय वस्तु या मानचित्र वस्तु सेट सिद्धांत में एक कार्य स्थान का श्रेणीबद्ध सामान्यीकरण है। सभी परिमित उत्पादों और घातीय वस्तुओं वाली श्रेणियों को कार्तीय बंद श्रेणियां कहा जाता है। संलग्न उत्पादों के बिना श्रेणियाँ (जैसे शीर्ष की उपश्रेणियाँ) अभी भी एक घातीय नियम हो सकती हैं।[1][2]
परिभाषा
मान लीजिये एक श्रेणी हो, और तथा की वस्तु (श्रेणी सिद्धांत) हो, और के पास के साथ सभी बाइनरी उत्पाद (श्रेणी सिद्धांत) हैं. एक वस्तु एक साथ एक आकारिकी के साथ किसी भी वस्तु के लिए एक चरघातीय वस्तु है किसी वस्तु के लिये और एक अद्वितीय आकारिकी (का स्थानांतरण कहा जाता है ) है, जैसे कि निम्न आरेख क्रमविनिमेय आरेख में बदलना:
प्रत्येक के लिए एक अद्वितीय का यह कार्य होम-सेट का एक समरूपता (आक्षेप) को स्थापित करता है
यदि सभी वस्तुओं के लिए उपस्थित है में , फिर गुणन द्वारा वस्तुओं पर परिभाषित और तीर पर , उत्पाद फ़ंक्टर के लिए एक सही आसन्न है . इस कारण से, आकारिकी तथा कभी-कभी एक दूसरे के चरघातांकी संलग्नक कहलाते हैं।[3]
समान परिभाषा
वैकल्पिक रूप से, घातीय वस्तु को समीकरणों के माध्यम से परिभाषित किया जा सकता है:
- उपस्थितगी में ऑपरेशन के अस्तित्व की गारंटी है .
- उपरोक्त आरेखों की क्रमविनिमेयता समानता द्वारा गारंटीकृत है .
- की विशिष्टता समानता की गारंटी है .
सार्वभौमिक संपत्ति
घातीय उत्पाद फ़ंक्टर से एक सार्वभौमिक आकारिकी द्वारा दिया गया है वस्तु को . इस सार्वभौमिक रूपवाद में एक वस्तु होती है और एक रूपवाद .
उदाहरण
सेट की श्रेणी में, एक घातीय वस्तु सभी कार्यों (गणित) का सेट है .[4] नक्शा केवल वह लागू होता है, जो जोड़ी भेजता है प्रति . किसी भी नक्शे के लिए नक्शा का करी रूप है :
एक हेटिंग बीजगणित केवल एक बंधी हुई जाली (क्रम) है जिसमें सभी घातीय वस्तुएँ हैं। हेटिंग निहितार्थ, , के लिए एक वैकल्पिक संकेतन है . उपरोक्त संयोजन परिणाम निहितार्थ में अनुवाद करते हैं () शामिल होने और मिलने के ठीक बगल में होना (). इस संयोजन को इस प्रकार लिखा जा सकता है , या अधिक पूरी तरह से:
कार्यात्मक प्रोग्रामिंग भाषाओं में, रूपवाद अक्सर होता है| बुलाया , और वाक्य रचना अक्सर कार्य अनुप्रयोग # प्रतिनिधित्व | लिखा जाता है . रूपवाद यहाँ eval के साथ भ्रमित नहीं होना चाहिएevalकुछ प्रोग्रामिंग भाषाओं में कार्य करता है, जो उद्धृत भावों का मूल्यांकन करता है।
यह भी देखें
- बंद मोनोइडल श्रेणी
टिप्पणियाँ
- ↑ Exponential law for spaces at the nLab
- ↑ Convenient category of topological spaces at the nLab
- ↑ Goldblatt, Robert (1984). "Chapter 3: Arrows instead of epsilon". टोपोई: तर्क का श्रेणीबद्ध विश्लेषण. Studies in Logic and the Foundations of Mathematics #98 (Revised ed.). North-Holland. p. 72. ISBN 978-0-444-86711-7.
- ↑ Mac Lane, Saunders (1978). "Chapter 4: Adjoints". कामकाजी गणितज्ञ के लिए श्रेणियाँ. graduate texts in mathematics. Vol. 5 (2nd ed.). Springer-Verlag. p. 98. doi:10.1007/978-1-4757-4721-8_5. ISBN 978-0387984032.
- ↑ Joseph J. Rotman, An Introduction to Algebraic Topology (1988) Springer-Verlag ISBN 0-387-96678-1 (See Chapter 11 for proof.)
संदर्भ
- Adámek, Jiří; Horst Herrlich; George Strecker (2006) [1990]. Abstract and Concrete Categories (The Joy of Cats). John Wiley & Sons.
- Awodey, Steve (2010). "Chapter 6: Exponentials". Category theory. Oxford New York: Oxford University Press. ISBN 978-0199237180.
- Mac Lane, Saunders (1998). "Chapter 4: Adjoints". Categories for the working mathematician. New York: Springer. ISBN 978-0387984032.
इस पेज में लापता आंतरिक लिंक की सूची
बाहरी संबंध
- Interactive Web page which generates examples of exponential objects and other categorical constructions. Written by Jocelyn Paine.