फ्रैक्टल एंटीना: Difference between revisions

From Vigyanwiki
No edit summary
Line 24: Line 24:


== फ्रैक्टल एंटेना, फ़्रीक्वेंसी इनवेरियन, और मैक्सवेल के समीकरण ==
== फ्रैक्टल एंटेना, फ़्रीक्वेंसी इनवेरियन, और मैक्सवेल के समीकरण ==
कुछ भग्न तत्व एंटेना की एक अलग और उपयोगी विशेषता उनका स्व-स्केलिंग पहलू है। 1957 में, वी.एच. रुम्सी<ref name="Rumsey, V.H pp.114-118"/>प्रस्तुत परिणाम बताते हैं कि कोण-परिभाषित स्केलिंग एक संख्या, या सीमा, आवृत्तियों पर एंटेना को अपरिवर्तनीय (समान विकिरण गुण) बनाने के लिए अंतर्निहित आवश्यकताओं में से एक थी। 1948 में जापान में वाई. मुशियाके द्वारा कार्य प्रारंभ<ref>{{Cite journal|url=http://www.sm.rim.or.jp/~ymushiak/sub.docu.1.htm##%% |first=Y. |last=Mushiake |title=स्व-पूरक संरचना की उत्पत्ति और इसकी निरंतर-प्रतिबाधा संपत्ति की खोज|journal=The Journal of the Institute of Electrical Engineers of Japan |volume=69 |issue=3 |page=88 |date=March 1949 |language=ja}}</ref> स्व-पूरक एंटीना वाले आवृत्ति स्वतंत्र एंटेना के समान परिणामों का प्रदर्शन किया। स्व-पूरकता।
कुछ फ्रैक्टल एलिमेंट एंटेना की एक अलग और उपयोगी विशेषता उनका सेल्फ-स्केलिंग पहलू है। 1957 में, वी.एच. रुम्सी<ref name="Rumsey, V.H pp.114-118"/> ने परिणाम प्रस्तुत किए कि कोण-परिभाषित स्केलिंग एंटेना को एक संख्या, या सीमा, आवृत्तियों पर अपरिवर्तनीय (समान विकिरण गुण) बनाने के लिए अंतर्निहित आवश्यकताओं में से एक थी। 1948 में जापान में वाई. मुशियाके के काम<ref>{{Cite journal|url=http://www.sm.rim.or.jp/~ymushiak/sub.docu.1.htm##%% |first=Y. |last=Mushiake |title=स्व-पूरक संरचना की उत्पत्ति और इसकी निरंतर-प्रतिबाधा संपत्ति की खोज|journal=The Journal of the Institute of Electrical Engineers of Japan |volume=69 |issue=3 |page=88 |date=March 1949 |language=ja}}</ref> ने स्व-पूरकता वाले फ्रीक्वेंसी-स्वतंत्र एंटेना के समान परिणाम प्रदर्शित किए।


ऐसा माना जाता था कि इसके सही होने के लिए एंटेना को कोणों द्वारा परिभाषित किया जाना था, लेकिन 1999 में इसकी खोज की गई<ref>{{cite journal | author = Hohlfeld R, Cohen N | year = 1999 | title = स्व-समानता और एंटीना में आवृत्ति स्वतंत्रता के लिए ज्यामितीय आवश्यकताएं| journal = Fractals | volume = 7 | issue = 1| pages = 79–84 | doi = 10.1142/S0218348X99000098 }}</ref> एंटेना आवृत्ति और बैंडविड्थ अपरिवर्तनीय बनाने के लिए स्व-समानता अंतर्निहित आवश्यकताओं में से एक थी। दूसरे शब्दों में, स्व-समान पहलू आवृत्ति स्वतंत्रता के लिए मूल समरूपता के साथ-साथ अंतर्निहित आवश्यकता थी। कोण-परिभाषित एंटेना स्व-समान हैं, लेकिन अन्य स्व-समान एंटेना आवृत्ति स्वतंत्र हैं, हालांकि कोण-परिभाषित नहीं हैं।
ऐसा माना जाता था कि इसे सच होने के लिए एंटेना को कोणों द्वारा परिभाषित किया जाना था, लेकिन 1999 में यह पता चला<ref>{{cite journal | author = Hohlfeld R, Cohen N | year = 1999 | title = स्व-समानता और एंटीना में आवृत्ति स्वतंत्रता के लिए ज्यामितीय आवश्यकताएं| journal = Fractals | volume = 7 | issue = 1| pages = 79–84 | doi = 10.1142/S0218348X99000098 }}</ref> कि एंटेना की आवृत्ति और बैंडविड्थ अपरिवर्तनीय बनाने के लिए स्व-समानता अंतर्निहित आवश्यकताओं में से एक थी। दूसरे शब्दों में, स्व-समान पहलू आवृत्ति स्वतंत्रता के लिए मूल समरूपता के साथ-साथ अंतर्निहित आवश्यकता थी। कोण-परिभाषित एंटेना स्व-समान हैं, लेकिन अन्य स्व-समान एंटेना आवृत्ति स्वतंत्र हैं, हालांकि कोण-परिभाषित नहीं हैं।


मैक्सवेल के समीकरणों पर आधारित इस विश्लेषण से पता चला है कि फ्रैक्टल एंटेना विद्युत चुम्बकीय घटना के एक प्रमुख पहलू में एक बंद रूप और अद्वितीय अंतर्दृष्टि प्रदान करते हैं। बुद्धि के लिए: मैक्सवेल के समीकरणों की अचल संपत्ति। इसे अब होहलफेल्ड-कोहेन-रुम्सी (HCR) सिद्धांत के रूप में जाना जाता है। स्व-संपूरकता पर मुशीके के पहले के कार्य को प्रतिबाधा सुगमता तक सीमित दिखाया गया था, जैसा कि बाबिनेट के सिद्धांत से अपेक्षित था, लेकिन आवृत्ति आक्रमण नहीं।
मैक्सवेल के समीकरणों पर आधारित इस विश्लेषण से पता चला है कि फ्रैक्टल एंटेना विद्युत चुम्बकीय घटना के एक प्रमुख पहलू में एक बंद रूप और अद्वितीय अंतर्दृष्टि प्रदान करते हैं। बुद्धि के लिए: मैक्सवेल के समीकरणों की अपरिवर्तनीय संपत्ति। इसे अब होहलफेल्ड-कोहेन-रुम्सी (एचसीआर) सिद्धांत के रूप में जाना जाता है। स्व-पूरकता पर मुशाइके के पहले के काम को बाबिनेट के सिद्धांत से अपेक्षित प्रतिबाधा सुगमता तक सीमित दिखाया गया था, लेकिन आवृत्ति आक्रमण नहीं।


== अन्य उपयोग ==
== अन्य उपयोग ==
एंटेना के रूप में उनके उपयोग के अलावा, फ्रैक्टल्स ने लोड, [[काउंटरपोइज़ (ग्राउंड सिस्टम)]], और ग्राउंड प्लेन सहित अन्य एंटीना सिस्टम घटकों में भी आवेदन पाया है।
एंटेना के रूप में उनके उपयोग के अलावा, फ्रैक्टल्स ने लोड, [[काउंटरपोइज़ (ग्राउंड सिस्टम)|काउंटरपोइज़]] और ग्राउंड प्लेन सहित अन्य एंटीना सिस्टम घटकों में भी आवेदन प्राप्त किया है।
 
फ्रैक्टल इंडक्टर्स और फ्रैक्टल-ट्यून सर्किट (फ्रैक्टल रेज़ोनेटर) भी फ्रैक्टल एलिमेंट एंटेना के साथ-साथ खोजे और आविष्कार किए गए थे।<ref name=r1/><ref>{{cite patent |inventor=Cohen, Nathan |pubdate=2007-08-14 |title=फ्रैक्टल एंटेना और फ्रैक्टल रेज़ोनेटर|number=7256751 |country=US}}</ref> इसका एक उभरता उदाहरण मेटामटेरियल है। एक हालिया आविष्कार माइक्रोवेव आवृत्तियों पर पहला वाइडबैंड [[मेटामेट्री]] अदृश्यता लबादा बनाने के लिए क्लोज-पैक्ड फ्रैक्टल रेज़ोनेटर का उपयोग करता है।<ref>{{US patent|8,253,639}}</ref><ref>{{cite journal |author=Cohen, N. |title=बॉडी साइज वाइड-बैंड हाई फिडेलिटी इनविजिबिलिटी क्लोक|journal=Fractals |volume=20 |issue=3n04 |pages=227–232 |year=2012 |doi=10.1142/s0218348x1250020x|bibcode=2012Fract..20..227C }}</ref>


फ्रैक्टल इंडक्टर्स और फ्रैक्टल ट्यून सर्किट (फ्रैक्टल रेज़ोनेटर) भी फ्रैक्टल एलिमेंट एंटेना के साथ-साथ खोजे और आविष्कार किए गए थे।<ref name=r1/><ref>{{cite patent |inventor=Cohen, Nathan |pubdate=2007-08-14 |title=फ्रैक्टल एंटेना और फ्रैक्टल रेज़ोनेटर|number=7256751 |country=US}}</ref> इसका एक उभरता हुआ उदाहरण मेटामटेरियल्स में है। एक हालिया आविष्कार माइक्रोवेव आवृत्तियों पर पहला वाइडबैंड [[मेटामेट्री]] अदृश्यता लबादा बनाने के लिए क्लोज-पैक्ड फ्रैक्टल रेज़ोनेटर का उपयोग करके प्रदर्शित करता है।<ref>{{US patent|8,253,639}}</ref><ref>{{cite journal |author=Cohen, N. |title=बॉडी साइज वाइड-बैंड हाई फिडेलिटी इनविजिबिलिटी क्लोक|journal=Fractals |volume=20 |issue=3n04 |pages=227–232 |year=2012 |doi=10.1142/s0218348x1250020x|bibcode=2012Fract..20..227C }}</ref>
फ्रैक्टल फिल्टर (एक प्रकार का ट्यून्ड सर्किट) एक और उदाहरण है जहां छोटे आकार और बेहतर अस्वीकृति के लिए फ्रैक्टल दृष्टिकोण की श्रेष्ठता सिद्ध हुई है।<ref>{{cite book |author1=Lancaster, M. |author2=Hong, Jia-Sheng |title=आरएफ/माइक्रोवेव अनुप्रयोगों के लिए माइक्रोस्ट्रिप फिल्टर|publisher=Wiley |location=New York |year=2001 |pages=410–411 |isbn=978-0-471-38877-7 |url=https://books.google.com/books?id=vj0hz1KUAXoC&pg=PA410}}</ref><ref>{{Cite journal |author1=Pourahmadazar, J. |author2=Ghobadi, C. |author3=Nourinia, J. |author4=Shirzad, H. |title=मोबाइल उपकरणों के लिए मल्टीबैंड रिंग फ्रैक्टल मोनोपोल एंटीना|journal=IEEE Antennas and Wireless Propagation Letters |volume=9 |year=2010 |pages=863–866 |doi=10.1109/LAWP.2010.2071372 |bibcode=2010IAWPL...9..863P|s2cid=19689050 }}</ref><ref>{{Cite journal |author1=Pourahmadazar, J. |author2=Ghobadi, C. |author3=Nourinia, J. |title=UWB अनुप्रयोगों के लिए उपन्यास संशोधित पाइथोगोरियन ट्री फ्रैक्टल मोनोपोल एंटेना|journal=IEEE Antennas and Wireless Propagation Letters |volume=10 |year=2011 |pages=484–487 |doi=10.1109/LAWP.2011.2154354 |bibcode=2011IAWPL..10..484P|s2cid=31823278 }}</ref>
फ्रैक्टल फिल्टर (एक प्रकार का ट्यून्ड सर्किट) एक और उदाहरण है जहां छोटे आकार और बेहतर अस्वीकृति के लिए फ्रैक्टल दृष्टिकोण की श्रेष्ठता सिद्ध हुई है।<ref>{{cite book |author1=Lancaster, M. |author2=Hong, Jia-Sheng |title=आरएफ/माइक्रोवेव अनुप्रयोगों के लिए माइक्रोस्ट्रिप फिल्टर|publisher=Wiley |location=New York |year=2001 |pages=410–411 |isbn=978-0-471-38877-7 |url=https://books.google.com/books?id=vj0hz1KUAXoC&pg=PA410}}</ref><ref>{{Cite journal |author1=Pourahmadazar, J. |author2=Ghobadi, C. |author3=Nourinia, J. |author4=Shirzad, H. |title=मोबाइल उपकरणों के लिए मल्टीबैंड रिंग फ्रैक्टल मोनोपोल एंटीना|journal=IEEE Antennas and Wireless Propagation Letters |volume=9 |year=2010 |pages=863–866 |doi=10.1109/LAWP.2010.2071372 |bibcode=2010IAWPL...9..863P|s2cid=19689050 }}</ref><ref>{{Cite journal |author1=Pourahmadazar, J. |author2=Ghobadi, C. |author3=Nourinia, J. |title=UWB अनुप्रयोगों के लिए उपन्यास संशोधित पाइथोगोरियन ट्री फ्रैक्टल मोनोपोल एंटेना|journal=IEEE Antennas and Wireless Propagation Letters |volume=10 |year=2011 |pages=484–487 |doi=10.1109/LAWP.2011.2154354 |bibcode=2011IAWPL..10..484P|s2cid=31823278 }}</ref>
चूंकि फ्रैक्टल्स को काउंटरपोइज़, लोड, ग्राउंड प्लेन और फिल्टर के रूप में इस्तेमाल किया जा सकता है, सभी भागों को एंटेना के साथ एकीकृत किया जा सकता है, उन्हें कुछ एंटीना सिस्टम के हिस्से माना जाता है और इस प्रकार फ्रैक्टल एंटेना के संदर्भ में चर्चा की जाती है।
 
चूंकि फ्रैक्टल को काउंटरपोइज़, लोड, ग्राउंड प्लेन और फिल्टर के रूप में इस्तेमाल किया जा सकता है, एंटेना के साथ एकीकृत किए जा सकने वाले सभी हिस्सों को कुछ एंटीना सिस्टम के हिस्से माना जाता है और इस प्रकार फ्रैक्टल एंटेना के संदर्भ में चर्चा की जाती है।


== यह भी देखें ==
== यह भी देखें ==

Revision as of 09:15, 3 January 2023

फ्रैक्टल एंटीना का एक उदाहरण: स्पेस-फिलिंग कर्व जिसे मिन्कोव्स्की द्वीप कहा जाता है[1] या मिन्कोव्स्की फ्रैक्टल[2]

एक फ्रैक्टल एंटीना एक एंटीना है जो प्रभावी लंबाई को अधिकतम करने के लिए एक फ्रैक्टल, स्व-समान डिज़ाइन का उपयोग करता है या किसी दिए गए कुल सतह क्षेत्र के भीतर विद्युत चुम्बकीय विकिरण प्राप्त या संचारित कर सकने वाली पदार्थ की परिधि (आंतरिक वर्गों या बाहरी संरचना पर) को बढ़ाता है।

इस तरह के फ्रैक्टल (आंशिक) एंटेना को बहुस्तरीय और स्थान-भरने वाले घटता के रूप में भी जाना जाता है, लेकिन मुख्य पहलू दो या दो से अधिक पैमाने के आकार,[3] या "पुनरावृत्ति" पर एक आकृति की पुनरावृत्ति में निहित है। इस कारण से, फ्रैक्टल एंटेना बहुत कॉम्पैक्ट, मल्टीबैंड या वाइडबैंड होते हैं, और सेलुलर टेलीफोन और माइक्रोवेव संचार में उपयोगी अनुप्रयोग होते हैं। एक आंशिक एंटीना की प्रतिक्रिया पारंपरिक एंटीना डिजाइनों से स्पष्ट रूप से भिन्न होती है, जिसमें यह एक साथ कई अलग-अलग आवृत्तियों पर अच्छे-से-उत्कृष्ट प्रदर्शन के साथ काम करने में सक्षम है। आम तौर पर मानक एंटेना को उस आवृत्ति के लिए "कट" करना पड़ता है जिसके लिए उनका उपयोग किया जाना है - और इस प्रकार मानक एंटेना केवल उस आवृत्ति पर अच्छी तरह से काम करते हैं।

इसके अलावा ऐन्टेना की भग्न प्रकृति इसके आकार को कम करती है, बिना किसी घटक के उपयोग के, जैसे कि प्रेरक या संधारित्र।

लॉग-पीरियोडिक एंटेना और फ्रैक्टल

लॉग-पीरियॉडिक एंटेना 1952 में आविष्कृत एरेज़ हैं और आमतौर पर टीवी एंटेना के रूप में देखे जाते हैं। यह 1975 में मैंडलब्रॉट द्वारा फ्रैक्टल शब्द गढ़े जाने से काफी पहले की बात है।[4] कुछ लेखक (उदाहरण के लिए कोहेन)[5] सभी पैमानों पर अपनी अनंत आत्म-समानता के कारण लॉग-पीरियडिक एंटेना को फ्रैक्टल एंटीना का प्रारंभिक रूप मानते हैं। हालांकि, उनके पास तत्वों की अनंत संख्या के साथ सैद्धांतिक सीमा में भी एक परिमित लंबाई है और इसलिए एक फ्रैक्टल आयाम नहीं है जो उनके टोपोलॉजिकल आयाम से अधिक है - जो भग्न को परिभाषित करने का एक तरीका है। अधिक विशिष्ट रूप से, (उदाहरण के लिए पाण्डेय)[6] लेखक उन्हें एक अलग, लेकिन संबंधित, ऐन्टेना की श्रेणी के रूप में मानते हैं।

फ्रैक्टल एलिमेंट एंटेना और प्रदर्शन

एक प्लानर ऐरे फ्रैक्टल एंटीना (एच पेड़)

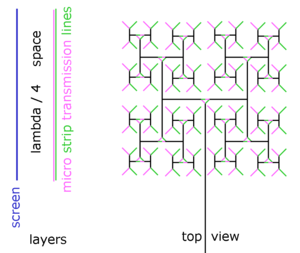
एंटीना तत्व (एंटीना सरणियों के विपरीत, जो आमतौर पर फ्रैक्टल एंटेना के रूप में शामिल नहीं होते हैं) स्व-समान आकृतियों से बने पहले नाथन कोहेन [7] और फिर बोस्टन विश्वविद्यालय के एक प्रोफेसर द्वारा 1988 में शुरू किए गए थे।[8] कोहेन के विभिन्न फ्रैक्टल एंटीना डिजाइनों के प्रयासों को पहली बार 1995 में प्रकाशित किया गया था।[1] कोहेन के प्रकाशन ने भग्न एंटेना पर उद्घाटन वैज्ञानिक प्रकाशन को चिन्हित किया।

कई फ्रैक्टल एलिमेंट एंटेना फ्रैक्टल संरचना का उपयोग संधारित्र और प्रेरकों के वर्चुअल संयोजन के रूप में करते हैं। यह ऐन्टेना बनाता है ताकि इसमें कई अलग-अलग अनुनाद हों जिन्हें उचित भग्न डिजाइन चुनकर चुना और समायोजित किया जा सके। यह जटिलता उत्पन्न होती है क्योंकि संरचना पर वर्तमान में अधिष्ठापन और आत्म-समाई के कारण जटिल व्यवस्था होती है। सामान्य तौर पर, हालांकि उनकी प्रभावी विद्युत लंबाई लंबी होती है, फिर भी इस प्रतिक्रियाशील भार के कारण फ्रैक्टल तत्व एंटेना खुद शारीरिक रूप से छोटे होते हैं।

इस प्रकार फ्रैक्टल तत्व एंटेना पारंपरिक डिजाइनों की तुलना में सिकुड़ जाते हैं और अतिरिक्त घटकों की आवश्यकता नहीं होती है, यह मानते हुए कि संरचना में वांछित गुंजयमान इनपुट प्रतिबाधा होती है। सामान्य तौर पर, फ्रैक्टल ऐन्टेना का फ्रैक्टल आयाम इसके प्रदर्शन और अनुप्रयोग का खराब भविष्यवक्ता होता है। किसी दिए गए एप्लिकेशन या एप्लिकेशन के सेट के लिए सभी फ्रैक्टल एंटेना अच्छी तरह से काम नहीं करते हैं। कंप्यूटर खोज विधियों और ऐन्टेना सिमुलेशन का उपयोग आमतौर पर यह पहचानने के लिए किया जाता है कि कौन से फ्रैक्टल ऐन्टेना डिज़ाइन एप्लिकेशन की ज़रूरतों को सर्वोत्तम रूप से पूरा करते हैं।

2000 के दशक के दौरान किए गए अध्ययनों ने आरएफआईडी[9] और सेल फोन जैसे वास्तविक जीवन के अनुप्रयोगों में फ्रैक्टल तत्व प्रौद्योगिकी के लाभों को दिखाया।[10] 2010 के बाद से एंटेना में फ्रैक्टल्स का व्यावसायिक रूप से उपयोग किया जाने लगा है। [11] उनके फायदे अच्छे मल्टीबैंड प्रदर्शन, व्यापक बैंडविड्थ और छोटे क्षेत्र हैं।[12] एक छोटे से क्षेत्र में विद्युत रूप से लंबी संरचना द्वारा वहन किए गए कई वर्तमान मैक्सिमा के साथ रचनात्मक हस्तक्षेप से छोटे आकार के परिणाम प्राप्त होते हैं।[13]

कुछ शोधकर्ताओं ने विवाद किया है कि फ्रैक्टल एंटेना का प्रदर्शन बेहतर है। स्टीवन आर. बेस्ट ने 2003 में कहा था, "एंटीना ज्यामिति अकेले, भग्न या अन्यथा, छोटे एंटीना के विद्युत चुम्बकीय गुणों को विशिष्ट रूप से निर्धारित नहीं करती है"।[14] 2011 में, रॉबर्ट सी. हैनसेन और रॉबर्ट ई. कॉलिन ने फ्रैक्टल एंटेना पर कई पेपरों की समीक्षा की और निष्कर्ष निकाला कि वे वसा द्विध्रुव, भारित द्विध्रुव, या साधारण लूप पर कोई लाभ नहीं देते हैं और यह कि गैर-भग्न हमेशा बेहतर होते हैं।[15] बालानिस ने कई फ्रैक्टल एंटेना पर सूचना दी और उनकी तुलना में विद्युत रूप से छोटे एंटेना के प्रदर्शन में उन्हें समकक्ष पाया।[16] लॉग पीरियॉडिक, फ्रैक्टल ऐन्टेना का एक रूप, उनकी विद्युत चुम्बकीय विशेषताओं को विशिष्ट रूप से एक प्रारंभिक कोण के माध्यम से ज्यामिति द्वारा निर्धारित किया जाता है।[17][18]

फ्रैक्टल एंटेना, फ़्रीक्वेंसी इनवेरियन, और मैक्सवेल के समीकरण

कुछ फ्रैक्टल एलिमेंट एंटेना की एक अलग और उपयोगी विशेषता उनका सेल्फ-स्केलिंग पहलू है। 1957 में, वी.एच. रुम्सी[18] ने परिणाम प्रस्तुत किए कि कोण-परिभाषित स्केलिंग एंटेना को एक संख्या, या सीमा, आवृत्तियों पर अपरिवर्तनीय (समान विकिरण गुण) बनाने के लिए अंतर्निहित आवश्यकताओं में से एक थी। 1948 में जापान में वाई. मुशियाके के काम[19] ने स्व-पूरकता वाले फ्रीक्वेंसी-स्वतंत्र एंटेना के समान परिणाम प्रदर्शित किए।

ऐसा माना जाता था कि इसे सच होने के लिए एंटेना को कोणों द्वारा परिभाषित किया जाना था, लेकिन 1999 में यह पता चला[20] कि एंटेना की आवृत्ति और बैंडविड्थ अपरिवर्तनीय बनाने के लिए स्व-समानता अंतर्निहित आवश्यकताओं में से एक थी। दूसरे शब्दों में, स्व-समान पहलू आवृत्ति स्वतंत्रता के लिए मूल समरूपता के साथ-साथ अंतर्निहित आवश्यकता थी। कोण-परिभाषित एंटेना स्व-समान हैं, लेकिन अन्य स्व-समान एंटेना आवृत्ति स्वतंत्र हैं, हालांकि कोण-परिभाषित नहीं हैं।

मैक्सवेल के समीकरणों पर आधारित इस विश्लेषण से पता चला है कि फ्रैक्टल एंटेना विद्युत चुम्बकीय घटना के एक प्रमुख पहलू में एक बंद रूप और अद्वितीय अंतर्दृष्टि प्रदान करते हैं। बुद्धि के लिए: मैक्सवेल के समीकरणों की अपरिवर्तनीय संपत्ति। इसे अब होहलफेल्ड-कोहेन-रुम्सी (एचसीआर) सिद्धांत के रूप में जाना जाता है। स्व-पूरकता पर मुशाइके के पहले के काम को बाबिनेट के सिद्धांत से अपेक्षित प्रतिबाधा सुगमता तक सीमित दिखाया गया था, लेकिन आवृत्ति आक्रमण नहीं।

अन्य उपयोग

एंटेना के रूप में उनके उपयोग के अलावा, फ्रैक्टल्स ने लोड, काउंटरपोइज़ और ग्राउंड प्लेन सहित अन्य एंटीना सिस्टम घटकों में भी आवेदन प्राप्त किया है।

फ्रैक्टल इंडक्टर्स और फ्रैक्टल-ट्यून सर्किट (फ्रैक्टल रेज़ोनेटर) भी फ्रैक्टल एलिमेंट एंटेना के साथ-साथ खोजे और आविष्कार किए गए थे।[3][21] इसका एक उभरता उदाहरण मेटामटेरियल है। एक हालिया आविष्कार माइक्रोवेव आवृत्तियों पर पहला वाइडबैंड मेटामेट्री अदृश्यता लबादा बनाने के लिए क्लोज-पैक्ड फ्रैक्टल रेज़ोनेटर का उपयोग करता है।[22][23]

फ्रैक्टल फिल्टर (एक प्रकार का ट्यून्ड सर्किट) एक और उदाहरण है जहां छोटे आकार और बेहतर अस्वीकृति के लिए फ्रैक्टल दृष्टिकोण की श्रेष्ठता सिद्ध हुई है।[24][25][26]

चूंकि फ्रैक्टल को काउंटरपोइज़, लोड, ग्राउंड प्लेन और फिल्टर के रूप में इस्तेमाल किया जा सकता है, एंटेना के साथ एकीकृत किए जा सकने वाले सभी हिस्सों को कुछ एंटीना सिस्टम के हिस्से माना जाता है और इस प्रकार फ्रैक्टल एंटेना के संदर्भ में चर्चा की जाती है।

यह भी देखें

संदर्भ

  1. ↑ 1.0 1.1 Cohen, Nathan (Summer 1995). "भग्न एंटेना भाग 1". Communications Quarterly. 5: 7–22. ISSN 1053-9433.
  2. ↑ Ghosh, Basudeb; Sinha, Sachendra N.; and Kartikeyan, M. V. (2014). Fractal Apertures in Waveguides, Conducting Screens and Cavities: Analysis and Design, p.88. Volume 187 of Springer Series in Optical Sciences. ISBN 9783319065359.
  3. ↑ 3.0 3.1 Nathan Cohen (2002) "Fractal antennas and fractal resonators" U.S. Patent 6,452,553
  4. ↑ Albers, Donald J.; Alexanderson, Gerald L. (2008). "Benoît Mandelbrot: In his own words". गणितीय लोग: प्रोफाइल और साक्षात्कार. Wellesley, MA: AK Peters. p. 214. ISBN 978-1-56881-340-0.
  5. ↑ Nathan Cohen, "Fractal antenna and fractal resonator primer", p. 218, ch.8 in, Michael Frame, Nathan Cohen (eds), Benoit Mandelbrot: A Life In Many Dimensions, World Scientific, 2015 ISBN 9814635537.
  6. ↑ Anil Pandey, Practical Microstrip and Printed Antenna Design, p. 5, Artech House, 2019 ISBN 1630816701.
  7. ↑ "फ्रैक्टल एंटीना सिस्टम्स, इंक". www.fractenna.com. Retrieved 22 April 2018.
  8. ↑ Cohen, N. (Summer 1995). "भग्न एंटेना भाग 1". Communications Quarterly: 12 sidebar, 'The First Fractal Antenna'. ISSN 1053-9433.
  9. ↑ Ukkonen L, Sydanheimo L, Kivikoski M (26–28 March 2007). "हैंडहेल्ड यूएचएफ आरएफआईडी रीडर के लिए कॉम्पैक्ट रीडर एंटेना की रेंज प्रदर्शन तुलना पढ़ें". IEEE International Conference on RFID, 2007. pp. 63–70. doi:10.1109/RFID.2007.346151. ISBN 978-1-4244-1013-2.
  10. ↑ N. A. Saidatul; A. A. H. Azremi; R. B. Ahmad; P. J. Soh; F. Malek (2009). "मोबाइल फोन एप्लिकेशन के लिए मल्टीबैंड फ्रैक्टल प्लानर इनवर्टेड एफ एंटीना (एफ-पीफा)।". Progress in Electromagnetics Research B. 14: 127–148. doi:10.2528/pierb09030802.
  11. ↑ Henry Lau, Practical Antenna Design for Wireless Products, p. 208, Artech House, 2019 ISBN 1630813265.
  12. ↑ John Volakis, Ch-Chi Chen, and Kyohei Fujimoto," Small Antennas", ch. 3.2.5, McGraw Hill, 2010 ISBN 9780071625531
  13. ↑ Michael Frame, and Nathan Cohen, "Benoit Mandelbrot: A Life in Many Dimensions", ch 8: "Fractal Antenna and Fractal Resonator Primer", ch 8.4, World Scientific Press, 2015 ISBN 9789814366069
  14. ↑ Best, S.R. (2003). "छोटे स्पेस-फिलिंग फ्रैक्टल एंटेना के गुंजयमान गुणों की तुलना". IEEE Antennas and Wireless Propagation Letters. 2 (1): 197–200. Bibcode:2003IAWPL...2..197B. doi:10.1109/1-awp.2003.819680. S2CID 15119380.
  15. ↑ Robert C. Hansen, Robert E. Collin, Small Antenna Handbook, ch. 5.13, John Wiley & Sons, 2011 ISBN 1118106857
  16. ↑ Constantine A. Balanis, "Modern Antenna Handbook", ch. 10.9, John Wiley & Sons, 2011 ISBN 978-1-118-20975-2
  17. ↑ Alois Krischke, "Rothammel's Antenna Book", 27.5, DARC Verlag, 2019 ISBN 9783000624278
  18. ↑ 18.0 18.1 Rumsey, V.H. "Frequency Independent Antennas", IRE International Convention Record, Vol. 5, Part 1, pp.114-118, 1957
  19. ↑ Mushiake, Y. (March 1949). "स्व-पूरक संरचना की उत्पत्ति और इसकी निरंतर-प्रतिबाधा संपत्ति की खोज". The Journal of the Institute of Electrical Engineers of Japan (in 日本語). 69 (3): 88.
  20. ↑ Hohlfeld R, Cohen N (1999). "स्व-समानता और एंटीना में आवृत्ति स्वतंत्रता के लिए ज्यामितीय आवश्यकताएं". Fractals. 7 (1): 79–84. doi:10.1142/S0218348X99000098.
  21. ↑ US 7256751, Cohen, Nathan, "फ्रैक्टल एंटेना और फ्रैक्टल रेज़ोनेटर", published 2007-08-14 
  22. ↑ U.S. Patent 8,253,639
  23. ↑ Cohen, N. (2012). "बॉडी साइज वाइड-बैंड हाई फिडेलिटी इनविजिबिलिटी क्लोक". Fractals. 20 (3n04): 227–232. Bibcode:2012Fract..20..227C. doi:10.1142/s0218348x1250020x.
  24. ↑ Lancaster, M.; Hong, Jia-Sheng (2001). आरएफ/माइक्रोवेव अनुप्रयोगों के लिए माइक्रोस्ट्रिप फिल्टर. New York: Wiley. pp. 410–411. ISBN 978-0-471-38877-7.
  25. ↑ Pourahmadazar, J.; Ghobadi, C.; Nourinia, J.; Shirzad, H. (2010). "मोबाइल उपकरणों के लिए मल्टीबैंड रिंग फ्रैक्टल मोनोपोल एंटीना". IEEE Antennas and Wireless Propagation Letters. 9: 863–866. Bibcode:2010IAWPL...9..863P. doi:10.1109/LAWP.2010.2071372. S2CID 19689050.
  26. ↑ Pourahmadazar, J.; Ghobadi, C.; Nourinia, J. (2011). "UWB अनुप्रयोगों के लिए उपन्यास संशोधित पाइथोगोरियन ट्री फ्रैक्टल मोनोपोल एंटेना". IEEE Antennas and Wireless Propagation Letters. 10: 484–487. Bibcode:2011IAWPL..10..484P. doi:10.1109/LAWP.2011.2154354. S2CID 31823278.

बाहरी कड़ियाँ

Retrieved from ‘https://www.vigyanwiki.in/index.php?title=फ्रैक्टल_एंटीना&oldid=63181’