समता (भौतिकी)

भौतिक विज्ञान में, एक समानता परिवर्तन (जिसे समता व्युत्क्रमण भी कहा जाता है) एक त्रिविम -आयामी अंतरिक्ष समन्वय के संकेत में घुमाव है। तीन आयामों में, यह तीनों स्थानिक निर्देशांक (एक बिंदु प्रतिबिंब) के संकेत में एक साथ घुमाव का भी उल्लेख कर सकता है:

$\mathbf {P} :{\begin{pmatrix}x\\y\\z\end{pmatrix}}\mapsto {\begin{pmatrix}-x\\-y\\-z\end{pmatrix}}.$

इसे एक भौतिक घटना के चिरायता (भौतिकी) के लिए एक परीक्षण के रूप में भी सोचा जा सकता है, जिसमें एक समता व्युत्क्रम एक घटना को अपनी दर्पण प्रतिबिम्ब में बदल देता है। मन्द अंतःक्रिया के अपवाद के साथ, प्राथमिक कणों की सभी मौलिक अंतःक्रिया समता के अंतर्गत होती हैं। मन्द अंतःक्रिया चिराल है और इस प्रकार भौतिक विज्ञान में चिरायता की परीक्षण के लिए एक साधन प्रदान किया जाता है। पारस्परिक क्रियाओं में जो समता के अंतर्गत हैं, जैसे कि परमाणु और आणविक भौतिक विज्ञान में विद्युत चुंबकत्व, समानता एक प्रभावशाली नियंत्रण सिद्धांत अंतर्निहित क्वांटम पारगमन के रूप में कार्य करता है।

P का एक आव्यूह निरूपण (किसी भी आयामों की संख्या में) निर्धारक 1 के समान होता है, और इसलिए एक घूर्णन से भिन्न होता है, जिसमें एक निर्धारक 1 के समान होता है। दो-आयामी विमान में, चिन्ह में सभी निर्देशांक का एक साथ घुमाव एक समता परिवर्तन नहीं है; यह 180° घुमाव के समान है।

क्वांटम यांत्रिकी में, एक समता परिवर्तन द्वारा अपरिवर्तित तरंग कार्यों को सम और विषम फलनों के कार्यों के रूप में परिभाषित किया जाता है, जबकि जो एक समता परिवर्तन के अंतर्गत चिन्ह बदलते हैं वे विषम फलन हैं।

सरल समरूपता संबंध

See also: SU(2) का प्रतिनिधित्व सिद्धांत

घूर्णन के अंतर्गत, पारम्परिक ज्यामितीय वस्तुओं को अदिश (भौतिकी), यूक्लिडियन सदिश और उच्च श्रेणी के टेंसर में वर्गीकृत किया जा सकता है। पारम्परिक भौतिक विज्ञान में, भौतिक विन्यास को प्रत्येक समरूपता समूह के अभ्यावेदन के अंतर्गत बदलने की आवश्यकता होती है।

क्वांटम यांत्रिकी की भविष्यवाणी है कि हिल्बर्ट अंतरिक्ष में अवस्थाओं को घूर्णन के समूह (गणित) के निरूपण के अंतर्गत बदलने की जरूरत नहीं है, लेकिन यह केवल प्रक्षेपीय अभ्यावेदन के अंतर्गत होता है। प्रक्षेपीय शब्द इस तथ्य को संदर्भित करता है कि यदि कोई प्रत्येक अवस्था के चरण का प्रक्षेपण करता है, वहाँ हम याद रखते हैं कि क्वांटम अवस्था का संपूर्ण चरण अवलोकन योग्य नहीं है, तो एक प्रक्षेपीय अभ्यावेदन सामान्य अभ्यावेदन में कम हो जाता है। सभी अभ्यावेदन भी प्रक्षेपी अभ्यावेदन हैं, लेकिन इसके विपरीत सत्य नहीं है, इसलिए क्वांटम अवस्थाओं पर प्रक्षेप्य निरूपण की स्थिति पारम्परिक अवस्थाओं पर निरूपण की स्थिति से मन्द है।

किसी भी समूह का प्रक्षेप्य निरूपण समूह विस्तार समूह के केंद्रीय विस्तार के सामान्य निरूपण के लिए समरूप है। उदाहरण के लिए, 3-आयामी घूर्णन समूह के प्रक्षेपी निरूपण, जो कि विशेष ऑर्थोगोनल समूह SO(3) है, विशेष एकात्मक समूह SU(2) के सामान्य निरूपण हैं। घूर्णन समूह के प्रक्षेपी अभ्यावेदन जो अभ्यावेदन नहीं हैं उन्हें स्पाइनर कहा जाता है और इसलिए क्वांटम अवस्था न केवल टेन्सर के रूप में बल्कि स्पिनर्स के रूप में भी परिवर्तित हो सकते हैं।

यदि कोई इसमें समता द्वारा वर्गीकरण जोड़ता है, तो इन्हें विस्तारित किया जा सकता है, उदाहरण के लिए, धारणाओं में

• अदिश (P = +1) और छद्म अदिश(भौतिकी) भौतिकी) (P = −1) जो घूर्णी रूप से अपरिवर्तनीय हैं।
• सदिश (P = −1) और अक्षीय सदिश (जिसे छद्म सदिश क्षेत्र भी कहा जाता है) (P = +1) जो दोनों घूर्णन के अंतर्गत सदिश के रूप में परिवर्तित हो जाते हैं।

कोई प्रतिबिंब को परिभाषित कर सकता है जैसे

$V_{x}:{\begin{pmatrix}x\\y\\z\end{pmatrix}}\mapsto {\begin{pmatrix}-x\\y\\z\end{pmatrix}},$

जिसका नकारात्मक निर्धारक भी है और एक वैध समता परिवर्तन बनाता है। फिर, उन्हें घूर्णन (या क्रमिक रूप से एक्स-, वाई-, और जेड-प्रतिबिंबों का संपादन) के साथ जोड़कर पहले से परिभाषित विशेष समता परिवर्तन को पुनः प्राप्त किया जा सकता है। दिया गया पहला समता परिवर्तन आयामों की एक समान संख्या में काम नहीं करता है, हालाँकि, इसका परिणाम एक सकारात्मक निर्धारक में होता है। सम आयामों में समता परिवर्तन (या निर्देशांक की विषम संख्या का कोई भी प्रतिबिंब) का केवल बाद वाला उदाहरण प्रयोग किया जा सकता है।

समानता ${\hat {\mathcal {P}}}^{2}={\hat {1}}$ संबंध के कारण.एबेलियन समूह $\mathbb {Z} _{2}$ बनाती है| सभी एबेलियन समूहों के पास $\mathbb {Z} _{2}$ के लिए केवल एक आयामी अलघुकरणीय निरूपण है। दो अलघुकरणीय अभ्यावेदन हैं: एक समता के अंतर्गत ${\hat {\mathcal {P}}}\phi =+\phi$ भी है, दूसरा विषम ${\hat {\mathcal {P}}}\phi =-\phi$ है| ये क्वांटम यांत्रिकी में उपयोगी हैं। हालाँकि, जैसा कि नीचे विस्तृत किया गया है, क्वांटम यांत्रिकी में अवस्थाओं को समानता के वास्तविक निरूपण के अंतर्गत बदलने की आवश्यकता नहीं है, बल्कि केवल प्रक्षेपीय अभ्यावेदन के अंतर्गत और इसलिए सिद्धांत रूप में एक समानता परिवर्तन किसी भी चरण (तरंगों) द्वारा अवस्था को घुमा सकता है।

ओ (3) का निरूपण

अदिशों, छद्म अदिश, सदिश और स्यूडोसदिश के उपरोक्त वर्गीकरण को लिखने का एक वैकल्पिक तरीका अभ्यावेदन स्थान के संदर्भ में है जिसमें प्रत्येक वस्तु रूपांतरित होती है। यह समूह समरूपता $\rho$ के संदर्भ में दिया जा सकता है, जो अभ्यावेदन को परिभाषित करता है। एक आव्यूह $R\in {\text{O}}(3),$के लिए,

• अदिशों : $\rho (R)=1$, तुच्छ निरूपण
• स्यूडोस्कालर: $\rho (R)=\det(R)$
• सदिश : $\rho (R)=R$, मौलिक निरूपण
• स्यूडो सदिश : $\rho (R)=\det(R)R.$

जब तक अभ्यावेदन ${\text{SO}}(3)$प्रतिबंधित है, अदिश और स्यूडोअदिश समान रूप से रूपांतरित होते हैं, जैसा कि सदिश और स्यूडोसदिश करते हैं।

पारम्परिक यांत्रिकी

न्यूटन का गति का समीकरण $\mathbf {F} =m\mathbf {a}$ (यदि द्रव्यमान स्थिर है) दो सदिशों के समान है, और इसलिए समता के अंतर्गत अपरिवर्तनीय है। गुरुत्व के नियम में भी केवल सदिश सम्मिलित होते हैं और इसलिए समता के अंतर्गत अपरिवर्तनीय भी है।

हालाँकि, कोणीय गति $\mathbf {L}$ एक अक्षीय सदिश है,

${\begin{aligned}\mathbf {L} &=\mathbf {r} \times \mathbf {p} \\{\hat {P}}\left(\mathbf {L} \right)&=(-\mathbf {r} )\times (-\mathbf {p} )=\mathbf {L} .\end{aligned}}$

पारम्परिक वैद्युतगतिकी में, चार्ज घनत्व $\rho$ एक अदिश राशि है, विद्युत क्षेत्र, $\mathbf {E}$, और धारा $\mathbf {j}$ सदिश हैं, लेकिन चुंबकीय क्षेत्र, $\mathbf {B}$ एक अक्षीय सदिश है। हालाँकि, मैक्सवेल के समीकरण समता के अंतर्गत अपरिवर्तनीय हैं क्योंकि अक्षीय सदिश का कर्ल (गणित) एक सदिश है।

पारम्परिक भौतिक विज्ञान के कुछ चरों पर स्थानिक व्युत्क्रमण का प्रभाव

पारम्परिक भौतिक चर के दो प्रमुख विभाजनों में या तो सम या विषम समता है। जिस तरह से विशेष चर और सदिश किसी भी श्रेणी में वर्गीकृत किये जाते हैं, वह इस बात पर निर्भर करता है कि अंतरिक्ष के आयामों की संख्या विषम या सम संख्या है या नहीं। समता परिवर्तन के लिए विषम या नीचे दी गई श्रेणियां एक अलग, लेकिन घनिष्ठ रूप से संबंधित वितरण है।

नीचे दिए गए उत्तर 3 स्थानिक आयामों के लिए सही हैं। उदाहरण के लिए, 2 आयामी अंतरिक्ष में, जब किसी ग्रह की सतह पर बने रहने के लिए बाध्य किया जाता है, तो कुछ चर पक्ष बदलते हैं।

विषम

पारम्परिक चर जिनके संकेत अंतरिक्ष के व्युत्क्रम में व्युत्क्रमणीय होने पर फ़्लिप करते हैं, वे मुख्य रूप से सदिश होते हैं। वे सम्मिलित करते हैं:

• $h$, the helicity
• $\Phi$, the magnetic flux
• $\mathbf {x}$, the position of a particle in three-space
• $\mathbf {v}$, the velocity of a particle
• $\mathbf {a}$, the acceleration of the particle
• $\mathbf {p}$, the linear momentum of a particle
• $\rho \,\mathbf {v}$, mass flow
• $\mathbf {F}$, the force exerted on a particle
• $\mathbf {J}$, the electric current density
• $\mathbf {E}$, the electric field
• $\mathbf {D}$, the electric displacement field
• $\mathbf {P}$, the electric polarization
• $\mathbf {A}$, the electromagnetic vector potential
• $\mathbf {S}$, the Poynting vector (flow of electromagnetic power).

सम

पारम्परिक चर, मुख्य रूप से अदिश राशियाँ, जो स्थानिक व्युत्क्रम पर नहीं बदलती हैं, उनमें सम्मिलित हैं:

• $t$, the time when an event occurs
• $m$, the mass of a particle
• $E$, the energy of the particle
• $P$, power (rate of work done)
• $\rho$, the electric charge density
• $V$, the scalar electric potential (voltage)
• $\rho$, energy density of the electromagnetic field
• $\mathbf {L}$, the angular momentum of a particle (both orbital and spin) (axial vector)
• $\mathbf {B}$, the magnetic field (axial vector)
• $\mathbf {H}$, the auxiliary magnetic field
• $\mathbf {M}$, the magnetization
• $T_{ij}$, Maxwell stress tensor.
• All masses, charges, coupling constants, and other scalar physical constants, except those associated with the weak force.

क्वांटम यांत्रिकी

संभावित आइगेनवैल्यू

समानता के दो आयामी निरूपण क्वांटम अवस्थाओं की एक जोड़ी द्वारा दिए जाते हैं जो समता के अंतर्गत एक दूसरे में जाते हैं। हालांकि, इस निरूपण को सदैव अवस्थाओं के रैखिक संयोजनों में घटाया जा सकता है, जिनमें से प्रत्येक समता के अंतर्गत या तो विषम या विषम है। एक का कहना है कि समता के सभी अलघुकरणीय निरूपण एक आयामी हैं।

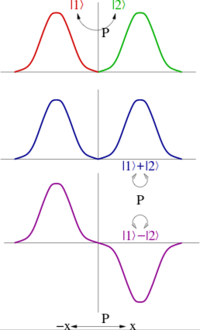
क्वांटम यांत्रिकी में, अंतरिक्षसमय परिवर्तन क्वांटम अवस्थाओं पर फलन करते हैं। समता परिवर्तन, ${\hat {\mathcal {P}}}$, एक एकात्मक संचालिका है, सामान्य रूप से अवस्था $\psi$ पर फलन करता है जो इस प्रकार है;

: ${\hat {\mathcal {P}}}\,\psi {\left(r\right)}=e^{{i\phi }/{2}}\psi {\left(-r\right)}$.

एक इस प्रकार होना चाहिए ${\hat {\mathcal {P}}}^{2}\,\psi {\left(r\right)}=e^{i\phi }\psi {\left(r\right)}$, चूंकि एक समग्र चरण अवकलन योग्य नहीं है। परिचालक ${\hat {\mathcal {P}}}^{2}$, जो एक अवस्था की समता को दो बार व्युत्क्रम करता है, अंतरिक्ष समय अपरिवर्तनीय छोड़ देता है, और इसी तरह एक आंतरिक समरूपता है जो चरणों द्वारा अपने आइजनस्टेट्स को घुमाती है जो अवयव $e^{i\phi }$ है| यदि ${\hat {\mathcal {P}}}^{2}$ एक अवयव है $e^{iQ}$ चरण घूर्णन के निरंतर U(1) समरूपता समूह की, फिर $e^{-iQ}$यह U(1) का भाग है और इसी प्रकार एक समरूपता भी है। विशेष रूप से, हम इस प्रकार परिभाषित कर सकते हैं ${\hat {\mathcal {P}}}'\equiv {\hat {\mathcal {P}}}\,e^{-{iQ}/{2}}$, जो एक समरूपता भी है, और इसलिए हम ${\hat {\mathcal {P}}}$. के के स्थान पर ${\hat {\mathcal {P}}}'$आवाहन के रूप में चुन सकते हैं| ध्यान दें कि ${{\hat {\mathcal {P}}}'}^{2}=1$ इसलिए ${\hat {\mathcal {P}}}'$ ईगेनवेल्यूज $\pm 1$ हैं| समता परिवर्तन के अंतर्गत ईगेनवेल्यूज +1 के साथ तरंग फलन सम और विषम फलन हैं, जबकि ईगेनवेल्यूज -1 विषम कार्यों से समरूप है। हालाँकि, जब ऐसा कोई समरूपता समूह उपस्थित नहीं होता है, तो यह हो सकता है कि सभी समता परिवर्तनों में कुछ ईजेनवेल्यूज़ हों जो $\pm 1$ के अलावा अन्य चरण हों |

इलेक्ट्रॉनिक तरंग फलन के लिए, यहां तक ​​​​कि अवस्थाओं को साधारणतः गेरेड (जर्मन: यहां तक) के लिए एक सबस्क्रिप्ट जी द्वारा इंगित किया जाता है और एक सबस्क्रिप्ट यू के लिए अनगेरेड (जर्मन: विषम) द्वारा विषम अवस्थाओं का संकेत दिया जाता है। उदाहरण के लिए, हाइड्रोजन अणु आयन का निम्नतम ऊर्जा स्तर (H₂⁺) $1\sigma _{g}$ चिह्नित किया गया है और अगला-निकटतम (उच्च) ऊर्जा स्तर $1\sigma _{u}$चिह्नित किया गया है|.

एक बाहरी क्षमता में जाने वाले कण के तरंग कार्य, जो कि सेंट्रोसिमेट्री है (अंतरिक्ष व्युत्क्रम के संबंध में संभावित ऊर्जा अपरिवर्तनीय, मूल के सममित), तरंग कार्यों की स्थिति या तो अपरिवर्तित रहते हैं या संकेत बदलते हैं: इन दो संभावित अवस्थाओं को सम अवस्था या विषम कहा जाता है ।

कणों की समता के संरक्षण के नियम में कहा गया है कि, यदि कणों के एक पृथक समूह में एक निश्चित समता है, तो समुच्चय के विकास की प्रक्रिया में समता अपरिवर्तित रहती है। हालांकि यह नाभिक के बीटा क्षय के लिए सही नहीं है) जो मन्द अंतःक्रिया समरूपता के उल्लंघन के कारण है। एक गोलाकार रूप से बाहरी क्षेत्र में गतिमान एक कण की अवस्थाओं की समता कोणीय संवेग संचालक द्वारा निर्धारित की जाती है, कुल ऊर्जा, कोणीय संवेग और कोणीय संवेग का प्रक्षेपण और कण अवस्था को तीन क्वांटम संख्याओं द्वारा परिभाषित किया जाता है।

समता समरूपता के परिणाम

जब समानता एबेलियन समूह ℤ उत्पन्न करती है₂, कोई सदैव क्वांटम अवस्थाओं के रैखिक संयोजन ले सकता है जैसे कि वे समता के अंतर्गत या तो विषम या विषम हैं (चित्र देखें)। इस प्रकार ऐसे अवस्थाओं की समता ±1 है। बहुकण अवस्था की समानता प्रत्येक अवस्था की समानता का उत्पाद है; दूसरे शब्दों में समता एक गुणक क्वांटम संख्या है।

क्वांटम यांत्रिकी में, हैमिल्टनियन (क्वांटम यांत्रिकी) एक समता परिवर्तन के अंतर्गत अपरिवर्तनीय (भौतिकी) (सममित) हैं यदि ${\hat {\mathcal {P}}}$ हैमिल्टन के साथ रूपान्तरित करते हैं। गैर-सापेक्षवादी क्वांटम यांत्रिकी में, यह किसी भी अदिश क्षमता के लिए होता है, अर्थात, $V=V{\left(r\right)}$, इसलिए क्षमता गोलाकार रूप से है। निम्नलिखित तथ्यों को आसानी से सिद्ध किया जा सकता है:

• यदि $\left|\varphi \right\rangle$ और $\left|\psi \right\rangle$ फिर समान समानता है $\left\langle \varphi \left|{\hat {X}}\right|\psi \right\rangle =0$ जहाँ ${\hat {X}}$ स्थिति संचालिका है।
• अवस्था के लिए $\left|{\vec {L}},L_{z}\right\rangle$ कक्षीय कोणीय गति का ${\vec {L}}$ जेड-अक्ष प्रक्षेपण के साथ $L_{z}$, तब ${\hat {\mathcal {P}}}\left|{\vec {L}},L_{z}\right\rangle =\left(-1\right)^{L}\left|{\vec {L}},L_{z}\right\rangle$.
• यदि $\left[{\hat {H}},{\hat {P}}\right]=0$, तो परमाणु द्विध्रुव पारगमन केवल विपरीत समता की अवस्थाओं के बीच होता है।
• यदि $\left[{\hat {H}},{\hat {P}}\right]=0$, फिर एक गैर-पतित स्वदेशी ${\hat {H}}$ समता संचालिका का आइजनस्टेट भी है; यानी, का एक गैर-पतित ईजेनफंक्शन ${\hat {H}}$ या तो अपरिवर्तनीय है ${\hat {\mathcal {P}}}$ या इसके द्वारा साइन इन करके बदला जाता है ${\hat {\mathcal {P}}}$... ...

के कुछ गैर-पतित ईजेनफंक्शन ${\hat {H}}$ समानता से अप्रभावित (अपरिवर्तनीय) हैं ${\hat {\mathcal {P}}}$ और अन्य केवल संकेत में उलट जाते हैं जब हैमिल्टनियन संचालक और समता संचालक कम्यूट करते हैं:

${\hat {\mathcal {P}}}\left|\psi \right\rangle =c\left|\psi \right\rangle ,$

जहाँ $c$ एक स्थिर है, का ईगेनवेल्यूज ${\hat {\mathcal {P}}}$,

${\hat {\mathcal {P}}}^{2}\left|\psi \right\rangle =c\,{\hat {\mathcal {P}}}\left|\psi \right\rangle .$

बहु-कण प्रणालियाँ: परमाणु, अणु, नाभिक

बहु-कण प्रणाली की समग्र समानता एक-कण अवस्थाओं की समानता का उत्पाद है। यह -1 है यदि विषम संख्या में कण विषम-समता अवस्था में हैं, और +1 अन्यथा। नाभिक, परमाणु और अणुओं की समानता को दर्शाने के लिए विभिन्न संकेतन उपयोग में हैं।

परमाणु

परमाणु कक्षकों में समता (−1) होती है^ℓ, जहां घातांक ℓ अज़ीमुथल क्वांटम संख्या है। ℓ = 1, 3, ... के साथ कक्षकों p, f, ... के लिए समता विषम होती है और यदि इन कक्षकों में इलेक्ट्रॉनों की विषम संख्या होती है तो परमाणु अवस्था में विषम समता होती है। उदाहरण के लिए, नाइट्रोजन परमाणु की मूल अवस्था में इलेक्ट्रॉन विन्यास 1s होता है²2s²2p³, और शब्द प्रतीक द्वारा पहचाना जाता है ⁴एस^o, जहां सुपरस्क्रिप्ट o विषम समता दर्शाता है। हालाँकि तीसरा उत्साहित शब्द लगभग 83,300 सेमी पर है^-1 जमीनी अवस्था के ऊपर इलेक्ट्रॉन विन्यास 1s है²2s²2p²3s में सम समानता है क्योंकि केवल दो 2p इलेक्ट्रॉन हैं, और इसका शब्द प्रतीक ⁴P है (ओ सुपरस्क्रिप्ट के बिना)|।

अणु

किसी भी अणु का पूर्ण (घूर्णी-कंपन-इलेक्ट्रॉनिक-परमाणु स्पिन) विद्युत चुम्बकीय हैमिल्टनियन समता संक्रिया पी (या ई *) के साथ (या अपरिवर्तनीय है) क्रिस्टोफर लॉन्गेट-हिगिंस द्वारा प्रस्तुत किए गए संकेत चिन्ह में। लॉन्गेट-हिगिंस।) और इसके आइगेनवैल्यू को समता समरूपता लेबल + या - दिया जा सकता है क्योंकि वे क्रमशः सम या विषम हैं। समता संक्रिया में द्रव्यमान के आणविक केंद्र पर इलेक्ट्रॉनिक और परमाणु स्थानिक निर्देशांक का व्युत्क्रम सम्मिलित होता है।

साम्यवस्था पर सेंट्रोसिमेट्रिक अणुओं में उनके मध्य बिंदु (द्रव्यमान का परमाणु केंद्र) पर समरूपता का केंद्र होता है। इसमें सभी समनाभिकीय डायटोमिक अणु ओं के साथ-साथ ईथीलीन, बेंजीन, क्सीनन टेट्राफ्लोराइड और सल्फर हेक्साफ्लोराइड जैसे कुछ अणु सम्मिलित हैं। सेंट्रोसिमेट्रिक अणुओं के लिए, बिंदु समूह में संक्रिया i होता है, जिसे पैरिटी संक्रिया के साथ भ्रमित नहीं होना है। संक्रिया i में द्रव्यमान के परमाणु केंद्र पर इलेक्ट्रॉनिक और कंपन विस्थापन निर्देशांक का व्युत्क्रम सम्मिलित है। सेंट्रोसिमेट्रिक अणुओं के लिए संक्रिया 'i' रोविब्रॉनिक (घूर्णन -कंपन-इलेक्ट्रॉनिक) हैमिल्टनियन के साथ शुरू होता है और ऐसे अवस्थाओं को लेबल करने के लिए प्रयोग किया जा सकता है। सेंट्रोसिमेट्रिक अणुओं के इलेक्ट्रॉनिक और कंपन अवस्था या तो संक्रिया 'i' द्वारा अपरिवर्तित हैं, या वे 'i' द्वारा साइन में बदल दिए गए हैं। पूर्व को सबस्क्रिप्ट जी द्वारा निरूपित किया जाता है और इसे गेरेड कहा जाता है, जबकि बाद वाले को सबस्क्रिप्ट यू द्वारा निरूपित किया जाता है और इसे अनग्रेड कहा जाता है। एक सेंट्रोसिमेट्रिक अणु का पूरा हैमिल्टनियन परमाणु हाइपरफाइन हैमिल्टनियन के प्रभाव के कारण पॉइंट ग्रुप इनवर्जन संक्रिया i के साथ कम्यूट नहीं करता है। परमाणु हाइपरफाइन हैमिल्टनियन जी और यू कंपट्रानीय अवस्था (जिसे ऑर्थो-पैरा मिक्सिंग कहा जाता है) के घूर्णी स्तरों को मिला सकते हैं और ऑर्थो-पैरा पारगमन को उत्तपन कर सकते हैं|

नाभिक

परमाणु नाभिक में, प्रत्येक न्यूक्लियॉन (प्रोटॉन या न्यूट्रॉन) की स्थिति सम या विषम समता होती है, और परमाणु कॉन्फ़िगरेशन का अनुमान परमाणु शेल मॉडल का उपयोग करके लगाया जा सकता है। परमाणुओं में इलेक्ट्रॉनों के लिए, न्यूक्लियॉन अवस्था में विषम समग्र समता होती है यदि और केवल विषम-समता वाले अवस्थाओं में न्यूक्लियंस की संख्या विषम होती है। समता को साधारणतः परमाणु स्पिन मान के बाद + (सम) या - (विषम) के रूप में लिखा जाता है। उदाहरण के लिए, ऑक्सीजन के समस्थानिक ों में सम्मिलित हैं ¹⁷O(5/2+), जिसका अर्थ है कि घुमाव 5/2 है और समता सम है। शेल मॉडल इसे समझाता है क्योंकि पहले 16 न्यूक्लियॉन जोड़े जाते हैं ताकि प्रत्येक जोड़ी में स्पिन शून्य और समता हो, और अंतिम न्यूक्लियॉन 1d में हो_5/2 खोल, जिसमें d कक्षक के लिए ℓ = 2 के बाद से समता है।

क्वांटम क्षेत्र सिद्धांत

इस खंड में आंतरिक समता असाइनमेंट सापेक्षवादी क्वांटम यांत्रिकी के साथ-साथ क्वांटम क्षेत्र सिद्धांत के लिए सही हैं।

यदि कोई दिखा सकता है कि निर्वात अवस्था समता के अंतर्गत अपरिवर्तनीय है, ${\hat {\mathcal {P}}}\left|0\right\rangle =\left|0\right\rangle$, हैमिल्टन समता $\left[{\hat {H}},{\hat {\mathcal {P}}}\right]$अपरिवर्तनीय है और परिमाणीकरण की स्थिति समता के अंतर्गत अपरिवर्तित रहती है, तो यह इस प्रकार है कि प्रत्येक अवस्था में अच्छी क्वांटम संख्या समानता है, और यह समता किसी भी प्रतिक्रिया में संरक्षित है।

यह दिखाने के लिए कि क्वांटम इलेक्ट्रोडायनामिक्स समता के अंतर्गत अपरिवर्तनीय है, हमें यह साबित करना होगा कि क्रिया अपरिवर्तनीय है और परिमाणीकरण भी अपरिवर्तनीय है। सरलता के लिए हम मानेंगे कि विहित परिमाणीकरण का उपयोग किया जाता है; निर्वात अवस्था तब निर्माण द्वारा समता के अंतर्गत अपरिवर्तनीय होती है। कार्रवाई का व्युत्क्रम मैक्सवेल के समीकरणों के पारम्परिक निश्चरता से अनुसरण करता है। विहित परिमाणीकरण प्रक्रिया के निश्चरता पर काम किया जा सकता है, और यह अभाव संचालक के परिवर्तन पर निर्भर करता है|:

पा (पी, ±) पी⁺ = −a(−p, ±)

जहाँ p एक फोटॉन की गति को दर्शाता है और ± इसकी ध्रुवीकरण अवस्था को दर्शाता है। यह इस कथन के समतुल्य है कि फोटॉन में विषम आंतरिक समता है। इसी प्रकार सभी सदिश बोसॉनों में विषम आंतरिक समता दिखाई जा सकती है, और सभी स्यूडोसदिश मेसन | अक्षीय-सदिश ों में समान आंतरिक समता दिखाई जा सकती है।

अदिश क्षेत्र सिद्धांतों के लिए इन तर्कों का सीधा विस्तार दर्शाता है कि अदिशों में समता है, चूँकि

पा (पी) पी⁺ = a(−p).

यह एक जटिल अदिश क्षेत्र के लिए भी सत्य है। (डिराक समीकरण पर लेख में स्पिनरों का विवरण दिया गया है, जहां यह दिखाया गया है कि फ़र्मियन और एंटी फर्मियन में विपरीत आंतरिक समानता है।)

फ़र्मियन्स के साथ, थोड़ी जटिलता है क्योंकि एक से अधिक स्पिन समूह हैं।

मानक मॉडल में समानता

वैश्विक समरूपता को ठीक करना

See also: (−1)^F

समता संचालक को दो बार लागू करने से निर्देशांक अपरिवर्तित रह जाते हैं, जिसका अर्थ है P² सिद्धांत के आंतरिक समरूपता में चरण को बदलने पर, एक अवस्था के रूप में कार्य करना चाहिए, अवस्था के चरण को बदलने पर। उदाहरण के लिए, मानक मॉडल में तीन वैश्विक वृत्त समूह हैं। यू (1) समरूपताएं बैरियन संख्या के समान शुल्क के साथ B, लेप्टान संख्या L, और बिजली का आवेश Q. इसलिए, समता संचालक संतुष्ट करता है P² = e^{iαB+iβL+iγQ} किसी विकल्प के लिए α, β, और γ. यह संचालक भी एक नए समता संचालक के रूप में अद्वितीय नहीं है P' इसे आंतरिक समरूपता जैसे गुणा करके सदैव बनाया जा सकता है P' = P e^iαB कुछ के लिए α.

यह देखने के लिए कि क्या समानता संचालक को सदैव संतुष्ट करने के लिए परिभाषित किया जा सकता है P² = 1, सामान्य मामले पर विचार करें जब P² = Q कुछ आंतरिक समरूपता के लिए Q सिद्धांत में उपस्थित है। वांछित समता संचालक होगा P' = PQ^−1/2. यदि Q एक सतत समरूपता समूह का भाग है Q^−1/2 उपस्थित है, लेकिन अगर यह असतत समरूपता का भाग है तो इस अवयव की उपस्थिति की आवश्यकता नहीं है और ऐसी पुनर्वितरण संभव नहीं हो सकता है।

मानक मॉडल एक (−1)^F समरूपता प्रदर्शित करता है (−1)^F, जहाँ F फर्मियन कण संख्या संचालक यह गिनता है कि एक अवस्था में कितने फ़र्मियन हैं। यदि समता संचालिका संतुष्ट है चूंकि मानक मॉडल में सभी कण संतुष्ट करते हैं F = B + Lअसतत समरूपता भी इसका भाग है e^{iα(B + L)} निरंतर समरूपता समूह।P² = (−1)^F, तो इसे एक नया समता संचालक संतोषजनक देने के लिए पुनर्परिभाषित किया जा सकता है P² = 1. लेकिन अगर मेजराना फर्मियन न्युट्रीनो को सम्मिलित करके स्टैंडर्ड मॉडल को बढ़ाया जाए, जिसमें है F = 1 और B + L = 0, फिर असतत समरूपता (−1)^F अब निरंतर समरूपता समूह का भाग नहीं है और समता संचालिका की वांछित पुनर्परिभाषा नहीं की जा सकती है। इसके बजाय यह संतुष्ट करता है P⁴ = 1 इसलिए मेजराना न्यूट्रिनो में आंतरिक समता ±i होगी|

पियन की समता

1954 में, विलियम चिनोवस्की और जैक स्टाइनबर्गर के एक पेपर ने प्रदर्शित किया कि पिओन में नकारात्मक समता है।

उन्होंने एक [[दूसरे | दूसरे (²
₁H⁺
)]] से बने परमाणु के क्षय का अध्ययन किया और एक नकारात्मक रूप से चार्ज किया गया पियन (
π⁻
) शून्य कक्षीय कोणीय गति वाली अवस्था में $~\mathbf {L} ={\boldsymbol {0}}~$ दो न्यूट्रॉन में ($n$) है|

न्यूट्रॉन फ़र्मियन हैं और इसलिए फ़र्मी-डिराक आँकड़ों का पालन करते हैं, जिसका अर्थ है कि अंतिम अवस्था विषम है। इस तथ्य का उपयोग करते हुए कि ड्यूटेरॉन में स्पिन एक है और पिओन स्पिन शून्य है, साथ में अंतिम अवस्था के एंटीसिमेट्री के साथ उन्होंने निष्कर्ष निकाला है कि दो न्यूट्रॉन में कक्षीय कोणीय $~L=1~.$गति होनी चाहिए | कुल समता कणों की आंतरिक समता और गोलाकार हार्मोनिक फ़ंक्शन की बाह्य समता का उत्पाद है $~\left(-1\right)^{L}~.$है | चूंकि इस प्रक्रिया में कक्षीय गति शून्य से एक में बदल जाती है, अगर प्रक्रिया को कुल समता को बनाए रखना है तो प्रारंभिक और अंतिम कणों के आंतरिक समता के उत्पादों के विपरीत संकेत होना चाहिए। एक ड्यूटेरॉन नाभिक एक प्रोटॉन और एक न्यूट्रॉन से बना है, और इसलिए पूर्वोक्त परिपाटी का उपयोग करते हुए कि प्रोटॉन और न्यूट्रॉन के समान आंतरिक समताएं $~+1~$ हैं उन्होंने तर्क दिया कि पिओन की समता दो न्यूट्रॉनों की समताओं के गुणनफल के ऋण के समान होती है, जिसे ड्यूटेरॉन में प्रोटॉन और न्यूट्रॉन द्वारा विभाजित किया जाता है, स्पष्ट रूप से ${\textstyle {\frac {(-1)(1)^{2}}{(1)^{2}}}=-1~,}$ जिससे उन्होंने निष्कर्ष निकाला कि पियन एक स्यूडोअदिश कण है।

समता उल्लंघन

See also: Wu experiment

हालांकि समानता विद्युत चुंबकत्व और गुरुत्वाकर्षण में संरक्षित है, यह मन्द अंतःक्रिया में उल्लंघन करती है, और शायद कुछ हद तक मजबूत अंतःक्रिया में।मानक मॉडल मन्द अंतःक्रिया को चिरायता (भौतिकी) गेज इंटरैक्शन के रूप में व्यक्त करके समता उल्लंघन को सम्मिलित करता है। कणों के केवल बाएं हाथ के घटक और एंटीपार्टिकल्स के दाएं हाथ के घटक मानक मॉडल में आवेशित मन्द अंतःक्रियाओं में भाग लेते हैं। इसका तात्पर्य यह है कि समता हमारे ब्रह्मांड की समरूपता नहीं है, जब तक कि कोई दर्पण पदार्थ उपस्थित नहीं है जिसमें समता का विपरीत तरीके से उल्लंघन किया जाता है।

आर.टी. कॉक्स, जी.सी. मैक्लव्रेथ, और बी. कुर्रेलमेयर द्वारा किए गए एक अस्पष्ट 1928 प्रयोग ने प्रभावी रूप से मन्द क्षय में समता उल्लंघन की सूचना दी थी, लेकिन चूंकि उपयुक्त अवधारणा अभी तक विकसित नहीं हुई थी, इसलिए उन परिणामों का कोई प्रभाव नहीं पड़ा। 1929 में, हरमन वेइल ने बिना किसी सबूत के, स्पिन के आधे हिस्से के दो-घटक द्रव्यमान रहित कण के अस्तित्व की खोज की। इस विचार को पाउली ने अस्वीकार कर दिया, क्योंकि इसमें समानता का उल्लंघन निहित था। 20वीं शताब्दी के मध्य तक, कई वैज्ञानिकों द्वारा यह सुझाव दिया गया था कि समता को (विभिन्न संदर्भों में) संरक्षित नहीं किया जा सकता है, लेकिन ठोस सबूत के बिना इन सुझावों को महत्वपूर्ण नहीं माना जाता था। फिर, 1956 में, सैद्धांतिक भौतिकविदों त्सुंग-दाओ ली और यांग चेन-एन आईएनजी | चेन-निंग यांग द्वारा सावधानीपूर्वक समीक्षा और विश्लेषण दिया गया है|

यह दर्शाता है कि समता संरक्षण को मजबूत या विद्युत चुम्बकीय अंतःक्रिया से क्षय में सत्यापित किया गया था, यह मन्द अंतःक्रिया में परीक्षण नहीं किया गया था। उन्होंने कई संभावित प्रत्यक्ष प्रयोगात्मक परीक्षण प्रस्तावित किए। उन्हें ज्यादातर नजरअंदाज कर दिया गया, लेकिन ली अपने कोलंबिया के सहयोगी χ en-shi UN GW यू को इसे आजमाने के लिए मनाने में सक्षम थे। उसे विशेष क्रायोजेनिक सुविधाओं और विशेषज्ञता की आवश्यकता थी, इसलिए प्रयोग राष्ट्रीय मानक ब्यूरो में किया गया था।

चिएन-शिउंग वू, अर्नेस्ट एंबलर, हेवर्ड, हॉप्स और हडसन (1957) ने कोबाल्ट-60 के बीटा क्षय में समता संरक्षण का स्पष्ट उल्लंघन पाया। जैसा कि प्रयोग समाप्त हो रहा था, डबल-चेकिंग प्रगति पर थी, वू ने ली और यांग को उनके सकारात्मक परिणामों के बारे में सूचित किया, और कहा कि परिणामों को आगे की परीक्षा की आवश्यकता है, उन्होंने उनसे पहले परिणामों को प्रचारित न करने के लिए कहा। हालांकि, ली ने 4 जनवरी 1957 को कोलंबिया के भौतिक विज्ञान विभाग के शुक्रवार दोपहर के भोजन समारोह में अपने कोलंबिया सहयोगियों के सामने परिणामों का खुलासा किया। उनमें से तीन, रिचर्ड गारविन|आर.एल. गारविन, लियोन लेडरमैन|एल.एम. लेडरमैन, और आर.एम. वेनरिच ने एक मौजूदा साइक्लोट्रॉन प्रयोग को संशोधित किया, और उन्होंने तुरंत समता उल्लंघन की पुष्टि की। वू के समूह के तैयार होने तक उन्होंने अपने परिणामों के प्रकाशन में देरी की, और दो पेपर एक ही भौतिक विज्ञान पत्रिका में बैक-टू-बैक दिखाई दिए।

समता उल्लंघन की खोज ने काओन की भौतिकी में उत्कृष्ट τ-θ पहेली को तुरंत समझाया।

2010 में, यह बताया गया कि सापेक्षवादी भारी आयन कोलाइडर के साथ काम करने वाले भौतिकविदों ने क्वार्क-ग्लूऑन प्लास्मा में एक अल्पकालिक समता समरूपता-भंग बुलबुला बनाया था। स्टार सहयोग में कई भौतिकविदों द्वारा किए गए एक प्रयोग ने सुझाव दिया कि मजबूत अंतःक्रिया में समता का भी उल्लंघन हो सकता है। यह भविष्यवाणी की जाती है कि यह स्थानीय समता उल्लंघन, जो उस प्रभाव के अनुरूप होगा जो अक्षीय क्षेत्र के उतार-चढ़ाव से प्रेरित होता है, खुद को चिरल चुंबकीय प्रभाव से प्रकट करता है।

हैड्रान की आंतरिक समता

जब तक प्रकृति समता को बनाए रखती है, तब तक प्रत्येक कण को ​​एक आंतरिक समानता प्रदान की जा सकती है। हालांकि मन्द अंतःक्रियाएं नहीं होती हैं, फिर भी कोई भी मजबूत अंतःक्रियात्मक प्रतिक्रिया की परीक्षण करके किसी भी हैड्रोन को समता प्रदान कर सकता है, या मन्द अंतःक्रिया को सम्मिलित नहीं करने वाले क्षय के माध्यम से, जैसे कि रो मेसन क्षय से लेकर पियन तक।

यह भी देखें

• सी-समरूपता
• सीपी उल्लंघन
• विद्युत मन्द सिद्धांत
• मिरर मैटर
• आणविक समरूपता
• टी-समरूपता

संदर्भ

Footnotes

Citations

स्रोत

• Perkins, Donald H. (2000). उच्च ऊर्जा भौतिकी का परिचय. ISBN 9780521621960.
• Sozzi, M. S. (2008). असतत समरूपता और सीपी उल्लंघन. Oxford University Press. ISBN 978-0-19-929666-8.
• Bigi, I. I.; Sanda, A. I. (2000). सीपी उल्लंघन. Cambridge Monographs on Particle Physics, Nuclear Physics and Cosmology. Cambridge University Press. ISBN 0-521-44349-0.
• Weinberg, S. (1995). खेतों की क्वांटम थ्योरी. Cambridge University Press. ISBN 0-521-67053-5.