प्रक्षेप (रैखिक बीजगणित): Difference between revisions
m (Abhishek moved page एक बिन्दु से एक रेखा की दूरी to बिन्दु से रेखा की दूरी without leaving a redirect) |
No edit summary |
||
| Line 2: | Line 2: | ||
[[यूक्लिडियन ज्यामिति]] में, एक बिंदु से एक रेखा तक की दूरी किसी दिए गए [[बिंदु (ज्यामिति)]] से एक अनंत [[रेखा (गणित)]] पर किसी भी बिंदु तक की सबसे छोटी [[यूक्लिडियन दूरी]] होती है। यह बिंदु की रेखा से [[लंबवत दूरी]] है, [[रेखा खंड]] की लंबाई जो बिंदु को रेखा पर निकटतम बिंदु से जोड़ती है। इसकी गणना करने का सूत्र कई तरीकों से निकाला और व्यक्त किया जा सकता है। | [[यूक्लिडियन ज्यामिति]] में, एक बिंदु से एक रेखा तक की दूरी किसी दिए गए [[बिंदु (ज्यामिति)]] से एक अनंत [[रेखा (गणित)]] पर किसी भी बिंदु तक की सबसे छोटी [[यूक्लिडियन दूरी]] होती है। यह बिंदु की रेखा से [[लंबवत दूरी]] है, [[रेखा खंड]] की लंबाई जो बिंदु को रेखा पर निकटतम बिंदु से जोड़ती है। इसकी गणना करने का सूत्र कई तरीकों से निकाला और व्यक्त किया जा सकता है। | ||
एक बिंदु से एक रेखा तक की दूरी को जानना विभिन्न स्थितियों में उपयोगी हो सकता है—उदाहरण के लिए, एक सड़क तक पहुँचने के लिए सबसे छोटी दूरी का पता लगाना, एक ग्राफ पर | एक बिंदु से एक रेखा तक की दूरी को जानना विभिन्न स्थितियों में उपयोगी हो सकता है—उदाहरण के लिए, एक सड़क तक पहुँचने के लिए सबसे छोटी दूरी का पता लगाना, एक ग्राफ पर प्रकीर्णन की मात्रा निर्धारित करना, आदि। [[डेमिंग प्रतिगमन]] में, एक प्रकार का रेखीय [[Index.php?title=वक्र समंजन|वक्र समंजन]], यदि आश्रित और स्वतंत्र चर के समान भिन्नता होती है जिसके परिणामस्वरूप [[Index.php?title=लांबिक प्रतिगमन|लांबिक प्रतिगमन]] होता है जिसमें योग्य की अपूर्णता की डिग्री प्रत्येक दत्तानुसारी बिन्दु के लिए प्रतिगमन रेखा से बिंदु की लंबवत दूरी के रूप में मापी जाती है। | ||
<!--''This '''picture''' is a stub. You can help Wikipedia by improving it.'' | <!--''This '''picture''' is a stub. You can help Wikipedia by improving it.'' | ||
| Line 10: | Line 10: | ||
== एक समीकरण द्वारा परिभाषित रेखा == | == एक समीकरण द्वारा परिभाषित रेखा == | ||
समीकरण द्वारा दिए गए | समीकरण द्वारा दिए गए समतल में एक रेखा के मामले में {{math|1=''ax'' + ''by'' + ''c'' = 0}}, जहाँ {{mvar|a}}, {{mvar|b}} और {{mvar|c}} [[वास्तविक संख्या]] स्थिरांक हैं {{mvar|a}} और {{mvar|b}} दोनों शून्य नहीं हैं, रेखा से एक बिंदु तक की दूरी {{math|(''x''<sub>0</sub>, ''y''<sub>0</sub>)}} है<ref>{{harvnb|Larson|Hostetler|2007|loc=p. 452}}</ref><ref>{{harvnb|Spain|2007}}</ref>{{rp|p.14}} | ||
:<math>\operatorname{distance}(ax+by+c=0, (x_0, y_0)) = \frac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}}. </math> | :<math>\operatorname{distance}(ax+by+c=0, (x_0, y_0)) = \frac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}}. </math> | ||
इस रेखा पर वह बिंदु जो सबसे निकट है {{math|(''x''<sub>0</sub>, ''y''<sub>0</sub>)}} निर्देशांक हैं:<ref name="Larson 2007 loc=p. 522">{{harvnb|Larson|Hostetler|2007|loc=p. 522}}</ref> | इस रेखा पर वह बिंदु जो सबसे निकट है {{math|(''x''<sub>0</sub>, ''y''<sub>0</sub>)}} निर्देशांक हैं:<ref name="Larson 2007 loc=p. 522">{{harvnb|Larson|Hostetler|2007|loc=p. 522}}</ref> | ||
:<math>x = \frac{b(bx_0 - ay_0)-ac}{a^2 + b^2} \text{ and } y = \frac{a(-bx_0 + ay_0) - bc}{a^2+b^2}.</math> | :<math>x = \frac{b(bx_0 - ay_0)-ac}{a^2 + b^2} \text{ and } y = \frac{a(-bx_0 + ay_0) - bc}{a^2+b^2}.</math> | ||
क्षैतिज और लंबवत रेखाएं | '''क्षैतिज और लंबवत रेखाएं''' | ||
एक रेखा के सामान्य समीकरण में, {{math|1=''ax'' + ''by'' + ''c'' = 0}}, {{mvar|a}} और {{mvar|b}} जब तक दोनों शून्य नहीं हो सकते {{mvar|c}} भी शून्य है, | एक रेखा के सामान्य समीकरण में, {{math|1=''ax'' + ''by'' + ''c'' = 0}}, {{mvar|a}} और {{mvar|b}} जब तक दोनों शून्य नहीं हो सकते {{mvar|c}} भी शून्य है, इस स्थिति में समीकरण एक रेखा को परिभाषित नहीं करता है। अगर {{math|1=''a'' = 0}} और {{math|''b'' ≠ 0}}, रेखा क्षैतिज है और समीकरण है {{math|1=''y'' = −{{sfrac|''c''|''b''}}}}. से दूरी {{math|(''x''<sub>0</sub>, ''y''<sub>0</sub>)}} इस रेखा को लंबाई के एक ऊर्ध्वाधर रेखा खंड के साथ मापा जाता है {{math|1={{!}}''y''<sub>0</sub> − (−{{sfrac|''c''|''b''}}){{!}} = {{sfrac|{{!}}''by''<sub>0</sub> + ''c''{{!}}|{{!}}''b''{{!}}}}}} सूत्र के अनुसार। इसी प्रकार, ऊर्ध्वाधर रेखाओं के लिए (b = 0) समान बिंदु और रेखा के बीच की दूरी है {{math|1={{sfrac|{{!}}''ax''<sub>0</sub> + ''c''{{!}}|{{!}}''a''{{!}}}} }}, जैसा कि एक क्षैतिज रेखा खंड के साथ मापा जाता है। | ||
== दो बिंदुओं द्वारा परिभाषित रेखा == | == दो बिंदुओं द्वारा परिभाषित रेखा == | ||
यदि रेखा दो बिन्दुओं से होकर गुजरती है {{math|1=''P''<sub>1</sub> = (''x''<sub>1</sub>, ''y''<sub>1</sub>)}} और {{math|1=''P''<sub>2</sub> = (''x<sub>2</sub>'', ''y<sub>2</sub>'')}} फिर | यदि रेखा दो बिन्दुओं से होकर गुजरती है {{math|1=''P''<sub>1</sub> = (''x''<sub>1</sub>, ''y''<sub>1</sub>)}} और {{math|1=''P''<sub>2</sub> = (''x<sub>2</sub>'', ''y<sub>2</sub>'')}} फिर लाइन से दूरी {{math|(''x''<sub>0</sub>, ''y''<sub>0</sub>)}} है:<ref name=GEO /> | ||
इस व्यंजक | |||
<nowiki>:</nowiki><math>\operatorname{distance}(P_1, P_2, (x_0, y_0)) = \frac{|(x_2-x_1)(y_1-y_0)-(x_1-x_0)(y_2-y_1)|}{\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}}. </math> | |||
इस व्यंजक के भाजक के बीच की दूरी है {{math|''P''<sub>1</sub>}} और {{math|''P''<sub>2</sub>}}. अंश तीन बिंदुओं पर इसके शीर्षों के साथ त्रिभुज के क्षेत्रफल का दुगुना है, {{math|(''x''<sub>0</sub>, ''y''<sub>0</sub>)}}, {{math|''P''<sub>1</sub>}} और {{math|''P''<sub>2</sub>}}. देखना: {{slink|त्रिभुज का क्षेत्रफल|निर्देशांकों का उपयोग}}. अभिव्यक्ति के बराबर है {{math|1=''h'' = {{sfrac|2''A''|''b''}}}}, जिसे त्रिभुज के क्षेत्रफल के लिए मानक सूत्र को पुनर्व्यवस्थित करके प्राप्त किया जा सकता है: {{math|1=''A'' = {{sfrac|1|2}} ''bh''}}, जहाँ {{mvar|b}} भुजा की लंबाई है, और {{mvar|h}} विपरीत शीर्ष से लंबवत ऊंचाई है। | |||
== बिंदु और कोण द्वारा परिभाषित रेखा == | == बिंदु और कोण द्वारा परिभाषित रेखा == | ||
| Line 33: | Line 36: | ||
यह प्रमाण केवल तभी मान्य होता है जब रेखा न तो लंबवत हो और न ही क्षैतिज, यानी हम मानते हैं कि न तो {{mvar|a}} और न {{mvar|b}} रेखा के समीकरण में शून्य है। | यह प्रमाण केवल तभी मान्य होता है जब रेखा न तो लंबवत हो और न ही क्षैतिज, यानी हम मानते हैं कि न तो {{mvar|a}} और न {{mvar|b}} रेखा के समीकरण में शून्य है। | ||
समीकरण वाली रेखा {{math|1=''ax'' + ''by'' + ''c'' = 0}} में | समीकरण वाली रेखा {{math|1=''ax'' + ''by'' + ''c'' = 0}} में ढाल है {{math|−''a''/''b''}}, इसलिए इसके लम्बवत किसी भी रेखा पर ढाल होगा {{math|''b''/''a''}} (नकारात्मक पारस्परिक)।माना (m, n) रेखा ax + by + c = 0 का प्रतिच्छेदन बिंदु है और रेखा इसके लंबवत है जो बिंदु (x0, y0) से गुजरती है। इन दो बिंदुओं के माध्यम से रेखा मूल रेखा के लंबवत है, इसलिए | ||
:<math>\frac{y_0 - n}{x_0 - m}=\frac{b}{a}.</math> | :<math>\frac{y_0 - n}{x_0 - m}=\frac{b}{a}.</math> | ||
इस प्रकार, | इस प्रकार, | ||
| Line 39: | Line 42: | ||
और इस समीकरण का वर्ग करके हम प्राप्त करते हैं: | और इस समीकरण का वर्ग करके हम प्राप्त करते हैं: | ||
:<math>a^2(y_0 - n)^2 + b^2(x_0 - m)^2 = 2ab(y_0 - n)(x_0 - m).</math> | :<math>a^2(y_0 - n)^2 + b^2(x_0 - m)^2 = 2ab(y_0 - n)(x_0 - m).</math> | ||
अब विचार | अब विचार कीजिए, | ||
:<math> | :<math> | ||
\begin{align} | \begin{align} | ||
| Line 46: | Line 49: | ||
\end{align} | \end{align} | ||
</math> | </math> | ||
उपरोक्त वर्ग समीकरण का उपयोग करना। लेकिन हमारे पास | उपरोक्त वर्ग समीकरण का उपयोग करना। लेकिन हमारे पास है, | ||
:<math> (a(x_0 - m) + b(y_0 - n))^2 = (ax_0 + by_0 - am - bn)^2 = (ax_0 + by_0 + c)^2</math> | :<math> (a(x_0 - m) + b(y_0 - n))^2 = (ax_0 + by_0 - am - bn)^2 = (ax_0 + by_0 + c)^2</math> | ||
चूँकि (m, n) ax + by + c = 0 पर है। इस प्रकार, | |||
इस प्रकार, | |||
:<math>\left(a^2 + b^2\right) \left((x_0 - m)^2 + (y_0 - n)^2\right) = (ax_0 + by_0 + c)^2 </math> | :<math>\left(a^2 + b^2\right) \left((x_0 - m)^2 + (y_0 - n)^2\right) = (ax_0 + by_0 + c)^2 </math> | ||
और हम इन दो बिंदुओं द्वारा निर्धारित रेखा खंड की लंबाई प्राप्त करते हैं, | और हम इन दो बिंदुओं द्वारा निर्धारित रेखा खंड की लंबाई प्राप्त करते हैं, | ||
| Line 57: | Line 59: | ||
=== एक ज्यामितीय प्रमाण === | === एक ज्यामितीय प्रमाण === | ||
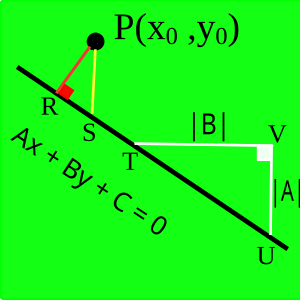
[[File:point-to-line2.svg|thumb|ज्यामितीय प्रमाण के लिए आरेख]]यह प्रमाण तभी मान्य होता है जब रेखा क्षैतिज या लंबवत न हो।<ref>{{harvnb|Ballantine|Jerbert|1952}} do not mention this restriction in their article</ref> | [[File:point-to-line2.svg|thumb|ज्यामितीय प्रमाण के लिए आरेख]]यह प्रमाण तभी मान्य होता है जब रेखा क्षैतिज या लंबवत न हो।<ref>{{harvnb|Ballantine|Jerbert|1952}} do not mention this restriction in their article</ref> | ||
निर्देशांक (x<sub>0</sub>, y<sub>0</sub>) वाले बिंदु P से समीकरण Ax + By + C = 0 वाली रेखा पर लंब डालें। लंब R के आधार को लेबल करें। P से होकर एक ऊर्ध्वाधर रेखा खींचें और दी गई रेखा S के साथ इसके प्रतिच्छेदन को चिह्नित करें। रेखा के किसी भी बिंदु T पर, एक समकोण त्रिभुज बनाएँ। TVU जिसकी भुजाएँ दी गई रेखा पर कर्ण TU के साथ क्षैतिज और ऊर्ध्वाधर रेखाखंड हैं और लंबाई की क्षैतिज भुजा |B| (आरेख देखें)। ∆TVU की उर्ध्वाधर भुजा की लंबाई |A| होगी चूँकि रेखा का ढाल -A/B है। | |||
∆PRS और ∆TVU समरूप त्रिभुज हैं, क्योंकि ये दोनों समकोण त्रिभुज हैं और ∠PSR ≅ ∠TUV क्योंकि ये समांतर रेखाओं PS और UV (दोनों लंबवत रेखाएँ हैं) के तिर्यक रेखा के संगत कोण हैं।<ref>If the two triangles are on opposite sides of the line, these angles are congruent because they are alternate interior angles.</ref> इन त्रिभुजों की संगत भुजाएँ समान अनुपात में हैं, इसलिए: | ∆PRS और ∆TVU समरूप त्रिभुज हैं, क्योंकि ये दोनों समकोण त्रिभुज हैं और ∠PSR ≅ ∠TUV हैं क्योंकि ये समांतर रेखाओं PS और UV (दोनों लंबवत रेखाएँ हैं) के तिर्यक रेखा के संगत कोण हैं।<ref>If the two triangles are on opposite sides of the line, these angles are congruent because they are alternate interior angles.</ref> इन त्रिभुजों की संगत भुजाएँ समान अनुपात में हैं, इसलिए: | ||
:<math>\frac{|\overline{PR}|}{|\overline{PS}|} = \frac{|\overline{TV}|}{|\overline{TU}|}.</math> | :<math>\frac{|\overline{PR}|}{|\overline{PS}|} = \frac{|\overline{TV}|}{|\overline{TU}|}.</math> | ||
यदि बिंदु S के निर्देशांक | यदि बिंदु S के निर्देशांक (x<sub>0</sub>, m)हैं तब |''PS''| = |''y''<sub>0</sub> - ''m''| P से लाइन की दूरी है: | ||
:<math> |\overline{PR} | = \frac{|y_0 - m||B|}{\sqrt{A^2 + B^2}}.</math> | :<math> |\overline{PR} | = \frac{|y_0 - m||B|}{\sqrt{A^2 + B^2}}.</math> | ||
चूँकि S रेखा पर है, हम m का मान ज्ञात कर सकते हैं, | चूँकि S रेखा पर है, हम m का मान ज्ञात कर सकते हैं, | ||
:<math>m = \frac{-Ax_0 - C}{B},</math> | :<math>m = \frac{-Ax_0 - C}{B},</math> | ||
और अंत में प्राप्त | और अंत में प्राप्त होगा:<ref>{{harvnb|Ballantine|Jerbert|1952}}</ref> | ||
:<math> |\overline{PR}| = \frac{|Ax_0 + By_0 + C|}{\sqrt{A^2 + B^2}}.</math> | :<math> |\overline{PR}| = \frac{|Ax_0 + By_0 + C|}{\sqrt{A^2 + B^2}}.</math> | ||
इस प्रमाण का एक रूपांतर V को P पर रखना है और त्रिभुज ∆UVT के क्षेत्रफल की गणना दो तरीकों से प्राप्त करना है। <math>D|\overline{TU}| = |\overline{VU}||\overline{VT}|</math> | इस प्रमाण का एक रूपांतर V को P पर रखना है और त्रिभुज ∆UVT के क्षेत्रफल की गणना दो तरीकों से प्राप्त करना है। <math>D|\overline{TU}| = |\overline{VU}||\overline{VT}|</math> | ||
| Line 71: | Line 73: | ||
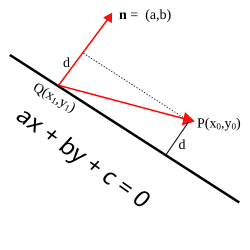
=== एक वेक्टर प्रोजेक्शन प्रूफ === | === एक वेक्टर प्रोजेक्शन प्रूफ === | ||
[[File:vectorpoint-to-line.svg|250px|left|वेक्टर प्रोजेक्शन प्रूफ के लिए आरेख]]मान लीजिए P निर्देशांक वाला बिंदु | [[File:vectorpoint-to-line.svg|250px|left|वेक्टर प्रोजेक्शन प्रूफ के लिए आरेख]]मान लीजिए P निर्देशांक वाला बिंदु (x<sub>0</sub>, y<sub>0</sub>)है और मान लीजिए कि दी गई रेखा का समीकरण ax + by + c = 0 है। साथ ही, मान लीजिए Q = (x<sub>1</sub>, और<sub>1</sub>) इस रेखा पर कोई बिंदु हो और n सदिश (''a'', ''b'') बिंदु ''Q'' से शुरू हो। सदिश n रेखा के लंबवत है, और बिंदु ''P'' से रेखा तक की दूरी ''d'' के लांबिक प्रतिगमन की लंबाई के बराबर है <math>\overrightarrow{QP}</math> n पर है। इस प्रक्षेपण की लंबाई इसके द्वारा दी गई है: | ||
:<math>d = \frac{|\overrightarrow{QP} \cdot \mathbf{n}|}{\| \mathbf{n}\|}.</math> | :<math>d = \frac{|\overrightarrow{QP} \cdot \mathbf{n}|}{\| \mathbf{n}\|}.</math> | ||
तब, | |||
:<math> \overrightarrow{QP} = (x_0 - x_1, y_0 - y_1),</math> इसलिए <math> \overrightarrow{QP} \cdot \mathbf{n} = a(x_0 - x_1) + b(y_0 - y_1)</math> और <math> \| \mathbf{n} \| = \sqrt{a^2 + b^2},</math> | :<math> \overrightarrow{QP} = (x_0 - x_1, y_0 - y_1),</math> इसलिए <math> \overrightarrow{QP} \cdot \mathbf{n} = a(x_0 - x_1) + b(y_0 - y_1)</math> और <math> \| \mathbf{n} \| = \sqrt{a^2 + b^2},</math> | ||
इस प्रकार | इस प्रकार | ||
Revision as of 21:22, 12 March 2023
यूक्लिडियन ज्यामिति में, एक बिंदु से एक रेखा तक की दूरी किसी दिए गए बिंदु (ज्यामिति) से एक अनंत रेखा (गणित) पर किसी भी बिंदु तक की सबसे छोटी यूक्लिडियन दूरी होती है। यह बिंदु की रेखा से लंबवत दूरी है, रेखा खंड की लंबाई जो बिंदु को रेखा पर निकटतम बिंदु से जोड़ती है। इसकी गणना करने का सूत्र कई तरीकों से निकाला और व्यक्त किया जा सकता है।
एक बिंदु से एक रेखा तक की दूरी को जानना विभिन्न स्थितियों में उपयोगी हो सकता है—उदाहरण के लिए, एक सड़क तक पहुँचने के लिए सबसे छोटी दूरी का पता लगाना, एक ग्राफ पर प्रकीर्णन की मात्रा निर्धारित करना, आदि। डेमिंग प्रतिगमन में, एक प्रकार का रेखीय वक्र समंजन, यदि आश्रित और स्वतंत्र चर के समान भिन्नता होती है जिसके परिणामस्वरूप लांबिक प्रतिगमन होता है जिसमें योग्य की अपूर्णता की डिग्री प्रत्येक दत्तानुसारी बिन्दु के लिए प्रतिगमन रेखा से बिंदु की लंबवत दूरी के रूप में मापी जाती है।
एक समीकरण द्वारा परिभाषित रेखा
समीकरण द्वारा दिए गए समतल में एक रेखा के मामले में ax + by + c = 0, जहाँ a, b और c वास्तविक संख्या स्थिरांक हैं a और b दोनों शून्य नहीं हैं, रेखा से एक बिंदु तक की दूरी (x0, y0) है[1][2]: p.14
इस रेखा पर वह बिंदु जो सबसे निकट है (x0, y0) निर्देशांक हैं:[3]
क्षैतिज और लंबवत रेखाएं
एक रेखा के सामान्य समीकरण में, ax + by + c = 0, a और b जब तक दोनों शून्य नहीं हो सकते c भी शून्य है, इस स्थिति में समीकरण एक रेखा को परिभाषित नहीं करता है। अगर a = 0 और b ≠ 0, रेखा क्षैतिज है और समीकरण है y = −c/b. से दूरी (x0, y0) इस रेखा को लंबाई के एक ऊर्ध्वाधर रेखा खंड के साथ मापा जाता है |y0 − (−c/b)| = |by0 + c|/|b| सूत्र के अनुसार। इसी प्रकार, ऊर्ध्वाधर रेखाओं के लिए (b = 0) समान बिंदु और रेखा के बीच की दूरी है |ax0 + c|/|a|, जैसा कि एक क्षैतिज रेखा खंड के साथ मापा जाता है।
दो बिंदुओं द्वारा परिभाषित रेखा
यदि रेखा दो बिन्दुओं से होकर गुजरती है P1 = (x1, y1) और P2 = (x2, y2) फिर लाइन से दूरी (x0, y0) है:[4]
:
इस व्यंजक के भाजक के बीच की दूरी है P1 और P2. अंश तीन बिंदुओं पर इसके शीर्षों के साथ त्रिभुज के क्षेत्रफल का दुगुना है, (x0, y0), P1 और P2. देखना: त्रिभुज का क्षेत्रफल § निर्देशांकों का उपयोग. अभिव्यक्ति के बराबर है h = 2A/b, जिसे त्रिभुज के क्षेत्रफल के लिए मानक सूत्र को पुनर्व्यवस्थित करके प्राप्त किया जा सकता है: A = 1/2 bh, जहाँ b भुजा की लंबाई है, और h विपरीत शीर्ष से लंबवत ऊंचाई है।
बिंदु और कोण द्वारा परिभाषित रेखा
यदि रेखा बिंदु से होकर गुजरती है P = (Px, Py) कोण के साथ θ, फिर किसी बिंदु की दूरी (x0, y0) लाइन के लिए है
प्रमाण
एक बीजगणितीय प्रमाण
यह प्रमाण केवल तभी मान्य होता है जब रेखा न तो लंबवत हो और न ही क्षैतिज, यानी हम मानते हैं कि न तो a और न b रेखा के समीकरण में शून्य है।
समीकरण वाली रेखा ax + by + c = 0 में ढाल है −a/b, इसलिए इसके लम्बवत किसी भी रेखा पर ढाल होगा b/a (नकारात्मक पारस्परिक)।माना (m, n) रेखा ax + by + c = 0 का प्रतिच्छेदन बिंदु है और रेखा इसके लंबवत है जो बिंदु (x0, y0) से गुजरती है। इन दो बिंदुओं के माध्यम से रेखा मूल रेखा के लंबवत है, इसलिए
इस प्रकार, और इस समीकरण का वर्ग करके हम प्राप्त करते हैं:
अब विचार कीजिए,
उपरोक्त वर्ग समीकरण का उपयोग करना। लेकिन हमारे पास है,
चूँकि (m, n) ax + by + c = 0 पर है। इस प्रकार,
और हम इन दो बिंदुओं द्वारा निर्धारित रेखा खंड की लंबाई प्राप्त करते हैं,
एक ज्यामितीय प्रमाण
यह प्रमाण तभी मान्य होता है जब रेखा क्षैतिज या लंबवत न हो।[6]
निर्देशांक (x0, y0) वाले बिंदु P से समीकरण Ax + By + C = 0 वाली रेखा पर लंब डालें। लंब R के आधार को लेबल करें। P से होकर एक ऊर्ध्वाधर रेखा खींचें और दी गई रेखा S के साथ इसके प्रतिच्छेदन को चिह्नित करें। रेखा के किसी भी बिंदु T पर, एक समकोण त्रिभुज बनाएँ। TVU जिसकी भुजाएँ दी गई रेखा पर कर्ण TU के साथ क्षैतिज और ऊर्ध्वाधर रेखाखंड हैं और लंबाई की क्षैतिज भुजा |B| (आरेख देखें)। ∆TVU की उर्ध्वाधर भुजा की लंबाई |A| होगी चूँकि रेखा का ढाल -A/B है।
∆PRS और ∆TVU समरूप त्रिभुज हैं, क्योंकि ये दोनों समकोण त्रिभुज हैं और ∠PSR ≅ ∠TUV हैं क्योंकि ये समांतर रेखाओं PS और UV (दोनों लंबवत रेखाएँ हैं) के तिर्यक रेखा के संगत कोण हैं।[7] इन त्रिभुजों की संगत भुजाएँ समान अनुपात में हैं, इसलिए:
यदि बिंदु S के निर्देशांक (x0, m)हैं तब |PS| = |y0 - m| P से लाइन की दूरी है:
चूँकि S रेखा पर है, हम m का मान ज्ञात कर सकते हैं,
और अंत में प्राप्त होगा:[8]
इस प्रमाण का एक रूपांतर V को P पर रखना है और त्रिभुज ∆UVT के क्षेत्रफल की गणना दो तरीकों से प्राप्त करना है। जहाँ D P से ∆UVT के कर्ण के लिए खींची गई ∆UVT की ऊँचाई है। तब दूरी सूत्र का उपयोग व्यक्त करने के लिए किया जा सकता है , , और संकेतित सूत्र प्राप्त करने के लिए P के निर्देशांक और रेखा के समीकरण के गुणांक के संदर्भ में।[citation needed]
एक वेक्टर प्रोजेक्शन प्रूफ
मान लीजिए P निर्देशांक वाला बिंदु (x0, y0)है और मान लीजिए कि दी गई रेखा का समीकरण ax + by + c = 0 है। साथ ही, मान लीजिए Q = (x1, और1) इस रेखा पर कोई बिंदु हो और n सदिश (a, b) बिंदु Q से शुरू हो। सदिश n रेखा के लंबवत है, और बिंदु P से रेखा तक की दूरी d के लांबिक प्रतिगमन की लंबाई के बराबर है n पर है। इस प्रक्षेपण की लंबाई इसके द्वारा दी गई है:
तब,
- इसलिए और
इस प्रकार
चूँकि Q रेखा पर एक बिंदु है, , इसलिए,[9]
हालांकि दूरी को मॉड्यूलस के रूप में दिया जाता है, संकेत सामान्य वेक्टर (ए, बी) की दिशा द्वारा निर्धारित अर्थ में, यह निर्धारित करने के लिए उपयोगी हो सकता है कि बिंदु किस तरफ है।
अन्य सूत्र
एक बिंदु से एक रेखा की सबसे छोटी दूरी का पता लगाने के लिए एक और अभिव्यक्ति उत्पन्न करना संभव है। इस व्युत्पत्ति के लिए यह भी आवश्यक है कि रेखा लंबवत या क्षैतिज न हो।
बिंदु P निर्देशांक के साथ दिया गया है (). एक रेखा का समीकरण किसके द्वारा दिया जाता है . बिंदु P से गुजरने वाली उस रेखा के अभिलम्ब का समीकरण दिया गया है .
जिस बिंदु पर ये दो रेखाएँ प्रतिच्छेद करती हैं, वह मूल रेखा पर बिंदु P का निकटतम बिंदु है। इसलिए:
हम इस समीकरण को x के लिए हल कर सकते हैं,
चौराहे के बिंदु का y निर्देशांक मूल रेखा के समीकरण में x के इस मान को प्रतिस्थापित करके पाया जा सकता है,
2 बिंदुओं के बीच की दूरी ज्ञात करने के लिए समीकरण का उपयोग करना, , हम यह निष्कर्ष निकाल सकते हैं कि एक रेखा और एक बिंदु के बीच की न्यूनतम दूरी ज्ञात करने का सूत्र निम्नलिखित है:
समीकरण ax + by + c = 0 वाली रेखा के लिए m = -a/b और k = - c/b को याद करते हुए, थोड़ा बीजगणितीय सरलीकरण इसे मानक अभिव्यक्ति में कम कर देता है।[3]
वेक्टर फॉर्मूलेशन
यूक्लिडियन सदिश रूप में एक रेखा का समीकरण दिया जा सकता है:
यहाँ a रेखा पर एक बिंदु है, और n रेखा की दिशा में एक इकाई सदिश है। फिर जैसे स्केलर टी भिन्न होता है, x रेखा का स्थान (गणित) देता है।
एक मनमाना बिंदु की दूरी p द्वारा इस पंक्ति को दिया गया है
यह सूत्र इस प्रकार निकाला जा सकता है: से एक वेक्टर है a मुद्दे पर p. तब लाइन पर अनुमानित लंबाई है और इसलिए
एक वेक्टर है जो कि प्रक्षेपण (रैखिक बीजगणित) है लाइन पर और निकटतम रेखा पर बिंदु का प्रतिनिधित्व करता है . इस प्रकार
का अंग है रेखा के लंबवत। बिंदु से रेखा तक की दूरी तब उस वेक्टर का आदर्श (गणित) है।[4] यह अधिक सामान्य सूत्र दो आयामों तक सीमित नहीं है।
एक और सदिश सूत्रीकरण
यदि सदिश स्थान orthonormality है और यदि रेखा बिंदु से होकर जाती है a और एक यूक्लिडियन वेक्टर है n, बिंदु के बीच की दूरी p और रेखा है[10]
ध्यान दें कि क्रॉस उत्पाद केवल आयाम 3 और 7 में मौजूद हैं।
यह भी देखें
- हेस्से सामान्य रूप
- लाइन-लाइन चौराहा
- दो रेखाओं के बीच की दूरी
- एक बिंदु से एक विमान की दूरी
- तिरछी रेखाएँ#दूरी
टिप्पणियाँ
- ↑ Larson & Hostetler 2007, p. 452
- ↑ Spain 2007
- ↑ 3.0 3.1 Larson & Hostetler 2007, p. 522
- ↑ 4.0 4.1 Sunday, Dan. "रेखाएँ और एक बिंदु से एक रेखा की दूरी". softSurfer. Archived from the original on 2021-05-07.
- ↑ Between Certainty and Uncertainty: Statistics and Probability in Five Units With Notes on Historical Origins and Illustrative Numerical Examples
- ↑ Ballantine & Jerbert 1952 do not mention this restriction in their article
- ↑ If the two triangles are on opposite sides of the line, these angles are congruent because they are alternate interior angles.
- ↑ Ballantine & Jerbert 1952
- ↑ Anton 1994, pp. 138-9
- ↑ Weisstein, Eric W. "Point-Line Distance--3-Dimensional". mathworld.wolfram.com (in English). Retrieved 2021-06-06.
संदर्भ
- Anton, Howard (1994), Elementary Linear Algebra (7th ed.), John Wiley & Sons, ISBN 0-471-58742-7
- Ballantine, J.P.; Jerbert, A.R. (1952), "Distance from a line or plane to a point", American Mathematical Monthly, 59 (4): 242–243, doi:10.2307/2306514, JSTOR 2306514
- Larson, Ron; Hostetler, Robert (2007), Precalculus: A Concise Course, Houghton Mifflin Co., ISBN 978-0-618-62719-6
- Spain, Barry (2007) [1957], Analytical Conics, Dover Publications, ISBN 978-0-486-45773-4
- Weisstein, Eric W. "Point-Line Distance--3-Dimensional". MathWorld.
अग्रिम पठन
- Deza, Michel Marie; Deza, Elena (2013), Encyclopedia of Distances (2nd ed.), Springer, p. 86, ISBN 9783642309588