अवक्षय क्षेत्र

अर्धचालक भौतिकी में, अवक्षय क्षेत्र, जिसे रिक्तीकरण परत, रिक्तीकरण क्षेत्र, जंक्शन क्षेत्र, अंतरिक्ष आवेश क्षेत्र या अंतरिक्ष आवेश परत भी कहा जाता है, जो एक प्रवाहकीय, डोप्ड अर्धचालक सामग्री के भीतर एक रोधक क्षेत्र है जहां मोबाइल आवेश वाहक दूर हो गए हैं, या बिजली के क्षेत्र से दूर हो गए हैं। अवक्षय क्षेत्र में एकमात्र तत्व आयनित दाता या स्वीकर्ता अशुद्धियाँ हैं।

अप्रकाशित धनात्मक और ऋणात्मक आयनों के इस क्षेत्र को इस क्षेत्र में वाहकों के ह्रास के कारण अवक्षय क्षेत्र कहा जाता है।

अवक्षय क्षेत्र का नाम इसलिए रखा गया है क्योंकि यह एक संवाहक क्षेत्र से बनता है सभी मुक्त आवेश कैरियर्स को हटाकर, धारा ले जाने के लिए कोई नहीं छोड़ता। आधुनिक अर्धचालक इलेक्ट्रॉनिक्स को समझाने के लिए कमी क्षेत्र को समझना महत्वपूर्ण है: डायोड, द्विध्रुवीय संधि ट्रांजिस्टर, क्षेत्रीय प्रभाव ट्रांजिस्टर, और चर (वैरियेबल) समाई डायोड सभी रिक्तीकरण क्षेत्र की घटनाओं पर निर्भर करते हैं।

पी-एन संधि (p-n जंक्शन) में गठन

चित्रा 1. शीर्ष: प्रसार से पहले पी-एन संधि (p-n जंक्शन);नीचे: संतुलन के बाद पहुंच गया है

चित्रा 2. ऊपर से नीचे तक;शीर्ष: जंक्शन के माध्यम से छेद और इलेक्ट्रॉन सांद्रता; दूसरा: आवेश घनत्व; तीसरा: विद्युत क्षेत्र; निचला: विद्युत क्षमता

चित्र 3. फॉरवर्ड बायस मोड में एक पीएन जंक्शन के घटने के क्रम में चौड़ाई कम हो जाती है। दोनों पी और एन जंक्शनों को 1E15/सेमी 3 डोपिंग स्तर पर डोप किया जाता है, जिससे ~ 0.59V की अंतर्निहित क्षमता होती है। एन (N) और पी (P) क्षेत्रों (लाल घटता) में चालन बैंड और वैलेंस बैंड के लिए अलग-अलग क्वासी फर्मी स्तरों का निरीक्षण किया जाता है।

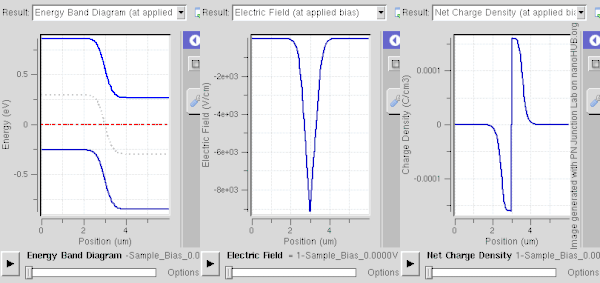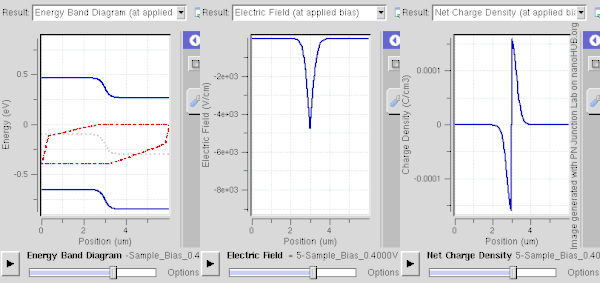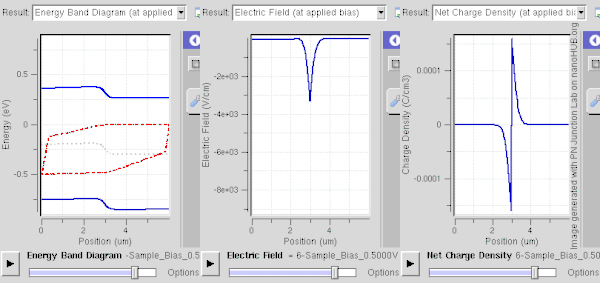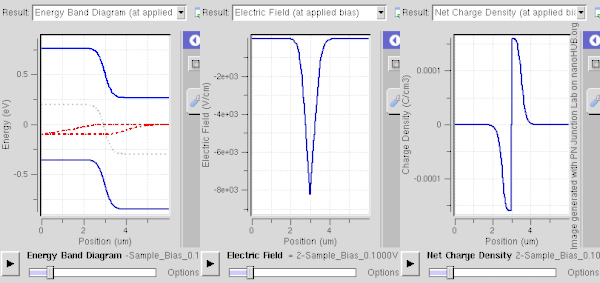
पी-एन संधि (p-n जंक्शन) के आर-पार एक ह्रास क्षेत्र तुरंत बनता है। यह सबसे आसानी से वर्णित है जब संधि (जंक्शन) ऊष्मीय संतुलन में या स्थिर अवस्था में होता है, इन दोनों मामलों में प्रणाली के गुण समय में भिन्न नहीं होते हैं; उन्हें गतिशील संतुलन कहा गया है।

इलेक्ट्रॉन और छिद्र कम सांद्रता वाले क्षेत्रों में फैल जाते हैं, यह उतना ही है जितना स्याही समान रूप से वितरित होने तक पानी में फैल जाता है। परिभाषा के अनुसार, एन-टाइप अर्धचालक में पी-टाइप अर्धचालक की तुलना में मुक्त इलेक्ट्रॉनों (चालन बैंड में) की अधिकता होती है, और पी (P)-प्रकार में एन (N)-प्रकार की तुलना में अधिक छिद्र (वैलेंस बैंड में) होते हैं। इसलिए, जब एन-डॉप्ड और पी-डॉप्ड अर्धचालकों को एक संधि (जंक्शन) बनाने के लिए एक साथ रखा जाता है, एन-साइड संवाहन बैंड में मुक्त इलेक्ट्रॉन पी-साइड संवाहन बैंड में फैलता हैं, और पी-साइड संयोजी बंध में छेद एन-साइड संयोजी बंध में चले जाते हैं।

स्थानांतरण के बाद, विसरित इलेक्ट्रॉन छिद्रों के संपर्क में आते हैं और पी (P)-साइड में पुनर्संयोजन द्वारा समाप्त हो जाते हैं। इसी तरह, विसरित छिद्रों को मुक्त इलेक्ट्रॉनों के साथ पुनर्संयोजित किया जाता है ताकि एन-साइड में समाप्त हो जाए। शुद्ध परिणाम यह है कि विसरित इलेक्ट्रॉन और छिद्र समाप्त हो जाते हैं। जंक्शन इंटरफेस के निकट एक एन-साइड क्षेत्र में, कंडक्शन बैंड में मुक्त इलेक्ट्रॉनों की कमी (1) पी (P)-साइड में इलेक्ट्रॉनों के प्रसार और (2) इलेक्ट्रॉनों के छिद्रों में पुनर्संयोजन के कारण होती है जो पी-साइड से विसरित होते हैं। इंटरफेस के पास पी-साइड क्षेत्र में छेद भी इसी तरह के कारण से चले गए हैं। नतीजतन, बहुसंख्यक आवेश वाहक (एन-टाइप सेमीकंडक्टर के लिए मुक्त इलेक्ट्रॉन, और पी-टाइप सेमीकंडक्टर के लिए छेद) और ये जंक्शन इंटरफेस के आसपास के क्षेत्र में समाप्त हो गए हैं, इसलिए इस क्षेत्र को अवक्षय क्षेत्र या अवक्षय क्षेत्र कहा जाता है। ऊपर वर्णित बहुसंख्यक आवेश वाहक प्रसार के कारण, कमी क्षेत्र आवेश किया जाता है; इसका एन-साइड सकारात्मक रूप से आवेश किया जाता है और इसका पी (P)-पक्ष ऋणात्मक रूप से आवेशित होता है। यह एक विद्युत क्षेत्र बनाता है जो आवेश प्रसार का विरोध करने वाला बल प्रदान करता है। जब विद्युत क्षेत्र छिद्रों और इलेक्ट्रॉनों के आगे प्रसार को रोकने के लिए पर्याप्त रूप से मजबूत होता है, ह्रास क्षेत्र संतुलन तक पहुँच जाता है। रिक्तीकरण क्षेत्र में विद्युत क्षेत्र का एकीकरण निर्धारित करता है जिसे बिल्ट-इन वोल्टेज कहा जाता है (जिसे जंक्शन वोल्टेज या बैरियर वोल्टेज या संपर्क क्षमता भी कहा जाता है)।

भौतिक रूप से, अर्धचालक उपकरणों में आवेश ट्रांसफर (1) विद्युत क्षेत्र द्वारा आवेश वाहक बहाव और (2) स्थानिक रूप से भिन्न वाहक एकाग्रता के कारण आवेश वाहक प्रसार से होता है। रिक्तीकरण क्षेत्र के पी-साइड में, जहां विद्युत क्षेत्र द्वारा विद्युत चालकता के साथ छेद बहते हैं और प्रसार स्थिरांक डी के साथ फैलते हैं, शुद्ध धारा घनत्व द्वारा दिया जाता है

${\bf {J}}=\sigma {\bf {E}}-eD\nabla p$,

जहाँ पर ${\bf {E}}$ विद्युत क्षेत्र है, ई प्राथमिक आवेश है (1.6 × 10⁻¹⁹ coulomb), और पी (P) छेद घनत्व (प्रति यूनिट मात्रा प्रति संख्या) है। विद्युत क्षेत्र, क्षेत्र की दिशा के साथ छिद्र द्वारा बहाव बनाता है, और प्रसार छिद्र के लिए एकाग्रता में कमी होने की दिशा में फिर यह आगे बढ़ता जाता है, इसलिए इस प्रकार छिद्र के लिए एक सकारात्मक घनत्व ढाल के लिए एक नकारात्मक वर्तमान परिणाम होता है। (यदि वाहक इलेक्ट्रॉन हैं, तो छिद्र घनत्व पी को इलेक्ट्रॉन घनत्व एन द्वारा नकारात्मक संकेत के साथ बदल दिया जाता है; ऐसे कुछ मामलों में, दोनों इलेक्ट्रॉनों और छिद्र को शामिल किया जाना आवश्यक है।) जब दो वर्तमान घटक संतुलन अवस्था में होते हैं, जैसा कि पी -एन जंक्शन की कमी में हम देखते है। गतिशील संतुलन पर क्षेत्र, वर्तमान आइंस्टीन संबंध के कारण इसका मान शून्य हो जाता है, जो डी द्वारा σ से संबंधित है।

अग्र पूर्वाग्रह (फॉरवर्ड बायस)

अग्र पूर्वाग्रह (फॉरवर्ड बायस) (एन-साइड के संबंध में पी-साइड के लिए यह एक सकारात्मक वोल्टेज को लागू करता है।) साथ ही यह घटने वाले क्षेत्र को कम करता है और वाहक इंजेक्शन (जैसा कि दाईं ओर चित्र में दिखाया गया है) के लिए बाधा को कम करता है। विस्तार में यदि हम बात करें तो, बहुसंख्यक वाहक पूर्वाग्रह क्षेत्र से कुछ ऊर्जा प्राप्त करता है, जिससे यह इस क्षेत्र में जा सके और विपरीत आरोपों को बेअसर कर सके। अधिक पूर्वाग्रह अधिक तटस्थता (या क्षेत्र में आयनों की स्क्रीनिंग) होता है। वाहक को आयनों के लिए पुनर्संयोजित किया जा सकता है, लेकिन ऊष्मीय ऊर्जा तुरंत पुनर्संयोजित वाहक को संक्रमण करती है क्योंकि फर्मी ऊर्जा निकट अवस्था में होती है। जब पूर्वाग्रह पर्याप्त रूप से मजबूत होता है तो ऐसी स्थिति में कमी क्षेत्र बहुत पतला हो जाता है, और वर्तमान का प्रसार घटक (जंक्शन इंटरफ़ेस के माध्यम से) बहुत बढ़ जाता है और बहाव घटक कम हो जाता है। इस तरह से यह शुद्ध वर्तमान पी-साइड से एन-साइड तक बहता है। वाहक घनत्व का मान ज्यादा होता है (यह लागू पूर्वाग्रह वोल्टेज के साथ तेजी से भिन्न होता है), जिसके कारण जंक्शन प्रवाहकीय बनता है और एक अग्र अभिनति वर्तमान की अनुमति देता है। वर्तमान का गणितीय विवरण यहाँ पर शॉक्ले डायोड समीकरण द्वारा प्रदान किया गया है। विपरीत पूर्वाग्रह के तहत आयोजित कम वर्तमान और अग्र पूर्वाग्रह के तहत बड़े वर्तमान सुधार का एक उदाहरण है।

विपरीत पूर्वाग्रह (रिवर्स बायस)

विपरीत पूर्वाग्रह (रिवर्स बायस) के तहत (एन-साइड के संबंध में पी-साइड में एक नकारात्मक वोल्टेज को लागू करता हैं), कमी क्षेत्र में संभावित ड्रॉप (यानी, वोल्टेज) का मान बढ़ जाता है। अनिवार्य रूप से, अधिकांश वाहक को जंक्शन से दूर धकेल दिया जाता है, जिससे अधिक आवेश किए गए आयनों को पीछे छोड़ दिया जाए। इस प्रकार कमी क्षेत्र को चौड़ा किया जाता है और इसका क्षेत्र मजबूत हो जाता है, जो वर्तमान के बहाव घटक (जंक्शन इंटरफ़ेस के माध्यम से) को बढ़ाता है और प्रसार घटक को कम करता है। इस तरह से शुद्ध धारा एन-साइड से पी-साइड तक बहती है। वाहक घनत्व (ज्यादातर, अल्पसंख्यक वाहक) का मान कम होता है और केवल एक बहुत छोटा विपरीत संतृप्ति वर्तमान प्रवाह सम्मलित होता है।

रिक्तिकरण परत की चौड़ाई का निर्धारण

एक पूर्ण रिक्तिकरण विश्लेषण से जैसा कि चित्र 2 में दिखाया गया है, आवेश को अचानक अपनी सीमा बिंदुओं पर गिरा देता है, जो वास्तव में धीरे -धीरे और पॉइसन के समीकरण द्वारा समझाया गया है। इस स्थिति में प्रवाह घनत्व की मात्रा होगी

${\begin{aligned}{\frac {Q_{n}}{x_{n}}}&=qN_{d}\\{\frac {Q_{p}}{x_{p}}}&=-qN_{a}\\\end{aligned}}$

जहाँ पर $Q_{n}$ तथा $Q_{p}$ क्रमशः नकारात्मक और सकारात्मक आवेश की मात्रा हैं, $x_{n}$ तथा $x_{p}$ केंद्र में शून्य के साथ क्रमशः नकारात्मक और सकारात्मक आवेश के लिए दूरी हैं, $N_{a}$ तथा $N_{d}$ क्रमशः स्वीकर्ता और दाता परमाणुओं की मात्रा हैं और $q$ इलेक्ट्रॉन आवेश है।

फ्लक्स घनत्व का अभिन्न अंग $D$ दूरी के संबंध में $dx$ विद्युत क्षेत्र निर्धारित करने के लिए $E$ (यानी गॉस का नियम) दूसरा ग्राफ बनाता है जैसा कि चित्र 2 में दिखाया गया है:

$E={\frac {\int D\,dx}{\epsilon _{s}}}$

जहाँ पर $\epsilon _{s}$पदार्थ की पारगम्यता है। इस प्रकार दूरी के संबंध में विद्युत क्षेत्र को एकीकृत करना विद्युत क्षमता निर्धारित करती है। यह भी वोल्टेज $V$ में निर्मित $\Delta V$ के बराबर होगा जैसा कि चित्र 2 में दिखाया गया है।

$V=\int Edx=\Delta V$

अंतिम समीकरण को इस स्थिति में व्यवस्थित किया जाएगा जिससे रिक्तीकरण की गई परत की चौड़ाई का कार्य $x_{n}$विद्युत क्षमता $V$ पर निर्भर हो .

${\begin{aligned}x_{n}&={\sqrt {{\frac {2\epsilon _{s}}{q}}{\frac {N_{a}}{N_{d}}}{\frac {1}{N_{a}+N_{d}}}(\Delta V)}}\\x_{p}&={\sqrt {{\frac {2\epsilon _{s}}{q}}{\frac {N_{d}}{N_{a}}}{\frac {1}{N_{a}+N_{d}}}(\Delta V)}}\\\end{aligned}}$

सारांश, $x_{n}$ तथा $x_{p}$ केंद्र के संबंध में क्रमशः नकारात्मक और सकारात्मक रिक्तीकरण परत की चौड़ाई हैं, $N_{a}$ तथा $N_{d}$ क्रमशः स्वीकर्ता और दाता परमाणुओं की मात्रा हैं, $q$ इलेक्ट्रॉन आवेश है और $\Delta V$ अंतर्निहित वोल्टेज है, जो आमतौर पर स्वतंत्र चर (वैरिएबल) है।

मौस (MOS) संधारित्र में गठन

पी-टाइप सिलिकॉन पर मेटल-ऑक्साइड-अर्धचालक संरचना

एक रिक्तीकरण क्षेत्र का एक और उदाहरण मौस (MOS) संधारित्र में होता है। यह एक पी-टाइप क्रियाधार के लिए दाईं ओर आंकड़े में दिखाया गया है। यह मानते हुए कि सेमीकंडक्टर शुरू में आवेश तटस्थ है, आवेश के साथ, स्वीकर्ता डोपिंग अशुद्धियों के कारण नकारात्मक आवेश द्वारा संतुलित छेद के कारण आवेश के साथ। यदि अब एक सकारात्मक विभव गेट पर लागू किया जाता है, जो कि गेट पर सकारात्मक आवेश q को पेश करके किया जाता है, तो गेट के पास अर्धचालक में कुछ सकारात्मक रूप से आवेशित किए गए छिद्र गेट पर सकारात्मक आवेश द्वारा निरस्त किए जाते हैं, और इस प्रकार निचला संपर्क होने के कारण उपकरण से बाहर निकलते हैं। वे एक क्षीण क्षेत्र को पीछे छोड़ देते हैं जो आवेशित कर रहा है क्योंकि कोई मोबाइल छेद नहीं रहता है; केवल इमोबाइल, नकारात्मक रूप से आवेश किए गए स्वीकर्ता अशुद्धियों। अधिक से अधिक सकारात्मक आवेश गेट पर रखा जाता है, अधिक सकारात्मक लागू गेट वोल्टेज, और अधिक छेद जो अर्धचालक सतह को छोड़ते हैं, घटाव क्षेत्र को बढ़ाते हैं। (इस उपकरण में एक सीमा है कि रिक्तीकरण की चौड़ाई कितनी व्यापक हो सकती है। यह सतह के पास एक पतली परत, या चैनल में वाहक की एक उलटी परत की शुरुआत द्वारा निर्धारित किया जाता है। उपरोक्त चर्चा सकारात्मक वोल्टेज के लिए लागू होती है जो काफी कम है। तो इस प्रकार उलटी परत नहीं बनती है।)

यदि गेट सामग्री थोक अर्धचालक के विपरीत प्रकार का पॉलीसिलिकॉन है, तो एक सहज रिक्तीकरण क्षेत्र बनाता है तो गेट को क्रियाधार के लिए विद्युत रूप से छोटा किया जाता है, ऐसे में बहुत से तरीके होते हैं जैसा कि ऊपर पी -एन जंक्शन के लिए वर्णित है। इस पर अधिक जानकारी के लिए, पॉलीसिलिकॉन की रिक्तीकरण प्रभाव को देखें।

रिक्तीकरण क्षेत्र की कुल चौड़ाई लागू रिवर्स-बायस और अशुद्धता एकाग्रता का एक कार्य है

आवेश तटस्थता का सिद्धांत कहता है कि सकारात्मक आरोपों का योग नकारात्मक आरोपों के योग के बराबर होना चाहिए:

$$n+N_{A}=p+N_{D}\,,$$

हां n और p मुक्त इलेक्ट्रॉनों और छेदों की संख्या हैं, और $N_{D}$ तथा $N_{A}$ क्रमशः आयनित दाताओं और स्वीकर्ताओं की संख्या प्रति यूनिट लंबाई की संख्या है। इस तरह, दोनों $N_{D}$ तथा $N_{A}$ स्थानिक घनत्व को डोपिंग के रूप में देखा जा सकता है। अगर हम पूर्ण आयनीकरण और मान लें $n,p\ll N_{D},N_{A}$,

फिर

$qN_{A}w_{P}\approx qN_{D}w_{N}\,$

जहाँ पर $w_{P}$ तथा $w_{N}$ क्रमशः पी और एन अर्धचालक में रिक्तीकरण की चौड़ाई हैं। यह स्थिति यह सुनिश्चित करती है कि शुद्ध नकारात्मक स्वीकर्ता आवेश पूर्ण धनात्मलक डोनर आवेश को बिल्कुल संतुलित करता है। इस मामले में कुल रिक्तीकरण की चौड़ाई राशि $w=w_{N}+w_{P}$ है। रिक्तीकरण की चौड़ाई के लिए एक पूर्ण व्युत्पत्ति संदर्भ में प्रस्तुत की गई है। यह व्युत्पत्ति एक आयाम में पॉइसन समीकरण को हल करने पर आधारित है - मेटालर्जिकल संधि (जंक्शन) के लिए सामान्य आयाम में। विद्युत क्षेत्र की रिक्तिकरण की चौड़ाई (उपरोक्त चित्र में देखा गया) के बाहर शून्य है और इसलिए गॉस के नियम का अर्थ है कि प्रत्येक क्षेत्र संतुलन में आवेश घनत्व-जैसा कि इस उप-धारा में पहले समीकरण द्वारा दिखाया गया है। प्रत्येक क्षेत्र का अलग -अलग इलाज करना और प्रत्येक क्षेत्र के लिए आवेश घनत्व को पॉइसन समीकरण में प्रतिस्थापित करना अंततः रिक्तीकरण की चौड़ाई के परिणामस्वरूप होता है। रिक्तीकरण की चौड़ाई के लिए यह परिणाम है:

$$w\approx \left[{\frac {2\epsilon _{r}\epsilon _{0}}{q}}\left({\frac {N_{A}+N_{D}}{N_{A}N_{D}}}\right)\left(V_{bi}-V\right)\right]^{\frac {1}{2}}$$

जहाँ पर $\epsilon _{r}$ अर्धचालक के सापेक्ष ढांकता हुआ पारगम्यता है, $V_{bi}$ अंतर्निहित वोल्टेज है, और $V$ लागू पूर्वाग्रह है।कमी क्षेत्र एन और पी क्षेत्रों के बीच सममित रूप से विभाजित नहीं है - यह हल्के से डोप किए गए पक्ष की ओर बढ़ेगा। एक अधिक पूर्ण विश्लेषण ध्यान में रखेगा कि रिक्तीकरण क्षेत्र के किनारों के पास अभी भी कुछ वाहक हैं। यह ऊपर के कोष्ठक के अंतिम सेट में एक अतिरिक्त -2kt/q शब्द की ओर जाता है।

मोस संधारित्र में रिक्तीकरण की चौड़ाई

जैसा कि पी -एन जंक्शनों में, यहां का शासी सिद्धांत आवेश तटस्थता है। आइए हम एक पी-टाइप क्रियाधार मानते हैं। यदि सकारात्मक आवेश Q को एरिया A के साथ गेट पर रखा जाता है, तो छेद को गेट आवेश को संतुलित करने के लिए पर्याप्त नकारात्मक स्वीकर्ताओं को उजागर करने वाले एक गहराई w तक कम कर दिया जाता है। डोपेंट घनत्व को मानते हुए $N_{A}$ प्रति यूनिट वॉल्यूम को स्वीकार करने वाले, फिर तटस्थता को आवेश करने के लिए संबंध को संतुष्ट करने के लिए रिक्तिकरण की चौड़ाई की आवश्यकता होती है:

$$Q/A=qN_{A}w\,$$

यदि रिक्तिकरण की चौड़ाई पर्याप्त चौड़ी हो जाती है, तो इलेक्ट्रॉनों को अर्धचालक-ऑक्साइड अंतराफलक में एक बहुत पतली परत में दिखाई देते हैं, जिसे एक उलटी परत कहा जाता है क्योंकि वे उन छेदों से विपरीत रूप से आवेशित करती है जो पी-प्रकार की सामग्री में प्रबल होते हैं। जब एक उलटी परत बन जाती है, तो रिक्तिकरण की चौड़ाई गेट आवेश Q में वृद्धि के साथ विस्तार करना बंद कर देती है। इस मामले में, तटस्थता को उलटी परत में अधिक इलेक्ट्रॉनों को आकर्षित करके प्राप्त किया जाता है। मोसफेट (MOSFET) में, इस उलटी परत को चैनल के रूप में संदर्भित किया जाता है।

रिक्तिकरण परत और बैंड झुकने में विद्युत क्षेत्र

रिक्तिकरण परत के साथ जुड़ा हुआ एक प्रभाव है जिसे झुके हुए बैंड के रूप में जाना जाता है। यह प्रभाव इसलिए होता है क्योंकि रिक्तिकरण परत में विद्युत क्षेत्र इसके (अधिकतम) मूल्य से अंतरिक्ष में रैखिक रूप से भिन्न होता है, $E_{m}$ घटते चौड़ाई के किनारे पर शून्य पर गेट पर:

$E_{m}={Q \over A\epsilon _{0}}=qN_{A}{w \over \epsilon _{0}},\,$

जहाँ पर $\epsilon _{0}$ = 8.854 × 10⁻¹² f/m, f farad है और m मीटर है।यह रैखिक रूप से अलग-अलग विद्युत क्षेत्र एक विद्युत क्षमता की ओर जाता है जो अंतरिक्ष में द्विघात रूप से भिन्न होता है। ऊर्जा स्तर, या ऊर्जा बैंड, इस क्षमता के जवाब में झुकते हैं।

यह भी देखें

• कैपेसिटेंस वोल्टेज प्रोफाइलिंग
• धातु -ऑक्साइड -सेमिकंडक्टर संरचना
• अर्धचालक डायोड

संदर्भ

]