केल्विन-वोइगट सामग्री: Difference between revisions
(Created page with "केल्विन-वोइग्ट सामग्री, जिसे वोइग्ट सामग्री भी कहा जाता है, सबसे सर...") |
mNo edit summary |
||
| Line 1: | Line 1: | ||
केल्विन-वोइग्ट सामग्री, जिसे वोइग्ट सामग्री भी कहा जाता है, सबसे सरल | '''केल्विन-वोइग्ट सामग्री''', जिसे '''वोइग्ट''' सामग्री भी कहा जाता है, सबसे सरल प्रतिरूप [[viscoelastic|श्यानप्रत्यास्थ]] सामग्री है जो विशिष्ट रबड़ जैसे गुण दिखाती है। यह लंबे समय के मानदंड (धीमी विरूपण) पर विशुद्ध रूप से लोचदार है, लेकिन तेजी से विरूपण के लिए अतिरिक्त प्रतिरोध दिखाता है। इसका नाम ब्रिटिश भौतिक विज्ञानी और इंजीनियर विलियम थॉमसन, प्रथम बैरन केल्विन और जर्मन भौतिक विज्ञानी [[वोल्डेमर वोइगट]] के नाम पर रखा गया है। | ||
== परिभाषा == | == परिभाषा == | ||
केल्विन-वोइग्ट | केल्विन-वोइग्ट प्रतिरूप, जिसे वोइग्ट प्रतिरूप भी कहा जाता है, चित्र में दिखाए गए अनुसार विशुद्ध रूप से चिपचिपा स्पंज और विशुद्ध रूप से [[लोच (भौतिकी)]] स्प्रिंग द्वारा समानांतर में जुड़ा हुआ है। | ||
[[Image:Kelvin Voigt diagram.svg|right|frame| केल्विन-वोइग | [[Image:Kelvin Voigt diagram.svg|right|frame| केल्विन-वोइग प्रतिरूप का योजनाबद्ध प्रतिनिधित्व।]]यदि, इसके विपरीत, हम इन दो तत्वों को श्रृंखला में जोड़ते हैं, तो हमें [[मैक्सवेल सामग्री]] का एक प्रतिरूप मिलता है। | ||
चूंकि | चूंकि प्रतिरूप के दो घटक समानांतर में व्यवस्थित होते हैं, प्रत्येक घटक में विकृति समान होती हैं: | ||
:<math> \varepsilon_\text{Total} = \varepsilon_S = \varepsilon_D. </math> | :<math> \varepsilon_\text{Total} = \varepsilon_S = \varepsilon_D. </math> | ||
जहां | जहां पादांक D डम्पर में प्रतिबल-विकृति को इंगित करता है और पादांक S स्प्रिंग में प्रतिबल-विकृति को इंगित करता है। इसी तरह, कुल प्रतिबल प्रत्येक घटक में प्रतिबल का योग होगा: | ||
:<math> \sigma_\text{Total} = \sigma_S + \sigma_D. </math> | :<math> \sigma_\text{Total} = \sigma_S + \sigma_D. </math> | ||
इन समीकरणों से हम पाते हैं कि एक केल्विन-वाॅइट सामग्री में, [[तनाव (भौतिकी)]] σ, [[तनाव (सामग्री विज्ञान)]] ε और समय | इन समीकरणों से हम पाते हैं कि एक केल्विन-वाॅइट सामग्री में, [[तनाव (भौतिकी)|प्रतिबल (भौतिकी)]] σ, [[तनाव (सामग्री विज्ञान)|विकृति (सामग्री विज्ञान)]] ε और समय T के संबंध में परिवर्तन की उनकी दरें फॉर्म के समीकरणों द्वारा नियंत्रित होती हैं: | ||
:<math>\sigma (t) = E \varepsilon(t) + \eta \frac {d\varepsilon(t)} {dt},</math> | :<math>\sigma (t) = E \varepsilon(t) + \eta \frac {d\varepsilon(t)} {dt},</math> | ||
| Line 19: | Line 19: | ||
:<math>\sigma = E \varepsilon + \eta \dot {\varepsilon},</math> | :<math>\sigma = E \varepsilon + \eta \dot {\varepsilon},</math> | ||
जहां | जहां E लोच का एक मापांक है और <math>\eta</math> चिपचिपापन है। समीकरण या तो अपरूपण प्रतिबल या किसी सामग्री के अभिलंब प्रतिबल पर लागू किया जा सकता है। | ||
== अचानक तनाव का प्रभाव == | == अचानक तनाव का प्रभाव == | ||
अगर हम अचानक कुछ निरंतर | अगर हम अचानक कुछ निरंतर प्रतिबल <math>\sigma_0</math> लागू करते हैं, केल्विन-वोइग सामग्री के लिए, तब विरूपण शुद्ध लोचदार सामग्री <math> \sigma_0/E</math> के लिए विरूपण के करीब पहुंच जाएगी, जिसमें अंतर तेजी से घट रहा है: | ||
:<math>\varepsilon(t)=\frac {\sigma_0}{E} (1-e^{-t/\tau_R }), </math> | :<math>\varepsilon(t)=\frac {\sigma_0}{E} (1-e^{-t/\tau_R }), </math> | ||
जहां | जहां T समय है और <math> \tau_R=\frac {\eta}{E} </math> मंदता का समय है। | ||
अगर हम समय | अगर हम समय <math>t_1</math>, पर सामग्री मुक्त कर देंगे तो लोचदार तत्व सामग्री को तब तक पीछे छोड़ देगा जब तक कि विरूपण शून्य न हो जाए। मंदता निम्नलिखित समीकरण का पालन करती है: | ||
:<math>\varepsilon(t>t_1)=\varepsilon(t_1)e^{-(t-t_1)/\tau_R}. </math> | :<math>\varepsilon(t>t_1)=\varepsilon(t_1)e^{-(t-t_1)/\tau_R}. </math> | ||
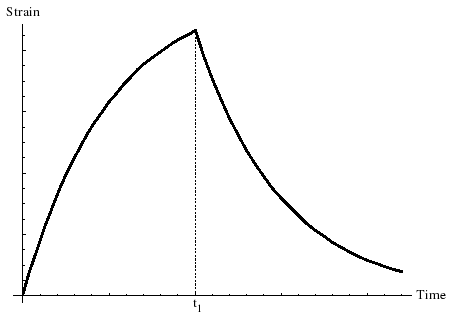
चित्र आयाम रहित विरूपण की निर्भरता को | चित्र आयाम रहित विरूपण की निर्भरता को <math>\frac {E\varepsilon(t)} {\sigma_0} </math> आयाम रहित समय <math>t/\tau_R</math>. पर दर्शाता है। | ||
वोइग्ट | चित्र में सामग्री पर प्रतिबल समय पर लोड होता है <math>t=0</math>, और बाद के आयाम रहित समय <math>t_1^*=t_1/\tau_R</math> पर जारी किया जाता है। | ||
[[Image:Kelvin deformation 2.png|right|frame|आयाम रहित विरूपण की निर्भरता निरंतर प्रतिबल के अधीन आयामहीन समय पर]]चूंकि सभी विरूपण उत्क्रमणीय हैं (हालांकि अचानक नहीं) केल्विन-वोइग सामग्री एक [[ठोस]] है। | |||
वोइग्ट प्रतिरूप मैक्सवेल प्रतिरूप की तुलना में अधिक वास्तविक रूप से रेंगने की भविष्यवाणी करता है, क्योंकि अनंत समय सीमा में तनाव स्थिर रहता है: | |||
:<math>\lim_{t\to\infty}\varepsilon = \frac{\sigma_0}{E},</math> | :<math>\lim_{t\to\infty}\varepsilon = \frac{\sigma_0}{E},</math> | ||
जबकि मैक्सवेल | जबकि मैक्सवेल प्रतिरूप प्रतिबल और समय के बीच एक रैखिक संबंध की भविष्यवाणी करता है, जो प्रायः ऐसा नहीं होता है। यद्यपि केल्विन-वोइगट प्रतिरूप रेंगने की भविष्यवाणी करने के लिए प्रभावी है, प्रतिबल भार हटा दिए जाने के बाद विश्रांति व्यवहार का वर्णन करने में यह ठीक नहीं है। | ||
== [[गतिशील मापांक]] == | == [[गतिशील मापांक|गतिक मापांक]] == | ||
केल्विन-वोइग सामग्री का जटिल | केल्विन-वोइग सामग्री का जटिल गतिक मापांक निम्न द्वारा दिया गया है: | ||
:<math>E^\star ( \omega ) = E + i \eta \omega. </math> | :<math>E^\star ( \omega ) = E + i \eta \omega. </math> | ||
इस प्रकार, गतिशील मापांक के वास्तविक और काल्पनिक घटक हैं: | इस प्रकार, गतिशील मापांक के वास्तविक और काल्पनिक घटक निम्न हैं: | ||
:<math>E_1 = \Re [E( \omega )] = E, </math> | :<math>E_1 = \Re [E( \omega )] = E, </math> | ||
| Line 59: | Line 60: | ||
== यह भी देखें == | == यह भी देखें == | ||
* [[बर्गर सामग्री]] | * [[बर्गर सामग्री]] | ||
* [[सामान्यीकृत मैक्सवेल मॉडल]] | * [[सामान्यीकृत मैक्सवेल मॉडल|सामान्यीकृत मैक्सवेल प्रतिरूप]] | ||
* मैक्सवेल सामग्री | * मैक्सवेल सामग्री | ||
* [[मानक रैखिक ठोस मॉडल]] | * [[मानक रैखिक ठोस मॉडल|मानक रैखिक ठोस प्रतिरूप]] | ||
{{DEFAULTSORT:Kelvin-Voigt Material}} | {{DEFAULTSORT:Kelvin-Voigt Material}} | ||
Revision as of 12:04, 29 March 2023
केल्विन-वोइग्ट सामग्री, जिसे वोइग्ट सामग्री भी कहा जाता है, सबसे सरल प्रतिरूप श्यानप्रत्यास्थ सामग्री है जो विशिष्ट रबड़ जैसे गुण दिखाती है। यह लंबे समय के मानदंड (धीमी विरूपण) पर विशुद्ध रूप से लोचदार है, लेकिन तेजी से विरूपण के लिए अतिरिक्त प्रतिरोध दिखाता है। इसका नाम ब्रिटिश भौतिक विज्ञानी और इंजीनियर विलियम थॉमसन, प्रथम बैरन केल्विन और जर्मन भौतिक विज्ञानी वोल्डेमर वोइगट के नाम पर रखा गया है।
परिभाषा
केल्विन-वोइग्ट प्रतिरूप, जिसे वोइग्ट प्रतिरूप भी कहा जाता है, चित्र में दिखाए गए अनुसार विशुद्ध रूप से चिपचिपा स्पंज और विशुद्ध रूप से लोच (भौतिकी) स्प्रिंग द्वारा समानांतर में जुड़ा हुआ है।
यदि, इसके विपरीत, हम इन दो तत्वों को श्रृंखला में जोड़ते हैं, तो हमें मैक्सवेल सामग्री का एक प्रतिरूप मिलता है।
चूंकि प्रतिरूप के दो घटक समानांतर में व्यवस्थित होते हैं, प्रत्येक घटक में विकृति समान होती हैं:
जहां पादांक D डम्पर में प्रतिबल-विकृति को इंगित करता है और पादांक S स्प्रिंग में प्रतिबल-विकृति को इंगित करता है। इसी तरह, कुल प्रतिबल प्रत्येक घटक में प्रतिबल का योग होगा:
इन समीकरणों से हम पाते हैं कि एक केल्विन-वाॅइट सामग्री में, प्रतिबल (भौतिकी) σ, विकृति (सामग्री विज्ञान) ε और समय T के संबंध में परिवर्तन की उनकी दरें फॉर्म के समीकरणों द्वारा नियंत्रित होती हैं:
या, डॉट नोटेशन में:
जहां E लोच का एक मापांक है और चिपचिपापन है। समीकरण या तो अपरूपण प्रतिबल या किसी सामग्री के अभिलंब प्रतिबल पर लागू किया जा सकता है।
अचानक तनाव का प्रभाव
अगर हम अचानक कुछ निरंतर प्रतिबल लागू करते हैं, केल्विन-वोइग सामग्री के लिए, तब विरूपण शुद्ध लोचदार सामग्री के लिए विरूपण के करीब पहुंच जाएगी, जिसमें अंतर तेजी से घट रहा है:
जहां T समय है और मंदता का समय है।
अगर हम समय , पर सामग्री मुक्त कर देंगे तो लोचदार तत्व सामग्री को तब तक पीछे छोड़ देगा जब तक कि विरूपण शून्य न हो जाए। मंदता निम्नलिखित समीकरण का पालन करती है:
चित्र आयाम रहित विरूपण की निर्भरता को आयाम रहित समय . पर दर्शाता है।
चित्र में सामग्री पर प्रतिबल समय पर लोड होता है , और बाद के आयाम रहित समय पर जारी किया जाता है।
चूंकि सभी विरूपण उत्क्रमणीय हैं (हालांकि अचानक नहीं) केल्विन-वोइग सामग्री एक ठोस है।
वोइग्ट प्रतिरूप मैक्सवेल प्रतिरूप की तुलना में अधिक वास्तविक रूप से रेंगने की भविष्यवाणी करता है, क्योंकि अनंत समय सीमा में तनाव स्थिर रहता है:
जबकि मैक्सवेल प्रतिरूप प्रतिबल और समय के बीच एक रैखिक संबंध की भविष्यवाणी करता है, जो प्रायः ऐसा नहीं होता है। यद्यपि केल्विन-वोइगट प्रतिरूप रेंगने की भविष्यवाणी करने के लिए प्रभावी है, प्रतिबल भार हटा दिए जाने के बाद विश्रांति व्यवहार का वर्णन करने में यह ठीक नहीं है।
गतिक मापांक
केल्विन-वोइग सामग्री का जटिल गतिक मापांक निम्न द्वारा दिया गया है:
इस प्रकार, गतिशील मापांक के वास्तविक और काल्पनिक घटक निम्न हैं:
ध्यान दें कि स्थिर है, जबकि आवृत्ति के सीधे आनुपातिक है (जहां स्पष्ट चिपचिपाहट, , आनुपातिकता का स्थिरांक है)।
संदर्भ
- Meyers and Chawla (1999): Section 13.11 of Mechanical Behaviors of Materials, Mechanical behavior of Materials, 570–580. Prentice Hall, Inc.
- http://stellar.mit.edu/S/course/3/fa06/3.032/index.html
यह भी देखें
- बर्गर सामग्री
- सामान्यीकृत मैक्सवेल प्रतिरूप
- मैक्सवेल सामग्री
- मानक रैखिक ठोस प्रतिरूप
श्रेणी:गैर-न्यूटोनियन तरल पदार्थ
श्रेणी:पदार्थ विज्ञान
श्रेणी:विलियम थॉमसन, प्रथम बैरन केल्विन