बूलियन पायथागॉरियन ट्रिपल समस्या: Difference between revisions
No edit summary |
m (added Category:Vigyan Ready using HotCat) |
||
| Line 48: | Line 48: | ||
[[Category: Machine Translated Page]] | [[Category: Machine Translated Page]] | ||
[[Category:Created On 17/03/2023]] | [[Category:Created On 17/03/2023]] | ||
[[Category:Vigyan Ready]] | |||
Revision as of 15:46, 11 April 2023
बूलियन पायथागॉरियन ट्रिपल समस्या रैमसे सिद्धांत से एक समस्या है कि क्या प्राकृतिक संख्या को लाल और नीले रंग में रंगा जा सकता है जिससे कोई पायथागॉरियन ट्रिपल में सभी लाल या सभी नीले सदस्य न हों। मई 2016 में एक कंप्यूटर-सहायता प्रमाण के माध्यम से बूलियन पायथागॉरियन ट्रिपल्स समस्या को मैरी ह्यूले, ओलिवर कुल्मन और विक्टर डब्ल्यू मारेक द्वारा समाधान किया गया था।[1]
कथन
समस्या पूछती है कि क्या प्रत्येक धनात्मक पूर्णांक को लाल या नीले रंग में रंगना संभव है, जिससे पूर्णांक a, b, c का कोई पायथागॉरियन ट्रिपल संतोषजनक न हो सब एक ही रंग के हैं।
उदाहरण के लिए, पायथागॉरियन ट्रिपल 3, 4 और 5 में (), यदि 3 और 4 को लाल रंग से रंगा गया है, तो 5 को नीले रंग से अवश्य रंगा जाना चाहिए।
समाधान
मेरिजन ह्यूले, ओलिवर कुलमैन और विक्टर डब्ल्यू मारेक ने दिखाया कि ऐसा रंग केवल 7824 संख्या तक ही संभव है। प्रमेय का वास्तविक कथन सिद्ध हुआ है
Theorem — समुच्चय {1, . . . , 7824} को दो भागों में विभाजित किया जा सकता है, जैसे कि किसी भी भाग में पायथागॉरियन ट्रिपल नहीं है, जबकि यह {1, . . . , 7825} के लिए असंभव है।[2]
7825 (संख्या) तक की संख्याओं के लिए 27825 ≈ 3.63×102355 संभावित रंग संयोजन हैं। इन संभावित रंगों को तार्किक और एल्गोरिदमिक रूप से लगभग एक ट्रिलियन (अभी भी अत्यधिक जटिल) स्थितियों तक सीमित कर दिया गया था, और बूलियन संतुष्टि समाधान का उपयोग करके उनकी जांच की गई थी। प्रमाण बनाने में टेक्सास एडवांस्ड कंप्यूटिंग सेंटर में स्टैम्पेड सुपरकंप्यूटर पर दो दिनों की अवधि में लगभग 4 सीपीयू-वर्ष की गणना हुई और एक 200 टेराबाइट प्रस्तावात्मक प्रमाण उत्पन्न हुआ, जिसे 68 गीगाबाइट तक संकुचित किया गया था।
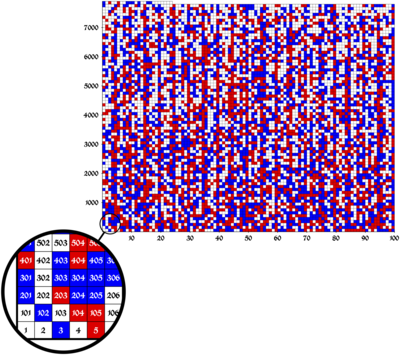
प्रमाण का वर्णन करने वाला पेपर एसएटी 2016 सम्मेलन में प्रकाशित हुआ था,[2] जहां इसने सर्वश्रेष्ठ पेपर का पुरस्कार जीता था।[3] नीचे दिया गया आंकड़ा समूह {1,...,7824} के लिए रंगों के एक संभावित परिवार को दिखाता है जिसमें कोई मोनोक्रोमैटिक पायथागॉरियन ट्रिपल नहीं है, और सफेद वर्गों को इस स्थिति को संतुष्ट करते हुए या तो लाल या नीला रंग दिया जा सकता है।
पुरस्कार
1980 के दशक में रोनाल्ड ग्राहम ने समस्या के समाधान के लिए $100 के पुरस्कार की प्रस्तुति की थी, जिसे अब मरिजन ह्यूले को प्रदान किया गया है।[1]
सामान्यीकरण
2018 तक, समस्या अभी भी 2 से अधिक रंगों के लिए खुली है, अर्थात, यदि धनात्मक पूर्णांकों का k-रंग (k ≥ 3) उपस्थित है, जैसे कि कोई पाइथागोरस ट्रिपल समान रंग नहीं है।[4]
यह भी देखें
संदर्भ
- ↑ 1.0 1.1 Lamb, Evelyn (26 May 2016). "दो सौ टेराबाइट मैथ्स प्रूफ अब तक का सबसे बड़ा है". Nature. 534 (7605): 17–18. Bibcode:2016Natur.534...17L. doi:10.1038/nature.2016.19990. PMID 27251254.
- ↑ 2.0 2.1 Heule, Marijn J. H.; Kullmann, Oliver; Marek, Victor W. (2016). "Solving and Verifying the Boolean Pythagorean Triples problem via Cube-and-Conquer". In Creignou, Nadia; Le Berre, Daniel (eds.). Theory and Applications of Satisfiability Testing – SAT 2016: 19th International Conference, Bordeaux, France, July 5-8, 2016, Proceedings. Lecture Notes in Computer Science. Vol. 9710. pp. 228–245. arXiv:1605.00723. doi:10.1007/978-3-319-40970-2_15.
- ↑ SAT 2016
- ↑ Eliahou, Shalom; Fromentin, Jean; Marion-Poty, Virginie; Robilliard, Denis (2018-10-02). "Are Monochromatic Pythagorean Triples Unavoidable under Morphic Colorings?". Experimental Mathematics (in English). 27 (4): 419–425. arXiv:1605.00859. doi:10.1080/10586458.2017.1306465. ISSN 1058-6458. S2CID 19035265.