एर्गोडिक परिकल्पना: Difference between revisions
(Created page with "{{Use American English|date=January 2019}} {{Use mdy dates|date=January 2019}} {{Short description|Statistical mechanics hypothesis that all microstates are equiprobable for a...") |
No edit summary |
||
| Line 3: | Line 3: | ||
{{Short description|Statistical mechanics hypothesis that all microstates are equiprobable for a given energy}} | {{Short description|Statistical mechanics hypothesis that all microstates are equiprobable for a given energy}} | ||
{{Technical|date=September 2016}} | {{Technical|date=September 2016}} | ||
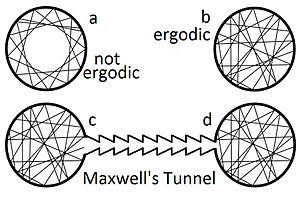
[[File:Ergodic hypothesis w reflecting rays.jpg|thumb|[[परावर्तक प्रतिबिंब]] के साथ पूरी तरह से टकराव रहित [[आदर्श गैस]] में एर्गोडिसिटी का | [[File:Ergodic hypothesis w reflecting rays.jpg|thumb|[[परावर्तक प्रतिबिंब|स्पेक्युलर प्रतिबिंब]] के साथ पूरी तरह से टकराव रहित [[आदर्श गैस]] में एर्गोडिसिटी का प्रश्न।]] | ||
[[Image:Fruit fly trap.jpg|150px|thumb|यह उपकरण फल मक्खियों को | [[Image:Fruit fly trap.jpg|150px|thumb|यह उपकरण फल मक्खियों को फंसा सकता है, लेकिन यदि यह गैस में रखे जाने पर परमाणुओं को फँसाता है जो पहले से ही समान रूप से उपलब्ध चरण स्थान को भरता है, तो लिउविले के प्रमेय और ऊष्मप्रवैगिकी के दूसरे नियम दोनों का उल्लंघन होगा।]]भौतिकी और [[ऊष्मप्रवैगिकी]] में, एर्गोडिक परिकल्पना<ref>Originally due to L. Boltzmann. See part 2 of {{cite book|title=Vorlesungen über Gastheorie|year= 1898 |location=Leipzig|publisher=J. A. Barth|url=https://archive.org/details/vorlesungenberg02boltgoog |oclc=01712811}} ('Ergoden' on p.89 in the 1923 reprint.) It was used to prove equipartition of energy in the kinetic theory of gases</ref> कहती है कि, लंबे [[समय]] तक, एक ही ऊर्जा के साथ माइक्रोस्टेट्स के चरण स्थान के कुछ क्षेत्र में एक प्रणाली द्वारा बिताया गया समय इस क्षेत्र के आयतन के समानुपाती होता है, अर्थात कि सभी सुलभ [[माइक्रोस्टेट (सांख्यिकीय यांत्रिकी)]] लंबे समय तक परिवर्तनीय हैं। '''लंबे तक, एक ही ऊर्जा के साथ के चरण स्थान के कुछ क्षेत्र में एक प्रणाली द्वारा बिताया गया समय इस क्षेत्र की मात्रा के समानुपाती होता है, अर्थात् कि सभी सुलभ माइक्रोस्टेट्स पर परिवर्तनीय हैं एक लंबी अवधि।''' | ||
लिउविले के प्रमेय में कहा गया है कि, [[हैमिल्टनियन प्रणाली]] के लिए, फेज स्पेस के माध्यम से एक कण पथ के बाद माइक्रोस्टेट्स का स्थानीय घनत्व स्थिर है जैसा कि एक पर्यवेक्षक द्वारा देखा जाता है जो पहनावा के साथ चलता है (अर्थात्, [[सामग्री व्युत्पन्न|संवहन समय व्युत्पन्न]] शून्य है)। इस प्रकार, यदि माइक्रोस्टेट समान रूप से चरण स्थान में [[समान वितरण (निरंतर)|समान रूप से वितरित]] किए जाते हैं, तो वे हर समय बने रहेंगे। लेकिन लिउविल के प्रमेय का अर्थ यह नहीं है कि एर्गोडिक परिकल्पना सभी हैमिल्टनियन प्रणालियों के लिए मान्य है। | |||
'''जैसा कि पहनावा के साथ चलने वाले एक पर्यवेक्षक द्वारा देखा गया है (अर्थात्, शून्य है)। इस प्रकार, यदि माइक्रोस्टेट प्रारंभ में चरण स्थान में हैं, तो वे हर समय ऐसा ही रहेंगे। लेकिन लिउविल के प्रमेय का अर्थ यह नहीं है कि एर्गोडिक परिकल्पना सभी हैमिल्टनियन प्रणालियों के लिए मान्य है।''' | |||
एर्गोडिक परिकल्पना | [[कम्प्यूटेशनल भौतिकी]] के [[सांख्यिकीय विश्लेषण]] में एर्गोडिक परिकल्पना को प्रायः माना जाता है। विश्लेषक यह मानेंगे कि समय के साथ एक प्रक्रिया पैरामीटर का [[औसत]] और सांख्यिकीय समेकन पर औसत समान हैं। यह धारणा - कि एक प्रणाली को लंबे समय तक अनुकरण करना उतना ही अच्छा है जितना कि एक ही प्रणाली के कई स्वतंत्र अनुभवों को बनाना - सदैव सही नहीं होता है। (उदाहरण के लिए, 1953 का फर्मी-पास्ता-उलम-त्सिंगौ प्रयोग देखें।) | ||
एर्गोडिक परिकल्पना की धारणा इस बात का प्रमाण देती है कि दूसरी तरह की सतत गति वाली मशीनें असंभव हैं। | |||
== | प्रणाली जो एर्गोडिक हैं कहा जाता है कि [[ ergodicity | एर्गोडिसिटी]] की संपत्ति है; [[ज्यामिति]], भौतिकी और [[अनेक संभावनाओं में से चुनी हूई प्रक्रिया|स्टोचैस्टिक]] संभावना सिद्धांत में प्रणालियों की एक विस्तृत श्रृंखला एर्गोडिक है। एर्गोडिक प्रणाली का अध्ययन [[एर्गोडिक सिद्धांत]] में किया जाता है। | ||
मैक्रोस्कोपिक प्रणालियों में, समय-सीमाएं जिस पर एक प्रणाली वास्तव में अपने स्वयं के चरण स्थान की संपूर्णता का पता लगा सकती है, वह पर्याप्त रूप से बड़ी हो सकती है कि थर्मोडायनामिक संतुलन | |||
== फेनोमेनोलॉजी == | |||
मैक्रोस्कोपिक प्रणालियों में, समय-सीमाएं जिस पर एक प्रणाली वास्तव में अपने स्वयं के चरण स्थान की संपूर्णता का पता लगा सकती है, वह पर्याप्त रूप से बड़ी हो सकती है कि थर्मोडायनामिक संतुलन स्थिति कुछ प्रकार के एर्गोडिसिटी ब्रेकिंग को प्रदर्शित करती है। एक सामान्य उदाहरण [[ लौह-चुंबकीय | लौह-चुंबकीय]] प्रणाली में सहज चुंबकत्व है, जिससे [[क्यूरी तापमान]] के नीचे प्रणाली अधिमानतः एक गैर-शून्य चुंबकत्व को अपनाता है, चूँकि एर्गोडिक परिकल्पना का अर्थ यह होगा कि सभी स्थितियों की खोज करने वाली प्रणाली के आधार पर कोई शुद्ध चुंबकत्व उपस्थित नहीं होना चाहिए, जिसका समय- औसत चुंबकीयकरण शून्य होना चाहिए। तथ्य यह है कि मैक्रोस्कोपिक प्रणाली अधिकांशतः एर्गोडिक परिकल्पना के शाब्दिक रूप का उल्लंघन करते हैं, यह सहज समरूपता तोड़ने का एक उदाहरण है। | |||
चूँकि, [[स्पिन ग्लास]] जैसी जटिल अव्यवस्थित प्रणालियां एर्गोडिसिटी ब्रेकिंग का और भी अधिक जटिल रूप दिखाती हैं, जहां व्यवहार में देखी जाने वाली थर्मोडायनामिक संतुलन स्थिति के गुणों को समरूपता तर्कों द्वारा विशुद्ध रूप से अनुमान लगाना अधिक कठिन होता है। इसके अतिरिक्त पारंपरिक कांच (जैसे खिड़की के शीशे) एक जटिल विधि से एर्गोडिसिटी का उल्लंघन करते हैं। व्यवहार में इसका अर्थ यह है कि पर्याप्त रूप से कम समय के पैमाने पर (जैसे सेकंड, मिनट या कुछ घंटों के कुछ हिस्सों में) प्रणाली 'ठोस' के रूप में व्यवहार कर सकते हैं, अर्थात् एक सकारात्मक अपरूपण मापांक के साथ, लेकिन बहुत लंबे पैमाने पर, उदाहरण: सहस्राब्दियों या युगों में, 'तरल पदार्थ' के रूप में, या दो या दो से अधिक समय के पैमाने और बीच में 'प्लैटॉक्स' के साथ।<ref>The introduction of the practical aspect of ergodicity breaking by introducing a "non-ergodicity time scale" is due to {{cite journal|first= R. G. |last=Palmer |title=Broken ergodicity |journal= Advances in Physics |volume =31|issue=6 |page= 669 |year=1982|bibcode = 1982AdPhy..31..669P |doi = 10.1080/00018738200101438 }}. Also related to these time-scale phenomena are the properties of [[ageing]] and the Mode-Coupling theory of {{cite book|first=W.|last= Götze|title=Dynamics of Glass Forming Liquids|publisher= Oxford Univ. Press|year=2008}}</ref> | |||
| Line 23: | Line 26: | ||
* [[एर्गोडिक प्रक्रिया]] | * [[एर्गोडिक प्रक्रिया]] | ||
* एर्गोडिक सिद्धांत, गणित की एक शाखा जो एर्गोडिसिटी के अधिक सामान्य सूत्रीकरण से संबंधित है | * एर्गोडिक सिद्धांत, गणित की एक शाखा जो एर्गोडिसिटी के अधिक सामान्य सूत्रीकरण से संबंधित है | ||
* | * एर्गोडिसिटी | ||
* लॉस्च्मिड्ट का विरोधाभास | * लॉस्च्मिड्ट का विरोधाभास | ||
* पॉइनकेयर पुनरावृत्ति प्रमेय | * पॉइनकेयर पुनरावृत्ति प्रमेय | ||
Revision as of 11:00, 7 April 2023
This article may be too technical for most readers to understand. (September 2016) (Learn how and when to remove this template message) |
भौतिकी और ऊष्मप्रवैगिकी में, एर्गोडिक परिकल्पना[1] कहती है कि, लंबे समय तक, एक ही ऊर्जा के साथ माइक्रोस्टेट्स के चरण स्थान के कुछ क्षेत्र में एक प्रणाली द्वारा बिताया गया समय इस क्षेत्र के आयतन के समानुपाती होता है, अर्थात कि सभी सुलभ माइक्रोस्टेट (सांख्यिकीय यांत्रिकी) लंबे समय तक परिवर्तनीय हैं। लंबे तक, एक ही ऊर्जा के साथ के चरण स्थान के कुछ क्षेत्र में एक प्रणाली द्वारा बिताया गया समय इस क्षेत्र की मात्रा के समानुपाती होता है, अर्थात् कि सभी सुलभ माइक्रोस्टेट्स पर परिवर्तनीय हैं एक लंबी अवधि।
लिउविले के प्रमेय में कहा गया है कि, हैमिल्टनियन प्रणाली के लिए, फेज स्पेस के माध्यम से एक कण पथ के बाद माइक्रोस्टेट्स का स्थानीय घनत्व स्थिर है जैसा कि एक पर्यवेक्षक द्वारा देखा जाता है जो पहनावा के साथ चलता है (अर्थात्, संवहन समय व्युत्पन्न शून्य है)। इस प्रकार, यदि माइक्रोस्टेट समान रूप से चरण स्थान में समान रूप से वितरित किए जाते हैं, तो वे हर समय बने रहेंगे। लेकिन लिउविल के प्रमेय का अर्थ यह नहीं है कि एर्गोडिक परिकल्पना सभी हैमिल्टनियन प्रणालियों के लिए मान्य है।
जैसा कि पहनावा के साथ चलने वाले एक पर्यवेक्षक द्वारा देखा गया है (अर्थात्, शून्य है)। इस प्रकार, यदि माइक्रोस्टेट प्रारंभ में चरण स्थान में हैं, तो वे हर समय ऐसा ही रहेंगे। लेकिन लिउविल के प्रमेय का अर्थ यह नहीं है कि एर्गोडिक परिकल्पना सभी हैमिल्टनियन प्रणालियों के लिए मान्य है।
कम्प्यूटेशनल भौतिकी के सांख्यिकीय विश्लेषण में एर्गोडिक परिकल्पना को प्रायः माना जाता है। विश्लेषक यह मानेंगे कि समय के साथ एक प्रक्रिया पैरामीटर का औसत और सांख्यिकीय समेकन पर औसत समान हैं। यह धारणा - कि एक प्रणाली को लंबे समय तक अनुकरण करना उतना ही अच्छा है जितना कि एक ही प्रणाली के कई स्वतंत्र अनुभवों को बनाना - सदैव सही नहीं होता है। (उदाहरण के लिए, 1953 का फर्मी-पास्ता-उलम-त्सिंगौ प्रयोग देखें।)
एर्गोडिक परिकल्पना की धारणा इस बात का प्रमाण देती है कि दूसरी तरह की सतत गति वाली मशीनें असंभव हैं।
प्रणाली जो एर्गोडिक हैं कहा जाता है कि एर्गोडिसिटी की संपत्ति है; ज्यामिति, भौतिकी और स्टोचैस्टिक संभावना सिद्धांत में प्रणालियों की एक विस्तृत श्रृंखला एर्गोडिक है। एर्गोडिक प्रणाली का अध्ययन एर्गोडिक सिद्धांत में किया जाता है।
फेनोमेनोलॉजी
मैक्रोस्कोपिक प्रणालियों में, समय-सीमाएं जिस पर एक प्रणाली वास्तव में अपने स्वयं के चरण स्थान की संपूर्णता का पता लगा सकती है, वह पर्याप्त रूप से बड़ी हो सकती है कि थर्मोडायनामिक संतुलन स्थिति कुछ प्रकार के एर्गोडिसिटी ब्रेकिंग को प्रदर्शित करती है। एक सामान्य उदाहरण लौह-चुंबकीय प्रणाली में सहज चुंबकत्व है, जिससे क्यूरी तापमान के नीचे प्रणाली अधिमानतः एक गैर-शून्य चुंबकत्व को अपनाता है, चूँकि एर्गोडिक परिकल्पना का अर्थ यह होगा कि सभी स्थितियों की खोज करने वाली प्रणाली के आधार पर कोई शुद्ध चुंबकत्व उपस्थित नहीं होना चाहिए, जिसका समय- औसत चुंबकीयकरण शून्य होना चाहिए। तथ्य यह है कि मैक्रोस्कोपिक प्रणाली अधिकांशतः एर्गोडिक परिकल्पना के शाब्दिक रूप का उल्लंघन करते हैं, यह सहज समरूपता तोड़ने का एक उदाहरण है।
चूँकि, स्पिन ग्लास जैसी जटिल अव्यवस्थित प्रणालियां एर्गोडिसिटी ब्रेकिंग का और भी अधिक जटिल रूप दिखाती हैं, जहां व्यवहार में देखी जाने वाली थर्मोडायनामिक संतुलन स्थिति के गुणों को समरूपता तर्कों द्वारा विशुद्ध रूप से अनुमान लगाना अधिक कठिन होता है। इसके अतिरिक्त पारंपरिक कांच (जैसे खिड़की के शीशे) एक जटिल विधि से एर्गोडिसिटी का उल्लंघन करते हैं। व्यवहार में इसका अर्थ यह है कि पर्याप्त रूप से कम समय के पैमाने पर (जैसे सेकंड, मिनट या कुछ घंटों के कुछ हिस्सों में) प्रणाली 'ठोस' के रूप में व्यवहार कर सकते हैं, अर्थात् एक सकारात्मक अपरूपण मापांक के साथ, लेकिन बहुत लंबे पैमाने पर, उदाहरण: सहस्राब्दियों या युगों में, 'तरल पदार्थ' के रूप में, या दो या दो से अधिक समय के पैमाने और बीच में 'प्लैटॉक्स' के साथ।[2]
यह भी देखें
- एर्गोडिक प्रक्रिया
- एर्गोडिक सिद्धांत, गणित की एक शाखा जो एर्गोडिसिटी के अधिक सामान्य सूत्रीकरण से संबंधित है
- एर्गोडिसिटी
- लॉस्च्मिड्ट का विरोधाभास
- पॉइनकेयर पुनरावृत्ति प्रमेय
संदर्भ
- ↑ Originally due to L. Boltzmann. See part 2 of Vorlesungen über Gastheorie. Leipzig: J. A. Barth. 1898. OCLC 01712811. ('Ergoden' on p.89 in the 1923 reprint.) It was used to prove equipartition of energy in the kinetic theory of gases
- ↑ The introduction of the practical aspect of ergodicity breaking by introducing a "non-ergodicity time scale" is due to Palmer, R. G. (1982). "Broken ergodicity". Advances in Physics. 31 (6): 669. Bibcode:1982AdPhy..31..669P. doi:10.1080/00018738200101438.. Also related to these time-scale phenomena are the properties of ageing and the Mode-Coupling theory of Götze, W. (2008). Dynamics of Glass Forming Liquids. Oxford Univ. Press.