आदर्श फाइलोजेनी: Difference between revisions
mNo edit summary |
mNo edit summary |
||
| Line 13: | Line 13: | ||
* <p>M की प्रत्येक पंक्ति T के एक सटीक सीमा बिंदु को वर्गीकरण करती है | * <p>M की प्रत्येक पंक्ति T के एक सटीक सीमा बिंदु को वर्गीकरण करती है | ||
* <p>''T'' के प्रत्येक आंतरिक सीमा बिंदु को ''M'' के कम से कम एक पंक्ति द्वारा वर्गीकरण किया जाता है | * <p>''T'' के प्रत्येक आंतरिक सीमा बिंदु को ''M'' के कम से कम एक पंक्ति द्वारा वर्गीकरण किया जाता है | ||
* <p>सीमा बिंदु से जुड़े वर्ण वेक्टर v को अद्वितीय पथ के साथ जड़ से पत्ती v तक सटीक रूप से निर्दिष्ट किया जाता है, अर्थात वर्ण वेक्टर में पथ सीमा बिंदुओं से संबंधित वर्णों के अनुरूप सभी पंक्तियों में 1 या 0 प्रविष्टि होती है।<br />यह ध्यान देने योग्य है कि वास्तविक वंशावली डेटा मिलना बहुत दुर्लभ है जो यहां विस्तृत अवधारणाओं और बाधाओं | * <p>सीमा बिंदु से जुड़े वर्ण वेक्टर v को अद्वितीय पथ के साथ जड़ से पत्ती v तक सटीक रूप से निर्दिष्ट किया जाता है, अर्थात वर्ण वेक्टर में पथ सीमा बिंदुओं से संबंधित वर्णों के अनुरूप सभी पंक्तियों में 1 या 0 प्रविष्टि होती है।<br />यह ध्यान देने योग्य है कि वास्तविक वंशावली डेटा मिलना बहुत दुर्लभ है जो यहां विस्तृत अवधारणाओं और बाधाओं का पालन करता हो। इसलिए, सामान्यतौर पर शोधकर्ताओं को वृक्षों को विकसित करके समाधान करने के लिए बाधित किया जाता है जो केवल [[ होमप्लासी |समाकृति]] को कम करने की कोशिश करते हैं, संयोज्य वर्णों का एक अधिकतम-एकल सूत्र समुच्चय ढूंढते हैं, या जैविक विकास का निर्माण करते हैं जो वर्णों द्वारा निहित विभाजनों से यथासंभव निकटता से मेल खाते हो। <br /><br /> | ||
== उदाहरण == | == उदाहरण == | ||
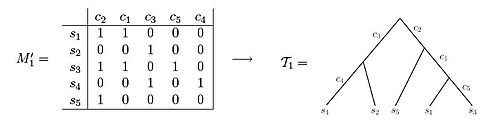
ये दोनों डेटा समुच्चय वर्ण अवस्था [[मैट्रिक्स (गणित)]] के उदाहरण दिखाते हैं। मैट्रिक्स M'<sub>1</sub>' का उपयोग करके कोई यह देखने में सक्षम है कि परिणामी वंशावली वृक्ष को इस तरह बनाया जाता है कि प्रत्येक वर्ण वृक्ष के एक सटीक सीमा बिंदु को वर्गीकरण | ये दोनों डेटा समुच्चय वर्ण अवस्था [[मैट्रिक्स (गणित)]] के उदाहरण दिखाते हैं। मैट्रिक्स M'<sub>1</sub>' का उपयोग करके कोई यह देखने में सक्षम है कि परिणामी वंशावली वृक्ष को इस तरह बनाया जाता है कि प्रत्येक वर्ण वृक्ष के एक सटीक सीमा बिंदु को वर्गीकरण कर सकते हैं। इसके विपरीत, मैट्रिक्स M'<sub>2</sub> का प्रेक्षण करते समय कोई भी देख सकता है कि वंशावली वृक्ष को स्थापित करने का कोई भी उपयुक्त तरीका नहीं है जिसमें प्रत्येक वर्ण केवल एक सीमा बिंदु की लंबाई को वर्गीकरण करता हो।<ref name="carolineuhler" />यदि अध्ययन के तहत नमूने कोशिकाओं की आबादी के रूपांतर गुणक आवृत्ति (वी ए एफ) डेटा से आते हैं, तो वर्ण मैट्रिक्स में प्रविष्टियाँ उत्परिवर्तन की आवृत्तियाँ होती हैं, और 0 और 1 के बीच का मान लेती हैं। अर्थात्, यदि <math>c_i</math> जीनोम में एक स्थिति का प्रतिनिधित्व करता है, फिर संबंधित प्रविष्टि <math>c_i</math> और नमूना <math>s_j</math> में जीनोम की आवृत्तियों में नमूने <math>s_j</math> को उत्परिवर्तन की स्थिति <math>c_i</math> के साथ धारण करेगा।<ref name=":1">{{cite journal | vauthors = El-Kebir M, Oesper L, Acheson-Field H, Raphael BJ | title = मल्टी-सैंपल सीक्वेंसिंग डेटा से क्लोनल ट्री और ट्यूमर कंपोजीशन का पुनर्निर्माण| journal = Bioinformatics | volume = 31 | issue = 12 | pages = i62-70 | date = June 2015 | pmid = 26072510 | pmc = 4542783 | doi = 10.1093/bioinformatics/btv261 }}</ref><ref name=":4">{{cite journal | vauthors = Satas G, Raphael BJ | title = वृक्ष-विवश महत्व नमूनाकरण का उपयोग करते हुए ट्यूमर फाइलोजेनी अनुमान| journal = Bioinformatics | volume = 33 | issue = 14 | pages = i152–i160 | date = July 2017 | pmid = 28882002 | pmc = 5870673 | doi = 10.1093/bioinformatics/btx270 }}</ref><ref name=":3">{{cite journal | vauthors = Malikic S, McPherson AW, Donmez N, Sahinalp CS | title = फाइलोजेनी का उपयोग करके कई ट्यूमर नमूनों में क्लोनलिटी का अनुमान| journal = Bioinformatics | volume = 31 | issue = 9 | pages = 1349–56 | date = May 2015 | pmid = 25568283 | doi = 10.1093/bioinformatics/btv003 | doi-access = free }}</ref><ref name=":0">{{Cite arXiv| vauthors = Ray S, Jia B, Safavi S, van Opijnen T, Isberg R, Rosch J, Bento J |date=2019-08-22|title=सही फाइलोजेनी मॉडल के तहत सटीक अनुमान|class=q-bio.QM|language=en|eprint=1908.08623}}</ref><ref name=":2">{{cite journal | vauthors = Deshwar AG, Vembu S, Yung CK, Jang GH, Stein L, Morris Q | title = PhyloWGS: reconstructing subclonal composition and evolution from whole-genome sequencing of tumors | journal = Genome Biology | volume = 16 | issue = 1 | pages = 35 | date = February 2015 | pmid = 25786235 | pmc = 4359439 | doi = 10.1186/s13059-015-0602-8 }}</ref> | ||
<gallery caption="Character state matrices" widths="500px" heights="300px" perrow="2"> | <gallery caption="Character state matrices" widths="500px" heights="300px" perrow="2"> | ||
File:PerfectPhylogenyExample.jpg|एक चरित्र मैट्रिक्स का एक उदाहरण जिसे एक पूर्ण फाइलोजेनी के रूप में चित्रित किया जा सकता है | File:PerfectPhylogenyExample.jpg|एक चरित्र मैट्रिक्स का एक उदाहरण जिसे एक पूर्ण फाइलोजेनी के रूप में चित्रित किया जा सकता है | ||
Revision as of 11:34, 5 April 2023
उत्तम जैविक विकास एक शब्द है जिसका उपयोग गणनीय वंशावली में एक वंशावली वृक्ष को निरूपित करने के लिए किया जाता है जिसमें सभी वर्ण समाकृति या समान बनावट के बिना वृक्ष के नीचे विकसित होते हैं और उनकी आंतरिक ग्रंथि को वर्गीकरण किया जा सकता है। इसलिए विशिष्ट गुण अभिसारी विकास पर निर्भर नहीं करते है, और उनकी संरचना भी एक समान (जीव विज्ञान) नहीं होती है। सांख्यिकीय रूप से, इसे प्रजनक के रूप में प्रदर्शित किया जा सकता है जिसमें सभी विशिष्ट गुणों की स्थिति 0 होती है जहां 0 उस विशिष्ट गुण की कमी का वर्णन करता है। इनमें से प्रत्येक विशिष्ट गुण 0 से 1 में ठीक एक बार बदलती है और कभी भी 0 की स्थिति पर वापस नहीं लौटती है। यह दुर्लभ है कि वास्तविक डेटा उत्तम जैविक विकास की अवधारणा का पालन करता है।[1][2]
निर्माण
सामान्य तौर पर वंशावली वृक्ष के निर्माण में दो अलग अलग प्रकार के डेटा का उपयोग किया जाता है। दूरी-आधारित संगणनाओं में प्रजातियों के बीच की दूरी और संबंधित वृक्ष की सीमा बिंदु की लंबाई के बीच संबंधों का विश्लेषण करके एक वंशावली वृक्ष बनाया जाता है। एक वर्ण आधारित दृष्टिकोण का उपयोग करते हुए प्रजातियों में वर्ण स्थितियों को एक निविष्ट के रूप में नियोजित किया जाता है ताकि सबसे उत्तम वंशावली वृक्ष को खोजने का प्रयास किया जा सके।[3][4]
एक उत्तम वंशावली वृक्ष के सांख्यिकीय अंशो को सबसे अच्छा इस प्रकार वर्णित किया जा सकता है:[3]
एक उत्तम जैविक विकास n x m के लिए वर्ण अवस्था मैट्रिक्स M एक जड़ वाला वृक्ष T है जिसमे पत्तियां n उपयुक्त है।
M की प्रत्येक पंक्ति T के एक सटीक पत्ती को वर्गीकरण करती है
M की प्रत्येक पंक्ति T के एक सटीक सीमा बिंदु को वर्गीकरण करती है
T के प्रत्येक आंतरिक सीमा बिंदु को M के कम से कम एक पंक्ति द्वारा वर्गीकरण किया जाता है
सीमा बिंदु से जुड़े वर्ण वेक्टर v को अद्वितीय पथ के साथ जड़ से पत्ती v तक सटीक रूप से निर्दिष्ट किया जाता है, अर्थात वर्ण वेक्टर में पथ सीमा बिंदुओं से संबंधित वर्णों के अनुरूप सभी पंक्तियों में 1 या 0 प्रविष्टि होती है।
यह ध्यान देने योग्य है कि वास्तविक वंशावली डेटा मिलना बहुत दुर्लभ है जो यहां विस्तृत अवधारणाओं और बाधाओं का पालन करता हो। इसलिए, सामान्यतौर पर शोधकर्ताओं को वृक्षों को विकसित करके समाधान करने के लिए बाधित किया जाता है जो केवल समाकृति को कम करने की कोशिश करते हैं, संयोज्य वर्णों का एक अधिकतम-एकल सूत्र समुच्चय ढूंढते हैं, या जैविक विकास का निर्माण करते हैं जो वर्णों द्वारा निहित विभाजनों से यथासंभव निकटता से मेल खाते हो।उदाहरण
ये दोनों डेटा समुच्चय वर्ण अवस्था मैट्रिक्स (गणित) के उदाहरण दिखाते हैं। मैट्रिक्स M'1' का उपयोग करके कोई यह देखने में सक्षम है कि परिणामी वंशावली वृक्ष को इस तरह बनाया जाता है कि प्रत्येक वर्ण वृक्ष के एक सटीक सीमा बिंदु को वर्गीकरण कर सकते हैं। इसके विपरीत, मैट्रिक्स M'2 का प्रेक्षण करते समय कोई भी देख सकता है कि वंशावली वृक्ष को स्थापित करने का कोई भी उपयुक्त तरीका नहीं है जिसमें प्रत्येक वर्ण केवल एक सीमा बिंदु की लंबाई को वर्गीकरण करता हो।[3]यदि अध्ययन के तहत नमूने कोशिकाओं की आबादी के रूपांतर गुणक आवृत्ति (वी ए एफ) डेटा से आते हैं, तो वर्ण मैट्रिक्स में प्रविष्टियाँ उत्परिवर्तन की आवृत्तियाँ होती हैं, और 0 और 1 के बीच का मान लेती हैं। अर्थात्, यदि जीनोम में एक स्थिति का प्रतिनिधित्व करता है, फिर संबंधित प्रविष्टि और नमूना में जीनोम की आवृत्तियों में नमूने को उत्परिवर्तन की स्थिति के साथ धारण करेगा।[5][6][7][8][9]
- Character state matrices
उपयोग
उत्तम जैविक विकास एक सैद्धांतिक ढांचा है जिसका उपयोग अधिक व्यावहारिक तरीकों में भी किया जा सकता है। इसका एक उदाहरण है अपरिपूर्ण निर्दिष्ट उत्तम जैविक विकास। इस अवधारणा में वास्तविक, अपरिपूर्ण और अउत्तम, डेटा समूह के साथ सही जैविक विकास का उपयोग करना सम्मिलित है। इस तरह की विधि विकासवादी समानता निर्धारित करने के लिए रेट्रोट्रांसपोज़न का उपयोग करती है। ये लघु अंतर्विभाजित तत्व कई जीनोम में सम्मिलित हैं और उनके सीमा बिंदु अनुक्रमों द्वारा पहचाने जा सकते हैं। रेट्रोट्रांसपोज़न विभिन्न प्रजातियों में कुछ गुणों की आनुवंशिकता के बारे में जानकारी प्रदान करते हैं। दुर्भाग्य से, यदि कोई रेट्रोट्रांसपोज़न अनुपस्थित है, तो यह जानना कठिन है कि क्या वे रेट्रोट्रांसपोज़न विलोपन से पहले उपस्थित थे। उत्तम जैविक विकास डेटा से प्राप्त एल्गोरिदम का उपयोग करके हम इन सीमाओं के प्रतिकूल एक वंशावली पेड़ के पुनर्निर्माण का प्रयास करने में सक्षम हैं।[10]
अंतरराष्ट्रीय हाप मानचित्र योजना के निर्माण में उत्तम जैविक विकास का भी उपयोग किया जाता है। उत्तम जैविक विकास में वर्णित अवधारणाओं और एल्गोरिदम का उपयोग करके अनुपस्थित और अनुपलब्ध हैप्लोटाइप डेटा के बारे में जानकारी निर्धारित कर सकते हैं।[11] यह मानते हुए कि जीनोटाइप मानचित्रण से उत्पन्न होने वाले हैप्लोटाइप्स का समूह मेल खाता है और उत्तम जैविक विकास की अवधारणा का पालन करता है (साथ ही साथ अन्य धारणाएं जैसे कि सही मेंडेलियन इनहेरिटेंस और तथ्य यह है कि प्रति एसएनपी केवल एक उत्परिवर्तन है), एक अनुमान लगाने में सक्षम है अनुपस्थित हैप्लोटाइप डेटा।[12][13][14] [15]
पीपीएम के तहत शोर वाले वीएएफ डेटा से जैविक विकास का उल्लेख करना एक कठिन समस्या है।[5]अधिकांश अनुमान उपकरणों में अनुमान लगाने के लिए कम्प्यूटेशनल रूप से ट्रैक्टेबल बनाने के लिए कुछ अनुमानी कदम शामिल हैं। उपकरण के उदाहरण जो शोर वाले VAF डेटा से जैविक विकास का अनुमान लगाते हैं, उनमें एन्सेस्ट्री, कैनोपी, सीआईटीयूपी, एग्जेक्ट और फाइलो डब्लूजीएस सम्मिलित हैं।[5][6][7][8][9]विशेष रूप से,एग्जेक्ट छोटे आकार की समस्याओं के लिए सभी संभावित वृक्षों पर पश्च संभाव्यता की गणना करने के लिए जीपीयू का उपयोग करके सटीक अनुमान लगाता है। संलग्न उपकरणों के साथ पीपीएम का विस्तार किया गया है।[16][17] उदाहरण के लिए,मेडिक, टुमुल, और फ़िष्ट्रीस जैसे उपकरण किसी दिए गए आनुवंशिक तत्व, या प्लोइडी की प्रतियों की संख्या को बढ़ाने या घटाने दोनों की अनुमति देते हैं, इस प्रकार प्रभावी रूप से उत्परिवर्तन को हटाने की अनुमति देते हैं।[18][19][20]
बाहरी संबंध
- List of phylogenetics software
- One of several programs available for analysis and creation of phylogenetic trees
- Another such program for phylogenetic tree analysis
- Additional program for tree analysis
- A paper detailing an example of how perfect phylogeny can be utilized outside of the field of genetics, as in language association
- Github for "Algorithm for clonal tree reconstruction from multi-sample cancer sequencing data" (AncesTree)
- Github for "Accessing Intra-Tumor Heterogeneity and Tracking Longitudinal and Spatial Clonal Evolutionary History by Next-Generation Sequencing" (Canopy)
- Github for "Clonality Inference in Tumors Using Phylogeny" (CITUP)
- Github for "Exact inference under the perfect phylogeny model" (EXACT)
- Github for "Reconstructing subclonal composition and evolution from whole-genome sequencing of tumors" (PhyloWGS)
संदर्भ
- ↑ Fernandez-Baca D. "बिल्कुल सही फाइलोजेनी समस्या" (PDF). Kluwer Academic Publishers. Retrieved 30 September 2012.
- ↑ Nakhleh L, Ringe D, Warnow T. "Perfect Phylogenetic Networks: A New Methodology for Reconstructing the Evolutionary History of Natural Languages" (PDF). Retrieved 1 October 2012.
- ↑ 3.0 3.1 3.2 Uhler C. "एक संपूर्ण फाइलोजेनी ढूँढना" (PDF). Archived from the original (PDF) on 4 March 2016. Retrieved 29 September 2012.
- ↑ Nikaido M, Rooney AP, Okada N (August 1999). "Phylogenetic relationships among cetartiodactyls based on insertions of short and long interpersed elements: hippopotamuses are the closest extant relatives of whales". Proceedings of the National Academy of Sciences of the United States of America. 96 (18): 10261–6. Bibcode:1999PNAS...9610261N. doi:10.1073/pnas.96.18.10261. PMC 17876. PMID 10468596.
- ↑ 5.0 5.1 5.2 El-Kebir M, Oesper L, Acheson-Field H, Raphael BJ (June 2015). "मल्टी-सैंपल सीक्वेंसिंग डेटा से क्लोनल ट्री और ट्यूमर कंपोजीशन का पुनर्निर्माण". Bioinformatics. 31 (12): i62-70. doi:10.1093/bioinformatics/btv261. PMC 4542783. PMID 26072510.
- ↑ 6.0 6.1 Satas G, Raphael BJ (July 2017). "वृक्ष-विवश महत्व नमूनाकरण का उपयोग करते हुए ट्यूमर फाइलोजेनी अनुमान". Bioinformatics. 33 (14): i152–i160. doi:10.1093/bioinformatics/btx270. PMC 5870673. PMID 28882002.
- ↑ 7.0 7.1 Malikic S, McPherson AW, Donmez N, Sahinalp CS (May 2015). "फाइलोजेनी का उपयोग करके कई ट्यूमर नमूनों में क्लोनलिटी का अनुमान". Bioinformatics. 31 (9): 1349–56. doi:10.1093/bioinformatics/btv003. PMID 25568283.
- ↑ 8.0 8.1 Ray S, Jia B, Safavi S, van Opijnen T, Isberg R, Rosch J, Bento J (2019-08-22). "सही फाइलोजेनी मॉडल के तहत सटीक अनुमान" (in English). arXiv:1908.08623 [q-bio.QM].
- ↑ 9.0 9.1 Deshwar AG, Vembu S, Yung CK, Jang GH, Stein L, Morris Q (February 2015). "PhyloWGS: reconstructing subclonal composition and evolution from whole-genome sequencing of tumors". Genome Biology. 16 (1): 35. doi:10.1186/s13059-015-0602-8. PMC 4359439. PMID 25786235.
- ↑ Pe'er I, Pupko T, Shamir R, Sharan R. "अधूरा निर्देशित बिल्कुल सही फाइलोजेनी". Tel-Aviv University. Archived from the original on 20 October 2013. Retrieved 30 October 2012.
{{cite web}}: CS1 maint: bot: original URL status unknown (link)- ↑ Eskin E, Halperin E, Karp RM (April 2003). "सही फाइलोजेनी के माध्यम से हैप्लोटाइप संरचना का कुशल पुनर्निर्माण" (PDF). Journal of Bioinformatics and Computational Biology. University of California, Berkeley. 1 (1): 1–20. doi:10.1142/S0219720003000174. PMID 15290779. Retrieved 30 October 2012.
- ↑ Gusfield D. "हाप्लोटाइप अनुमान के लिए कम्प्यूटेशनल विधियों का अवलोकन" (PDF). University of California, Davis. Retrieved 18 November 2012.
- ↑ Ding Z, Filkov V, Gusfield D. "बिल्कुल सही फाइलोजेनी हैप्लोटाइपिंग समस्या के लिए एक रेखीय समय एल्गोरिथम". University of California, Davis. Retrieved 18 November 2012.
- ↑ Bafna V, Gusfield D, Lancia G, Yooseph S (2003). "Haplotyping as perfect phylogeny: a direct approach". Journal of Computational Biology. 10 (3–4): 323–40. doi:10.1089/10665270360688048. PMID 12935331.
- ↑ Seyalioglu H. "परफेक्ट फाइलोजेनी के रूप में हाप्लोटाइपिंग" (PDF). Archived from the original (PDF) on 30 September 2011. Retrieved 30 October 2012.
- ↑ Bonizzoni P, Carrieri AP, Della Vedova G, Trucco G (October 2014). "विवश निरंतर परिपूर्ण फाइलोजेनी के माध्यम से विकास की व्याख्या करना". BMC Genomics. 15 Suppl 6 (S6): S10. doi:10.1186/1471-2164-15-S6-S10. PMC 4240218. PMID 25572381.
- ↑ Hajirasouliha I, Raphael BJ (2014), Brown D, Morgenstern B (eds.), "Reconstructing Mutational History in Multiply Sampled Tumors Using Perfect Phylogeny Mixtures", Algorithms in Bioinformatics, Springer Berlin Heidelberg, vol. 8701, pp. 354–367, doi:10.1007/978-3-662-44753-6_27, ISBN 9783662447529
- ↑ Schwarz RF, Trinh A, Sipos B, Brenton JD, Goldman N, Markowetz F (April 2014). Beerenwinkel N (ed.). "इंट्रा-ट्यूमर विषमता का फाइलोजेनेटिक मात्रा का ठहराव". PLOS Computational Biology. 10 (4): e1003535. arXiv:1306.1685. Bibcode:2014PLSCB..10E3535S. doi:10.1371/journal.pcbi.1003535. PMC 3990475. PMID 24743184.
- ↑ Letouzé E, Allory Y, Bollet MA, Radvanyi F, Guyon F (2010). "एक ही मरीज के कई ट्यूमर नमूनों की कॉपी नंबर प्रोफाइल के विश्लेषण से ट्यूमरजेनिसिस में क्रमिक चरणों का पता चलता है". Genome Biology. 11 (7): R76. doi:10.1186/gb-2010-11-7-r76. PMC 2926787. PMID 20649963.
- ↑ Gertz EM, Chowdhury SA, Lee WJ, Wangsa D, Heselmeyer-Haddad K, Ried T, et al. (2016-06-30). "FISHtrees 3.0: Tumor Phylogenetics Using a Ploidy Probe". PLOS ONE. 11 (6): e0158569. Bibcode:2016PLoSO..1158569G. doi:10.1371/journal.pone.0158569. PMC 4928784. PMID 27362268.