सबसे छोटा बहुभुज: Difference between revisions
(Created page with "File:Biggest little polygon.svg|thumb|upright=1.3|6 भुजाओं वाला सबसे बड़ा छोटा बहुभुज (बाईं ओर); दा...") |
(text) |
||
| Line 1: | Line 1: | ||
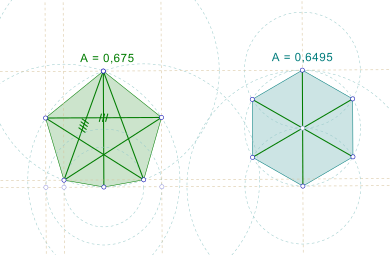
[[File:Biggest little polygon.svg|thumb|upright=1.3|6 भुजाओं वाला सबसे बड़ा छोटा बहुभुज (बाईं ओर); दाईं ओर नियमित बहुभुज समान व्यास लेकिन निचले क्षेत्र के साथ।]]ज्यामिति में, किसी संख्या ''n'' के लिए सबसे बड़ा छोटा [[बहुभुज]] ''n''-पक्षीय बहुभुज होता है जिसका [[व्यास]] एक होता है (अर्थात, इसके प्रत्येक दो [[बिंदु (ज्यामिति)]] एक दूसरे से इकाई दूरी के भीतर होते हैं) और जिसमें सभी व्यास-एक ''एन''-गोंन्स के बीच सबसे बड़ा [[क्षेत्र]] है। | [[File:Biggest little polygon.svg|thumb|upright=1.3|6 भुजाओं वाला सबसे बड़ा छोटा बहुभुज (बाईं ओर); दाईं ओर नियमित बहुभुज समान व्यास लेकिन निचले क्षेत्र के साथ।]]ज्यामिति में, किसी संख्या ''n'' के लिए सबसे बड़ा छोटा [[बहुभुज]] ''n''-पक्षीय बहुभुज होता है जिसका [[व्यास]] एक होता है (अर्थात, इसके प्रत्येक दो [[बिंदु (ज्यामिति)]] एक दूसरे से इकाई दूरी के भीतर होते हैं) और जिसमें सभी व्यास-एक ''एन''-गोंन्स के बीच सबसे बड़ा [[क्षेत्र]] है। गैर-अद्वितीय समाधान जब ''n'' = 4 एक [[वर्ग]] है, और समाधान एक नियमित बहुभुज है जब n एक विषम संख्या है, लेकिन अन्यथा समाधान अनियमित है। | ||
== चतुर्भुज == | == चतुर्भुज == | ||
n = 4 के लिए, एक स्वेच्छ चतुर्भुज का क्षेत्रफल सूत्र S = pq sin(θ)/2 द्वारा दिया जाता है, जहां p और q चतुर्भुज के दो विकर्ण हैं और θ उन कोणों में से एक है जो वे एक दूसरे के साथ बनाते हैं। व्यास अधिकतम 1 होने के लिए, p और q दोनों स्वयं अधिकतम 1 होने चाहिए। इसलिए, चतुर्भुज का क्षेत्रफल सबसे बड़ा होता है, जब क्षेत्र सूत्र के तीन कारकों को व्यक्तिगत रूप से | n = 4 के लिए, एक स्वेच्छ चतुर्भुज का क्षेत्रफल सूत्र S = pq sin(θ)/2 द्वारा दिया जाता है, जहां p और q चतुर्भुज के दो विकर्ण हैं और θ उन कोणों में से एक है जो वे एक दूसरे के साथ बनाते हैं। व्यास अधिकतम 1 होने के लिए, p और q दोनों स्वयं अधिकतम 1 होने चाहिए। इसलिए, चतुर्भुज का क्षेत्रफल सबसे बड़ा होता है, जब क्षेत्र सूत्र के तीन कारकों को व्यक्तिगत रूप से p = q = 1 और sin( θ) = 1 के साथ अधिकतम किया जाता है। जब स्तिथि p = q है तो इसका अर्थ है कि चतुर्भुज एक [[समबाहु चतुर्भुज]] है (इसके विकर्णों की लंबाई समान है), और जब स्तिथि sin(θ) = 1 है तो इसका अर्थ है कि यह एक लंब अक्ष विकर्ण चतुर्भुज है (इसके विकर्ण लम्बकोण की ओर काटते हैं)। इस प्रकार के चतुर्भुजों में इकाई-लंबाई वाले विकर्णों वाला [[वर्ग (ज्यामिति)]] सम्मिलित है, जिसका क्षेत्रफल 1/2 है। हालांकि, अपरिमित रूप से कई अन्य लंब अक्ष विकर्ण और समबाहु चतुर्भुजों का भी व्यास 1 होता है और उनका क्षेत्रफल वर्ग के समान होता है, इसलिए इस स्तिथि में समाधान अद्वितीय नहीं है।<ref>{{citation|first=J. J.|last=Schäffer|title=Nachtrag zu Ungelöste Prob. 12|journal=Elemente der Math.|volume=13|year=1958|pages=85–86}}. As cited by {{harvtxt|Graham|1975}}.</ref> | ||
| Line 10: | Line 10: | ||
== भुजाओं की सम संख्या == | == भुजाओं की सम संख्या == | ||
n = 6 स्तिथि में, अद्वितीय इष्टतम बहुभुज नियमित नहीं है। इस स्तिथि का समाधान 1975 में [[रोनाल्ड ग्राहम]] द्वारा प्रकाशित किया गया था, 1956 में [[हैनफ्रीड लेंज]] द्वारा पूछे गए एक प्रश्न का उत्तर देते हुए;<ref>{{citation|first=H.|last=Lenz|authorlink=Hanfried Lenz|title=Ungelöste Prob. 12|journal=EIemente der Math. |volume=11|year=1956|page=86}}. As cited by {{harvtxt|Graham|1975}}.</ref> यह एक अनियमित समद्विबाहु पंचभुज का रूप ले लेता है, जिसके एक भुजा से जुड़ा एक अधिक समद्विबाहु त्रिभुज होता है, जिसमें त्रिभुज के शीर्ष से विपरीत पंचकोणीय शीर्ष तक की दूरी पंचकोण के विकर्णों के बराबर होती है।<ref name="Graham">{{citation|last=Graham|first=R. L.|authorlink=Ronald Graham|title=The largest small hexagon|journal=[[Journal of Combinatorial Theory]]|series=Series A|volume=18|pages=165–170|year=1975|issue=2|url=http://www.math.ucsd.edu/~ronspubs/75_02_hexagon.pdf|doi=10.1016/0097-3165(75)90004-7|doi-access=free}}.</ref> इसका क्षेत्रफल 0.674981 है।... {{OEIS|id=A111969}}, एक संख्या जो निम्न समीकरण को संतुष्ट करती है | |||
: 4096 x<sup>10</sup> +8192x<sup>9</sup> − 3008x<sup>8</sup> − 30848x<sup>7</sup> + 21056x<sup>6</sup> + 146496x<sup>5</sup> − 221360x<sup>4</sup> + 1232x<sup>3</sup> + 144464x<sup>2</sup> − 78488x + 11993 = 0। | : 4096 x<sup>10</sup> +8192x<sup>9</sup> − 3008x<sup>8</sup> − 30848x<sup>7</sup> + 21056x<sup>6</sup> + 146496x<sup>5</sup> − 221360x<sup>4</sup> + 1232x<sup>3</sup> + 144464x<sup>2</sup> − 78488x + 11993 = 0। | ||
ग्राहम ने अनुमान लगाया कि n के सम मानों के सामान्य | ग्राहम ने अनुमान लगाया कि n के सम मानों के सामान्य स्तिथि के लिए इष्टतम समाधान एक समान विकर्ण (n − 1)-गॉन के समान होता है, जिसके एक तरफ एक समद्विबाहु त्रिभुज जुड़ा होता है, इसका शीर्ष विपरीत ( n − 1)-गॉन कोणबिंदु से इकाई दूरी पर होता है। n = 8 स्तिथि में यह ऑडिट एट अल द्वारा एक कंप्यूटर गणना द्वारा सत्यापित किया गया था।<ref>{{citation | ||
| last1 = Audet | first1 = Charles | | last1 = Audet | first1 = Charles | ||
| last2 = Hansen | first2 = Pierre | | last2 = Hansen | first2 = Pierre | ||
| Line 27: | Line 27: | ||
| volume = 98 | | volume = 98 | ||
| year = 2002| doi-access = free | | year = 2002| doi-access = free | ||
}}.</ref> | }}.</ref> ग्राहम का प्रमाण कि उसका षट्भुज इष्टतम है, और n = 8 स्थिति का कंप्यूटर प्रमाण, दोनों में सीधे किनारों के साथ सभी संभावित n-कोणबिंदु [[थ्रैकल]] की स्तिथि विश्लेषण सम्मिलित है। | ||
ग्राहम का प्रमाण कि उसका षट्भुज इष्टतम है, और n = 8 | |||
ग्राहम का पूर्ण अनुमान, n के सभी सम मानों के लिए सबसे बड़ी छोटी बहुभुज समस्या के समाधान की विशेषता, फोस्टर और स्जाबो द्वारा 2007 में सिद्ध किया गया था।<ref>{{citation | ग्राहम का पूर्ण अनुमान, n के सभी सम मानों के लिए सबसे बड़ी छोटी बहुभुज समस्या के समाधान की विशेषता, फोस्टर और स्जाबो द्वारा 2007 में सिद्ध किया गया था।<ref>{{citation | ||
| Line 46: | Line 45: | ||
== यह भी देखें == | == यह भी देखें == | ||
* हैनसेन का छोटा | * हैनसेन का छोटा अष्टकोण | ||
*रीनहार्ट बहुभुज, बहुभुज अपने व्यास के लिए परिधि को अधिकतम करते हैं, उनके व्यास के लिए अधिकतम चौड़ाई, और उनके परिधि के लिए चौड़ाई को अधिकतम करते हैं | *रीनहार्ट बहुभुज, बहुभुज अपने व्यास के लिए परिधि को अधिकतम करते हैं, उनके व्यास के लिए अधिकतम चौड़ाई, और उनके परिधि के लिए चौड़ाई को अधिकतम करते हैं | ||
| Line 54: | Line 53: | ||
==बाहरी संबंध== | ==बाहरी संबंध== | ||
*{{mathworld|title= | *{{mathworld|title=सबसे बड़ा छोटा बहुभुज|id=सबसे बड़ा छोटा बहुभुज|mode=cs2}} | ||
*[http://www.drking.org.uk/hexagons/grahams/index.html | *[http://www.drking.org.uk/hexagons/grahams/index.html ग्राहम का सबसे बड़ा छोटा षट्कोण], षट्कोण के हॉल से | ||
[[Category: बहुभुज के प्रकार]] [[Category: क्षेत्र]] [[Category: सर्वोत्कृष्ट]] | [[Category: बहुभुज के प्रकार]] [[Category: क्षेत्र]] [[Category: सर्वोत्कृष्ट]] | ||
Revision as of 14:35, 23 April 2023
ज्यामिति में, किसी संख्या n के लिए सबसे बड़ा छोटा बहुभुज n-पक्षीय बहुभुज होता है जिसका व्यास एक होता है (अर्थात, इसके प्रत्येक दो बिंदु (ज्यामिति) एक दूसरे से इकाई दूरी के भीतर होते हैं) और जिसमें सभी व्यास-एक एन-गोंन्स के बीच सबसे बड़ा क्षेत्र है। गैर-अद्वितीय समाधान जब n = 4 एक वर्ग है, और समाधान एक नियमित बहुभुज है जब n एक विषम संख्या है, लेकिन अन्यथा समाधान अनियमित है।
चतुर्भुज
n = 4 के लिए, एक स्वेच्छ चतुर्भुज का क्षेत्रफल सूत्र S = pq sin(θ)/2 द्वारा दिया जाता है, जहां p और q चतुर्भुज के दो विकर्ण हैं और θ उन कोणों में से एक है जो वे एक दूसरे के साथ बनाते हैं। व्यास अधिकतम 1 होने के लिए, p और q दोनों स्वयं अधिकतम 1 होने चाहिए। इसलिए, चतुर्भुज का क्षेत्रफल सबसे बड़ा होता है, जब क्षेत्र सूत्र के तीन कारकों को व्यक्तिगत रूप से p = q = 1 और sin( θ) = 1 के साथ अधिकतम किया जाता है। जब स्तिथि p = q है तो इसका अर्थ है कि चतुर्भुज एक समबाहु चतुर्भुज है (इसके विकर्णों की लंबाई समान है), और जब स्तिथि sin(θ) = 1 है तो इसका अर्थ है कि यह एक लंब अक्ष विकर्ण चतुर्भुज है (इसके विकर्ण लम्बकोण की ओर काटते हैं)। इस प्रकार के चतुर्भुजों में इकाई-लंबाई वाले विकर्णों वाला वर्ग (ज्यामिति) सम्मिलित है, जिसका क्षेत्रफल 1/2 है। हालांकि, अपरिमित रूप से कई अन्य लंब अक्ष विकर्ण और समबाहु चतुर्भुजों का भी व्यास 1 होता है और उनका क्षेत्रफल वर्ग के समान होता है, इसलिए इस स्तिथि में समाधान अद्वितीय नहीं है।[1]
पक्षों की विषम संख्या
n के विषम मानों के लिए, 1922 में कार्ल रेनहार्ट (गणितज्ञ) द्वारा यह दिखाया गया था कि एक नियमित बहुभुज में सभी व्यास-एक बहुभुज का क्षेत्रफल सबसे बड़ा होता है।[2]
भुजाओं की सम संख्या
n = 6 स्तिथि में, अद्वितीय इष्टतम बहुभुज नियमित नहीं है। इस स्तिथि का समाधान 1975 में रोनाल्ड ग्राहम द्वारा प्रकाशित किया गया था, 1956 में हैनफ्रीड लेंज द्वारा पूछे गए एक प्रश्न का उत्तर देते हुए;[3] यह एक अनियमित समद्विबाहु पंचभुज का रूप ले लेता है, जिसके एक भुजा से जुड़ा एक अधिक समद्विबाहु त्रिभुज होता है, जिसमें त्रिभुज के शीर्ष से विपरीत पंचकोणीय शीर्ष तक की दूरी पंचकोण के विकर्णों के बराबर होती है।[4] इसका क्षेत्रफल 0.674981 है।... (sequence A111969 in the OEIS), एक संख्या जो निम्न समीकरण को संतुष्ट करती है
- 4096 x10 +8192x9 − 3008x8 − 30848x7 + 21056x6 + 146496x5 − 221360x4 + 1232x3 + 144464x2 − 78488x + 11993 = 0।
ग्राहम ने अनुमान लगाया कि n के सम मानों के सामान्य स्तिथि के लिए इष्टतम समाधान एक समान विकर्ण (n − 1)-गॉन के समान होता है, जिसके एक तरफ एक समद्विबाहु त्रिभुज जुड़ा होता है, इसका शीर्ष विपरीत ( n − 1)-गॉन कोणबिंदु से इकाई दूरी पर होता है। n = 8 स्तिथि में यह ऑडिट एट अल द्वारा एक कंप्यूटर गणना द्वारा सत्यापित किया गया था।[5] ग्राहम का प्रमाण कि उसका षट्भुज इष्टतम है, और n = 8 स्थिति का कंप्यूटर प्रमाण, दोनों में सीधे किनारों के साथ सभी संभावित n-कोणबिंदु थ्रैकल की स्तिथि विश्लेषण सम्मिलित है।
ग्राहम का पूर्ण अनुमान, n के सभी सम मानों के लिए सबसे बड़ी छोटी बहुभुज समस्या के समाधान की विशेषता, फोस्टर और स्जाबो द्वारा 2007 में सिद्ध किया गया था।[6]
यह भी देखें
- हैनसेन का छोटा अष्टकोण
- रीनहार्ट बहुभुज, बहुभुज अपने व्यास के लिए परिधि को अधिकतम करते हैं, उनके व्यास के लिए अधिकतम चौड़ाई, और उनके परिधि के लिए चौड़ाई को अधिकतम करते हैं
संदर्भ
- ↑ Schäffer, J. J. (1958), "Nachtrag zu Ungelöste Prob. 12", Elemente der Math., 13: 85–86. As cited by Graham (1975).
- ↑ Reinhardt, K. (1922), "Extremale Polygone gegebenen Durchmessers", Jahresbericht der Deutschen Mathematiker-Vereinigung, 31: 251–270.
- ↑ Lenz, H. (1956), "Ungelöste Prob. 12", EIemente der Math., 11: 86. As cited by Graham (1975).
- ↑ Graham, R. L. (1975), "The largest small hexagon" (PDF), Journal of Combinatorial Theory, Series A, 18 (2): 165–170, doi:10.1016/0097-3165(75)90004-7.
- ↑ Audet, Charles; Hansen, Pierre; Messine, Frédéric; Xiong, Junjie (2002), "The largest small octagon", Journal of Combinatorial Theory, Series A, 98 (1): 46–59, doi:10.1006/jcta.2001.3225, MR 1897923.
- ↑ Foster, Jim; Szabo, Tamas (2007), "Diameter graphs of polygons and the proof of a conjecture of Graham", Journal of Combinatorial Theory, Series A, 114 (8): 1515–1525, doi:10.1016/j.jcta.2007.02.006, MR 2360684.
बाहरी संबंध
- Weisstein, Eric W., बड़ा छोटा बहुभुज.html "सबसे बड़ा छोटा बहुभुज", MathWorld
{{cite web}}: Check|url=value (help) - ग्राहम का सबसे बड़ा छोटा षट्कोण, षट्कोण के हॉल से