रेनहार्ड्ट बहुभुज: Difference between revisions
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
{{Short description|Polygon with many longest diagonals}} | {{Short description|Polygon with many longest diagonals}} | ||
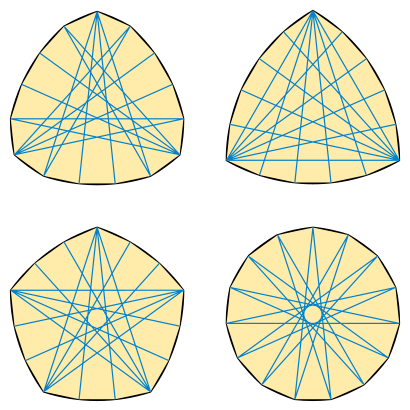
[[File:Reinhardt 15-gons.svg|thumb|upright=1.35|चार 15-तरफा रेनहार्ड्ट बहुभुज (पीला), रेलेक्स बहुभुज (घुमावदार काली बाहरी सीमाएँ) में खुदा हुआ। प्रत्येक बहुभुज के भीतर व्यास को नीली रेखा खंडों के रूप में दिखाया गया है।]]ज्यामिति में, रेइनहार्ट बहुभुज [[समबाहु बहुभुज]] है जो रेयूलॉक्स बहुभुज में खुदा हुआ है। [[नियमित बहुभुज]] | [[File:Reinhardt 15-gons.svg|thumb|upright=1.35|चार 15-तरफा रेनहार्ड्ट बहुभुज (पीला), रेलेक्स बहुभुज (घुमावदार काली बाहरी सीमाएँ) में खुदा हुआ। प्रत्येक बहुभुज के भीतर व्यास को नीली रेखा खंडों के रूप में दिखाया गया है।]]ज्यामिति में, रेइनहार्ट बहुभुज [[समबाहु बहुभुज]] है जो रेयूलॉक्स बहुभुज में खुदा हुआ है। [[नियमित बहुभुज|नियमित बहुभुजों]] की तरह, रेनहार्ड्ट बहुभुज का प्रत्येक शीर्ष बहुभुज के [[व्यास]] के कम से कम परिभाषित युग्म में भाग लेता है। रेनहार्ड्ट बहुभुज के साथ <math>n</math> पक्ष उपस्थित हैं, अधिकांशतः कई रूपों के साथ जब भी <math>n</math> [[विनम्र संख्या]] है। सभी बहुभुजों के बीच <math>n</math> पक्षों, रेनहार्ड्ट बहुभुजों में उनके व्यास के लिए सबसे बड़ा संभव परिधि है, उनके व्यास के लिए निरंतर चौड़ाई का सबसे बड़ा संभव वक्र है, और उनके परिधि के लिए सबसे बड़ी संभव चौड़ाई है। उनका नाम [[कार्ल रेनहार्ड्ट (गणितज्ञ)]] के नाम पर रखा गया है, जिन्होंने 1922 में उनका अध्ययन किया था।{{r|m|hm}} | ||
== परिभाषा और निर्माण == | == परिभाषा और निर्माण == | ||
एक रिउलेक्स बहुभुज वृत्ताकार-चाप भुजाओं वाला उत्तल आकार है, प्रत्येक आकृति के शीर्ष पर केंद्रित होता है और सभी में समान त्रिज्या होती है; उदाहरण रेउलेक्स त्रिकोण है। ये आकृतियाँ स्थिर चौड़ाई के वक्र हैं। कुछ रेउलॉक्स बहुभुजों की पार्श्व लंबाई होती है जो दूसरे के अपरिमेय गुणक होते हैं, | एक रिउलेक्स बहुभुज वृत्ताकार-चाप भुजाओं वाला उत्तल आकार है, प्रत्येक आकृति के शीर्ष पर केंद्रित होता है और सभी में समान त्रिज्या होती है; उदाहरण रेउलेक्स त्रिकोण है। ये आकृतियाँ स्थिर चौड़ाई के वक्र हैं। कुछ रेउलॉक्स बहुभुजों की पार्श्व लंबाई होती है जो दूसरे के अपरिमेय गुणक होते हैं, किन्तु यदि रेलेक्स बहुभुज के पक्ष होते हैं जिन्हें समान लंबाई के चापों की प्रणाली में विभाजित किया जा सकता है, तो इन चापों के अंतबिंदुओं के उत्तल हल के रूप में गठित बहुभुज को परिभाषित किया जाता है रेनहार्ड्ट बहुभुज के रूप में आवश्यक रूप से, अंतर्निहित रीलॉक्स बहुभुज के कोने भी रेनहार्ड्ट बहुभुज के चाप और कोने के अंत बिंदु हैं, किन्तु रेनहार्ड्ट बहुभुज में रेलेक्स बहुभुज के किनारों के आंतरिक अतिरिक्त कोने भी हो सकते हैं।{{r|d}} | ||
यदि <math>n</math> [[दो की शक्ति]] है, तो <math>n</math> रेनहार्ड्ट बहुभुज बनाना संभव नहीं है। यदि <math>n</math> [[विषम संख्या]] है, तो <math>n</math> भुजाओं वाला नियमित बहुभुज एक रेनहार्ड्ट बहुभुज है। किसी अन्य प्राकृत संख्या में विषम [[भाजक]] <math>d</math> अवश्य होना चाहिए , और रेनहार्ड्ट बहुभुज के साथ <math>n</math> पक्षों को नियमित के प्रत्येक चाप को उपविभाजित करके बनाया जा सकता है नियमित <math>d</math>-साइडेड रेलेक्स बहुभुज में <math>n/d</math> छोटे चाप। इसलिए, रेनहार्ड्ट बहुभुजों की भुजाओं की संभावित संख्या विनम्र संख्याएँ हैं, संख्याएँ जो दो की घात नहीं हैं। कब <math>n</math> विषम [[अभाज्य संख्या]] है, या दो बार अभाज्य संख्या है, '''का केवल ही आकार है''' <math>n</math>-पक्षीय रेनहार्ड्ट बहुभुज का केवल एक आकार है , किन्तु <math>n</math> के अन्य सभी मान कई आकृतियों के साथ रेनहार्ड्ट बहुभुज हैं।{{r|m}} | |||
== आयाम और इष्टतमता == | == आयाम और इष्टतमता == | ||
| Line 14: | Line 14: | ||
*उनकी सबसे बड़ी संभावित चौड़ाई है <math>n</math>-भुजा वाले बहुभुज उनकी परिधि के साथ, और सभी के बीच सबसे छोटा संभव परिमाप <math>n</math>उनकी चौड़ाई के साथ पक्षीय बहुभुज।{{r|m}} | *उनकी सबसे बड़ी संभावित चौड़ाई है <math>n</math>-भुजा वाले बहुभुज उनकी परिधि के साथ, और सभी के बीच सबसे छोटा संभव परिमाप <math>n</math>उनकी चौड़ाई के साथ पक्षीय बहुभुज।{{r|m}} | ||
इन बहुभुजों के लिए परिधि और व्यास के बीच का संबंध रेनहार्ड्ट द्वारा सिद्ध किया गया था,{{r|r}} और कई बार स्वतंत्र रूप से फिर से खोजा गया।{{r|v|lt}} 2000 में बेजडेक और फोडोर द्वारा व्यास और चौड़ाई के बीच संबंध सिद्ध किया गया था; उनका काम इस समस्या के लिए इष्टतम बहुभुजों की भी जांच करता है जब पक्षों की संख्या दो की शक्ति होती है (जिसके लिए रेनहार्ड्ट बहुभुज | इन बहुभुजों के लिए परिधि और व्यास के बीच का संबंध रेनहार्ड्ट द्वारा सिद्ध किया गया था,{{r|r}} और कई बार स्वतंत्र रूप से फिर से खोजा गया।{{r|v|lt}} 2000 में बेजडेक और फोडोर द्वारा व्यास और चौड़ाई के बीच संबंध सिद्ध किया गया था; उनका काम इस समस्या के लिए इष्टतम बहुभुजों की भी जांच करता है जब पक्षों की संख्या दो की शक्ति होती है (जिसके लिए रेनहार्ड्ट बहुभुज उपस्थित नहीं होते हैं)।{{r|bf}} | ||
== समरूपता और गणना == <math>n</math>वें>-पक्षीय रेनहार्ड्ट बहुभुज से बने <math>d</math>-पक्षीय नियमित रेलेक्स बहुभुज सममित होते हैं: उन्हें के कोण से घुमाया जा सकता है <math>2\pi/d</math> समान बहुभुज प्राप्त करने के लिए। इस प्रकार की घूर्णी समरूपता वाले रेनहार्ड्ट बहुभुजों को आवधिक कहा जाता है, और बिना घूर्णी समरूपता वाले रेनहार्ड्ट बहुभुजों को छिटपुट कहा जाता है। | == समरूपता और गणना == <math>n</math>वें>-पक्षीय रेनहार्ड्ट बहुभुज से बने <math>d</math>-पक्षीय नियमित रेलेक्स बहुभुज सममित होते हैं: उन्हें के कोण से घुमाया जा सकता है <math>2\pi/d</math> समान बहुभुज प्राप्त करने के लिए। इस प्रकार की घूर्णी समरूपता वाले रेनहार्ड्ट बहुभुजों को आवधिक कहा जाता है, और बिना घूर्णी समरूपता वाले रेनहार्ड्ट बहुभुजों को छिटपुट कहा जाता है। यदि <math>n</math> [[ semiprime |semiprime]] है, या विषम प्रधान शक्ति के साथ दो की शक्ति का उत्पाद है, तो सभी <math>n</math>-पक्षीय रेनहार्ड्ट बहुभुज आवधिक होते हैं। शेष मामलों में कब <math>n</math> दो भिन्न विषम अभाज्य गुणनखंड हैं और इन दो कारकों का गुणनफल नहीं है, छिटपुट रेनहार्ड्ट बहुभुज भी उपस्थित हैं।{{r|hm}} | ||
प्रत्येक के लिए <math>n</math>, केवल निश्चित रूप से अनेक भिन्न हैं <math>n</math>-पक्षीय रेनहार्ड्ट बहुभुज।{{r|d}} | प्रत्येक के लिए <math>n</math>, केवल निश्चित रूप से अनेक भिन्न हैं <math>n</math>-पक्षीय रेनहार्ड्ट बहुभुज।{{r|d}} यदि <math>p</math> का सबसे छोटा प्रधान कारक है <math>n</math>, फिर अलग की संख्या <math>n</math>पक्षीय आवधिक रेनहार्ड्ट बहुभुज है | ||
<math display=block>\frac{p2^{n/p}}{4n}\bigl(1+o(1)\bigr),</math> | <math display=block>\frac{p2^{n/p}}{4n}\bigl(1+o(1)\bigr),</math> | ||
जहां <math>o(1)</math> टर्म [[बिग ओ नोटेशन]] का उपयोग करता है। हालाँकि, छिटपुट रेनहार्ड्ट बहुभुजों की संख्या कम अच्छी तरह से समझी जाती है, और के अधिकांश मूल्यों के लिए <math>n</math> रेनहार्ड्ट बहुभुजों की कुल संख्या में छिटपुट बहुभुजों का प्रभुत्व है।{{r|hm}} | जहां <math>o(1)</math> टर्म [[बिग ओ नोटेशन]] का उपयोग करता है। हालाँकि, छिटपुट रेनहार्ड्ट बहुभुजों की संख्या कम अच्छी तरह से समझी जाती है, और के अधिकांश मूल्यों के लिए <math>n</math> रेनहार्ड्ट बहुभुजों की कुल संख्या में छिटपुट बहुभुजों का प्रभुत्व है।{{r|hm}} | ||
| Line 30: | Line 30: | ||
|} | |} | ||
'''<br />टपुट रेनहार्ड्ट बहुभुजों की संख्या कम अच्छी तरह से समझी जाती है, और के अधिकांश मूल्यों के लिए <math>n</math> रेनहार्ड्ट बहुभुजों की कुल संख्या में छिटपुट बहुभुजों का प्रभुत्व है।{{r|hm}}''' | |||
== यह भी देखें == | == यह भी देखें == | ||
*[[सबसे बड़ा छोटा बहुभुज]], बहुभुज अपने व्यास के लिए क्षेत्रफल को अधिकतम करता है | *[[सबसे बड़ा छोटा बहुभुज]], बहुभुज अपने व्यास के लिए क्षेत्रफल को अधिकतम करता है | ||
Revision as of 09:53, 23 April 2023
ज्यामिति में, रेइनहार्ट बहुभुज समबाहु बहुभुज है जो रेयूलॉक्स बहुभुज में खुदा हुआ है। नियमित बहुभुजों की तरह, रेनहार्ड्ट बहुभुज का प्रत्येक शीर्ष बहुभुज के व्यास के कम से कम परिभाषित युग्म में भाग लेता है। रेनहार्ड्ट बहुभुज के साथ पक्ष उपस्थित हैं, अधिकांशतः कई रूपों के साथ जब भी विनम्र संख्या है। सभी बहुभुजों के बीच पक्षों, रेनहार्ड्ट बहुभुजों में उनके व्यास के लिए सबसे बड़ा संभव परिधि है, उनके व्यास के लिए निरंतर चौड़ाई का सबसे बड़ा संभव वक्र है, और उनके परिधि के लिए सबसे बड़ी संभव चौड़ाई है। उनका नाम कार्ल रेनहार्ड्ट (गणितज्ञ) के नाम पर रखा गया है, जिन्होंने 1922 में उनका अध्ययन किया था।[1][2]
परिभाषा और निर्माण
एक रिउलेक्स बहुभुज वृत्ताकार-चाप भुजाओं वाला उत्तल आकार है, प्रत्येक आकृति के शीर्ष पर केंद्रित होता है और सभी में समान त्रिज्या होती है; उदाहरण रेउलेक्स त्रिकोण है। ये आकृतियाँ स्थिर चौड़ाई के वक्र हैं। कुछ रेउलॉक्स बहुभुजों की पार्श्व लंबाई होती है जो दूसरे के अपरिमेय गुणक होते हैं, किन्तु यदि रेलेक्स बहुभुज के पक्ष होते हैं जिन्हें समान लंबाई के चापों की प्रणाली में विभाजित किया जा सकता है, तो इन चापों के अंतबिंदुओं के उत्तल हल के रूप में गठित बहुभुज को परिभाषित किया जाता है रेनहार्ड्ट बहुभुज के रूप में आवश्यक रूप से, अंतर्निहित रीलॉक्स बहुभुज के कोने भी रेनहार्ड्ट बहुभुज के चाप और कोने के अंत बिंदु हैं, किन्तु रेनहार्ड्ट बहुभुज में रेलेक्स बहुभुज के किनारों के आंतरिक अतिरिक्त कोने भी हो सकते हैं।[3]
यदि दो की शक्ति है, तो रेनहार्ड्ट बहुभुज बनाना संभव नहीं है। यदि विषम संख्या है, तो भुजाओं वाला नियमित बहुभुज एक रेनहार्ड्ट बहुभुज है। किसी अन्य प्राकृत संख्या में विषम भाजक अवश्य होना चाहिए , और रेनहार्ड्ट बहुभुज के साथ पक्षों को नियमित के प्रत्येक चाप को उपविभाजित करके बनाया जा सकता है नियमित -साइडेड रेलेक्स बहुभुज में छोटे चाप। इसलिए, रेनहार्ड्ट बहुभुजों की भुजाओं की संभावित संख्या विनम्र संख्याएँ हैं, संख्याएँ जो दो की घात नहीं हैं। कब विषम अभाज्य संख्या है, या दो बार अभाज्य संख्या है, का केवल ही आकार है -पक्षीय रेनहार्ड्ट बहुभुज का केवल एक आकार है , किन्तु के अन्य सभी मान कई आकृतियों के साथ रेनहार्ड्ट बहुभुज हैं।[1]
आयाम और इष्टतमता
रेनहार्ड्ट बहुभुज के व्यास जोड़े त्रिभुज की भुजाओं के साथ शीर्ष कोण के साथ कई समद्विबाहु त्रिभुज बनाते हैं , जिससे बहुभुज के आयामों की गणना की जा सकती है। यदि रेनहार्ड्ट बहुभुज की भुजा की लंबाई 1 है, तो इसका परिमाप न्यायसंगत है . बहुभुज का व्यास (इसके किन्हीं दो बिंदुओं के बीच की सबसे लंबी दूरी) इन समद्विबाहु त्रिभुजों की भुजाओं की लंबाई के बराबर है, . बहुभुज की निरंतर चौड़ाई का वक्र (किसी भी दो समानांतर सहायक रेखाओं के बीच की सबसे छोटी दूरी) इस त्रिभुज की ऊंचाई के बराबर है, . ये बहुभुज तीन प्रकार से इष्टतम हैं:
- उनके पास सबसे बड़ा संभावित परिमाप है -साइड वाले बहुभुज उनके व्यास के साथ, और सभी के बीच सबसे छोटा संभव व्यास -भुजा वाले बहुभुज उनकी परिधि के साथ।[1]
- उनकी सबसे बड़ी संभावित चौड़ाई है -साइड वाले बहुभुज उनके व्यास के साथ, और सभी के बीच सबसे छोटा संभव व्यास उनकी चौड़ाई के साथ पक्षीय बहुभुज।[1]
- उनकी सबसे बड़ी संभावित चौड़ाई है -भुजा वाले बहुभुज उनकी परिधि के साथ, और सभी के बीच सबसे छोटा संभव परिमाप उनकी चौड़ाई के साथ पक्षीय बहुभुज।[1]
इन बहुभुजों के लिए परिधि और व्यास के बीच का संबंध रेनहार्ड्ट द्वारा सिद्ध किया गया था,[4] और कई बार स्वतंत्र रूप से फिर से खोजा गया।[5][6] 2000 में बेजडेक और फोडोर द्वारा व्यास और चौड़ाई के बीच संबंध सिद्ध किया गया था; उनका काम इस समस्या के लिए इष्टतम बहुभुजों की भी जांच करता है जब पक्षों की संख्या दो की शक्ति होती है (जिसके लिए रेनहार्ड्ट बहुभुज उपस्थित नहीं होते हैं)।[7]
== समरूपता और गणना == वें>-पक्षीय रेनहार्ड्ट बहुभुज से बने -पक्षीय नियमित रेलेक्स बहुभुज सममित होते हैं: उन्हें के कोण से घुमाया जा सकता है समान बहुभुज प्राप्त करने के लिए। इस प्रकार की घूर्णी समरूपता वाले रेनहार्ड्ट बहुभुजों को आवधिक कहा जाता है, और बिना घूर्णी समरूपता वाले रेनहार्ड्ट बहुभुजों को छिटपुट कहा जाता है। यदि semiprime है, या विषम प्रधान शक्ति के साथ दो की शक्ति का उत्पाद है, तो सभी -पक्षीय रेनहार्ड्ट बहुभुज आवधिक होते हैं। शेष मामलों में कब दो भिन्न विषम अभाज्य गुणनखंड हैं और इन दो कारकों का गुणनफल नहीं है, छिटपुट रेनहार्ड्ट बहुभुज भी उपस्थित हैं।[2]
प्रत्येक के लिए , केवल निश्चित रूप से अनेक भिन्न हैं -पक्षीय रेनहार्ड्ट बहुभुज।[3] यदि का सबसे छोटा प्रधान कारक है , फिर अलग की संख्या पक्षीय आवधिक रेनहार्ड्ट बहुभुज है
के छोटे मानों के लिए इन बहुभुजों की संख्या (दो बहुभुजों को उसी के रूप में गिनना जब उन्हें घुमाया जा सकता है या दूसरे को बनाने के लिए फ़्लिप किया जा सकता है) हैं:[1]
| : | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| #: | 1 | 0 | 1 | 1 | 1 | 0 | 2 | 1 | 1 | 2 | 1 | 1 | 5 | 0 | 1 | 5 | 1 | 2 | 10 | 1 | 1 | 12 |
टपुट रेनहार्ड्ट बहुभुजों की संख्या कम अच्छी तरह से समझी जाती है, और के अधिकांश मूल्यों के लिए रेनहार्ड्ट बहुभुजों की कुल संख्या में छिटपुट बहुभुजों का प्रभुत्व है।[2]
यह भी देखें
- सबसे बड़ा छोटा बहुभुज, बहुभुज अपने व्यास के लिए क्षेत्रफल को अधिकतम करता है
संदर्भ
- ↑ 1.0 1.1 1.2 1.3 1.4 1.5 Mossinghoff, Michael J. (2011), "Enumerating isodiametric and isoperimetric polygons", Journal of Combinatorial Theory, Series A, 118 (6): 1801–1815, doi:10.1016/j.jcta.2011.03.004, MR 2793611
- ↑ 2.0 2.1 2.2 2.3 Hare, Kevin G.; Mossinghoff, Michael J. (2019), "Most Reinhardt polygons are sporadic", Geometriae Dedicata, 198: 1–18, arXiv:1405.5233, doi:10.1007/s10711-018-0326-5, MR 3933447, S2CID 119629098
- ↑ 3.0 3.1 Datta, Basudeb (1997), "A discrete isoperimetric problem", Geometriae Dedicata, 64 (1): 55–68, doi:10.1023/A:1004997002327, MR 1432534, S2CID 118797507
- ↑ Reinhardt, Karl (1922), "Extremale Polygone gegebenen Durchmessers", Jahresbericht der Deutschen Mathematiker-Vereinigung, 31: 251–270
- ↑ Vincze, Stephen (1950), "On a geometrical extremum problem", Acta Universitatis Szegediensis, 12: 136–142, MR 0038087
- ↑ Larman, D. G.; Tamvakis, N. K. (1984), "The decomposition of the -sphere and the boundaries of plane convex domains", Convexity and graph theory (Jerusalem, 1981), North-Holland Math. Stud., vol. 87, Amsterdam: North-Holland, pp. 209–214, doi:10.1016/S0304-0208(08)72828-7, MR 0791034
- ↑ Bezdek, A.; Fodor, F. (2000), "On convex polygons of maximal width", Archiv der Mathematik, 74 (1): 75–80, doi:10.1007/PL00000413, MR 1728365, S2CID 123299791