स्व ऊर्जा: Difference between revisions
(एक) |
No edit summary |
||
| Line 1: | Line 1: | ||
{{Short description|Energy quantum particles contribute to themselves}} | {{Short description|Energy quantum particles contribute to themselves}} | ||
[[ क्वांटम क्षेत्र सिद्धांत |क्वांटम क्षेत्र सिद्धांत]] में, एक कण में जो ऊर्जा होती है, वह परिवर्तनों के परिणामस्वरूप होती है जो इसके वातावरण में उत्पन्न होती है, वह स्व ऊर्जा को परिभाषित करती है <math>\Sigma</math>, और कण और उसके पर्यावरण के बीच परस्पर क्रिया के कारण कण की [[ऊर्जा]], या [[प्रभावी द्रव्यमान (ठोस अवस्था भौतिकी)]]के योगदान का प्रतिनिधित्व करता है। [[ इलेक्ट्रोस्टाटिक्स |विद्युत्दर्शी]] में आवेश वितरण को इकट्ठा करने के लिए आवश्यक ऊर्जा अनंत से संघटक आवेशों में लाकर स्व ऊर्जा का रूप ले लेती है, जहाँ विद्युत बल शून्य तक चला जाता है। एक सामग्री में चलने वाले इलेक्ट्रॉनों के लिए प्रासंगिक एक संघनित मामले के संदर्भ में, स्व-ऊर्जा इलेक्ट्रॉन द्वारा महसूस की गई क्षमता का प्रतिनिधित्व करता है आसपास के माध्यम के साथ | [[ क्वांटम क्षेत्र सिद्धांत |क्वांटम क्षेत्र सिद्धांत]] में, एक कण में जो ऊर्जा होती है, वह परिवर्तनों के परिणामस्वरूप होती है जो इसके वातावरण में उत्पन्न होती है, वह स्व ऊर्जा को परिभाषित करती है <math>\Sigma</math>, और कण और उसके पर्यावरण के बीच परस्पर क्रिया के कारण कण की [[ऊर्जा]], या [[प्रभावी द्रव्यमान (ठोस अवस्था भौतिकी)]] के योगदान का प्रतिनिधित्व करता है। [[ इलेक्ट्रोस्टाटिक्स |विद्युत्दर्शी]] में आवेश वितरण को इकट्ठा करने के लिए आवश्यक ऊर्जा अनंत से संघटक आवेशों में लाकर स्व ऊर्जा का रूप ले लेती है, जहाँ विद्युत बल शून्य तक चला जाता है। एक सामग्री में चलने वाले इलेक्ट्रॉनों के लिए प्रासंगिक एक संघनित मामले के संदर्भ में, स्व-ऊर्जा इलेक्ट्रॉन द्वारा महसूस की गई क्षमता का प्रतिनिधित्व करता है आसपास के माध्यम के साथ पारस्परिक प्रभाव के कारण। चूंकि इलेक्ट्रॉन एक दूसरे को ध्रुवीय करते हैं, या इसके आसपास के क्षेत्रों में इलेक्ट्रॉनों को विस्थापित करने का कारण बनते हैं और फिर गतिशील इलेक्ट्रॉन की क्षमता बदलते हैं। ये स्व-ऊर्जा के उदाहरण हैं। | ||
== विशेषताएं == | == विशेषताएं == | ||
| Line 8: | Line 8: | ||
सामान्य रूप से संवेग-ऊर्जा निरूपण में स्वऊर्जा ऑपरेटर का ऑन-मास-शैल मान [[जटिल संख्या]] होता है। ऐसे मामलों में, यह इस आत्म-ऊर्जा का वास्तविक भाग है जिसकी पहचान भौतिक आत्म-ऊर्जा से की जाती है (ऊपर से कण के "आत्म-ऊर्जा" के रूप में संदर्भित); काल्पनिक भाग का व्युत्क्रम जांच के अधीन कण के जीवनकाल के लिए एक माप है। स्पष्टता के लिए, प्रारंभिक उत्तेजन, या ड्रेस्ड कण (अर्ध-कण देखें), अंतर्क्रिया प्रणालियों में निर्वात में स्थिर कणों से भिन्न होते हैं; उनकी स्थिति फ़ंक्शंस में अंतर्निहित कई-कण प्रणाली की आइगेनवैल्यू और ईजेनवेक्टर अवस्थाओं की जटिल अतिस्थिति होती है, जो केवल क्षणिक रूप से, यदि बिल्कुल भी, अलग-थलग कणों के लिए उन विशिष्ट स्थितियों की तरह व्यवहार करते हैं; उपर्युक्त जीवनकाल वह समय है जब एक ड्रेस्ड कण इस प्रकार व्यवहार करता है मानो वह सुपरिभाषित संवेग और ऊर्जा वाला एक एकल कण हो। | सामान्य रूप से संवेग-ऊर्जा निरूपण में स्वऊर्जा ऑपरेटर का ऑन-मास-शैल मान [[जटिल संख्या]] होता है। ऐसे मामलों में, यह इस आत्म-ऊर्जा का वास्तविक भाग है जिसकी पहचान भौतिक आत्म-ऊर्जा से की जाती है (ऊपर से कण के "आत्म-ऊर्जा" के रूप में संदर्भित); काल्पनिक भाग का व्युत्क्रम जांच के अधीन कण के जीवनकाल के लिए एक माप है। स्पष्टता के लिए, प्रारंभिक उत्तेजन, या ड्रेस्ड कण (अर्ध-कण देखें), अंतर्क्रिया प्रणालियों में निर्वात में स्थिर कणों से भिन्न होते हैं; उनकी स्थिति फ़ंक्शंस में अंतर्निहित कई-कण प्रणाली की आइगेनवैल्यू और ईजेनवेक्टर अवस्थाओं की जटिल अतिस्थिति होती है, जो केवल क्षणिक रूप से, यदि बिल्कुल भी, अलग-थलग कणों के लिए उन विशिष्ट स्थितियों की तरह व्यवहार करते हैं; उपर्युक्त जीवनकाल वह समय है जब एक ड्रेस्ड कण इस प्रकार व्यवहार करता है मानो वह सुपरिभाषित संवेग और ऊर्जा वाला एक एकल कण हो। | ||
स्व-ऊर्जा ऑपरेटर (अक्सर द्वारा निरूपित किया जाता है <math>\Sigma_{}^{}</math>, और कम बार द्वारा <math>M_{}^{}</math>) मात्र और प्रसाधित प्रचारकों से संबंधित है (प्रायः द्वारा निरूपित किया जाता है <math>G_0^{}</math> और <math>G_{}^{}</math> क्रमशः) डायसन समीकरण के माध्यम से ([[फ्रीमैन डायसन]] के नाम पर): | |||
स्व-ऊर्जा ऑपरेटर (अक्सर द्वारा निरूपित किया जाता है <math>\Sigma_{}^{}</math>, और कम बार द्वारा <math>M_{}^{}</math>) मात्र और प्रसाधित प्रचारकों से संबंधित है ( | |||
:<math>G = G_0^{} + G_0 \Sigma G.</math> | :<math>G = G_0^{} + G_0 \Sigma G.</math> | ||
बाईं ओर व्युत्क्रम से गुणा करना <math>G_0^{-1}</math> ऑपरेटर का <math>G_0</math> | बाईं ओर व्युत्क्रम से गुणा करना <math>G_0^{-1}</math> ऑपरेटर का <math>G_0</math> | ||
| Line 18: | Line 17: | ||
:[[File:electron self energy.svg]] | :[[File:electron self energy.svg]] | ||
:[[File:Dyson.svg]]फोटॉन और ग्लूऑन को [[पुनर्सामान्यीकरण]] के माध्यम से द्रव्यमान नहीं मिलता है क्योंकि [[गेज समरूपता]] उन्हें द्रव्यमान प्राप्त करने से बचाती | :[[File:Dyson.svg]] | ||
: | |||
:फोटॉन और ग्लूऑन को [[पुनर्सामान्यीकरण]] के माध्यम से द्रव्यमान नहीं मिलता है क्योंकि [[गेज समरूपता]] उन्हें द्रव्यमान प्राप्त करने से बचाती है।यह वार्ड पहचान का ही एक परिणाम है। [[W-बोसोन]] और Z-बोसोन अपना द्रव्यमान [[हिग्स तंत्र]] के माध्यम से प्राप्त करते हैं; वे [[विद्युत]] सिद्धांत के पुनर्सामान्यीकरण के माध्यम से बड़े पैमाने पर पुनर्सामान्यीकरण से गुजरते हैं। | |||
आंतरिक क्वांटम संख्याओं के साथ न्यूट्रल कण [[आभासी जोड़ी]] उत्पादन के माध्यम से एक दूसरे के साथ मिल सकते हैं। इस घटना का प्राथमिक उदाहरण [[तटस्थ कण दोलन|तटस्थ कण दोलनों]] का मिश्रण है। उचित सरलीकरण धारणाओं के अंतर्गत बिना क्वांटम क्षेत्र सिद्धांत के इसका वर्णन किया जा सकता है। | आंतरिक क्वांटम संख्याओं के साथ न्यूट्रल कण [[आभासी जोड़ी]] उत्पादन के माध्यम से एक दूसरे के साथ मिल सकते हैं। इस घटना का प्राथमिक उदाहरण [[तटस्थ कण दोलन|तटस्थ कण दोलनों]] का मिश्रण है। उचित सरलीकरण धारणाओं के अंतर्गत बिना क्वांटम क्षेत्र सिद्धांत के इसका वर्णन किया जा सकता है। | ||
== अन्य उपयोग == | == अन्य उपयोग == | ||
[[रसायन विज्ञान]] में, एक आयन की स्वयं ऊर्जा या जनित ऊर्जा स्वयं आयन के क्षेत्र से जुड़ी ऊर्जा है। | [[रसायन विज्ञान]] में, एक आयन की स्वयं ऊर्जा या जनित ऊर्जा स्वयं आयन के क्षेत्र से जुड़ी ऊर्जा है। | ||
[[ भौतिक विज्ञान की ठोस अवस्था | | [[ भौतिक विज्ञान की ठोस अवस्था |भौतिक विज्ञान की ठोस अवस्था]] और [[ संघनित पदार्थ भौतिकी | संघनित पदार्थ भौतिकी]] में स्व ऊर्जा और संबंधित [[ quisiparticle |क्वैस्कण]] गुणों के एक असंख्य अप्रकट की गणना ग्रीन की कार्य विधियों द्वारा की जाती है और [[इलेक्ट्रॉनिक बैंड संरचना]] गणना के आधार पर कम-ऊर्जा उत्तेजित करने के ग्रीन के कार्य (कई-निकाय सिद्धांत). स्व ऊर्जा, खुले क्वांटम प्रणालियों के माध्यम से कण परिवहन की गणना में और उप-क्षेत्रों को बड़ी प्रणालियों में एम्बेड करने (उदाहरण के लिए एक अर्ध-अनन्त क्रिस्टल की सतह) में भी व्यापक अनुप्रयोग पाते हैं। | ||
== यह भी देखें == | == यह भी देखें == | ||
Revision as of 11:15, 28 April 2023
क्वांटम क्षेत्र सिद्धांत में, एक कण में जो ऊर्जा होती है, वह परिवर्तनों के परिणामस्वरूप होती है जो इसके वातावरण में उत्पन्न होती है, वह स्व ऊर्जा को परिभाषित करती है , और कण और उसके पर्यावरण के बीच परस्पर क्रिया के कारण कण की ऊर्जा, या प्रभावी द्रव्यमान (ठोस अवस्था भौतिकी) के योगदान का प्रतिनिधित्व करता है। विद्युत्दर्शी में आवेश वितरण को इकट्ठा करने के लिए आवश्यक ऊर्जा अनंत से संघटक आवेशों में लाकर स्व ऊर्जा का रूप ले लेती है, जहाँ विद्युत बल शून्य तक चला जाता है। एक सामग्री में चलने वाले इलेक्ट्रॉनों के लिए प्रासंगिक एक संघनित मामले के संदर्भ में, स्व-ऊर्जा इलेक्ट्रॉन द्वारा महसूस की गई क्षमता का प्रतिनिधित्व करता है आसपास के माध्यम के साथ पारस्परिक प्रभाव के कारण। चूंकि इलेक्ट्रॉन एक दूसरे को ध्रुवीय करते हैं, या इसके आसपास के क्षेत्रों में इलेक्ट्रॉनों को विस्थापित करने का कारण बनते हैं और फिर गतिशील इलेक्ट्रॉन की क्षमता बदलते हैं। ये स्व-ऊर्जा के उदाहरण हैं।
विशेषताएं
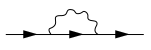
गणितीय रूप से, यह ऊर्जा संवेग-ऊर्जा निरूपण (अधिक संक्षेप में, करने के लिए, उचित स्व ऊर्जा ऑपरेटर (या उचित द्रव्यमान ऑपरेटर) के उचित द्रव्यमान ऑन शेल और ऑफ शेल मान पर तथाकथित के बराबर होती है, बार इस मान का समय देता है). इसमें, या अन्य निरूपण (जैसे अंतरिक्ष-समय का प्रतिनिधित्व), स्व ऊर्जा को फेनमैन आरेखों के माध्यम से प्रतिनिधित्व करते हुए, चित्ररूप से (और आर्थिक रूप से) किया जाता है, जैसे कि नीचे दिखाया गया एक। इस विशेष आरेख में, तीन आरोवेदार सीधी रेखाएँ कणों, या कण प्रचारक का प्रतिनिधित्व करती हैं, और लहरदार रेखा एक कण-कण की पारस्परिक क्रिया; नीचे दिखाए गए आरेख में बाईं-सबसे और दाईं-सबसे सीधी रेखाओं को निकालना (या एम्पुटिंग) (ये तथाकथित बाह्य रेखाएँ, उदाहरण के लिए, संवेग और ऊर्जा, या चार-संवेग) के लिए निर्धारित मानों के अनुरूप होती हैं, इनमें से एक स्व ऊर्जा ऑपरेटर के लिए योगदान को बनाए रखती हैं (उदाहरण के लिए, संवेग-ऊर्जा प्रतिनिधित्व). सरल नियमों की एक छोटी संख्या का उपयोग करते हुए प्रत्येक फेनमैन आरेख को अपने संगत बीजगणितीय रूप में सरलता से व्यक्त किया जा सकता है।
सामान्य रूप से संवेग-ऊर्जा निरूपण में स्वऊर्जा ऑपरेटर का ऑन-मास-शैल मान जटिल संख्या होता है। ऐसे मामलों में, यह इस आत्म-ऊर्जा का वास्तविक भाग है जिसकी पहचान भौतिक आत्म-ऊर्जा से की जाती है (ऊपर से कण के "आत्म-ऊर्जा" के रूप में संदर्भित); काल्पनिक भाग का व्युत्क्रम जांच के अधीन कण के जीवनकाल के लिए एक माप है। स्पष्टता के लिए, प्रारंभिक उत्तेजन, या ड्रेस्ड कण (अर्ध-कण देखें), अंतर्क्रिया प्रणालियों में निर्वात में स्थिर कणों से भिन्न होते हैं; उनकी स्थिति फ़ंक्शंस में अंतर्निहित कई-कण प्रणाली की आइगेनवैल्यू और ईजेनवेक्टर अवस्थाओं की जटिल अतिस्थिति होती है, जो केवल क्षणिक रूप से, यदि बिल्कुल भी, अलग-थलग कणों के लिए उन विशिष्ट स्थितियों की तरह व्यवहार करते हैं; उपर्युक्त जीवनकाल वह समय है जब एक ड्रेस्ड कण इस प्रकार व्यवहार करता है मानो वह सुपरिभाषित संवेग और ऊर्जा वाला एक एकल कण हो।
स्व-ऊर्जा ऑपरेटर (अक्सर द्वारा निरूपित किया जाता है , और कम बार द्वारा ) मात्र और प्रसाधित प्रचारकों से संबंधित है (प्रायः द्वारा निरूपित किया जाता है और क्रमशः) डायसन समीकरण के माध्यम से (फ्रीमैन डायसन के नाम पर):
बाईं ओर व्युत्क्रम से गुणा करना ऑपरेटर का और दाईं ओर पैदावार

- फोटॉन और ग्लूऑन को पुनर्सामान्यीकरण के माध्यम से द्रव्यमान नहीं मिलता है क्योंकि गेज समरूपता उन्हें द्रव्यमान प्राप्त करने से बचाती है।यह वार्ड पहचान का ही एक परिणाम है। W-बोसोन और Z-बोसोन अपना द्रव्यमान हिग्स तंत्र के माध्यम से प्राप्त करते हैं; वे विद्युत सिद्धांत के पुनर्सामान्यीकरण के माध्यम से बड़े पैमाने पर पुनर्सामान्यीकरण से गुजरते हैं।
आंतरिक क्वांटम संख्याओं के साथ न्यूट्रल कण आभासी जोड़ी उत्पादन के माध्यम से एक दूसरे के साथ मिल सकते हैं। इस घटना का प्राथमिक उदाहरण तटस्थ कण दोलनों का मिश्रण है। उचित सरलीकरण धारणाओं के अंतर्गत बिना क्वांटम क्षेत्र सिद्धांत के इसका वर्णन किया जा सकता है।
अन्य उपयोग
रसायन विज्ञान में, एक आयन की स्वयं ऊर्जा या जनित ऊर्जा स्वयं आयन के क्षेत्र से जुड़ी ऊर्जा है।
भौतिक विज्ञान की ठोस अवस्था और संघनित पदार्थ भौतिकी में स्व ऊर्जा और संबंधित क्वैस्कण गुणों के एक असंख्य अप्रकट की गणना ग्रीन की कार्य विधियों द्वारा की जाती है और इलेक्ट्रॉनिक बैंड संरचना गणना के आधार पर कम-ऊर्जा उत्तेजित करने के ग्रीन के कार्य (कई-निकाय सिद्धांत). स्व ऊर्जा, खुले क्वांटम प्रणालियों के माध्यम से कण परिवहन की गणना में और उप-क्षेत्रों को बड़ी प्रणालियों में एम्बेड करने (उदाहरण के लिए एक अर्ध-अनन्त क्रिस्टल की सतह) में भी व्यापक अनुप्रयोग पाते हैं।
यह भी देखें
- क्वांटम क्षेत्र सिद्धांत
- क्यूईडी वैक्यूम
- पुनर्सामान्यीकरण
- आत्म बल
- GW सन्निकटन
- व्हीलर-फेनमैन अवशोषक सिद्धांत
संदर्भ
- A. L. Fetter, and J. D. Walecka, Quantum Theory of Many-Particle Systems (McGraw-Hill, New York, 1971); (Dover, New York, 2003)
- J. W. Negele, and H. Orland, Quantum Many-Particle Systems (Westview Press, Boulder, 1998)
- A. A. Abrikosov, L. P. Gorkov and I. E. Dzyaloshinski (1963): Methods of Quantum Field Theory in Statistical Physics Englewood Cliffs: Prentice-Hall.
- Alexei M. Tsvelik (2007). Quantum Field Theory in Condensed Matter Physics (2nd ed.). Cambridge University Press. ISBN 978-0-521-52980-8.
- A. N. Vasil'ev The Field Theoretic Renormalization Group in Critical Behavior Theory and Stochastic Dynamics (Routledge Chapman & Hall 2004); ISBN 0-415-31002-4; ISBN 978-0-415-31002-4
- John E. Inglesfield (2015). The Embedding Method for Electronic Structure. IOP Publishing. ISBN 978-0-7503-1042-0.