हॉसडॉर्फ दूरी: Difference between revisions
(Created page with "{{Short description|Distance between two metric-space subsets}} गणित में, हॉसडॉर्फ दूरी, या हॉसडॉर्फ मीट्र...") |
No edit summary |
||
| Line 1: | Line 1: | ||
{{Short description|Distance between two metric-space subsets}} | {{Short description|Distance between two metric-space subsets}} | ||
गणित में | गणित में हॉसडॉर्फ दूरी या हॉसडॉर्फ मीट्रिक को पोम्पेउ-हॉउसडॉर्फ दूरी भी कहा जाता है<ref name="rock">{{cite book |author-link=R. Tyrrell Rockafellar |first1=R. Tyrrell |last1=Rockafellar |author-link2=Roger J-B Wets |first2=Roger J-B |last2=Wets |title=परिवर्तनशील विश्लेषण|publisher=Springer-Verlag |year=2005 |isbn=3-540-62772-3 |page=117 }}</ref><ref>{{Citation|last1=Bîrsan|first1=Temistocle|contribution=One hundred years since the introduction of the set distance by Dimitrie Pompeiu| year=2006|title=System Modeling and Optimization|volume=199|pages=35–39|editor-last=Ceragioli|editor-first=Francesca|place=Boston|publisher=[[Springer Science+Business Media|Kluwer Academic Publishers]]|language=en|doi=10.1007/0-387-33006-2_4|isbn=978-0-387-32774-7|last2=Tiba|first2=Dan|editor2-last=Dontchev|editor2-first=Asen|editor3-last=Futura|editor3-first=Hitoshi|editor4-last=Marti|editor4-first=Kurt|editor5-last=Pandolfi|editor5-first=Luciano|mr=2249320|doi-access=free}} | ||
</ref> | </ref> यह एक [[मीट्रिक स्थान]] के दो उपसमुच्चयों की एक दूसरे से दूरी मापता हैं। यह [[गैर-खाली सेट|गैर-रिक्त समुच्चय]] के समुच्चय को परिवर्तित कर देता है | मीट्रिक स्पेस के गैर-रिक्त[[ कॉम्पैक्ट जगह ]] [[सबसेट|उपसमुच्चय]] को अपने आप को मीट्रिक स्थान में परिवर्तित कर देता है। इसका नाम [[फेलिक्स हॉसडॉर्फ]] और [[डेमेट्रियस पॉम्पी]] के नाम पर रखा गया है। | ||
अनौपचारिक रूप से | अनौपचारिक रूप से हॉसडॉर्फ दूरी में दो समुच्चय निकट होते हैं यदि समुच्चय के प्रत्येक बिंदु दूसरे समुच्चय के किसी बिंदु के निकट है। हॉसडॉर्फ दूरी वह सबसे लंबी दूरी है जहाँ आपको विपक्षी द्वारा जाने के लिए प्रेरित किया जाता है जो दो समुच्चयों में से एक में बिंदु का चुनाव करता है जहां से आपको दूसरे समुच्चय की ओर जाना चाहिये। दूसरे शब्दों में यह दूरी समुच्चय में एक बिंदु से दूसरे समुच्चय में निकटतम बिंदु तक की सभी दूरियों में से सबसे बड़ी है। | ||
इस दूरी को हॉसडॉर्फ ने पहली बार 1914 में | इस दूरी को हॉसडॉर्फ ने पहली बार 1914 में प्रथम बार प्रकाशित अपनी पुस्तक ग्रंडजुगे डेर मेंजेनलेह्रे में प्रस्तुत किया था जबकि मौरिस रेने फ्रेचेट के डॉक्टरेट थीसिस में एक बहुत निकटतम सम्बन्धी <math>[0,1] \to \R^3</math> सम्मुख आया था। | ||
== परिभाषा == | == परिभाषा == | ||
[[Image:Hausdorff distance sample.svg|thumb|250px|right|ग्रीन कर्व X और ब्लू कर्व Y के बीच हॉसडॉर्फ दूरी की गणना के घटक।]] | [[Image:Hausdorff distance sample.svg|thumb|250px|right|ग्रीन कर्व X और ब्लू कर्व Y के बीच हॉसडॉर्फ दूरी की गणना के घटक।]]माना कि X और Y मीट्रिक स्पेस के दो गैर-रिक्त उपसमुच्चय <math>(M,d)</math> हैं, हम उनकी हॉसडॉर्फ दूरी को <math>d_{\mathrm H}(X,Y)</math> द्वारा | ||
परिभाषित करते हैं, | |||
जहाँ sup सर्वोच्चता का प्रतिनिधित्व करता है, [[infimum]] का प्रतिनिधित्व करता है | |||
<math> d_{\mathrm H}(X,Y) = \max\left\{\,\sup_{x \in X} d(x,Y),\, \sup_{y \in Y} d(X,y) \,\right\}, \! </math> | |||
जहाँ sup सर्वोच्चता का प्रतिनिधित्व करता है, [[infimum]] का प्रतिनिधित्व करता है और जहाँ <math>d(a, B) = \inf_{b \in B} d(a,b)</math> एक बिंदु <math>a \in X</math> उपसमुच्चय की <math>B\subseteq X</math> से दूरी की गणना करता है। | |||
समान रूप से, | समान रूप से, | ||
:<math>d_H(X,Y) = \inf\{\varepsilon \geq 0\,;\ X \subseteq Y_\varepsilon \text{ and } Y \subseteq X_\varepsilon\},\quad</math><ref>{{cite book |last=Munkres |first=James |author-link=James Munkres|title=टोपोलॉजी|edition=2nd |publisher=[[Prentice Hall]] |year=1999 |isbn=0-13-181629-2 |pages=280–281 |url={{Google books |plainurl=yes |id=XjoZAQAAIAAJ |page=280 }} }}</ref> | :<math>d_H(X,Y) = \inf\{\varepsilon \geq 0\,;\ X \subseteq Y_\varepsilon \text{ and } Y \subseteq X_\varepsilon\},\quad</math><ref>{{cite book |last=Munkres |first=James |author-link=James Munkres|title=टोपोलॉजी|edition=2nd |publisher=[[Prentice Hall]] |year=1999 |isbn=0-13-181629-2 |pages=280–281 |url={{Google books |plainurl=yes |id=XjoZAQAAIAAJ |page=280 }} }}</ref> | ||
जहाँ | |||
:<math> X_\varepsilon := \bigcup_{x \in X} \{z \in M\,;\ d(z,x) \leq \varepsilon\},</math> | :<math> X_\varepsilon := \bigcup_{x \in X} \{z \in M\,;\ d(z,x) \leq \varepsilon\},</math> | ||
अर्थात् | अर्थात् भीतर सभी बिंदुओं का समुच्चय <math>\varepsilon</math> समुच्चय <math>X</math> का (कभी-कभी <math>X</math> का <math>\varepsilon</math>- मोटा होना या त्रिज्या <math>\varepsilon</math> की सामान्यीकृत [[गेंद (गणित)]] <math>X</math> के आस-पास कहा जाता है). | ||
समान रूप से, | समान रूप से, | ||
| Line 28: | Line 31: | ||
</math><ref name="rock"/> | </math><ref name="rock"/> | ||
वह है | वह है <math>d_{\mathrm H}(X, Y) = \sup_{w \in M} | d(w, X) - d(w, Y)|</math> | ||
जहाँ समुच्चय <math>X</math> की बिंदु <math>w</math> से दूरी <math>d(w, X)</math> है। | |||
=== टिप्पणी === | === टिप्पणी === | ||
यह | यह स्वेच्छाचारी उपसमुच्चय <math>X, Y \subset M</math> जो कि <math> d_{\mathrm H}(X,Y) = \varepsilon </math> हेतु सत्य नहीं है तात्पर्य | ||
:<math> X\subseteq Y_\varepsilon \ \mbox{and} \ Y\subseteq X_\varepsilon.</math> | :<math> X\subseteq Y_\varepsilon \ \mbox{and} \ Y\subseteq X_\varepsilon.</math> | ||
उदाहरण के लिए | उदाहरण के लिए वास्तविक संख्याओं के मीट्रिक स्थान <math>\mathbb{R}</math> पर विचार करें सामान्य मीट्रिक के साथ <math>d</math> निरपेक्ष मूल्य से प्रेरित, | ||
:<math>d(x,y) := |y - x|, \quad x,y \in \R.</math> | :<math>d(x,y) := |y - x|, \quad x,y \in \R.</math> | ||
लेते हैं | |||
:<math>X := (0, 1] \quad \mbox{and} \quad Y := [-1,0). </math> | :<math>X := (0, 1] \quad \mbox{and} \quad Y := [-1,0). </math> | ||
तब <math>d_{\mathrm H}(X,Y) = 1\ </math> | तब <math>d_{\mathrm H}(X,Y) = 1\ </math>जबकि <math>X \nsubseteq Y_1</math> क्योंकि <math>Y_1 = [-2,1)\ </math>, परन्तु <math>1 \in X</math>. | ||
परन्तु यह सत्य है <math> X\subseteq \overline{Y_\varepsilon} </math> और <math> Y\subseteq \overline{X_\varepsilon}</math>; विशेष रूप से यह सच है यदि <math>X, Y</math> बंद हो जाते हैं। | |||
== गुण == | == गुण == | ||
*सामान्य रूप में | *सामान्य रूप में <math>d_{\mathrm H}(X,Y)</math> अनंत हो सकता है। यदि X और Y दोनों समुच्चय हैं तो <math>d_{\mathrm H}(X,Y)</math> परिमित होने की गारंटी है। | ||
*<math>d_{\mathrm H}(X,Y)=0</math> | *अगर <math>d_{\mathrm H}(X,Y)=0</math> और केवल अगर X और Y का एक ही प्रकार बंद होना है। | ||
*M के प्रत्येक बिंदु x के लिए और किसी भी गैर- | *M के प्रत्येक बिंदु x के लिए और किसी भी गैर-रिक्त समुच्चय Y, M के Z के लिए: d(x,Y) ≤ d(x,Z) + d<sub>H</sub>(वाई, जेड), जहां D (X, Y) बिंदु X और समुच्चय Y में निकटतम बिंदु के मध्य की दूरी है। | ||
*|व्यास(Y)-व्यास(X)| ≤ 2 | *|व्यास(Y)-व्यास(X)| ≤ 2 d<sub>H</sub>(X, Y)।<ref>[https://math.stackexchange.com/q/375296 Diameter and Hausdorff Distance], Math.SE</ref> | ||
*यदि प्रतिच्छेदन X ∩ Y का आंतरिक भाग | *यदि प्रतिच्छेदन X ∩ Y का आंतरिक भाग रिक्त नहीं है तो स्थिरांक r > 0 उपस्थित है जैसे कि प्रत्येक समुच्चय X' जिसकी हॉसडॉर्फ की दूरी X से कम है, Y को भी प्रतिच्छेद करता है।<ref>[https://math.stackexchange.com/q/732850 Hausdorff Distance and Intersection], Math.SE</ref> | ||
*M के सभी उपसमुच्चयों के समुच्चय पर, d<sub>H</sub> एक विस्तारित [[स्यूडोमेट्रिक स्पेस]] देता है। | *M के सभी उपसमुच्चयों के समुच्चय पर, d<sub>H</sub> एक विस्तारित [[स्यूडोमेट्रिक स्पेस]] देता है। | ||
* | * M, D<sub>H</sub> के सभी गैर-रिक्त सघन उपसमुच्चय के समुच्चय F(M) पर एक पैमाना है। | ||
**यदि M [[पूर्ण मीट्रिक स्थान]] है, तो F(M) भी है।<ref>{{cite journal|title=हॉसडॉर्फ मीट्रिक की पूर्णता और कुल सीमा|first=Jeff |last=Henrikson |journal=MIT Undergraduate Journal of Mathematics |year=1999 |pages=69–80 |url=http://www-math.mit.edu/phase2/UJM/vol1/HAUSF.PDF |url-status=dead |archive-url=https://web.archive.org/web/20020623095720/http://www-math.mit.edu/phase2/UJM/vol1/HAUSF.PDF |archive-date=June 23, 2002 }}</ref> | **यदि M [[पूर्ण मीट्रिक स्थान]] है, तो F(M) भी है।<ref>{{cite journal|title=हॉसडॉर्फ मीट्रिक की पूर्णता और कुल सीमा|first=Jeff |last=Henrikson |journal=MIT Undergraduate Journal of Mathematics |year=1999 |pages=69–80 |url=http://www-math.mit.edu/phase2/UJM/vol1/HAUSF.PDF |url-status=dead |archive-url=https://web.archive.org/web/20020623095720/http://www-math.mit.edu/phase2/UJM/vol1/HAUSF.PDF |archive-date=June 23, 2002 }}</ref> | ||
**यदि | **यदि M सघन है तो F(M) भी है। | ||
**F(M) का [[टोपोलॉजिकल स्पेस]] केवल M के टोपोलॉजी पर निर्भर करता है | **F(M) का [[टोपोलॉजिकल स्पेस|टोपोलॉजिकल स्थान]] केवल M के टोपोलॉजी पर निर्भर करता है मेट्रिक d पर नहीं। | ||
== प्रेरणा == | == प्रेरणा == | ||
हॉसडॉर्फ दूरी की परिभाषा दूरी समारोह के प्राकृतिक विस्तार की | हॉसडॉर्फ दूरी की परिभाषा दूरी समारोह के प्राकृतिक विस्तार की श्रृंखला <math>d(x,y)</math> से प्राप्त की जा सकती है जहाँ अंतर्निहित मीट्रिक स्थान M में इस प्रकार है:<ref>{{cite book | ||
| last = Barnsley | | last = Barnsley | ||
| first = Michael | | first = Michael | ||
| Line 67: | Line 72: | ||
| isbn = 0-12-079069-6}} | | isbn = 0-12-079069-6}} | ||
</ref> | </ref> | ||
* M के किसी भी बिंदु x और M के किसी भी गैर-रिक्त | * M के किसी भी बिंदु x और M के किसी भी गैर-रिक्त समुच्चय Y के मध्य दूरी फ़ंक्शन को परिभाषित करें: | ||
::<math>d(x,Y)=\inf \{ d(x,y) \mid y \in Y \}.\ </math> | ::<math>d(x,Y)=\inf \{ d(x,y) \mid y \in Y \}.\ </math> | ||
: उदाहरण के लिए, | : उदाहरण के लिए, d (1, {3,6}) = 2 और डी (7, {3,6}) = 1। | ||
* | * M के किसी भी दो गैर-रिक्त समुच्चय X और Y के मध्य (सममित-आवश्यक-नहीं) दूरी फ़ंक्शन परिभाषित करें: | ||
::<math>d(X,Y)=\sup \{ d(x,Y) \mid x \in X \}.\ </math> | ::<math>d(X,Y)=\sup \{ d(x,Y) \mid x \in X \}.\ </math> | ||
:उदाहरण के लिए | :उदाहरण के लिए <math display="inline"> d(\{1,7\},\{3,6\}) = \sup\{ d(1,\{3,6\}), d(7,\{3,6\})\} = \sup\{ d(1,3),d(7,6) \} = 2. </math> | ||
*यदि | *यदि X और Y सघन हैं तो d (X, Y) परिमित होगा; d (X, X) = 0; और d त्रिभुज असमानता संपत्ति को M में दूरी फंक्शन से प्राप्त करता है। जैसा कि स्थित है कि d (X, Y) मीट्रिक नहीं है क्योंकि d (X, Y) सदैव सममित नहीं है और {{nowrap|1=''d''(''X'',''Y'') = 0}} का अर्थ {{nowrap|1=''X'' = ''Y''}} (इसका मतलब यह है <math> X \subseteq Y</math>) नहीं है उदाहरण के लिए, {{nowrap|1=''d''({1,3,6,7}, {3,6}) = 2}} किन्तु {{nowrap|1=''d''({3,6}, {1,3,6,7}) = 0}}, जबकि हम हॉसडॉर्फ दूरी को परिभाषित करके मीट्रिक बना सकते हैं: | ||
::<math>d_{\mathrm H}(X,Y) = \max\{d(X,Y),d(Y,X) \} \, .</math> | ::<math>d_{\mathrm H}(X,Y) = \max\{d(X,Y),d(Y,X) \} \, .</math> | ||
== अनुप्रयोग == | == अनुप्रयोग == | ||
[[कंप्यूटर दृष्टि]] में | [[कंप्यूटर दृष्टि]] में हॉसडॉर्फ दूरी का उपयोग एकपक्षीय लक्ष्य छवि में दिए गए टेम्पलेट को खोजने के लिए किया जा सकता है। नमूना और छवि को अधिकतर [[किनारे का पता लगाना|सीमा सूचकांक]] के माध्यम से पूर्व-प्रक्रमक किया जाता है जिससे [[ द्विआधारी छवि ]] मिलती है। टेम्पलेट की बाइनरी छवि में प्रत्येक 1 (सक्रिय) बिंदु को समुच्चय में एक बिंदु टेम्पलेट का आकार के रूप में माना जाता है। इसी प्रकार बाइनरी लक्ष्य छवि के क्षेत्र को बिंदुओं के समूह के रूप में माना जाता है। एल्गोरिथ्म तब टेम्पलेट और लक्ष्य छवि के कुछ क्षेत्र के बीच हॉसडॉर्फ की दूरी को कम करने की कोशिश करता है। लक्ष्य छवि में टेम्पलेट के लिए न्यूनतम हॉसडॉर्फ दूरी वाले क्षेत्र को लक्ष्य में टेम्पलेट का पता लगाने के लिए सबसे अच्छा उम्मीदवार माना जा सकता है। | ||
[[कंप्यूटर चित्रलेख]] में हॉसडॉर्फ दूरी का उपयोग एक ही 3डी ऑब्जेक्ट के दो अलग-अलग प्रतिनिधित्वों के बीच अंतर को मापने के लिए किया जाता है<ref>{{cite journal |first1=P. |last1=Cignoni |first2=C. |last2=Rocchini |first3=R. |last3=Scopigno |title=Metro: Measuring Error on Simplified Surfaces |journal=Computer Graphics Forum |volume=17 |issue=2 |year=1998 |pages=167–174 |doi=10.1111/1467-8659.00236 |citeseerx=10.1.1.95.9740 |s2cid=17783159 }}</ref> विशेष रूप से जटिल 3डी मॉडल के कुशल प्रदर्शन के लिए विस्तार का स्तर (कंप्यूटर ग्राफिक्स) उत्पन्न करते समय। | [[कंप्यूटर चित्रलेख]] में हॉसडॉर्फ दूरी का उपयोग एक ही 3डी ऑब्जेक्ट के दो अलग-अलग प्रतिनिधित्वों के बीच अंतर को मापने के लिए किया जाता है<ref>{{cite journal |first1=P. |last1=Cignoni |first2=C. |last2=Rocchini |first3=R. |last3=Scopigno |title=Metro: Measuring Error on Simplified Surfaces |journal=Computer Graphics Forum |volume=17 |issue=2 |year=1998 |pages=167–174 |doi=10.1111/1467-8659.00236 |citeseerx=10.1.1.95.9740 |s2cid=17783159 }}</ref> विशेष रूप से जटिल 3डी मॉडल के कुशल प्रदर्शन के लिए विस्तार का स्तर (कंप्यूटर ग्राफिक्स) उत्पन्न करते समय। | ||
Revision as of 23:56, 30 April 2023
गणित में हॉसडॉर्फ दूरी या हॉसडॉर्फ मीट्रिक को पोम्पेउ-हॉउसडॉर्फ दूरी भी कहा जाता है[1][2] यह एक मीट्रिक स्थान के दो उपसमुच्चयों की एक दूसरे से दूरी मापता हैं। यह गैर-रिक्त समुच्चय के समुच्चय को परिवर्तित कर देता है | मीट्रिक स्पेस के गैर-रिक्तकॉम्पैक्ट जगह उपसमुच्चय को अपने आप को मीट्रिक स्थान में परिवर्तित कर देता है। इसका नाम फेलिक्स हॉसडॉर्फ और डेमेट्रियस पॉम्पी के नाम पर रखा गया है।
अनौपचारिक रूप से हॉसडॉर्फ दूरी में दो समुच्चय निकट होते हैं यदि समुच्चय के प्रत्येक बिंदु दूसरे समुच्चय के किसी बिंदु के निकट है। हॉसडॉर्फ दूरी वह सबसे लंबी दूरी है जहाँ आपको विपक्षी द्वारा जाने के लिए प्रेरित किया जाता है जो दो समुच्चयों में से एक में बिंदु का चुनाव करता है जहां से आपको दूसरे समुच्चय की ओर जाना चाहिये। दूसरे शब्दों में यह दूरी समुच्चय में एक बिंदु से दूसरे समुच्चय में निकटतम बिंदु तक की सभी दूरियों में से सबसे बड़ी है।
इस दूरी को हॉसडॉर्फ ने पहली बार 1914 में प्रथम बार प्रकाशित अपनी पुस्तक ग्रंडजुगे डेर मेंजेनलेह्रे में प्रस्तुत किया था जबकि मौरिस रेने फ्रेचेट के डॉक्टरेट थीसिस में एक बहुत निकटतम सम्बन्धी सम्मुख आया था।
परिभाषा
माना कि X और Y मीट्रिक स्पेस के दो गैर-रिक्त उपसमुच्चय हैं, हम उनकी हॉसडॉर्फ दूरी को द्वारा
परिभाषित करते हैं,
जहाँ sup सर्वोच्चता का प्रतिनिधित्व करता है, infimum का प्रतिनिधित्व करता है और जहाँ एक बिंदु उपसमुच्चय की से दूरी की गणना करता है।
समान रूप से,
जहाँ
अर्थात् भीतर सभी बिंदुओं का समुच्चय समुच्चय का (कभी-कभी का - मोटा होना या त्रिज्या की सामान्यीकृत गेंद (गणित) के आस-पास कहा जाता है).
समान रूप से,
वह है
जहाँ समुच्चय की बिंदु से दूरी है।
टिप्पणी
यह स्वेच्छाचारी उपसमुच्चय जो कि हेतु सत्य नहीं है तात्पर्य
उदाहरण के लिए वास्तविक संख्याओं के मीट्रिक स्थान पर विचार करें सामान्य मीट्रिक के साथ निरपेक्ष मूल्य से प्रेरित,
लेते हैं
तब जबकि क्योंकि , परन्तु .
परन्तु यह सत्य है और ; विशेष रूप से यह सच है यदि बंद हो जाते हैं।
गुण
- सामान्य रूप में अनंत हो सकता है। यदि X और Y दोनों समुच्चय हैं तो परिमित होने की गारंटी है।
- अगर और केवल अगर X और Y का एक ही प्रकार बंद होना है।
- M के प्रत्येक बिंदु x के लिए और किसी भी गैर-रिक्त समुच्चय Y, M के Z के लिए: d(x,Y) ≤ d(x,Z) + dH(वाई, जेड), जहां D (X, Y) बिंदु X और समुच्चय Y में निकटतम बिंदु के मध्य की दूरी है।
- |व्यास(Y)-व्यास(X)| ≤ 2 dH(X, Y)।[4]
- यदि प्रतिच्छेदन X ∩ Y का आंतरिक भाग रिक्त नहीं है तो स्थिरांक r > 0 उपस्थित है जैसे कि प्रत्येक समुच्चय X' जिसकी हॉसडॉर्फ की दूरी X से कम है, Y को भी प्रतिच्छेद करता है।[5]
- M के सभी उपसमुच्चयों के समुच्चय पर, dH एक विस्तारित स्यूडोमेट्रिक स्पेस देता है।
- M, DH के सभी गैर-रिक्त सघन उपसमुच्चय के समुच्चय F(M) पर एक पैमाना है।
- यदि M पूर्ण मीट्रिक स्थान है, तो F(M) भी है।[6]
- यदि M सघन है तो F(M) भी है।
- F(M) का टोपोलॉजिकल स्थान केवल M के टोपोलॉजी पर निर्भर करता है मेट्रिक d पर नहीं।
प्रेरणा
हॉसडॉर्फ दूरी की परिभाषा दूरी समारोह के प्राकृतिक विस्तार की श्रृंखला से प्राप्त की जा सकती है जहाँ अंतर्निहित मीट्रिक स्थान M में इस प्रकार है:[7]
- M के किसी भी बिंदु x और M के किसी भी गैर-रिक्त समुच्चय Y के मध्य दूरी फ़ंक्शन को परिभाषित करें:
- उदाहरण के लिए, d (1, {3,6}) = 2 और डी (7, {3,6}) = 1।
- M के किसी भी दो गैर-रिक्त समुच्चय X और Y के मध्य (सममित-आवश्यक-नहीं) दूरी फ़ंक्शन परिभाषित करें:
- उदाहरण के लिए
- यदि X और Y सघन हैं तो d (X, Y) परिमित होगा; d (X, X) = 0; और d त्रिभुज असमानता संपत्ति को M में दूरी फंक्शन से प्राप्त करता है। जैसा कि स्थित है कि d (X, Y) मीट्रिक नहीं है क्योंकि d (X, Y) सदैव सममित नहीं है और d(X,Y) = 0 का अर्थ X = Y (इसका मतलब यह है ) नहीं है उदाहरण के लिए, d({1,3,6,7}, {3,6}) = 2 किन्तु d({3,6}, {1,3,6,7}) = 0, जबकि हम हॉसडॉर्फ दूरी को परिभाषित करके मीट्रिक बना सकते हैं:
अनुप्रयोग
कंप्यूटर दृष्टि में हॉसडॉर्फ दूरी का उपयोग एकपक्षीय लक्ष्य छवि में दिए गए टेम्पलेट को खोजने के लिए किया जा सकता है। नमूना और छवि को अधिकतर सीमा सूचकांक के माध्यम से पूर्व-प्रक्रमक किया जाता है जिससे द्विआधारी छवि मिलती है। टेम्पलेट की बाइनरी छवि में प्रत्येक 1 (सक्रिय) बिंदु को समुच्चय में एक बिंदु टेम्पलेट का आकार के रूप में माना जाता है। इसी प्रकार बाइनरी लक्ष्य छवि के क्षेत्र को बिंदुओं के समूह के रूप में माना जाता है। एल्गोरिथ्म तब टेम्पलेट और लक्ष्य छवि के कुछ क्षेत्र के बीच हॉसडॉर्फ की दूरी को कम करने की कोशिश करता है। लक्ष्य छवि में टेम्पलेट के लिए न्यूनतम हॉसडॉर्फ दूरी वाले क्षेत्र को लक्ष्य में टेम्पलेट का पता लगाने के लिए सबसे अच्छा उम्मीदवार माना जा सकता है। कंप्यूटर चित्रलेख में हॉसडॉर्फ दूरी का उपयोग एक ही 3डी ऑब्जेक्ट के दो अलग-अलग प्रतिनिधित्वों के बीच अंतर को मापने के लिए किया जाता है[8] विशेष रूप से जटिल 3डी मॉडल के कुशल प्रदर्शन के लिए विस्तार का स्तर (कंप्यूटर ग्राफिक्स) उत्पन्न करते समय।
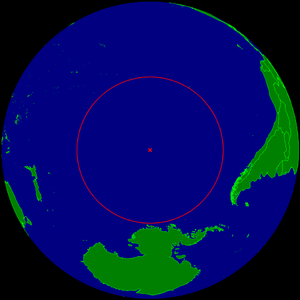
अगर पृथ्वी की सतह है, और पृथ्वी की भूमि-सतह है, तो निमो बिंदु खोजने पर, हम देखते हैं लगभग 2,704.8 किमी है।
संबंधित अवधारणाएं
आइसोमेट्री तक हॉसडॉर्फ दूरी द्वारा दो आकृतियों की असमानता के लिए एक उपाय दिया गया है, जिसे डी निरूपित किया गया हैH. अर्थात्, X और Y को मीट्रिक स्पेस M (आमतौर पर एक यूक्लिडियन अंतरिक्ष ) में दो कॉम्पैक्ट आंकड़े होने दें; तब डीH(एक्स, वाई) डी का न्यूनतम हैH(I(X),Y) मीट्रिक स्पेस M के सभी आइसोमेट्री I के साथ ही। यह दूरी मापती है कि आकार X और Y सममितीय होने से कितनी दूर हैं।
ग्रोमोव-हॉसडॉर्फ अभिसरण एक संबंधित विचार है: हम दो मीट्रिक रिक्त स्थान एम और एन की दूरी को कम से कम लेते हुए मापते हैं सभी आइसोमेट्रिक एम्बेडिंग के साथ और कुछ सामान्य मीट्रिक स्थान एल में।
यह भी देखें
- विज्समैन अभिसरण
- कुराटोव्स्की अभिसरण
- अर्ध निरंतरता
- फ्रेचेट दूरी
संदर्भ
- ↑ 1.0 1.1 Rockafellar, R. Tyrrell; Wets, Roger J-B (2005). परिवर्तनशील विश्लेषण. Springer-Verlag. p. 117. ISBN 3-540-62772-3.
- ↑ Bîrsan, Temistocle; Tiba, Dan (2006), "One hundred years since the introduction of the set distance by Dimitrie Pompeiu", in Ceragioli, Francesca; Dontchev, Asen; Futura, Hitoshi; Marti, Kurt; Pandolfi, Luciano (eds.), System Modeling and Optimization (in English), vol. 199, Boston: Kluwer Academic Publishers, pp. 35–39, doi:10.1007/0-387-33006-2_4, ISBN 978-0-387-32774-7, MR 2249320
- ↑ Munkres, James (1999). टोपोलॉजी (2nd ed.). Prentice Hall. pp. 280–281. ISBN 0-13-181629-2.
- ↑ Diameter and Hausdorff Distance, Math.SE
- ↑ Hausdorff Distance and Intersection, Math.SE
- ↑ Henrikson, Jeff (1999). "हॉसडॉर्फ मीट्रिक की पूर्णता और कुल सीमा" (PDF). MIT Undergraduate Journal of Mathematics: 69–80. Archived from the original (PDF) on June 23, 2002.
- ↑ Barnsley, Michael (1993). Fractals Everywhere. Morgan Kaufmann. pp. Ch. II.6. ISBN 0-12-079069-6.
- ↑ Cignoni, P.; Rocchini, C.; Scopigno, R. (1998). "Metro: Measuring Error on Simplified Surfaces". Computer Graphics Forum. 17 (2): 167–174. CiteSeerX 10.1.1.95.9740. doi:10.1111/1467-8659.00236. S2CID 17783159.
बाहरी संबंध
- Hausdorff distance between convex polygons.
- Using MeshLab to measure difference between two surfaces A short tutorial on how to compute and visualize the Hausdorff distance between two triangulated 3D surfaces using the open source tool MeshLab.
- MATLAB code for Hausdorff distance: [1]