टायचोनॉफ स्पेस: Difference between revisions
No edit summary |
No edit summary |
||
| Line 6: | Line 6: | ||
== परिभाषाएँ == | == परिभाषाएँ == | ||
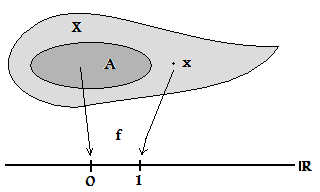
[[File:vollständigRegulärerRaum.png|right|frame|सतत क्रिया के माध्यम से बंद समुच्चय से एक बिंदु का पृथक्करण।]]टोपोलॉजिकल स्थान <math>X</math> {{em|पूर्णतया नियमित}} कहा जाता है यदि बिंदुओं को [[बंद सेट|बंद समुच्चयों]] से (बाध्य) निरंतर वास्तविक-मूल्यवान कार्यों के माध्यम से अलग किया जा सकता है। तकनीकी शब्दों में इसका अर्थ है किसी भी बंद समुच्चय <math>A \subseteq X</math> के लिए और कोई [[बिंदु (ज्यामिति)]] <math>x \in X \setminus A</math> ,अस्तित्वगत मात्रा का ठहराव वास्तविक-मूल्यवान [[निरंतर कार्य (टोपोलॉजी)]] <math>f : X \to \R</math> इस प्रकार उपस्थित है कि <math>f(x)=1</math> और <math>f\vert_{A} = 0</math> (समतुल्य रूप से इसके अतिरिक्त अन्य दो मान <math>0</math> और <math>1</math> चुन सकते हैं और यहां तक कि मांग करते हैं कि <math>f</math> एक बाध्य कार्य | [[File:vollständigRegulärerRaum.png|right|frame|सतत क्रिया के माध्यम से बंद समुच्चय से एक बिंदु का पृथक्करण।]]टोपोलॉजिकल स्थान <math>X</math> {{em|पूर्णतया नियमित}} कहा जाता है यदि बिंदुओं को [[बंद सेट|बंद समुच्चयों]] से (बाध्य) निरंतर वास्तविक-मूल्यवान कार्यों के माध्यम से अलग किया जा सकता है। तकनीकी शब्दों में इसका अर्थ है किसी भी बंद समुच्चय <math>A \subseteq X</math> के लिए और कोई [[बिंदु (ज्यामिति)]] <math>x \in X \setminus A</math> ,अस्तित्वगत मात्रा का ठहराव वास्तविक-मूल्यवान [[निरंतर कार्य (टोपोलॉजी)]] <math>f : X \to \R</math> इस प्रकार उपस्थित है कि <math>f(x)=1</math> और <math>f\vert_{A} = 0</math> (समतुल्य रूप से इसके अतिरिक्त अन्य दो मान <math>0</math> और <math>1</math> चुन सकते हैं और यहां तक कि मांग करते हैं कि <math>f</math> एक बाध्य कार्य हो)। | ||
टोपोलॉजिकल स्थान को टाइकोनॉफ़ स्थान कहा जाता है (वैकल्पिक रूप से:{{em|T<sub>3½</sub> स्थान}}, या {{em|T<sub>π</sub> स्थान}}, या {{em|पूर्णतया T<sub>3</sub> स्थान}}) यदि यह पूर्ण रूप से नियमित हौसडॉर्फ स्थान है। | टोपोलॉजिकल स्थान को टाइकोनॉफ़ स्थान कहा जाता है (वैकल्पिक रूप से:{{em|T<sub>3½</sub> स्थान}}, या {{em|T<sub>π</sub> स्थान}}, या {{em|पूर्णतया T<sub>3</sub> स्थान}}) यदि यह पूर्ण रूप से नियमित हौसडॉर्फ स्थान है। | ||
| Line 30: | Line 30: | ||
* प्रत्येक सांस्थितिक समूह पूर्णतः नियमित होता है। | * प्रत्येक सांस्थितिक समूह पूर्णतः नियमित होता है। | ||
* मेट्रिक स्थान और [[ टोपोलॉजिकल समूह | टोपोलॉजिकल समूह]] दोनों का सामान्यीकरण करते हुए प्रत्येक [[एक समान स्थान]] पूर्ण रूप से नियमित है। इसका विलोम भी सत्य है कि प्रत्येक पूर्णतः नियमित स्थान एकरूपता योग्य होता है। | * मेट्रिक स्थान और [[ टोपोलॉजिकल समूह | टोपोलॉजिकल समूह]] दोनों का सामान्यीकरण करते हुए प्रत्येक [[एक समान स्थान]] पूर्ण रूप से नियमित है। इसका विलोम भी सत्य है कि प्रत्येक पूर्णतः नियमित स्थान एकरूपता योग्य होता है। | ||
* प्रत्येक [[सीडब्ल्यू कॉम्प्लेक्स]] टाइकोनॉफ है। | * प्रत्येक [[सीडब्ल्यू कॉम्प्लेक्स|सीडब्ल्यू जटिल]] टाइकोनॉफ है। | ||
* प्रत्येक [[सामान्य स्थान|सामान्य]] नियमित स्थान पूर्ण रूप से नियमित है और प्रत्येक सामान्य हौसडॉर्फ स्थान टाइकोनॉफ़ है। | * प्रत्येक [[सामान्य स्थान|सामान्य]] नियमित स्थान पूर्ण रूप से नियमित है और प्रत्येक सामान्य हौसडॉर्फ स्थान टाइकोनॉफ़ है। | ||
* नीमेत्ज़की प्लेन टाइकोनॉफ़ स्थान का उदाहरण है जो सामान्य स्थान नहीं है। | * नीमेत्ज़की प्लेन टाइकोनॉफ़ स्थान का उदाहरण है जो सामान्य स्थान नहीं है। | ||
| Line 50: | Line 50: | ||
पूर्ण रूप से नियमित रिक्त स्थान को इस तथ्य से चित्रित किया जा सकता है कि उनकी टोपोलॉजी पूर्ण रूप से <math>C(X)</math> या <math>C_b(X)</math> निर्धारित होती है। विशेष रूप से: | पूर्ण रूप से नियमित रिक्त स्थान को इस तथ्य से चित्रित किया जा सकता है कि उनकी टोपोलॉजी पूर्ण रूप से <math>C(X)</math> या <math>C_b(X)</math> निर्धारित होती है। विशेष रूप से: | ||
* स्थान <math>X</math> पूर्ण रूप से नियमित है यदि और केवल यदि इसके द्वारा प्रेरित प्रारंभिक टोपोलॉजी | * स्थान <math>X</math> पूर्ण रूप से नियमित है यदि और केवल यदि इसके द्वारा प्रेरित प्रारंभिक टोपोलॉजी <math>C(X)</math> या <math>C_b(X)</math> है | ||
* स्थान <math>X</math> पूर्ण रूप से नियमित है यदि और केवल यदि प्रत्येक बंद समुच्चय <math>X</math> को [[शून्य सेट|शून्य समुच्चय]] के समूह के प्रतिच्छेदन के रूप में लिखा जा सकता है (अर्थात शून्य समुच्चय के बंद समुच्चय के लिए आधार बनाते हैं <math>X</math>) | * स्थान <math>X</math> पूर्ण रूप से नियमित है यदि और केवल यदि प्रत्येक बंद समुच्चय <math>X</math> को [[शून्य सेट|शून्य समुच्चय]] के समूह के प्रतिच्छेदन के रूप में लिखा जा सकता है (अर्थात शून्य समुच्चय के बंद समुच्चय के लिए आधार बनाते हैं <math>X</math>) | ||
* स्थान <math>X</math> पूर्ण रूप से नियमित है यदि और केवल यदि [[कोज़ीरो सेट|कोज़ीरो समुच्चय]] करता है <math>X</math> की टोपोलॉजी के लिए [[आधार (टोपोलॉजी)]] <math>X</math> बनाते हैं | * स्थान <math>X</math> पूर्ण रूप से नियमित है यदि और केवल यदि [[कोज़ीरो सेट|कोज़ीरो समुच्चय]] करता है <math>X</math> की टोपोलॉजी के लिए [[आधार (टोपोलॉजी)]] <math>X</math> बनाते हैं | ||
एकपक्षीय | एकपक्षीय रूप से टोपोलॉजिकल स्थान <math>(X, \tau)</math> को देखते हुए <math>(X, \tau)</math> के साथ एक पूरी तरह से नियमित स्थान को जोड़ने का सार्वभौमिक तरीका है। माना कि ρ, <math>X</math> पर प्रारंभिक टोपोलॉजी <math>C_{\tau}(X)</math> द्वारा प्रेरित है या समकक्ष <math>(X, \tau)</math> में कोज़रो सेट के आधार पर उत्पन्न टोपोलॉजी है तब ρ [[बेहतरीन टोपोलॉजी|उन्नत टोपोलॉजी]] होगी जिस पर पूर्ण रूप से नियमित <math>X</math> टोपोलॉजी होगी, वह <math>\tau</math> इससे मोटा है अतः यह निर्माण इस अर्थ में [[सार्वभौमिक संपत्ति]] है कि कोई भी निरंतर कार्य करता है<math display=block>f : (X, \tau) \to Y</math> | ||
पूर्ण रूप से नियमित स्थान <math>Y</math> पर निरंतर <math>(X, \rho)</math> चालू रहेगा [[श्रेणी सिद्धांत]] की भाषा में जो [[ऑपरेटर]] <math>(X, \tau)</math> को <math>(X, \rho)</math> भेजता है, समावेशन फ़ैक्टर CReg → शीर्ष के निकट छोड़ दिया गया है। इस प्रकार पूर्ण रूप से नियमित रिक्त स्थान की श्रेणी CReg, उच्चतम [[चिंतनशील उपश्रेणी|प्रतिबिंबित उपश्रेणी]] है जो स्थलीय रिक्त स्थान की श्रेणी है। कोलमोगोरोव उद्धरण से प्राप्त होता है कि टाइकोनॉफ़ रिक्त स्थान की उपश्रेणी भी प्रतिबंधित है। | पूर्ण रूप से नियमित स्थान <math>Y</math> पर निरंतर <math>(X, \rho)</math> चालू रहेगा [[श्रेणी सिद्धांत]] की भाषा में जो [[ऑपरेटर]] <math>(X, \tau)</math> को <math>(X, \rho)</math> भेजता है, समावेशन फ़ैक्टर CReg → शीर्ष के निकट छोड़ दिया गया है। इस प्रकार पूर्ण रूप से नियमित रिक्त स्थान की श्रेणी CReg, उच्चतम [[चिंतनशील उपश्रेणी|प्रतिबिंबित उपश्रेणी]] है जो स्थलीय रिक्त स्थान की श्रेणी है। कोलमोगोरोव उद्धरण से प्राप्त होता है कि टाइकोनॉफ़ रिक्त स्थान की उपश्रेणी भी प्रतिबंधित है। | ||
| Line 72: | Line 71: | ||
=== संघनन === | === संघनन === | ||
विशेष रूप से रुचि वे अंत: स्थापन हैं जहां | विशेष रूप से रुचि वे अंत: स्थापन हैं जहां <math>X</math> की छवि में <math>K</math> घना उपसमुच्चय है इन्हें <math>X</math> का हॉसडॉर्फ [[संघनन (गणित)|संघनन]] (गणित) कहा जाता है। | ||
टाइकोनॉफ स्थान के किसी भी अंतःस्थापन को देखते हुए <math>X</math> एक सघन हौसडॉर्फ स्थान में <math>K</math> की छवि का समापन (टोपोलॉजी) <math>X</math> में <math>K</math> का संघनन <math>X</math> है। | टाइकोनॉफ स्थान के किसी भी अंतःस्थापन को देखते हुए <math>X</math> एक सघन हौसडॉर्फ स्थान में <math>K</math> की छवि का समापन (टोपोलॉजी) <math>X</math> में <math>K</math> का संघनन <math>X</math> है। | ||
सन 1930 के उसी लेख में जहां टाइकोनॉफ़ ने पूर्ण रूप से नियमित रिक्त स्थान को परिभाषित किया | सन 1930 के उसी लेख में जहां टाइकोनॉफ़ ने पूर्ण रूप से नियमित रिक्त स्थान को परिभाषित किया था। उन्होंने यह भी प्रमाणित किया कि प्रत्येक टाइकोनॉफ़ स्थान में हौसडॉर्फ संघनन होता है।{{sfn|Narici|Beckenstein|2011|pp=225–273}} | ||
उन हॉसडॉर्फ संघनन में एक अनोखा सबसे सामान्य स्टोन-चेक संघनन <math>\beta X</math> है | उन हॉसडॉर्फ संघनन में एक अनोखा सबसे सामान्य स्टोन-चेक संघनन <math>\beta X</math> है तथा यह सार्वभौमिक संपत्ति की विशेषता है जिसने <math>X</math> से किसी भी अन्य सघन हौसडॉर्फ स्थान <math>Y</math> के लिए एक निरंतर मानचित्र <math>f</math> दिया गया है एवं किसी अन्य सघन हौसडॉर्फ स्थान एक अद्वितीय (गणित) निरंतर मानचित्र <math>g : \beta X \to Y</math> देता है जो <math>f</math> को इस अर्थ में विस्तारित करता है कि <math>f</math>, <math>g</math> और <math>j</math> की [[रचना (कार्य)|संरचना (कार्य)]] है। | ||
यह सार्वभौमिक संपत्ति की विशेषता है | |||
=== समान संरचना === | === समान संरचना === | ||
सामयिक स्थान पर पूर्ण नियमितता समान संरचनाओं के अस्तित्व के लिए एक आवश्यक परिस्थिति है। दूसरे शब्दों में प्रत्येक समान स्थान में पूर्ण रूप से नियमित टोपोलॉजी और प्रत्येक पूर्ण रूप से नियमित स्थान <math>X</math> होता है और यह [[एकरूप करने योग्य]] है। टोपोलॉजिकल स्थान | सामयिक स्थान पर पूर्ण नियमितता समान संरचनाओं के अस्तित्व के लिए एक आवश्यक परिस्थिति है। दूसरे शब्दों में प्रत्येक समान स्थान में पूर्ण रूप से नियमित टोपोलॉजी और प्रत्येक पूर्ण रूप से नियमित स्थान <math>X</math> होता है और यह [[एकरूप करने योग्य]] है। टोपोलॉजिकल स्थान अलग समान संरचना को स्वीकार करता है यदि और केवल यदि यह टाइकोनॉफ़ है। | ||
पूर्ण रूप से नियमित स्थान <math>X</math> को देखते हुए सामान्यतः <math>X</math> पर एक से अधिक एकरूपता होती है जो <math>X</math> टोपोलॉजी के के साथ संगत होती है जबकि सदैव एक उन्नत संगत एकरूपता होगी जिसे <math>X</math> पर सूक्ष्म एकरूपता कहा जाता है यदि <math>X</math> टेक्नोऑफ है तो समान संरचना <math>\beta X</math> को चुना जा सकता है जहाँ एक समान स्थान का [[समापन (टोपोलॉजी)]] <math>X</math> हो जाता है। | |||
== यह भी देखें == | == यह भी देखें == | ||
* {{annotated link| | * {{annotated link|स्टोन-सेच संघनन}} | ||
==उद्धरण== | ==उद्धरण== | ||
Revision as of 08:29, 3 May 2023
| Separation axioms in topological spaces | |
|---|---|
| Kolmogorov classification | |
| T0 | (Kolmogorov) |
| T1 | (Fréchet) |
| T2 | (Hausdorff) |
| T2½ | (Urysohn) |
| completely T2 | (completely Hausdorff) |
| T3 | (regular Hausdorff) |
| T3½ | (Tychonoff) |
| T4 | (normal Hausdorff) |
| T5 | (completely normal Hausdorff) |
| T6 | (perfectly normal Hausdorff) |
टोपोलॉजी और गणित की संबंधित शाखाओं में टाइकोनॉफ़ स्थान और पूर्ण रूप से नियमित स्थान टोपोलॉजिकल स्थान के प्रकार हैं। ये स्थितियाँ पृथक्करण अभिगृहीतों के उदाहरण हैं। टाइकोनॉफ़ स्थान किसी भी पूर्ण रूप से नियमित स्थान को संदर्भित करता है जो हॉसडॉर्फ स्थान भी है वहाँ पूर्ण रूप से नियमित स्थान उपस्थित हैं जो टाइकोनॉफ नहीं हैं (अर्थात हौसडॉर्फ नहीं हैं)।
टायकोनॉफ़ रिक्त स्थान का नाम एंड्री निकोलाइविच तिखोनॉफ के नाम पर रखा गया है जिनके रूसी भाषा के नाम (Тихонов) को विभिन्न रूप से "ताइकोनोव", "तिखोनोव", "तिहोनोव", "तिचोनोव" आदि के रूप में प्रस्तुत किया गया है जिन्होंने सन 1930 में हौसडॉर्फ रिक्त स्थान की पैथोलॉजिकल स्थिति से सुरक्षा के लिए उनका परिचय दिया था जिसकी एकमात्र निरंतर वास्तविक- मूल्यवान क्रिया स्थायी मानचित्र हैं।[1]
परिभाषाएँ
टोपोलॉजिकल स्थान पूर्णतया नियमित कहा जाता है यदि बिंदुओं को बंद समुच्चयों से (बाध्य) निरंतर वास्तविक-मूल्यवान कार्यों के माध्यम से अलग किया जा सकता है। तकनीकी शब्दों में इसका अर्थ है किसी भी बंद समुच्चय के लिए और कोई बिंदु (ज्यामिति) ,अस्तित्वगत मात्रा का ठहराव वास्तविक-मूल्यवान निरंतर कार्य (टोपोलॉजी) इस प्रकार उपस्थित है कि और (समतुल्य रूप से इसके अतिरिक्त अन्य दो मान और चुन सकते हैं और यहां तक कि मांग करते हैं कि एक बाध्य कार्य हो)।
टोपोलॉजिकल स्थान को टाइकोनॉफ़ स्थान कहा जाता है (वैकल्पिक रूप से:T3½ स्थान, या Tπ स्थान, या पूर्णतया T3 स्थान) यदि यह पूर्ण रूप से नियमित हौसडॉर्फ स्थान है।
टिप्पणी- पूर्ण रूप से नियमित रिक्त स्थान और टाइकोनॉफ़ रिक्त स्थान कोलमोगोरोव तुल्यता की धारणा से संबंधित हैं। यदि टोपोलॉजिकल स्थान टायकोनॉफ़ है और यदि यह पूर्ण रूप से नियमित और कोलमोगोरोव स्थान दोनों T0 है। दूसरी ओर एक स्थान पूर्ण रूप से नियमित है यदि और केवल यदि उसका कोलमोगोरोव भागफल टाइकोनॉफ़ है।
नामकरण परंपराएं
जब बात "पूर्ण रूप से से नियमित" और "T"-सिद्धांतों की आती है तो गणितीय साहित्य में भिन्न-भिन्न परंपराएँ लागू होती हैं। इस खंड की परिभाषाएँ विशिष्ट आधुनिक उपयोग में हैं। जबकि कुछ लेखक दो प्रकार के शब्दों के अर्थ परिवर्तित कर देते हैं या सभी शब्दों का परस्पर उपयोग करते हैं। विकिपीडिया में "पूर्ण रूप से नियमित" और "टाइकोनॉफ" शब्द स्वतंत्र रूप से उपयोग किए जाते हैं और "T" -नोटेशन सामान्य रूप से टाला जाता है। मानक साहित्य में इस प्रकार सावधानी की सलाह दी जाती है यह पता लगाने के लिए कि लेखक किन परिभाषाओं का उपयोग कर रहा है। इस विवाद पर अधिक जानकारी के लिए पृथक्करण अभिगृहीतों का इतिहास देखें।
उदाहरण और प्रति उदाहरण
गणितीय विश्लेषण में अध्ययन किया गया लगभग हर टोपोलॉजिकल स्थान टाइकोनॉफ़ है या कम से कम पूर्ण रूप से नियमित है।
उदाहरण के लिए मानक यूक्लिडियन स्थान के अंतर्गत वास्तविक रेखा टाइकोनॉफ़ है।
अन्य उदाहरणों में सम्मिलित हैं:
- प्रत्येक मीट्रिक स्थान टाइकोनॉफ़ है जहाँ हर स्यूडोमेट्रिक स्थान पूर्ण रूप से नियमित है।
- प्रत्येक स्थानीय रूप से सघन नियमित स्थान पूर्ण रूप से नियमित है और इसलिए प्रत्येक स्थानीय रूप से सघन हौसडॉर्फ स्थान टाइकोनॉफ़ है।
- विशेष रूप से प्रत्येक टोपोलॉजिकल बहुविध टाइकोनॉफ़ है।
- आर्डर टोपोलॉजी के साथ प्रत्येक पूर्ण रूप से ऑर्डर किया गया समुच्चय, टाइकोनॉफ़ है।
- प्रत्येक सांस्थितिक समूह पूर्णतः नियमित होता है।
- मेट्रिक स्थान और टोपोलॉजिकल समूह दोनों का सामान्यीकरण करते हुए प्रत्येक एक समान स्थान पूर्ण रूप से नियमित है। इसका विलोम भी सत्य है कि प्रत्येक पूर्णतः नियमित स्थान एकरूपता योग्य होता है।
- प्रत्येक सीडब्ल्यू जटिल टाइकोनॉफ है।
- प्रत्येक सामान्य नियमित स्थान पूर्ण रूप से नियमित है और प्रत्येक सामान्य हौसडॉर्फ स्थान टाइकोनॉफ़ है।
- नीमेत्ज़की प्लेन टाइकोनॉफ़ स्थान का उदाहरण है जो सामान्य स्थान नहीं है।
गुण
संरक्षण
प्रारंभिक टोपोलॉजी के संबंध में पूर्ण नियमितता और टाइकोनॉफ विशेषता अच्छे प्रकार से व्यवहार की जाती है। विशेष रूप से स्वैक्षिक प्रारंभिक टोपोलॉजी के साथ पूर्ण नियमितता को संरक्षित किया जाता है और टाइकोनॉफ संपत्ति को बिंदु-पृथक्करण प्रारंभिक टोपोलॉजी के साथ संरक्षित किया जाता है। यह इस प्रकार है कि:
- पूर्ण रूप से नियमित या टाइकोनॉफ स्थान के प्रत्येक उपस्थान (टोपोलॉजी) में एक ही संपत्ति होती है।
- गैर-रिक्त उत्पाद स्थान पूर्ण रूप से नियमित (क्रमशः टाइकोनॉफ़) होता है यदि और केवल यदि प्रत्येक कारक स्थान पूर्ण रूप से नियमित (क्रमशः टाइकोनॉफ़) हो।
सभी अलगाव सिद्धांतों की तरह अंतिम टोपोलॉजी के उपयोग से पूर्ण नियमितता संरक्षित नहीं होती है। विशेष रूप से पूर्ण रूप से नियमित रिक्त स्थान के भागफल स्थान (टोपोलॉजी) को नियमित स्थान नहीं होना चाहिए। टाइकोनॉफ़ रिक्त स्थान के भागफलों को हॉसडॉर्फ स्थान की भी आवश्यकता नहीं है जिसमें एक प्राथमिक प्रत्युत्तर उदाहरण दो मूल के साथ रेखा है। मूर प्लेन के बंद भागफल हैं जो प्रति उदाहरण प्रदान करते हैं।
वास्तविक-मूल्यवान निरंतर कार्य
किसी भी टोपोलॉजिकल स्थान के लिए माना कि वास्तविक-मूल्यवान सतत कार्य (टोपोलॉजी) के परिवार को निरूपित करते हैं और जानें परिबद्ध फलन वास्तविक-मूल्यवान सतत फलन का उपसमुच्चय हो।
पूर्ण रूप से नियमित रिक्त स्थान को इस तथ्य से चित्रित किया जा सकता है कि उनकी टोपोलॉजी पूर्ण रूप से या निर्धारित होती है। विशेष रूप से:
- स्थान पूर्ण रूप से नियमित है यदि और केवल यदि इसके द्वारा प्रेरित प्रारंभिक टोपोलॉजी या है
- स्थान पूर्ण रूप से नियमित है यदि और केवल यदि प्रत्येक बंद समुच्चय को शून्य समुच्चय के समूह के प्रतिच्छेदन के रूप में लिखा जा सकता है (अर्थात शून्य समुच्चय के बंद समुच्चय के लिए आधार बनाते हैं )
- स्थान पूर्ण रूप से नियमित है यदि और केवल यदि कोज़ीरो समुच्चय करता है की टोपोलॉजी के लिए आधार (टोपोलॉजी) बनाते हैं
एकपक्षीय रूप से टोपोलॉजिकल स्थान को देखते हुए के साथ एक पूरी तरह से नियमित स्थान को जोड़ने का सार्वभौमिक तरीका है। माना कि ρ, पर प्रारंभिक टोपोलॉजी द्वारा प्रेरित है या समकक्ष में कोज़रो सेट के आधार पर उत्पन्न टोपोलॉजी है तब ρ उन्नत टोपोलॉजी होगी जिस पर पूर्ण रूप से नियमित टोपोलॉजी होगी, वह इससे मोटा है अतः यह निर्माण इस अर्थ में सार्वभौमिक संपत्ति है कि कोई भी निरंतर कार्य करता है
पूर्ण रूप से नियमित स्थान पर निरंतर चालू रहेगा श्रेणी सिद्धांत की भाषा में जो ऑपरेटर को भेजता है, समावेशन फ़ैक्टर CReg → शीर्ष के निकट छोड़ दिया गया है। इस प्रकार पूर्ण रूप से नियमित रिक्त स्थान की श्रेणी CReg, उच्चतम प्रतिबिंबित उपश्रेणी है जो स्थलीय रिक्त स्थान की श्रेणी है। कोलमोगोरोव उद्धरण से प्राप्त होता है कि टाइकोनॉफ़ रिक्त स्थान की उपश्रेणी भी प्रतिबंधित है।
उपरोक्त निर्माण में दिख सकता है जिससे छल्ले और सामान्य रूप से केवल पूर्ण रूप से नियमित रिक्त स्थान के लिए अध्ययन किया जाता है।
वास्तविकसघन स्थान टाइकोनॉफ़ स्थान की श्रेणी छल्लों की श्रेणी के मानचित्र के रूप में रिंग होमोमोर्फिज्म के साथ समकक्ष नहीं है (जहाँ वास्तविकसघन है)। उदाहरण के लिए कोई पुनर्निर्माण से कर सकता है जब (वास्तविक) सघन है। इसलिए इन छल्लों का बीजगणितीय सिद्धांत गहन अध्ययन का विषय है।
छल्ले के इस वर्ग का विशाल सामान्यीकरण जो अभी भी टाइकोनॉफ रिक्त स्थान के कई गुणों जैसा दिखता है परन्तु वास्तविक बीजगणितीय ज्यामिति में भी लागू होता है जो वास्तविक बंद छल्ले का वर्ग है।
अंत: स्थापन
टेक्नोऑफ रिक्त स्थान ठीक वे स्थान हैं जो सघन हौसडॉर्फ स्थान में टोपोलॉजिकल अंत: स्थापक हो सकते हैं। अधिक सटीक रूप से प्रत्येक टाइकोनॉफ़ स्थान के लिए सघन हौसडॉर्फ स्थान उपस्थित है, ऐसा है कि की उपसमष्टि के लिए होमियोमॉर्फिक है।
वास्तव में टाइकोनॉफ क्यूब के हेतु सदैव का चुनाव (अर्थात इकाई अंतराल का संभवतः अनंत उत्पाद) कर सकता है। टाइकोनॉफ के प्रमेय के परिणामस्वरूप प्रत्येक टाइकोनॉफ घन सघन हॉसडॉर्फ है। चूंकि सघन हौसडॉर्फ स्थान के प्रत्येक उप-स्थान टाइकोनॉफ के समीप है: टोपोलॉजिकल स्थान टाइकोनॉफ़ है यदि और केवल यदि इसे टाइकोनॉफ़ घन में अंत: स्थापित किया जा सकता है।
संघनन
विशेष रूप से रुचि वे अंत: स्थापन हैं जहां की छवि में घना उपसमुच्चय है इन्हें का हॉसडॉर्फ संघनन (गणित) कहा जाता है।
टाइकोनॉफ स्थान के किसी भी अंतःस्थापन को देखते हुए एक सघन हौसडॉर्फ स्थान में की छवि का समापन (टोपोलॉजी) में का संघनन है।
सन 1930 के उसी लेख में जहां टाइकोनॉफ़ ने पूर्ण रूप से नियमित रिक्त स्थान को परिभाषित किया था। उन्होंने यह भी प्रमाणित किया कि प्रत्येक टाइकोनॉफ़ स्थान में हौसडॉर्फ संघनन होता है।[2]
उन हॉसडॉर्फ संघनन में एक अनोखा सबसे सामान्य स्टोन-चेक संघनन है तथा यह सार्वभौमिक संपत्ति की विशेषता है जिसने से किसी भी अन्य सघन हौसडॉर्फ स्थान के लिए एक निरंतर मानचित्र दिया गया है एवं किसी अन्य सघन हौसडॉर्फ स्थान एक अद्वितीय (गणित) निरंतर मानचित्र देता है जो को इस अर्थ में विस्तारित करता है कि , और की संरचना (कार्य) है।
समान संरचना
सामयिक स्थान पर पूर्ण नियमितता समान संरचनाओं के अस्तित्व के लिए एक आवश्यक परिस्थिति है। दूसरे शब्दों में प्रत्येक समान स्थान में पूर्ण रूप से नियमित टोपोलॉजी और प्रत्येक पूर्ण रूप से नियमित स्थान होता है और यह एकरूप करने योग्य है। टोपोलॉजिकल स्थान अलग समान संरचना को स्वीकार करता है यदि और केवल यदि यह टाइकोनॉफ़ है।
पूर्ण रूप से नियमित स्थान को देखते हुए सामान्यतः पर एक से अधिक एकरूपता होती है जो टोपोलॉजी के के साथ संगत होती है जबकि सदैव एक उन्नत संगत एकरूपता होगी जिसे पर सूक्ष्म एकरूपता कहा जाता है यदि टेक्नोऑफ है तो समान संरचना को चुना जा सकता है जहाँ एक समान स्थान का समापन (टोपोलॉजी) हो जाता है।
यह भी देखें
उद्धरण
- ↑ Narici & Beckenstein 2011, p. 240.
- ↑ Narici & Beckenstein 2011, pp. 225–273.
ग्रन्थसूची
- Gillman, Leonard; Jerison, Meyer (1960). Rings of continuous functions. Graduate Texts in Mathematics, No. 43 (Dover reprint ed.). NY: Springer-Verlag. p. xiii. ISBN 978-048681688-3.
- Narici, Lawrence; Beckenstein, Edward (2011). Topological Vector Spaces. Pure and applied mathematics (Second ed.). Boca Raton, FL: CRC Press. ISBN 978-1584888666. OCLC 144216834.
- Willard, Stephen (1970). General Topology (Dover reprint ed.). Reading, Massachusetts: Addison-Wesley Publishing Company. ISBN 0-486-43479-6.