लाफलिन वेवफंक्शन: Difference between revisions
(Created page with "संघनित पदार्थ भौतिकी में, लाफलिन वेवफंक्शन <रेफरी नाम= लाफलिन पीप...") |
No edit summary |
||
| Line 1: | Line 1: | ||
[[संघनित पदार्थ भौतिकी]] में, लाफलिन वेवफंक्शन | [[संघनित पदार्थ भौतिकी]] में, लाफलिन वेवफंक्शन <ref>{{cite book | author=Z. F. Ezewa | title=क्वांटम हॉल प्रभाव, दूसरा संस्करण| publisher= World Scientific| year=2008 | isbn=978-981-270-032-2}} pp. 210-213</ref> एक एन्सैट्ज है, जिसे रॉबर्ट लाफलिन द्वारा एक समान जेलियम पृष्ठभूमि की उपस्थिति में एक समान पृष्ठभूमि चुंबकीय क्षेत्र में रखी गई दो-आयामी इलेक्ट्रॉन गैस की जमीनी स्थिति के लिए प्रस्तावित किया गया है। निम्नतम लन्दौ स्तर का भरण कारक (क्वांटम हॉल प्रभाव) <math>\nu=1/n</math> है जहाँ n एक विषम धनात्मक पूर्णांक है। इसका निर्माण <math>\nu=1/3</math> भिन्नात्मक क्वांटम हॉल प्रभाव के अवलोकन की व्याख्या करने के लिए किया गया था और अतिरिक्त <math>\nu = 1/n</math> अवस्थाओं के साथ-साथ भिन्नात्मक विद्युत आवेश <math>e/n</math> के साथ क्वासिपार्टिकल उद्दीपन के अस्तित्व की भविष्यवाणी की गई थी, दोनों बाद में प्रायोगिक तौर पर देखे गए थे। लाफलिन को इस खोज के लिए 1998 में भौतिकी के नोबेल पुरस्कार का एक तिहाई हिस्सा मिला था। ट्रायल वेवफंक्शन होने के नाते, यह सटीक नहीं है, लेकिन गुणात्मक रूप से, यह सटीक समाधान की कई विशेषताओं को पुन: पेश करता है और मात्रात्मक रूप से, छोटे प्रणाली के लिए सटीक जमीनी स्थिति के साथ इसका बहुत अधिक अतिव्यापन होता है। | ||
यदि हम शून्य क्रम सन्निकटन के रूप में इलेक्ट्रॉनों के बीच जेलियम और आपसी [[कूलम्ब प्रतिकर्षण]] | यदि हम एक शून्य क्रम सन्निकटन के रूप में इलेक्ट्रॉनों के बीच जेलियम और आपसी [[कूलम्ब प्रतिकर्षण]] को अनदेखा करते हैं, तो हमारे पास एक असीम रूप से निम्नतम लैंडौ स्तर (LLL) है और 1/n के भरण कारक के साथ, हम उम्मीद करेंगे कि सभी इलेक्ट्रॉन LLL में स्थित होंगे। अन्योन्यक्रियाओं को चालू करते हुए, हम अनुमान लगा सकते हैं कि सभी इलेक्ट्रॉन LLL में हैं। यदि <math>\psi_0</math> सबसे कम कक्षीय [[कोणीय गति ऑपरेटर|कोणीय]] संवेग के साथ LLL अवस्था का एकल कण तरंग है, तो मल्टीपार्टिकल वेवफंक्शन के लिए लाफलिन एनाट्ज़ है। | ||
:<math> | :<math> | ||
| Line 10: | Line 10: | ||
D \left[ \prod_{N \geqslant i > j \geqslant 1}\left( z_i-z_j \right)^n \right] \prod^N_{k=1}\exp\left( - \mid z_k \mid^2 \right) | D \left[ \prod_{N \geqslant i > j \geqslant 1}\left( z_i-z_j \right)^n \right] \prod^N_{k=1}\exp\left( - \mid z_k \mid^2 \right) | ||
</math> | </math> | ||
जहां स्थिति द्वारा | जहां स्थिति द्वारा दर्शाया गया है | ||
:<math>z={1 \over 2 \mathit l_B} \left( x + iy\right) </math> | :<math>z={1 \over 2 \mathit l_B} \left( x + iy\right) </math> | ||
(गाऊसी इकाइयों) में | |||
:<math> \mathit l_B = \sqrt{\hbar c\over e B} </math> | :<math> \mathit l_B = \sqrt{\hbar c\over e B} </math> | ||
और <math> x </math> और <math> y </math> xy | और <math> x </math> और <math> y </math>, xy समतल में निर्देशांक हैं। यहाँ <math> \hbar </math> घटी हुई प्लैंक नियतांक है, <math> e </math> इलेक्ट्रॉन आवेश है, <math> N </math> कणों की कुल संख्या है, और <math> B </math> चुंबकीय क्षेत्र है, जो xy तल के लम्बवत् है। Z पर सबस्क्रिप्ट कण की पहचान करते हैं। वेव फंक्शन के लिए फ़र्मियन का वर्णन करने के लिए, n को एक विषम पूर्णांक होना चाहिए। यह कण इंटरचेंज के तहत वेव फ़ंक्शन को एंटीसिमेट्रिक होने के लिए मजबूर करता है। इस स्थिति के लिए कोणीय गति <math> n\hbar </math> है। | ||
== दो कणों के लिए परस्पर क्रिया की ऊर्जा == | == दो कणों के लिए परस्पर क्रिया की ऊर्जा == | ||
Revision as of 08:48, 3 May 2023
संघनित पदार्थ भौतिकी में, लाफलिन वेवफंक्शन [1] एक एन्सैट्ज है, जिसे रॉबर्ट लाफलिन द्वारा एक समान जेलियम पृष्ठभूमि की उपस्थिति में एक समान पृष्ठभूमि चुंबकीय क्षेत्र में रखी गई दो-आयामी इलेक्ट्रॉन गैस की जमीनी स्थिति के लिए प्रस्तावित किया गया है। निम्नतम लन्दौ स्तर का भरण कारक (क्वांटम हॉल प्रभाव) है जहाँ n एक विषम धनात्मक पूर्णांक है। इसका निर्माण भिन्नात्मक क्वांटम हॉल प्रभाव के अवलोकन की व्याख्या करने के लिए किया गया था और अतिरिक्त अवस्थाओं के साथ-साथ भिन्नात्मक विद्युत आवेश के साथ क्वासिपार्टिकल उद्दीपन के अस्तित्व की भविष्यवाणी की गई थी, दोनों बाद में प्रायोगिक तौर पर देखे गए थे। लाफलिन को इस खोज के लिए 1998 में भौतिकी के नोबेल पुरस्कार का एक तिहाई हिस्सा मिला था। ट्रायल वेवफंक्शन होने के नाते, यह सटीक नहीं है, लेकिन गुणात्मक रूप से, यह सटीक समाधान की कई विशेषताओं को पुन: पेश करता है और मात्रात्मक रूप से, छोटे प्रणाली के लिए सटीक जमीनी स्थिति के साथ इसका बहुत अधिक अतिव्यापन होता है।
यदि हम एक शून्य क्रम सन्निकटन के रूप में इलेक्ट्रॉनों के बीच जेलियम और आपसी कूलम्ब प्रतिकर्षण को अनदेखा करते हैं, तो हमारे पास एक असीम रूप से निम्नतम लैंडौ स्तर (LLL) है और 1/n के भरण कारक के साथ, हम उम्मीद करेंगे कि सभी इलेक्ट्रॉन LLL में स्थित होंगे। अन्योन्यक्रियाओं को चालू करते हुए, हम अनुमान लगा सकते हैं कि सभी इलेक्ट्रॉन LLL में हैं। यदि सबसे कम कक्षीय कोणीय संवेग के साथ LLL अवस्था का एकल कण तरंग है, तो मल्टीपार्टिकल वेवफंक्शन के लिए लाफलिन एनाट्ज़ है।
जहां स्थिति द्वारा दर्शाया गया है
(गाऊसी इकाइयों) में
और और , xy समतल में निर्देशांक हैं। यहाँ घटी हुई प्लैंक नियतांक है, इलेक्ट्रॉन आवेश है, कणों की कुल संख्या है, और चुंबकीय क्षेत्र है, जो xy तल के लम्बवत् है। Z पर सबस्क्रिप्ट कण की पहचान करते हैं। वेव फंक्शन के लिए फ़र्मियन का वर्णन करने के लिए, n को एक विषम पूर्णांक होना चाहिए। यह कण इंटरचेंज के तहत वेव फ़ंक्शन को एंटीसिमेट्रिक होने के लिए मजबूर करता है। इस स्थिति के लिए कोणीय गति है।
दो कणों के लिए परस्पर क्रिया की ऊर्जा
लॉफलिन वेवफंक्शन quisiparticle ्स के लिए मल्टीपार्टिकल वेवफंक्शन है। क्वासिपार्टिकल्स की एक जोड़ी के लिए अंतःक्रियात्मक ऊर्जा का अपेक्षित मूल्य है
जहां स्क्रीन की क्षमता है (स्थैतिक बल और आभासी-कण विनिमय देखें # एक चुंबकीय क्षेत्र में एम्बेडेड दो मौजूदा छोरों के बीच कूलम्ब क्षमता)
कहाँ एक मिला हुआ हाइपरज्यामितीय कार्य है और प्रथम प्रकार का बेसेल फलन है। यहाँ, दो मौजूदा लूप के केंद्रों के बीच की दूरी है, इलेक्ट्रॉन आवेश का परिमाण है, Larmor त्रिज्या का क्वांटम संस्करण है, और चुंबकीय क्षेत्र की दिशा में इलेक्ट्रॉन गैस की मोटाई है। दो अलग-अलग वर्तमान लूपों की कोणीय गति है और कहाँ . व्युत्क्रम स्क्रीनिंग लंबाई (गाऊसी इकाइयों) द्वारा दी गई है
कहाँ साइक्लोट्रॉन आवृत्ति है, और xy तल में इलेक्ट्रॉन गैस का क्षेत्र है।
अंतःक्रियात्मक ऊर्जा इसका मूल्यांकन करती है:
इस परिणाम को प्राप्त करने के लिए हमने एकीकरण चरों का परिवर्तन किया है
और
और नोट किया गया (क्वांटम फील्ड थ्योरी में कॉमन इंटीग्रल्स देखें # मैग्नेटिक वेव फंक्शन पर इंटीग्रेशन)
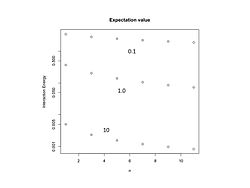
अंतःक्रियात्मक ऊर्जा के लिए मिनिमा है (चित्र 1)
और
कोणीय संवेग के अनुपात के इन मूल्यों के लिए, ऊर्जा को चित्र 2 में एक फलन के रूप में अंकित किया गया है .
संदर्भ
- ↑ Z. F. Ezewa (2008). क्वांटम हॉल प्रभाव, दूसरा संस्करण. World Scientific. ISBN 978-981-270-032-2. pp. 210-213
यह भी देखें
- लैंडौ स्तर
- आंशिक क्वांटम हॉल प्रभाव
- स्थैतिक बल और आभासी-कण विनिमय # एक चुंबकीय क्षेत्र में एम्बेडेड दो वर्तमान लूपों के बीच कूलम्ब क्षमता
श्रेणी:हॉल प्रभाव श्रेणी:संघनित पदार्थ भौतिकी श्रेणी:क्वांटम चरण