एक्सट ऑपरेटर: Difference between revisions
(Created page with "{{Short description|Construction in homological algebra}} गणित में, Ext functors मैं एक आदमी के रूप में काम करत...") |
No edit summary |
||
| Line 1: | Line 1: | ||
{{Short description|Construction in homological algebra}} | {{Short description|Construction in homological algebra}} | ||
गणित में, | गणित में, एक्सट प्रकार्यक [[मैं एक आदमी के रूप में काम करता हूं]] के व्युत्पन्न प्रकार्यक हैं। [[Tor functor|Tor प्रकार्यक]] के साथ, एक्सट [[समरूप बीजगणित]] की मूल अवधारणाओं में से एक है, जिसमें [[बीजगणितीय टोपोलॉजी|बीजगणितीय सांस्थितिकी]] के विचारों का उपयोग बीजगणितीय संरचनाओं के आक्रमणकारियों को परिभाषित करने के लिए किया जाता है। [[समूह कोहोलॉजी|समूह सह-समरूपता]], लाई बीजगणित सह-समरूपता और [[होशचाइल्ड कोहोलॉजी|होशचाइल्ड सह-समरूपता]] सभी को एक्सट के संदर्भ में परिभाषित किया जा सकता है। यह नाम इस तथ्य से आता है कि पहला एक्सट समूह एक्सट<sup>1</sup> एक [[मॉड्यूल (गणित)|मापांक (गणित)]] के [[समूह विस्तार]] को दूसरे द्वारा वर्गीकृत करता है। | ||
[[एबेलियन समूह]]ों के विशेष | [[एबेलियन समूह]]ों के विशेष स्थिति में, [[रेनहोल्ड बेयर]] (1934) द्वारा एक्सट प्रस्तुत किया गया था। इसका नाम [[सैमुअल एलेनबर्ग]] और [[सॉन्डर्स मैकलेन]] (1942) द्वारा रखा गया था, और सांस्थितिकी ([[कोहोलॉजी के लिए सार्वभौमिक गुणांक प्रमेय|सह-समरूपता के लिए सार्वभौमिक गुणांक प्रमेय]]) पर अनुप्रयुक्त किया गया था। किसी भी वलय (गणित) पर मापांक के लिए, एक्सट को [[ हेनरी कर्तन ]]और ईलेनबर्ग द्वारा उनकी 1956 की पुस्तक तुल्य बीजगणित में परिभाषित किया गया था।<ref>Weibel (1999); Cartan & Eilenberg (1956), section VI.1.</ref> | ||
== परिभाषा == | == परिभाषा == | ||
R को एक वलय होने दें और R-अत्याधुनिक को R पर मापांक की [[श्रेणी (गणित)]] होने दें। ''T''(''B'') = Hom<sub>''R''</sub>(''A'', ''B'') R-अत्याधुनिक में B के लिए। (यहाँ होम<sub>''R''</sub>(ए, B) ए से B तक R-रैखिक मानचित्रों का एबेलियन समूह है; यह एक R-मापांक है यदि R [[ क्रमविनिमेय अंगूठी | क्रमविनिमेय वलय]] है)। यह R-अत्याधुनिक से एबेलियन समूह एB की श्रेणी के लिए बाएं सटीक प्रकार्यक है, और इसलिए इसमें दाएं व्युत्पन्न प्रकार्यक R हैं<sup>मैंटी. एक्सट समूह द्वारा परिभाषित एबेलियन समूह हैं | |||
:<math>\operatorname{Ext}_R^i(A,B)=(R^iT)(B),</math> | :<math>\operatorname{Ext}_R^i(A,B)=(R^iT)(B),</math> | ||
एक [[पूर्णांक]] i के लिए परिभाषा के अनुसार, इसका अर्थ है: कोई भी [[इंजेक्शन संकल्प]] लें | एक [[पूर्णांक]] i के लिए परिभाषा के अनुसार, इसका अर्थ है: कोई भी [[इंजेक्शन संकल्प|अंतःक्षेपक संकल्प]] लें | ||
:<math>0 \to B \to I^0 \to I^1 \to \cdots,</math> | :<math>0 \to B \to I^0 \to I^1 \to \cdots,</math> | ||
B शब्द को हटा दें, और [[कोचेन कॉम्प्लेक्स|सह श्रृंखला समष्टि]] बनाएं: | |||
:<math>0 \to \operatorname{Hom}_R(A,I^0) \to \operatorname{Hom}_R(A,I^1) \to \cdots.</math> | :<math>0 \to \operatorname{Hom}_R(A,I^0) \to \operatorname{Hom}_R(A,I^1) \to \cdots.</math> | ||
प्रत्येक पूर्णांक i के लिए, | प्रत्येक पूर्णांक i के लिए, एक्सट{{supsub|''i''|''R''}}(ए, B) स्थिति i पर इस समष्टि का [[चेन कॉम्प्लेक्स|श्रृंखला समष्टि]] है। यह i ऋणात्मक के लिए शून्य है। उदाहरण के लिए, एक्सट{{supsub|0|''R''}}(ए, B) होम मैप का कर्नेल (रैखिक बीजगणित) है<sub>''R''</sub>(ए, आई<sup>0</sup>) → होम<sub>''R''</sub>(ए, आई<sup>1</sup>), जो कि होम के लिए तुल्याकारी है<sub>''R''</sub>(ए, B)। | ||
एक वैकल्पिक परिभाषा | एक वैकल्पिक परिभाषा प्रकार्यक G(A)=Hom का उपयोग करती है<sub>''R''</sub>(ए, B), एक निश्चित R-मापांक B के लिए। यह प्रकार्यक प्रकार्यक का सहप्रसरण और विरोधाभास है, जिसे [[विपरीत श्रेणी]] (R-अत्याधुनिक) से बाएं सटीक प्रकार्यक के रूप में देखा जा सकता है।<sup>ऑप</sup> से अब तक। एक्सट समूहों को सही व्युत्पन्न प्रकार्यक R के रूप में परिभाषित किया गया है<sup>मैं</sup>जी: | ||
:<math>\operatorname{Ext}_R^i(A,B)=(R^iG)(A).</math> | :<math>\operatorname{Ext}_R^i(A,B)=(R^iG)(A).</math> | ||
| Line 23: | Line 23: | ||
:<math>\cdots \to P_1 \to P_0 \to A \to 0, </math> | :<math>\cdots \to P_1 \to P_0 \to A \to 0, </math> | ||
शब्द A को हटा दें, और | शब्द A को हटा दें, और सह श्रृंखला समष्टि बनाएं: | ||
:<math>0\to \operatorname{Hom}_R(P_0,B)\to \operatorname{Hom}_R(P_1,B) \to \cdots.</math> | :<math>0\to \operatorname{Hom}_R(P_0,B)\to \operatorname{Hom}_R(P_1,B) \to \cdots.</math> | ||
अगला{{supsub|''i''|''R''}}(ए, | अगला{{supsub|''i''|''R''}}(ए, B) स्थिति i पर इस परिसर का सह-समरूपता है। | ||
कार्टन और ईलेनबर्ग ने दिखाया कि ये निर्माण प्रक्षेपी या अंतःक्षेपी संकल्प की पसंद से स्वतंत्र हैं | कार्टन और ईलेनबर्ग ने दिखाया कि ये निर्माण प्रक्षेपी या अंतःक्षेपी संकल्प की पसंद से स्वतंत्र हैं और यह कि दोनों निर्माण एक ही एक्सटी समूह उत्पन्न करते हैं।<ref>Weibel (1994), sections 2.4 and 2.5 and Theorem 2.7.6.</ref> इसके अतिरिक्त, एक निश्चित वलय R के लिए, एक्सट प्रत्येक चर में एक प्रकार्यक है (A में contravariant, B में सहसंयोजक)। | ||
एक | एक क्रमविनिमेय वलय R और R-मापांक ए और B के लिए, एक्सट{{supsub|''i''|''R''}}(ए, B) एक R-मापांक है (होम<sub>''R''</sub>(ए, B) इस स्थिति में एक R-मापांक है)। एक गैर-क्रमविनिमेय वलय R, एक्सट के लिए{{supsub|''i''|''R''}}(ए, B) सामान्यतः केवल एक एबेलियन समूह है। यदि R एक वलय S पर एक बीजगणित है (जिसका विशेष रूप से अर्थ है कि S क्रमविनिमेय है), तो एक्सट{{supsub|''i''|''R''}}(ए, B) कम से कम एक एस-मापांक है। | ||
एक्सट के गुण | |||
*एक्स्ट{{su|b=''R''|p=''i''}}( | यहाँ एक्सट समूहों के कुछ मूलभूत गुण और संगणनाएँ दी गई हैं।<ref>Weibel (1994), Chapters 2 and 3.</ref> | ||
*एक्स्ट{{supsub|0|''R''}}(''A'', B) ≅ होम<sub>''R''</sub>(''A'', B) किसी भी R-मापांक ''A'' और ''B'' के लिए। | |||
*एक्स्ट{{su|b=''R''|p=''i''}}(''A'', B) = 0 सभी i> 0 के लिए यदि R-मापांक ''A'' [[ प्रक्षेपी मॉड्यूल | प्रक्षेपी मापांक]] है (उदाहरण के लिए,[[ मुफ्त मॉड्यूल | मुफ्त मापांक]] ) या यदि B [[इंजेक्शन मॉड्यूल|अंतःक्षेपक मापांक]] है। | |||
*बातचीत भी रखती है: | *बातचीत भी रखती है: | ||
**यदि एक्सट{{su|b=''R''|p=1}}(A, B) = 0 सभी B के लिए, तो A प्रक्षेपी है (और इसलिए | **यदि एक्सट{{su|b=''R''|p=1}}(A, B) = 0 सभी B के लिए, तो A प्रक्षेपी है (और इसलिए एक्सट{{su|b=''R''|p=''i''}}(A, B) = 0 सभी के लिए i> 0)। | ||
**यदि एक्सट{{su|b=''R''|p=1}}( | **यदि एक्सट{{su|b=''R''|p=1}}(''A'', B) = 0 सभी ए के लिए, फिर B अंतःक्षेपी है (और इसलिए एक्सट{{su|b=''R''|p=''i''}}(''A'', B) = 0 सभी के लिए i> 0)। | ||
*<math>\operatorname{Ext}^i_{\Z}(A,B) = 0</math> सभी i ≥ 2 और सभी एबेलियन समूहों A और B के लिए।<ref>Weibeil (1994), Lemma 3.3.1.</ref> | *<math>\operatorname{Ext}^i_{\Z}(A,B) = 0</math> सभी i ≥ 2 और सभी एबेलियन समूहों A और B के लिए।<ref>Weibeil (1994), Lemma 3.3.1.</ref> | ||
*यदि R एक क्रमविनिमेय वलय है और u in R एक [[शून्य भाजक]] नहीं है, तो | *यदि R एक क्रमविनिमेय वलय है और u in R एक [[शून्य भाजक]] नहीं है, तो | ||
::<math>\operatorname{Ext}_R^i(R/(u),B)\cong\begin{cases} B[u] & i=0\\ B/uB & i=1\\ 0 &\text{otherwise,}\end{cases}</math> | ::<math>\operatorname{Ext}_R^i(R/(u),B)\cong\begin{cases} B[u] & i=0\\ B/uB & i=1\\ 0 &\text{otherwise,}\end{cases}</math> | ||
:किसी भी | :किसी भी R-मापांक B के लिए। यहां B [यू] B के यू-टोरसन उपसमूह को दर्शाता है, {x ∈ B: ux = 0}। R को वलय मान लेना <math>\Z</math> पूर्णांकों की, इस गणना का उपयोग गणना करने के लिए किया जा सकता है <math>\operatorname{Ext}^1_{\Z}(A,B)</math> किसी भी [[अंतिम रूप से उत्पन्न एबेलियन समूह]] ए के लिए। | ||
* पिछले उदाहरण को सामान्य करते हुए, जब कोई | * पिछले उदाहरण को सामान्य करते हुए, जब कोई मापांक [[जटिल शर्ट]] का उपयोग करके किसी भी [[नियमित अनुक्रम]] द्वारा एक क्रमविनिमेय वलय का भागफल होता है, तो कोई एक्सट समूह की गणना कर सकता है।<ref>Weibel (1994), section 4.5.</ref> उदाहरण के लिए, यदि R बहुपद वलय k[x<sub>1</sub>,...,एक्स<sub>''n''</sub>] क्षेत्र k पर, फिर एक्सट{{supsub|*|''R''}}(k,k) एक्सट में n जनक पर k के ऊपर [[बाहरी बीजगणित]] S है<sup>1</उप>। इसके अतिरिक्त, एक्सट{{supsub|*|''S''}}(k,k) बहुपद वलय R है; यह कोज़ुल द्वैत का एक उदाहरण है। | ||
*व्युत्पन्न | *व्युत्पन्न प्रकार्यकों के सामान्य गुणों के अनुसार, एक्सट के लिए दो मूल सटीक अनुक्रम हैं।<ref>Weibel (1994), Definition 2.1.1.</ref> सबसे पहले, R-मापांक का एक छोटा सटीक अनुक्रम 0 → K → L → M → 0 प्रपत्र के एक लंबे सटीक अनुक्रम को प्रेरित करता है | ||
::<math>0 \to \mathrm{Hom}_R(A,K) \to \mathrm{Hom}_R(A,L) \to \mathrm{Hom}_R(A,M) \to \mathrm{Ext}^1_R(A,K) \to \mathrm{Ext}^1_R(A,L) \to \cdots | ::<math>0 \to \mathrm{Hom}_R(A,K) \to \mathrm{Hom}_R(A,L) \to \mathrm{Hom}_R(A,M) \to \mathrm{Ext}^1_R(A,K) \to \mathrm{Ext}^1_R(A,L) \to \cdots</math> | ||
: किसी भी | : किसी भी R-मापांक ए के लिए। इसके अतिरिक्त, एक छोटा सटीक अनुक्रम 0 → के → एल → एम → 0 फॉर्म के एक लंबे सटीक अनुक्रम को प्रेरित करता है | ||
::<math>0 \to \mathrm{Hom}_R(M,B) \to \mathrm{Hom}_R(L,B) \to \mathrm{Hom}_R(K,B) \to \mathrm{Ext}^1_R(M,B) \to \mathrm{Ext}^1_R(L,B) \to \cdots | ::<math>0 \to \mathrm{Hom}_R(M,B) \to \mathrm{Hom}_R(L,B) \to \mathrm{Hom}_R(K,B) \to \mathrm{Ext}^1_R(M,B) \to \mathrm{Ext}^1_R(L,B) \to \cdots</math> | ||
: किसी भी | : किसी भी R-मापांक B के लिए। | ||
* | *एक्सट पहले चर में मापांक (संभवतः अनंत) का प्रत्यक्ष योग लेता है और प्रत्यक्ष उत्पाद#दूसरा चर में मापांक का प्रत्यक्ष उत्पाद उत्पादों के लिए।<ref>Weibel (1994), Proposition 3.3.4.</ref> वह है: | ||
::<math>\begin{align} | ::<math>\begin{align} | ||
\operatorname{Ext}^i_R \left(\bigoplus_\alpha M_\alpha,N \right) &\cong\prod_\alpha \operatorname{Ext}^i_R (M_\alpha,N) \\ | \operatorname{Ext}^i_R \left(\bigoplus_\alpha M_\alpha,N \right) &\cong\prod_\alpha \operatorname{Ext}^i_R (M_\alpha,N) \\ | ||
\operatorname{Ext}^i_R \left(M,\prod_\alpha N_\alpha \right ) &\cong\prod_\alpha \operatorname{Ext}^i_R (M,N_\alpha) | \operatorname{Ext}^i_R \left(M,\prod_\alpha N_\alpha \right ) &\cong\prod_\alpha \operatorname{Ext}^i_R (M,N_\alpha) | ||
\end{align}</math> | \end{align}</math> | ||
* चलो ए एक | * चलो ए एक क्रमविनिमेय [[नोथेरियन रिंग|नोथेरियन वलय]] R पर एक अंतिम रूप से उत्पन्न मापांक है। फिर एक्स एक वलय के स्थानीयकरण के साथ प्रारंभ होता है, इस अर्थ में कि R में प्रत्येक गुणक रूप से बंद समुच्चय एस के लिए, प्रत्येक R-मापांक B, और प्रत्येक पूर्णांक i,<ref>Weibel (1994), Proposition 3.3.10.</ref> | ||
::<math>S^{-1} \operatorname{Ext}_R^i(A, B) \cong \operatorname{Ext}_{S^{-1} R}^i \left (S^{-1} A, S^{-1} B \right ) | ::<math>S^{-1} \operatorname{Ext}_R^i(A, B) \cong \operatorname{Ext}_{S^{-1} R}^i \left (S^{-1} A, S^{-1} B \right )</math> | ||
== एक्सट और | == एक्सट और विस्तारण == <!-- "मापांक का विस्तार" यहां पुनर्निर्देश करता है --> | ||
=== | === विस्तारण की समानता === | ||
एक्सट समूह | एक्सट समूह मापांक के विस्तार से उनके संबंध से अपना नाम प्राप्त करते हैं। दिए गए R-मापांक ए और B, 'B द्वारा A का विस्तार' R-मापांक का एक छोटा सटीक अनुक्रम है | ||
:<math>0\to B\to E\to A\to 0 | :<math>0\to B\to E\to A\to 0</math> | ||
दो | दो विस्तारण | ||
:<math>0\to B\to E\to A\to 0</math> | :<math>0\to B\to E\to A\to 0</math> | ||
:<math>0\to B\to E' \to A\to 0</math> | :<math>0\to B\to E' \to A\to 0</math> | ||
एक | एक क्रमविनिमेय Rेख होने पर समतुल्य कहा जाता है ('A' द्वारा ''B'' के विस्तार के रूप में): | ||
:[[Image:EquivalenceOfExtensions.png]]ध्यान दें कि [[पाँच लेम्मा]] का तात्पर्य है कि मध्य तीर एक समरूपता है। | :[[Image:EquivalenceOfExtensions.png]]ध्यान दें कि [[पाँच लेम्मा]] का तात्पर्य है कि मध्य तीर एक समरूपता है। A द्वारा B के विस्तार को 'विभाजन' कहा जाता है यदि यह 'तुच्छ विस्तार' के समान है | ||
:<math>0\to B\to A\oplus B\to A\to 0.</math> | :<math>0\to B\to A\oplus B\to A\to 0.</math> | ||
A बटा B के विस्तारण के समतुल्य वर्गों और एक्सट के तत्वों के Bच एक-से-एक पत्राचार है{{supsub|1|''R''}}(ए, B)।<ref>Weibel (1994), Theorem 3.4.3.</ref> तुच्छ विस्तार एक्सट के शून्य तत्व से मेल खाता है{{supsub|1|''R''}}(ए, B)। | |||
=== | === विस्तारण का बायर योग === | ||
बेयर योग | बेयर योग एक्सट पर एबेलियन समूह संरचना का एक स्पष्ट विवरण है{{supsub|1|''R''}}(ए, B), B द्वारा A के विस्तारण के समतुल्य वर्गों के समुच्चय के रूप में देखा जाता है।<ref>Weibel (1994), Corollary 3.4.5.</ref> अर्थात्, दो विस्तारण दिए गए | ||
:<math>0\to B\xrightarrow[f]{} E \xrightarrow[g]{} A\to 0</math> | :<math>0\to B\xrightarrow[f]{} E \xrightarrow[g]{} A\to 0</math> | ||
| Line 92: | Line 93: | ||
पहले [[पुलबैक (श्रेणी सिद्धांत)]] तैयार करें <math>A</math>, | पहले [[पुलबैक (श्रेणी सिद्धांत)]] तैयार करें <math>A</math>, | ||
:<math>\Gamma = \left\{ (e, e') \in E \oplus E' \; | \; g(e) = g'(e')\right\} | :<math>\Gamma = \left\{ (e, e') \in E \oplus E' \; | \; g(e) = g'(e')\right\}</math> | ||
फिर [[भागफल मॉड्यूल]] बनाएं | फिर [[भागफल मॉड्यूल|भागफल मापांक]] बनाएं | ||
:<math>Y = \Gamma / \{(f(b), -f'(b)) \;|\;b \in B\}.</math> | :<math>Y = \Gamma / \{(f(b), -f'(b)) \;|\;b \in B\}.</math> | ||
| Line 99: | Line 100: | ||
:<math>0\to B\to Y\to A\to 0,</math> | :<math>0\to B\to Y\to A\to 0,</math> | ||
जहां पहला | जहां पहला प्रतिचित्र है <math>b \mapsto [(f(b), 0)] = [(0, f'(b))]</math> और दूसरा <math>(e, e') \mapsto g(e) = g'(e')</math> है। | ||
विस्तारण की समतुल्यता [[तक]], बायर राशि क्रमविनिमेय है और पहचान तत्व के रूप में तुच्छ विस्तार है। एक विस्तार 0 → B → ई → ए → 0 का ऋणात्मक एक ही मापांक ई को सम्मिलित करने वाला विस्तार है, परन्तु समरूपता B → ई के साथ इसके ऋणात्मक द्वारा प्रतिस्थापित किया गया है। | |||
== एबेलियन श्रेणियों में एक्सट का निर्माण == | == एबेलियन श्रेणियों में एक्सट का निर्माण == | ||
[[ नोबुओ योनेदा ]] ने एबेलियन समूहों को परिभाषित किया{{su|b='''C'''|p=''n''}}(ए, | [[ नोबुओ योनेदा ]]ने एबेलियन समूहों को परिभाषित किया{{su|b='''C'''|p=''n''}}(ए, B) किसी [[एबेलियन श्रेणी]] 'सी' में वस्तुओं ए और B के लिए; यह संकल्पों के संदर्भ में परिभाषा से सहमत है यदि 'सी' में प्रोजेक्टिव ऑब्जेक्ट # पर्याप्त प्रक्षेपीय या अंतःक्षेपक ऑब्जेक्ट # पर्याप्त अंतःक्षेपक और अंतःक्षेपक हल्स हैं। सबसे पहले, एक्सट{{supsub|0|'''C'''}}(ए, B) = आदमी<sub>'''C'''</sub>(ए, B)। अगला, एक्सट{{su|b='''C'''|p=1}}(ए, B) B द्वारा ए के विस्तार के समतुल्य वर्गों का समुच्चय है, जो बायर योग के अंतर्गत एक एबेलियन समूह बनाता है। अंत में, उच्च एक्सट समूह एक्सट{{su|b='''C'''|p=''n''}}(ए, B) को एन-विस्तारण के समतुल्य वर्ग के रूप में परिभाषित किया गया है, जो सटीक अनुक्रम हैं | ||
:<math>0\to B\to X_n\to\cdots\to X_1\to A\to 0 | :<math>0\to B\to X_n\to\cdots\to X_1\to A\to 0</math> | ||
दो | दो विस्तारण की पहचान करने वाले संबंध से उत्पन्न [[तुल्यता संबंध]] के अंतर्गत | ||
:<math>\begin{align} | :<math>\begin{align} | ||
| Line 113: | Line 114: | ||
\xi': 0 &\to B\to X'_n\to\cdots\to X'_1\to A\to 0 | \xi': 0 &\to B\to X'_n\to\cdots\to X'_1\to A\to 0 | ||
\end{align}</math> | \end{align}</math> | ||
यदि प्रतिचित्र <math>X_m \to X'_m</math>है, {1, 2, ..., n} में सभी m के लिए ताकि प्रत्येक परिणामी वर्ग परिवर्तित हो जाए। | |||
यदि कोई श्रृंखला मानचित्र ξ → ξ' है जो A और B पर तत्समक है। | |||
उपर्युक्त दो n- | उपर्युक्त दो n-आयामों का बायर योग देने से बनता है, ''A'' पर <math>X_1</math> और <math>X'_1</math> का पुलबैक <math>X''_1</math> हो और B के अंतर्गत <math>X_n</math> और <math>X'_n</math> का [[पुशआउट (श्रेणी सिद्धांत)|बहिकर्षी]] <math>X''_n</math> हो,<ref>Weibel (1994), Vists 3.4.6. Some minor corrections are in the [http://www.math.rutgers.edu/~weibel/Hbook.errors.edition2.pdf errata].</ref> फिर विस्तारण का बायर योग है। | ||
:<math>0\to B\to X''_n\to X_{n-1}\oplus X'_{n-1}\to\cdots\to X_2\oplus X'_2\to X''_1\to A\to 0 | :<math>0\to B\to X''_n\to X_{n-1}\oplus X'_{n-1}\to\cdots\to X_2\oplus X'_2\to X''_1\to A\to 0</math> | ||
== | == व्युत्पन्न श्रेणी और योनेदा उत्पाद == | ||
एक महत्वपूर्ण बिंदु यह है कि एबेलियन श्रेणी | एक महत्वपूर्ण बिंदु यह है कि एबेलियन श्रेणी '''C''' में एक्सट समूहों को '''C''' व्युत्पन्न श्रेणी ''D''('''C''') से संबंधित श्रेणी में आकारिकी के समुच्चय के रूप में देखा जा सकता है।<ref>Weibel (1994), sections 10.4 and 10.7; Gelfand & Manin (2003), Chapter III.</ref> व्युत्पन्न श्रेणी की वस्तुएं '''C''' में वस्तुओं के परिसर हैं। विशेष रूप से, किसी के पास है | ||
:<math>\operatorname{Ext}^i_{\mathbf C}(A,B) = \operatorname{Hom}_{D({\mathbf C})}(A,B[i]) | :<math>\operatorname{Ext}^i_{\mathbf C}(A,B) = \operatorname{Hom}_{D({\mathbf C})}(A,B[i])</math> | ||
जहां C की एक वस्तु को डिग्री शून्य में केंद्रित एक जटिल के रूप में देखा जाता है | जहां C की एक वस्तु को डिग्री शून्य में केंद्रित एक जटिल के रूप में देखा जाता है और [''i''] का अर्थ है। एक जटिल ''i'' चरणों को बाईं ओर स्थानांतरित करना है। इस व्याख्या से, एक [[द्विरेखीय नक्शा|द्विरेखीय प्रतिचित्र]] है, जिसे कभी-कभी [[योनेदा उत्पाद]] कहा जाता है: | ||
:<math>\operatorname{Ext}^i_{\mathbf C}(A,B) \times \operatorname{Ext}^j_{\mathbf C}(B,C) \to \operatorname{Ext}^{i+j}_{\mathbf C}(A,C) | :<math>\operatorname{Ext}^i_{\mathbf C}(A,B) \times \operatorname{Ext}^j_{\mathbf C}(B,C) \to \operatorname{Ext}^{i+j}_{\mathbf C}(A,C)</math> | ||
जो केवल व्युत्पन्न श्रेणी में | जो केवल व्युत्पन्न श्रेणी में आकारिता की रचना है। | ||
योनेडा उत्पाद को अधिक प्राथमिक शब्दों में भी वर्णित किया जा सकता है। i = j = 0 के लिए, गुणनफल C श्रेणी के प्रतिचित्रों का संघटन है। सामान्यतः, उत्पाद को दो योनेडा विस्तारण को एक साथ जोड़कर परिभाषित किया जा सकता है। | |||
वैकल्पिक रूप से, | वैकल्पिक रूप से, योनेडा उत्पाद को विश्लेषण के संदर्भ में परिभाषित किया जा सकता है (यह व्युत्पन्न श्रेणी की परिभाषा के समीप है)। उदाहरण के लिए, R-मापांक ''A'', ''B'', ''C'' के साथ R को वलय होने दें और ''P'', ''Q'', और ''T'' को ''A'', ''B'', ''C'' के अनुमानित विश्लेषण होने दें। फिर Ext{{supsub|''i''|''R''}}(''A'', B) को श्रृंखला प्रतिचित्र ''P'' → ''Q''[''i''] के [[चेन होमोटॉपी|श्रृंखला समस्थेयता]] कक्षाओं के समूह के साथ पहचाना जा सकता है। योनेदा उत्पाद श्रृंखला प्रतिचित्र बनाकर दिया गया है: | ||
:<math>P\to Q[i]\to T[i+j] | :<math>P\to Q[i]\to T[i+j]</math> | ||
इनमें से किसी भी व्याख्या से, योनेदा उत्पाद साहचर्य है। | इनमें से किसी भी व्याख्या से, योनेदा उत्पाद साहचर्य है। फलस्वरूप, <math>\operatorname{Ext}^*_R(A,A)</math> किसी भी R-मापांक ''A'' के लिए एक [[ वर्गीकृत अंगूठी |श्रेणीबद्ध वलय]] है। उदाहरण के लिए, यह समूह सह-समरूपता <math>H^*(G, \Z)</math> पर वलय संरचना देता है, चूंकि इसे <math>\operatorname{Ext}^*_{\Z[G]}(\Z,\Z)</math> के रूप में देखा जा सकता है। योनेडा उत्पाद की सहचारिता द्वारा भी: किसी भी R-मापांक ''A'' और B के लिए, <math>\operatorname{Ext}^*_R(A,B)</math> पर एक मापांक <math>\operatorname{Ext}^*_R(A,A)</math> है। | ||
== महत्वपूर्ण विशेष | == महत्वपूर्ण विशेष स्थिति == | ||
*समूह | *समूह सह-समरूपता <math>H^*(G,M)=\operatorname{Ext}_{\Z[G]}^*(\Z, M)</math> द्वारा परिभाषित किया गया है, जहाँ G एक समूह है, M पूर्णांकों पर G का एक [[समूह प्रतिनिधित्व]] है और <math>\Z[G]</math> G का [[ समूह की अंगूठी |समूह वलय]] है। | ||
* | *क्षेत्र k और A-[[bimodule|द्विप्रतिरूपक]] M पर बीजगणित A के लिए, होशचाइल्ड सह-समरूपता द्वारा परिभाषित किया गया है: | ||
::<math>HH^*(A,M)=\operatorname{Ext}^*_{A\otimes_k A^{\text{op}}} (A, M) | ::<math>HH^*(A,M)=\operatorname{Ext}^*_{A\otimes_k A^{\text{op}}} (A, M)</math> | ||
*लाई | *लाई बीजगणितीय सह-समरूपता <math>H^*(\mathfrak g,M)=\operatorname{Ext}^*_{U\mathfrak g}(k,M)</math> द्वारा परिभाषित किया गया है, जहाँ <math>\mathfrak g</math> क्रमविनिमेय वलय k पर एक लाई बीजगणित है, M एक <math>\mathfrak g</math>-मापांक है और <math>U\mathfrak g</math> सार्वभौमिक आवृत बीजगणित है। | ||
* एक [[टोपोलॉजिकल स्पेस]] | * एक [[टोपोलॉजिकल स्पेस|सांस्थितिक समष्टि]] ''X'' के लिए, [[शेफ कोहोलॉजी|पूली सह-समरूपता]] को इस <math>H^*(X, A) = \operatorname{Ext}^*(\Z_X, A)</math> रूप में परिभाषित किया जा सकता है। यहाँ एक्सट को X पर एबेलियन के [[शीफ (गणित)|पुली]] की एबेलियन श्रेणी में लिया गया है और <math>\Z_X</math> स्थानीय स्थिरांक <math>\Z</math>-मूल्यवान फलन का [[शीफ (गणित)|पुली]] है। | ||
* | *अवशिष्ट क्षेत्र k के साथ क्रमविनिमेय नोथेरियन स्थानीय वलय R के लिए, <math>\operatorname{Ext}^*_R(k,k)</math> एक श्रेणीबद्ध लाई बीजगणितीय π*(R) पर k का सार्वभौमिक आवृत बीजगणित है, जिसे R के समस्थेयता लाई बीजगणित के रूप में जाना जाता है (सटीक होने के लिए, जब k की विलक्षणता 2 होती है, π*(R) को एक समायोजित लाई बीजगणितीय के रूप में देखा जा सकता है)।<ref>Sjödin (1980), Notation 14.</ref> एंड्रे-क्विलन सह-समरूपता ''D''*(''k''/''R'',''k'') से π*(R) तक श्रेणीबद्ध लाई बीजगणितीय का एक प्राकृतिक समरूपता है, जो एक समरूपता है यदि ''k'' में विलक्षणता शून्य है।<ref>Avramov (2010), section 10.2.</ref> | ||
== यह भी देखें == | == यह भी देखें == | ||
* [[वैश्विक आयाम]] | * [[वैश्विक आयाम]] | ||
* [[बार संकल्प]] | * [[बार संकल्प|अवरोध विश्लेषण]] | ||
*ग्रोथेंडिक | *ग्रोथेंडिक समूह | ||
* ग्रोथेंडिक स्थानीय | * ग्रोथेंडिक स्थानीय द्वंद्व | ||
==टिप्पणियाँ== | ==टिप्पणियाँ== | ||
Revision as of 21:33, 17 May 2023
गणित में, एक्सट प्रकार्यक मैं एक आदमी के रूप में काम करता हूं के व्युत्पन्न प्रकार्यक हैं। Tor प्रकार्यक के साथ, एक्सट समरूप बीजगणित की मूल अवधारणाओं में से एक है, जिसमें बीजगणितीय सांस्थितिकी के विचारों का उपयोग बीजगणितीय संरचनाओं के आक्रमणकारियों को परिभाषित करने के लिए किया जाता है। समूह सह-समरूपता, लाई बीजगणित सह-समरूपता और होशचाइल्ड सह-समरूपता सभी को एक्सट के संदर्भ में परिभाषित किया जा सकता है। यह नाम इस तथ्य से आता है कि पहला एक्सट समूह एक्सट1 एक मापांक (गणित) के समूह विस्तार को दूसरे द्वारा वर्गीकृत करता है।
एबेलियन समूहों के विशेष स्थिति में, रेनहोल्ड बेयर (1934) द्वारा एक्सट प्रस्तुत किया गया था। इसका नाम सैमुअल एलेनबर्ग और सॉन्डर्स मैकलेन (1942) द्वारा रखा गया था, और सांस्थितिकी (सह-समरूपता के लिए सार्वभौमिक गुणांक प्रमेय) पर अनुप्रयुक्त किया गया था। किसी भी वलय (गणित) पर मापांक के लिए, एक्सट को हेनरी कर्तन और ईलेनबर्ग द्वारा उनकी 1956 की पुस्तक तुल्य बीजगणित में परिभाषित किया गया था।[1]
परिभाषा
R को एक वलय होने दें और R-अत्याधुनिक को R पर मापांक की श्रेणी (गणित) होने दें। T(B) = HomR(A, B) R-अत्याधुनिक में B के लिए। (यहाँ होमR(ए, B) ए से B तक R-रैखिक मानचित्रों का एबेलियन समूह है; यह एक R-मापांक है यदि R क्रमविनिमेय वलय है)। यह R-अत्याधुनिक से एबेलियन समूह एB की श्रेणी के लिए बाएं सटीक प्रकार्यक है, और इसलिए इसमें दाएं व्युत्पन्न प्रकार्यक R हैंमैंटी. एक्सट समूह द्वारा परिभाषित एबेलियन समूह हैं
एक पूर्णांक i के लिए परिभाषा के अनुसार, इसका अर्थ है: कोई भी अंतःक्षेपक संकल्प लें
B शब्द को हटा दें, और सह श्रृंखला समष्टि बनाएं:
प्रत्येक पूर्णांक i के लिए, एक्सटi
R(ए, B) स्थिति i पर इस समष्टि का श्रृंखला समष्टि है। यह i ऋणात्मक के लिए शून्य है। उदाहरण के लिए, एक्सट0
R(ए, B) होम मैप का कर्नेल (रैखिक बीजगणित) हैR(ए, आई0) → होमR(ए, आई1), जो कि होम के लिए तुल्याकारी हैR(ए, B)।
एक वैकल्पिक परिभाषा प्रकार्यक G(A)=Hom का उपयोग करती हैR(ए, B), एक निश्चित R-मापांक B के लिए। यह प्रकार्यक प्रकार्यक का सहप्रसरण और विरोधाभास है, जिसे विपरीत श्रेणी (R-अत्याधुनिक) से बाएं सटीक प्रकार्यक के रूप में देखा जा सकता है।ऑप से अब तक। एक्सट समूहों को सही व्युत्पन्न प्रकार्यक R के रूप में परिभाषित किया गया हैमैंजी:
यानी कोई भी प्रक्षेपी संकल्प चुनें
शब्द A को हटा दें, और सह श्रृंखला समष्टि बनाएं:
अगलाi
R(ए, B) स्थिति i पर इस परिसर का सह-समरूपता है।
कार्टन और ईलेनबर्ग ने दिखाया कि ये निर्माण प्रक्षेपी या अंतःक्षेपी संकल्प की पसंद से स्वतंत्र हैं और यह कि दोनों निर्माण एक ही एक्सटी समूह उत्पन्न करते हैं।[2] इसके अतिरिक्त, एक निश्चित वलय R के लिए, एक्सट प्रत्येक चर में एक प्रकार्यक है (A में contravariant, B में सहसंयोजक)।
एक क्रमविनिमेय वलय R और R-मापांक ए और B के लिए, एक्सटi
R(ए, B) एक R-मापांक है (होमR(ए, B) इस स्थिति में एक R-मापांक है)। एक गैर-क्रमविनिमेय वलय R, एक्सट के लिएi
R(ए, B) सामान्यतः केवल एक एबेलियन समूह है। यदि R एक वलय S पर एक बीजगणित है (जिसका विशेष रूप से अर्थ है कि S क्रमविनिमेय है), तो एक्सटi
R(ए, B) कम से कम एक एस-मापांक है।
एक्सट के गुण
यहाँ एक्सट समूहों के कुछ मूलभूत गुण और संगणनाएँ दी गई हैं।[3]
- एक्स्ट0
R(A, B) ≅ होमR(A, B) किसी भी R-मापांक A और B के लिए।
- एक्स्टi
R(A, B) = 0 सभी i> 0 के लिए यदि R-मापांक A प्रक्षेपी मापांक है (उदाहरण के लिए, मुफ्त मापांक ) या यदि B अंतःक्षेपक मापांक है।
- बातचीत भी रखती है:
- यदि एक्सट1
R(A, B) = 0 सभी B के लिए, तो A प्रक्षेपी है (और इसलिए एक्सटi
R(A, B) = 0 सभी के लिए i> 0)। - यदि एक्सट1
R(A, B) = 0 सभी ए के लिए, फिर B अंतःक्षेपी है (और इसलिए एक्सटi
R(A, B) = 0 सभी के लिए i> 0)।
- यदि एक्सट1
- सभी i ≥ 2 और सभी एबेलियन समूहों A और B के लिए।[4]
- यदि R एक क्रमविनिमेय वलय है और u in R एक शून्य भाजक नहीं है, तो
- किसी भी R-मापांक B के लिए। यहां B [यू] B के यू-टोरसन उपसमूह को दर्शाता है, {x ∈ B: ux = 0}। R को वलय मान लेना पूर्णांकों की, इस गणना का उपयोग गणना करने के लिए किया जा सकता है किसी भी अंतिम रूप से उत्पन्न एबेलियन समूह ए के लिए।
- पिछले उदाहरण को सामान्य करते हुए, जब कोई मापांक जटिल शर्ट का उपयोग करके किसी भी नियमित अनुक्रम द्वारा एक क्रमविनिमेय वलय का भागफल होता है, तो कोई एक्सट समूह की गणना कर सकता है।[5] उदाहरण के लिए, यदि R बहुपद वलय k[x1,...,एक्सn] क्षेत्र k पर, फिर एक्सट*
R(k,k) एक्सट में n जनक पर k के ऊपर बाहरी बीजगणित S है1</उप>। इसके अतिरिक्त, एक्सट*
S(k,k) बहुपद वलय R है; यह कोज़ुल द्वैत का एक उदाहरण है।
- व्युत्पन्न प्रकार्यकों के सामान्य गुणों के अनुसार, एक्सट के लिए दो मूल सटीक अनुक्रम हैं।[6] सबसे पहले, R-मापांक का एक छोटा सटीक अनुक्रम 0 → K → L → M → 0 प्रपत्र के एक लंबे सटीक अनुक्रम को प्रेरित करता है
- किसी भी R-मापांक ए के लिए। इसके अतिरिक्त, एक छोटा सटीक अनुक्रम 0 → के → एल → एम → 0 फॉर्म के एक लंबे सटीक अनुक्रम को प्रेरित करता है
- किसी भी R-मापांक B के लिए।
- एक्सट पहले चर में मापांक (संभवतः अनंत) का प्रत्यक्ष योग लेता है और प्रत्यक्ष उत्पाद#दूसरा चर में मापांक का प्रत्यक्ष उत्पाद उत्पादों के लिए।[7] वह है:
- चलो ए एक क्रमविनिमेय नोथेरियन वलय R पर एक अंतिम रूप से उत्पन्न मापांक है। फिर एक्स एक वलय के स्थानीयकरण के साथ प्रारंभ होता है, इस अर्थ में कि R में प्रत्येक गुणक रूप से बंद समुच्चय एस के लिए, प्रत्येक R-मापांक B, और प्रत्येक पूर्णांक i,[8]
एक्सट और विस्तारण
विस्तारण की समानता
एक्सट समूह मापांक के विस्तार से उनके संबंध से अपना नाम प्राप्त करते हैं। दिए गए R-मापांक ए और B, 'B द्वारा A का विस्तार' R-मापांक का एक छोटा सटीक अनुक्रम है
दो विस्तारण
एक क्रमविनिमेय Rेख होने पर समतुल्य कहा जाता है ('A' द्वारा B के विस्तार के रूप में):
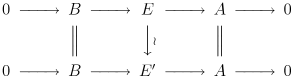 ध्यान दें कि पाँच लेम्मा का तात्पर्य है कि मध्य तीर एक समरूपता है। A द्वारा B के विस्तार को 'विभाजन' कहा जाता है यदि यह 'तुच्छ विस्तार' के समान है
ध्यान दें कि पाँच लेम्मा का तात्पर्य है कि मध्य तीर एक समरूपता है। A द्वारा B के विस्तार को 'विभाजन' कहा जाता है यदि यह 'तुच्छ विस्तार' के समान है
A बटा B के विस्तारण के समतुल्य वर्गों और एक्सट के तत्वों के Bच एक-से-एक पत्राचार है1
R(ए, B)।[9] तुच्छ विस्तार एक्सट के शून्य तत्व से मेल खाता है1
R(ए, B)।
विस्तारण का बायर योग
बेयर योग एक्सट पर एबेलियन समूह संरचना का एक स्पष्ट विवरण है1
R(ए, B), B द्वारा A के विस्तारण के समतुल्य वर्गों के समुच्चय के रूप में देखा जाता है।[10] अर्थात्, दो विस्तारण दिए गए
और
पहले पुलबैक (श्रेणी सिद्धांत) तैयार करें ,
फिर भागफल मापांक बनाएं
E और E' का बेयर योग विस्तार है
जहां पहला प्रतिचित्र है और दूसरा है।
विस्तारण की समतुल्यता तक, बायर राशि क्रमविनिमेय है और पहचान तत्व के रूप में तुच्छ विस्तार है। एक विस्तार 0 → B → ई → ए → 0 का ऋणात्मक एक ही मापांक ई को सम्मिलित करने वाला विस्तार है, परन्तु समरूपता B → ई के साथ इसके ऋणात्मक द्वारा प्रतिस्थापित किया गया है।
एबेलियन श्रेणियों में एक्सट का निर्माण
नोबुओ योनेदा ने एबेलियन समूहों को परिभाषित कियाn
C(ए, B) किसी एबेलियन श्रेणी 'सी' में वस्तुओं ए और B के लिए; यह संकल्पों के संदर्भ में परिभाषा से सहमत है यदि 'सी' में प्रोजेक्टिव ऑब्जेक्ट # पर्याप्त प्रक्षेपीय या अंतःक्षेपक ऑब्जेक्ट # पर्याप्त अंतःक्षेपक और अंतःक्षेपक हल्स हैं। सबसे पहले, एक्सट0
C(ए, B) = आदमीC(ए, B)। अगला, एक्सट1
C(ए, B) B द्वारा ए के विस्तार के समतुल्य वर्गों का समुच्चय है, जो बायर योग के अंतर्गत एक एबेलियन समूह बनाता है। अंत में, उच्च एक्सट समूह एक्सटn
C(ए, B) को एन-विस्तारण के समतुल्य वर्ग के रूप में परिभाषित किया गया है, जो सटीक अनुक्रम हैं
दो विस्तारण की पहचान करने वाले संबंध से उत्पन्न तुल्यता संबंध के अंतर्गत
यदि प्रतिचित्र है, {1, 2, ..., n} में सभी m के लिए ताकि प्रत्येक परिणामी वर्ग परिवर्तित हो जाए।
यदि कोई श्रृंखला मानचित्र ξ → ξ' है जो A और B पर तत्समक है।
उपर्युक्त दो n-आयामों का बायर योग देने से बनता है, A पर और का पुलबैक हो और B के अंतर्गत और का बहिकर्षी हो,[11] फिर विस्तारण का बायर योग है।
व्युत्पन्न श्रेणी और योनेदा उत्पाद
एक महत्वपूर्ण बिंदु यह है कि एबेलियन श्रेणी C में एक्सट समूहों को C व्युत्पन्न श्रेणी D(C) से संबंधित श्रेणी में आकारिकी के समुच्चय के रूप में देखा जा सकता है।[12] व्युत्पन्न श्रेणी की वस्तुएं C में वस्तुओं के परिसर हैं। विशेष रूप से, किसी के पास है
जहां C की एक वस्तु को डिग्री शून्य में केंद्रित एक जटिल के रूप में देखा जाता है और [i] का अर्थ है। एक जटिल i चरणों को बाईं ओर स्थानांतरित करना है। इस व्याख्या से, एक द्विरेखीय प्रतिचित्र है, जिसे कभी-कभी योनेदा उत्पाद कहा जाता है:
जो केवल व्युत्पन्न श्रेणी में आकारिता की रचना है।
योनेडा उत्पाद को अधिक प्राथमिक शब्दों में भी वर्णित किया जा सकता है। i = j = 0 के लिए, गुणनफल C श्रेणी के प्रतिचित्रों का संघटन है। सामान्यतः, उत्पाद को दो योनेडा विस्तारण को एक साथ जोड़कर परिभाषित किया जा सकता है।
वैकल्पिक रूप से, योनेडा उत्पाद को विश्लेषण के संदर्भ में परिभाषित किया जा सकता है (यह व्युत्पन्न श्रेणी की परिभाषा के समीप है)। उदाहरण के लिए, R-मापांक A, B, C के साथ R को वलय होने दें और P, Q, और T को A, B, C के अनुमानित विश्लेषण होने दें। फिर Exti
R(A, B) को श्रृंखला प्रतिचित्र P → Q[i] के श्रृंखला समस्थेयता कक्षाओं के समूह के साथ पहचाना जा सकता है। योनेदा उत्पाद श्रृंखला प्रतिचित्र बनाकर दिया गया है:
इनमें से किसी भी व्याख्या से, योनेदा उत्पाद साहचर्य है। फलस्वरूप, किसी भी R-मापांक A के लिए एक श्रेणीबद्ध वलय है। उदाहरण के लिए, यह समूह सह-समरूपता पर वलय संरचना देता है, चूंकि इसे के रूप में देखा जा सकता है। योनेडा उत्पाद की सहचारिता द्वारा भी: किसी भी R-मापांक A और B के लिए, पर एक मापांक है।
महत्वपूर्ण विशेष स्थिति
- समूह सह-समरूपता द्वारा परिभाषित किया गया है, जहाँ G एक समूह है, M पूर्णांकों पर G का एक समूह प्रतिनिधित्व है और G का समूह वलय है।
- क्षेत्र k और A-द्विप्रतिरूपक M पर बीजगणित A के लिए, होशचाइल्ड सह-समरूपता द्वारा परिभाषित किया गया है:
- लाई बीजगणितीय सह-समरूपता द्वारा परिभाषित किया गया है, जहाँ क्रमविनिमेय वलय k पर एक लाई बीजगणित है, M एक -मापांक है और सार्वभौमिक आवृत बीजगणित है।
- एक सांस्थितिक समष्टि X के लिए, पूली सह-समरूपता को इस रूप में परिभाषित किया जा सकता है। यहाँ एक्सट को X पर एबेलियन के पुली की एबेलियन श्रेणी में लिया गया है और स्थानीय स्थिरांक -मूल्यवान फलन का पुली है।
- अवशिष्ट क्षेत्र k के साथ क्रमविनिमेय नोथेरियन स्थानीय वलय R के लिए, एक श्रेणीबद्ध लाई बीजगणितीय π*(R) पर k का सार्वभौमिक आवृत बीजगणित है, जिसे R के समस्थेयता लाई बीजगणित के रूप में जाना जाता है (सटीक होने के लिए, जब k की विलक्षणता 2 होती है, π*(R) को एक समायोजित लाई बीजगणितीय के रूप में देखा जा सकता है)।[13] एंड्रे-क्विलन सह-समरूपता D*(k/R,k) से π*(R) तक श्रेणीबद्ध लाई बीजगणितीय का एक प्राकृतिक समरूपता है, जो एक समरूपता है यदि k में विलक्षणता शून्य है।[14]
यह भी देखें
- वैश्विक आयाम
- अवरोध विश्लेषण
- ग्रोथेंडिक समूह
- ग्रोथेंडिक स्थानीय द्वंद्व
टिप्पणियाँ
- ↑ Weibel (1999); Cartan & Eilenberg (1956), section VI.1.
- ↑ Weibel (1994), sections 2.4 and 2.5 and Theorem 2.7.6.
- ↑ Weibel (1994), Chapters 2 and 3.
- ↑ Weibeil (1994), Lemma 3.3.1.
- ↑ Weibel (1994), section 4.5.
- ↑ Weibel (1994), Definition 2.1.1.
- ↑ Weibel (1994), Proposition 3.3.4.
- ↑ Weibel (1994), Proposition 3.3.10.
- ↑ Weibel (1994), Theorem 3.4.3.
- ↑ Weibel (1994), Corollary 3.4.5.
- ↑ Weibel (1994), Vists 3.4.6. Some minor corrections are in the errata.
- ↑ Weibel (1994), sections 10.4 and 10.7; Gelfand & Manin (2003), Chapter III.
- ↑ Sjödin (1980), Notation 14.
- ↑ Avramov (2010), section 10.2.
संदर्भ
- Avramov, Luchezar (2010), "Infinite free resolutions", Six lectures on commutative algebra, Birkhäuser, pp. 1–108, doi:10.1007/978-3-0346-0329-4_1, ISBN 978-3-7643-5951-5, MR 2641236
- Baer, Reinhold (1934), "Erweiterung von Gruppen und ihren Isomorphismen", Mathematische Zeitschrift, 38 (1): 375–416, doi:10.1007/BF01170643, Zbl 0009.01101
- Cartan, Henri; Eilenberg, Samuel (1999) [1956], Homological algebra, Princeton: Princeton University Press, ISBN 0-691-04991-2, MR 0077480
- Eilenberg, Samuel; MacLane, Saunders (1942), "Group extensions and homology", Annals of Mathematics, 43 (4): 757–931, doi:10.2307/1968966, JSTOR 1968966, MR 0007108
- Gelfand, Sergei I.; Manin, Yuri Ivanovich (2003), Methods of homological algebra, Berlin, New York: Springer-Verlag, doi:10.1007/978-3-662-12492-5, ISBN 978-3-540-43583-9, MR 1950475
- Sjödin, Gunnar (1980), "Hopf algebras and derivations", Journal of Algebra, 64: 218–229, doi:10.1016/0021-8693(80)90143-X, MR 0575792
- Weibel, Charles A. (1994). An introduction to homological algebra. Cambridge Studies in Advanced Mathematics. Vol. 38. Cambridge University Press. ISBN 978-0-521-55987-4. MR 1269324. OCLC 36131259.
- Weibel, Charles A. (1999), "History of homological algebra" (PDF), History of topology, Amsterdam: North-Holland, pp. 797–836, ISBN 9780444823755, MR 1721123