गैर-विश्लेषणात्मक सुचारू कार्य: Difference between revisions
(Created page with "{{Short description|Mathematical functions which are smooth but not analytic}} गणित में, सुचारू कार्य (जिसे असीम रूप...") |
No edit summary |
||
| Line 1: | Line 1: | ||
{{Short description|Mathematical functions which are smooth but not analytic}} | {{Short description|Mathematical functions which are smooth but not analytic}} | ||
गणित में, | गणित में, समतल फलन (जिसे अधिकतम सीमा तक अवकलन फलन भी कहा जाता है) और विश्लेषणात्मक फलन दो बहुत महत्वपूर्ण प्रकार के फलन (गणित) होते हैं। कोई आसानी से प्रमाणित कर सकता है कि वास्तविक तर्क का कोई भी विश्लेषणात्मक फलन समतल है। इसका उत्क्रम सत्य नहीं है, जैसा कि नीचे दिए गए प्रति-उदाहरण के साथ प्रदर्शित किया गया है। | ||
[[कॉम्पैक्ट समर्थन]] के साथ | [[कॉम्पैक्ट समर्थन|सुसंहति समर्थन]] के साथ समतल फलनों के सबसे महत्वपूर्ण अनुप्रयोगों में से एक तथाकथित मोलिफायर का निर्माण है, जो सामान्यीकृत फलनों के सिद्धांतों में महत्वपूर्ण हैं, जैसे कि [[लॉरेंट श्वार्ट्ज]] के बंटन का सिद्धांत (गणित) होता है। | ||
समतल लेकिन गैर-विश्लेषणात्मक फलनों का अस्तित्व [[अंतर ज्यामिति|अवकल ज्यामिति]] विश्लेषणात्मक ज्यामिति के बीच मुख्य अंतरों में से एक का प्रतिनिधित्व करता है। [[शीफ सिद्धांत]] के संदर्भ में, इस अंतर को निम्नानुसार कहा जा सकता है: विश्लेषणात्मक स्थितियों के विपरीत, अवकलनीय प्रसमष्टि पर अवकलनीय फलनों का शीफ परिशुद्ध है। | |||
नीचे दिए गए | नीचे दिए गए फलन सामान्य रूप से अवकलनीय प्रसमष्टि पर समानता के विभाजन को बनाने के लिए उपयोग किए जाते हैं। | ||
== एक उदाहरण | == एक उदाहरण फलन == | ||
=== | === फलन की परिभाषा === | ||
[[Image:Non-analytic smooth function.png|right|frame|लेख में माना गया गैर-विश्लेषणात्मक | [[Image:Non-analytic smooth function.png|right|frame|लेख में माना गया गैर-विश्लेषणात्मक समतल फलन f(x)।]]फलन पर विचार करें | ||
:<math>f(x)=\begin{cases}e^{-\frac{1}{x}}&\text{if }x>0,\\ 0&\text{if }x\le0,\end{cases}</math> | :<math>f(x)=\begin{cases}e^{-\frac{1}{x}}&\text{if }x>0,\\ 0&\text{if }x\le0,\end{cases}</math> | ||
प्रत्येक वास्तविक संख्या x के लिए | प्रत्येक वास्तविक संख्या x के लिए परिभाषित है। | ||
=== | === फलन समतल है === | ||
फलन f में [[वास्तविक रेखा]] के प्रत्येक बिंदु x पर सभी फलन के सतत फलन [[ यौगिक |अवकल]] हैं। इन अवकलों का सूत्र है | |||
:<math>f^{(n)}(x) = \begin{cases}\displaystyle\frac{p_n(x)}{x^{2n}}\,f(x) & \text{if }x>0, \\ 0 &\text{if }x \le 0,\end{cases}</math> | :<math>f^{(n)}(x) = \begin{cases}\displaystyle\frac{p_n(x)}{x^{2n}}\,f(x) & \text{if }x>0, \\ 0 &\text{if }x \le 0,\end{cases}</math> | ||
जहां | जहां ''p<sub>n</sub>''(''x'') एक [[बहुपद]] n − 1 की घात का एक बहुपद है जिसे ''p''<sub>1</sub>(''x'') = 1 द्वारा पुनरावर्तन दिया गया है और | ||
:<math>p_{n+1}(x)=x^2p_n'(x)-(2nx-1)p_n(x)</math> | :<math>p_{n+1}(x)=x^2p_n'(x)-(2nx-1)p_n(x)</math> | ||
किसी भी धनात्मक [[पूर्णांक]] n के | किसी भी धनात्मक [[पूर्णांक]] n के लिए इस सूत्र से, यह पूरी तरह से स्पष्ट नहीं है कि अवकल 0 पर सतत हैं; यह [[एक तरफा सीमा|एकपक्षीय लिमिट]] से अनुसरण करता है | ||
:<math>\lim_{x\searrow 0} \frac{e^{-\frac{1}{x}}}{x^m} = 0</math> | :<math>\lim_{x\searrow 0} \frac{e^{-\frac{1}{x}}}{x^m} = 0</math> | ||
किसी भी गैर- | किसी भी गैर-ऋणात्मक पूर्णांक m के लिए होता है। | ||
{{Collapse top|title= | {{Collapse top|title=समतलता का विस्तृत प्रमाण}} | ||
घातीय फलन | घातीय फलन के घात श्रेणी निरूपण से, हमारे पास प्रत्येक प्राकृत संख्या <math>m</math> (शून्य सहित) के लिए है | ||
:<math>\frac1{x^m}=x\Bigl(\frac1{x}\Bigr)^{m+1}\le (m+1)!\,x\sum_{n=0}^\infty\frac1{n!}\Bigl(\frac1x\Bigr)^n | :<math>\frac1{x^m}=x\Bigl(\frac1{x}\Bigr)^{m+1}\le (m+1)!\,x\sum_{n=0}^\infty\frac1{n!}\Bigl(\frac1x\Bigr)^n | ||
=(m+1)!\,x e^{\frac{1}{x}},\qquad x>0,</math> | =(m+1)!\,x e^{\frac{1}{x}},\qquad x>0,</math> | ||
क्योंकि | क्योंकि <math>n \neq m+1</math> के लिए सभी धनात्मक पद जोड़े गए हैं। इसलिए, इस असमानता को <math>e^{\frac{1}{x}}</math> से विभाजित करके ऊपर से लिमिट लेकर, | ||
:<math>\lim_{x\searrow0}\frac{e^{-\frac{1}{x}}}{x^m} | :<math>\lim_{x\searrow0}\frac{e^{-\frac{1}{x}}}{x^m} | ||
\le (m+1)!\lim_{x\searrow0}x=0.</math> | \le (m+1)!\lim_{x\searrow0}x=0.</math> | ||
अब हम गणितीय | अब हम गणितीय प्रेरण द्वारा f के nवें अवकलज के सूत्र को सिद्ध करते हैं। [[श्रृंखला नियम]], [[व्युत्क्रम नियम]], और इस तथ्य का उपयोग करते हुए कि घातीय फलन का व्युत्पन्न फिर से घातीय फलन है, हम देखते हैं कि सूत्र सभी x > 0 के लिए f के पहले अवकल के लिए सही है और वह p<sub>1</sub>(x) घात 0 का एक बहुपद है। तथापि, f का अवकल x < 0 के लिए शून्य है। | ||
यह दिखाना | यह दिखाना शेष है कि x = 0 पर f का दक्षिणावर्ती पथ अवकल शून्य है। उपरोक्त सीमा का उपयोग करते हुए, हम देखते हैं | ||
:<math>f'(0)=\lim_{x\searrow0}\frac{f(x)-f(0)}{x-0}=\lim_{x\searrow0}\frac{e^{-\frac{1}{x}}}{x}=0.</math> | :<math>f'(0)=\lim_{x\searrow0}\frac{f(x)-f(0)}{x-0}=\lim_{x\searrow0}\frac{e^{-\frac{1}{x}}}{x}=0.</math> | ||
n से n + 1 तक का | n से n + 1 तक का प्रेरण चरण समान है। और x > 0 के लिए हम अवकल के लिए प्राप्त करते हैं | ||
:<math>\begin{align}f^{(n+1)}(x) | :<math>\begin{align}f^{(n+1)}(x) | ||
&=\biggl(\frac{p'_n(x)}{x^{2n}}-2n\frac{p_n(x)}{x^{2n+1}}+\frac{p_n(x)}{x^{2n+2}}\biggr)f(x)\\ | &=\biggl(\frac{p'_n(x)}{x^{2n}}-2n\frac{p_n(x)}{x^{2n+1}}+\frac{p_n(x)}{x^{2n+2}}\biggr)f(x)\\ | ||
&=\frac{x^2p'_n(x)-(2nx-1)p_n(x)}{x^{2n+2}}f(x)\\ | &=\frac{x^2p'_n(x)-(2nx-1)p_n(x)}{x^{2n+2}}f(x)\\ | ||
&=\frac{p_{n+1}(x)}{x^{2(n+1)}}f(x),\end{align}</math> | &=\frac{p_{n+1}(x)}{x^{2(n+1)}}f(x),\end{align}</math> | ||
जहां | जहां p<sub>''n''+1</sub>(x) घात n = (n + 1) − 1 का एक बहुपद है। परंतु, f का (n + 1)वां अवकलज x < 0 के लिए शून्य है। f के दक्षिण पथ के अवकलज के लिए<sup>(n)</sup> x = 0 पर हम उपरोक्त सीमा के साथ प्राप्त करते हैं | ||
:<math>\lim_{x\searrow0} \frac{f^{(n)}(x) - f^{(n)}(0)}{x-0} = \lim_{x\searrow0} \frac{p_n(x)}{x^{2n+1}}\,e^{-1/x} = 0.</math> | :<math>\lim_{x\searrow0} \frac{f^{(n)}(x) - f^{(n)}(0)}{x-0} = \lim_{x\searrow0} \frac{p_n(x)}{x^{2n+1}}\,e^{-1/x} = 0.</math> | ||
{{Collapse bottom}} | {{Collapse bottom}} | ||
=== | === फलन विश्लेषणात्मक नहीं है === | ||
जैसा कि पहले देखा गया है, | जैसा कि पहले देखा गया है, फलन f समतल है, और मूल (गणित) पर इसके सभी अवकल 0 हैं। इसलिए, उत्पत्ति पर f की [[टेलर श्रृंखला]] प्रत्येक समष्टि शून्य फलन में परिवर्तित हो जाती है, | ||
:<math>\sum_{n=0}^\infty \frac{f^{(n)}(0)}{n!}x^n=\sum_{n=0}^\infty \frac{0}{n!}x^n = 0,\qquad x\in\mathbb{R},</math> | :<math>\sum_{n=0}^\infty \frac{f^{(n)}(0)}{n!}x^n=\sum_{n=0}^\infty \frac{0}{n!}x^n = 0,\qquad x\in\mathbb{R},</math> | ||
और इसलिए टेलर श्रृंखला x > 0 के लिए f(x) के बराबर नहीं है। | और इसलिए टेलर श्रृंखला x > 0 के लिए f(x) के बराबर नहीं है। परिणामस्वरूप, f मूल बिंदु पर विश्लेषणात्मक फलन नहीं है। | ||
=== | === समतल संक्रमण फलन === | ||
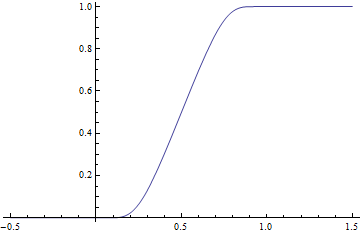
[[Image:Smooth transition from 0 to 1.png|right|frame|यहाँ परिभाषित 0 से 1 तक का | [[Image:Smooth transition from 0 to 1.png|right|frame|यहाँ परिभाषित 0 से 1 तक का समतल संक्रमण g है।]]फलन | ||
:<math>g(x)=\frac{f(x)}{f(x)+f(1-x)},\qquad x\in\mathbb{R},</math> | :<math>g(x)=\frac{f(x)}{f(x)+f(1-x)},\qquad x\in\mathbb{R},</math> | ||
वास्तविक रेखा पर | वास्तविक रेखा पर प्रत्येक समष्टि दृढ़ता से धनात्मक भाजक होता है, इसलिए g भी समतल होता है। इसके अतिरिक्त, x ≤ 0 के लिए g(x) = 0 और x ≥ 1 के लिए g(x) = 1 इसलिए यह [[इकाई अंतराल]] <nowiki>[</nowiki> 0, 1] में स्तर 0 से स्तर 1 तक एक सामान्य संक्रमण प्रदान करता है। वास्तविक अंतराल a < b मे <nowiki>[</nowiki>a, b<nowiki>]</nowiki> के साथ सामान्य संक्रमण के लिए, फलन पर विचार करें | ||
:<math>\mathbb{R}\ni x\mapsto g\Bigl(\frac{x-a}{b-a}\Bigr).</math> | :<math>\mathbb{R}\ni x\mapsto g\Bigl(\frac{x-a}{b-a}\Bigr).</math> | ||
वास्तविक संख्या | वास्तविक संख्या {{math|''a'' < ''b'' < ''c'' < ''d''}}, समतल फलन के लिए | ||
:<math>\mathbb{R}\ni x\mapsto g\Bigl(\frac{x-a}{b-a}\Bigr)\,g\Bigl(\frac{d-x}{d-c}\Bigr)</math> | :<math>\mathbb{R}\ni x\mapsto g\Bigl(\frac{x-a}{b-a}\Bigr)\,g\Bigl(\frac{d-x}{d-c}\Bigr)</math> | ||
संवृत अंतराल <nowiki>[</nowiki>b, c<nowiki>]</nowiki> पर 1 के बराबर होता है और विवृत अंतराल (a, d) के बाहर समाप्त हो जाता है, इसलिए यह एक [[टक्कर समारोह|संघट्टन फलन]] के रूप में काम कर सकता है। | |||
== | == सामान्य फलन जो कहीं भी वास्तविक विश्लेषणात्मक नहीं है == | ||
[[File:Smooth non-analytic function.png|thumb|सुचारू-हर जगह, लेकिन कहीं नहीं-विश्लेषणात्मक कार्य का उल्लेख यहाँ किया गया है। यह आंशिक योग k=2 से लिया गया है<sup>0</sup> से 2<sup>500</sup>.|सही]] | [[File:Smooth non-analytic function.png|thumb|सुचारू-हर जगह, लेकिन कहीं नहीं-विश्लेषणात्मक कार्य का उल्लेख यहाँ किया गया है। यह आंशिक योग k=2 से लिया गया है<sup>0</sup> से 2<sup>500</sup>.|सही]]अधिक [[पैथोलॉजिकल (गणित)|तर्कहीन (गणित)]] उदाहरण अधिकतम सीमा तक अवकलन फलन है जो किसी भी बिंदु पर विश्लेषणात्मक नहीं है। इसका निर्माण निम्नानुसार फूरियर श्रृंखला के माध्यम से किया जा सकता है। सभी <math>x \in \mathbb{R}</math> के लिए परिभाषित करें | ||
:<math>F(x):=\sum_{k\in \mathbb{N}} e^{-\sqrt{2^k}}\cos(2^k x)\ .</math> | :<math>F(x):=\sum_{k\in \mathbb{N}} e^{-\sqrt{2^k}}\cos(2^k x)\ .</math> | ||
श्रृंखला | चूंकि श्रृंखला <math>\sum_{k\in \mathbb{N}} e^{-\sqrt{2^k}}{(2^k)}^n</math> अभिसरित होती है सभी <math>n \in \mathbb{N}</math> के लिए, यह फलन अवकलों की प्रत्येक श्रृंखला के एकसमान अभिसरण को प्रदर्शित करने के लिए वीयरस्ट्रैस m-परीक्षण के एक मानक प्रेरण अनुप्रयोग द्वारा आसानी से वर्ग C∞ का देखा जाता है। | ||
अब हम दिखाते हैं <math>F(x)</math> π के किसी भी द्विअर्थी परिमेय गुणज, | अब हम दिखाते हैं <math>F(x)</math> π के किसी भी द्विअर्थी परिमेय गुणज, अर्थात किसी भी <math>x := \pi \cdot p \cdot 2^{-q}</math> पर <math>p \in \mathbb{Z}</math> और <math>q \in \mathbb{N}</math> भी विश्लेषणात्मक नहीं है। चूँकि पहले <math>q</math> पदों का योग विश्लेषणात्मक है, हमें केवल <math>F_{>q}(x)</math> पर विचार करने की आवश्यकता है और <math>k>q</math> के साथ पदों का योग अवकलों के सभी कर्मों के लिए <math>n = 2^m</math> साथ मे <math>m \in \mathbb{N}</math>, <math>m \geq 2</math> और <math>m > q/2</math> हमे प्राप्त है | ||
:<math>F_{>q}^{(n)}(x):=\sum_{k\in \mathbb{N}\atop k>q} e^{-\sqrt{2^k}} {(2^k)}^n\cos(2^k x) = \sum_{k\in \mathbb{N}\atop k>q} e^{-\sqrt{2^k}} {(2^k)}^n \ge e^{-n} n^{2n}\quad (\mathrm{as}\; n\to \infty)</math> | :<math>F_{>q}^{(n)}(x):=\sum_{k\in \mathbb{N}\atop k>q} e^{-\sqrt{2^k}} {(2^k)}^n\cos(2^k x) = \sum_{k\in \mathbb{N}\atop k>q} e^{-\sqrt{2^k}} {(2^k)}^n \ge e^{-n} n^{2n}\quad (\mathrm{as}\; n\to \infty)</math> | ||
जहां हमने इस तथ्य का उपयोग किया <math>\cos(2^k x) = 1</math> सभी | जहां हमने इस तथ्य का उपयोग किया कि <math>\cos(2^k x) = 1</math> सभी <math>2^k > 2^q</math> के लिए और हमने पहले योग को नीचे से पद <math>2^k=2^{2m}=n^2</math> के साथ परिबद्ध किया। परिणामस्वरूप, ऐसे किसी भी <math>x \in \mathbb{R}</math> पर | ||
:<math>\limsup_{n\to\infty} \left(\frac{|F_{>q}^{(n)}(x)|}{n!}\right)^{1/n}=+\infty\, ,</math> | :<math>\limsup_{n\to\infty} \left(\frac{|F_{>q}^{(n)}(x)|}{n!}\right)^{1/n}=+\infty\, ,</math> | ||
ताकि टेलर श्रृंखला | ताकि कॉची-हैडमार्ड सूत्र द्वारा x पर टेलर श्रृंखला की अभिसरण की त्रिज्या <math>F_{>q}</math> हो। चूंकि किसी फ़ंक्शन की विश्लेषणात्मकता का समुच्चय एक विवृत समुच्चय है, और चूंकि युग्मकीय परिमेय सुसंहत हैं, इसलिए हम निष्कर्ष निकालते हैं कि <math>F_{>q}</math>,, और इसलिए <math>F</math>, <math>\mathbb{R}</math> में कहीं भी विश्लेषणात्मक नहीं है। | ||
== टेलर श्रृंखला के लिए | == टेलर श्रृंखला के लिए अनुप्रयोग == | ||
{{main|बोरेल लेम्मा}} | |||
हर क्रम के लिए α0, α1, α2, . . . वास्तविक या सम्मिश्र संख्याओं के लिए, निम्नलिखित निर्माण वास्तविक रेखा पर एक समतल फलन F के अस्तित्व को दर्शाता है, जिसके मूल में ये संख्याएँ अवकल के रूप में हैं।<ref>Exercise 12 on page 418 in Walter Rudin, ''Real and Complex Analysis''. McGraw-Hill, New Delhi 1980, ISBN 0-07-099557-5</ref> विशेष रूप से, संख्याओं का प्रत्येक क्रम टेलर श्रृंखला के समतल फलनों के गुणांक के रूप में प्रकट हो सकता है। एमिल बोरेल के बाद इस परिणाम को बोरेल लेम्मा के रूप में जाना जाता है। | |||
:<math>h(x)=g(2+x)\,g(2-x),\qquad x\in\mathbb{R}.</math> | :<math>h(x)=g(2+x)\,g(2-x),\qquad x\in\mathbb{R}.</math> | ||
यह | यह फलन h भी समतल है; यह संवृत अंतराल <nowiki>[</nowiki>−1,1<nowiki>]</nowiki> पर 1 के बराबर होता है और विवृत अंतराल (−2,2) के बाहर नष्ट हो जाता है। h का उपयोग करते हुए, प्रत्येक प्राकृतिक संख्या n (शून्य सहित) के लिए समतल फलन को परिभाषित करें | ||
:<math>\psi_n(x)=x^n\,h(x),\qquad x\in\mathbb{R},</math> | :<math>\psi_n(x)=x^n\,h(x),\qquad x\in\mathbb{R},</math> | ||
जो [ | जो [−1,1] पर एकपदी ''x<sup>n</sup>'' के साथ सहमत है और अंतराल (−2,2) के बाहर नष्ट हो जाता है। इसलिए, मूल बिंदु पर ''ψ<sub>n</sub>'' का k-वाँ अवकलज संतुष्ट करता है | ||
:<math>\psi_n^{(k)}(0)=\begin{cases}n!&\text{if }k=n,\\0&\text{otherwise,}\end{cases}\quad k,n\in\mathbb{N}_0,</math> | :<math>\psi_n^{(k)}(0)=\begin{cases}n!&\text{if }k=n,\\0&\text{otherwise,}\end{cases}\quad k,n\in\mathbb{N}_0,</math> | ||
और | और परिबद्धता प्रमेय का तात्पर्य है कि ''ψ<sub>n</sub>'' और ''ψ<sub>n</sub>'' का प्रत्येक अवकलज परिबद्ध है। इसलिए, स्थिरांक | ||
:<math>\lambda_n=\max\bigl\{1,|\alpha_n|,\|\psi_n\|_\infty,\|\psi_n^{(1)}\|_\infty,\ldots,\|\psi_n^{(n)}\|_\infty\bigr\},\qquad n\in\mathbb{N}_0,</math> | :<math>\lambda_n=\max\bigl\{1,|\alpha_n|,\|\psi_n\|_\infty,\|\psi_n^{(1)}\|_\infty,\ldots,\|\psi_n^{(n)}\|_\infty\bigr\},\qquad n\in\mathbb{N}_0,</math> | ||
ψ | ψ<sub>n</sub> के सर्वोच्च मानक को सम्मिलित करनाऔर इसके पहले n अवकल, अच्छी तरह से परिभाषित वास्तविक संख्याएँ हैं। माप किए गए फलनों को परिभाषित करें | ||
:<math>f_n(x)=\frac{\alpha_n}{n!\,\lambda_n^n}\psi_n(\lambda_n x),\qquad n\in\mathbb{N}_0,\;x\in\mathbb{R}.</math> | :<math>f_n(x)=\frac{\alpha_n}{n!\,\lambda_n^n}\psi_n(\lambda_n x),\qquad n\in\mathbb{N}_0,\;x\in\mathbb{R}.</math> | ||
| Line 106: | Line 105: | ||
:<math>f_n^{(k)}(x)=\frac{\alpha_n}{n!\,\lambda_n^{n-k}}\psi_n^{(k)}(\lambda_n x),\qquad k,n\in\mathbb{N}_0,\;x\in\mathbb{R},</math> | :<math>f_n^{(k)}(x)=\frac{\alpha_n}{n!\,\lambda_n^{n-k}}\psi_n^{(k)}(\lambda_n x),\qquad k,n\in\mathbb{N}_0,\;x\in\mathbb{R},</math> | ||
और, ψ के k-वें | और शून्य पर, ψ<sub>n</sub> के k-वें अवकल के लिए पूर्व परिणाम का उपयोग करना | ||
:<math>f_n^{(k)}(0)=\begin{cases}\alpha_n&\text{if }k=n,\\0&\text{otherwise,}\end{cases}\qquad k,n\in\mathbb{N}_0.</math> | :<math>f_n^{(k)}(0)=\begin{cases}\alpha_n&\text{if }k=n,\\0&\text{otherwise,}\end{cases}\qquad k,n\in\mathbb{N}_0.</math> | ||
यह दिखाना | यह दिखाना शेष है कि फलन | ||
:<math>F(x)=\sum_{n=0}^\infty f_n(x),\qquad x\in\mathbb{R},</math> | :<math>F(x)=\sum_{n=0}^\infty f_n(x),\qquad x\in\mathbb{R},</math> | ||
अच्छी तरह से परिभाषित है और | अच्छी तरह से परिभाषित है और पद-दर-अवधि में असीमित रूप से कई बार अवकलित किया जा सकता है।<ref>See e.g. Chapter V, Section 2, Theorem 2.8 and Corollary 2.9 about the differentiability of the limits of sequences of functions in {{Citation | ||
| last = Amann | | last = Amann | ||
| first = Herbert | | first = Herbert | ||
| Line 122: | Line 121: | ||
| year = 2005 | | year = 2005 | ||
| pages = 373–374 | | pages = 373–374 | ||
| isbn = 3-7643-7153-6}}</ref> इसके लिए, देखें कि | | isbn = 3-7643-7153-6}}</ref> इसके लिए, देखें कि प्रत्येक k के लिए | ||
:<math>\sum_{n=0}^\infty\|f_n^{(k)}\|_\infty | :<math>\sum_{n=0}^\infty\|f_n^{(k)}\|_\infty | ||
| Line 133: | Line 132: | ||
जहां शेष अनंत श्रृंखला अनुपात परीक्षण द्वारा अभिसरित होती है। | जहां शेष अनंत श्रृंखला अनुपात परीक्षण द्वारा अभिसरित होती है। | ||
== उच्च आयामों के लिए | == उच्च आयामों के लिए अनुप्रयोग == | ||
[[File:Mollifier Illustration.svg|right|thumb|280px| | [[File:Mollifier Illustration.svg|right|thumb|280px|फलन Ψ<sub>1</sub>(x) एक आयाम में।]]प्रत्येक त्रिज्या r > 0 के लिए, | ||
:<math>\mathbb{R}^n\ni x\mapsto \Psi_r(x)=f(r^2-\|x\|^2)</math> | :<math>\mathbb{R}^n\ni x\mapsto \Psi_r(x)=f(r^2-\|x\|^2)</math> | ||
[[यूक्लिडियन मानदंड]] के साथ ||x|| त्रिज्या आर की [[गेंद (गणित)]] में [[समर्थन (गणित)]] के साथ | [[यूक्लिडियन मानदंड]] के साथ ||x|| त्रिज्या आर की [[गेंद (गणित)|गोला (गणित)]] में [[समर्थन (गणित)]] के साथ n-आयामी [[यूक्लिडियन अंतरिक्ष|यूक्लिडियन]] समष्टि पर एक समतल फलन को परिभाषित करता है, लेकिन <math>\Psi_r(0)>0</math> होता है। | ||
== [[जटिल विश्लेषण]] == | == [[जटिल विश्लेषण]] == | ||
यह विकृति एक वास्तविक चर के | यह विकृति एक वास्तविक चर के अतिरिक्त अवकलनीय जटिल विश्लेषण के साथ नहीं हो सकती है। वास्तव में, सभी होलोमॉर्फिक(पूर्ण-सममितिक) फलन विश्लेषणात्मक होते हैं, इसलिए इस लेख में परिभाषित फलन f की विफलता विश्लेषणात्मक होने के बाद भी अधिकतम सीमा तक अवकल होने के बाद भी वास्तविक-चर और जटिल-चर विश्लेषण के बीच सबसे प्रभावशाली अंतरों में से एक का संकेत है। | ||
ध्यान दें कि यद्यपि | ध्यान दें कि यद्यपि फलन f में वास्तविक रेखा पर सभी फलन के अवकल हैं, धनात्मक अर्ध-रेखा x > 0 से [[जटिल विमान|सम्मिश्र तल]] तक f की [[विश्लेषणात्मक निरंतरता]], अर्थात फलन | ||
:<math>\mathbb{C}\setminus\{0\}\ni z\mapsto e^{-\frac{1}{z}}\in\mathbb{C},</math> | :<math>\mathbb{C}\setminus\{0\}\ni z\mapsto e^{-\frac{1}{z}}\in\mathbb{C},</math> | ||
मूल में एक | मूल में एक अनिवार्य विलक्षणता है, और इसलिए यह निरंतर भी नहीं है, बहुत कम विश्लेषणात्मक है। [[महान पिकार्ड प्रमेय]] द्वारा, यह उत्पत्ति के प्रत्येक प्रतिवेश में असीमित रूप से कई बार प्रत्येक सम्मिश्र मान (शून्य के अपवाद के साथ) प्राप्त करता है। | ||
== यह भी देखें == | == यह भी देखें == | ||
* | * संघट्ट फलन | ||
* [[फैबियस समारोह]] | * [[फैबियस समारोह|फैबियस फलन]] | ||
* [[फ्लैट समारोह]] | * [[फ्लैट समारोह|समतल फलन]] | ||
* मोलिफायर | * मोलिफायर | ||
Revision as of 09:44, 23 May 2023
गणित में, समतल फलन (जिसे अधिकतम सीमा तक अवकलन फलन भी कहा जाता है) और विश्लेषणात्मक फलन दो बहुत महत्वपूर्ण प्रकार के फलन (गणित) होते हैं। कोई आसानी से प्रमाणित कर सकता है कि वास्तविक तर्क का कोई भी विश्लेषणात्मक फलन समतल है। इसका उत्क्रम सत्य नहीं है, जैसा कि नीचे दिए गए प्रति-उदाहरण के साथ प्रदर्शित किया गया है।
सुसंहति समर्थन के साथ समतल फलनों के सबसे महत्वपूर्ण अनुप्रयोगों में से एक तथाकथित मोलिफायर का निर्माण है, जो सामान्यीकृत फलनों के सिद्धांतों में महत्वपूर्ण हैं, जैसे कि लॉरेंट श्वार्ट्ज के बंटन का सिद्धांत (गणित) होता है।
समतल लेकिन गैर-विश्लेषणात्मक फलनों का अस्तित्व अवकल ज्यामिति विश्लेषणात्मक ज्यामिति के बीच मुख्य अंतरों में से एक का प्रतिनिधित्व करता है। शीफ सिद्धांत के संदर्भ में, इस अंतर को निम्नानुसार कहा जा सकता है: विश्लेषणात्मक स्थितियों के विपरीत, अवकलनीय प्रसमष्टि पर अवकलनीय फलनों का शीफ परिशुद्ध है।
नीचे दिए गए फलन सामान्य रूप से अवकलनीय प्रसमष्टि पर समानता के विभाजन को बनाने के लिए उपयोग किए जाते हैं।
एक उदाहरण फलन
फलन की परिभाषा
फलन पर विचार करें
प्रत्येक वास्तविक संख्या x के लिए परिभाषित है।
फलन समतल है
फलन f में वास्तविक रेखा के प्रत्येक बिंदु x पर सभी फलन के सतत फलन अवकल हैं। इन अवकलों का सूत्र है
जहां pn(x) एक बहुपद n − 1 की घात का एक बहुपद है जिसे p1(x) = 1 द्वारा पुनरावर्तन दिया गया है और
किसी भी धनात्मक पूर्णांक n के लिए इस सूत्र से, यह पूरी तरह से स्पष्ट नहीं है कि अवकल 0 पर सतत हैं; यह एकपक्षीय लिमिट से अनुसरण करता है
किसी भी गैर-ऋणात्मक पूर्णांक m के लिए होता है।
| style="background: #F0F2F5; font-size:87%; padding:0.2em 0.3em; text-align:center; " | समतलता का विस्तृत प्रमाण
|
|---|
|
घातीय फलन के घात श्रेणी निरूपण से, हमारे पास प्रत्येक प्राकृत संख्या (शून्य सहित) के लिए है क्योंकि के लिए सभी धनात्मक पद जोड़े गए हैं। इसलिए, इस असमानता को से विभाजित करके ऊपर से लिमिट लेकर, अब हम गणितीय प्रेरण द्वारा f के nवें अवकलज के सूत्र को सिद्ध करते हैं। श्रृंखला नियम, व्युत्क्रम नियम, और इस तथ्य का उपयोग करते हुए कि घातीय फलन का व्युत्पन्न फिर से घातीय फलन है, हम देखते हैं कि सूत्र सभी x > 0 के लिए f के पहले अवकल के लिए सही है और वह p1(x) घात 0 का एक बहुपद है। तथापि, f का अवकल x < 0 के लिए शून्य है। यह दिखाना शेष है कि x = 0 पर f का दक्षिणावर्ती पथ अवकल शून्य है। उपरोक्त सीमा का उपयोग करते हुए, हम देखते हैं n से n + 1 तक का प्रेरण चरण समान है। और x > 0 के लिए हम अवकल के लिए प्राप्त करते हैं जहां pn+1(x) घात n = (n + 1) − 1 का एक बहुपद है। परंतु, f का (n + 1)वां अवकलज x < 0 के लिए शून्य है। f के दक्षिण पथ के अवकलज के लिए(n) x = 0 पर हम उपरोक्त सीमा के साथ प्राप्त करते हैं |
फलन विश्लेषणात्मक नहीं है
जैसा कि पहले देखा गया है, फलन f समतल है, और मूल (गणित) पर इसके सभी अवकल 0 हैं। इसलिए, उत्पत्ति पर f की टेलर श्रृंखला प्रत्येक समष्टि शून्य फलन में परिवर्तित हो जाती है,
और इसलिए टेलर श्रृंखला x > 0 के लिए f(x) के बराबर नहीं है। परिणामस्वरूप, f मूल बिंदु पर विश्लेषणात्मक फलन नहीं है।
समतल संक्रमण फलन
फलन
वास्तविक रेखा पर प्रत्येक समष्टि दृढ़ता से धनात्मक भाजक होता है, इसलिए g भी समतल होता है। इसके अतिरिक्त, x ≤ 0 के लिए g(x) = 0 और x ≥ 1 के लिए g(x) = 1 इसलिए यह इकाई अंतराल [ 0, 1] में स्तर 0 से स्तर 1 तक एक सामान्य संक्रमण प्रदान करता है। वास्तविक अंतराल a < b मे [a, b] के साथ सामान्य संक्रमण के लिए, फलन पर विचार करें
वास्तविक संख्या a < b < c < d, समतल फलन के लिए
संवृत अंतराल [b, c] पर 1 के बराबर होता है और विवृत अंतराल (a, d) के बाहर समाप्त हो जाता है, इसलिए यह एक संघट्टन फलन के रूप में काम कर सकता है।
सामान्य फलन जो कहीं भी वास्तविक विश्लेषणात्मक नहीं है
अधिक तर्कहीन (गणित) उदाहरण अधिकतम सीमा तक अवकलन फलन है जो किसी भी बिंदु पर विश्लेषणात्मक नहीं है। इसका निर्माण निम्नानुसार फूरियर श्रृंखला के माध्यम से किया जा सकता है। सभी के लिए परिभाषित करें
चूंकि श्रृंखला अभिसरित होती है सभी के लिए, यह फलन अवकलों की प्रत्येक श्रृंखला के एकसमान अभिसरण को प्रदर्शित करने के लिए वीयरस्ट्रैस m-परीक्षण के एक मानक प्रेरण अनुप्रयोग द्वारा आसानी से वर्ग C∞ का देखा जाता है।
अब हम दिखाते हैं π के किसी भी द्विअर्थी परिमेय गुणज, अर्थात किसी भी पर और भी विश्लेषणात्मक नहीं है। चूँकि पहले पदों का योग विश्लेषणात्मक है, हमें केवल पर विचार करने की आवश्यकता है और के साथ पदों का योग अवकलों के सभी कर्मों के लिए साथ मे , और हमे प्राप्त है
जहां हमने इस तथ्य का उपयोग किया कि सभी के लिए और हमने पहले योग को नीचे से पद के साथ परिबद्ध किया। परिणामस्वरूप, ऐसे किसी भी पर
ताकि कॉची-हैडमार्ड सूत्र द्वारा x पर टेलर श्रृंखला की अभिसरण की त्रिज्या हो। चूंकि किसी फ़ंक्शन की विश्लेषणात्मकता का समुच्चय एक विवृत समुच्चय है, और चूंकि युग्मकीय परिमेय सुसंहत हैं, इसलिए हम निष्कर्ष निकालते हैं कि ,, और इसलिए , में कहीं भी विश्लेषणात्मक नहीं है।
टेलर श्रृंखला के लिए अनुप्रयोग
हर क्रम के लिए α0, α1, α2, . . . वास्तविक या सम्मिश्र संख्याओं के लिए, निम्नलिखित निर्माण वास्तविक रेखा पर एक समतल फलन F के अस्तित्व को दर्शाता है, जिसके मूल में ये संख्याएँ अवकल के रूप में हैं।[1] विशेष रूप से, संख्याओं का प्रत्येक क्रम टेलर श्रृंखला के समतल फलनों के गुणांक के रूप में प्रकट हो सकता है। एमिल बोरेल के बाद इस परिणाम को बोरेल लेम्मा के रूप में जाना जाता है।
यह फलन h भी समतल है; यह संवृत अंतराल [−1,1] पर 1 के बराबर होता है और विवृत अंतराल (−2,2) के बाहर नष्ट हो जाता है। h का उपयोग करते हुए, प्रत्येक प्राकृतिक संख्या n (शून्य सहित) के लिए समतल फलन को परिभाषित करें
जो [−1,1] पर एकपदी xn के साथ सहमत है और अंतराल (−2,2) के बाहर नष्ट हो जाता है। इसलिए, मूल बिंदु पर ψn का k-वाँ अवकलज संतुष्ट करता है
और परिबद्धता प्रमेय का तात्पर्य है कि ψn और ψn का प्रत्येक अवकलज परिबद्ध है। इसलिए, स्थिरांक
ψn के सर्वोच्च मानक को सम्मिलित करनाऔर इसके पहले n अवकल, अच्छी तरह से परिभाषित वास्तविक संख्याएँ हैं। माप किए गए फलनों को परिभाषित करें
श्रृंखला नियम के बार-बार प्रयोग से,
और शून्य पर, ψn के k-वें अवकल के लिए पूर्व परिणाम का उपयोग करना
यह दिखाना शेष है कि फलन
अच्छी तरह से परिभाषित है और पद-दर-अवधि में असीमित रूप से कई बार अवकलित किया जा सकता है।[2] इसके लिए, देखें कि प्रत्येक k के लिए
जहां शेष अनंत श्रृंखला अनुपात परीक्षण द्वारा अभिसरित होती है।
उच्च आयामों के लिए अनुप्रयोग
प्रत्येक त्रिज्या r > 0 के लिए,
यूक्लिडियन मानदंड के साथ ||x|| त्रिज्या आर की गोला (गणित) में समर्थन (गणित) के साथ n-आयामी यूक्लिडियन समष्टि पर एक समतल फलन को परिभाषित करता है, लेकिन होता है।
जटिल विश्लेषण
यह विकृति एक वास्तविक चर के अतिरिक्त अवकलनीय जटिल विश्लेषण के साथ नहीं हो सकती है। वास्तव में, सभी होलोमॉर्फिक(पूर्ण-सममितिक) फलन विश्लेषणात्मक होते हैं, इसलिए इस लेख में परिभाषित फलन f की विफलता विश्लेषणात्मक होने के बाद भी अधिकतम सीमा तक अवकल होने के बाद भी वास्तविक-चर और जटिल-चर विश्लेषण के बीच सबसे प्रभावशाली अंतरों में से एक का संकेत है।
ध्यान दें कि यद्यपि फलन f में वास्तविक रेखा पर सभी फलन के अवकल हैं, धनात्मक अर्ध-रेखा x > 0 से सम्मिश्र तल तक f की विश्लेषणात्मक निरंतरता, अर्थात फलन
मूल में एक अनिवार्य विलक्षणता है, और इसलिए यह निरंतर भी नहीं है, बहुत कम विश्लेषणात्मक है। महान पिकार्ड प्रमेय द्वारा, यह उत्पत्ति के प्रत्येक प्रतिवेश में असीमित रूप से कई बार प्रत्येक सम्मिश्र मान (शून्य के अपवाद के साथ) प्राप्त करता है।
यह भी देखें
- संघट्ट फलन
- फैबियस फलन
- समतल फलन
- मोलिफायर
टिप्पणियाँ
- ↑ Exercise 12 on page 418 in Walter Rudin, Real and Complex Analysis. McGraw-Hill, New Delhi 1980, ISBN 0-07-099557-5
- ↑ See e.g. Chapter V, Section 2, Theorem 2.8 and Corollary 2.9 about the differentiability of the limits of sequences of functions in Amann, Herbert; Escher, Joachim (2005), Analysis I, Basel: Birkhäuser Verlag, pp. 373–374, ISBN 3-7643-7153-6