वर्णक्रमीय क्रम

For खगोल विज्ञान में तारों का वर्गीकरण, see तारकीय वर्गीकरण.

तुल्य बीजगणित और बीजगणितीय सांस्थिति में, एक वर्णक्रमीय अनुक्रम क्रमिक सन्निकटन लेकर अनुरूपता समूहों की गणना करने का एक साधन है। वर्णक्रमीय अनुक्रम यथार्थ अनुक्रमों का एक सामान्यीकरण है, और Jean Leray (1946a, 1946b) द्वारा उनके परिचय के बाद से , वे महत्वपूर्ण संगणनात्मक उपकरण बन गए हैं, विशेष रूप से बीजीय सांस्थिति, बीजगणितीय ज्यामिति और समरूप बीजगणित में।

आविष्कार और प्रेरणा

बीजगणितीय सांस्थिति में समस्याओं से प्रेरित, जीन लेरे ने एक शेफ (गणित) की धारणा प्रस्तुत की और स्वयं को संगणना शेफ सह समरूपता की समस्या का सामना करना पड़ा। शेफ सह समरूपता की गणना करने के लिए, लेरे ने एक संगणनात्मक तकनीक प्रस्तुत की जिसे अब लेरे वर्णक्रमीय अनुक्रम के रूप में जाना जाता है। इसने एक शेफ के सह समरूपता समूहों और एक शेफ की प्रत्यक्ष प्रतिरूप के सह समरूपता समूहों के बीच एक संबंध दिया। संबंध में एक अनंत प्रक्रिया सम्मिलित थी। लेरे ने पाया कि ज़ारी रखने के सह समरूपता समूहों ने एक प्राकृतिक श्रृंखला सम्मिश्र का गठन किया, ताकि वह सह समरूपता के सह समरूपता को ले सकें। यह अभी भी मूल शेफ की सह समरूपता नहीं थी, परन्तु यह एक अर्थ में एक चरण और निकट था। सह समरूपता के सह समरूपता ने फिर से एक मिश्रित शृंखला का गठन किया, और इसके सह समरूपता ने एक मिश्रित शृंखला का निर्माण किया, और इसी प्रकार। इस अनंत प्रक्रिया की सीमा अनिवार्य रूप से वही थी जो मूल शेफ के सह समरूपता समूहों के रूप में थी।

शीघ्र ही यह समझा गया किया गया कि लेरे की संगणनात्मक तकनीक एक अधिक सामान्य घटना का एक उदाहरण थी। विभिन्न स्थितियों में वर्णक्रमीय अनुक्रम पाए गए, और उन्होंने अनुरूपता और सह समरूपता समूहों के बीच सम्मिश्र संबंध दिए, जो ज्यामितीय स्थितियों जैसे कंपन और बीजगणितीय स्थितियों से व्युत्पन्न प्रकार्यक से जुड़े थे। जबकि व्युत्पन्न श्रेणी की प्रारंभ के बाद से उनका सैद्धांतिक महत्व कम हो गया है, वे अभी भी सबसे प्रभावी संगणनात्मक उपकरण उपलब्ध हैं। यह तब भी सत्य है जब वर्णक्रमीय अनुक्रम के कई पद अगणनीय हैं।

दुर्भाग्य से, बड़ी मात्रा में सूचना वर्णक्रमीय अनुक्रमों में ले जाने के कारण, उन्हें समझना जटिल है। यह सूचना सामान्यतः एबेलियन समूहों या मॉड्यूल (गणित) के पद तीन जाली में निहित होती है। निपटने के लिए सबसे सरल स्थिति वे हैं जिनमें वर्णक्रमीय अनुक्रम अंततः पतन हो जाता है, जिसका अर्थ है कि अनुक्रम में आगे जाने से कोई नवीन सूचना नहीं मिलती है। यहां तक ​​कि जब ऐसा नहीं होता है, तब भी विभिन्न क्रमभंग से वर्णक्रमीय अनुक्रम से उपयोगी सूचना प्राप्त करना प्रायः संभव होता है।

औपचारिक परिभाषा

सह समरूपी वर्णक्रमीय अनुक्रम

एक एबेलियन श्रेणी को ठीक करें, जैसे कि एक वलय (गणित) पर मॉड्यूल (गणित) की श्रेणी, और एक गैर-ऋणात्मक पूर्णांक $r_{0}$। सह समरूपी वर्णक्रमीय अनुक्रम वस्तु $E_{r}$ और समरूपता $d_{r}:E_{r}\to E_{r}$ का अनुक्रम $\{E_{r},d_{r}\}_{r\geq r_{0}}$ है, जैसे कि प्रत्येक $r\geq r_{0}$ के लिए,

1. $d_{r}\circ d_{r}=0$,
2. $E_{r+1}\cong H_{*}(E_{r},d_{r})$, $d_{r}$ के संबंध में $E_{r}$ की समरूपता (गणित)।

सामान्यतः समरूपताओं को दबा दिया जाता है और हम इसके अतिरिक्त $E_{r+1}=H_{*}(E_{r},d_{r})$ लिखते हैं। एक वस्तु $E_{r}$को पत्रक (पृष्ठ के पत्रक के रूप में), या कभी-कभी एक पृष्ठ या पद कहा जाता है; एक समरूपता $d_{r}$ को सीमा प्रतिचित्र या अवकलन कहा जाता है। कभी-कभी $E_{r+1}$ को $E_{r}$ की व्युत्पन्न वस्तु कहा जाता है।

द्वि वर्गीकृत वर्णक्रमीय अनुक्रम

वस्तुतः वर्णक्रमीय अनुक्रम अधिकतर एक वलय (गणित) R (या द्वि वर्गीकृत शेफ (गणित) मॉड्यूल के वलय के एक शेफ पर) पर द्वि वर्गीकृत मॉड्यूल (गणित) की श्रेणी में होते हैं, अर्थात प्रत्येक पत्रक एक द्वि वर्गीकृत R-मॉड्यूल ${\textstyle E_{r}=\bigoplus _{p,q\in \mathbb {Z} ^{2}}E_{r}^{p,q}}$ है। तो इस स्थिति में एक सह-समरूपता वर्णक्रमीय अनुक्रम द्वि वर्गीकृत R-मॉड्यूल $\{E_{r}^{p,q}\}_{p,q}$ का अनुक्रम $\{E_{r},d_{r}\}_{r\geq r_{0}}$ है और प्रत्येक मॉड्यूल के लिए द्वि वर्गीकृत $(r,1-r)$ के समरूपता $d_{r}=(d_{r}^{p,q}:E_{r}^{p,q}\to E_{r}^{p+r,q-r+1})_{p,q\in \mathbb {Z} ^{2}}$ का प्रत्यक्ष योग है, जैसे कि प्रत्येक $r\geq r_{0}$ के लिए यह धारण करता है:

1. $d_{r}^{p+r,q-r+1}\circ d_{r}^{p,q}=0$,
2. $E_{r+1}\cong H_{*}(E_{r},d_{r})$।

यहाँ प्रयुक्त अंकन को पूरक घात कहा जाता है। कुछ लेखक इसके अतिरिक्त $E_{r}^{d,q}$ लिखते हैं , जहाँ $d=p+q$ कुल घात है। वर्णक्रमीय अनुक्रम के आधार पर, पहली पत्रक पर सीमा प्रतिचित्र में एक घात हो सकती है जो R = 0, R = 1, या R = 2 से मेल खाती है। उदाहरण के लिए, निस्यंदित किए गए सम्मिश्र के वर्णक्रमीय अनुक्रम के लिए, नीचे वर्णित, R₀ = 0, परन्तु ग्रोथेंडिक वर्णक्रमीय अनुक्रम के लिए, R₀ = 2। सामान्यतः R₀ शून्य, एक या दो है। ऊपर वर्णित अश्रेणीकृत स्थिति में, r₀ अप्रासंगिक है।

सजातीय वर्णक्रमीय अनुक्रम

अधिकतर जिन वस्तुओं के विषय में हम बात कर रहे हैं वे मिश्रित शृंखला हैं, जो अवरोही (जैसे ऊपर) या आरोही क्रम में होते हैं। बाद की स्थिति में, $E_{r}^{p,q}$ को $E_{p,q}^{r}$ और $d_{r}^{p,q}:E_{r}^{p,q}\to E_{r}^{p+r,q-r+1}$ के साथ $d_{p,q}^{r}:E_{p,q}^{r}\to E_{p-r,q+r-1}^{r}$, (द्विपद $(-r,r-1)$) के साथ प्रतिस्थापित करके, सह समरूपी स्थिति के अनुरूप एक तुल्य वर्णक्रमीय अनुक्रम की परिभाषा प्राप्त करता है।

एक श्रृंखला सम्मिश्र से वर्णक्रमीय अनुक्रम

अक्रमिक स्थिति में सबसे प्राथमिक उदाहरण एक मिश्रित शृंखला C• है। एक वस्तु C• मिश्रित शृंखला की एबेलियन श्रेणी में स्वाभाविक रूप से एक अवकलन d के साथ आता है। मान लीजिए R₀ = 0, और मान लीजिए E₀ C_• है। यह E₁ को सम्मिश्र H (C•) होने के लिए बाध्य करता है: iवें स्थान पर यह C _• का iवां समरूपता समूह है। इस नवीन सम्मिश्र पर एकमात्र प्राकृतिक अवकलन शून्य प्रतिचित्र है, इसलिए हम d₁ = 0 करते हैं। यह $E_{2}$ को $E_{1}$के बराबर बनाता है, और फिर से हमारा एकमात्र प्राकृतिक अवकलन शून्य प्रतिचित्र है। हमारी शेष सभी पत्रकों पर शून्य अवकलन डालने से वर्णक्रमीय क्रम मिलता है जिसकी पद हैं:

• E₀ = C•
• सभी R ≥ 1 के लिए E_r= H (C•)।

इस वर्णक्रमीय अनुक्रम की पद पहली पत्रक पर स्थिर होती हैं क्योंकि इसका एकमात्र असतहीय अवकल शून्यवाँ पत्रक पर था। फलस्वरूप, हम बाद के चरणों में और अधिक सूचना प्राप्त नहीं कर सकते हैं। सामान्यतः, बाद की पत्रक से उपयोगी सूचना प्राप्त करने के लिए, हमें $E_{r}$ पर अतिरिक्त संरचना की आवश्यकता होती है ।

प्रत्यक्षण

E₂ सह समरूपी वर्णक्रमीय अनुक्रम की पत्रक

एक द्वि वर्गीकृत वर्णक्रमीय अनुक्रम में ट्रैक रखने के लिए डेटा की विलक्षण मात्रा होती है, परन्तु एक सामान्य प्रत्यक्षण तकनीक है जो वर्णक्रमीय अनुक्रम की संरचना को स्पष्ट बनाती है। हमारे निकट तीन सूचकांक हैं, R, पी और q। एक वस्तु $E_{r}$को एक पुस्तक के $r^{th}$ विविध पृष्ठ के रूप में देखा जा सकता है। इन पत्रकों पर, हम p को क्षैतिज दिशा और q को उर्ध्वाधर दिशा मानेंगे। प्रत्येक जाली बिंदु पर हमारे निकट वस्तु $E_{r}^{p,q}$ है । अब अगले पृष्ठ की ओर मुड़ने का अर्थ है समरूपता लेना, अर्थात $r^{th}$ पृष्ठ $(r+1)^{th}$ पृष्ठ का एक उपभाग है। कुल घात n = p + q प्रत्येक पत्रक के पार तिरछे, उत्तर-पश्चिम से दक्षिण-पूर्व तक चलता है। समरूपी स्थिति में, अवकलों का द्विपद (−r, r − 1) होता है, इसलिए वे n से एक घटाते हैं। सह समरूपी स्थिति में, n एक से बढ़ जाता है। r के संबंध में अवकल प्रत्येक मोड़ के साथ अपनी दिशा बदलते हैं।

सह समरूपी वर्णक्रमीय अनुक्रम के चार पृष्ठ

लाल तीर पहले चतुर्थांश अनुक्रम की स्थिति को प्रदर्शित करता है (उदाहरण वर्णक्रमीय अनुक्रम देखें), जहां मात्र पहले चतुर्थांश की वस्तुएं गैर-शून्य हैं। पृष्ठों को पलटते समय, सभी अवकलनों का प्रांत या उपप्रांत शून्य हो जाता है।

गुण

श्रेणीबद्ध गुण

उपयोग वर्णक्रमीय अनुक्रमों का सम्मुचय एक श्रेणी बनाता है: वर्णक्रमीय अनुक्रमों का एक रूपवाद $f:E\to E'$ परिभाषा के अनुसार प्रतिचित्रों $f_{r}:E_{r}\to E'_{r}$ का एक संग्रह हैजो अवकलन के साथ संगत हैं, अर्थात $f_{r}\circ d_{r}=d'_{r}\circ f_{r}$, और दिए गए समरूपताओं के साथ क्रमशः E और E' के Rवें चरण और (R + 1) वें पत्रक के सह समरूपता के बीच: $f_{r+1}(E_{r+1})\,=\,f_{r+1}(H(E_{r}))\,=\,H(f_{r}(E_{r}))$। द्वि वर्गीकृत स्थिति में, उन्हेंक्रमस्थापनका भी सम्मान करना चाहिए: $f_{r}(E_{r}^{p,q})\subset {E'_{r}}^{p,q}.$

गुणक संरचना

एक कप उत्पाद सह समरूपता समूह को एक वलय (गणित) देता है, इसे एक सह समरूपता वलय में बदल देता है। इस प्रकार, वलय संरचना के साथ-साथ वर्णक्रमीय अनुक्रम पर विचार करना स्वाभाविक है। $E_{r}^{p,q}$ को सह समरूपी प्रकार का एक वर्णक्रमीय अनुक्रम होने दें। हम कहते हैं कि इसकी गुणात्मक संरचना है यदि (i) $E_{r}$ (द्वि वर्गीकृत)अवकल वर्गीकृत बीजगणित और (ii) $E_{r+1}$ पर गुणा सह समरूपता केमाध्यम से $E_{r}$ पर प्रेरित किया जाता है।

एक विशिष्ट उदाहरण एक कंपन $F\to E\to B$ के लिए उपयोग सेरे वर्णक्रमीय अनुक्रम है , जब गुणांक समूह एक वलय R है। इसमें फाइबर $E_{2}$-पृष्ठ के कप उत्पादों और आधार पर गुणक संरचना होती है । यद्यपि, सामान्यतःसीमित पद $E_{\infty }$ H (E; R) के लिए एक वर्गीकृत बीजगणित के रूप मेंसमरूपी नहीं है। गुणात्मक संरचना अनुक्रम पर अवकलन की गणना के लिए बहुत उपयोगी हो सकती है।

वर्णक्रमीय अनुक्रमों का निर्माण

वर्णक्रमीय दृश्यों का निर्माण विभिन्न विधियों से किया जा सकता है। बीजगणितीय सांस्थिति में, एक यथार्थ युग्म संभवतः निर्माण के लिए सबसे सामान्य उपकरण है। बीजगणितीय ज्यामिति में, वर्णक्रमीय अनुक्रम सामान्यतः उप शृंखला सम्मिश्रों के निस्पंदन से निर्मित होते हैं।

एक यथार्थ युग्म का वर्णक्रमीय अनुक्रम

Main article: यथार्थ युगल

वर्णक्रमीय अनुक्रमों के निर्माण के लिए एक और तकनीक विलियम शूमाकर मैसी की यथार्थ युग्मों की विधि है। बीजगणितीय सांस्थिति में यथार्थ युग्म विशेष रूप से सामान्य हैं। इसके अतिरिक्त वे अमूर्त बीजगणित में अलोकप्रिय हैं, जहां अधिकांश वर्णक्रमीय अनुक्रम निस्यंदित किए गए सम्मिश्रों से आते हैं।

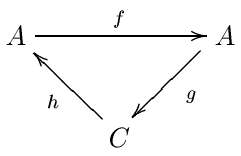
यथार्थ युग्मों को परिभाषित करने के लिए, हम फिर से एक एबेलियन श्रेणी से प्रारंभकरते हैं। पहले के जैसे, व्यवहार में यह सामान्यतः वलय के ऊपर दोगुने क्रमिक वाले मॉड्यूल की श्रेणी है। एक यथार्थ युग्म वस्तुओं की एक युग्म है (A, C), साथ में इन वस्तुओं के बीच तीन समरूपताएं हैं: f : A → A, g : A → C और h : C → A कुछ यथार्थ प्रतिबन्धों के अधीन:

• प्रतिरूप (गणित) f = कर्नेल (बीजगणित) g
• प्रतिरूप g = कर्नेल H
• प्रतिरूप H = कर्नेल f

हम इस डेटा को (A, C, f, g, h) द्वारा संक्षिप्त करेंगे। यथार्थ युग्म को सामान्यतः त्रिकोण के रूप में दर्शाया जाता है। हम देखेंगे किC वर्णक्रमीय अनुक्रम के E ₀ वपद से मेल खाता है और A कुछ सहायक डेटा है।

वर्णक्रमीय अनुक्रम की अगली पत्रक पर जाने के लिए, हम 'व्युत्पन्न युग्म' बनाएंगे। हम लोग तैयार हैं:

• d = g o H
• A' = f(A)
• C' = Ker d / Im d
• f' = f|_A', f से A' का प्रतिबंध
• h' : C' → A' h से प्रेरित है। यह देखना सरल है कि h ऐसे प्रतिचित्र को प्रेरित करता है।
• g' : A' → C' को तत्वों पर इस प्रकार परिभाषित किया गया है: A' में प्रत्येक के लिए , A में कुछ b के लिए a को f(b) के रूप में लिखें। g'(a) को C' में g(b) की प्रतिरूप के रूप में परिभाषित किया गया है। सामान्यतः , एबेलियन श्रेणियों के लिए एम्बेडिंग प्रमेयों में से एक का उपयोग करके g' का निर्माण किया जा सकता है।

यहां से यह जांचना सरल है कि (A', C', f', g', h ') एक यथार्थ युग्म है। C' वर्णक्रमीय अनुक्रम के E₁ पद से मेल खाता है। हम यथार्थ युग्म (A⁽ⁿ⁾, सी⁽ⁿ⁾, f⁽ⁿ⁾, g⁽ⁿ⁾, H⁽ⁿ⁾) प्राप्त करने के लिए इस प्रक्रिया को दोहरा सकते हैं।

वर्णक्रमीय अनुक्रम बनाने के लिए, E_n को C⁽ⁿ⁾ और D_n को G^{(n) o h(n) होने दें।}

इस पद्धति से निर्मित वर्णक्रमीय अनुक्रम

• सेरे वर्णक्रमीय अनुक्रम - एक कंपन की समरूपता की गणना (सह) करने के लिए उपयोग किया जाता है
• अत्यायाह-हिर्जेब्रूच वर्णक्रमीय अनुक्रम - असाधारण सह समरूपता सिद्धांतों की गणना (सह) समरूपता के लिए उपयोग किया जाता है, जैसे कि K-सिद्धांत
• बॉकस्टीन वर्णक्रमीय अनुक्रम।
• निस्यंदित किए गए सम्मिश्रों के वर्णक्रमीय क्रम

निस्यंदित किए गए सम्मिश्र का वर्णक्रमीय अनुक्रम

एक बहुत ही सामान्य प्रकार का वर्णक्रमीय अनुक्रम निस्यंदित (अमूर्त बीजगणित) उपशृंखला मिश्रित से आता है, क्योंकि यह स्वाभाविक रूप से एक बड़ी श्रेणी वाली वस्तु को प्रेरित करता है। अवरोही निस्पंदन ${\textstyle ...\supset \,F^{-2}C^{\bullet }\,\supset \,F^{-1}C^{\bullet }\supset F^{0}C^{\bullet }\,\supset \,F^{1}C^{\bullet }\,\supset \,F^{2}C^{\bullet }\,\supset \,F^{3}C^{\bullet }\,\supset ...\,}$ के साथ एक उपशृंखला मिश्रित $(C^{\bullet },d)$ पर विचार करें। हमें आवश्यकता है कि सीमा प्रतिचित्र निस्पंदन के अनुकूल हो, अर्थात ${\textstyle d(F^{p}C^{n})\subset F^{p}C^{n+1}}$, और यह कि निस्पंदन संपूर्ण है, अर्थात सभी ${\textstyle F^{p}C^{\bullet }}$ के समुच्चय का मिलन संपूर्ण श्रृंखला सम्मिश्र ${\textstyle C^{\bullet }}$ है। फिर ${\textstyle E_{0}^{p,q}=F^{p}C^{p+q}/F^{p+1}C^{p+q}}$ और ${\textstyle E_{1}^{p,q}=H^{p+q}(F^{p}C^{\bullet }/F^{p+1}C^{\bullet })}$ के साथ एक वर्णक्रमीय अनुक्रम स्थित है।। बाद में, हम यह भी मान लेंगे कि निस्पंदन हॉसडॉर्फ या अलग है, अर्थात सभी ${\textstyle F^{p}C^{\bullet }}$ के सम्मुचय का प्रतिच्छेदन शून्य है।

निस्यंदन उपयोगी है क्योंकि यह शून्य की निकटता का माप देता है: जैसे-जैसे p बढ़ता है, ${\textstyle F^{p}C^{\bullet }}$ शून्य के और निकट आता जाता है। हम इस निस्यंदित से एक वर्णक्रमीय अनुक्रम का निर्माण करेंगे जहां बाद की पत्रक में उपसीमाओं और उपचक्र मूल सम्मिश्र में उपसीमाओं और उपचक्र के निकट और निकट आते हैं। इस वर्णक्रमीय अनुक्रम को निस्पंदन घात p और पूरक घात q = n − p द्वारा दोगुना वर्गीकृत किया गया है।

निर्माण

$C^{\bullet }$ में मात्र एक श्रेणीकरण और एक निस्यंदित है, इसलिए हम पहले वर्णक्रमीय अनुक्रम के पहले पृष्ठ के लिए एक दोगुनी श्रेणीबद्ध वस्तु का निर्माण करते हैं। दूसरी श्रेणीकरण प्राप्त करने के लिए, हम निस्यंदित के संबंध में संबंधित क्रमिक वस्तु लेंगे। हम इसे एक असामान्य विधि से लिखेंगे जो $E_{1}$ चरण पर उचित होगा:

$Z_{-1}^{p,q}=Z_{0}^{p,q}=F^{p}C^{p+q}$

$B_{0}^{p,q}=0$

$E_{0}^{p,q}={\frac {Z_{0}^{p,q}}{B_{0}^{p,q}+Z_{-1}^{p+1,q-1}}}={\frac {F^{p}C^{p+q}}{F^{p+1}C^{p+q}}}$

$E_{0}=\bigoplus _{p,q\in \mathbf {Z} }E_{0}^{p,q}$

चूँकि हमने माना कि सीमा प्रतिचित्र निस्पंदन के साथ संगत था, $E_{0}$ एक दोगुनी वर्गीकृत वस्तु है और $E_{0}$ पर एक प्राकृतिक दोगुनी वर्गीकृत सीमा प्रतिचित्र $d_{0}$ है। $E_{1}$प्राप्त करने के लिए $E_{0}$ की समरूपता लेते हैं।

${\bar {Z}}_{1}^{p,q}=\ker d_{0}^{p,q}:E_{0}^{p,q}\rightarrow E_{0}^{p,q+1}=\ker d_{0}^{p,q}:F^{p}C^{p+q}/F^{p+1}C^{p+q}\rightarrow F^{p}C^{p+q+1}/F^{p+1}C^{p+q+1}$

${\bar {B}}_{1}^{p,q}={\mbox{im }}d_{0}^{p,q-1}:E_{0}^{p,q-1}\rightarrow E_{0}^{p,q}={\mbox{im }}d_{0}^{p,q-1}:F^{p}C^{p+q-1}/F^{p+1}C^{p+q-1}\rightarrow F^{p}C^{p+q}/F^{p+1}C^{p+q}$

$E_{1}^{p,q}={\frac {{\bar {Z}}_{1}^{p,q}}{{\bar {B}}_{1}^{p,q}}}={\frac {\ker d_{0}^{p,q}:E_{0}^{p,q}\rightarrow E_{0}^{p,q+1}}{{\mbox{im }}d_{0}^{p,q-1}:E_{0}^{p,q-1}\rightarrow E_{0}^{p,q}}}$

$E_{1}=\bigoplus _{p,q\in \mathbf {Z} }E_{1}^{p,q}=\bigoplus _{p,q\in \mathbf {Z} }{\frac {{\bar {Z}}_{1}^{p,q}}{{\bar {B}}_{1}^{p,q}}}$

ध्यान दें कि ${\bar {Z}}_{1}^{p,q}$ और ${\bar {B}}_{1}^{p,q}$ को

$Z_{1}^{p,q}=\ker d_{0}^{p,q}:F^{p}C^{p+q}\rightarrow C^{p+q+1}/F^{p+1}C^{p+q+1}$

$B_{1}^{p,q}=({\mbox{im }}d_{0}^{p,q-1}:F^{p}C^{p+q-1}\rightarrow C^{p+q})\cap F^{p}C^{p+q}$

के $E_{0}^{p,q}$ में प्रतिरूपों के रूप में लिखा जा सकता है और फिर हमारे निकट

$E_{1}^{p,q}={\frac {Z_{1}^{p,q}}{B_{1}^{p,q}+Z_{0}^{p+1,q-1}}}$ है।

$Z_{1}^{p,q}$ वस्तुतः वे तत्व हैं जो अवकलन निस्पंदन में एक स्तर ऊपर धकेलते हैं, और $B_{1}^{p,q}$ वस्तुतः उन तत्वों की प्रतिरूप हैं जो अवकलन निस्पंदन में शून्य स्तर ऊपर धकेलते हैं। इससे पता चलता है कि हमें $Z_{r}^{p,q}$ को उन तत्वों के रूप में चुनना चाहिए जो अवकलन निस्पंदन में r स्तरों को ऊपर धकेलता है और $B_{r}^{p,q}$ उन तत्वों की प्रतिरूप है जो अवकलन निस्पंदन में r-1 स्तरों को ऊपर धकेलता है। दूसरे पदों में, वर्णक्रमीय अनुक्रम को

$Z_{r}^{p,q}=\ker d_{0}^{p,q}:F^{p}C^{p+q}\rightarrow C^{p+q+1}/F^{p+r}C^{p+q+1}$

$B_{r}^{p,q}=({\mbox{im }}d_{0}^{p-r+1,q+r-2}:F^{p-r+1}C^{p+q-1}\rightarrow C^{p+q})\cap F^{p}C^{p+q}$

$E_{r}^{p,q}={\frac {Z_{r}^{p,q}}{B_{r}^{p,q}+Z_{r-1}^{p+1,q-1}}}$

को संतुष्ट करना चाहिए और हमारे निकट संबंध

$B_{r}^{p,q}=d_{0}^{p,q}(Z_{r-1}^{p-r+1,q+r-2})$ होना चाहिए।

इसे समझने के लिए, हमें प्रत्येक $E_{r}$ पर एक अवकलन $d_{r}$ खोजना होगा और यह सत्यापित करना होगा कि यह समरूपी समरूपता को $E_{r+1}$ की ओर ले जाता है। अवकलन

$d_{r}^{p,q}:E_{r}^{p,q}\rightarrow E_{r}^{p+r,q-r+1}$

को $C^{p+q}$ $d$ पर परिभाषित मूल अवकलन d को उपवस्तु $Z_{r}^{p,q}$ तक सीमित करके परिभाषित किया गया है। यह जाँचना सरल है कि इस अवकलन के संबंध में $E_{r}$ की समरूपता $E_{r+1}$है, इसलिए यह वर्णक्रमीय अनुक्रम देता है। दुर्भाग्य से, अवकलन बहुत स्पष्ट नहीं है। वर्णक्रमीय अनुक्रम को सफलतापूर्वक लागू करने के लिए अवकलन निर्धारित करना या उनके निकट काम करने के विधि खोजना मुख्य चुनौतियों में से एक है।

इस पद्धति से निर्मित वर्णक्रमीय अनुक्रम

• हॉज-डे राम वर्णक्रमीय अनुक्रम
• एक दोहरे सम्मिश्र का वर्णक्रमीय क्रम
• मिश्रित हॉज संरचनाओं के निर्माण के लिए उपयोग किया जा सकता है

एक दोहरे सम्मिश्र का वर्णक्रमीय अनुक्रम

एक अन्य सामान्य वर्णक्रमीय अनुक्रम एक दोहरे सम्मिश्र का वर्णक्रमीय क्रम है। एक द्वि सम्मिश्र सभी पूर्णांकों i और j के लिए दो अवकलन, वस्तुओं का एक संग्रह है C_i,j के साथ , d ^I और d ^{II के साथ वस्तुओं Cij का एक संग्रह है। d I को i घटता माना जाता है, और d II को j घटता हुआ माना जाता है। इसके अतिरिक्त, हम मानते हैं कि अवकलन विरोधी आवागमन है, ताकि d i d II + d II d I = 0। हमारा लक्ष्य पुनरावृत्त समरूपता $H_{i}^{I}(H_{j}^{II}(C_{\bullet ,\bullet }))$ और $H_{j}^{II}(H_{i}^{I}(C_{\bullet ,\bullet }))$ की तुलना करना है। हम अपने द्वि सम्मिश्र को दो अलग-अलग विधियों से निस्यंदित करके ऐसा करेंगे। यहां हमारे निस्यंदित हैं:}

$(C_{i,j}^{I})_{p}={\begin{cases}0&{\text{if }}i<p\\C_{i,j}&{\text{if }}i\geq p\end{cases}}$

$(C_{i,j}^{II})_{p}={\begin{cases}0&{\text{if }}j<p\\C_{i,j}&{\text{if }}j\geq p\end{cases}}$

वर्णक्रमीय अनुक्रम प्राप्त करने के लिए, हम पिछले उदाहरण को कम कर देंगे। हम कुल सम्मिश्र T(C_•,•) को उस सम्मिश्र के रूप में परिभाषित करते हैं जिसका n'वाँ पद$\bigoplus _{i+j=n}C_{i,j}$ और जिसका अवकलन d^I+ d^II है। ^{यह एक सम्मिश्र है क्योंकि d I और d II विरोधी आवागमन अवकल हैं। C_{i,j पर दो निस्यंदित} कुल सम्मिश्र पर दो _{निस्यंदक} देते हैं:}

$T_{n}(C_{\bullet ,\bullet })_{p}^{I}=\bigoplus _{i+j=n \atop i>p-1}C_{i,j}$

$T_{n}(C_{\bullet ,\bullet })_{p}^{II}=\bigoplus _{i+j=n \atop j>p-1}C_{i,j}$

यह दिखाने के लिए कि ये वर्णक्रमीय अनुक्रम पुनरावृत्त समरूपता के विषय में सूचना देते हैं, हम T(C•,•) पर I निस्पंदन के E^{0, E1, औरE2 के प्रतिबन्ध पर काम करेंगे। E0 पद स्पष्ट है:}

${}^{I}E_{p,q}^{0}=T_{n}(C_{\bullet ,\bullet })_{p}^{I}/T_{n}(C_{\bullet ,\bullet })_{p+1}^{I}=\bigoplus _{i+j=n \atop i>p-1}C_{i,j}{\Big /}\bigoplus _{i+j=n \atop i>p}C_{i,j}=C_{p,q},$

जहाँ n = p + q।

E¹ ज्ञात करने के लिए, हमें ^{E0 पर dI + d II निर्धारित करने की आवश्यकता है। पर द्वितीय </उप>। ध्यान दें कि n के संबंध में अवकलन की घात -1 होनी चाहिए, इसलिए हमें एक प्रतिचित्र}

$d_{p,q}^{I}+d_{p,q}^{II}:T_{n}(C_{\bullet ,\bullet })_{p}^{I}/T_{n}(C_{\bullet ,\bullet })_{p+1}^{I}=C_{p,q}\rightarrow T_{n-1}(C_{\bullet ,\bullet })_{p}^{I}/T_{n-1}(C_{\bullet ,\bullet })_{p+1}^{I}=C_{p,q-1}$ मिलता है

फलस्वरूप, E⁰ पर अवकलन प्रतिचित्र C_p,q → सी_p,q−1 d ^I + d^{II द्वारा प्रेरित है। परन्तु d I के निकट ऐसे प्रतिचित्र को प्रेरित करने के लिए अनुचित घात है, इसलिए d I को E0 पर शून्य होना चाहिए। इसका अर्थ है कि अवकलन पूर्णतः dII है, इसलिए हमें}

${}^{I}E_{p,q}^{1}=H_{q}^{II}(C_{p,\bullet })$ मिलता है।

E² ज्ञात करने के लिए, हमें

$d_{p,q}^{I}+d_{p,q}^{II}:H_{q}^{II}(C_{p,\bullet })\rightarrow H_{q}^{II}(C_{p+1,\bullet })$ ज्ञात करना होगा

क्योंकि E¹ यथार्थ में d ^II के संबंध में समरूपता थी, d ^II E^{1 पर शून्य है। फलस्वरूप, हमें}

${}^{I}E_{p,q}^{2}=H_{p}^{I}(H_{q}^{II}(C_{\bullet ,\bullet }))$ मिलता है।

अन्य निस्पंदन का उपयोग करने से हमें समान E² पद

${}^{II}E_{p,q}^{2}=H_{q}^{II}(H_{p}^{I}(C_{\bullet ,\bullet }))$ के साथ एक अलग वर्णक्रमीय क्रम मिलता है :

इन दो वर्णक्रमीय अनुक्रमों के बीच संबंध खोजने के लिए क्या बचा है। यह पता चलेगा कि जैसे-जैसे r बढ़ता है, उपयोगी तुलना की अनुमति देने के लिए दो क्रम समान हो जाएंगे।

अभिसरण, पतन और अभिसरण

चक्रों और सीमाओं के निस्पंदन के रूप में व्याख्या

माना कि R = 1 से प्रारंभ होकर E_r एक वर्णक्रमीय क्रम है। फिर उपवस्तु

$0=B_{0}\subset B_{1}\subset B_{2}\subset \dots \subset B_{r}\subset \dots \subset Z_{r}\subset \dots \subset Z_{2}\subset Z_{1}\subset Z_{0}=E_{1}$

का अनुक्रम होता है जैसे कि $E_{r}\simeq Z_{r-1}/B_{r-1}$; वस्तुतः, पुनरावर्ती रूप से हम $Z_{0}=E_{1},B_{0}=0$ और $Z_{r},B_{r}$ होने देते हैं ताकि $E_{r}{\overset {d_{r}}{\to }}E_{r}$ कर्नेल और$Z_{r}/B_{r-1},B_{r}/B_{r-1}$ की प्रतिरूप हो।

फिर हम $Z_{\infty }=\cap _{r}Z_{r},B_{\infty }=\cup _{r}B_{r}$ और

$E_{\infty }=Z_{\infty }/B_{\infty }$;

देते हैं: इसे सीमांत पद कहते हैं। (अवश्य, इस प्रकार के $E_{\infty }$ को श्रेणी में मौजूद होने की आवश्यकता नहीं है, परन्तु यह सामान्यतः एक गैर-समस्या है क्योंकि उदाहरण के लिए मॉड्यूल की श्रेणी में ऐसी सीमाएं स्थित हैं या चूंकि व्यवहार में एक वर्णक्रमीय अनुक्रम पतित होने की प्रवृत्ति के साथ काम करता है; ऊपर दिए गए क्रम में मात्र सूक्ष्म रूप से कई समावेशन हैं।)

अभिसरण की पद

हम कहते हैं कि वर्णक्रमीय अनुक्रम निर्बल रूप से अभिसरण करता है यदि प्रत्येक $n$ के लिए एक निस्पंदन $F^{\bullet }H^{n}$ के साथ एक वर्गीकृत वस्तु $H^{\bullet }$ है, और प्रत्येक $p$ के लिए एक समरूपता $E_{\infty }^{p,q}\cong F^{p}H^{p+q}/F^{p+1}H^{p+q}$ स्थित है। यह $H^{\bullet }$ में परिवर्तित हो जाता है यदि निस्पंदन $F^{\bullet }H^{n}$ हौसडॉर्फ है, अर्थात$\cap _{p}F^{p}C^{\bullet }=0$। हम

$E_{r}^{p,q}\Rightarrow _{p}E_{\infty }^{n}$

लिखते हैं जिसका अर्थ है कि जब भी p + q = n, $E_{r}^{p,q}$ ,$E_{\infty }^{p,q}$ में परिवर्तित होता है। हम कहते हैं कि एक वर्णक्रमीय अनुक्रम $E_{r}^{p,q}$ $E_{\infty }^{p,q}$ से जुड़ा हुआ है यदि प्रत्येक $p,q$ के लिए $r(p,q)$ ऐसा है कि सभी $r\geq r(p,q)$, $E_{r}^{p,q}=E_{r(p,q)}^{p,q}$के लिए। तब $E_{r(p,q)}^{p,q}=E_{\infty }^{p,q}$ सीमित पद है। वर्णक्रमीय क्रम नियमित है या $r_{0}$ पर पतित होता है यदि अवकलन $d_{r}^{p,q}$ सभी $r\geq r_{0}$ के लिए शून्य है। यदि विशेष रूप से $r_{0}\geq 2$ है, जैसे कि $r_{0}^{th}$ पत्रक एक पंक्ति या एक स्तंभ पर केंद्रित होती है, तो हम कहते हैं कि यह पतित हो जाती है। प्रतीकों में हम लिखते हैं:

$E_{r}^{p,q}\Rightarrow _{p}E_{\infty }^{p,q}$

p निस्पंदन सूचकांक को इंगित करता है। $E_{2}^{p,q}$ पद आधार के बाईं ओर लिखना बहुत सामान्य है, क्योंकि यह अधिकांश वर्णक्रमीय अनुक्रमों का सबसे उपयोगी पद है। एक अनिस्यंदित मिश्रित शृंखला का वर्णक्रमीय अनुक्रम पहली पत्रक पर घटता है (पहला उदाहरण देखें): चूँकि शून्यवाँ पत्रक के बाद कुछ भी नहीं होता है, प्रतिबंधक पत्रक $E_{\infty }$ $E_{1}$ के समान है।

वर्णक्रमीय अनुक्रम का पांच-पद का यथार्थ अनुक्रम कुछ निम्न-घात प्रतिबन्धों और E_∞ प्रतिबन्धों से संबंधित है।

अध: पतन के उदाहरण

निस्यंदित किए गए सम्मिश्र का वर्णक्रमीय अनुक्रम, जारी

ध्यान दें कि हमारे निकट समावेशन की एक श्रृंखला है:

$Z_{0}^{p,q}\supseteq Z_{1}^{p,q}\supseteq Z_{2}^{p,q}\supseteq \cdots \supseteq B_{2}^{p,q}\supseteq B_{1}^{p,q}\supseteq B_{0}^{p,q}$

हम पूछ सकते हैं कि क्या होता है यदि हम

$Z_{\infty }^{p,q}=\bigcap _{r=0}^{\infty }Z_{r}^{p,q},$

$B_{\infty }^{p,q}=\bigcup _{r=0}^{\infty }B_{r}^{p,q},$

$E_{\infty }^{p,q}={\frac {Z_{\infty }^{p,q}}{B_{\infty }^{p,q}+Z_{\infty }^{p+1,q-1}}}$ को परिभाषित करते हैं।

$E_{\infty }^{p,q}$ इस वर्णक्रमीय अनुक्रम के निरस्तीकरण के लिए एक स्वाभाविक प्रत्याशी है। अभिसरण स्वत: नहीं होता है, परन्तु कई स्थितियों में होता है। विशेष रूप से, यदि निस्पंदन परिमित है और इसमें ठीक r असतहीय चरण होते हैं, तो वर्णक्रमीय क्रम rवे पत्रक के बाद पतित हो जाता है। अभिसरण तब भी होता है जब सम्मिश्र और निस्यंदित दोनों नीचे से बंधे होते हैं या दोनों ऊपर से बंधे होते हैं।

अधिक विस्तार से हमारे वर्णक्रमीय अनुक्रम के निरस्तीकरण का वर्णन करने के लिए, ध्यान दें कि हमारे निकट सूत्र हैं:

$Z_{\infty }^{p,q}=\bigcap _{r=0}^{\infty }Z_{r}^{p,q}=\bigcap _{r=0}^{\infty }\ker(F^{p}C^{p+q}\rightarrow C^{p+q+1}/F^{p+r}C^{p+q+1})$

$B_{\infty }^{p,q}=\bigcup _{r=0}^{\infty }B_{r}^{p,q}=\bigcup _{r=0}^{\infty }({\mbox{im }}d^{p,q-r}:F^{p-r}C^{p+q-1}\rightarrow C^{p+q})\cap F^{p}C^{p+q}$

यह देखने के लिए कि $Z_{\infty }^{p,q}$ का क्या तात्पर्य है याद रखें कि हमने मान लिया था कि निस्पंदन अलग हो गया था। इसका तात्पर्य यह है कि जैसे-जैसे r बढ़ता है, कर्नेल सिकुड़ती जाती है, जब तक कि हमारे निकट $Z_{\infty }^{p,q}=\ker(F^{p}C^{p+q}\rightarrow C^{p+q+1})$ नहीं रह जाती। $B_{\infty }^{p,q}$ के लिए , याद रखें कि हमने माना था कि निस्यंदित संपूर्ण था। इसका तात्पर्य यह है कि जैसे-जैसे r बढ़ता है, तब तक प्रतिरूप बढ़ते हैं जब तक हम $B_{\infty }^{p,q}={\text{im }}(C^{p+q-1}\rightarrow C^{p+q})\cap F^{p}C^{p+q}$ तक नहीं पहुँच जाते। हम निष्कर्ष निकालते हैं कि

$E_{\infty }^{p,q}={\mbox{gr}}_{p}H^{p+q}(C^{\bullet })$,

अर्थात्, वर्णक्रमीय अनुक्रम का निरसन, C के (p+q)वें अनुरूपता का pवां श्रेणीबद्ध भाग है। यदि हमारा वर्णक्रमीय अनुक्रम अभिसरण करता है, तो हम यह निष्कर्ष निकालते हैं कि:

$E_{r}^{p,q}\Rightarrow _{p}H^{p+q}(C^{\bullet })$

लंबे यथार्थ क्रम

निस्यंदित किए गए सम्मिश्र के वर्णक्रमीय अनुक्रम का उपयोग करके, हम लंबे यथार्थ अनुक्रमों के अस्तित्व को प्राप्त कर सकते हैं। उपशृंखला मिश्रित का संक्षिप्त यथार्थ अनुक्रम 0 → A ^• → B^• → C• → 0 चुनें, और पहले प्रतिचित्र को f^• :A^• → B^• कहते हैं। हमें अनुरूपता वस्तु Hⁿ(A^•) → Hⁿ(B^•) → Hⁿ(C•) के प्राकृतिक प्रतिचित्र मिलते हैं, और हम जानते हैं कि यह ठीक बीच में है। हम संयोजक समरूपता को खोजने के लिए निस्यंदित किए गए सम्मिश्र के वर्णक्रमीय अनुक्रम का उपयोग करेंगे और यह सिद्ध करने के लिए कि परिणामी अनुक्रम यथार्थ है। प्रारंभकरने के लिए, हम B^•:

$F^{0}B^{n}=B^{n}$

$F^{1}B^{n}=A^{n}$

$F^{2}B^{n}=0$ निस्यंदित करते हैं

यह:

$E_{0}^{p,q}={\frac {F^{p}B^{p+q}}{F^{p+1}B^{p+q}}}={\begin{cases}0&{\text{if }}p<0{\text{ or }}p>1\\C^{q}&{\text{if }}p=0\\A^{q+1}&{\text{if }}p=1\end{cases}}$

$E_{1}^{p,q}={\begin{cases}0&{\text{if }}p<0{\text{ or }}p>1\\H^{q}(C^{\bullet })&{\text{if }}p=0\\H^{q+1}(A^{\bullet })&{\text{if }}p=1\end{cases}}$ देता है

अवकल में द्विपद (1, 0) होता है, इसलिए d_0,q: H^q(C•) → H^q+1(A)। ये स्नेक लेम्मा से संयोजक समरूपता हैं, और प्रतिचित्र A^• → B^• → C• के साथ, वे एक क्रम देते हैं:

$\cdots \rightarrow H^{q}(B^{\bullet })\rightarrow H^{q}(C^{\bullet })\rightarrow H^{q+1}(A^{\bullet })\rightarrow H^{q+1}(B^{\bullet })\rightarrow \cdots$

यह दिखाना शेष है कि यह क्रम A और C स्थान पर यथार्थ है। ध्यान दें कि यह वर्णक्रमीय क्रम E₂ पद पर पतित होता है क्योंकि अवकलों का द्विपद (2, −1) होता है। फलस्वरूप, E₂ पद E_∞ पद के समान है :

$E_{2}^{p,q}\cong {\text{gr}}_{p}H^{p+q}(B^{\bullet })={\begin{cases}0&{\text{if }}p<0{\text{ or }}p>1\\H^{q}(B^{\bullet })/H^{q}(A^{\bullet })&{\text{if }}p=0\\{\text{im }}H^{q+1}f^{\bullet }:H^{q+1}(A^{\bullet })\rightarrow H^{q+1}(B^{\bullet })&{\text{if }}p=1\end{cases}}$

परन्तु हमारे निकट E₂ पद का प्रत्यक्ष वर्णन E₁ पद की समरूपता के रूप में भी है। ये दो विवरण समरूपी होने चाहिए:

$H^{q}(B^{\bullet })/H^{q}(A^{\bullet })\cong \ker d_{0,q}^{1}:H^{q}(C^{\bullet })\rightarrow H^{q+1}(A^{\bullet })$

${\text{im }}H^{q+1}f^{\bullet }:H^{q+1}(A^{\bullet })\rightarrow H^{q+1}(B^{\bullet })\cong H^{q+1}(A^{\bullet })/({\mbox{im }}d_{0,q}^{1}:H^{q}(C^{\bullet })\rightarrow H^{q+1}(A^{\bullet }))$

पूर्व C स्थान पर यथार्थता देता है, और बाद वाला A स्थान पर यथार्थता देता है।

एक दोहरे सम्मिश्र का वर्णक्रमीय अनुक्रम, जारी

निस्यंदित सम्मिश्र के लिए आधार का उपयोग करते हुए, हम पाते हैं कि:

$H_{p}^{I}(H_{q}^{II}(C_{\bullet ,\bullet }))\Rightarrow _{p}H^{p+q}(T(C_{\bullet ,\bullet }))$

$H_{q}^{II}(H_{p}^{I}(C_{\bullet ,\bullet }))\Rightarrow _{q}H^{p+q}(T(C_{\bullet ,\bullet }))$

सामान्यतः , H^p+q(T(C•_,•)) पर दो श्रेणीकरण अलग हैं। इसके अतिरिक्त, इन दो वर्णक्रमीय अनुक्रमों से उपयोगी सूचना प्राप्त करना अभी भी संभव है।

Tor की क्रमविनिमेयता

R को वलय होने दें, M को दाएँ R-मॉड्यूल और n को बाएँ R-मॉड्यूल होने दें। याद रखें कि टेंसर उत्पाद के व्युत्पन्न प्रकार्यक को टॉर फलन के रूप में दर्शाया गया है। टॉर को इसके पहले तर्क के प्रक्षेपी संकल्प का उपयोग करके परिभाषित किया गया है। यद्यपि, यह पता चला है कि $\operatorname {Tor} _{i}(M,N)=\operatorname {Tor} _{i}(N,M)$। जबकि यह वर्णक्रमीय अनुक्रम के बिना सत्यापित किया जा सकता है, यह वर्णक्रमीय अनुक्रमों के साथ बहुत सरल है।

क्रमशः M और N के प्रक्षेपी विभेदन $P_{\bullet }$ और $Q_{\bullet }$ चुनें। इन्हें ऐसे सम्मिश्रों के रूप में मानें जो क्रमशः d और ई के अवकलन वाले ऋणात्मक घात में लुप्त हो जाते हैं। हम एक द्वि सम्मिश्र का निर्माण कर सकते हैं जिसकी पद $C_{i,j}=P_{i}\otimes Q_{j}$ हैं और जिनके अवकलन $d\otimes 1$ और $(-1)^{i}(1\otimes e)$ हैं। (-1 का कारक इतना है कि अवकलन विरोधी आवागमन है।) चूंकि प्रक्षेपी मॉड्यूल समतल हैं, एक प्रक्षेपी मॉड्यूल के साथ टेंसर उत्पाद लेना अनुरूपता लेने के साथ प्रारंभहोता है, इसलिए हम प्राप्त करते हैं:

$H_{p}^{I}(H_{q}^{II}(P_{\bullet }\otimes Q_{\bullet }))=H_{p}^{I}(P_{\bullet }\otimes H_{q}^{II}(Q_{\bullet }))$

$H_{q}^{II}(H_{p}^{I}(P_{\bullet }\otimes Q_{\bullet }))=H_{q}^{II}(H_{p}^{I}(P_{\bullet })\otimes Q_{\bullet })$

चूंकि दो सम्मिश्र संकल्प हैं, उनकी अनुरूपता घात शून्य के बाहर लुप्त हो जाती है। घात शून्य में, हम

$H_{p}^{I}(P_{\bullet }\otimes N)=\operatorname {Tor} _{p}(M,N)$

$H_{q}^{II}(M\otimes Q_{\bullet })=\operatorname {Tor} _{q}(N,M)$ के साथ रह जाते हैं

विशेष रूप से, $E_{p,q}^{2}$ पद पंक्ति q = 0 (I वर्णक्रमीय अनुक्रम के लिए) और p = 0 (II वर्णक्रमीय अनुक्रम के लिए) को छोड़कर लुप्त हो जाते हैं। इसका तात्पर्य यह है कि वर्णक्रमीय क्रम दूसरी पत्रक पर पतित हो जाता है, इसलिए E^∞ पद E ² प्रतिबन्धों के लिए तुल्याकारी हैं:

$\operatorname {Tor} _{p}(M,N)\cong E_{p}^{\infty }=H_{p}(T(C_{\bullet ,\bullet }))$

$\operatorname {Tor} _{q}(N,M)\cong E_{q}^{\infty }=H_{q}(T(C_{\bullet ,\bullet }))$

अंत में, जब p और q बराबर होते हैं, तो दाएँ हाथ की दो भुजाएँ बराबर होती हैं, और Tor की क्रमविनिमेयता इस प्रकार होती है।

हल निकालने के उदाहरण

प्रथम-चतुर्थांश पत्रक

एक वर्णक्रमीय अनुक्रम पर विचार करें जहाँ $E_{r}^{p,q}$ कुछ $p_{0}$ से कम सभी $p$ के लिए और कुछ $q_{0}$ से कम सभी $q$ के लिए लुप्त हो जाता है। यदि $p_{0}$ और $q_{0}$ को शून्य के रूप में चुना जा सकता है, तो इसे प्रथम-चतुर्थांश वर्णक्रमीय अनुक्रम कहा जाता है। क्रम समाप्त हो जाता है क्योंकि $E_{r+i}^{p,q}=E_{r}^{p,q}$ सभी $i\geq 0$ लिए धारण करता है यदि $r>p$ और $r>q+1$। इसे देखने के लिए, ध्यान दें कि माने गए स्थितियों के लिए या तो अवकलन का प्रांत या उपप्रांत शून्य है। दृश्य पदों में, पत्रक एक बढ़ती हुई आयत में स्थिर हो जाती हैं (ऊपर चित्र देखें)। यद्यपि, वर्णक्रमीय अनुक्रम को पतित होने की आवश्यकता नहीं है, क्योंकि अवकलन प्रतिचित्र सभी एक बार में शून्य नहीं हो सकते हैं। इसी प्रकार, वर्णक्रमीय क्रम भी अभिसरण करता है यदि $E_{r}^{p,q}$ कुछ $p_{0}$से अधिक सभी $p$ के लिए लुप्त हो जाता है और कुछ $q_{0}$ से अधिक सभी $q$ के लिए लुप्त हो जाता है।

2 गैर-शून्य आसन्न स्तंभ

मान लीजिए कि $E_{p,q}^{r}$ एक सजातीय वर्णक्रमीय अनुक्रम है जैसे कि $E_{p,q}^{2}=0$ 0, 1 को छोड़कर सभी p के लिए है। दृष्टिगत रूप से, यह $E^{2}$-पृष्ठ

${\begin{matrix}&\vdots &\vdots &\vdots &\vdots &\\\cdots &0&E_{0,2}^{2}&E_{1,2}^{2}&0&\cdots \\\cdots &0&E_{0,1}^{2}&E_{1,1}^{2}&0&\cdots \\\cdots &0&E_{0,0}^{2}&E_{1,0}^{2}&0&\cdots \\\cdots &0&E_{0,-1}^{2}&E_{1,-1}^{2}&0&\cdots \\&\vdots &\vdots &\vdots &\vdots &\end{matrix}}$ के साथ वर्णक्रमीय अनुक्रम है

दूसरे पृष्ठ पर अवकलन की घात (-2, 1) है, इसलिए वे

$d_{p,q}^{2}:E_{p,q}^{2}\to E_{p-2,q+1}^{2}$ के रूप में हैं

ये प्रतिचित्र सभी शून्य हैं क्योंकि वे

$d_{0,q}^{2}:E_{0,q}^{2}\to 0$, $d_{1,q}^{2}:E_{1,q}^{2}\to 0$

हैं इसलिए वर्णक्रमीय अनुक्रम पतित होता है: $E^{\infty }=E^{2}$। कहते हैं, यह एक निस्पंदन

$0=F_{-1}H_{n}\subset F_{0}H_{n}\subset \dots \subset F_{n}H_{n}=H_{n}$

के साथ $H_{*}$ में परिवर्तित होता है जैसे कि $E_{p,q}^{\infty }=F_{p}H_{p+q}/F_{p-1}H_{p+q}$। तब $F_{0}H_{n}=E_{0,n}^{2}$, $F_{1}H_{n}/F_{0}H_{n}=E_{1,n-1}^{2}$, $F_{2}H_{n}/F_{1}H_{n}=0$, $F_{3}H_{n}/F_{2}H_{n}=0$, आदि। इस प्रकार, यथार्थ क्रम है:

$0\to E_{0,n}^{2}\to H_{n}\to E_{1,n-1}^{2}\to 0$।

अगला, मान लीजिए कि $E_{p,q}^{r}$ एक वर्णक्रमीय अनुक्रम है जिसके दूसरे पृष्ठ में मात्र दो पंक्तियाँ q = 0, 1 हैं। यह दूसरे पृष्ठ पर पतित होने की आवश्यकता नहीं है, परन्तु यह अभी भी तीसरे पृष्ठ पर पतित होता है क्योंकि अवकलन में घात (-3, 2) होती है। टिप्पणी $E_{p,0}^{3}=\operatorname {ker} (d:E_{p,0}^{2}\to E_{p-2,1}^{2})$, क्योंकि भाजक शून्य है। इसी प्रकार, $E_{p,1}^{3}=\operatorname {coker} (d:E_{p+2,0}^{2}\to E_{p,1}^{2})$। इस प्रकार,

$0\to E_{p,0}^{\infty }\to E_{p,0}^{2}{\overset {d}{\to }}E_{p-2,1}^{2}\to E_{p-2,1}^{\infty }\to 0$।

अब, कहते हैं, वर्णक्रमीय अनुक्रम पिछले उदाहरण के जैसे एक निस्पंदन f के साथ H में परिवर्तित हो जाता है। चूंकि $F_{p-2}H_{p}/F_{p-3}H_{p}=E_{p-2,2}^{\infty }=0$, $F_{p-3}H_{p}/F_{p-4}H_{p}=0$, आदि, हमारे निकट है: $0\to E_{p-1,1}^{\infty }\to H_{p}\to E_{p,0}^{\infty }\to 0$। सब कुछ एक साथ रखकर, एक मिलता है:

$\cdots \to H_{p+1}\to E_{p+1,0}^{2}{\overset {d}{\to }}E_{p-1,1}^{2}\to H_{p}\to E_{p,0}^{2}{\overset {d}{\to }}E_{p-2,1}^{2}\to H_{p-1}\to \dots .$

वांग अनुक्रम

पिछले खंड में की गई गणना सरल विधि से सामान्यीकरण करती है। एक क्षेत्र पर एक कंपन पर विचार करें:

$F{\overset {i}{\to }}E{\overset {p}{\to }}S^{n}$

जिसमें n कम से कम 2 हो। सेर वर्णक्रमीय अनुक्रम है:

$E_{p,q}^{2}=H_{p}(S^{n};H_{q}(F))\Rightarrow H_{p+q}(E)$;

यही कहना है, $E_{p,q}^{\infty }=F_{p}H_{p+q}(E)/F_{p-1}H_{p+q}(E)$ कुछ निस्पंदन $F_{\bullet }$ के साथ।

चूँकि $H_{p}(S^{n})$ मात्र शून्य नहीं है जब p शून्य या n है और उस स्थिति में 'Z' के बराबर है, हम देखते हैं कि $E_{p,q}^{2}$ में मात्र दो रेखाएँ $p=0,n$ हैं, इसलिए $E^{2}$-पृष्ठ

${\begin{matrix}&\vdots &\vdots &\vdots &&\vdots &\vdots &\vdots &\\\cdots &0&E_{0,2}^{2}&0&\cdots &0&E_{n,2}^{2}&0&\cdots \\\cdots &0&E_{0,1}^{2}&0&\cdots &0&E_{n,1}^{2}&0&\cdots \\\cdots &0&E_{0,0}^{2}&0&\cdots &0&E_{n,0}^{2}&0&\cdots \\\end{matrix}}$ द्वारा दिया गया है।

इसके अतिरिक्त सार्वभौमिक गुणांक प्रमेय द्वारा $p=0,n$ के लिए

$E_{p,q}^{2}=H_{p}(S^{n};H_{q}(F))=H_{q}(F)$

के बाद से, $E^{2}$ पृष्ठ

${\begin{matrix}&\vdots &\vdots &\vdots &&\vdots &\vdots &\vdots &\\\cdots &0&H_{2}(F)&0&\cdots &0&H_{2}(F)&0&\cdots \\\cdots &0&H_{1}(F)&0&\cdots &0&H_{1}(F)&0&\cdots \\\cdots &0&H_{0}(F)&0&\cdots &0&H_{0}(F)&0&\cdots \\\end{matrix}}$ जैसा दिखता है।

चूंकि $E^{n}$-पृष्ठ मात्र गैर-शून्य अवकलन हैं,

$d_{n,q}^{n}:E_{n,q}^{n}\to E_{0,q+n-1}^{n}$

द्वारा दिया गया है जो कि

$d_{n,q}^{n}:H_{q}(F)\to H_{q+n-1}(F)$

है वर्णक्रमीय अनुक्रम $E^{n+1}=E^{\infty }$पर अभिसरण करता है। $E^{n+1}$ की गणना करके हम एक यथार्थ क्रम

$0\to E_{n,q-n}^{\infty }\to E_{n,q-n}^{n}{\overset {d}{\to }}E_{0,q-1}^{n}\to E_{0,q-1}^{\infty }\to 0$ प्राप्त करते हैं।

और अनुरूपता समूहों का उपयोग करके लिखा गया है, यह

$0\to E_{n,q-n}^{\infty }\to H_{q-n}(F){\overset {d}{\to }}H_{q-1}(F)\to E_{0,q-1}^{\infty }\to 0$ है।

यह स्थापित करने के लिए कि दो $E^{\infty }$-पद क्या हैं, $H=H(E)$, लिखें, और चूंकि $F_{1}H_{q}/F_{0}H_{q}=E_{1,q-1}^{\infty }=0$, आदि, हमारे निकट: $E_{n,q-n}^{\infty }=F_{n}H_{q}/F_{0}H_{q}$ और इस प्रकार, के बाद से $F_{n}H_{q}=H_{q}$,

$0\to E_{0,q}^{\infty }\to H_{q}\to E_{n,q-n}^{\infty }\to 0$ है।

यह ठीक क्रम

$0\to H_{q}(F)\to H_{q}(E)\to H_{q-n}(F)\to 0$ है

सभी गणनाओं को एक साथ रखकर, एक प्राप्त होता है:

$\dots \to H_{q}(F){\overset {i_{*}}{\to }}H_{q}(E)\to H_{q-n}(F){\overset {d}{\to }}H_{q-1}(F){\overset {i_{*}}{\to }}H_{q-1}(E)\to H_{q-n-1}(F)\to \dots$

(ग्य्सिन अनुक्रम इसी प्रकार से प्राप्त किया जाता है।)

कम-घात पद

एक स्पष्ट सांकेतिक परिवर्तन के साथ, पिछले उदाहरणों में संगणना के प्रकार को उपयोग वर्णक्रमीय अनुक्रम के लिए भी किया जा सकता है। माना $E_{r}^{p,q}$ घटते निस्पंदन

$0=F^{n+1}H^{n}\subset F^{n}H^{n}\subset \dots \subset F^{0}H^{n}=H^{n}$

के साथ H में परिवर्तित होने वाला प्रथम-चतुर्थांश वर्णक्रमीय अनुक्रम है ताकि $E_{\infty }^{p,q}=F^{p}H^{p+q}/F^{p+1}H^{p+q}.$

चूँकि $E_{2}^{p,q}$ शून्य है यदि p या q ऋणात्मक है, तो हमारे निकट:

$0\to E_{\infty }^{0,1}\to E_{2}^{0,1}{\overset {d}{\to }}E_{2}^{2,0}\to E_{\infty }^{2,0}\to 0.$

चूँकि $E_{\infty }^{1,0}=E_{2}^{1,0}$ उसी कारण से और चूँकि $F^{2}H^{1}=0,$

$0\to E_{2}^{1,0}\to H^{1}\to E_{\infty }^{0,1}\to 0$।

$F^{3}H^{2}=0$, $E_{\infty }^{2,0}\subset H^{2}$ के बाद से। अनुक्रमों को एक साथ जोड़कर, हम तथाकथित पांच-पद यथार्थ अनुक्रम प्राप्त करते हैं:

$0\to E_{2}^{1,0}\to H^{1}\to E_{2}^{0,1}{\overset {d}{\to }}E_{2}^{2,0}\to H^{2}.$

किनारे के प्रतिचित्र और अतिक्रमण

तुल्य वर्णक्रमीय अनुक्रम

मान लीजिए कि $E_{p,q}^{r}$ एक वर्णक्रमीय क्रम है। यदि प्रत्येक q < 0 के लिए $E_{p,q}^{r}=0$ है, तो यह होना चाहिए: r ≥ 2 के लिए, भाजक के रूप में

$E_{p,0}^{r+1}=\operatorname {ker} (d:E_{p,0}^{r}\to E_{p-r,r-1}^{r})$

शून्य है। इसलिए, एकरूपता का एक क्रम है:

$E_{p,0}^{r}\to E_{p,0}^{r-1}\to \dots \to E_{p,0}^{3}\to E_{p,0}^{2}$।

उन्हें किनारे के प्रतिचित्र कहा जाता है। इसी प्रकार, यदि प्रत्येक p <0 के लिए $E_{p,q}^{r}=0$ तो एपिमोर्फिज्म का एक क्रम होता है (जिसे एज प्रतिचित्र भी कहा जाता है):

$E_{0,q}^{2}\to E_{0,q}^{3}\to \dots \to E_{0,q}^{r-1}\to E_{0,q}^{r}$।

अतिक्रमण प्रतिचित्र आंशिक रूप से परिभाषित प्रतिचित्र है (अधिक यथार्थ, एक योजक संबंध)

$\tau :E_{p,0}^{2}\to E_{0,p-1}^{2}$

रचना के रूप में दिया $E_{p,0}^{2}\to E_{p,0}^{p}{\overset {d}{\to }}E_{0,p-1}^{p}\to E_{0,p-1}^{2}$, पहला और आखिरी प्रतिचित्र किनारे के प्रतिचित्र के व्युत्क्रम हैं।

सह समरूपी वर्णक्रमीय अनुक्रम

वर्णक्रमीय अनुक्रम के लिए $E_{r}^{p,q}$ सह समरूपी प्रकार के, अनुरूप कथन धारण करते हैं। यदि $E_{r}^{p,q}=0$ प्रत्येक q < 0 के लिए, फिर एपिमोर्फिज्म का एक क्रम होता है

$E_{2}^{p,0}\to E_{3}^{p,0}\to \dots \to E_{r-1}^{p,0}\to E_{r}^{p,0}$।

और यदि $E_{r}^{p,q}=0$ प्रत्येक p < 0 के लिए, मोनोमोर्फिज्म का एक क्रम होता है:

$E_{r}^{0,q}\to E_{r-1}^{0,q}\to \dots \to E_{3}^{0,q}\to E_{2}^{0,q}$।

अतिक्रमण जरूरी ठीक रूप से परिभाषित प्रतिचित्र नहीं है:

$\tau :E_{2}^{0,q-1}\to E_{2}^{q,0}$

प्रेरक $d:E_{q}^{0,q-1}\to E_{q}^{q,0}$।

आवेदन

इन प्रतिचित्रों का निर्धारण Serre वर्णक्रमीय अनुक्रम में कई अवकलनों की गणना के लिए मौलिक है। उदाहरण के लिए अतिक्रमण प्रतिचित्र अवकलन को निर्धारित करता है

$d_{n}:E_{n,0}^{n}\to E_{0,n-1}^{n}$

तुल्य वर्णक्रमीय अनुक्रम के लिए, इसलिए कंपन के लिए सेरे वर्णक्रमीय अनुक्रम पर $F\to E\to B$ प्रतिचित्र देता है

$d_{n}:H_{n}(B)\to H_{n-1}(F)$।

आगे के उदाहरण

कुछ उल्लेखनीय वर्णक्रमीय अनुक्रम हैं:

सांस्थिति और ज्यामिति

• एक असाधारण सह समरूपता सिद्धांत का अतियाह-हिर्जेब्रुक वर्णक्रमीय अनुक्रम
• एक समूह के वर्गीकरण स्थान की समरूपता के लिए बार वर्णक्रमीय अनुक्रम।
• बॉकस्टीन वर्णक्रमीय अनुक्रम, मॉड पी गुणांक के साथ अनुरूपता से संबंधित है और अनुरूपता ने मॉड पी को कम कर दिया है।
• कार्टन-लेरे वर्णक्रमीय अनुक्रम भागफल स्थान के अनुरूपता में परिवर्तित हो रहा है।
• एक कंपन के ठहराना के एकवचन सह समरूपता के लिए ईलेनबर्ग-मूर वर्णक्रमीय अनुक्रम
• एक कंपन का गंभीर वर्णक्रमीय क्रम

होमोटॉपी सिद्धांत

• स्थिर समरूपता सिद्धांत में ईHपी वर्णक्रमीय अनुक्रम
• एडम्स-नोविकोव वर्णक्रमीय अनुक्रम, असाधारण सह समरूपता सिद्धांत के लिए एक सामान्यीकरण।
• बैराट वर्णक्रमीय अनुक्रम एक कोफिब्रेशन के प्रारंभिक स्थान के होमोटॉपी में परिवर्तित हो रहा है।
• बाउसफ़ील्ड-कान वर्णक्रमीय अनुक्रम एक फ़ैक्टर के होमोटॉपी कोलिमिट में परिवर्तित हो रहा है।
• एडम्स-नोविकोव वर्णक्रमीय अनुक्रम की प्रारंभिक प्रतिबन्धों की गणना होमोटॉपी निश्चित बिंदु वर्णक्रमीय अनुक्रम
• कोबर वर्णक्रमीय अनुक्रम
• ईHपी वर्णक्रमीय अनुक्रम क्षेत्रों के स्थिर होमोटोपी समूहों में परिवर्तित हो रहा है
• फेडरर वर्णक्रमीय अनुक्रम एक फ़ंक्शन स्पेस के होमोटॉपी समूहों में परिवर्तित हो रहा है।
• होमोटॉपी फिक्स्ड फेडरर वर्णक्रमीय अनुक्रम
• Hurewicz वर्णक्रमीय अनुक्रम किसी स्थान की समरूपता की समरूपता की गणना के लिए।
• मिलर वर्णक्रमीय अनुक्रम एक अवकलनिक्ष के मॉड पी स्थिर अनुरूपता में परिवर्तित हो रहा है।
• मिल्नोर वर्णक्रमीय अनुक्रम बार वर्णक्रमीय अनुक्रम का दूसरा नाम है।
• मूर वर्णक्रमीय अनुक्रम बार वर्णक्रमीय अनुक्रम का दूसरा नाम है।
• एक साधारण समूह की होमोटॉपी की गणना के लिए क्विलन वर्णक्रमीय अनुक्रम
• रोथेनबर्ग-स्टीनरोड वर्णक्रमीय अनुक्रम बार वर्णक्रमीय अनुक्रम का दूसरा नाम है।
• वैन कम्पेन वर्णक्रमीय अनुक्रम रिक्त स्थान की कील की होमोटॉपी की गणना के लिए।

बीजगणित

• चेक सह समरूपता से शेफ सह समरूपता तक चेक-टू-डेराइव्ड फंक्शनल वर्णक्रमीय सीक्वेंस।
• मॉड्यूल के टॉर और एक्सटी समूहों की गणना के लिए वलय वर्णक्रमीय अनुक्रमों का परिवर्तन।
• एक बीजगणित के चक्रीय समरूपता में अभिसरण कोन्स वर्णक्रमीय अनुक्रम।
• गेर्स्टन-विट वर्णक्रमीय अनुक्रम
• सह समरूपता शर्ट के लिए ग्रीन का वर्णक्रमीय अनुक्रम
• व्युत्पन्न फंक्टर बनाने के लिए ग्रोथेंडिक वर्णक्रमीय अनुक्रम
• हाइपरअनुरूपता की गणना के लिए हाइपरअनुरूपता वर्णक्रमीय अनुक्रम
• अवकलन बीजगणित के टेंसर उत्पाद के अनुरूपता की गणना के लिए कुनेथ वर्णक्रमीय अनुक्रम।
• लेरे वर्णक्रमीय अनुक्रम एक शेफ के सह समरूपता में परिवर्तित हो रहा है।
• स्थानीय-से-वैश्विक एक्सट वर्णक्रमीय अनुक्रम
• लिंडन-होच्स्चाइल्ड-सेरे वर्णक्रमीय सीक्वेंस इन समूह सह समरूपता |ग्रुप (को)अनुरूपता
• एक बीजगणित के Tor या Ext समूहों की गणना के लिए मई वर्णक्रमीय अनुक्रम
• एक विभेदक निस्यंदित समूह का वर्णक्रमीय क्रम: इस लेख में वर्णित है।
• एक दोहरे सम्मिश्र का वर्णक्रमीय क्रम: इस लेख में वर्णित है।
• एक यथार्थ युग्म का वर्णक्रमीय क्रम: इस लेख में वर्णित है।
• सार्वभौमिक गुणांक वर्णक्रमीय अनुक्रम
• वैन एस्ट वर्णक्रमीय अनुक्रम सापेक्ष लाई बीजगणित सह समरूपता में परिवर्तित हो रहा है।

सम्मिश्र और बीजगणितीय ज्यामिति

• एकवचन सिद्धांत में अर्नोल्ड का वर्णक्रमीय क्रम।
• बलोच-लिक्टेनबौम वर्णक्रमीय अनुक्रम एक क्षेत्र के बीजगणितीय के-सिद्धांत में परिवर्तित हो रहा है।
• Frölicher वर्णक्रमीय अनुक्रम Dolbeault cohomology से प्रारंभहोता है और विभिन्न प्रकार के बीजगणितीय de Rham cohomology में परिवर्तित होता है।
• हॉज-डी राम वर्णक्रमीय अनुक्रम विभिन्न प्रकार के बीजगणितीय d राम सह समरूपता में परिवर्तित हो रहा है।
• मोटिविक-टू-के-थ्योरी वर्णक्रमीय सीक्वेंस|मोटिविक-टू-के-थ्योरी वर्णक्रमीय सीक्वेंस

संदर्भ

परिचयात्मक

• Fomenko, Anatoly; Fuchs, Dmitry, Homotopical Topology
• Hatcher, Allen. "बीजगणितीय टोपोलॉजी में वर्णक्रमीय अनुक्रम" (PDF).

संदर्भ

• Leray, Jean (1946a), "L'anneau d'homologie d'une représentation", Les Comptes rendus de l'Académie des sciences, 222: 1366–1368
• Leray, Jean (1946b), "Structure de l'anneau d'homologie d'une représentation", Les Comptes rendus de l'Académie des sciences, 222: 1419–1422
• Koszul, Jean-Louis (1947). "Sur les opérateurs de dérivation dans un anneau". Comptes rendus de l'Académie des Sciences. 225: 217–219.
• Massey, William S. (1952). "Exact couples in algebraic topology. I, II". Annals of Mathematics. Second Series. Annals of Mathematics. 56 (2): 363–396. doi:10.2307/1969805. JSTOR 1969805.
• Massey, William S. (1953). "Exact couples in algebraic topology. III, IV, V". Annals of Mathematics. Second Series. Annals of Mathematics. 57 (2): 248–286. doi:10.2307/1969858. JSTOR 1969858.
• May, J. Peter. "A primer on spectral sequences" (PDF). Archived (PDF) from the original on 21 Jun 2020. Retrieved 21 Jun 2020.
• McCleary, John (2001). A User's Guide to Spectral Sequences. Cambridge Studies in Advanced Mathematics. Vol. 58 (2nd ed.). Cambridge University Press. ISBN 978-0-521-56759-6. MR 1793722.
• Mosher, Robert; Tangora, Martin (1968), Cohomology Operations and Applications in Homotopy Theory, Harper and Row, ISBN 978-0-06-044627-7
• Weibel, Charles A. (1994). An introduction to homological algebra. Cambridge Studies in Advanced Mathematics. Vol. 38. Cambridge University Press. ISBN 978-0-521-55987-4. MR 1269324. OCLC 36131259.

अग्रिम पठन

• Chow, Timothy Y. (2006). "You Could Have Invented Spectral Sequences" (PDF). Notices of the American Mathematical Society. 53: 15–19.

बाहरी संबंध

• "What is so "spectral" about spectral sequences?". MathOverflow.
• "SpectralSequences — a package for working with filtered complexes and spectral sequences". Macaulay2.