कर्नेल प्रधान घटक विश्लेषण

बहुभिन्नरूपी आँकड़े के क्षेत्र में, कर्नेल प्रधान घटक विश्लेषण (कर्नेल पीसीए) कर्नेल विधियों की तकनीकों का उपयोग करके प्रधान घटक विश्लेषण (पीसीए) का एक विस्तार है। कर्नेल का उपयोग करते हुए, पीसीए का मूल रूप से रैखिक संचालन एक पुनरुत्पादन कर्नेल हिल्बर्ट स्पेस (आरकेएचएस) में किया जाता है।

पृष्ठभूमि: रैखिक पीसीए

याद रखें कि पारंपरिक पीसीए शून्य-केंद्रित डेटा पर काम करता है; वह है,

${\frac {1}{N}}\sum _{i=1}^{N}\mathbf {x} _{i}=\mathbf {0}$,

जहां $\mathbf {x} _{i}$ इनमें से एक है $N$ बहुभिन्नरूपी अवलोकन। यह सहप्रसरण मैट्रिक्स को विकर्ण करके संचालित होता है,

$C={\frac {1}{N}}\sum _{i=1}^{N}\mathbf {x} _{i}\mathbf {x} _{i}^{\top }$

दूसरे शब्दों में, यह सहप्रसरण मैट्रिक्स का एक आइगेनअपघटन देता है:

$\lambda \mathbf {v} =C\mathbf {v}$

जिसे फिर से लिखा जा सकता है

$\lambda \mathbf {x} _{i}^{\top }\mathbf {v} =\mathbf {x} _{i}^{\top }C\mathbf {v} \quad {\textrm {for}}~i=1,\ldots ,N$.

(यह भी देखें: सहप्रसरण मैट्रिक्स एक रैखिक संचालक के रूप में)

पीसीए के लिए कर्नेल का परिचय

कर्नेल पीसीए की उपयोगिता को समझने के लिए, विशेष रूप से क्लस्टरिंग के लिए, निरीक्षण करें कि, जबकि एन अंक सामान्य रूप से रैखिक पृथक्करणीयता नहीं हो सकते हैं $d<N$ आयाम, वे लगभग हमेशा रैखिक रूप से अलग हो सकते हैं $d\geq N$ आयाम। अर्थात एन अंक दिए गए हैं, $\mathbf {x} _{i}$, यदि हम उन्हें एन-आयाम स्थान के साथ मैप करते हैं

$\Phi (\mathbf {x} _{i})$ जहां $\Phi :\mathbb {R} ^{d}\to \mathbb {R} ^{N}$,

एक हाइपरप्लेन का निर्माण करना आसान है जो बिंदुओं को मनमाना समूहों में विभाजित करता है। बेशक, यह $\Phi$ रैखिक रूप से स्वतंत्र सदिश बनाता है, इसलिए ऐसा कोई सहप्रसरण नहीं है जिस पर स्पष्ट रूप से आइगेनअपघटन किया जा सके जैसा कि हम रैखिक पीसीए में करते हैं।

इसके अतिरिक्त, कर्नेल पीसीए में, एक गैर-तुच्छ, मनमाना $\Phi$ फलन 'चयनित' है जिसकी कभी भी स्पष्ट रूप से गणना नहीं की जाती है, जिससे संभावना को बहुत उच्च-आयामी उपयोग करने की अनुमति मिलती है $\Phi$ यदि हमें वास्तव में उस स्थान में डेटा का मूल्यांकन नहीं करना है। चूंकि हम सामान्यतः काम करने से बचने की प्रयास करते हैं $\Phi$-स्पेस, जिसे हम 'फीचर स्पेस' कहेंगे, हम एन-बाय-एन कर्नेल बना सकते हैं

$K=k(\mathbf {x} ,\mathbf {y} )=(\Phi (\mathbf {x} ),\Phi (\mathbf {y} ))=\Phi (\mathbf {x} )^{T}\Phi (\mathbf {y} )$

जो आंतरिक उत्पाद स्थान (ग्रामियन मैट्रिक्स देखें) का प्रतिनिधित्व करता है। एक कर्नेल के निर्माण में उत्पन्न होने वाला दोहरा रूप हमें गणितीय रूप से पीसीए के एक संस्करण को तैयार करने की अनुमति देता है जिसमें हम वास्तव में सहप्रसरण मैट्रिक्स के अभिलक्षणिक सदिश और अभिलक्षणिक मान को हल नहीं करते हैं। $\Phi (\mathbf {x} )$-स्पेस (कर्नेल चाल देखें)। K के प्रत्येक स्तंभ में N-तत्व सभी रूपांतरित बिंदुओं (N बिंदुओं) के संबंध में रूपांतरित डेटा के एक बिंदु के डॉट उत्पाद का प्रतिनिधित्व करते हैं। नीचे दिए गए उदाहरण में कुछ जाने-माने कर्नेल दिखाए गए हैं।

क्योंकि हम कभी भी फीचर स्पेस में सीधे काम नहीं कर रहे हैं, पीसीए का कर्नेल-फॉर्मूलेशन प्रतिबंधित है, क्योंकि यह स्वयं प्रमुख घटकों की गणना नहीं करता है, बल्कि उन घटकों पर हमारे डेटा के अनुमानों की गणना करता है। फीचर स्पेस में एक बिंदु से प्रक्षेपण का मूल्यांकन करने के लिए $\Phi (\mathbf {x} )$ kवें प्रमुख घटक पर $V^{k}$ (जहाँ सुपरस्क्रिप्ट k का अर्थ है घटक k, k की शक्तियाँ नहीं)

${V^{k}}^{T}\Phi (\mathbf {x} )=\left(\sum _{i=1}^{N}\mathbf {a} _{i}^{k}\Phi (\mathbf {x} _{i})\right)^{T}\Phi (\mathbf {x} )$

हमने ध्यान दिया कि $\Phi (\mathbf {x} _{i})^{T}\Phi (\mathbf {x} )$ डॉट उत्पाद को दर्शाता है, जो केवल कर्नेल के तत्व $K$ है। ऐसा लगता है कि जो कुछ बचा है, उसकी गणना और सामान्यीकरण करना है $\mathbf {a} _{i}^{k}$, जो अभिलक्षणिक सदिश समीकरण को हल करके किया जा सकता है

$N\lambda \mathbf {a} =K\mathbf {a}$

जहां $N$ समुच्चय में डेटा बिंदुओं की संख्या है, और $\lambda$ और $\mathbf {a}$ के अभिलक्षणिक मान ​​​​और अभिलक्षणिक सदिश हैं $K$. फिर अभिलक्षणिक सदिश को सामान्य करने के लिए $\mathbf {a} ^{k}$,की हमें आवश्यकता होती है

$1=(V^{k})^{T}V^{k}$

इस बात का ध्यान रखा जाना चाहिए कि $x$ अपने मूल स्थान में शून्य-माध्य है या नहीं है, यह सुविधा स्थान में केंद्रित होने की गारंटी नहीं है (जिसे हम कभी भी स्पष्ट रूप से गणना नहीं करते हैं)। चूंकि एक प्रभावी प्रमुख घटक विश्लेषण करने के लिए केंद्रित डेटा की आवश्यकता होती है, इसलिए हमें 'केंद्रित मैट्रिक्स' $K$ बनना $K'$है।

$K'=K-\mathbf {1_{N}} K-K\mathbf {1_{N}} +\mathbf {1_{N}} K\mathbf {1_{N}}$

जहां $\mathbf {1_{N}}$ एन-बाय-एन मैट्रिक्स को दर्शाता है जिसके लिए प्रत्येक तत्व मान लेता है $1/N$. हम उपयोग करते हैं $K'$ ऊपर वर्णित कर्नेल पीसीए एल्गोरिथम को निष्पादित करने के लिए।

कर्नेल पीसीए की एक चेतावनी को यहाँ उदाहरण से स्पष्ट किया जाना चाहिए। रैखिक पीसीए में, हम प्रत्येक प्रमुख घटक द्वारा डेटा की कितनी भिन्नता पर आधारित अभिलक्षणिक सदिशों को रैंक करने के लिए अभिलक्षणिक मान ​​​​ का उपयोग कर सकते हैं। यह डेटा आयाम में कमी के लिए उपयोगी है और इसे केपीसीए पर भी लागू किया जा सकता है। चूंकि, व्यवहार में ऐसे स्थितियों होते हैं कि डेटा की सभी विविधताएँ समान होती हैं। यह सामान्यतः कर्नेल स्केल के गलत चुनाव के कारण होता है।

बड़ा डेटासमुच्चय

व्यवहार में, एक बड़ा डेटा समुच्चय एक बड़े K की ओर ले जाता है, और K को स्टोर करना एक समस्या बन सकता है। इससे निपटने का एक उपाय डेटासमुच्चय पर क्लस्टरिंग करना है, और उन क्लस्टर्स के माध्यम से कर्नेल को पॉप्युलेट करना है। चूँकि यह विधि भी अपेक्षाकृत बड़ा K उत्पन्न कर सकती है, केवल शीर्ष पी अभिलक्षणिक मान ​​​​की गणना करना सामान्य है और अभिलक्षणिक मान ​​​​के अभिलक्षणिक सदिश की गणना इस तरह से की जाती है।

उदाहरण

कर्नेल पीसीए से पहले इनपुट बिंदु

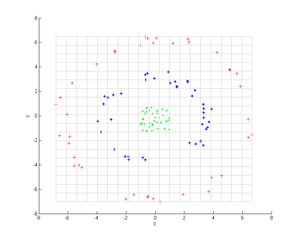
बिंदुओं के तीन संकेंद्रित समूहों पर विचार करें (दिखाया गया है); हम इन समूहों की पहचान करने के लिए कर्नेल पीसीए का उपयोग करना चाहते हैं। बिंदुओं का रंग एल्गोरिथम में सम्मलित जानकारी का प्रतिनिधित्व नहीं करता है, लेकिन केवल यह दर्शाता है कि परिवर्तन डेटा बिंदुओं को कैसे स्थानांतरित करता है।

पहले कर्नेल पर विचार करें

$k({\boldsymbol {x}},{\boldsymbol {y}})=({\boldsymbol {x}}^{\mathrm {T} }{\boldsymbol {y}}+1)^{2}$

इसे कर्नेल पीसीए पर लागू करने से अगली आकृति प्राप्त होती है।

कर्नेल पीसीए के पश्चात आउटपुट $k({\boldsymbol {x}},{\boldsymbol {y}})=({\boldsymbol {x}}^{\mathrm {T} }{\boldsymbol {y}}+1)^{2}$. तीन समूहों को केवल पहले घटक का उपयोग करके पहचाना जा सकता है।

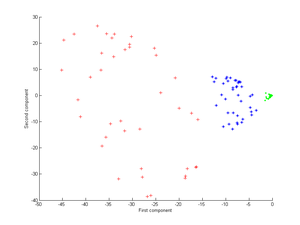
अब गॉसियन कर्नेल पर विचार करें:

$k({\boldsymbol {x}},{\boldsymbol {y}})=e^{\frac {-||{\boldsymbol {x}}-{\boldsymbol {y}}||^{2}}{2\sigma ^{2}}},$

यही है, यह कर्नेल निकटता का माप है, 1 के बराबर जब अंक मिलते हैं और अनंत पर तब 0 के बराबर होते हैं।

विशेष रूप से ध्यान दें कि पहला प्रमुख घटक तीन अलग-अलग समूहों को अलग करने के लिए पर्याप्त है, जब कि केवल रैखिक पीसीए का उपयोग करना असंभव है, चूंकि रैखिक पीसीए केवल दिए गए (इस मामले में द्वि-आयामी) स्थान में संचालित होता है, जिसमें ये बिंदुओं के तीन संकेंद्रित समूह हैं रैखिक रूप से वियोज्य नहीं।

अनुप्रयोग

कर्नेल पीसीए को नवीनता का पता लगाना और आकृति फैलने में कमी के लिए उपयोगी दिखाया गया है।

यह भी देखें

• क्लस्टर विश्लेषण
• गैर रेखीय आयामीता में कमी
• स्पेक्ट्रल क्लस्टरिंग