पथ (ग्राफ सिद्धांत): Difference between revisions
mNo edit summary |
mNo edit summary |
||
| Line 2: | Line 2: | ||
{{For|the family of graphs known as paths|Path graph}} | {{For|the family of graphs known as paths|Path graph}} | ||
[[File:Snake-in-the-box and Hamiltonian path.svg|thumb|right|एक त्रि-आयामी [[हाइपरक्यूब ग्राफ]]़ लाल रंग में [[हैमिल्टनियन पथ]] और | [[File:Snake-in-the-box and Hamiltonian path.svg|thumb|right|एक त्रि-आयामी [[हाइपरक्यूब ग्राफ|अतिविम ग्राफ]]़ लाल रंग में [[हैमिल्टनियन पथ]] और गहरा काला रंग सबसे लंबा प्रेरित पथ दिखा रहा है।।]]ग्राफ़ सिद्धांत में, ग्राफ़ में एक पथ किनारों का एक परिमित या अनंत अनुक्रम होता है जो शीर्षों के अनुक्रम में शामिल होता है, जो कि अधिकांश परिभाषाओं से अलग होते हैं (और चूंकि कोने अलग होते हैं, इसलिए किनारे भी होते हैं)। एक निर्देशित पथ (कभी-कभी द्विपथ {{sfn|Bender|Williamson|2010|p=162}} कहा जाता है) एक निर्देशित ग्राफ में किनारों का एक परिमित या अनंत अनुक्रम होता है जो अलग-अलग शीर्षों के अनुक्रम में शामिल होता है, लेकिन अतिरिक्त प्रतिबंध के साथ कि किनारों को एक ही दिशा में निर्देशित किया जाता है। | ||
पथ ग्राफ सिद्धांत की मूलभूत अवधारणाएँ हैं, जिनका वर्णन अधिकांश ग्राफ सिद्धांत ग्रंथों के परिचयात्मक खंडों में वर्णित है। उदाहरण देखें बॉन्डी और मूर्ति (1976), गिबन्स (1985), या डायस्टेल (2005) कोर्टे एट अल। (1990) रेखांकन में पथों से संबंधित अधिक उन्नत [[ कलन विधि |कलन विधि]] विषयों को कवर करते हैं। | पथ ग्राफ सिद्धांत की मूलभूत अवधारणाएँ हैं, जिनका वर्णन अधिकांश ग्राफ सिद्धांत ग्रंथों के परिचयात्मक खंडों में वर्णित है। उदाहरण देखें बॉन्डी और मूर्ति (1976), गिबन्स (1985), या डायस्टेल (2005) कोर्टे एट अल। (1990) रेखांकन में पथों से संबंधित अधिक उन्नत [[ कलन विधि |कलन विधि]] विषयों को कवर करते हैं। | ||
| Line 8: | Line 8: | ||
== परिभाषाएँ == | == परिभाषाएँ == | ||
=== | === चाल, निशान, और पथ === | ||
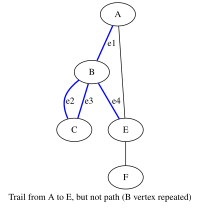
[[File:Trail but not path.svg|200px|thumb|right]]* | [[File:Trail but not path.svg|200px|thumb|right]]* चाल किनारों का एक परिमित या अनंत क्रम है जो शीर्षों के अनुक्रम में शामिल होता है{{sfn|Bender|Williamson|2010|p=162}} | ||
: मान लीजिए कि G = (V, E, ϕ) एक ग्राफ है। एक परिमित चाल किनारों (e1, e2, …, en − 1) का एक क्रम है जिसके लिए | : मान लीजिए कि G = (V, E, ϕ) एक ग्राफ है। एक परिमित चाल किनारों (e1, e2, …, en − 1) का एक क्रम है जिसके लिए सीधा (v1, v2, …, vn) का एक क्रम है जैसे कि ϕ(ei) = {vi, vi 1} के लिए i = 1, 2, …, n − 1. (v1, v2, …, vn) चाल का शीर्ष अनुक्रम है।अगर v1 = vn चलना बंद है,अन्यथा यह खुला है। एक अनंत चाल यहाँ वर्णित एक ही प्रकार के किनारों का एक क्रम है, लेकिन कोई पहला या अंतिम शीर्ष नहीं है, और एक अर्ध-अनंत चाल (या किरण) का पहला शीर्ष है लेकिन कोई अंतिम शीर्ष नहीं है। | ||
* | * संकेत एक ऐसा चाल है जिसके सभी किनारे अलग-अलग होते हैं।{{sfn|Bender|Williamson|2010|p=162}} | ||
* एक पथ एक | * एक पथ एक संकेत है जिसमें सभी कोने (और सभी किनारे भी) अलग-अलग हैं।{{sfn|Bender|Williamson|2010|p=162}} | ||
इसी प्रकार एक निर्देशित निशान या पथ के लिए यदि w = (e1, e2, …, en − 1) शीर्ष अनुक्रम (v1, v2, …, vn) के साथ एक परिमित निर्देशित चाल है, तो w को v1 से vn तक की चाल कहा जाता है। यदि दो अलग-अलग शीर्षों के बीच एक परिमित निर्देशित चाल है तो एक परिमित निर्देशित निशान और उनके बीच एक परिमित निर्देशित पथ भी है। | |||
कुछ लेखकों की आवश्यकता नहीं है कि पथ के सभी कोने अलग-अलग हों और इसके बजाय ऐसे पथ को संदर्भित करने के लिए 'सरल पथ' शब्द का उपयोग करें जहां सभी कोने अलग-अलग हों। | कुछ लेखकों की आवश्यकता नहीं है कि पथ के सभी कोने अलग-अलग हों और इसके बजाय ऐसे पथ को संदर्भित करने के लिए 'सरल पथ' शब्द का उपयोग करें जहां सभी कोने अलग-अलग हों। | ||
एक | एक भारित ग्राफ में प्रत्येक किनारे के साथ एक मान (वजन) को जोड़ता है। भारित ग्राफ़ में चलने (या निशान या पथ) का भार पार किए हुए किनारे के भार का योग होता है। कभी-कभी वजन के स्थान पर लागत या लंबाई शब्दों का प्रयोग किया जाता है। | ||
=== निर्देशित चलना, निर्देशित | === निर्देशित चलना, निर्देशित निशान, और निर्देशित पथ === | ||
* एक निर्देशित | * एक निर्देशित चाल किनारा (ग्राफ सिद्धांत) का एक परिमित या अनंत अनुक्रम है जो उसी दिशा में निर्देशित होता है जो शीर्ष (ग्राफ सिद्धांत) के अनुक्रम में शामिल होता है।{{sfn|Bender|Williamson|2010|p=162}} | ||
: होने देना {{nowrap|1=''G'' = (''V'', ''E'', ''ϕ'')}} एक निर्देशित ग्राफ बनें। एक परिमित निर्देशित चलना किनारों का एक क्रम है {{nowrap|(''e''<sub>1</sub>, ''e''<sub>2</sub>, …, ''e''<sub>''n'' − 1</sub>)}} जिसके लिए वर्टिकल का एक क्रम है {{nowrap|(''v''<sub>1</sub>, ''v''<sub>2</sub>, …, ''v''<sub>''n''</sub>)}} ऐसा है कि {{nowrap|1=''ϕ''(''e''<sub>''i''</sub>) = (''v''<sub>''i''</sub>, ''v''<sub>''i'' + 1</sub>)}} के लिए {{nowrap|1=''i'' = 1, 2, …, ''n'' − 1}}. {{nowrap|(''v''<sub>1</sub>, ''v''<sub>2</sub>, …, ''v''<sub>''n''</sub>)}} निर्देशित चलने का शीर्ष क्रम है। निर्देशित चलना बंद है अगर {{nowrap begin}}में<sub>1</sub> = वि<sub>''n''</sub>{{nowrap end}}, और यह अन्यथा खुला है। एक अनंत निर्देशित चाल यहाँ वर्णित एक ही प्रकार के किनारों का एक क्रम है, लेकिन कोई पहला या अंतिम शीर्ष नहीं है, और एक अर्ध-अनंत निर्देशित चलना (या अंत (ग्राफ सिद्धांत)) का पहला शीर्ष है लेकिन कोई अंतिम शीर्ष नहीं है। | : होने देना {{nowrap|1=''G'' = (''V'', ''E'', ''ϕ'')}} एक निर्देशित ग्राफ बनें। एक परिमित निर्देशित चलना किनारों का एक क्रम है {{nowrap|(''e''<sub>1</sub>, ''e''<sub>2</sub>, …, ''e''<sub>''n'' − 1</sub>)}} जिसके लिए वर्टिकल का एक क्रम है {{nowrap|(''v''<sub>1</sub>, ''v''<sub>2</sub>, …, ''v''<sub>''n''</sub>)}} ऐसा है कि {{nowrap|1=''ϕ''(''e''<sub>''i''</sub>) = (''v''<sub>''i''</sub>, ''v''<sub>''i'' + 1</sub>)}} के लिए {{nowrap|1=''i'' = 1, 2, …, ''n'' − 1}}. {{nowrap|(''v''<sub>1</sub>, ''v''<sub>2</sub>, …, ''v''<sub>''n''</sub>)}} निर्देशित चलने का शीर्ष क्रम है। निर्देशित चलना बंद है अगर {{nowrap begin}}में<sub>1</sub> = वि<sub>''n''</sub>{{nowrap end}}, और यह अन्यथा खुला है। एक अनंत निर्देशित चाल यहाँ वर्णित एक ही प्रकार के किनारों का एक क्रम है, लेकिन कोई पहला या अंतिम शीर्ष नहीं है, और एक अर्ध-अनंत निर्देशित चलना (या अंत (ग्राफ सिद्धांत)) का पहला शीर्ष है लेकिन कोई अंतिम शीर्ष नहीं है। | ||
* 'डायरेक्टेड ट्रेल' एक निर्देशित वॉक है जिसमें सभी किनारे अलग-अलग होते हैं।{{sfn|Bender|Williamson|2010|p=162}} | * 'डायरेक्टेड ट्रेल' एक निर्देशित वॉक है जिसमें सभी किनारे अलग-अलग होते हैं।{{sfn|Bender|Williamson|2010|p=162}} | ||
| Line 28: | Line 28: | ||
अगर {{nowrap|1=''w'' = (''e''<sub>1</sub>, ''e''<sub>2</sub>, …, ''e''<sub>''n'' − 1</sub>)}} वर्टेक्स अनुक्रम के साथ एक परिमित निर्देशित चलना है {{nowrap|(''v''<sub>1</sub>, ''v''<sub>2</sub>, …, ''v''<sub>''n''</sub>)}} तो w को v से चलना कहा जाता है<sub>1</sub> पत्र बी<sub>''n''</sub>. इसी प्रकार एक निर्देशित निशान या पथ के लिए। यदि दो अलग-अलग शीर्षों के बीच एक परिमित निर्देशित चाल है तो एक परिमित निर्देशित मार्ग और उनके बीच एक परिमित निर्देशित मार्ग भी है। | अगर {{nowrap|1=''w'' = (''e''<sub>1</sub>, ''e''<sub>2</sub>, …, ''e''<sub>''n'' − 1</sub>)}} वर्टेक्स अनुक्रम के साथ एक परिमित निर्देशित चलना है {{nowrap|(''v''<sub>1</sub>, ''v''<sub>2</sub>, …, ''v''<sub>''n''</sub>)}} तो w को v से चलना कहा जाता है<sub>1</sub> पत्र बी<sub>''n''</sub>. इसी प्रकार एक निर्देशित निशान या पथ के लिए। यदि दो अलग-अलग शीर्षों के बीच एक परिमित निर्देशित चाल है तो एक परिमित निर्देशित मार्ग और उनके बीच एक परिमित निर्देशित मार्ग भी है। | ||
एक सरल निर्देशित पथ एक | एक सरल निर्देशित पथ एक ऐसी चाल है जहाँ सभी शीर्ष भिन्न होते हैं। | ||
एक भारित ग्राफ़ निर्देशित ग्राफ़ में प्रत्येक किनारे के साथ एक मान (वजन) को जोड़ता है। भारित निर्देशित ग्राफ़ में एक निर्देशित चाल (या | एक भारित ग्राफ़ निर्देशित ग्राफ़ में प्रत्येक किनारे के साथ एक मान (वजन) को जोड़ता है। भारित निर्देशित ग्राफ़ में एक निर्देशित चाल (या निशान या पथ) का भार अनुप्रस्थ किनारों के भार का योग होता है। कभी-कभी वजन के स्थान पर लागत या लंबाई शब्दों का प्रयोग किया जाता है। | ||
== उदाहरण == | == उदाहरण == | ||
* एक ग्राफ | * एक ग्राफ जुड़ा हुआ है यदि प्रत्येक जोड़े के शीर्ष वाले पथ हैं। | ||
* एक निर्देशित ग्राफ | *एक निर्देशित ग्राफ दृढ़ता से जुड़ा हुआ है यदि विपरीत दिशा में निर्देशित पथ जिनमें प्रत्येक जोड़ी के कोने हैं। | ||
* एक पथ ऐसा है कि कोई ग्राफ किनारा दो गैर-लगातार पथ के शीर्षों को जोड़ता है, एक | * एक पथ ऐसा है कि कोई भी ग्राफ किनारा दो गैर-लगातार पथ के शीर्षों को जोड़ता है,वह एक प्रेरित पथ कहलाता है। | ||
* एक पथ जिसमें बिना | *एक पथ जिसमें दोहराए बिना ग्राफ़ के प्रत्येक शीर्ष को शामिल किया गया है, हैमिल्टनियन पथ के रूप में जाना जाता है। | ||
* दो | * दो पथ शीर्ष स्वतंत्र (वैकल्पिक रूप से, आंतरिक रूप से शीर्ष -विभिन्न करना) हैं यदि उनके पास कोई आंतरिक शीर्ष उभयनिष्ठ नहीं है। इसी तरह, दो रास्ते किनारे से स्वतंत्र (या किनारे से विभिन्न करना) हैं, अगर उनमें कोई आंतरिक किनारा समान नहीं है। दो आंतरिक रूप से शीर्ष-विभिन्न करना पथ किनारे से विभिन्न करना हैं, लेकिन इसका विलोम आवश्यक रूप से सत्य नहीं है। | ||
* एक ग्राफ़ में दो शीर्षों के बीच की दूरी (ग्राफ़ सिद्धांत) उनके बीच सबसे छोटे पथ की लंबाई है, यदि कोई मौजूद है, | *एक ग्राफ़ में दो शीर्षों के बीच की दूरी (ग्राफ़ सिद्धांत) उनके बीच सबसे छोटे पथ की लंबाई है, यदि कोई मौजूद है, अन्यथा दूरी अनंत है। | ||
* जुड़े हुए ग्राफ़ का व्यास, ग्राफ़ के शीर्षों के युग्मों के बीच की सबसे बड़ी दूरी (ऊपर परिभाषित) है। | * जुड़े हुए ग्राफ़ का व्यास, ग्राफ़ के शीर्षों के युग्मों के बीच की सबसे बड़ी दूरी (ऊपर परिभाषित) है। | ||
== पथ ढूँढना == | == पथ ढूँढना == | ||
ग्राफ़ में | ग्राफ़ में सबसे छोटा और सबसे लंबापथ खोजने के लिए कई कलन विधि मौजूद हैं, इस महत्वपूर्ण अंतर के साथ कि पूर्व की समस्या गणना रूप से बाद की मिलान में बहुत आसान है। | ||
दिज्क्स्ट्रा का एल्गोरिथ्म गैर-नकारात्मक एज वेट (या कोई एज वेट) के साथ निर्देशित और अप्रत्यक्ष ग्राफ़ में स्रोत वर्टेक्स से हर दूसरे वर्टेक्स तक सबसे छोटे रास्तों की एक सूची तैयार करता है, जबकि बेलमैन-फोर्ड एल्गोरिथ्म को नेगेटिव एज वेट के साथ निर्देशित ग्राफ़ पर लागू किया जा सकता है। . फ़्लॉइड-वॉर्शल एल्गोरिथम का उपयोग भारित निर्देशित ग्राफ़ में सभी जोड़े के बीच सबसे छोटा रास्ता खोजने के लिए किया जा सकता है। | दिज्क्स्ट्रा का एल्गोरिथ्म गैर-नकारात्मक एज वेट (या कोई एज वेट) के साथ निर्देशित और अप्रत्यक्ष ग्राफ़ में स्रोत वर्टेक्स से हर दूसरे वर्टेक्स तक सबसे छोटे रास्तों की एक सूची तैयार करता है, जबकि बेलमैन-फोर्ड एल्गोरिथ्म को नेगेटिव एज वेट के साथ निर्देशित ग्राफ़ पर लागू किया जा सकता है। . फ़्लॉइड-वॉर्शल एल्गोरिथम का उपयोग भारित निर्देशित ग्राफ़ में सभी जोड़े के बीच सबसे छोटा रास्ता खोजने के लिए किया जा सकता है। | ||
| Line 50: | Line 50: | ||
* [[पथ ग्राफ]] | * [[पथ ग्राफ]] | ||
* [[बहुभुज श्रृंखला]] | * [[बहुभुज श्रृंखला]] | ||
* सबसे छोटा | * सबसे छोटा पथसमस्या | ||
* सबसे लंबी पथ समस्या | * सबसे लंबी पथ समस्या | ||
* दिज्क्स्ट्रा का | * दिज्क्स्ट्रा का कलन विधि | ||
* बेलमैन-फोर्ड | * बेलमैन-फोर्ड कलन विधि | ||
* फ्लोयड-वॉर्शल | * फ्लोयड-वॉर्शल कलन विधि | ||
* स्वयं से परहेज करना | * स्वयं से परहेज करना | ||
* [[सबसे छोटा पथ ग्राफ]] | * [[सबसे छोटा पथ ग्राफ]] | ||
Revision as of 17:59, 25 May 2023

ग्राफ़ सिद्धांत में, ग्राफ़ में एक पथ किनारों का एक परिमित या अनंत अनुक्रम होता है जो शीर्षों के अनुक्रम में शामिल होता है, जो कि अधिकांश परिभाषाओं से अलग होते हैं (और चूंकि कोने अलग होते हैं, इसलिए किनारे भी होते हैं)। एक निर्देशित पथ (कभी-कभी द्विपथ [1] कहा जाता है) एक निर्देशित ग्राफ में किनारों का एक परिमित या अनंत अनुक्रम होता है जो अलग-अलग शीर्षों के अनुक्रम में शामिल होता है, लेकिन अतिरिक्त प्रतिबंध के साथ कि किनारों को एक ही दिशा में निर्देशित किया जाता है।
पथ ग्राफ सिद्धांत की मूलभूत अवधारणाएँ हैं, जिनका वर्णन अधिकांश ग्राफ सिद्धांत ग्रंथों के परिचयात्मक खंडों में वर्णित है। उदाहरण देखें बॉन्डी और मूर्ति (1976), गिबन्स (1985), या डायस्टेल (2005) कोर्टे एट अल। (1990) रेखांकन में पथों से संबंधित अधिक उन्नत कलन विधि विषयों को कवर करते हैं।
परिभाषाएँ
चाल, निशान, और पथ
* चाल किनारों का एक परिमित या अनंत क्रम है जो शीर्षों के अनुक्रम में शामिल होता है[1]
- मान लीजिए कि G = (V, E, ϕ) एक ग्राफ है। एक परिमित चाल किनारों (e1, e2, …, en − 1) का एक क्रम है जिसके लिए सीधा (v1, v2, …, vn) का एक क्रम है जैसे कि ϕ(ei) = {vi, vi 1} के लिए i = 1, 2, …, n − 1. (v1, v2, …, vn) चाल का शीर्ष अनुक्रम है।अगर v1 = vn चलना बंद है,अन्यथा यह खुला है। एक अनंत चाल यहाँ वर्णित एक ही प्रकार के किनारों का एक क्रम है, लेकिन कोई पहला या अंतिम शीर्ष नहीं है, और एक अर्ध-अनंत चाल (या किरण) का पहला शीर्ष है लेकिन कोई अंतिम शीर्ष नहीं है।
- संकेत एक ऐसा चाल है जिसके सभी किनारे अलग-अलग होते हैं।[1]
- एक पथ एक संकेत है जिसमें सभी कोने (और सभी किनारे भी) अलग-अलग हैं।[1]
इसी प्रकार एक निर्देशित निशान या पथ के लिए यदि w = (e1, e2, …, en − 1) शीर्ष अनुक्रम (v1, v2, …, vn) के साथ एक परिमित निर्देशित चाल है, तो w को v1 से vn तक की चाल कहा जाता है। यदि दो अलग-अलग शीर्षों के बीच एक परिमित निर्देशित चाल है तो एक परिमित निर्देशित निशान और उनके बीच एक परिमित निर्देशित पथ भी है।
कुछ लेखकों की आवश्यकता नहीं है कि पथ के सभी कोने अलग-अलग हों और इसके बजाय ऐसे पथ को संदर्भित करने के लिए 'सरल पथ' शब्द का उपयोग करें जहां सभी कोने अलग-अलग हों।
एक भारित ग्राफ में प्रत्येक किनारे के साथ एक मान (वजन) को जोड़ता है। भारित ग्राफ़ में चलने (या निशान या पथ) का भार पार किए हुए किनारे के भार का योग होता है। कभी-कभी वजन के स्थान पर लागत या लंबाई शब्दों का प्रयोग किया जाता है।
निर्देशित चलना, निर्देशित निशान, और निर्देशित पथ
- एक निर्देशित चाल किनारा (ग्राफ सिद्धांत) का एक परिमित या अनंत अनुक्रम है जो उसी दिशा में निर्देशित होता है जो शीर्ष (ग्राफ सिद्धांत) के अनुक्रम में शामिल होता है।[1]
- होने देना G = (V, E, ϕ) एक निर्देशित ग्राफ बनें। एक परिमित निर्देशित चलना किनारों का एक क्रम है (e1, e2, …, en − 1) जिसके लिए वर्टिकल का एक क्रम है (v1, v2, …, vn) ऐसा है कि ϕ(ei) = (vi, vi + 1) के लिए i = 1, 2, …, n − 1. (v1, v2, …, vn) निर्देशित चलने का शीर्ष क्रम है। निर्देशित चलना बंद है अगर में1 = विn, और यह अन्यथा खुला है। एक अनंत निर्देशित चाल यहाँ वर्णित एक ही प्रकार के किनारों का एक क्रम है, लेकिन कोई पहला या अंतिम शीर्ष नहीं है, और एक अर्ध-अनंत निर्देशित चलना (या अंत (ग्राफ सिद्धांत)) का पहला शीर्ष है लेकिन कोई अंतिम शीर्ष नहीं है।
- 'डायरेक्टेड ट्रेल' एक निर्देशित वॉक है जिसमें सभी किनारे अलग-अलग होते हैं।[1]
- एक निर्देशित पथ एक निर्देशित पथ है जिसमें सभी शीर्ष भिन्न होते हैं।[1]
अगर w = (e1, e2, …, en − 1) वर्टेक्स अनुक्रम के साथ एक परिमित निर्देशित चलना है (v1, v2, …, vn) तो w को v से चलना कहा जाता है1 पत्र बीn. इसी प्रकार एक निर्देशित निशान या पथ के लिए। यदि दो अलग-अलग शीर्षों के बीच एक परिमित निर्देशित चाल है तो एक परिमित निर्देशित मार्ग और उनके बीच एक परिमित निर्देशित मार्ग भी है।
एक सरल निर्देशित पथ एक ऐसी चाल है जहाँ सभी शीर्ष भिन्न होते हैं।
एक भारित ग्राफ़ निर्देशित ग्राफ़ में प्रत्येक किनारे के साथ एक मान (वजन) को जोड़ता है। भारित निर्देशित ग्राफ़ में एक निर्देशित चाल (या निशान या पथ) का भार अनुप्रस्थ किनारों के भार का योग होता है। कभी-कभी वजन के स्थान पर लागत या लंबाई शब्दों का प्रयोग किया जाता है।
उदाहरण
- एक ग्राफ जुड़ा हुआ है यदि प्रत्येक जोड़े के शीर्ष वाले पथ हैं।
- एक निर्देशित ग्राफ दृढ़ता से जुड़ा हुआ है यदि विपरीत दिशा में निर्देशित पथ जिनमें प्रत्येक जोड़ी के कोने हैं।
- एक पथ ऐसा है कि कोई भी ग्राफ किनारा दो गैर-लगातार पथ के शीर्षों को जोड़ता है,वह एक प्रेरित पथ कहलाता है।
- एक पथ जिसमें दोहराए बिना ग्राफ़ के प्रत्येक शीर्ष को शामिल किया गया है, हैमिल्टनियन पथ के रूप में जाना जाता है।
- दो पथ शीर्ष स्वतंत्र (वैकल्पिक रूप से, आंतरिक रूप से शीर्ष -विभिन्न करना) हैं यदि उनके पास कोई आंतरिक शीर्ष उभयनिष्ठ नहीं है। इसी तरह, दो रास्ते किनारे से स्वतंत्र (या किनारे से विभिन्न करना) हैं, अगर उनमें कोई आंतरिक किनारा समान नहीं है। दो आंतरिक रूप से शीर्ष-विभिन्न करना पथ किनारे से विभिन्न करना हैं, लेकिन इसका विलोम आवश्यक रूप से सत्य नहीं है।
- एक ग्राफ़ में दो शीर्षों के बीच की दूरी (ग्राफ़ सिद्धांत) उनके बीच सबसे छोटे पथ की लंबाई है, यदि कोई मौजूद है, अन्यथा दूरी अनंत है।
- जुड़े हुए ग्राफ़ का व्यास, ग्राफ़ के शीर्षों के युग्मों के बीच की सबसे बड़ी दूरी (ऊपर परिभाषित) है।
पथ ढूँढना
ग्राफ़ में सबसे छोटा और सबसे लंबापथ खोजने के लिए कई कलन विधि मौजूद हैं, इस महत्वपूर्ण अंतर के साथ कि पूर्व की समस्या गणना रूप से बाद की मिलान में बहुत आसान है।
दिज्क्स्ट्रा का एल्गोरिथ्म गैर-नकारात्मक एज वेट (या कोई एज वेट) के साथ निर्देशित और अप्रत्यक्ष ग्राफ़ में स्रोत वर्टेक्स से हर दूसरे वर्टेक्स तक सबसे छोटे रास्तों की एक सूची तैयार करता है, जबकि बेलमैन-फोर्ड एल्गोरिथ्म को नेगेटिव एज वेट के साथ निर्देशित ग्राफ़ पर लागू किया जा सकता है। . फ़्लॉइड-वॉर्शल एल्गोरिथम का उपयोग भारित निर्देशित ग्राफ़ में सभी जोड़े के बीच सबसे छोटा रास्ता खोजने के लिए किया जा सकता है।
यह भी देखें
- ग्राफ सिद्धांत की शब्दावली
- पथ ग्राफ
- बहुभुज श्रृंखला
- सबसे छोटा पथसमस्या
- सबसे लंबी पथ समस्या
- दिज्क्स्ट्रा का कलन विधि
- बेलमैन-फोर्ड कलन विधि
- फ्लोयड-वॉर्शल कलन विधि
- स्वयं से परहेज करना
- सबसे छोटा पथ ग्राफ
संदर्भ
- Bender, Edward A.; Williamson, S. Gill (2010). Lists, Decisions and Graphs. With an Introduction to Probability.
- Bondy, J. A.; Murty, U. S. R. (1976). Graph Theory with Applications. North Holland. p. 12-21. ISBN 0-444-19451-7.
- Diestel, Reinhard (2005). Graph Theory. Springer-Verlag. pp. 6–9. ISBN 3-540-26182-6.
- Gibbons, A. (1985). Algorithmic Graph Theory. Cambridge University Press. pp. 5–6. ISBN 0-521-28881-9.
- Korte, Bernhard; Lovász, László; Prömel, Hans Jürgen; Schrijver, Alexander (1990). Paths, Flows, and VLSI-Layout. Springer-Verlag. ISBN 0-387-52685-4.