चरण मॉडुलन: Difference between revisions
No edit summary |
No edit summary |
||
| Line 2: | Line 2: | ||
{{Modulation techniques}} | {{Modulation techniques}} | ||
चरण [[मॉडुलन]] (पीएम) [[ट्रांसमिशन (दूरसंचार)]] के लिए कंडीशनिंग संचार संकेतों के लिए एक मॉड्यूलेशन | चरण [[मॉडुलन]] (पीएम) [[ट्रांसमिशन (दूरसंचार)]] के लिए कंडीशनिंग संचार संकेतों के लिए एक मॉड्यूलेशन प्रतिरूप है। यह एक वाहक [[तरंग]] के [[तात्कालिक चरण]] में बदलाव के रूप में एक संदेश संकेत को एनकोड करता है। चरण मॉडुलन आवृत्ति मॉडुलन के साथ, [[कोण मॉडुलन]] के दो प्रमुख रूपों में से एक है। | ||
चरण मॉडुलन में, बेसबैंड | चरण मॉडुलन में, बेसबैंड संकेत का तात्कालिक आयाम अपने आयाम और आवृत्ति को स्थिर रखते हुए वाहक संकेत के चरण को संशोधित करता है। संदेश संकेत के बदलते संकेत स्तर (आयाम) का पालन करने के लिए वाहक संकेत के चरण को संशोधित किया जाता है। शिखर आयाम और वाहक संकेत की आवृत्ति स्थिर बनी हुई है, किंतु जैसे ही संदेश संकेत के आयाम में परिवर्तन होता है, वाहक का चरण तदनुसार बदलता है। | ||
चरण मॉडुलन व्यापक रूप से [[रेडियो]] तरंगों को प्रसारित करने के लिए उपयोग किया जाता है और यह कई डिजिटल ट्रांसमिशन कोडिंग योजनाओं का एक अभिन्न अंग है जो वाई-फाई, [[जीएसएम]] और उपग्रह टेलीविजन जैसी | चरण मॉडुलन व्यापक रूप से [[रेडियो]] तरंगों को प्रसारित करने के लिए उपयोग किया जाता है और यह कई डिजिटल ट्रांसमिशन कोडिंग योजनाओं का एक अभिन्न अंग है जो वाई-फाई, [[जीएसएम]] और उपग्रह टेलीविजन जैसी विधियों की एक विस्तृत श्रृंखला को रेखांकित करता है। [[एफएम संश्लेषण]] को प्रयुक्त करने के लिए [[यामाहा ने सफाई की]] 7 जैसे [[डिजिटल सिंथेसाइज़र]] में संकेत और तरंग उत्पादन के लिए भी इसका उपयोग किया जाता है। [[कैसियो सीजेड सिंथेसाइज़र]] में एक संबंधित प्रकार का ध्वनि संश्लेषण जिसे [[चरण विरूपण संश्लेषण]] कहा जाता है, का उपयोग किया जाता है। | ||
== सिद्धांत == | == सिद्धांत == | ||
[[File:Phase-modulation.gif|290px|thumb|right|मॉड्यूलेटिंग वेव ({{font color|blue|'''blue'''}}) वाहक तरंग को संशोधित कर रहा है ({{font color|red|'''red'''}}), जिसके परिणामस्वरूप पीएम संकेत ({{font color|green|'''green'''}}). {{center| {{nobr|{{math| ''g''(''t'') {{=}} {{sfrac| ''π'' |2}}×sin[ 2×2''π t'' + {{sfrac| ''π'' |2}}×sin( 3×2''π t'' ) ] }} }} }}]]चरण मॉडुलन संदेश संकेत के अनुपात में जटिल लिफाफे के चरण (तरंगों) को बदलता है। | [[File:Phase-modulation.gif|290px|thumb|right|मॉड्यूलेटिंग वेव ({{font color|blue|'''blue'''}}) वाहक तरंग को संशोधित कर रहा है ({{font color|red|'''red'''}}), जिसके परिणामस्वरूप पीएम संकेत ({{font color|green|'''green'''}}). {{center| {{nobr|{{math| ''g''(''t'') {{=}} {{sfrac| ''π'' |2}}×sin[ 2×2''π t'' + {{sfrac| ''π'' |2}}×sin( 3×2''π t'' ) ] }} }} }}]]चरण मॉडुलन संदेश संकेत के अनुपात में जटिल लिफाफे के चरण (तरंगों) को बदलता है। | ||
यदि m(t) संचरित होने वाला संदेश संकेत है और वाहक जिस पर संकेत संग्राहक है, | यदि m(t) संचरित होने वाला संदेश संकेत है और वाहक जिस पर संकेत संग्राहक है, | ||
: <math>c(t) = A_\text{c}\sin\left(\omega_\text{c}t + \phi_\text{c}\right),</math> | : <math>c(t) = A_\text{c}\sin\left(\omega_\text{c}t + \phi_\text{c}\right),</math> | ||
तो संग्राहक संकेत है | तो संग्राहक संकेत है | ||
: <math>y(t) = A_\text{c}\sin\left(\omega_\text{c}t + m(t) + \phi_\text{c}\right).</math> | : <math>y(t) = A_\text{c}\sin\left(\omega_\text{c}t + m(t) + \phi_\text{c}\right).</math> | ||
यह | |||
यह दर्शाता है कि कैसे <math>m(t)</math> चरण को संशोधित करता है - एक समय में जितना अधिक <math>m(t)</math> होता है, उस बिंदु पर संग्राहक संकेत का चरण बदलाव उतना ही अधिक होता है। इसे वाहक संकेत की आवृत्ति में परिवर्तन के रूप में भी देखा जा सकता है, और इस प्रकार चरण मॉडुलन को एफएम का एक विशेष स्थिति माना जा सकता है जिसमें वाहक आवृत्ति मॉडुलन चरण मॉडुलन के समय व्युत्पन्न द्वारा दिया जाता है। | |||
मॉडुलन संकेत यहाँ हो सकता है | मॉडुलन संकेत यहाँ हो सकता है | ||
: <math>m(t) = \cos\left(\omega_\text{c} t + h\omega_\text{m}(t)\right).</math> | : <math>m(t) = \cos\left(\omega_\text{c} t + h\omega_\text{m}(t)\right).</math> | ||
[[वर्णक्रमीय घनत्व]] | [[वर्णक्रमीय घनत्व]] संबंध के गणित से पता चलता है कि विशेष रुचि के दो क्षेत्र हैं: | ||
{{unordered list | {{unordered list | ||
| | | छोटे [[आयाम]] संकेतों के लिए, पीएम [[आयाम मॉड्यूलेशन]] (एएम) के समान है और [[बेसबैंड]] [[बैंडविड्थ (सिग्नल प्रोसेसिंग)|बैंडविड्थ]] के दुर्भाग्यपूर्ण दोहरीकरण और खराब दक्षता को प्रदर्शित करता है। | ||
| | |एक बड़े [[साइनसोइडल]] सिग्नल के लिए, पीएम एफएम के समान है, और इसकी [[बैंडविड्थ (सिग्नल प्रोसेसिंग)|बैंडविड्थ]] लगभग है | ||
: <math>2\left(h + 1\right)f_\text{M}</math>, | : <math>2\left(h + 1\right)f_\text{M}</math>, | ||
Where <math>f_\text{M} = \omega_\text{m}/2\pi</math> and <math>h</math> | Where <math>f_\text{M} = \omega_\text{m}/2\pi</math> and <math>h</math> मॉडुलन सूचकांक नीचे परिभाषित किया गया है। इसे पीएम के लिए [[कार्सन बैंडविड्थ रूल|कार्सन रूल]] के रूप में भी जाना जाता है।}} | ||
}} | |||
== [[ मॉडुलन सूचकांक ]] == | == [[ मॉडुलन सूचकांक ]] == | ||
जैसा कि अन्य मॉड्यूलेशन | जैसा कि अन्य मॉड्यूलेशन सूचकांक के साथ होता है, यह मात्रा इस बात को इंगित करती है कि मॉड्यूलेटेड चर अपने अनमॉड्यूलेटेड स्तर के आसपास कितना भिन्न होता है। यह वाहक संकेत के चरण में भिन्नता से संबंधित है: | ||
: <math>h = \Delta \theta ,</math> | : <math>h = \Delta \theta ,</math> | ||
जहाँ <math>\Delta \theta</math> शिखर चरण विचलन है। आवृत्ति मॉड्यूलेशन या मॉड्यूलेशन सूचकांक के लिए मॉड्यूलेशन सूचकांक से तुलना करें। | |||
<!-- in analog communication . phase modulation how to change phase of carrier with accordance modulating signal--> | <!-- in analog communication . phase modulation how to change phase of carrier with accordance modulating signal--> | ||
<!-- the above text makes no sense. I do not understand why it is there.--> | <!-- the above text makes no sense. I do not understand why it is there.--> | ||
| Line 36: | Line 37: | ||
* कोण मॉडुलन | * कोण मॉडुलन | ||
* [[स्वचालित आवृत्ति नियंत्रण]] | * [[स्वचालित आवृत्ति नियंत्रण]] | ||
* अन्य मॉड्यूलेशन | * अन्य मॉड्यूलेशन विधियों की सूची के लिए मॉड्यूलेशन | ||
* [[मॉडुलन क्षेत्र]] | * [[मॉडुलन क्षेत्र]] | ||
* [[ध्रुवीय मॉडुलन]] | * [[ध्रुवीय मॉडुलन]] | ||
Revision as of 15:26, 11 May 2023
| Passband modulation |
|---|
 |
| Analog modulation |
| Digital modulation |
| Hierarchical modulation |
| Spread spectrum |
| See also |
चरण मॉडुलन (पीएम) ट्रांसमिशन (दूरसंचार) के लिए कंडीशनिंग संचार संकेतों के लिए एक मॉड्यूलेशन प्रतिरूप है। यह एक वाहक तरंग के तात्कालिक चरण में बदलाव के रूप में एक संदेश संकेत को एनकोड करता है। चरण मॉडुलन आवृत्ति मॉडुलन के साथ, कोण मॉडुलन के दो प्रमुख रूपों में से एक है।
चरण मॉडुलन में, बेसबैंड संकेत का तात्कालिक आयाम अपने आयाम और आवृत्ति को स्थिर रखते हुए वाहक संकेत के चरण को संशोधित करता है। संदेश संकेत के बदलते संकेत स्तर (आयाम) का पालन करने के लिए वाहक संकेत के चरण को संशोधित किया जाता है। शिखर आयाम और वाहक संकेत की आवृत्ति स्थिर बनी हुई है, किंतु जैसे ही संदेश संकेत के आयाम में परिवर्तन होता है, वाहक का चरण तदनुसार बदलता है।
चरण मॉडुलन व्यापक रूप से रेडियो तरंगों को प्रसारित करने के लिए उपयोग किया जाता है और यह कई डिजिटल ट्रांसमिशन कोडिंग योजनाओं का एक अभिन्न अंग है जो वाई-फाई, जीएसएम और उपग्रह टेलीविजन जैसी विधियों की एक विस्तृत श्रृंखला को रेखांकित करता है। एफएम संश्लेषण को प्रयुक्त करने के लिए यामाहा ने सफाई की 7 जैसे डिजिटल सिंथेसाइज़र में संकेत और तरंग उत्पादन के लिए भी इसका उपयोग किया जाता है। कैसियो सीजेड सिंथेसाइज़र में एक संबंधित प्रकार का ध्वनि संश्लेषण जिसे चरण विरूपण संश्लेषण कहा जाता है, का उपयोग किया जाता है।
सिद्धांत
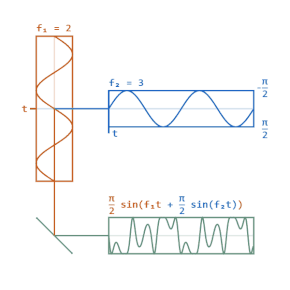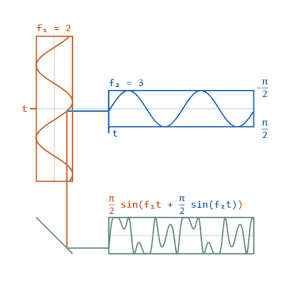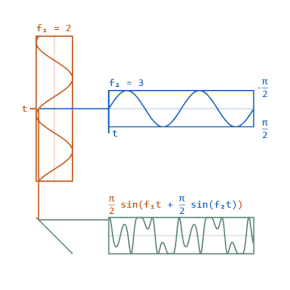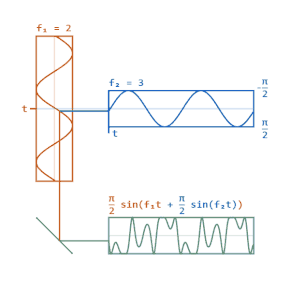
चरण मॉडुलन संदेश संकेत के अनुपात में जटिल लिफाफे के चरण (तरंगों) को बदलता है।
यदि m(t) संचरित होने वाला संदेश संकेत है और वाहक जिस पर संकेत संग्राहक है,
तो संग्राहक संकेत है
यह दर्शाता है कि कैसे चरण को संशोधित करता है - एक समय में जितना अधिक होता है, उस बिंदु पर संग्राहक संकेत का चरण बदलाव उतना ही अधिक होता है। इसे वाहक संकेत की आवृत्ति में परिवर्तन के रूप में भी देखा जा सकता है, और इस प्रकार चरण मॉडुलन को एफएम का एक विशेष स्थिति माना जा सकता है जिसमें वाहक आवृत्ति मॉडुलन चरण मॉडुलन के समय व्युत्पन्न द्वारा दिया जाता है।
मॉडुलन संकेत यहाँ हो सकता है
वर्णक्रमीय घनत्व संबंध के गणित से पता चलता है कि विशेष रुचि के दो क्षेत्र हैं:
- छोटे आयाम संकेतों के लिए, पीएम आयाम मॉड्यूलेशन (एएम) के समान है और बेसबैंड बैंडविड्थ के दुर्भाग्यपूर्ण दोहरीकरण और खराब दक्षता को प्रदर्शित करता है।
- एक बड़े साइनसोइडल सिग्नल के लिए, पीएम एफएम के समान है, और इसकी बैंडविड्थ लगभग है
- ,
मॉडुलन सूचकांक
जैसा कि अन्य मॉड्यूलेशन सूचकांक के साथ होता है, यह मात्रा इस बात को इंगित करती है कि मॉड्यूलेटेड चर अपने अनमॉड्यूलेटेड स्तर के आसपास कितना भिन्न होता है। यह वाहक संकेत के चरण में भिन्नता से संबंधित है:
जहाँ शिखर चरण विचलन है। आवृत्ति मॉड्यूलेशन या मॉड्यूलेशन सूचकांक के लिए मॉड्यूलेशन सूचकांक से तुलना करें।
यह भी देखें
- कोण मॉडुलन
- स्वचालित आवृत्ति नियंत्रण
- अन्य मॉड्यूलेशन विधियों की सूची के लिए मॉड्यूलेशन
- मॉडुलन क्षेत्र
- ध्रुवीय मॉडुलन
- पॉकेल के प्रभाव चरण मॉड्यूलेशन के लिए इलेक्ट्रो-ऑप्टिक न्यूनाधिक एक मोनोक्रोमैटिक तरंग के साइडबैंड लगाने के लिए