हबर्ड मॉडल: Difference between revisions
(Created page with "{{Use dmy dates|date=October 2021}} thumb|2-आयामी हबर्ड मॉडल।हबर्ड मॉडल एक अनुमान...") |
No edit summary |
||
| Line 1: | Line 1: | ||
{{Use dmy dates|date=October 2021}} | {{Use dmy dates|date=October 2021}} | ||
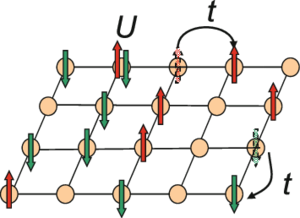
[[File:2D-Hubbard-model.png|thumb|2-आयामी हबर्ड मॉडल।]]हबर्ड मॉडल एक अनुमान है जिसका उपयोग [[ | [[File:2D-Hubbard-model.png|thumb|2-आयामी हबर्ड मॉडल।]]हबर्ड मॉडल एक अनुमान है जिसका उपयोग [[Index.php?title=चालन|चालन]] और विद्युत अवरोधी के बीच संक्रमण का वर्णन करने के लिए किया जाता है।<ref name="Altland"> | ||
{{cite book | {{cite book | ||
|last1=Altland |first=A. | |last1=Altland |first=A. | ||
| Line 13: | Line 13: | ||
}}</ref> यह ठोस अवस्था भौतिकी में विशेष रूप से उपयोगी है। मॉडल का नाम [[जॉन हबर्ड (भौतिक विज्ञानी)]] के नाम पर रखा गया है। | }}</ref> यह ठोस अवस्था भौतिकी में विशेष रूप से उपयोगी है। मॉडल का नाम [[जॉन हबर्ड (भौतिक विज्ञानी)]] के नाम पर रखा गया है। | ||
हबर्ड मॉडल कहता है कि प्रत्येक इलेक्ट्रॉन प्रतिस्पर्धी बलों का अनुभव करता है: एक इसे सुरंग में पड़ोसी परमाणुओं की ओर धकेलता है, जबकि दूसरा इसे अपने पड़ोसियों से दूर धकेलता है।<ref name=":0" />इस प्रकार इसके [[हैमिल्टनियन (क्वांटम यांत्रिकी)]] में दो शब्द हैं: | हबर्ड मॉडल कहता है कि प्रत्येक इलेक्ट्रॉन प्रतिस्पर्धी बलों का अनुभव करता है: एक इसे सुरंग में पड़ोसी परमाणुओं की ओर धकेलता है, जबकि दूसरा इसे अपने पड़ोसियों से दूर धकेलता है।<ref name=":0" />इस प्रकार इसके [[हैमिल्टनियन (क्वांटम यांत्रिकी)]] में दो शब्द हैं:जालक साइटों के बीच कणों की [[Index.php?title=क्वांटम सुरंग|क्वांटम सुरंग]] (hopping) के लिए अनुमति देने वाला एक काइनेटिक शब्द और ऑन-साइट इंटरैक्शन को दर्शाने वाला एक संभावित शब्द। कण या तो [[फरमिओन्स]] हो सकते हैं, जैसा कि हबर्ड के मूल कार्य में है, या बोसोन, जिस स्थिति में मॉडल को बोस-हबर्ड मॉडल कहा जाता है। | ||
The Hubbard model states that each electron experiences competing forces: one pushes it to tunnel to neighboring atoms, while the other pushes it away from its neighbors. Its Hamiltonian thus has two terms: a kinetic term allowing for tunneling ("hopping") of particles between lattice sites and a potential term reflecting on-site interaction. The particles can either be fermions, as in Hubbard's original work, or bosons, in which case the model is referred to as the "Bose–Hubbard model". | |||
हबर्ड मॉडल पर्याप्त रूप से कम तापमान पर आवधिक क्षमता में कणों के लिए एक उपयोगी सन्निकटन है, जहां सभी कणों को सबसे कम बलोच प्रमेय में माना जा सकता है, और कणों के बीच लंबी दूरी की बातचीत को नजरअंदाज किया जा सकता है। यदि जाली के विभिन्न स्थलों पर कणों के बीच परस्पर क्रियाओं को शामिल किया जाता है, तो मॉडल को अक्सर विस्तारित हबर्ड मॉडल कहा जाता है। विशेष रूप से, हबर्ड शब्द, जिसे आमतौर पर यू द्वारा निरूपित किया जाता है, घनत्व कार्यात्मक सिद्धांत, डीएफटी का उपयोग करते हुए पहले सिद्धांतों पर आधारित सिमुलेशन में लागू होता है। डीएफटी सिमुलेशन में हबर्ड शब्द को शामिल करना महत्वपूर्ण है क्योंकि यह इलेक्ट्रॉन स्थानीयकरण की भविष्यवाणी में सुधार करता है और इस प्रकार यह इन्सुलेट सिस्टम में धातु चालन की गलत भविष्यवाणी को रोकता है।<ref>{{Cite journal |doi = 10.1016/j.apsusc.2019.01.208|title = Theoretical insights into the hydrophobicity of low index CeO2 surfaces|journal = Applied Surface Science|volume = 478|pages = 68–74|year = 2019|last1 = Fronzi|first1 = Marco|last2 = Assadi|first2 = M. Hussein N.|last3 = Hanaor|first3 = Dorian A.H.|arxiv = 1902.02662|bibcode = 2019ApSS..478...68F|s2cid = 118895100}}</ref> हबर्ड मॉडल [[टाइट बाइंडिंग]] | टाइट-बाइंडिंग मॉडल के लिए इलेक्ट्रॉनों के बीच शॉर्ट-रेंज इंटरैक्शन का परिचय देता है, जिसमें केवल गतिज ऊर्जा (एक होपिंग टर्म) और जाली के परमाणुओं (एक परमाणु क्षमता) के साथ बातचीत शामिल है। जब इलेक्ट्रॉनों के बीच परस्पर क्रिया मजबूत होती है, तो हबर्ड मॉडल का व्यवहार टाइट-बाइंडिंग मॉडल से गुणात्मक रूप से भिन्न हो सकता है। उदाहरण के लिए, हबर्ड मॉडल सही ढंग से [[मोट इंसुलेटर]] के अस्तित्व की भविष्यवाणी करता है: सामग्री जो इलेक्ट्रॉनों के बीच मजबूत प्रतिकर्षण के कारण इन्सुलेट होती है, भले ही वे कंडक्टर के लिए सामान्य मानदंडों को पूरा करते हैं, जैसे कि प्रति यूनिट सेल में विषम संख्या में इलेक्ट्रॉन होते हैं। | हबर्ड मॉडल पर्याप्त रूप से कम तापमान पर आवधिक क्षमता में कणों के लिए एक उपयोगी सन्निकटन है, जहां सभी कणों को सबसे कम बलोच प्रमेय में माना जा सकता है, और कणों के बीच लंबी दूरी की बातचीत को नजरअंदाज किया जा सकता है। यदि जाली के विभिन्न स्थलों पर कणों के बीच परस्पर क्रियाओं को शामिल किया जाता है, तो मॉडल को अक्सर विस्तारित हबर्ड मॉडल कहा जाता है। विशेष रूप से, हबर्ड शब्द, जिसे आमतौर पर यू द्वारा निरूपित किया जाता है, घनत्व कार्यात्मक सिद्धांत, डीएफटी का उपयोग करते हुए पहले सिद्धांतों पर आधारित सिमुलेशन में लागू होता है। डीएफटी सिमुलेशन में हबर्ड शब्द को शामिल करना महत्वपूर्ण है क्योंकि यह इलेक्ट्रॉन स्थानीयकरण की भविष्यवाणी में सुधार करता है और इस प्रकार यह इन्सुलेट सिस्टम में धातु चालन की गलत भविष्यवाणी को रोकता है।<ref>{{Cite journal |doi = 10.1016/j.apsusc.2019.01.208|title = Theoretical insights into the hydrophobicity of low index CeO2 surfaces|journal = Applied Surface Science|volume = 478|pages = 68–74|year = 2019|last1 = Fronzi|first1 = Marco|last2 = Assadi|first2 = M. Hussein N.|last3 = Hanaor|first3 = Dorian A.H.|arxiv = 1902.02662|bibcode = 2019ApSS..478...68F|s2cid = 118895100}}</ref> हबर्ड मॉडल [[टाइट बाइंडिंग]] | टाइट-बाइंडिंग मॉडल के लिए इलेक्ट्रॉनों के बीच शॉर्ट-रेंज इंटरैक्शन का परिचय देता है, जिसमें केवल गतिज ऊर्जा (एक होपिंग टर्म) और जाली के परमाणुओं (एक परमाणु क्षमता) के साथ बातचीत शामिल है। जब इलेक्ट्रॉनों के बीच परस्पर क्रिया मजबूत होती है, तो हबर्ड मॉडल का व्यवहार टाइट-बाइंडिंग मॉडल से गुणात्मक रूप से भिन्न हो सकता है। उदाहरण के लिए, हबर्ड मॉडल सही ढंग से [[मोट इंसुलेटर]] के अस्तित्व की भविष्यवाणी करता है: सामग्री जो इलेक्ट्रॉनों के बीच मजबूत प्रतिकर्षण के कारण इन्सुलेट होती है, भले ही वे कंडक्टर के लिए सामान्य मानदंडों को पूरा करते हैं, जैसे कि प्रति यूनिट सेल में विषम संख्या में इलेक्ट्रॉन होते हैं। | ||
Revision as of 10:02, 10 May 2023
हबर्ड मॉडल एक अनुमान है जिसका उपयोग चालन और विद्युत अवरोधी के बीच संक्रमण का वर्णन करने के लिए किया जाता है।[1] यह ठोस अवस्था भौतिकी में विशेष रूप से उपयोगी है। मॉडल का नाम जॉन हबर्ड (भौतिक विज्ञानी) के नाम पर रखा गया है।
हबर्ड मॉडल कहता है कि प्रत्येक इलेक्ट्रॉन प्रतिस्पर्धी बलों का अनुभव करता है: एक इसे सुरंग में पड़ोसी परमाणुओं की ओर धकेलता है, जबकि दूसरा इसे अपने पड़ोसियों से दूर धकेलता है।[2]इस प्रकार इसके हैमिल्टनियन (क्वांटम यांत्रिकी) में दो शब्द हैं:जालक साइटों के बीच कणों की क्वांटम सुरंग (hopping) के लिए अनुमति देने वाला एक काइनेटिक शब्द और ऑन-साइट इंटरैक्शन को दर्शाने वाला एक संभावित शब्द। कण या तो फरमिओन्स हो सकते हैं, जैसा कि हबर्ड के मूल कार्य में है, या बोसोन, जिस स्थिति में मॉडल को बोस-हबर्ड मॉडल कहा जाता है।
The Hubbard model states that each electron experiences competing forces: one pushes it to tunnel to neighboring atoms, while the other pushes it away from its neighbors. Its Hamiltonian thus has two terms: a kinetic term allowing for tunneling ("hopping") of particles between lattice sites and a potential term reflecting on-site interaction. The particles can either be fermions, as in Hubbard's original work, or bosons, in which case the model is referred to as the "Bose–Hubbard model".
हबर्ड मॉडल पर्याप्त रूप से कम तापमान पर आवधिक क्षमता में कणों के लिए एक उपयोगी सन्निकटन है, जहां सभी कणों को सबसे कम बलोच प्रमेय में माना जा सकता है, और कणों के बीच लंबी दूरी की बातचीत को नजरअंदाज किया जा सकता है। यदि जाली के विभिन्न स्थलों पर कणों के बीच परस्पर क्रियाओं को शामिल किया जाता है, तो मॉडल को अक्सर विस्तारित हबर्ड मॉडल कहा जाता है। विशेष रूप से, हबर्ड शब्द, जिसे आमतौर पर यू द्वारा निरूपित किया जाता है, घनत्व कार्यात्मक सिद्धांत, डीएफटी का उपयोग करते हुए पहले सिद्धांतों पर आधारित सिमुलेशन में लागू होता है। डीएफटी सिमुलेशन में हबर्ड शब्द को शामिल करना महत्वपूर्ण है क्योंकि यह इलेक्ट्रॉन स्थानीयकरण की भविष्यवाणी में सुधार करता है और इस प्रकार यह इन्सुलेट सिस्टम में धातु चालन की गलत भविष्यवाणी को रोकता है।[3] हबर्ड मॉडल टाइट बाइंडिंग | टाइट-बाइंडिंग मॉडल के लिए इलेक्ट्रॉनों के बीच शॉर्ट-रेंज इंटरैक्शन का परिचय देता है, जिसमें केवल गतिज ऊर्जा (एक होपिंग टर्म) और जाली के परमाणुओं (एक परमाणु क्षमता) के साथ बातचीत शामिल है। जब इलेक्ट्रॉनों के बीच परस्पर क्रिया मजबूत होती है, तो हबर्ड मॉडल का व्यवहार टाइट-बाइंडिंग मॉडल से गुणात्मक रूप से भिन्न हो सकता है। उदाहरण के लिए, हबर्ड मॉडल सही ढंग से मोट इंसुलेटर के अस्तित्व की भविष्यवाणी करता है: सामग्री जो इलेक्ट्रॉनों के बीच मजबूत प्रतिकर्षण के कारण इन्सुलेट होती है, भले ही वे कंडक्टर के लिए सामान्य मानदंडों को पूरा करते हैं, जैसे कि प्रति यूनिट सेल में विषम संख्या में इलेक्ट्रॉन होते हैं।
इतिहास
मॉडल को मूल रूप से 1963 में ठोस पदार्थों में इलेक्ट्रॉनों का वर्णन करने के लिए प्रस्तावित किया गया था।[4] हबर्ड, मार्टिन गुत्ज़विलर और जुन्जिरो कनामोरी प्रत्येक ने स्वतंत्र रूप से इसे प्रस्तावित किया।[2] तब से, इसे उच्च तापमान अतिचालकता, क्वांटम चुंबकत्व और आवेश घनत्व तरंगों के अध्ययन के लिए लागू किया गया है।[5]
संकीर्ण ऊर्जा बैंड सिद्धांत
हबर्ड मॉडल सॉलिड-स्टेट फिजिक्स से टाइट बाइंडिंग | टाइट-बाइंडिंग सन्निकटन पर आधारित है, जो आवधिक क्षमता में चलने वाले कणों का वर्णन करता है, जिसे आमतौर पर जाली समूह के रूप में संदर्भित किया जाता है। वास्तविक सामग्रियों के लिए, प्रत्येक जाली साइट एक आयनिक कोर के अनुरूप हो सकती है, और कण इन आयनों के संयोजी इलेक्ट्रॉन होंगे। तंग-बाध्यकारी सन्निकटन में, हैमिल्टनियन को वानियर समारोह के संदर्भ में लिखा गया है, जो प्रत्येक जाली साइट पर केंद्रित स्थानीयकृत राज्य हैं। पड़ोसी जाली साइटों पर वानियर राज्य युग्मित हैं, जिससे एक साइट पर कण दूसरे स्थान पर जा सकते हैं। गणितीय रूप से, इस युग्मन की ताकत पास की साइटों के बीच एक हॉपिंग इंटीग्रल या ट्रांसफर इंटीग्रल द्वारा दी जाती है। सिस्टम को टाइट-बाइंडिंग लिमिट में कहा जाता है जब होपिंग इंटीग्रल्स की ताकत दूरी के साथ तेजी से गिरती है। यह युग्मन प्रत्येक जाली साइट से जुड़े राज्यों को संकरण करने की अनुमति देता है, और इस तरह के एक क्रिस्टलीय प्रणाली के खुद के राज्यों बलोच के प्रमेय हैं। बलोच के कार्य, अलग-अलग इलेक्ट्रॉनिक बैंड संरचना में विभाजित ऊर्जा स्तरों के साथ। बैंड की चौड़ाई होपिंग इंटीग्रल के मूल्य पर निर्भर करती है।
हबर्ड मॉडल जाली के प्रत्येक स्थल पर विपरीत स्पिन के कणों के बीच एक संपर्क संपर्क का परिचय देता है। जब इलेक्ट्रॉन प्रणालियों का वर्णन करने के लिए हबर्ड मॉडल का उपयोग किया जाता है, तो इलेक्ट्रिक-फील्ड स्क्रीनिंग से उपजी इन अंतःक्रियाओं के प्रतिकारक होने की उम्मीद की जाती है। हालाँकि, आकर्षक बातचीत पर भी अक्सर विचार किया गया है। हबर्ड मॉडल की भौतिकी को होपिंग इंटीग्रल की ताकत के बीच प्रतिस्पर्धा द्वारा निर्धारित किया जाता है, जो सिस्टम की गतिज ऊर्जा की विशेषता है, और अंतःक्रियात्मक शब्द की ताकत है। हबर्ड मॉडल इसलिए कुछ अंतःक्रियात्मक प्रणालियों में धातु से इन्सुलेटर में संक्रमण की व्याख्या कर सकता है। उदाहरण के लिए, इसका उपयोग धातु के आक्साइड का वर्णन करने के लिए किया गया है क्योंकि वे गर्म होते हैं, जहां निकटतम-पड़ोसी रिक्ति में इसी वृद्धि से उस बिंदु पर hopping अभिन्न अंग कम हो जाता है जहां ऑन-साइट क्षमता प्रमुख होती है। इसी तरह, हबर्ड मॉडल दुर्लभ-पृथ्वी pyrochlor जैसे सिस्टम में कंडक्टर से इंसुलेटर तक संक्रमण की व्याख्या कर सकता है क्योंकि दुर्लभ-पृथ्वी धातु की परमाणु संख्या बढ़ जाती है, क्योंकि जालीदार मापदंड बढ़ता है (या परमाणुओं के बीच का कोण भी बदल सकता है) दुर्लभ-पृथ्वी तत्व परमाणु संख्या बढ़ जाती है, इस प्रकार ऑन-साइट प्रतिकर्षण की तुलना में होपिंग इंटीग्रल के सापेक्ष महत्व को बदल देता है।
उदाहरण: एक आयामी हाइड्रोजन परमाणु श्रृंखला
तथाकथित s कक्षीय में हाइड्रोजन परमाणु में एक इलेक्ट्रॉन होता है, जिसे या तो स्पिन किया जा सकता है () या स्पिन डाउन (). इस कक्षीय में अधिकतम दो इलेक्ट्रॉन हो सकते हैं, एक स्पिन (भौतिकी) के साथ ऊपर और एक नीचे (पाउली अपवर्जन सिद्धांत देखें)।
बैंड सिद्धांत के तहत, हाइड्रोजन परमाणुओं की 1डी श्रृंखला के लिए, 1एस कक्षीय एक सतत बैंड बनाता है, जो बिल्कुल आधा भरा होगा। इस प्रकार हाइड्रोजन परमाणुओं की 1डी श्रृंखला पारंपरिक बैंड सिद्धांत के तहत एक कंडक्टर होने की भविष्यवाणी की जाती है। यह 1D स्ट्रिंग एकमात्र कॉन्फ़िगरेशन है जो सीधे हल करने के लिए पर्याप्त सरल है।[2]
लेकिन उस मामले में जहां हाइड्रोजन परमाणुओं के बीच की दूरी धीरे-धीरे बढ़ जाती है, किसी बिंदु पर श्रृंखला को एक इन्सुलेटर बनना चाहिए।
हबर्ड मॉडल का उपयोग करके व्यक्त किया गया, हैमिल्टनियन दो शब्दों से बना है। पहला शब्द सिस्टम की गतिज ऊर्जा का वर्णन करता है, जो होपिंग इंटीग्रल द्वारा परिचालित होता है, . दूसरा कार्यकाल शक्ति की ऑन-साइट सहभागिता है जो इलेक्ट्रॉन प्रतिकर्षण का प्रतिनिधित्व करता है। दूसरे क्वांटिज़ेशन नोटेशन में लिखा गया, हबर्ड हैमिल्टनियन (क्वांटम यांत्रिकी) तब रूप लेता है
कहाँ स्पिन के लिए स्पिन-घनत्व ऑपरेटर है पर -थ साइट। घनत्व ऑपरेटर है और का कब्जा वेवफंक्शन के लिए -th साइट है . आमतौर पर टी को सकारात्मक माना जाता है, और यू या तो सकारात्मक या नकारात्मक हो सकता है, लेकिन इलेक्ट्रॉनिक सिस्टम पर विचार करते समय इसे सकारात्मक माना जाता है।
दूसरे कार्यकाल के योगदान के बिना, हैमिल्टन नियमित बैंड सिद्धांत से तंग बाध्यकारी सूत्र का समाधान करता है।
दूसरे कार्यकाल को शामिल करने से एक यथार्थवादी मॉडल उत्पन्न होता है जो कंडक्टर से इंसुलेटर तक एक संक्रमण की भविष्यवाणी करता है, जो कि होपिंग के लिए बातचीत के अनुपात के रूप में होता है, , विविध है। इस अनुपात को संशोधित किया जा सकता है, उदाहरण के लिए, अंतर-परमाणु रिक्ति को बढ़ाकर, जिससे परिमाण कम हो जाएगा प्रभावित किए बिना . सीमा में कहाँ , श्रृंखला बस पृथक चुंबकीय क्षणों के एक सेट में हल हो जाती है। अगर बहुत बड़ा नहीं है, ओवरलैप इंटीग्रल पड़ोसी चुंबकीय क्षणों के बीच superexchange इंटरैक्शन प्रदान करता है, जिससे मॉडल मापदंडों के आधार पर विभिन्न प्रकार के दिलचस्प चुंबकीय सहसंबंध हो सकते हैं, जैसे कि फेरोमैग्नेटिक, एंटीफेरोमैग्नेटिक आदि। एक आयामी हबर्ड मॉडल को इलियट एच. लीब और वू ने बेथे दृष्टिकोण का उपयोग करके हल किया था। 1990 के दशक में आवश्यक प्रगति हासिल की गई थी: एक यांग्यान की खोज की गई थी, और एस मैट्रिक्स , सहसंबंध समारोह (सांख्यिकीय यांत्रिकी), thermodynamic और क्वांटम उलझाव का मूल्यांकन किया गया था।[6]
अधिक जटिल प्रणालियाँ
यद्यपि हबर्ड हाइड्रोजन परमाणुओं की 1डी श्रृंखला जैसी प्रणालियों का वर्णन करने में उपयोगी है, यह ध्यान रखना महत्वपूर्ण है कि अधिक जटिल प्रणालियां अन्य प्रभावों का अनुभव कर सकती हैं जिन पर हबर्ड मॉडल विचार नहीं करता है। सामान्य तौर पर, इंसुलेटर को मेटल-इंसुलेटर ट्रांजिशन | मॉट-हबर्ड इंसुलेटर और चार्ज-ट्रांसफर इंसुलेटर में विभाजित किया जा सकता है।
एक मॉट-हबर्ड इन्सुलेटर के रूप में वर्णित किया जा सकता है
इसे हाइड्रोजन श्रृंखलाओं के लिए हबर्ड मॉडल के अनुरूप देखा जा सकता है, जहां इकाई कोशिकाओं के बीच प्रवाहकत्त्व को स्थानांतरण अभिन्न द्वारा वर्णित किया जा सकता है।
हालाँकि, इलेक्ट्रॉनों के लिए दूसरे प्रकार का व्यवहार प्रदर्शित करना संभव है:
इसे चार्ज ट्रांसफर के रूप में जाना जाता है और चार्ज-ट्रांसफर इंसुलेटर में परिणाम होता है। मॉट-हबर्ड इंसुलेटर के विपरीत इलेक्ट्रॉन स्थानांतरण केवल एक इकाई सेल के भीतर होता है।
ये दोनों प्रभाव मौजूद हो सकते हैं और जटिल आयनिक प्रणालियों में प्रतिस्पर्धा कर सकते हैं।
संख्यात्मक उपचार
तथ्य यह है कि हबर्ड मॉडल को मनमाना आयामों में विश्लेषणात्मक रूप से हल नहीं किया गया है, इन दृढ़ता से सहसंबद्ध इलेक्ट्रॉन प्रणालियों के लिए संख्यात्मक तरीकों में गहन शोध किया गया है।[7][8] इस शोध का एक प्रमुख लक्ष्य इस मॉडल के निम्न-तापमान चरण आरेख को निर्धारित करना है, विशेष रूप से दो-आयामों में। विभिन्न तरीकों से परिमित प्रणालियों पर हबर्ड मॉडल का अनुमानित संख्यात्मक उपचार संभव है।
ऐसी ही एक विधि, लैंक्ज़ोस एल्गोरिथम, सिस्टम के स्थिर और गतिशील गुणों का उत्पादन कर सकती है। इस पद्धति का उपयोग करके जमीनी स्थिति की गणना के लिए राज्यों की संख्या के आकार के तीन वैक्टरों के भंडारण की आवश्यकता होती है। सिस्टम के आकार के साथ राज्यों की संख्या तेजी से बढ़ती है, जो जाली में साइटों की संख्या को 21 वीं सदी के हार्डवेयर पर लगभग 20 तक सीमित करती है। प्रोजेक्टर और परिमित-तापमान सहायक-क्षेत्र मोंटे कार्लो के साथ, दो सांख्यिकीय विधियां मौजूद हैं जो सिस्टम के कुछ गुणों को प्राप्त कर सकती हैं। कम तापमान के लिए, अभिसरण समस्याएं दिखाई देती हैं जो तथाकथित फर्मियन साइन समस्या के कारण घटते तापमान के साथ एक घातीय कम्प्यूटेशनल प्रयास की ओर ले जाती हैं।
हबर्ड मॉडल का अध्ययन गतिशील माध्य-क्षेत्र सिद्धांत (DMFT) के भीतर किया जा सकता है। यह योजना हबर्ड हैमिल्टनियन को एंडरसन अशुद्धता मॉडल | एकल-साइट अशुद्धता मॉडल पर मैप करती है, एक मैपिंग जो केवल अनंत आयामों में औपचारिक रूप से सटीक है और परिमित आयामों में केवल सभी विशुद्ध रूप से स्थानीय सहसंबंधों के सटीक उपचार से मेल खाती है। डीएमएफटी किसी को दिए गए हबर्ड मॉडल के स्थानीय ग्रीन के कार्य की गणना करने की अनुमति देता है और एक दिया गया तापमान। DMFT के भीतर, वर्णक्रमीय कार्य के विकास की गणना की जा सकती है और ऊपरी और निचले हबर्ड बैंड की उपस्थिति को सहसंबंध बढ़ने के रूप में देखा जा सकता है।
सिम्युलेटर
विषम 2-आयामी संक्रमण धातु डाइक्लोजेनाइड मोनोलेयर्स के ढेर | संक्रमण धातु डाइक्लोजेनाइड्स (टीएमडी) का उपयोग एक से अधिक आयामों में ज्यामिति का अनुकरण करने के लिए किया गया है। टंगस्टन सेलेनाइड और टंगस्टन सल्फाइड को ढेर कर दिया गया था। इसने हेक्सागोनल सुपरसेल (क्रिस्टल) (दो सामग्रियों के संबंध द्वारा परिभाषित पुनरावृत्ति इकाइयों) से मिलकर एक मोरी सुपरलैटिस बनाया। प्रत्येक सुपरसेल तब ऐसा व्यवहार करता है जैसे कि वह एक ही परमाणु हो। सुपरसेल के बीच की दूरी उनके भीतर के परमाणुओं की दूरी से लगभग 100 गुना है। यह बड़ी दूरी सुपरसेल्स में इलेक्ट्रॉन टनलिंग को काफी कम कर देती है।[9] उनका उपयोग विग्नर क्रिस्टल बनाने के लिए किया जा सकता है। विद्युत क्षेत्र को विनियमित करने के लिए इलेक्ट्रोड संलग्न किए जा सकते हैं। विद्युत क्षेत्र नियंत्रित करता है कि प्रत्येक सुपरसेल में कितने इलेक्ट्रॉन भरते हैं। सुपरसेल प्रति इलेक्ट्रॉनों की संख्या प्रभावी ढंग से निर्धारित करती है कि जाली किस परमाणु का अनुकरण करती है। एक इलेक्ट्रॉन/सेल हाइड्रोजन की तरह व्यवहार करता है, दो/सेल हीलियम की तरह, आदि। 2022 तक, आठ इलेक्ट्रॉनों (ऑक्सीजन) तक के सुपरसेल को सिम्युलेट किया जा सकता है। सिमुलेशन के एक परिणाम से पता चला है कि धातु और इन्सुलेटर के बीच का अंतर विद्युत क्षेत्र की ताकत का एक सतत कार्य है।[9]
एक बैकवर्ड स्टैकिंग व्यवस्था विषम क्वांटम हॉल प्रभाव के माध्यम से एक चेर्न इंसुलेटर के निर्माण की अनुमति देती है (डिवाइस के किनारों के साथ एक कंडक्टर के रूप में कार्य करता है जबकि इंटीरियर एक इन्सुलेटर के रूप में कार्य करता है।) डिवाइस 5 केल्विन के तापमान पर काम करता है, जो कि ऊपर है। तापमान जिस पर पहली बार प्रभाव देखा गया था।[9]
यह भी देखें
- एंडरसन अशुद्धता मॉडल
- बलोच की प्रमेय
- इलेक्ट्रॉनिक बैंड संरचना
- भौतिक विज्ञान की ठोस अवस्था
- बोस-हबर्ड मॉडल
- टी-जे मॉडल
- हाइजेनबर्ग मॉडल (क्वांटम)
- डायनेमिकल मीन-फील्ड थ्योरी
- स्टोनर कसौटी
संदर्भ
- ↑ Altland, A.; Simons, B. (2006). "Interaction effects in the tight-binding system". Condensed Matter Field Theory. Cambridge University Press. pp. 58 ff. ISBN 978-0-521-84508-3.
- ↑ 2.0 2.1 2.2 Wood, Charlie (16 August 2022). "फिजिक्स डुओ को दो आयामों में जादू लगता है". Quanta Magazine (in English). Retrieved 21 August 2022.
- ↑ Fronzi, Marco; Assadi, M. Hussein N.; Hanaor, Dorian A.H. (2019). "Theoretical insights into the hydrophobicity of low index CeO2 surfaces". Applied Surface Science. 478: 68–74. arXiv:1902.02662. Bibcode:2019ApSS..478...68F. doi:10.1016/j.apsusc.2019.01.208. S2CID 118895100.
- ↑ Hubbard, J. (26 November 1963). "संकीर्ण ऊर्जा बैंड में इलेक्ट्रॉन सहसंबंध". Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences. 276 (1365): 238–257. Bibcode:1963RSPSA.276..238H. doi:10.1098/rspa.1963.0204. ISSN 0080-4630. S2CID 35439962.
- ↑ Auerbach, Assa. (1994). इंटरेक्टिंग इलेक्ट्रॉन और क्वांटम चुंबकत्व. New York: Springer-Verlag. ISBN 0-387-94286-6. OCLC 30028928.
- ↑ Essler, F. H. L.; Frahm, H.; Göhmann, F.; Klümper, A.; Korepin, V. E. (2005). The One-Dimensional Hubbard Model. Cambridge University Press. ISBN 978-0-521-80262-8.
- ↑
Scalapino, D. J. (2006). "Numerical Studies of the 2D Hubbard Model": cond–mat/0610710. arXiv:cond-mat/0610710. Bibcode:2006cond.mat.10710S.
{{cite journal}}: Cite journal requires|journal=(help) - ↑ LeBlanc, J. (2015). "Solutions of the Two-Dimensional Hubbard Model: Benchmarks and Results from a Wide Range of Numerical Algorithms". Physical Review X. 5 (4): 041041. arXiv:1505.02290. Bibcode:2015PhRvX...5d1041L. doi:10.1103/PhysRevX.5.041041.
- ↑ 9.0 9.1 9.2 Wood, Charlie (16 August 2022). "फिजिक्स डुओ को दो आयामों में जादू लगता है". Quanta Magazine (in English). Retrieved 21 August 2022.
अग्रिम पठन
- Hubbard, J. (1963). "Electron Correlations in Narrow Energy Bands". Proceedings of the Royal Society of London. 276 (1365): 238–257. Bibcode:1963RSPSA.276..238H. doi:10.1098/rspa.1963.0204. JSTOR 2414761. S2CID 35439962.
- Bach, V.; Lieb, E. H.; Solovej, J. P. (1994). "Generalized Hartree–Fock Theory and the Hubbard Model". Journal of Statistical Physics. 76 (1–2): 3. arXiv:cond-mat/9312044. Bibcode:1994JSP....76....3B. doi:10.1007/BF02188656. S2CID 207143.
- Lieb, E. H. (1995). "The Hubbard Model: Some Rigorous Results and Open Problems". Xi Int. Cong. Mp, Int. Press (?). 1995: cond–mat/9311033. arXiv:cond-mat/9311033. Bibcode:1993cond.mat.11033L.
- Gebhard, F. (1997). "Metal–Insulator Transition". The Mott Metal–Insulator Transition: Models and Methods. Springer Tracts in Modern Physics. Vol. 137. Springer. pp. 1–48. ISBN 9783540614814.
- Lieb, E. H.; Wu, F. Y. (2003). "The one-dimensional Hubbard model: A reminiscence". Physica A. 321 (1): 1–27. arXiv:cond-mat/0207529. Bibcode:2003PhyA..321....1L. doi:10.1016/S0378-4371(02)01785-5. S2CID 44758937.