टेलर कोन: Difference between revisions
No edit summary |
No edit summary |
||
| Line 9: | Line 9: | ||
== सिद्धांत == | == सिद्धांत == | ||
1964 में सर जेफ्री इनग्राम टेलर ने इस घटना का वर्णन | 1964 में सर जेफ्री इनग्राम टेलर ने इस घटना का वर्णन सैद्धांतिक रूप से सामान्य धारणाओं के आधार पर किया था कि ऐसी परिस्थितियों में एक पूर्ण शंकु बनाने की आवश्यकताओं के लिए 49.3 डिग्री (98.6 डिग्री का एक पूर्ण कोण) के अर्ध-ऊर्ध्वाधर कोण की आवश्यकता होती है और यह प्रदर्शित करता है कि इस प्रकार के आकार जेट गठन से ठीक पहले एक शंकु सैद्धांतिक आकार के पास पहुंचा। इस कोण को '''टेलर कोण''' के नाम से जाना जाता है। यह कोण अधिक त्रुटिहीन <math>\pi-\theta _0\,</math> है जहाँ <math>\theta _0\,</math><math>P _{1/2} (\cos\theta _0)\,</math>(आदेश 1/2 का [[लेजेंड्रे समारोह|लेजेंड्रे फलन]]) का प्रथम शून्य है। | ||
टेलर की व्युत्पत्ति दो धारणाओं पर आधारित है: (1) कि शंकु की सतह एक समविभव सतह है और (2) कि शंकु स्थिर अवस्था संतुलन में | टेलर की व्युत्पत्ति दो धारणाओं पर आधारित है: (1) कि शंकु की सतह एक समविभव सतह है और (2) कि शंकु स्थिर अवस्था संतुलन में उपस्थित है। इन दोनों मानदंडों को पूरा करने के लिए विद्युत क्षेत्र में [[दिगंश]] समरूपता होनी चाहिए और शंकु का उत्पादन करने के लिए सतह के तनाव का मुकाबला करने के लिए <math>\sqrt{R}\,</math> निर्भरता होनी चाहिए। इस समस्या का समाधान है: | ||
:<math>V=V_0+AR^{1/2}P _{1/2} (\cos\theta _0)\,</math> | :<math>V=V_0+AR^{1/2}P _{1/2} (\cos\theta _0)\,</math> | ||
जहाँ <math>V=V_0\,</math> (समविभव सतह) एक समविभव शंकु का निर्माण करने वाले <math>\theta _0</math> (R का ध्यान दिए बिना) के मान पर उपस्थित है। सभी R के लिए <math>V=V_0\,</math> के लिए आवश्यक कोण 0 और <math>\pi\,</math> के बीच <math>P _{1/2} (\cos\theta _0)\,</math> का एक शून्य है, जो 130.7099° पर केवल एक है। इस कोण का पूरक टेलर कोण है। | |||
== संदर्भ == | == संदर्भ == | ||
Revision as of 08:17, 15 June 2023
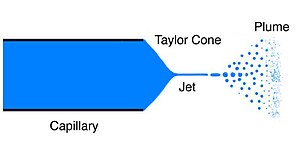
टेलर कोन इलेक्ट्रोस्पिनिंग, इलेक्ट्रोस्प्रेइंग और हाइड्रोडायनेमिक स्प्रे प्रक्रियाओं में देखे गए शंकु को संदर्भित करता है, जिसमें से आवेशित कणों का जेट एक थ्रेशोल्ड वोल्टेज से ऊपर निकलता है। मास स्पेक्ट्रोमेट्री में इलेक्ट्रोस्प्रे आयनीकरण के अतिरिक्त, टेलर शंकु क्षेत्र-उत्सर्जन विद्युत प्रणोदन (एफईईपी) और कोलाइड थ्रस्टर्स में महत्वपूर्ण नियंत्रण और उच्च दक्षता (कम शक्ति) अंतरिक्ष यान के थ्रस्ट में उपयोग किया जाता है।
इतिहास
इलेक्ट्रोस्प्रे की खोज से पहले 1964 में सर जेफ्री इनग्राम टेलर द्वारा इस शंकु का वर्णन किया गया था।[1] इस काम के बाद जॉन ज़ेलेनी के काम का अनुसरण किया गया,[2] जिन्होंने एक शक्तिशाली विद्युत क्षेत्र में ग्लिसरीन के एक शंकु-जेट और कई अन्य लोगों: विल्सन और टेलर (1925),[3] नोलन (1926)[4] और मैकी (1931) के काम का छायांकन किया था।[5] टेलर मुख्य रूप से तेज बिजली के क्षेत्रों जैसे आंधी में पानी की बूंदों के व्यवहार में रुचि रखते थे।
गठन
जब विद्युत प्रवाहकीय तरल की छोटी मात्रा एक विद्युत क्षेत्र के संपर्क में आती है, तो तरल का आकार केवल सतह तनाव के कारण होने वाले आकार से ख़राब होने लगता है। जैसे ही वोल्टेज बढ़ता है विद्युत क्षेत्र का प्रभाव अधिक प्रमुख हो जाता है। जैसे ही विद्युत क्षेत्र का यह प्रभाव छोटी बूंद पर बल के समान परिमाण को प्रायुक्त करना प्रारंभ करता है, जैसा कि सतह तनाव करता है, एक शंकु आकार उत्तल पक्षों और एक गोल टिप के साथ बनना प्रारंभ होता है। यह 98.6° के पूरे कोण (चौड़ाई) के साथ एक शंकु (ज्यामिति) के आकार तक पहुंचता है।[1] जब एक निश्चित थ्रेसहोल्ड वोल्टेज कुछ गोलाकार टिप तक पहुंच जाता है और तरल के एक जेट का उत्सर्जन करता है। इसे कोन-जेट कहा जाता है और यह इलेक्ट्रोस्प्रेइंग प्रक्रिया का प्रारंभ है जिसमें आयनों को गैस चरण में स्थानांतरित किया जा सकता है। यह सामान्यतः पाया जाता है कि स्थिर शंकु-जेट प्राप्त करने के लिए थ्रेसहोल्ड वोल्टेज से कुछ अधिक उपयोग किया जाना चाहिए। जैसे ही वोल्टेज और भी अधिक बढ़ जाता है, छोटी बूंदों के विघटन के अन्य विधि पाए जाते हैं। टेलर कोन शब्द विशेष रूप से पूर्वानुमानित कोण के पूर्ण शंकु की सैद्धांतिक सीमा को संदर्भित कर सकता है या सामान्यतः विद्युतप्रसार प्रक्रिया प्रारंभ होने के बाद शंकु-जेट के लगभग शंक्वाकार भाग को संदर्भित करता है।
सिद्धांत
1964 में सर जेफ्री इनग्राम टेलर ने इस घटना का वर्णन सैद्धांतिक रूप से सामान्य धारणाओं के आधार पर किया था कि ऐसी परिस्थितियों में एक पूर्ण शंकु बनाने की आवश्यकताओं के लिए 49.3 डिग्री (98.6 डिग्री का एक पूर्ण कोण) के अर्ध-ऊर्ध्वाधर कोण की आवश्यकता होती है और यह प्रदर्शित करता है कि इस प्रकार के आकार जेट गठन से ठीक पहले एक शंकु सैद्धांतिक आकार के पास पहुंचा। इस कोण को टेलर कोण के नाम से जाना जाता है। यह कोण अधिक त्रुटिहीन है जहाँ (आदेश 1/2 का लेजेंड्रे फलन) का प्रथम शून्य है।
टेलर की व्युत्पत्ति दो धारणाओं पर आधारित है: (1) कि शंकु की सतह एक समविभव सतह है और (2) कि शंकु स्थिर अवस्था संतुलन में उपस्थित है। इन दोनों मानदंडों को पूरा करने के लिए विद्युत क्षेत्र में दिगंश समरूपता होनी चाहिए और शंकु का उत्पादन करने के लिए सतह के तनाव का मुकाबला करने के लिए निर्भरता होनी चाहिए। इस समस्या का समाधान है:
जहाँ (समविभव सतह) एक समविभव शंकु का निर्माण करने वाले (R का ध्यान दिए बिना) के मान पर उपस्थित है। सभी R के लिए के लिए आवश्यक कोण 0 और के बीच का एक शून्य है, जो 130.7099° पर केवल एक है। इस कोण का पूरक टेलर कोण है।
संदर्भ
- ↑ 1.0 1.1 Sir Geoffrey Taylor (1964). "एक विद्युत क्षेत्र में पानी की बूंदों का विघटन". Proceedings of the Royal Society A. 280 (1382): 383–397. Bibcode:1964RSPSA.280..383T. doi:10.1098/rspa.1964.0151. JSTOR 2415876.
- ↑ Zeleny, J. (1914). "तरल बिंदुओं से विद्युत निर्वहन, और उनकी सतहों पर विद्युत तीव्रता को मापने का एक हाइड्रोस्टेटिक तरीका।". Physical Review. 3 (2): 69–91. Bibcode:1914PhRv....3...69Z. doi:10.1103/PhysRev.3.69.
- ↑ Wilson, C. T.; G. I Taylor (1925). "एक समान विद्युत क्षेत्र में साबुन के बुलबुले का फूटना". Proc. Cambridge Philos. Soc. 22 (5): 728. Bibcode:1925PCPS...22..728W. doi:10.1017/S0305004100009609.
- ↑ Nolan, J. J. (1926). "विद्युत क्षेत्रों द्वारा जल-बूंदों का टूटना". Proc. R. Ir. Acad. A. 37: 28.
- ↑ Macky, W. A. (October 1, 1931). "मजबूत विद्युत क्षेत्रों में पानी की बूंदों के विरूपण और टूटने पर कुछ जांच". Proceedings of the Royal Society A. 133 (822): 565–587. Bibcode:1931RSPSA.133..565M. doi:10.1098/rspa.1931.0168.