द्वि-आयामी फ़िल्टर: Difference between revisions
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
कई डोमेन में उनके महत्व और उच्च प्रयोज्यता के कारण | कई डोमेन में उनके महत्व और उच्च प्रयोज्यता के कारण द्वि आयामी फिल्टर ने पर्याप्त विकास प्रयास देखा है। 2-डी स्थितियों में स्थिति 1-डी स्थितियों से अत्यधिक भिन्न होती है, क्योंकि बहु-आयामी बहुपदों को सामान्य रूप से कारक नहीं बनाया जा सकता है। इसका तात्पर्य यह है कि इच्छानुसार स्थानांतरण फलन सामान्यतः किसी विशेष कार्यान्वयन के लिए आवश्यक रूप में हेरफेर नहीं किया जा सकता है। 2-डी आईआईआर फिल्टर का इनपुट-आउटपुट संबंध निरंतर-गुणांक रैखिक आंशिक विभेदक समीकरण का पालन करता है, जिससे इनपुट नमूनों और पहले से गणना किए गए आउटपुट नमूनों का उपयोग करके आउटपुट नमूने का मूल्य गणना किया जा सकता है। चूंकि आउटपुट नमूने के मूल्यों को वापस खिलाया जाता है, 2-डी फ़िल्टर, इसके 1-डी समकक्ष की प्रकार, अस्थिर हो सकता है। | ||
== प्रेरणा और अनुप्रयोग == | == प्रेरणा और अनुप्रयोग == | ||
सूचना विज्ञान और [[ कम्प्यूटिंग |कम्प्यूटिंग]] प्रौद्योगिकी के तेजी से विकास के कारण, डिजिटल फिल्टर डिजाइन और अनुप्रयोग के सिद्धांत ने आगे छलांग लगाई है। हम वास्तविक जीवन में विभिन्न प्रकार के संकेतों का सामना करते हैं, जैसे कि [[प्रसारण]] संकेत, [[टेलीविजन]] संकेत, [[राडार]] संकेत, [[ चल दूरभाष |चल दूरभाष]] संकेत, [[ मार्गदर्शन |मार्गदर्शन]] संकेत, [[रेडियो खगोल विज्ञान]] संकेत, जैव चिकित्सा संकेत, नियंत्रण संकेत, मौसम संकेत, भूकंपीय संकेत, यांत्रिक कंपन संकेत, [[रिमोट सेंसिंग]] और [[ टेलीमेटरी |टेलीमेटरी]] सिग्नल | सूचना विज्ञान और [[ कम्प्यूटिंग |कम्प्यूटिंग]] प्रौद्योगिकी के तेजी से विकास के कारण, डिजिटल फिल्टर डिजाइन और अनुप्रयोग के सिद्धांत ने आगे छलांग लगाई है। हम वास्तविक जीवन में विभिन्न प्रकार के संकेतों का सामना करते हैं, जैसे कि [[प्रसारण]] संकेत, [[टेलीविजन]] संकेत, [[राडार]] संकेत, [[ चल दूरभाष |चल दूरभाष]] संकेत, [[ मार्गदर्शन |मार्गदर्शन]] संकेत, [[रेडियो खगोल विज्ञान]] संकेत, जैव चिकित्सा संकेत, नियंत्रण संकेत, मौसम संकेत, भूकंपीय संकेत, यांत्रिक कंपन संकेत, [[रिमोट सेंसिंग]] और [[ टेलीमेटरी |टेलीमेटरी]] सिग्नल इत्यादि इस प्रकार है । इनमें से अधिकतर सिग्नल एनालॉग सिग्नल हैं और उनमें से एकमात्र छोटा सा भाग डिजिटल सिग्नल हैं। एनालॉग सिग्नल स्वतंत्र चर के [[निरंतर कार्य]] हैं, जो एक-आयामी, द्वि-आयामी या बहुआयामी हो सकते हैं। अधिकतर स्थितियों में, आयामी एनालॉग सिग्नल का चर समय होता है। समय के नमूने और परिमाण के [[विवेक]] के बाद, ऐसा एनालॉग सिग्नल आयामी डिजिटल सिग्नल बन जाएगा। परिणामी डिजिटल सिग्नल को असतत अनुक्रम द्वारा दर्शाया जा सकता है। उदाहरण के लिए, सामान्य संकेत ध्वनि संकेत है। द्वि-आयामी संकेत का उदाहरण छवि है। फ़िल्टर ऐसी प्रणाली है जो सिग्नल को दूसरे सिग्नल में बदल सकती है। इस प्रकार के परिवर्तन के उदाहरणों में शोर हटाने के लिए सिग्नल को चिकना करना, सिग्नल से आवृत्ति घटकों को हटाना और सिग्नल बढ़ाने के लिए आवृत्ति घटकों को बढ़ाना सम्मलित है। फ़िल्टर का डिज़ाइन और कार्यान्वयन सिग्नल विश्लेषण और प्रसंस्करण प्रौद्योगिकी की महत्वपूर्ण शाखा है। फ़िल्टर सिग्नल अधिग्रहण, ट्रांसमिशन, प्रोसेसिंग और एक्सचेंज में भी मुख्य भूमिका निभाते हैं। | ||
== समस्या कथन और बुनियादी अवधारणाएँ == | == समस्या कथन और बुनियादी अवधारणाएँ == | ||
| Line 12: | Line 12: | ||
=== द्वि-आयामी डिजिटल फ़िल्टर === | === द्वि-आयामी डिजिटल फ़िल्टर === | ||
द्वि-आयामी डिजिटल संकेतों को संसाधित करने के लिए द्वि-आयामी फ़िल्टर का उपयोग किया जाता है। 1-डी और 2-डी डिजिटल फ़िल्टर समस्याओं के डिज़ाइन के बीच महत्वपूर्ण अंतर है। 1-डी स्थितियों में, फिल्टर के डिजाइन और कार्यान्वयन को अलग से अधिक आसानी से माना जा सकता है। फ़िल्टर को पहले डिज़ाइन किया जा सकता है और फिर, स्थानांतरण | द्वि-आयामी डिजिटल संकेतों को संसाधित करने के लिए द्वि-आयामी फ़िल्टर का उपयोग किया जाता है। 1-डी और 2-डी डिजिटल फ़िल्टर समस्याओं के डिज़ाइन के बीच महत्वपूर्ण अंतर है। 1-डी स्थितियों में, फिल्टर के डिजाइन और कार्यान्वयन को अलग से अधिक आसानी से माना जा सकता है। फ़िल्टर को पहले डिज़ाइन किया जा सकता है और फिर, स्थानांतरण फलन के उचित जोड़-तोड़ के माध्यम से, किसी विशेष नेटवर्क संरचना के लिए आवश्यक गुणांक निर्धारित किया जा सकता है। चूँकि 2-डी स्थितियों में, डिजाइन और कार्यान्वयन अधिक निकटता से संबंधित हैं। चूंकि बहुआयामी बहुपदों को सामान्य रूप से कारक नहीं बनाया जा सकता है। इसका तात्पर्य यह है कि इच्छानुसार से बहु-आयामी हस्तांतरण फलन को सामान्यतः किसी विशेष कार्यान्वयन के लिए आवश्यक रूप में हेरफेर नहीं किया जा सकता है। यदि हमारा कार्यान्वयन एकमात्र कारक हस्तांतरण कार्यों को अनुभूत कर सकता है, तो हमारे डिज़ाइन एल्गोरिदम को इस वर्ग के एकमात्र फ़िल्टर डिज़ाइन करने के लिए तैयार किया जाना चाहिए। इसका डिजाइन की समस्या को जटिल बनाने और व्यावहारिक कार्यान्वयन की संख्या को सीमित करने का प्रभाव है। डिजिटल फिल्टर को दो मुख्य प्रकारों में वर्गीकृत किया जा सकता है, अर्थात् [[परिमित आवेग प्रतिक्रिया]] (परिमित आवेग प्रतिक्रिया) और [[अनंत आवेग प्रतिक्रिया]] (अनंत आवेग प्रतिक्रिया) होती है । 2-डी एफआईआर डिजिटल फिल्टर गैर-पुनरावर्ती एल्गोरिथ्म संरचना द्वारा प्राप्त किया जाता है चूँकि 2-डी आईआईआर डिजिटल फिल्टर पुनरावर्ती प्रतिक्रिया एल्गोरिथ्म संरचना द्वारा प्राप्त किया जाता है।<ref name=":0">T. S. Huang, “Stability of two-dimensional recursive filters,” IEEE ''Transactions on Audio and Electroacoustics'', vol. 20, no. 2, pp. 158–163, 1972.</ref> | ||
| Line 18: | Line 18: | ||
=== 2-डी आईआईआर फिल्टर का प्रत्यक्ष रूप कार्यान्वयन === | === 2-डी आईआईआर फिल्टर का प्रत्यक्ष रूप कार्यान्वयन === | ||
इनपुट नमूने और पहले से गणना किए गए आउटपुट नमूने के संदर्भ में आउटपुट नमूना व्यक्त करने के लिए अपने अंतर समीकरण को पुनर्व्यवस्थित करके आईआईआर फ़िल्टर प्रत्यक्ष रूप में कार्यान्वित किया जा सकता है।<ref name=":1">J. S. Lim, Two-Dimensional Signal and Image Processing, Prentice-Hall International, 1990.</ref> प्रथम-चतुर्थांश फ़िल्टर के लिए, इनपुट सिग्नल <math>x\left(n_1,n_2\right)</math> और आउटपुट सिग्नल <math>y\left(n_1,n_2\right)</math> से संबंधित हैं | इनपुट नमूने और पहले से गणना किए गए आउटपुट नमूने के संदर्भ में आउटपुट नमूना व्यक्त करने के लिए अपने अंतर समीकरण को पुनर्व्यवस्थित करके आईआईआर फ़िल्टर प्रत्यक्ष रूप में कार्यान्वित किया जा सकता है।<ref name=":1">J. S. Lim, Two-Dimensional Signal and Image Processing, Prentice-Hall International, 1990.</ref> प्रथम-चतुर्थांश फ़िल्टर के लिए, इनपुट सिग्नल <math>x\left(n_1,n_2\right)</math> और आउटपुट सिग्नल <math>y\left(n_1,n_2\right)</math> से संबंधित हैं । | ||
<math>y\left(n_1,n_2\right)=\sum_{l_1=0}^{L_1-1}\sum_{l_2=0}^{L_2-1}a(l_1,l_2)x(n_1-l_1,n_2-l_2)-\sum_{k_1=0}^{K_1-1}\sum_{k_2=0}^{K_2-1}b(k_1,k_2)y(n_1-k_1,n_2-k_2)</math> | <math>y\left(n_1,n_2\right)=\sum_{l_1=0}^{L_1-1}\sum_{l_2=0}^{L_2-1}a(l_1,l_2)x(n_1-l_1,n_2-l_2)-\sum_{k_1=0}^{K_1-1}\sum_{k_2=0}^{K_2-1}b(k_1,k_2)y(n_1-k_1,n_2-k_2)</math> | ||
आवेग के लिए फ़िल्टर की प्रतिक्रिया के बाद से <math>\delta(n_1,n_2)</math> परिभाषा के अनुसार [[आवेग प्रतिक्रिया]] है <math>h\left(n_1,n_2\right)</math>, हम संबंध प्राप्त कर सकते हैं | आवेग के लिए फ़िल्टर की प्रतिक्रिया के बाद से <math>\delta(n_1,n_2)</math> परिभाषा के अनुसार [[आवेग प्रतिक्रिया]] है <math>h\left(n_1,n_2\right)</math>, हम संबंध प्राप्त कर सकते हैं । | ||
<math>h\left(n_1,n_2\right)=a(l_1,l_2)-\sum_{k_1=0}^{K_1-1}\sum_{k_2=0}^{K_2-1}b(k_1,k_2)h(n_1-k_1,n_2-k_2)</math> | <math>h\left(n_1,n_2\right)=a(l_1,l_2)-\sum_{k_1=0}^{K_1-1}\sum_{k_2=0}^{K_2-1}b(k_1,k_2)h(n_1-k_1,n_2-k_2)</math> | ||
दोनों पक्षों के 2-डी जेड-रूपांतरण को लेकर, हम | दोनों पक्षों के 2-डी जेड-रूपांतरण को लेकर, हम प्रणाली फलन के लिए हल कर सकते हैं <math>H\left(z_1,z_2\right)</math>द्वारा दिया गया है। | ||
<math>H_z(z_1,z_2)=\frac{\sum_{l_1=0}^{L_1-1}\sum_{l_2=0}^{L_2-1}a(l_1,l_2)z_1^{-l_1}z_2^{-l_2}}{\sum_{k_1=0}^{K_1-1}\sum_{k_2=0}^{K_2-1}b(k_1,k_2)z_1^{-k_1}z_2^{-k_2}}=\frac{A_z(z_1,z_2)}{B_z(z_1,z_2)}</math> | <math>H_z(z_1,z_2)=\frac{\sum_{l_1=0}^{L_1-1}\sum_{l_2=0}^{L_2-1}a(l_1,l_2)z_1^{-l_1}z_2^{-l_2}}{\sum_{k_1=0}^{K_1-1}\sum_{k_2=0}^{K_2-1}b(k_1,k_2)z_1^{-k_1}z_2^{-k_2}}=\frac{A_z(z_1,z_2)}{B_z(z_1,z_2)}</math> | ||
इस अनुपात को दो फिल्टर के कैस्केड के परिणाम के रूप में देखा जा सकता है, | इस अनुपात को दो फिल्टर के कैस्केड के परिणाम के रूप में देखा जा सकता है, प्रणाली फलन के समान एफआईआर फ़िल्टर<math>A(z_1,z_2)</math> और प्रणाली फलन के समान [[आईआईआर फिल्टर]] <math>1/B(z_1,z_2)</math>, जैसा कि नीचे चित्र में दिखाया गया है।<ref name=":2">Dan E. Dudgeon, Russell M. Mersereau, “Multidimensional Digital Signal Processing”, Prentice-Hall Signal Processing Series, {{ISBN|0136049591}}, 1983.</ref> | ||
[[File:Two-dimensional filter diagram.jpg|frame|center| | [[File:Two-dimensional filter diagram.jpg|frame|center|प्रणाली फलन के साथ फ़िल्टर के लिए प्रतिनिधित्व <math>H(z_1,z_2)</math>. [3] से अनुकूलित होता है। ]] | ||
=== 2-डी आईआईआर फिल्टर के समानांतर कार्यान्वयन === | === 2-डी आईआईआर फिल्टर के समानांतर कार्यान्वयन === | ||
जटिल 2-डी | जटिल 2-डी आईआईआर फिल्टर बनाने की अन्य विधि सबफिल्टरों के समानांतर इंटरकनेक्शन द्वारा है। इस स्थिति में, समग्र स्थानांतरण कार्य बन जाता है | ||
<math>H_z^p(z_1,z_2)=\sum_{i=1}^NH_z^{(i)}(z_1,z_2) </math> | <math>H_z^p(z_1,z_2)=\sum_{i=1}^NH_z^{(i)}(z_1,z_2) </math> | ||
समीकरण का उपयोग करना | समीकरण का उपयोग करना होता है। | ||
<math>H_z^{(i)}(z_1,z_2)=\frac{A_z^{(i)}(z_1,z_2)}{B_z^{(i)}(z_1,z_2)}</math> | <math>H_z^{(i)}(z_1,z_2)=\frac{A_z^{(i)}(z_1,z_2)}{B_z^{(i)}(z_1,z_2)}</math> | ||
| Line 46: | Line 46: | ||
<math>H_z^{p}(z_1,z_2)=\frac{A_z^{p}(z_1,z_2)}{B_z^{p}(z_1,z_2)}=\frac{\sum_{j=1}^N\prod_{i \neq j}A_z^{(j)}(z_1,z_2)B_z^{(i)}(z_1,z_2)}{\prod_{i=1}^NB_z^{(i)}(z_1,z_2)}</math> | <math>H_z^{p}(z_1,z_2)=\frac{A_z^{p}(z_1,z_2)}{B_z^{p}(z_1,z_2)}=\frac{\sum_{j=1}^N\prod_{i \neq j}A_z^{(j)}(z_1,z_2)B_z^{(i)}(z_1,z_2)}{\prod_{i=1}^NB_z^{(i)}(z_1,z_2)}</math> | ||
इच्छानुसार 2-डी तर्कसंगत प्रणाली फलन को लागू करने के लिए समांतर रूप का उपयोग नहीं किया जा सकता है।<ref name=":3">M. Ahmadi, “Design of 2-Dimensional recursive digital filters”, Control and Dynamics System, vol. 78, pp. 131-181, 1996.</ref> फिर भी, हम रोचक 2-डी आईआईआर फिल्टर को संश्लेषित कर सकते हैं जिसे समांतर वास्तुकला द्वारा कार्यान्वित किया जा सकता है। उदाहरण के लिए, एकाधिक [[पासबैंड]] वाले फ़िल्टर को डिज़ाइन करते समय समांतर रूप फायदेमंद हो सकता है। समांतर कार्यान्वयन 2-डी अनंत आवेग प्रतिक्रिया फ़िल्टर को लागू करने के लिए भी उपयोगी हो सकता है जिसका आवेग प्रतिक्रिया एकल चतुर्भुज तक ही सीमित नहीं है, जैसे सममित फ़िल्टर सम्मिलित है। | |||
[[File:tp1.jpg|frame|center|नया 2-डी आईआईआर फिल्टर बनाने के लिए एन सरल 2-डी आईआईआर फिल्टर के समानांतर इंटरकनेक्शन। [3] से | [[File:tp1.jpg|frame|center|नया 2-डी आईआईआर फिल्टर बनाने के लिए एन सरल 2-डी आईआईआर फिल्टर के समानांतर इंटरकनेक्शन। [3] से अनुकूलित है।]] | ||
==== '''जेनेटिक एल्गोरिदम के साथ 2-डी आईआईआर फिल्टर का डिजाइन''' ==== | ==== '''जेनेटिक एल्गोरिदम के साथ 2-डी आईआईआर फिल्टर का डिजाइन''' ==== | ||
| Line 57: | Line 57: | ||
नीचे दिया गया चित्र प्रस्तावित GA-आधारित डिज़ाइन प्रवाह दिखाता है। फ़िल्टर गुणांक उनके सीएसडी संख्या प्रतिनिधित्व में एन्कोड किए गए हैं। जनसंख्या आरंभीकरण में, गुणसूत्र अनियमित रूप से उत्पन्न होते हैं। प्रत्येक गुणांक में पूर्व-निर्दिष्ट शब्द लंबाई और गैर-शून्य अंकों की अधिकतम संख्या होती है, जिसे किसी भी वांछित मान पर सेट किया जा सकता है।<ref>Li Liang, Majid Ahmadi, Maher Sid-Ahmed, “Design of 2-D IIR FIlters with Canonical signed-digit coefficients using genetic algorithm”, Department of Electrical & Computer Engineering, University of Windsor, Canada.</ref> | नीचे दिया गया चित्र प्रस्तावित GA-आधारित डिज़ाइन प्रवाह दिखाता है। फ़िल्टर गुणांक उनके सीएसडी संख्या प्रतिनिधित्व में एन्कोड किए गए हैं। जनसंख्या आरंभीकरण में, गुणसूत्र अनियमित रूप से उत्पन्न होते हैं। प्रत्येक गुणांक में पूर्व-निर्दिष्ट शब्द लंबाई और गैर-शून्य अंकों की अधिकतम संख्या होती है, जिसे किसी भी वांछित मान पर सेट किया जा सकता है।<ref>Li Liang, Majid Ahmadi, Maher Sid-Ahmed, “Design of 2-D IIR FIlters with Canonical signed-digit coefficients using genetic algorithm”, Department of Electrical & Computer Engineering, University of Windsor, Canada.</ref> | ||
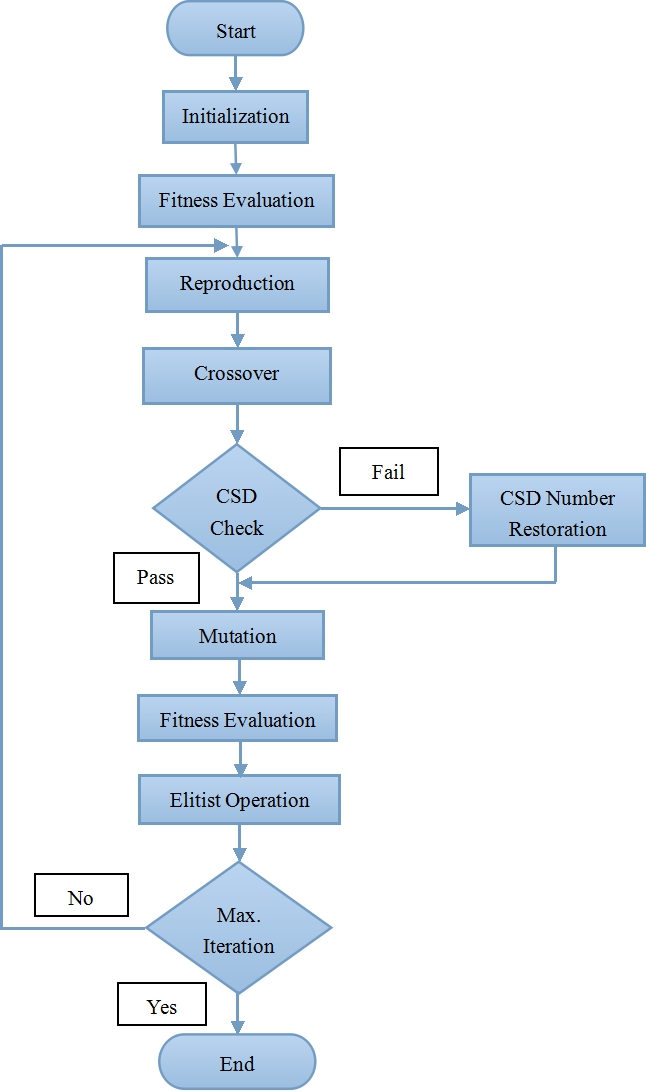
[[File:tppt.jpg|frame|center|GA-आधारित डिज़ाइन फ़्लो चार्ट। [5] से | [[File:tppt.jpg|frame|center|GA-आधारित डिज़ाइन फ़्लो चार्ट। [5] से अनुकूलित है।]] | ||
==== जेनेटिक ऑपरेटर ==== | ==== जेनेटिक ऑपरेटर ==== | ||
| Line 65: | Line 65: | ||
==== फिटनेस मूल्यांकन और प्रतिस्थापन रणनीति ==== | ==== फिटनेस मूल्यांकन और प्रतिस्थापन रणनीति ==== | ||
फिटनेस मूल्यांकन दो चरणों वाली प्रक्रिया होती है। पहला कदम स्थिरता त्रिकोण का उपयोग करके प्रत्येक दूसरे क्रम खंड की स्थिरता की जांच करना है। जाँच में असफल होने वाले गुणसूत्रों को फिटनेस मान 0 दिया जाता है। प्राचीन पीढ़ी के प्रतिस्थापन के लिए अभिजात्य रणनीति लागू की जाती है। प्रजनन के बाद संतान में सबसे अच्छा गुणसूत्र और सबसे खराब गुणसूत्र पाया जाता है। डिज़ाइन किए गए फ़िल्टर में गैर-वियोज्य अंश और वियोज्य भाजक स्थानांतरण | फिटनेस मूल्यांकन दो चरणों वाली प्रक्रिया होती है। पहला कदम स्थिरता त्रिकोण का उपयोग करके प्रत्येक दूसरे क्रम खंड की स्थिरता की जांच करना है। जाँच में असफल होने वाले गुणसूत्रों को फिटनेस मान 0 दिया जाता है। प्राचीन पीढ़ी के प्रतिस्थापन के लिए अभिजात्य रणनीति लागू की जाती है। प्रजनन के बाद संतान में सबसे अच्छा गुणसूत्र और सबसे खराब गुणसूत्र पाया जाता है। डिज़ाइन किए गए फ़िल्टर में गैर-वियोज्य अंश और वियोज्य भाजक स्थानांतरण फलन है।<ref>A. Mazinani, M. Ahmadi, M. Shridhar and R. S. Lashkari, “A novel approach to the design of 2-D recursive digital filters”, Journal of the Franklin Institute, Pergamon Press Ltd, vol. 329, no. 1, pp. 127-133, 1992.</ref> संख्या बहाली कार्यपद्धति का उपयोग यह सुनिश्चित करने के लिए किया जाता है कि फ़िल्टर गुणांक पूर्व-निर्दिष्ट सीएसडी प्रारूप में दर्शाए गए हैं। | ||
==संदर्भ== | ==संदर्भ== | ||
Revision as of 19:56, 21 June 2023
कई डोमेन में उनके महत्व और उच्च प्रयोज्यता के कारण द्वि आयामी फिल्टर ने पर्याप्त विकास प्रयास देखा है। 2-डी स्थितियों में स्थिति 1-डी स्थितियों से अत्यधिक भिन्न होती है, क्योंकि बहु-आयामी बहुपदों को सामान्य रूप से कारक नहीं बनाया जा सकता है। इसका तात्पर्य यह है कि इच्छानुसार स्थानांतरण फलन सामान्यतः किसी विशेष कार्यान्वयन के लिए आवश्यक रूप में हेरफेर नहीं किया जा सकता है। 2-डी आईआईआर फिल्टर का इनपुट-आउटपुट संबंध निरंतर-गुणांक रैखिक आंशिक विभेदक समीकरण का पालन करता है, जिससे इनपुट नमूनों और पहले से गणना किए गए आउटपुट नमूनों का उपयोग करके आउटपुट नमूने का मूल्य गणना किया जा सकता है। चूंकि आउटपुट नमूने के मूल्यों को वापस खिलाया जाता है, 2-डी फ़िल्टर, इसके 1-डी समकक्ष की प्रकार, अस्थिर हो सकता है।
प्रेरणा और अनुप्रयोग
सूचना विज्ञान और कम्प्यूटिंग प्रौद्योगिकी के तेजी से विकास के कारण, डिजिटल फिल्टर डिजाइन और अनुप्रयोग के सिद्धांत ने आगे छलांग लगाई है। हम वास्तविक जीवन में विभिन्न प्रकार के संकेतों का सामना करते हैं, जैसे कि प्रसारण संकेत, टेलीविजन संकेत, राडार संकेत, चल दूरभाष संकेत, मार्गदर्शन संकेत, रेडियो खगोल विज्ञान संकेत, जैव चिकित्सा संकेत, नियंत्रण संकेत, मौसम संकेत, भूकंपीय संकेत, यांत्रिक कंपन संकेत, रिमोट सेंसिंग और टेलीमेटरी सिग्नल इत्यादि इस प्रकार है । इनमें से अधिकतर सिग्नल एनालॉग सिग्नल हैं और उनमें से एकमात्र छोटा सा भाग डिजिटल सिग्नल हैं। एनालॉग सिग्नल स्वतंत्र चर के निरंतर कार्य हैं, जो एक-आयामी, द्वि-आयामी या बहुआयामी हो सकते हैं। अधिकतर स्थितियों में, आयामी एनालॉग सिग्नल का चर समय होता है। समय के नमूने और परिमाण के विवेक के बाद, ऐसा एनालॉग सिग्नल आयामी डिजिटल सिग्नल बन जाएगा। परिणामी डिजिटल सिग्नल को असतत अनुक्रम द्वारा दर्शाया जा सकता है। उदाहरण के लिए, सामान्य संकेत ध्वनि संकेत है। द्वि-आयामी संकेत का उदाहरण छवि है। फ़िल्टर ऐसी प्रणाली है जो सिग्नल को दूसरे सिग्नल में बदल सकती है। इस प्रकार के परिवर्तन के उदाहरणों में शोर हटाने के लिए सिग्नल को चिकना करना, सिग्नल से आवृत्ति घटकों को हटाना और सिग्नल बढ़ाने के लिए आवृत्ति घटकों को बढ़ाना सम्मलित है। फ़िल्टर का डिज़ाइन और कार्यान्वयन सिग्नल विश्लेषण और प्रसंस्करण प्रौद्योगिकी की महत्वपूर्ण शाखा है। फ़िल्टर सिग्नल अधिग्रहण, ट्रांसमिशन, प्रोसेसिंग और एक्सचेंज में भी मुख्य भूमिका निभाते हैं।
समस्या कथन और बुनियादी अवधारणाएँ
डिजिटल फिल्टर
डिजिटल सिग्नल फ़िल्टरिंग डिजिटल फ़िल्टर लागू कर रहा है। डिजिटल फिल्टर ऐसी प्रणाली है जो उस सिग्नल के कुछ पहलुओं को कम करने या बढ़ाने के लिए नमूनाकृत, असतत-समय संकेत पर गणितीय संचालन करता है। इनपुट और आउटपुट सिग्नल सभी डिजिटल सिग्नल हैं। यह अन्य प्रमुख प्रकार के इलेक्ट्रॉनिक फिल्टर, एनालॉग फिल्टर के विपरीत है, जो इलेक्ट्रॉनिक सर्किट है जो निरंतर-समय के एनालॉग संकेत पर काम करता है। दरअसल डिजिटल फिल्टर और एनालॉग फिल्टर की मूल अवधारणा ही है। फर्क सिर्फ इतना है कि संकेतों के प्रकार और फ़िल्टरिंग के विधि हैं। डिजिटल फिल्टर को सॉफ्टवेयर में संख्यात्मक रूप से लागू किया जा सकता है और इसमें उच्च प्रसंस्करण त्रुटिहीनता, स्थिर प्रणाली, कम मात्रा और हल्के वजन के फायदे हैं। डिजिटल फिल्टर में कोई प्रतिबाधा मिलान नहीं है और डिजिटल फिल्टर कुछ विशेष फ़िल्टरिंग कार्यों को पूर्ण कर सकते हैं जिन्हें एनालॉग फिल्टर द्वारा पूर्ण नहीं किया जा सकता है। एनॉलॉग से डिजिटल परिवर्तित करने वाला उपकरण का उपयोग करके एनालॉग सिग्नल को डिजिटल फिल्टर के माध्यम से भी संसाधित किया जा सकता है।
द्वि-आयामी डिजिटल फ़िल्टर
द्वि-आयामी डिजिटल संकेतों को संसाधित करने के लिए द्वि-आयामी फ़िल्टर का उपयोग किया जाता है। 1-डी और 2-डी डिजिटल फ़िल्टर समस्याओं के डिज़ाइन के बीच महत्वपूर्ण अंतर है। 1-डी स्थितियों में, फिल्टर के डिजाइन और कार्यान्वयन को अलग से अधिक आसानी से माना जा सकता है। फ़िल्टर को पहले डिज़ाइन किया जा सकता है और फिर, स्थानांतरण फलन के उचित जोड़-तोड़ के माध्यम से, किसी विशेष नेटवर्क संरचना के लिए आवश्यक गुणांक निर्धारित किया जा सकता है। चूँकि 2-डी स्थितियों में, डिजाइन और कार्यान्वयन अधिक निकटता से संबंधित हैं। चूंकि बहुआयामी बहुपदों को सामान्य रूप से कारक नहीं बनाया जा सकता है। इसका तात्पर्य यह है कि इच्छानुसार से बहु-आयामी हस्तांतरण फलन को सामान्यतः किसी विशेष कार्यान्वयन के लिए आवश्यक रूप में हेरफेर नहीं किया जा सकता है। यदि हमारा कार्यान्वयन एकमात्र कारक हस्तांतरण कार्यों को अनुभूत कर सकता है, तो हमारे डिज़ाइन एल्गोरिदम को इस वर्ग के एकमात्र फ़िल्टर डिज़ाइन करने के लिए तैयार किया जाना चाहिए। इसका डिजाइन की समस्या को जटिल बनाने और व्यावहारिक कार्यान्वयन की संख्या को सीमित करने का प्रभाव है। डिजिटल फिल्टर को दो मुख्य प्रकारों में वर्गीकृत किया जा सकता है, अर्थात् परिमित आवेग प्रतिक्रिया (परिमित आवेग प्रतिक्रिया) और अनंत आवेग प्रतिक्रिया (अनंत आवेग प्रतिक्रिया) होती है । 2-डी एफआईआर डिजिटल फिल्टर गैर-पुनरावर्ती एल्गोरिथ्म संरचना द्वारा प्राप्त किया जाता है चूँकि 2-डी आईआईआर डिजिटल फिल्टर पुनरावर्ती प्रतिक्रिया एल्गोरिथ्म संरचना द्वारा प्राप्त किया जाता है।[1]
उपस्थिता दृष्टिकोण
2-डी आईआईआर फिल्टर का प्रत्यक्ष रूप कार्यान्वयन
इनपुट नमूने और पहले से गणना किए गए आउटपुट नमूने के संदर्भ में आउटपुट नमूना व्यक्त करने के लिए अपने अंतर समीकरण को पुनर्व्यवस्थित करके आईआईआर फ़िल्टर प्रत्यक्ष रूप में कार्यान्वित किया जा सकता है।[2] प्रथम-चतुर्थांश फ़िल्टर के लिए, इनपुट सिग्नल और आउटपुट सिग्नल से संबंधित हैं ।
आवेग के लिए फ़िल्टर की प्रतिक्रिया के बाद से परिभाषा के अनुसार आवेग प्रतिक्रिया है , हम संबंध प्राप्त कर सकते हैं ।
दोनों पक्षों के 2-डी जेड-रूपांतरण को लेकर, हम प्रणाली फलन के लिए हल कर सकते हैं द्वारा दिया गया है।
इस अनुपात को दो फिल्टर के कैस्केड के परिणाम के रूप में देखा जा सकता है, प्रणाली फलन के समान एफआईआर फ़िल्टर और प्रणाली फलन के समान आईआईआर फिल्टर , जैसा कि नीचे चित्र में दिखाया गया है।[3]
2-डी आईआईआर फिल्टर के समानांतर कार्यान्वयन
जटिल 2-डी आईआईआर फिल्टर बनाने की अन्य विधि सबफिल्टरों के समानांतर इंटरकनेक्शन द्वारा है। इस स्थिति में, समग्र स्थानांतरण कार्य बन जाता है
समीकरण का उपयोग करना होता है।
और योग को आम भाजक के ऊपर स्थानांतरण प्रकार्य में रखने पर हमें विस्तारित रूप मिलता है
इच्छानुसार 2-डी तर्कसंगत प्रणाली फलन को लागू करने के लिए समांतर रूप का उपयोग नहीं किया जा सकता है।[4] फिर भी, हम रोचक 2-डी आईआईआर फिल्टर को संश्लेषित कर सकते हैं जिसे समांतर वास्तुकला द्वारा कार्यान्वित किया जा सकता है। उदाहरण के लिए, एकाधिक पासबैंड वाले फ़िल्टर को डिज़ाइन करते समय समांतर रूप फायदेमंद हो सकता है। समांतर कार्यान्वयन 2-डी अनंत आवेग प्रतिक्रिया फ़िल्टर को लागू करने के लिए भी उपयोगी हो सकता है जिसका आवेग प्रतिक्रिया एकल चतुर्भुज तक ही सीमित नहीं है, जैसे सममित फ़िल्टर सम्मिलित है।
जेनेटिक एल्गोरिदम के साथ 2-डी आईआईआर फिल्टर का डिजाइन
साहित्य में 2-डी आईआईआर डिजिटल फिल्टर के लिए कई डिजाइन तकनीकों की सूचना दी गई है।[1][2][3][4]2013 में, अधिकतर दशक तक डिजिटल फ़िल्टर डिज़ाइन के लिए जेनेटिक एल्गोरिद्म का सफलतापूर्वक उपयोग किया गया था।[citation needed] यहां हम जीए-आधारित डिजाइन विधि नामक 2-डी आईआईआर फ़िल्टर डिजाइन करने के लिए विधि प्रस्तुत करते हैं।
प्रारंभ
नीचे दिया गया चित्र प्रस्तावित GA-आधारित डिज़ाइन प्रवाह दिखाता है। फ़िल्टर गुणांक उनके सीएसडी संख्या प्रतिनिधित्व में एन्कोड किए गए हैं। जनसंख्या आरंभीकरण में, गुणसूत्र अनियमित रूप से उत्पन्न होते हैं। प्रत्येक गुणांक में पूर्व-निर्दिष्ट शब्द लंबाई और गैर-शून्य अंकों की अधिकतम संख्या होती है, जिसे किसी भी वांछित मान पर सेट किया जा सकता है।[5]
जेनेटिक ऑपरेटर
रूले व्हील चयन का उपयोग प्रजनन ऑपरेटर के रूप में किया जाता है। प्रत्येक क्रॉसओवर ऑपरेशन के बाद, गुणांक जहां क्रॉसओवर पॉइंट स्थित है, को सीएसडी प्रारूप पर चेक किया जाएगा। म्यूटेशन ऑपरेशन सरल सिंगल बिट फ्लिप है। म्यूटेशन के बाद, संतति में प्रत्येक गुणांक को सीएसडी प्रारूप पर जांचा जाता है।
फिटनेस मूल्यांकन और प्रतिस्थापन रणनीति
फिटनेस मूल्यांकन दो चरणों वाली प्रक्रिया होती है। पहला कदम स्थिरता त्रिकोण का उपयोग करके प्रत्येक दूसरे क्रम खंड की स्थिरता की जांच करना है। जाँच में असफल होने वाले गुणसूत्रों को फिटनेस मान 0 दिया जाता है। प्राचीन पीढ़ी के प्रतिस्थापन के लिए अभिजात्य रणनीति लागू की जाती है। प्रजनन के बाद संतान में सबसे अच्छा गुणसूत्र और सबसे खराब गुणसूत्र पाया जाता है। डिज़ाइन किए गए फ़िल्टर में गैर-वियोज्य अंश और वियोज्य भाजक स्थानांतरण फलन है।[6] संख्या बहाली कार्यपद्धति का उपयोग यह सुनिश्चित करने के लिए किया जाता है कि फ़िल्टर गुणांक पूर्व-निर्दिष्ट सीएसडी प्रारूप में दर्शाए गए हैं।
संदर्भ
- ↑ 1.0 1.1 T. S. Huang, “Stability of two-dimensional recursive filters,” IEEE Transactions on Audio and Electroacoustics, vol. 20, no. 2, pp. 158–163, 1972.
- ↑ 2.0 2.1 J. S. Lim, Two-Dimensional Signal and Image Processing, Prentice-Hall International, 1990.
- ↑ 3.0 3.1 Dan E. Dudgeon, Russell M. Mersereau, “Multidimensional Digital Signal Processing”, Prentice-Hall Signal Processing Series, ISBN 0136049591, 1983.
- ↑ 4.0 4.1 M. Ahmadi, “Design of 2-Dimensional recursive digital filters”, Control and Dynamics System, vol. 78, pp. 131-181, 1996.
- ↑ Li Liang, Majid Ahmadi, Maher Sid-Ahmed, “Design of 2-D IIR FIlters with Canonical signed-digit coefficients using genetic algorithm”, Department of Electrical & Computer Engineering, University of Windsor, Canada.
- ↑ A. Mazinani, M. Ahmadi, M. Shridhar and R. S. Lashkari, “A novel approach to the design of 2-D recursive digital filters”, Journal of the Franklin Institute, Pergamon Press Ltd, vol. 329, no. 1, pp. 127-133, 1992.