बैकप्रेशर रूटिंग

For the term "back pressure" in describing fluid flow in piping and air vent systems, see back pressure.

कतार सिद्धांत में, गणितीय संभाव्यता सिद्धांत के भीतर एक अनुशासन, बैकप्रेशर रूटिंग एल्गोरिदम एक क्यूइंग नेटवर्क के आसपास ट्रैफ़िक को निर्देशित करने की एक विधि है जो अधिकतम नेटवर्क थ्रूपुट प्राप्त करता है,जिसे Lyapunov अनुकूलन की अवधारणाओं का उपयोग करके स्थापित किया गया है। बैकप्रेशर रूटिंग उस स्थिति पर विचार करता है जहां प्रत्येक कार्य नेटवर्क में कई सर्विस नोड्स पर जा सकता है। यह अधिकतम वजन निर्धारण का विस्तार है जहां प्रत्येक कार्य केवल एक सेवा नोड पर जाता है।

परिचय

बैकप्रेशर रूटिंग कंजेशन ग्रेडिएंट्स का उपयोग करके मल्टी-हॉप नेटवर्क पर गतिशील रूप से ट्रैफ़िक को रूट करने के लिए एक एल्गोरिथ्म है। एल्गोरिथ्म वायरलेस संचार नेटवर्क पर लागू किया जा सकता है, जिसमें वायरलेस सेंसर नेटवर्क, मोबाइल तदर्थ नेटवर्क (मोबाइल तदर्थ नेटवर्क), और वायरलेस और वायरलाइन घटकों के साथ विषम नेटवर्क शामिल हैं। बैकप्रेशर सिद्धांतों को अन्य क्षेत्रों में भी लागू किया जा सकता है, जैसे कि अध्ययन के लिए उत्पाद असेंबली सिस्टम और प्रोसेसिंग नेटवर्क। यह लेख संचार नेटवर्क पर केंद्रित है, जहां कई डेटा स्ट्रीम से पैकेट आते हैं और उपयुक्त स्थलों पर पहुंचाना चाहिए। बैकप्रेशर एल्गोरिथ्म स्लॉटेड समय में काम करता है। हर बार स्लॉट में यह डेटा को उस दिशा में रूट करना चाहता है पड़ोसी नोड्स के बीच अंतर बैकलॉग को अधिकतम करें। यह कैसे पानी के समान है दबाव प्रवणताओं के माध्यम से पाइपों के एक नेटवर्क के माध्यम से बहती है। हालांकि, बैकप्रेशर एल्गोरिदम मल्टी-कमोडिटी नेटवर्क पर लागू किया जा सकता है (जहां अलग-अलग पैकेट के अलग-अलग गंतव्य हो सकते हैं), और नेटवर्क के लिए जहां ट्रांसमिशन दरों का चयन किया जा सकता है (संभवतः समय-भिन्न) विकल्पों के एक सेट से। आकर्षक विशेषताएं बैकप्रेशर एल्गोरिथम हैं: (i) यह अधिकतम नेटवर्क थ्रूपुट की ओर ले जाता है, (ii) यह समय-भिन्न नेटवर्क स्थितियों के लिए काफी मजबूत है, (iii) यह ट्रैफ़िक आगमन दरों या चैनल स्थिति को जाने बिना लागू किया जा सकता है संभावनाओं। हालाँकि, एल्गोरिथ्म बड़ी देरी का परिचय दे सकता है, और हो सकता है हस्तक्षेप वाले नेटवर्क में सटीक रूप से लागू करना मुश्किल हो सकता है। का संशोधन बैकप्रेशर जो देरी को कम करता है और कार्यान्वयन को आसान बनाता है, नीचे वर्णित हैं

1. देरी में सुधार और #वितरित बैकप्रेशर के तहत।

बैकप्रेशर रूटिंग का अध्ययन मुख्य रूप से सैद्धांतिक रूप से किया गया है प्रसंग। व्यवहार में, तदर्थ वायरलेस नेटवर्क में आमतौर पर शॉर्टेस्ट के आधार पर वैकल्पिक रूटिंग विधियों को लागू किया पथ संगणना या नेटवर्क बाढ़, जैसे तदर्थ तदर्थ ऑन-डिमांड दूरी वेक्टर रूटिंग| तदर्थ ऑन-डिमांड डिस्टेंस वेक्टर रूटिंग (AODV), भौगोलिक रूटिंग, और ExOR (वायरलेस नेटवर्क प्रोटोकॉल) (ExOR)। हालाँकि, बैकप्रेशर की गणितीय इष्टतमता गुण इसके उपयोग के हाल के प्रायोगिक प्रदर्शनों को प्रेरित किया है दक्षिणी कैलिफोर्निया विश्वविद्यालय में वायरलेस टेस्टबेड पर और उत्तरी कैरोलिना स्टेट यूनिवर्सिटी में।

उत्पत्ति

मूल बैकप्रेशर एल्गोरिथम को टैसियुलास और एफ़्रेमाइड्स द्वारा विकसित किया गया था।उन्होंने मल्टी-हॉप रूटिंग | मल्टी-हॉप पैकेट रेडियो नेटवर्क पर यादृच्छिक पैकेट आगमन और लिंक चयन विकल्पों के एक निश्चित सेट पर विचार किया। उनके एल्गोरिदम में अधिकतम-भार लिंक चयन चरण और अंतर बैकलॉग रूटिंग चरण शामिल था। बैकप्रेसर से संबंधित एक एल्गोरिदम, मल्टी-कमोडिटी कंप्यूटिंग के लिए डिज़ाइन किया गया नेटवर्क प्रवाह, Awerbuch और Leighton में विकसित किया गया था। बैकप्रेशर एल्गोरिथम को बाद में नेली, मोडियानो और रोहर्स द्वारा मोबाइल नेटवर्क के लिए शेड्यूलिंग का इलाज करने के लिए बढ़ाया गया था। बैकप्रेशर का गणितीय रूप से लाइपुनोव अनुकूलन के सिद्धांत के माध्यम से विश्लेषण किया जाता है, और नेटवर्क उपयोगिता अधिकतमकरण प्रदान करने के लिए प्रवाह नियंत्रण तंत्र के साथ संयुक्त रूप से उपयोग किया जा सकता है। (यूटिलिटी ऑप्टिमाइज़ेशन और पेनल्टी न्यूनीकरण के साथ #बैकप्रेशर भी देखें)।

यह कैसे काम करता है

बैकप्रेशर रूटिंग को निर्णय लेने के लिए डिज़ाइन किया गया है जो (मोटे तौर पर) क्यू बैकलॉग के वर्गों के योग को कम करता है नेटवर्क में एक समयावधि से दूसरे समय तक। इस तकनीक का सटीक गणितीय विकास में वर्णित है बाद के खंड। यह खंड सामान्य नेटवर्क मॉडल और सम्मान के साथ बैकप्रेशर रूटिंग के संचालन का वर्णन करता है इस मॉडल को।

मल्टी-हॉप क्यूइंग नेटवर्क मॉडल

अंजीर। 1: एक 6-नोड मल्टीहॉप नेटवर्क। नोड्स के बीच तीर दिखाता है वर्तमान पड़ोसी।

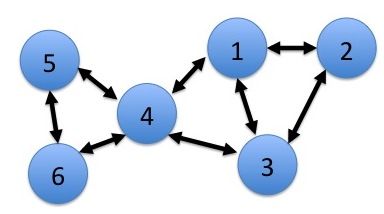
एन नोड्स के साथ एक बहु-हॉप नेटवर्क पर विचार करें (एन = 6 के साथ उदाहरण के लिए चित्र 1 देखें)।

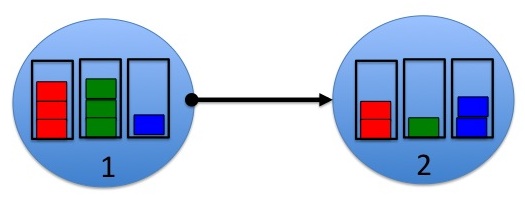
नेटवर्क में काम करता है स्लॉटेड समय $t\in \{0,1,2,\ldots \}$. हर स्लॉट पर नया डेटा आ सकता है नेटवर्क, और रूटिंग और ट्रांसमिशन शेड्यूलिंग निर्णय लिए जाते हैं सभी डेटा को उसके उचित गंतव्य तक पहुंचाने के प्रयास में। नियत डेटा दें नोड के लिए $c\in \{1,\dots ,N\}$ कमोडिटी सी डेटा के रूप में लेबल किया जाना चाहिए। प्रत्येक नोड में डेटा को उसकी वस्तु के अनुसार संग्रहीत किया जाता है। के लिए $n\in \{1,\ldots ,N\}$ और $c\in \{1,\ldots ,N\}$, होने देना $Q_{n}^{(c)}(t)$ नोड एन में कमोडिटी सी डेटा की वर्तमान मात्रा हो, जिसे क्यू बैकलॉग भी कहा जाता है। एक नोड के अंदर क्यू बैकलॉग का क्लोज़अप चित्र 2 में दिखाया गया है। की इकाइयां $Q_{n}^{(c)}(t)$ समस्या के संदर्भ पर निर्भर करता है। उदाहरण के लिए, बैकलॉग पैकेट की पूर्णांक इकाइयाँ ले सकता है, जो उन मामलों में उपयोगी होता है जब डेटा को निश्चित लंबाई के पैकेट में विभाजित किया जाता है। वैकल्पिक रूप से, यह बिट्स की वास्तविक मूल्यवान इकाइयां ले सकता है। यह मान लिया है कि $Q_{c}^{(c)}(t)=0$ सभी के लिए $c\in \{1,\ldots ,N\}$ और सभी टाइम स्लॉट टी, क्योंकि कोई भी नोड डेटा को अपने लिए निर्धारित नहीं करता है। प्रत्येक टाइमलॉट, नोड दूसरों को डेटा संचारित कर सकते हैं। डेटा जो एक नोड से दूसरे नोड में प्रेषित होता है, उसे पहले नोड की कतार से हटा दिया जाता है और दूसरे नोड की कतार में जोड़ दिया जाता है। अपने डेस्टिनेशन पर ट्रांसमिट होने वाले डेटा को नेटवर्क से हटा दिया जाता है। डेटा भी बाहरी रूप से नेटवर्क में आ सकता है, और $A_{n}^{(c)}(t)$ स्लॉट टी पर नोड एन में आने वाले नए डेटा की मात्रा के रूप में परिभाषित किया गया है जो अंततः होना चाहिए नोड सी को वितरित किया जाएगा।

होने देना $\mu _{ab}(t)$ स्लॉट टी पर लिंक (ए, बी) पर नेटवर्क द्वारा उपयोग की जाने वाली ट्रांसमिशन दर हो, यह वर्तमान स्लॉट पर नोड ए से नोड बी में स्थानांतरित किए जा सकने वाले डेटा की मात्रा का प्रतिनिधित्व करता है। होने देना $(\mu _{ab}(t))$ संचरण दर मैट्रिक्स हो। इन संचरण दरों को संभवतः समय-भिन्न विकल्पों के एक सेट के भीतर चुना जाना चाहिए। विशेष रूप से, नेटवर्क में समय-भिन्न चैनल और नोड हो सकते हैं गतिशीलता, और यह इसकी संचरण क्षमताओं को हर स्लॉट को प्रभावित कर सकता है। इसे मॉडल करने के लिए, एस (टी) नेटवर्क की टोपोलॉजी स्थिति का प्रतिनिधित्व करते हैं, जो कैप्चर करता है स्लॉट टी पर नेटवर्क के गुण जो ट्रांसमिशन को प्रभावित करते हैं। होने देना $\Gamma _{S(t)}$ सेट का प्रतिनिधित्व करें टोपोलॉजी राज्य एस (टी) के तहत उपलब्ध संचरण दर मैट्रिक्स विकल्प। प्रत्येक स्लॉट टी, नेटवर्क नियंत्रक एस (टी) को देखता है और ट्रांसमिशन चुनता है दरें $(\mu _{ab}(t))$ सेट के भीतर $\Gamma _{S(t)}$. जिसका चुनाव $(\mu _{ab}(t))$ आव्यूह प्रत्येक स्लॉट टी पर चयन करने के लिए अगले उपधारा में वर्णित किया गया है।

यह समय-भिन्न नेटवर्क मॉडल पहली बार मामले के लिए विकसित किया गया था जब प्रत्येक स्लॉट टी को चैनल राज्य मैट्रिक्स के सामान्य कार्यों और बिजली आवंटन मैट्रिक्स द्वारा निर्धारित किया गया था। मॉडल का उपयोग तब भी किया जा सकता है जब दरें अन्य नियंत्रण निर्णयों द्वारा निर्धारित की जाती हैं, जैसे सर्वर आवंटन, उप-बैंड चयन, कोडिंग प्रकार, और इसी तरह। यह मानता है कि सहायक संचरण दर ज्ञात हैं और कोई संचरण त्रुटि नहीं है। बहु-रिसीवर विविधता के माध्यम से वायरलेस प्रसारण लाभ का फायदा उठाने वाले नेटवर्क सहित संभाव्य चैनल त्रुटियों वाले नेटवर्क के लिए बैकप्रेशर रूटिंग के विस्तारित फॉर्मूलेशन का उपयोग किया जा सकता है।

बैकप्रेसर नियंत्रण निर्णय

प्रत्येक स्लॉट टी बैकप्रेशर नियंत्रक एस (टी) को देखता है और निम्नलिखित 3 चरणों का पालन करता है:

• सबसे पहले, प्रत्येक लिंक (ए, बी) के लिए, यह एक इष्टतम वस्तु का चयन करता है $c_{ab}^{opt}(t)$ उपयोग करने के लिए।
• अगला, यह निर्धारित करता है कि क्या $(\mu _{ab}(t))$ मैट्रिक्स में $\Gamma _{S(t)}$ उपयोग करने के लिए।
• अंत में, यह वस्तु की मात्रा निर्धारित करता है $c_{ab}^{opt}(t)$ यह लिंक (ए, बी) पर संचारित होगा (ज्यादा से ज्यादा $\mu _{ab}(t)$, लेकिन संभवतः कुछ मामलों में कम हो रहा है)।

इष्टतम वस्तु का चयन

प्रत्येक नोड अपनी कतार के बैकलॉग और अपने वर्तमान में बैकलॉग को देखता है पड़ोसियों। नोड ए का वर्तमान पड़ोसी एक नोड बी है जैसे कि इसे चुनना संभव है गैर-शून्य संचरण दर $\mu _{ab}(t)$ वर्तमान स्लॉट पर। इस प्रकार, पड़ोसियों को सेट द्वारा निर्धारित किया जाता है $\Gamma _{S(t)}$. चरम मामले में, ए नोड में पड़ोसी के रूप में सभी N − 1 अन्य नोड हो सकते हैं। हालाँकि, सेट का उपयोग करना आम है $\Gamma _{S(t)}$ जो एक निश्चित भौगोलिक दूरी से अधिक अलग किए गए नोड्स के बीच प्रसारण को रोकते हैं, या जिसकी एक निश्चित सीमा के नीचे प्रचारित सिग्नल शक्ति होगी। इस प्रकार, यह पड़ोसियों की संख्या के लिए विशिष्ट है N − 1 से बहुत कम होना। चित्र 1 में उदाहरण पड़ोसियों को लिंक कनेक्शन द्वारा दिखाता है, ताकि नोड 5 में पड़ोसी 4 और 6 हों। उदाहरण पड़ोसियों के बीच एक सममित संबंध का सुझाव देता है (ताकि यदि 5, 4 का पड़ोसी हो, तो 4 5 का पड़ोसी है), लेकिन यह सामान्य रूप से मामला नहीं होना चाहिए।

किसी दिए गए नोड के पड़ोसियों का सेट आउटगोइंग लिंक के सेट को निर्धारित करता है जिसका उपयोग वह वर्तमान स्लॉट पर प्रसारण के लिए कर सकता है। प्रत्येक आउटगोइंग लिंक (ए, बी) के लिए, इष्टतम वस्तु $c_{ab}^{opt}(t)$ वस्तु के रूप में परिभाषित किया गया है $c\in \{1,\ldots ,N\}$ जो निम्नलिखित विभेदक बैकलॉग मात्रा को अधिकतम करता है:

$Q_{a}^{(c)}(t)-Q_{b}^{(c)}(t)$

इष्टतम वस्तु को चुनने में कोई भी संबंध मनमाने ढंग से टूट जाता है।

अंजीर। 2: नोड 1 और 2 का क्लोजअप। लिंक (1,2) पर भेजने के लिए इष्टतम वस्तु हरी वस्तु है। दूसरी दिशा में भेजने के लिए इष्टतम वस्तु (लिंक (2,1) पर) नीली वस्तु है।

एक उदाहरण चित्र 2 में दिखाया गया है। उदाहरण मानता है कि प्रत्येक कतार में वर्तमान में केवल 3 वस्तुएं हैं: लाल, हरा और

नीला, और इन्हें पैकेट की पूर्णांक इकाइयों में मापा जाता है। निर्देशित लिंक (1,2) पर ध्यान केंद्रित करते हुए, अंतर बैकलॉग हैं:

$Q_{1}^{({\text{red}})}(t)-Q_{2}^{({\text{red}})}(t)=1$

$Q_{1}^{({\text{green}})}(t)-Q_{2}^{({\text{green}})}(t)=2$

$Q_{1}^{({\text{blue}})}(t)-Q_{2}^{({\text{blue}})}(t)=-1$

इसलिए, स्लॉट टी पर लिंक (1,2) पर भेजने के लिए इष्टतम वस्तु हरी वस्तु है। दूसरी ओर, स्लॉट टी पर रिवर्स लिंक (2,1) भेजने के लिए इष्टतम कमोडिटी ब्लू कमोडिटी है।

μ चुनना_ab(टी) मैट्रिक्स

एक बार प्रत्येक लिंक (ए, बी) के लिए इष्टतम वस्तुओं का निर्धारण हो जाने के बाद, नेटवर्क नियंत्रक निम्नलिखित भारों की गणना करता है $W_{ab}(t)$:

$W_{ab}(t)=\max \left[Q_{a}^{(c_{ab}^{\mathrm {opt} }(t))}(t)-Q_{b}^{(c_{ab}^{opt}(t))}(t),0\right]$

भार $W_{ab}(t)$ इष्टतम कमोडिटी से जुड़े डिफरेंशियल बैकलॉग का मूल्य है लिंक (ए, बी) के लिए, 0 के साथ अधिकतम। नियंत्रक तब संचरण दरों को समाधान के रूप में चुनता है निम्नलिखित अधिकतम वजन समस्या (मनमाने ढंग से संबंध तोड़ना):

${\text{(Eq. 1)}}\qquad {\text{Maximize: }}\sum _{a=1}^{N}\sum _{b=1}^{N}\mu _{ab}(t)W_{ab}(t)$

${\text{(Eq. 2)}}\qquad {\text{Subject to: }}(\mu _{ab}(t))\in \Gamma _{S(t)}$

अधिकतम-भार निर्णय के एक उदाहरण के रूप में, मान लीजिए कि वर्तमान स्लॉट टी पर, 6 नोड नेटवर्क के प्रत्येक लिंक पर अंतर बैकलॉग से लिंक वज़न होता है $W_{ab}(t)$ द्वारा दिए गए:

$(W_{ab}(t))=\left[{\begin{array}{cccccc}0&2&1&1&6&0\\1&0&1&2&5&6\\0&7&0&0&0&0\\1&0&1&0&0&0\\1&0&7&5&0&0\\0&0&0&0&5&0\end{array}}\right]$

जबकि सेट $\Gamma _{S(t)}$ एक बेशुमार अनंत संख्या हो सकती है संभव संचरण दर मैट्रिसेस, सादगी के लिए मान लें कि वर्तमान टोपोलॉजी राज्य केवल 4 संभावितों को स्वीकार करता है विकल्प:

$\Gamma _{S(t)}=\{{\boldsymbol {\mu }}_{a},{\boldsymbol {\mu }}_{b},{\boldsymbol {\mu }}_{c},{\boldsymbol {\mu }}_{d}\}$

वर्तमान टोपोलॉजी राज्य एस (टी) के तहत 4 संभावित संचरण दर चयनों का चित्रण। विकल्प (ए) सक्रिय करता है एकल लिंक (1,5) की संचरण दर के साथ $\mu _{15}=2$. अन्य सभी विकल्प दो लिंक का उपयोग करते हैं, प्रत्येक सक्रिय लिंक पर 1 की संचरण दर के साथ।

इन चार संभावनाओं को मैट्रिक्स रूप में निम्न द्वारा दर्शाया गया है:

${\boldsymbol {\mu }}_{a}=\left[{\begin{array}{cccccc}0&0&0&0&2&0\\0&0&0&0&0&0\\0&0&0&0&0&0\\0&0&0&0&0&0\\0&0&0&0&0&0\\0&0&0&0&0&0\end{array}}\right],\quad {\boldsymbol {\mu }}_{b}=\left[{\begin{array}{cccccc}0&0&0&0&0&0\\0&0&1&0&0&0\\0&0&0&0&0&0\\0&0&0&0&1&0\\0&0&0&0&0&0\\0&0&0&0&0&0\end{array}}\right]$

${\boldsymbol {\mu }}_{c}=\left[{\begin{array}{cccccc}0&0&0&0&0&0\\1&0&0&0&0&0\\0&0&0&0&0&0\\0&0&0&0&1&0\\0&0&0&0&0&0\\0&0&0&0&0&0\end{array}}\right],\quad {\boldsymbol {\mu }}_{d}=\left[{\begin{array}{cccccc}0&0&0&0&0&0\\0&0&0&0&0&0\\0&1&0&0&0&0\\0&0&0&0&0&0\\0&0&0&1&0&0\\0&0&0&0&0&0\end{array}}\right]$

गौर करें कि इनमें से किसी भी संभावना के तहत नोड 6 न तो भेज सकता है और न ही प्राप्त कर सकता है। यह उत्पन्न हो सकता है क्योंकि नोड 6 वर्तमान में संचार सीमा से बाहर है। 4 संभावनाओं में से प्रत्येक के लिए दरों का भारित योग है:

• पसंद (ए): $\sum _{ab}W_{ab}(t)\mu _{ab}(t)=12$.
• विकल्प (बी): $\sum _{ab}W_{ab}(t)\mu _{ab}(t)=1$.
• विकल्प (सी): $\sum _{ab}W_{ab}(t)\mu _{ab}(t)=1$.
• पसंद (डी): $\sum _{ab}W_{ab}(t)\mu _{ab}(t)=12$.

क्योंकि 12 के अधिकतम वजन के लिए एक टाई है, नेटवर्क नियंत्रक टाई को मनमाने ढंग से तोड़ सकता है कोई भी विकल्प चुनना ${\boldsymbol {\mu }}_{a}$ या विकल्प ${\boldsymbol {\mu }}_{d}$.

रूटिंग वेरिएबल्स को अंतिम रूप देना

अब मान लीजिए कि इष्टतम वस्तुओं $c_{ab}^{opt}(t)$ प्रत्येक लिंक और ट्रांसमिशन के लिए निर्धारित किया गया है दरें $(\mu _{ab}(t))$ भी निर्धारित किया गया है। यदि दिए गए लिंक (ए, बी) पर इष्टतम वस्तु के लिए अंतर बैकलॉग ऋणात्मक है, तो कोई डेटा स्थानांतरित नहीं किया जाता है वर्तमान स्लॉट पर इस लिंक पर। अन्यथा, नेटवर्क भेजने की पेशकश करता है $\mu _{ab}(t)$ वस्तु की इकाइयाँ $c_{ab}^{\mathrm {opt} }(t)$ इस लिंक पर डेटा। यह रूटिंग वेरिएबल्स को परिभाषित करके किया जाता है $\mu _{ab}^{(c)}(t)$ प्रत्येक लिंक के लिए (ए, बी) और प्रत्येक वस्तु सी, जहां:

$\mu _{ab}^{(c)}(t)={\begin{cases}\mu _{ab}(t)&{\text{ if }}c=c_{ab}^{opt}(t){\text{ and }}Q_{a}^{(c_{ab}^{opt}(t))}(t)-Q_{b}^{(c_{ab}^{opt}(t))}(t)\geq 0\\0&{\text{ otherwise}}\end{cases}}$

का मान है $\mu _{ab}^{(c)}(t)$ लिंक पर कमोडिटी सी डेटा को दी जाने वाली ट्रांसमिशन दर का प्रतिनिधित्व करता है (ए, बी) स्लॉट टी पर। हालाँकि, ट्रांसमिशन का समर्थन करने के लिए नोड्स के पास एक निश्चित वस्तु के लिए पर्याप्त नहीं हो सकता है उनके सभी आउटगोइंग लिंक्स पर प्रस्तावित दरों पर। यह नोड एन और कमोडिटी सी के लिए स्लॉट टी पर उत्पन्न होता है यदि:

$Q_{n}^{(c)}(t)<\sum _{b=1}^{N}\mu _{nb}^{(c)}(t)$

इस मामले में, सभी $Q_{n}^{(c)}(t)$ डेटा भेजा जाता है, और अशक्त डेटा का उपयोग प्रस्तावित दरों के अप्रयुक्त भागों को भरने के लिए किया जाता है, संबंधित आउटगोइंग लिंक्स (प्रस्तावित दरों के अनुसार) पर मनमाने ढंग से वास्तविक डेटा और अशक्त डेटा आवंटित करना। इसे क्यू अंडरफ्लो स्थिति कहा जाता है। इस तरह के अंडरफ्लो थ्रूपुट को प्रभावित नहीं करते हैं या नेटवर्क की स्थिरता गुण। सहज रूप से, यह अंडरफ्लो के कारण है केवल तभी उत्पन्न होता है जब संचारण नोड में बैकलॉग की मात्रा कम होती है, जिसका अर्थ है नोड को अस्थिरता का खतरा नहीं है।

देरी में सुधार

बैकप्रेशर एल्गोरिथम किसी भी पूर्व-निर्दिष्ट पथ का उपयोग नहीं करता है। रास्ते सीखे जाते हैं गतिशील रूप से, और विभिन्न पैकेटों के लिए भिन्न हो सकते हैं। देरी बहुत बड़ी हो सकती है, खासकर जब सिस्टम हल्का हो लोड किया गया ताकि गंतव्य की ओर डेटा पुश करने के लिए पर्याप्त दबाव न हो। उदाहरण के तौर पर, एक पैकेट मान लीजिए नेटवर्क में प्रवेश करता है, और कुछ भी कभी प्रवेश नहीं करता है। यह पैकेट नेटवर्क के माध्यम से चक्कर लगा सकता है और कभी नहीं पहुंचेगा अपने गंतव्य पर क्योंकि कोई दबाव प्रवणता नहीं बनती है। यह थ्रूपुट इष्टतमता या स्थिरता का खंडन नहीं करता है बैकप्रेशर के गुण क्योंकि नेटवर्क में किसी भी समय अधिकतम एक पैकेट होता है और इसलिए तुच्छ रूप से स्थिर होता है (0 की डिलीवरी दर प्राप्त करना, आगमन दर के बराबर)।

पूर्व-निर्दिष्ट पथों के एक सेट पर बैकप्रेशर लागू करना भी संभव है। यह क्षमता क्षेत्र को प्रतिबंधित कर सकता है, लेकिन इन-ऑर्डर में सुधार कर सकता है वितरण और देरी। क्षमता क्षेत्र को प्रभावित किए बिना देरी में सुधार करने का एक और तरीका है, एन्हांस्ड का उपयोग करना संस्करण जो पूर्वाग्रहों को वांछित दिशाओं की ओर जोड़ता है। इस तरह के पक्षपात के अनुकरण ने महत्वपूर्ण देरी में सुधार दिखाया है।ध्यान दें कि बैकप्रेशर को कतारों में फर्स्ट-इन-फर्स्ट-आउट (FIFO (कंप्यूटिंग और इलेक्ट्रॉनिक्स)) सेवा की आवश्यकता नहीं है। यह देखा गया है लास्ट-इन-फर्स्ट-आउट (एलआईएफओ (कंप्यूटिंग)) सेवा नाटकीय रूप से पैकेटों के विशाल बहुमत के लिए देरी में सुधार कर सकती है, थ्रूपुट को प्रभावित किए बिना।

वितरित बैकप्रेशर

ध्यान दें कि एक बार संचरण दर $(\mu _{ab}(t))$ चयनित किया गया है, रूटिंग निर्णय चर $\mu _{ab}^{(c)}(t)$ सरल वितरित तरीके से गणना की जा सकती है, जहां प्रत्येक नोड को केवल ज्ञान की आवश्यकता होती है क्यू बैकलॉग अपने और अपने पड़ोसियों के बीच अंतर करता है। हालाँकि, संचरण दरों के चयन के लिए एक समाधान की आवश्यकता होती है Eq में अधिकतम वजन की समस्या। (1)-(2). विशेष मामले में जब चैनल ओर्थोगोनल होते हैं, एल्गोरिथ्म में एक प्राकृतिक वितरित कार्यान्वयन होता है और प्रत्येक नोड पर अलग-अलग निर्णयों को कम करता है। हालाँकि, अधिकतम-भार समस्या इंटर-चैनल हस्तक्षेप वाले नेटवर्क के लिए एक केंद्रीकृत नियंत्रण समस्या है। केंद्रीकृत तरीके से भी इसे हल करना बहुत मुश्किल हो सकता है।

सिग्नल-टू-शोर-प्लस-हस्तक्षेप अनुपात (एसआईएनआर) द्वारा निर्धारित लिंक दरों के साथ हस्तक्षेप नेटवर्क के लिए एक वितरित दृष्टिकोण यादृच्छिककरण का उपयोग करके किया जा सकता है। प्रत्येक नोड बेतरतीब ढंग से प्रत्येक स्लॉट टी को प्रसारित करने का निर्णय लेता है (यदि यह वर्तमान में नहीं है तो एक अशक्त पैकेट को प्रेषित करता है भेजने के लिए एक पैकेट है)। वास्तविक संचरण दर, और भेजने के लिए संबंधित वास्तविक पैकेट, 2-स्टेप हैंडशेक द्वारा निर्धारित किया जाता है: पहले चरण में, बेतरतीब ढंग से चुने गए ट्रांसमीटर नोड सिग्नल की शक्ति के आनुपातिक के साथ एक पायलट सिग्नल भेजते हैं एक वास्तविक संचरण के लिए। दूसरे चरण पर, सभी संभावित रिसीवर नोड परिणामी हस्तक्षेप को मापते हैं और उस जानकारी को वापस भेजते हैं ट्रांसमीटर। सभी आउटगोइंग लिंक्स (एन, बी) के लिए एसआईएनआर स्तर तब सभी नोड्स एन के लिए जाना जाता है, और प्रत्येक नोड n तय कर सकता है इसका $\mu _{nb}(t)$ और $(\mu _{nb}^{(c)}(t))$ इस जानकारी के आधार पर चर। परिणामी थ्रूपुट आवश्यक रूप से इष्टतम नहीं है। हालाँकि, यादृच्छिक संचरण प्रक्रिया को चैनल राज्य प्रक्रिया के एक भाग के रूप में देखा जा सकता है (बशर्ते कि अशक्त पैकेट अंडरफ़्लो के मामलों में भेजे जाते हैं, ताकि चैनल राज्य प्रक्रिया पिछले निर्णयों पर निर्भर न हो)। इसलिए, इस वितरित कार्यान्वयन का परिणामी थ्रूपुट सभी रूटिंग और शेड्यूलिंग एल्गोरिदम के वर्ग पर इष्टतम है जो इस तरह के यादृच्छिक प्रसारण का उपयोग करते हैं।

वैकल्पिक वितरित कार्यान्वयन को मोटे तौर पर दो वर्गों में बांटा जा सकता है: एल्गोरिद्म का प्रथम वर्ग अधिकतम-भार समस्या के लिए निरंतर गुणक कारक सन्निकटन पर विचार करता है, और निरंतर-कारक थ्रूपुट परिणाम प्राप्त करें। एल्गोरिदम की दूसरी श्रेणी अधिकतम वजन के लिए योगात्मक सन्निकटन पर विचार करती है समस्या, समय के साथ अधिकतम-वजन समस्या के समाधान को अद्यतन करने पर आधारित है। इस द्वितीय श्रेणी के एल्गोरिद्म को स्थैतिक चैनल की आवश्यकता प्रतीत होती है स्थितियां और लंबा (अक्सर गैर-बहुपद) अभिसरण समय, हालांकि वे अधिकतम थ्रूपुट प्राप्त कर सकते हैं उपयुक्त मान्यताओं के तहत।योगात्मक सन्निकटन अक्सर उपयोगी होते हैं आउट-ऑफ-डेट कतार बैकलॉग जानकारी के साथ कार्यान्वित किए जाने पर बैकप्रेशर की इष्टतमता साबित करने के लिए (नीली पाठ का अभ्यास 4.10 देखें)।

लयपुनोव बहाव के माध्यम से गणितीय निर्माण

यह भाग प्रदर्शित करता है कि एक व्याकरणिक स्थान से दूसरे व्याकरणिक स्थान में क्यू बैकलॉग के वर्गों के योग में परिवर्तन पर बाध्यता को कम करने के स्वाभाविक परिणाम के रूप में पश्चदाब एल्गोरिदम कैसे उत्पन्न होता है।

नियंत्रण निर्णय बाध्यताएं और पंक्ति अद्यतन समीकरण

उपरोक्त खंड में वर्णित N बिंदु के साथ एक बहुपद नेटवर्क पर विचार करें। प्रत्येक व्याकरणिक स्थान t नेटवर्क नियंत्रक सांस्थिति स्थिति S(t) को प्रेक्षित करता है तथा निम्नलिखित बाधाओं के अधीन संचरण दर $(\mu _{ab}(t))$ परिसंचरण चर राशि $(\mu _{ab}^{(c)}(t))$ का चयन करता है:

${\text{(Eq. 3)}}\qquad (\mu _{ab}(t))\in \Gamma _{S(t)}$

${\text{(Eq. 4)}}\qquad 0\leq \mu _{ab}^{(c)}(t)\qquad \forall a,b,c,\forall t$

${\text{(Eq. 5)}}\qquad \sum _{c=1}^{N}\mu _{ab}^{(c)}(t)\leq \mu _{ab}(t)\qquad \forall (a,b),\forall t$

एक बार परिसंचरण चर निर्धारित हो जाने के पश्चात ही प्रसारण किया जाता है (यदि आवश्यक हो तो निष्क्रिय भरण का उपयोग करके) तथा परिणामी क्यू बैकलॉग निम्नलिखित को संतुष्ट करते हैं:

${\text{(Eq. 6)}}\qquad Q_{n}^{(c)}(t+1)\leq \max \left[Q_{n}^{(c)}(t)-\sum _{b=1}^{N}\mu _{nb}^{(c)}(t),0\right]+\sum _{a=1}^{N}\mu _{an}^{(c)}(t)+A_{n}^{(c)}(t)$

जहाँ $A_{n}^{(c)}(t)$ नए पण्य c डेटा की यादृच्छिक मात्रा है जो वाह्य रूप से व्याकरणिक स्थान t पर बिंदु n पर आता है और $\mu _{nb}^{(c)}(t)$ व्याकरणिक स्थान t से संबद्ध (एन, बी) पर पण्य c परिवहन के लिए आवंटित संचरण दर है। ध्यान दें कि $\mu _{nb}^{(c)}(t)$ पण्य c डेटा की मात्रा से अधिक हो सकता है जो वस्तुतः व्याकरणिक स्थान t से संबद्ध (a,b) पर प्रसारित होता है। ऐसा इसलिए है क्योंकि बिंदु n में पर्याप्त संचित कार्य नहीं हो सकता है। इसी कारण से समीकरण (6) एक समानता की जगह एक असमानता है क्योंकि व्याकरणिक स्थान t पर बिंदु n के लिए पण्य c के वास्तविक अंतर्जात आगमन से $\sum _{a=1}^{N}\mu _{an}^{(c)}(t)$ अधिक हो सकता है। समीकरण (6) की एक महत्वपूर्ण विशेषता यह है कि यद्यपि $\mu _{ab}^{(c)}(t)$ निर्णय चर क्यू बैकलॉग से स्वतंत्र रूप से चुने गए हों।

यह माना जाता है कि सभी व्याकरणिक स्थान t और सभी $c\in \{1,\ldots ,N\}$ के लिए $Q_{c}^{(c)}(t)=0$ क्योंकि कोई क्रमित डेटा को स्वयं के लिए नियत नहीं करता है।

लायपुनोव बहाव

परिभाषित करना ${\boldsymbol {Q}}(t)=(Q_{n}^{(c)}(t))$ वर्तमान कतार बैकलॉग के मैट्रिक्स के रूप में। निम्नलिखित गैर-नकारात्मक फ़ंक्शन को परिभाषित करें, जिसे लायपुनोव समारोह कहा जाता है:

$L(t)={\frac {1}{2}}\sum _{n=1}^{N}\sum _{c=1}^{N}Q_{n}^{(c)}(t)^{2}$ यह कतार बैकलॉग के वर्गों का योग है (बाद के विश्लेषण में सुविधा के लिए केवल 1/2 से गुणा)। उपरोक्त राशि सभी n, c के योग के समान है जैसे कि $n\neq c$ क्योंकि $Q_{c}^{(c)}(t)=0$ सभी के लिए $c\in \{1,\ldots ,N\}$ और सभी स्लॉट टी.

सशर्त Lyapunov बहाव $\Delta (t)$ परिभाषित किया गया:

$\Delta (t)=E\left[L(t+1)-L(t)\mid {\boldsymbol {Q}}(t)\right]$

ध्यान दें कि निम्नलिखित असमानता सभी के लिए लागू होती है $q\geq 0$, $a\geq 0$, $b\geq 0$:

$(\max[q-b,0]+a)^{2}\leq q^{2}+b^{2}+a^{2}+2q(a-b)$

कतार अद्यतन समीकरण (Eq। (6)) को चुकता करके और उपरोक्त असमानता का उपयोग करके, यह मुश्किल नहीं है यह दिखाने के लिए कि सभी स्लॉट टी के लिए और ट्रांसमिशन और रूटिंग वेरिएबल्स चुनने के लिए किसी भी एल्गोरिदम के तहत $(\mu _{ab}(t))$ और $(\mu _{ab}^{(c)}(t))$:

${\text{(Eq. 7)}}\qquad \Delta (t)\leq B+\sum _{n=1}^{N}\sum _{c=1}^{N}Q_{n}^{(c)}(t)E\left[\lambda _{n}^{(c)}(t)+\sum _{a=1}^{N}\mu _{an}^{(c)}(t)-\sum _{b=1}^{N}\mu _{nb}^{(c)}(t)|{\boldsymbol {Q}}(t)\right]$

जहां बी एक परिमित स्थिरांक है जो आगमन के दूसरे क्षणों और संचरण दरों के अधिकतम संभव दूसरे क्षणों पर निर्भर करता है।

राशियों को स्विच करके बहाव को कम करना

बैकप्रेसर एल्गोरिदम को निरीक्षण करने के लिए डिज़ाइन किया गया है ${\boldsymbol {Q}}(t)$ और एस (टी) हर स्लॉट टी और चुनें $(\mu _{ab}(t))$ और $(\mu _{ab}^{(c)}(t))$ ड्रिफ्ट बाउंड Eq के दाईं ओर को कम करने के लिए। (7)। क्योंकि बी एक स्थिर है और $\lambda _{n}^{(c)}$ स्थिरांक हैं, यह अधिकतम करने के बराबर है:

$E\left[\sum _{n=1}^{N}\sum _{c=1}^{N}Q_{n}^{(c)}(t)\left[\sum _{b=1}^{N}\mu _{nb}^{(c)}(t)-\sum _{a=1}^{N}\mu _{an}^{(c)}(t)\right]|{\boldsymbol {Q}}(t)\right]$

जहां अधिकतम निर्णय को रोशन करने के लिए उम्मीदों के माध्यम से परिमित रकम को धक्का दिया गया है। अवसरवादी रूप से एक अपेक्षा को अधिकतम करने के सिद्धांत द्वारा, उपरोक्त अपेक्षा को अधिकतम किया जाता है इसके अंदर फ़ंक्शन को अधिकतम करना (देखा गया ${\boldsymbol {Q}}(t)$, $S(t)$). इस प्रकार, कोई चुनता है $(\mu _{ab}(t))$ और $(\mu _{ab}^{(c)}(t))$ बाधाओं Eqs के अधीन। (3)-(5) अधिकतम करने के लिए:

$\sum _{n=1}^{N}\sum _{c=1}^{N}Q_{n}^{(c)}(t)\left[\sum _{b=1}^{N}\mu _{nb}^{(c)}(t)-\sum _{a=1}^{N}\mu _{an}^{(c)}(t)\right]$

यह तत्काल स्पष्ट नहीं है कि कौन से निर्णय उपरोक्त को अधिकतम करते हैं। राशियों को स्विच करके इसे प्रकाशित किया जा सकता है। वास्तव में, उपरोक्त अभिव्यक्ति नीचे के समान है:

$\sum _{a=1}^{N}\sum _{b=1}^{N}\sum _{c=1}^{N}\mu _{ab}^{(c)}(t)[Q_{a}^{(c)}(t)-Q_{b}^{(c)}(t)]$

भार $Q_{a}^{(c)}(t)-Q_{b}^{(c)}(t)$ कमोडिटी सी के बीच वर्तमान अंतर बैकलॉग कहा जाता है नोड्स ए और बी। निर्णय चर चुनने का विचार है $(\mu _{ab}^{(c)}(t))$ ताकि उपरोक्त को अधिकतम किया जा सके भारित राशि, जहाँ भार विभेदक बैकलॉग हैं। सहज रूप से, इसका अर्थ है दिशाओं में बड़ी दरें आवंटित करना बड़े अंतर बैकलॉग का।

स्पष्ट रूप से किसी को चुनना चाहिए $\mu _{ab}^{(c)}(t)=0$ जब कभी भी $Q_{a}^{(c)}(t)-Q_{b}^{(c)}(t)<0$. आगे, दिया $\mu _{ab}(t)$ किसी विशेष लिंक के लिए $(a,b)$, यह दिखाना मुश्किल नहीं है कि इष्टतम $\mu _{ab}^{(c)}(t)$ चयन, Eqs के अधीन। (3) - (5), निम्नानुसार निर्धारित किए जाते हैं: पहले कमोडिटी खोजें $c_{ab}^{opt}(t)\in \{1,\ldots ,N\}$ जो लिंक (ए, बी) के लिए अंतर बैकलॉग को अधिकतम करता है। यदि लिंक (ए, बी) के लिए अधिकतम अंतर बैकलॉग नकारात्मक है, सौंपना $\mu _{ab}^{(c)}(t)=0$ सभी वस्तुओं के लिए $c\in \{1,\ldots ,N\}$ लिंक पर (ए, बी)। अन्यथा, पूरी लिंक दर आवंटित करें $\mu _{ab}(t)$ कमोडिटी को $c_{ab}^{opt}(t)$, और इस लिंक पर अन्य सभी वस्तुओं के लिए शून्य दर। इस विकल्प के साथ, यह इस प्रकार है:

$\sum _{c=1}^{N}\mu _{ab}^{(c)}(t)[Q_{a}^{(c)}(t)-Q_{b}^{(c)}(t)]=\mu _{ab}(t)W_{ab}(t)$

कहाँ $W_{ab}(t)$ स्लॉट टी (0 के साथ अधिकतम) पर लिंक (ए, बी) के लिए इष्टतम वस्तु का अंतर बैकलॉग है:

$W_{ab}(t)=\max[Q_{a}^{(c_{ab}^{opt}(t))}(t)-Q_{b}^{(c_{ab}^{opt}(t))}(t),0]$

यह केवल चुनना बाकी है $(\mu _{ab}(t))\in \Gamma _{S(t)}$. यह निम्नलिखित को हल करके किया जाता है:

$\mathrm {Maximize:} \sum _{a=1}^{N}\sum _{b=1}^{N}\mu _{ab}(t)W_{ab}(t)$

$\mathrm {Subjectto:} (\mu _{ab}(t))\in \Gamma _{S(t)}$

उपरोक्त समस्या Eqs में अधिकतम-भार समस्या के समान है। (1)-(2). बैकप्रेशर एल्गोरिथम के लिए अधिकतम-वजन निर्णयों का उपयोग करता है $(\mu _{ab}(t))$, और फिर रूटिंग वेरिएबल चुनता है $(\mu _{ab}^{(c)}(t))$ ऊपर वर्णित अधिकतम अंतर बैकलॉग के माध्यम से।

बैकप्रेसर एल्गोरिथम की एक उल्लेखनीय संपत्ति यह है कि यह केवल देखी गई टोपोलॉजी स्थिति S(t) और क्यू बैकलॉग के आधार पर हर स्लॉट टी पर लालच से काम करता है। ${\boldsymbol {Q}}(t)$ उस स्लॉट के लिए। इस प्रकार, इसे आगमन दरों के ज्ञान की आवश्यकता नहीं है $(\lambda _{n}^{(c)})$ या टोपोलॉजी राज्य संभावनाएं $\pi _{S}=Pr[S(t)=S]$.

प्रदर्शन विश्लेषण

यह भाग पश्चदाब एल्गोरिथम की साद्यांत इष्टतमता को सिद्ध करता है।सरलता के लिए उस परिदृश्य पर विचार किया जाता है जहाँ घटनाएँ स्वतंत्र तथा व्याकरणिक स्थान पर समान रूप से वितरित (i.i.d.) होती हैं, हालाँकि समान एल्गोरिथ्म को गैर-i.i.d परिदृश्यों में कार्य करने के लिए प्रदर्शित किया जा सकता है (गैर-i.i.d. ऑपरेशन और सार्वभौमिक अनुसूचीकरण के अंतर्गत नीचे देखें)।

गतिक आगमन

मान लें कि$(A_{n}^{(c)}(t))$ व्याकरणिक स्थान t पर बहिर्जात आगमन का आव्यूह है। मान लें कि यह आव्यूह स्वतंत्र और समान रूप से वितरित (i.i.d.) व्याकरणिक स्थान पर परिमित दूसरे क्षणों तथा साधनों के साथ है:

$\lambda _{n}^{(c)}=E\left[A_{n}^{(c)}(t)\right]$

यह माना जाता है कि सभी $c\in \{1,\ldots ,N\}$ के लिए $\lambda _{c}^{(c)}=0$ क्योंकि स्वयं के लिए नियत कोई डेटा प्राप्त नहीं होता है। इस प्रकार, आगमन दर $(\lambda _{n}^{(c)})$ का आव्यूह विकर्ण पर शून्य के साथ गैर-ऋणात्मक वास्तविक संख्याओं का $N\times N$ आव्यूह है।

नेटवर्क क्षमता क्षेत्र

मान लें कि टोपोलॉजी स्थिति S(t) i.i.d है। संभावनाओं के साथ स्लॉट्स पर $\pi _{S}=Pr[S(t)=S]$ (यदि एस (टी) वास्तविक मूल्यवान प्रविष्टियों वाले वैक्टरों के अनगिनत अनंत सेट में मान लेता है, तब $\pi _{S}$ संभाव्यता वितरण है, संभाव्यता द्रव्यमान समारोह नहीं)। नेटवर्क के लिए एक सामान्य एल्गोरिद्म S(t) प्रत्येक स्लॉट t को देखता है और ट्रांसमिशन दरों को चुनता है $(\mu _{ab}(t))$ और रूटिंग चर $(\mu _{ab}^{(c)}(t))$ Eq में बाधाओं के अनुसार। (3) - (5)। नेटवर्क क्षमता क्षेत्र $\Lambda$ सभी आगमन दर आव्यूहों के सेट का समापन है $(\lambda _{n}^{(c)})$ जिसके लिए एक एल्गोरिथ्म मौजूद है जो नेटवर्क को स्थिर करता है। सभी कतारों की स्थिरता का अर्थ है कि नेटवर्क में ट्रैफ़िक की कुल इनपुट दर अपने गंतव्य तक पहुँचाए गए डेटा की कुल दर के समान है। यह दिखाया जा सकता है कि किसी भी आगमन दर मैट्रिक्स के लिए $(\lambda _{n}^{(c)})$ क्षमता क्षेत्र में $\Lambda$, एक स्थिर और यादृच्छिक एल्गोरिदम है जो निर्णय चर चुनता है $(\mu _{ab}^{*}(t))$ और $(\mu _{ab}^{*(c)}(t))$ प्रत्येक स्लॉट टी केवल एस (टी) पर आधारित है (और इसलिए क्यू बैकलॉग से स्वतंत्र) जो सभी के लिए निम्नलिखित देता है $n\neq c$:

${\text{(Eq. 8)}}\qquad E\left[\lambda _{n}^{(c)}+\sum _{a=1}^{N}\mu _{an}^{*(c)}(t)-\sum _{b=1}^{N}\mu _{nb}^{*(c)}(t)\right]\leq 0$

इस तरह के एक स्थिर और यादृच्छिक एल्गोरिदम जो केवल एस (टी) पर निर्णय लेते हैं, एस-ओनली एल्गोरिदम कहलाते हैं। यह मान लेना अक्सर उपयोगी होता है $(\lambda _{n}^{(c)})$ का आंतरिक है $\Lambda$, ताकि वहाँ एक है $\epsilon >0$ ऐसा है कि $(\lambda _{n}^{(c)}+\epsilon 1_{n}^{(c)})\in \Lambda$, कहाँ $1_{n}^{(c)}$ 1 है अगर $n\neq c$, और शून्य। उस स्थिति में, एक एस-ओनली एल्गोरिथम है जो सभी के लिए निम्नलिखित उत्पन्न करता है $n\neq c$:

${\text{(Eq. 9)}}\qquad E\left[\lambda _{n}^{(c)}+\sum _{a=1}^{N}\mu _{an}^{*(c)}(t)-\sum _{b=1}^{N}\mu _{nb}^{*(c)}(t)\right]\leq -\epsilon$

तकनीकी आवश्यकता के रूप में, यह माना जाता है कि संचरण दर के दूसरे क्षण $\mu _{ab}(t)$ इन दरों को चुनने के लिए किसी भी एल्गोरिदम के तहत परिमित हैं। यह तुच्छ रूप से धारण करता है यदि कोई अधिकतम अधिकतम दर है $\mu _{max}$.

केवल-एस एल्गोरिदम की तुलना

क्योंकि पश्चदाब एल्गोरिथ्म ${\boldsymbol {Q}}(t)$ और S(t) प्रत्येक व्याकरणिक स्थान t को देखता है और बाध्य धारा समीकरण (7) के दाहिने हाथ की ओर कम करने के लिए $(\mu _{ab}(t))$ और $(\mu _{ab}^{(c)}(t))$ निर्णय का चयन करता है। हमें प्राप्त है:

${\text{(Eq. 10)}}\qquad \Delta (t)\leq B+\sum _{n=1}^{N}\sum _{c=1}^{N}Q_{n}^{(c)}(t)E\left[\lambda _{n}^{(c)}(t)+\sum _{a=1}^{N}\mu _{an}^{*(c)}(t)-\sum _{b=1}^{N}\mu _{nb}^{*(c)}(t)|{\boldsymbol {Q}}(t)\right]$

जहाँ $(\mu _{ab}^{*}(t))$ और $(\mu _{ab}^{*(c)}(t))$ कोई वैकल्पिक निर्णय हैं जो समीकरण (3) - (5) को संतुष्ट करते हैं जिसमें यादृच्छिक निर्णय सम्मिलित हैं।

अब$(\lambda _{n}^{(c)})\in \Lambda$ मान लीजिए। तब एक केवल-S एल्गोरिथम उपस्थित होता है जो समीकरण (8) को संतुष्ट करता है। इसे समीकरण (10) के दाईं ओर यह देखते हुए प्लग करना कि इस केवल-S एल्गोरिथम के अंतर्गत ${\boldsymbol {Q}}(t)$ अशर्त अपेक्षा (क्योंकि S(t) i.i.d. स्लॉट्स पर है और S-only एल्गोरिथम वर्तमान क्यू बैकलॉग से स्वतंत्र है) के समान है:

$\Delta (t)\leq B\,$

इस प्रकार द्विघात लायपुनोव फलन का आशय सभी व्याकरणिक स्थान t के लिए नियतांक B से कम या उसके समान है। यह तथ्य इस धारणा के साथ है कि पंक्ति आगमन ने दूसरे क्षणों को सीमित कर दिया है, सभी नेटवर्क पंक्ति के लिए निम्नलिखित का अर्थ है:

$\lim _{t\rightarrow \infty }{\frac {Q_{n}^{(c)}(t)}{t}}=0{\text{ with probability 1}}$

औसत कतार आकार की एक मजबूत समझ के लिए, आगमन दर मान सकते हैं $(\lambda _{n}^{(c)})$ के आंतरिक हैं $\Lambda$, तो वहाँ एक है $\epsilon >0$ ऐसा है कि Eq। (9) किसी विकल्प के लिए है एस-केवल एल्गोरिदम। समीकरण (9) को समीकरण (10) के दाएँ पक्ष में लगाने पर यह प्राप्त होता है:

$\Delta (t)\leq B-\epsilon \sum _{n=1}^{N}\sum _{c=1}^{N}Q_{n}^{(c)}(t)$

जिससे तत्काल प्राप्त हो जाता है (देखें):

$\limsup _{t\rightarrow \infty }{\frac {1}{t}}\sum _{\tau =0}^{t-1}\sum _{n=1}^{N}\sum _{c=1}^{N}E\left[Q_{n}^{(c)}(\tau )\right]\leq {\frac {B}{\epsilon }}$

जैसे-जैसे क्षमता क्षेत्र $\Lambda$ की सीमा से दूरी $\epsilon$ शून्य हो जाती है, यह औसत पंक्ति आकार सीमा बढ़ जाती है। यह आगमन दर $\lambda$ और सेवा दर $\mu$ के साथ एकल M/M/1 पंक्ति के समान गुणात्मक प्रदर्शन है जहां औसत पंक्ति का आकार $1/\epsilon$ के समानुपाती होता है जहां $\epsilon =\mu -\lambda$ होता है।

उपरोक्त फॉर्मूलेशन के एक्सटेंशन

गैर-आई.आई.डी. ऑपरेशन और यूनिवर्सल शेड्यूलिंग

उपरोक्त विश्लेषण i.i.d. सादगी के लिए गुण। हालांकि, वही बैकप्रेशर एल्गोरिद्म गैर-आई.आई.डी. स्थितियों। जब आगमन प्रक्रियाएँ और टोपोलॉजी अवस्थाएँ एर्गोडिक होती हैं, लेकिन जरूरी नहीं कि i.i.d., बैकप्रेशर तब भी सिस्टम को स्थिर करता है जब भी $(\lambda _{n}^{(c)})\in \Lambda$. अधिक आम तौर पर, एक सार्वभौमिक शेड्यूलिंग दृष्टिकोण का उपयोग करते हुए, यह यादृच्छिक (संभवतः गैर-एर्गोडिक) नमूना पथों के लिए स्थिरता और इष्टतम गुणों की पेशकश करने के लिए दिखाया गया है।

यूटिलिटी ऑप्टिमाइज़ेशन और पेनल्टी मिनिमाइज़ेशन के साथ बैकप्रेशर

ड्रिफ्ट प्लस पेनल्टी|ड्रिफ्ट-प्लस-पेनल्टी तकनीक के माध्यम से बैकप्रेशर को प्रवाह नियंत्रण के संयोजन के साथ काम करने के लिए दिखाया गया है। यह तकनीक लालच से बहाव की मात्रा और भारित जुर्माना अभिव्यक्ति को अधिकतम करती है। जुर्माना एक पैरामीटर V द्वारा भारित होता है जो एक प्रदर्शन ट्रेडऑफ़ निर्धारित करता है। यह तकनीक सुनिश्चित करती है कि थ्रूपुट उपयोगिता इष्टतमता के O(1/V) के भीतर है जबकि औसत विलंब O(V) है। इस प्रकार, उपयोगिता को मनमाने ढंग से इष्टतमता के करीब धकेला जा सकता है, औसत देरी में एक समान व्यापार के साथ। औसत शक्ति न्यूनीकरण के लिए समान गुण दिखाए जा सकते हैं और अधिक सामान्य नेटवर्क विशेषताओं के अनुकूलन के लिए।

नेटवर्क उपयोगिता को अधिकतम करते हुए कतारों को स्थिर करने के लिए वैकल्पिक एल्गोरिदम विकसित किए गए हैं द्रव मॉडल विश्लेषण का उपयोग करना,संयुक्त द्रव विश्लेषण और लैग्रेंज गुणक विश्लेषण, उत्तल अनुकूलन, और स्टोकेस्टिक ग्रेडिएंट्स। ये दृष्टिकोण O(1/V), O(V) उपयोगिता-विलंब परिणाम प्रदान नहीं करते हैं।

यह भी देखें

• एड हॉक ऑन-डिमांड डिस्टेंस वेक्टर रूटिंग
• विविधता बैकप्रेशर रूटिंग (DIVBAR)* ड्रिफ्ट प्लस पेनल्टी
• ExOR (वायरलेस नेटवर्क प्रोटोकॉल)
• भौगोलिक मार्ग
• एड तदर्थ रूटिंग प्रोटोकॉल की सूची
• लायपुनोव अनुकूलन

प्राथमिक स्रोत

• एल. तस्सिउलास और ए. एफ़्रेमाइड्स, मल्टीहॉप रेडियो नेटवर्क में अधिकतम थ्रूपुट के लिए विवश क्यूइंग सिस्टम और शेड्यूलिंग नीतियों की स्थिरता गुण, स्वचालित नियंत्रण पर IEEE लेनदेन, वॉल्यूम। 37, नहीं. 12, पीपी. 1936-1948, दिसंबर 1992.
• एल. जोर्जियाडिस, एम.जे. नीली, और एल. तासीउलास, संसाधन आवंटन और वायरलेस नेटवर्क में क्रॉस-लेयर नियंत्रण, नेटवर्किंग में नींव और रुझान, वॉल्यूम। 1, नहीं। 1, पीपी। 1–149, 2006।
• एम जे नीली। स्टोचैस्टिक नेटवर्क ऑप्टिमाइजेशन विथ एप्लीकेशन टू कम्युनिकेशन एंड क्यूइंग सिस्टम्स, मॉर्गन एंड क्लेपूल, 2010।

श्रेणी:नेटवर्किंग एल्गोरिदम श्रेणी:पंक्ति सिद्धांत श्रेणी:रूटिंग एल्गोरिथम