नैपसैक समस्या

आयामी (बाधा) नैकपैक समस्या का उदाहरण: कुल वजन को 15 किग्रा से कम या समान रखते हुए धन की मात्रा को अधिकतम करने के लिए कौन से बक्सों को चुना जाना चाहिए? नैपसैक समस्याओं की सूची # एकाधिक प्रतिबंध बॉक्स के वजन और मात्रा दोनों पर विचार कर सकते हैं।
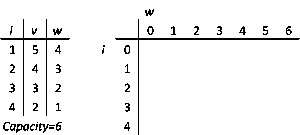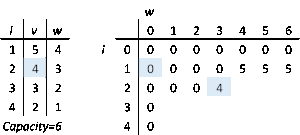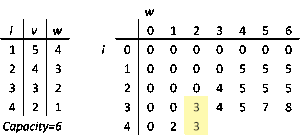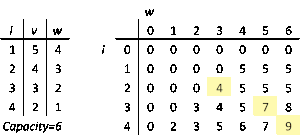
(समाधान: यदि प्रत्येक बॉक्स की कोई संख्या उपलब्ध है, तो तीन पीले बॉक्स और तीन ग्रे बॉक्स; यदि केवल दिखाए गए बॉक्स उपलब्ध हैं, तो हरे बॉक्स को छोड़कर सभी।)

संयोजी अनुकूलन में नैपसैक समस्या निम्नलिखित समस्या है:

वस्तुओं का समुच्चय दिया गया है प्रत्येक वजन और मूल्य के साथ यह निर्धारित करें कि संग्रह में कौन सी वस्तुओं को सम्मिलित करना है जिससे कुल वजन दी गई सीमा से कम या उसके समान हो और कुल मूल्य जितना संभव हो उतना बड़ा हो।' '

इसका नाम किसी ऐसे व्यक्ति के सामने आने वाली समस्या से लिया गया है जो निश्चित आकार के थैले से विवश है और इसे सबसे मूल्यवान वस्तुओं से भरना चाहिए। समस्या अधिकांशतः संसाधन आवंटन में उत्पन्न होती है जहां निर्णय लेने वालों को क्रमशः निश्चित बजट या समय की कमी के अनुसार गैर-विभाज्य परियोजनाओं या कार्यों के समुच्चय से चुनना पड़ता है।

नैकपैक समस्या का अध्ययन सदी से भी अधिक समय से किया जा रहा है, जिसमें प्रारंभिक कार्य 1897 तक के हैं। नैपसेक नाम की समस्या गणितज्ञ टोबियास डेंजिग (1884-1956) के प्रारंभिक कार्यों से मिलती है, और सामान को ओवरलोड किए बिना सबसे मूल्यवान या उपयोगी वस्तुओं को पैक करने की सामान्य समस्या को संदर्भित करता है।

अनुप्रयोग

विभिन्न प्रकार के क्षेत्रों में वास्तविक विश्व की निर्णय लेने की प्रक्रियाओं में नैपसैक समस्याएं दिखाई देती हैं जैसे कच्चे माल को कम से कम व्यर्थ करने का प्रणाली खोजना निवेश और पोर्टफोलियो (वित्त) का चयन संपत्ति-समर्थित प्रतिभूतिकरण के लिए संपत्ति का चयन और मेर्कले-हेलमैन और अन्य नैकपैक क्रिप्टोप्रणाली के लिए जनरेटिंग कुंजियां है ।

क्नाप्सैक एल्गोरिदम का प्रारंभिक अनुप्रयोग परीक्षणों के निर्माण और स्कोरिंग में था जिसमें परीक्षार्थियों के पास यह विकल्प होता है कि वे किस प्रश्न का उत्तर दें और छोटे उदाहरणों के लिए परीक्षार्थियों को इस तरह का विकल्प प्रदान करना अधिक सरल प्रक्रिया है। उदाहरण के लिए यदि किसी परीक्षा में 10 अंकों के 12 प्रश्न हैं तो परीक्षार्थी को अधिकतम 100 अंक प्राप्त करने के लिए केवल 10 प्रश्नों के उत्तर देने की आवश्यकता है। चूंकि बिंदु मानों के विषम वितरण वाले परीक्षणों पर विकल्प प्रदान करना अधिक कठिन होता है। फ़्यूरमैनऔर वेइसने प्रणाली प्रस्तावित की जिसमें छात्रों को कुल 125 संभावित अंकों के साथ विषम परीक्षा दी जाती है। छात्रों को अपनी क्षमताओं के अनुसार सभी प्रश्नों के उत्तर देने के लिए कहा जाता है। समस्याओं के संभावित उपसमुच्चयों में से जिनके कुल अंक मान 100 तक जोड़ते हैं नैपसैक एल्गोरिथ्म यह निर्धारित करेगा कि कौन सा उपसमुच्चय प्रत्येक छात्र को उच्चतम संभव स्कोर देता है।

1999 में स्टोनी ब्रुक यूनिवर्सिटी एल्गोरिथम रिपॉजिटरी के अध्ययन से पता चला है कि कॉम्बिनेटरियल एल्गोरिदम और एल्गोरिथम इंजीनियरिंग के क्षेत्र से संबंधित 75 एल्गोरिथम समस्याओं में से, नैपसैक समस्या 19वीं सबसे लोकप्रिय और प्रत्यय पेड़ों और बिन पैकिंग समस्या के बाद तीसरी सबसे अधिक आवश्यक थी। .

परिभाषा

हल की जा रही सबसे समान समस्या 0-1 नैपसैक समस्या है, जो प्रत्येक प्रकार के आइटम की प्रतियों की संख्या $x_{i}$ को शून्य या एक तक सीमित कर देती है। अधिकतम वजन क्षमता $W$ के साथ, 1 से $n$ तक की संख्या वाली $n$ वस्तुओं का एक सेट दिया गया है, प्रत्येक का वजन $w_{i}$ और एक मान $v_{i}$ है।

अधिकतम करें $\sum _{i=1}^{n}v_{i}x_{i}$

का विषय है $\sum _{i=1}^{n}w_{i}x_{i}\leq W$ और $x_{i}\in \{0,1\}$.

यहाँ $x_{i}$ नैपसैक में सम्मिलित करने के लिए आइटम $i$ के उदाहरणों की संख्या का प्रतिनिधित्व करता है। अनौपचारिक रूप से समस्या थैले में वस्तुओं के मूल्यों के योग को अधिकतम करने की है जिससे वजन का योग थैले की क्षमता से कम या उसके समान हो।

बाउंडेड नैपसैक प्रॉब्लम (बीकेपी) प्रतिबंध को हटाती है कि प्रत्येक आइटम में से केवल है, किन्तु प्रत्येक प्रकार के आइटम की प्रतियों की संख्या $x_{i}$ को अधिकतम गैर-ऋणात्मक पूर्णांक मान $c$ तक सीमित करती है:

अधिकतम करें $\sum _{i=1}^{n}v_{i}x_{i}$

का विषय है $\sum _{i=1}^{n}w_{i}x_{i}\leq W$ और $x_{i}\in \{0,1,2,\dots ,c\}.$

अनबाउंड नैपसैक प्रॉब्लम (यूकेपी) प्रत्येक प्रकार के आइटम की प्रतियों की संख्या पर कोई ऊपरी सीमा नहीं रखती है और इसे ऊपर के रूप में तैयार किया जा सकता है सिवाय इसके कि $x_{i}$ पर एकमात्र प्रतिबंध यह है कि यह गैर-नकारात्मक पूर्णांक है।

अधिकतम करें $\sum _{i=1}^{n}v_{i}x_{i}$

का विषय है $\sum _{i=1}^{n}w_{i}x_{i}\leq W$ और $x_{i}\in \mathbb {Z} ,\ x_{i}\geq 0.$

असीमित नैपसैक समस्या का उदाहरण इस आलेख के आरंभ में दिखाए गए चित्र और उस चित्र के शीर्षक में प्रत्येक बॉक्स की कोई संख्या उपलब्ध होने पर पाठ का उपयोग करके दिया गया है।

कम्प्यूटेशनल जटिलता

कंप्यूटर विज्ञान के दृष्टिकोण से नैकपैक समस्या कई कारणों से रोचक है:

• क्नाप्सैक समस्या का निर्णय समस्या रूप (क्या कम से कम V का मान W से अधिक वजन के बिना प्राप्त किया जा सकता है?) NP-पूर्ण है, इस प्रकार कोई ज्ञात एल्गोरिथम नहीं है जो सभी स्थितियों में सही और तेज़ (बहुपद-समय) दोनों हो .
• जबकि निर्णय समस्या एनपी-पूर्ण है, अनुकूलन समस्या नहीं है, इसका समाधान कम से कम उतना ही कठिन है जितना कि निर्णय समस्या और कोई ज्ञात बहुपद एल्गोरिथ्म नहीं है जो यह बता सके कि समाधान दिया गया है कि क्या यह इष्टतम है (जो होगा) इसका कारण है कि बड़े वी के साथ कोई समाधान नहीं है, इस प्रकार एनपी-पूर्ण निर्णय समस्या को हल करना)।
• गतिशील प्रोग्रामिंग का उपयोग करते हुए छद्म-बहुपद समय एल्गोरिथ्म है।
• बहुपद-समय सन्निकटन योजना है।
• कई स्थितियों जो व्यवहार में उत्पन्न होते हैं, और कुछ वितरणों से यादृच्छिक उदाहरण फिर भी ठीक से हल किए जा सकते हैं।

इसमें निर्णय और अनुकूलन समस्याओं के बीच लिंक है, यदि कोई बहुपद एल्गोरिदम उपस्थित है जो निर्णय की समस्या को हल करता है तो बहुपद समय में अनुकूलन समस्या के लिए अधिकतम मूल्य पा सकते हैं, इस एल्गोरिथ्म को k के मान में वृद्धि करते हुए पुनरावृत्त रूप से प्रयुक्त कर सकते हैं। दूसरी ओर, यदि एल्गोरिथ्म बहुपद समय में अनुकूलन समस्या का इष्टतम मूल्य पाता है, तो बहुपद समय में इस एल्गोरिथ्म द्वारा समाधान आउटपुट के मूल्य की तुलना k के मान से करके निर्णय समस्या को हल किया जा सकता है। इस प्रकार, समस्या के दोनों संस्करण समान कठिनाई वाले हैं।

शोध साहित्य में विषय यह पहचानना है कि नैकपैक समस्या के कठिन उदाहरण क्या दिखते हैं, या किसी अन्य विधि से देखा जाता है, यह पहचानने के लिए कि व्यवहार में उदाहरणों के कौन से गुण उन्हें उनके सबसे खराब स्थिति वाले एनपी-पूर्ण व्यवहार से अधिक उत्तरदायी बना सकते हैं। इन कठिन उदाहरणों को खोजने का लक्ष्य सार्वजनिक कुंजी क्रिप्टोग्राफ़ी प्रणाली में उनके उपयोग के लिए है, जैसे मर्कल-हेलमैन नैपसैक क्रिप्टोसिस्टम है

इसके अतिरिक्त उल्लेखनीय तथ्य यह है कि नैकपैक समस्या की कठोरता इनपुट के रूप पर निर्भर करती है। यदि वजन और लाभ पूर्णांक के रूप में दिया जाता है, तो यह अशक्त रूप से एनपी-पूर्ण होता है, जबकि वजन और लाभ को तर्कसंगत संख्या के रूप में दिया जाता है, जबकि यह दृढ़ता से एनपी-पूर्ण होता है। चूंकि तर्कसंगत वजन और लाभ के स्थितियों में यह अभी भी बहुपद-समय सन्निकटन योजना को स्वीकार करता है। पूरी तरह से बहुपद-समय सन्निकटन योजना है ।

सुलझाना

गतिशील प्रोग्रामिंग दृष्टिकोण, शाखा और बाध्य दृष्टिकोण या दोनों दृष्टिकोणों के संकरण के आधार पर, नैपसैक समस्याओं को हल करने के लिए कई एल्गोरिदम उपलब्ध हैं।

डायनेमिक प्रोग्रामिंग इन-एडवांस एल्गोरिथम

असीमित नैपसैक समस्या (यूकेपी) प्रत्येक प्रकार के आइटम की प्रतियों की संख्या पर कोई प्रतिबंध नहीं लगाती है। इसके अतिरिक्त यहाँ हम मानते हैं $x_{i}>0$

$m[w']=\max \left(\sum _{i=1}^{n}v_{i}x_{i}\right)$

का विषय है $\sum _{i=1}^{n}w_{i}x_{i}\leq w'$ और $x_{i}>0$

उसका अवलोकन करो $m[w]$ निम्नलिखित गुण हैं:

1. $m[0]=0\,\!$ (शून्य मदों का योग, अर्थात खाली समुच्चय का योग)।

2. $m[w]=\max(v_{1}+m[w-w_{1}],v_{2}+m[w-w_{2}],...,v_{n}+m[w-w_{n}])$

, $w_{i}\leq w$, जहाँ $v_{i}$ का मूल्य है $i$-वें प्रकार की वस्तु।

दूसरी संपत्ति को विस्तार से समझाने की आवश्यकता है। इस पद्धति के चलने की प्रक्रिया के समय हम वजन $w$ कैसे प्राप्त करते हैं? केवल $i$ विधि हैं और पिछले वजन हैं $w-w_{1},w-w_{2},...,w-w_{i}$ जहां कुल $i$ प्रकार के अलग-अलग आइटम हैं (यह कहकर अलग, हमारा कारण है कि वजन और मूल्य पूरी तरह से समान नहीं हैं)। यदि हम इन वस्तुओं के प्रत्येक मूल्य और संबंधित अधिकतम मूल्य को पहले से जानते हैं, तो हम बस उनकी दूसरे से तुलना करते हैं और अंततः अधिकतम मूल्य प्राप्त करते हैं और हम कर रहे हैं।

यहां खाली समुच्चय का अधिकतम शून्य लिया जाता है। $m[0]$ से $m[W]$ तक परिणामों को सारणीबद्ध करने से समाधान मिलता है। चूंकि प्रत्येक $m[w]$ की गणना में अधिकांश $n$ मदों की जांच सम्मिलित है, और गणना करने के लिए $m[w]$ के अधिकतम $W$ मान हैं, गतिशील प्रोग्रामिंग समाधान का चलने का समय $O(nW)$ है।$w_{1},\,w_{2},\,\ldots ,\,w_{n},\,W$ को उनके सबसे बड़े सामान्य भाजक से विभाजित करना चलने के समय को बढ़िया बनाने का प्रणाली है।

तथापि P≠NP, $O(nW)$ जटिलता इस तथ्य का खंडन नहीं करती है कि नैपसैक समस्या NP-पूर्ण है, क्योंकि $W$, $n$ के विपरीत, समस्या के इनपुट की लंबाई में बहुपद नहीं है। समस्या के लिए $W$ इनपुट की लंबाई $W$ , $\log W$ , में बिट्स की संख्या के समानुपाती होती है, स्वयं $W$ के लिए नहीं। चूंकि , चूंकि यह रनटाइम छद्मबहुपद है, यह (निर्णय संस्करण) नैपसैक समस्या को अशक्त एनपी-पूर्ण समस्या बनाता है।

0-1 बस्ता समस्या

गतिशील प्रोग्रामिंग दृष्टिकोण का प्रदर्शन।

0-1 नैपसैक समस्या के लिए समान गतिशील प्रोग्रामिंग समाधान छद्म-बहुपद समय में भी चलता है मान लें $w_{1},\,w_{2},\,\ldots ,\,w_{n},\,W$ सख्ती से सकारात्मक पूर्णांक हैं। $m[i,w]$ को अधिकतम मान के रूप में परिभाषित करें जिसे $i$ (प्रथम $i$ आइटम) तक के आइटम का उपयोग करके $w$ से कम या उसके समान वजन के साथ प्राप्त किया जा सकता है।

हम $m[i,w]$ को पुनरावर्ती रूप से निम्नानुसार परिभाषित कर सकते हैं: (परिभाषा ए)

• $m[0,\,w]=0$
• $m[i,\,w]=m[i-1,\,w]$ यदि $w_{i}>w\,\!$ (नया आइटम वर्तमान वजन सीमा से अधिक है)
• $m[i,\,w]=\max(m[i-1,\,w],\,m[i-1,w-w_{i}]+v_{i})$ यदि $w_{i}\leqslant w$.

समाधान तब $m[n,W]$ की गणना करके पाया जा सकता है। इसे कुशलतापूर्वक करने के लिए, हम पिछली संगणनाओं को संग्रहीत करने के लिए तालिका का उपयोग कर सकते हैं।

निम्नलिखित गतिशील कार्यक्रम के लिए स्यूडोकोड है:

// Input:
// Values (stored in array v)
// Weights (stored in array w)
// Number of distinct items (n)
// Knapsack capacity (W)
// NOTE: The array "v" and array "w" are assumed to store all relevant values starting at index 1.

array m[0..n, 0..W];
for j from 0 to W do:
    m[0, j] := 0
for i from 1 to n do:
    m[i, 0] := 0

for i from 1 to n do:
    for j from 0 to W do:
        if w[i] > j then:
            m[i, j] := m[i-1, j]
        else:
            m[i, j] := max(m[i-1, j], m[i-1, j-w[i]] + v[i])

इसलिए यह समाधान $O(nW)$ समय और $O(nW)$ स्थान में चलेगा। (यदि हमें केवल m [n, W] मान की आवश्यकता है, तो हम कोड को संशोधित कर सकते हैं जिससे आवश्यक मेमोरी की मात्रा O (W) हो जो सरणी "m" की दो पंक्तियों को संग्रहीत करती है।)

चूँकि यदि हम इसे या दो कदम आगे ले जाते हैं, तो हमें पता होना चाहिए कि विधि $O(nW)$ और $O(2^{n})$ के बीच के समय में चलेगी। परिभाषा ए से, हम जानते हैं कि सभी भारों की गणना करने की कोई आवश्यकता नहीं है जब वस्तुओं की संख्या और हमारे द्वारा चुने गए आइटम स्वयं तय होते हैं। कहने का तात्पर्य यह है कि ऊपर दिया गया प्रोग्राम आवश्यकता से अधिक गणना करता है क्योंकि वजन अधिकांशतः 0 से W में बदलता रहता है। इस दृष्टिकोण से, हम इस पद्धति को प्रोग्राम कर सकते हैं जिससे यह पुनरावर्ती रूप से चलता है ।

// Input:
// Values (stored in array v)
// Weights (stored in array w)
// Number of distinct items (n)
// Knapsack capacity (W)
// NOTE: The array "v" and array "w" are assumed to store all relevant values starting at index 1.

Define value[n, W]

Initialize all value[i, j] = -1

Define m:=(i,j)         // Define function m so that it represents the maximum value we can get under the condition: use first i items, total weight limit is j
{
    if i == 0 or j <= 0 then:
        value[i, j] = 0
        return

    if (value[i-1, j] == -1) then:     // m[i-1, j] has not been calculated, we have to call function m
        m(i-1, j)

    if w[i] > j then:                      // item cannot fit in the bag
        value[i, j] = value[i-1, j]
    else: 
        if (value[i-1, j-w[i]] == -1) then:     // m[i-1,j-w[i]] has not been calculated, we have to call function m
            m(i-1, j-w[i])
        value[i, j] = max(value[i-1,j], value[i-1, j-w[i]] + v[i])
}

Run m(n, W)

उदाहरण के लिए, 10 अलग-अलग आइटम हैं और वज़न की सीमा 67 है। इसलिए,

$${\begin{aligned}&w[1]=23,w[2]=26,w[3]=20,w[4]=18,w[5]=32,w[6]=27,w[7]=29,w[8]=26,w[9]=30,w[10]=27\\&v[1]=505,v[2]=352,v[3]=458,v[4]=220,v[5]=354,v[6]=414,v[7]=498,v[8]=545,v[9]=473,v[10]=543\\\end{aligned}}$$

यदि आप $m(10,67)$ के लिए गणना करने के लिए उपरोक्त विधि का उपयोग करते हैं, तो $m(i,j)=0$ उत्पन्न करने वाली कॉलों को छोड़कर, आपको यह मिलेगा::

इसके अतिरिक्त हम रिकर्सन को तोड़ सकते हैं और इसे पेड़ में बदल सकते हैं। तब हम कुछ पत्तियों को काट सकते हैं और समानांतर कंप्यूटिंग का उपयोग करके इस पद्धति को चलाने में तेजी ला सकते हैं।

वस्तुओं के वास्तविक उपसमुच्चय को खोजने के लिए केवल उनके कुल मूल्य के अतिरिक्त हम इसे ऊपर दिए गए फलन को चलाने के बाद चला सकते हैं

/**
 * Returns the indices of the items of the optimal knapsack.
 * i: We can include items 1 through i in the knapsack
 * j: maximum weight of the knapsack
 */
function knapsack(i: int, j: int): Set<int> {
    if i == 0 then:
        return {}
    if m[i, j] > m[i-1, j] then:
        return {i} ∪ knapsack(i-1, j-w[i])
    else:
        return knapsack(i-1, j)
}

knapsack(n, W)

बीच-बीच में मिलना

1974 में खोजे गए 0-1 नैपसैक के लिए और एल्गोरिथ्म , जिसे कभी-कभी क्रिप्टोग्राफी में समान नाम वाले एल्गोरिदम के समानांतर होने के कारण "मीट-इन-द-मिडल" कहा जाता है, विभिन्न मदों की संख्या में घातीय है किन्तु इसके लिए बढ़िया हो सकता है डीपी एल्गोरिथम जब $W$ n की तुलना में बड़ा होता है। विशेष रूप से, यदि $w_{i}$ गैर-नकारात्मक हैं, किन्तु पूर्णांक नहीं हैं, तब भी हम स्केलिंग और राउंडिंग (अर्थात निश्चित-बिंदु अंकगणितीय का उपयोग करके) द्वारा गतिशील प्रोग्रामिंग एल्गोरिदम का उपयोग कर सकते हैं, किन्तु यदि समस्या के लिए त्रुटिहीन के भिन्नात्मक अंकों की आवश्यकता होती है सही उत्तर, $W$ को $10^{d}$ से स्केल करने की आवश्यकता होगी, और डीपी एल्गोरिदम को $O(W10^{d})$ स्पेस और $O(nW10^{d})$ समय की आवश्यकता होगी।

algorithm Meet-in-the-middle is
    input: A set of items with weights and values.
    output: The greatest combined value of a subset.

    partition the set {1...n} into two sets A and B of approximately equal size
    compute the weights and values of all subsets of each set

    for each subset of A do
        find the subset of B of greatest value such that the combined weight is less than W

    keep track of the greatest combined value seen so far

एल्गोरिदम $O(2^{n/2})$ स्थान लेता है, और चरण 3 के कुशल कार्यान्वयन (उदाहरण के लिए, वजन के आधार पर B के उपसमुच्चय को छांटना, B के उपसमुच्चय को छोड़ना जो अधिक या समान मूल्य के B के अन्य उपसमुच्चय से अधिक वजन का होता है , और सर्वोत्तम मिलान खोजने के लिए बाइनरी खोज का उपयोग करके) $O(n2^{n/2})$ के रनटाइम में परिणामित होता है। क्रिप्टोग्राफी में मीट इन मिडल अटैक के साथ, यह $O(n2^{n})$ रनटाइम पर भोली क्रूर बल दृष्टिकोण ($\{1...n\}$ के सभी उपसमुच्चय की जांच) के रनटाइम में सुधार करता है, इसकी कीमत पर निरंतर स्थान के अतिरिक्त घातांक का उपयोग करना (बेबी-स्टेप जाइंट-स्टेप भी देखें)। मीट-इन-द-मिडल एल्गोरिथम में सुधार की वर्तमान स्थिति, उपसमुच्चय योग के लिए श्रोएप्पेल और शमीर के एल्गोरिथम से अंतर्दृष्टि का उपयोग करते हुए, नैपसैक के लिए यादृच्छिक एल्गोरिथम के रूप में प्रदान करता है जो $O^{*}(2^{n/2})$ (बहुपद कारकों तक) चलने का समय और स्थान की आवश्यकताओं को $O^{*}(2^{0.249999n})$ तक कम कर देता है (देखें [24] परिणाम 1.4) । इसके विपरीत, सबसे प्रसिद्ध नियतात्मक एल्गोरिथ्म $O^{*}(2^{n/2})$ समय में$O^{*}(2^{n/4})$ है ।

सन्निकटन एल्गोरिदम

अधिकांश एनपी-पूर्ण समस्याओं के लिए यह व्यावहारिक समाधान खोजने के लिए पर्याप्त हो सकता है, तथापि वे इष्टतम न हों। अधिमानतः चूंकि सन्निकटन समाधान के मूल्य और इष्टतम समाधान के मूल्य के बीच अंतर की आश्वासन के साथ आता है।

कई उपयोगी किन्तु कम्प्यूटेशनल रूप से जटिल एल्गोरिदम के साथ एल्गोरिदम बनाने और विश्लेषण करने पर पर्याप्त शोध किया गया है जो समाधान का अनुमान लगाता है। नैपसैक समस्या चूंकि एनपी-हार्ड एल्गोरिदम के संग्रह में से है जिसे अभी भी किसी निर्दिष्ट डिग्री तक अनुमानित किया जा सकता है। इसका कारण है कि समस्या में बहुपद समय सन्निकटन योजना है। स्पष्ट होने के लिए, नैकपैक समस्या में पूर्ण बहुपद समय सन्निकटन योजना (एफपीटीएएस ) है।

लालची सन्निकटन एल्गोरिथम

जॉर्ज डेंटज़िग ने असीम नैपसैक समस्या को हल करने के लिए लालची सन्निकटन एल्गोरिथम प्रस्तावित किया जाता है । उसका संस्करण वजन की प्रति इकाई मूल्य के घटते क्रम में वस्तुओं को क्रमबद्ध करता है, $v_{1}/w_{1}\geq \cdots \geq v_{n}/w_{n}$। यह तब उन्हें बोरी में डालने के लिए आगे बढ़ता है, पहले प्रकार के आइटम की जितनी संभव हो उतनी प्रतियों के साथ प्रारंभ होता है जब तक कि बोरी में और अधिक स्थान न हो। परंतु कि प्रत्येक प्रकार की वस्तु की असीमित आपूर्ति हो, यदि m बोरी में फिट होने वाली वस्तुओं का अधिकतम मूल्य है, तो लालची एल्गोरिथ्म को कम से कम $m/2$ का मान प्राप्त करने की आश्वासन है।

परिबद्ध समस्या के लिए जहाँ प्रत्येक प्रकार की वस्तु की आपूर्ति सीमित है उपरोक्त एल्गोरिथम इष्टतम से बहुत दूर हो सकता है। फिर भी साधारण संशोधन हमें इस स्थितियों को हल करने की अनुमति देता है: सादगी के लिए मान लें कि सभी आइटम अलग-अलग बोरी में फिट होते हैं ($w_{i}\leq W$ सभी के लिए $i$) यथासंभव लंबे समय तक वस्तुओं को लालच से पैक करके समाधान $S_{1}$ का निर्माण करें, अर्थात $S_{1}=\left\{1,\ldots ,k\right\}$जहां $k=\textstyle \max _{1\leq k'\leq n}\textstyle \sum _{i=1}^{k'}w_{i}\leq W$. इसके अतिरिक्त दूसरे समाधान का निर्माण करें $S_{2}=\left\{k+1\right\}$ जिसमें पहला आइटम फिट नहीं हुआ। चूँकि $S_{1}\cup S_{2}$ समस्या के LP रैखिक प्रोग्रामिंग छूट के लिए ऊपरी सीमा प्रदान करता है, समुच्चय में से का मान कम से कम $m/2$ होना चाहिए; हम इस प्रकार $S_{1}$ और $S_{2}$ में से जो भी लौटाते हैं उसका $1/2$-सन्निकटन प्राप्त करने के लिए बढ़िया मूल्य है।

यह दिखाया जा सकता है कि औसत प्रदर्शन त्रुटि दर $n^{-1/2}$ पर वितरण में इष्टतम समाधान में परिवर्तित हो जाता है

पूरी तरह से बहुपद समय सन्निकटन योजना

नैपसैक समस्या के लिए पूरी तरह से बहुपद समय सन्निकटन योजना (एफपीटीएएस) इस तथ्य का लाभ उठाती है कि समस्या का कोई ज्ञात बहुपद समय समाधान नहीं है क्योंकि वस्तुओं से जुड़े लाभ प्रतिबंधित नहीं हैं। यदि कोई लाभ मूल्यों के कम से कम महत्वपूर्ण अंकों में से कुछ को गोल करता है तो वे बहुपद और 1/ε से बंधे होंगे जहां ε समाधान की शुद्धता पर बाध्य है। इस प्रतिबंध का कारण है कि एल्गोरिदम बहुपद समय में समाधान ढूंढ सकता है जो इष्टतम समाधान के (1-ε) के कारक के अंदर सही है।

एल्गोरिथम एफपीटीएएस है

 algorithm FPTAS i

input: ε ∈ (0,1]

a list A of n items, specified by their values, , and weights output: S' the FPTAS solution

P := max $\{v_{i}\mid 1\leq i\leq n\}$ // the highest item value

K= ε ${\frac {P}{n}}$

for i from 1 to n do

$v'_{i}$ := $\left\lfloor {\frac {v_{i}}{K}}\right\rfloor$

end for

return the solution, S', using the values in the dynamic program outlined above

प्रमेय: $S'$उपरोक्त एल्गोरिथ्म द्वारा संगणित समुच्चय $\mathrm {profit} (S')\geq (1-\varepsilon )\cdot \mathrm {profit} (S^{*})$ को संतुष्ट करता है, जहाँ $S^{*}$ इष्टतम उपाय है।

प्रभुत्व संबंध

असीमित नैपसेक समस्या का समाधान उन वस्तुओं को फेंक कर आसान बनाया जा सकता है जिनकी कभी आवश्यकता नहीं होगी। किसी दिए गए आइटम $i$ के लिए मान लीजिए कि हम आइटम $J$ का समुच्चय पा सकते हैं जैसे कि उनका कुल वजन $i$ के वजन से कम है, और उनका कुल मूल्य i के मान से अधिक है। तब मैं इष्टतम समाधान में प्रकट नहीं हो सकता, क्योंकि हम समुच्चय जे के साथ $i$ को बदलकर सदैव किसी भी संभावित समाधान में सुधार कर सकते हैं। इसलिए, हम $i$-वें आइटम को पूरी तरह से अनदेखा कर सकते हैं। ऐसे स्थितियों में, $J$ को $i$ पर प्रभावित कहा जाता है। (ध्यान दें कि यह बंधी हुई नैकपैक समस्याओं पर प्रयुक्त नहीं होता है, क्योंकि हो सकता है कि हमने पहले ही $J$ में आइटम का उपयोग कर लिया हो।)

प्रभुत्व संबंध खोजना हमें खोज स्थान के आकार को महत्वपूर्ण रूप से कम करने की अनुमति देता है। कई अलग-अलग प्रकार के प्रभुत्व संबंध हैं,जो सभी फॉर्म की असमानता को पूरा करते हैं:

$\qquad \sum _{j\in J}w_{j}\,x_{j}\ \leq \alpha \,w_{i}$, और $\sum _{j\in J}v_{j}\,x_{j}\ \geq \alpha \,v_{i}\,$ कुछ के लिए $x\in Z_{+}^{n}$ जहाँ $\alpha \in Z_{+}\,,J\subsetneq N$ और $i\not \in J$. सदिश $x$ , $J$ के प्रत्येक सदस्य की प्रतियों की संख्या को दर्शाता है .

सामूहिक प्रभुत्व:

$i$वें>-वें आइटम का सामूहिक रूप से प्रभुत्व है $J$, के रूप में लिखा गया है $i\ll J$, यदि मदों के कुछ संयोजन का कुल भार $J$ w_i से कम है और उनका कुल मान v_i से अधिक है औपचारिक रूप से, $\sum _{j\in J}w_{j}\,x_{j}\ \leq w_{i}$ और $\sum _{j\in J}v_{j}\,x_{j}\ \geq v_{i}$ कुछ के लिए $x\in Z_{+}^{n}$, अर्थात। $\alpha =1$. इस प्रभुत्व को सत्यापित करना कम्प्यूटेशनल रूप से कठिन है, इसलिए इसका उपयोग केवल गतिशील प्रोग्रामिंग दृष्टिकोण के साथ किया जा सकता है। वास्तव में, यह छोटी नैकपैक निर्णय समस्या को हल करने के समान है जहां $V=v_{i}$ , $W=w_{i}$, और आइटम $J$ प्रतिबंधित हैं .

सीमा प्रभुत्व:

$i$ वां>-वां आइटम सीमा का प्रभुत्व है $J$, के रूप में लिखा गया है $i\prec \prec J$, यदि $i$ कुछ प्रतियों की संख्या $J$ से प्रभावित है। औपचारिक रूप से, $\sum _{j\in J}w_{j}\,x_{j}\ \leq \alpha \,w_{i}$, और $\sum _{j\in J}v_{j}\,x_{j}\ \geq \alpha \,v_{i}\,$ कुछ के लिए $x\in Z_{+}^{n}$ और $\alpha \geq 1$. यह सामूहिक प्रभुत्व का सामान्यीकरण है, जिसे पहली बार में प्रस्तुत किया गया थाऔर EDUK एल्गोरिथ्म में उपयोग किया जाता है। इस तरह का सबसे छोटा $\alpha$ आइटम $i$ की सीमा को परिभाषित करता है, जिसे $t_{i}=(\alpha -1)w_{i}$ लिखा जाता है। इस स्थितियों में, इष्टतम समाधान में 0 की अधिकतम $\alpha -1$ प्रतियां हो सकती हैं।

एकाधिक प्रभुत्व:

$i$वें>-वें आइटम में ही आइटम का गुणन होता है $j$, के रूप में लिखा गया है $i\ll _{m}j$, यदि $i$ की कुछ प्रतियों का प्रभुत्व है $j$. औपचारिक रूप से, $w_{j}\,x_{j}\ \leq w_{i}$, और $v_{j}\,x_{j}\ \geq v_{i}$ कुछ के लिए $x_{j}\in Z_{+}$ अर्थात। $J=\{j\},\alpha =1,x_{j}=\lfloor {\frac {w_{i}}{w_{j}}}\rfloor$. प्रीप्रोसेसिंग के समय इस प्रभुत्व का कुशलता से उपयोग किया जा सकता है क्योंकि इसका अपेक्षाकृत आसानी से पता लगाया जा सकता है।

मॉड्यूलर प्रभुत्व:

माना कि $b$ सर्वोत्तम वस्तु है अर्थात् ${\frac {v_{b}}{w_{b}}}\geq {\frac {v_{i}}{w_{i}}}\,$ सभी के लिए $i$. यह मूल्य के सबसे बड़े घनत्व वाला आइटम है। $i$th>-th आइटम मॉड्यूलर रूप से एकल आइटम $j$ का प्रभुत्व है के रूप में लिखा गया है जिसे $i\ll _{\equiv }j$, के रूप में लिखा गया है, यदि $i$ पर $j$ और $b$.की कई प्रतियों का प्रभुत्व है। औपचारिक रूप से, $w_{j}+tw_{b}\leq w_{i}$, और $v_{j}+tv_{b}\geq v_{i}$ अर्थात $J=\{b,j\},\alpha =1,x_{b}=t,x_{j}=1$.

विविधताएं

Main article: बैकपैक समस्याओं की सूची

नैकपैक समस्या के कई रूप हैं जो मूल समस्या के अनुप्रयोगों की विशाल संख्या से उत्पन्न हुए हैं। मुख्य विविधताएं कुछ समस्या पैरामीटरों की संख्या जैसे मदों की संख्या, उद्देश्यों की संख्या, या यहां तक ​​कि नैपैक्स की संख्या को बदलकर उत्पन्न होती हैं।

बहुउद्देश्यीय नैकपैक समस्या

यह भिन्नता थैला भरने वाले व्यक्ति के लक्ष्य को बदल देती है। उद्देश्य के अतिरिक्त जैसे कि मौद्रिक लाभ को अधिकतम करना, उद्देश्य के कई आयाम हो सकते हैं। उदाहरण के लिए, पर्यावरण या सामाजिक सरोकार के साथ-साथ आर्थिक लक्ष्य भी हो सकते हैं। जिन समस्याओं को अधिकांशतः संबोधित किया जाता है उनमें पोर्टफोलियो और परिवहन रसद अनुकूलन सम्मिलित हैं।

उदाहरण के रूप से मान लीजिए कि आप क्रूज जहाज चलाते हैं। आपको यह तय करना होगा कि कितने प्रसिद्ध कॉमेडियन को भर्ती करना है। यह नाव टन से अधिक यात्रियों को नहीं संभाल सकती है और मनोरंजन करने वालों का वजन 1000 पाउंड से कम होना चाहिए। प्रत्येक कॉमेडियन का वजन होता है, उनकी लोकप्रियता के आधार पर व्यवसाय में लाता है और विशिष्ट वेतन मांगता है। इस उदाहरण में, आपके पास कई उद्देश्य हैं। निस्संदेह आप अपने मनोरंजनकर्ताओं की लोकप्रियता को अधिकतम करना चाहते हैं जबकि उनके वेतन को कम करना चाहते हैं। साथ ही आप अधिक से अधिक मनोरंजनकर्ता चाहते हैं।

बहुआयामी नैकपैक समस्या

इस भिन्नता में, नैकपैक आइटम i का वजन डी-आयामी वेक्टर ${\overline {w_{i}}}=(w_{i1},\ldots ,w_{iD})$ द्वारा दिया जाता है और नैपसैक में डी- आयामी क्षमता वेक्टर $(W_{1},\ldots ,W_{D})$। लक्ष्य बैकपैक में वस्तुओं के मूल्यों के योग को अधिकतम करना है जिससे प्रत्येक आयाम $d$ में वजन का योग $W_{d}$ से अधिक न हो।

बहु-आयामी नैकपैक कम्प्यूटेशनल रूप से नैपसैक की तुलना में कठिन है; $D=2$ के लिए भी, समस्या में इप्टास नहीं है जब तक कि P=NP नहीं है। चूंकि में एल्गोरिथ्म विरल उदाहरणों को कुशलतापूर्वक हल करने के लिए दिखाया गया है। बहु-आयामी नैपसैक का उदाहरण विरल है यदि $m<D$ के लिए समुच्चय $J=\{1,2,\ldots ,m\}$ है जैसे कि प्रत्येक नैपसैक आइटम के लिए $i$,> ऐसा है कि $\forall j\in J\cup \{z\},\ w_{ij}\geq 0$ और $\forall y\notin J\cup \{z\},w_{iy}=0$. उदाहरण के लिए, ऐसे उदाहरण होते हैं, जब रिले नोड्स के साथ वायरलेस नेटवर्क में पैकेट शेड्यूल करते हैं। से एल्गोरिथ्म बहुविकल्पी संस्करण, बहुविकल्पी बहु-आयामी नैकपैक के विरल उदाहरणों को भी हल करता है।

आईएचएस (बढ़ती ऊंचाई शेल्फ़) एल्गोरिथम 2D नैकपैक (वर्गों को द्वि-आयामी इकाई आकार वर्ग में पैक करना) के लिए इष्टतम है: जब इष्टतम पैकिंग में अधिकतम पाँच वर्ग होते हैं।

एकाधिक बस्ता समस्या

यह भिन्नता बिन पैकिंग समस्या के समान है। यह बिन पैकिंग समस्या से भिन्न है जिसमें वस्तुओं का उपसमुच्चय चुना जा सकता है जबकि बिन पैकिंग समस्या में सभी वस्तुओं को कुछ डिब्बे में पैक करना पड़ता है। अवधारणा यह है कि कई थैले हैं। यह तुच्छ परिवर्तन की तरह लग सकता है, किन्तु यह प्रारंभिक नैकपैक की क्षमता को जोड़ने के समान नहीं है। इस भिन्नता का उपयोग ऑपरेशंस रिसर्च में कई लोडिंग और शेड्यूलिंग समस्याओं में किया जाता है और इसमें बहुपद-समय सन्निकटन योजना है।

द्विघाती नैपसैक समस्या

द्विघातीय नैपसैक समस्या द्विघाती और रेखीय क्षमता प्रतिबंधों के अधीन द्विघात उद्देश्य फलन को अधिकतम करती है। समस्या को 1980 में गैलो हैमर और शिमोन द्वारा प्रस्तुत किया गया था। चूँकि समस्या का पहला उपचार 1975 में विट्जगल में हुआ था।

सबसेट-योग समस्या

उपसमुच्चय योग समस्या निर्णय का विशेष स्थिति है और 0-1 समस्याएं हैं जहां प्रत्येक प्रकार की वस्तु, वजन मूल्य के समान होती है: $w_{i}=v_{i}$. क्रिप्टोग्राफी के क्षेत्र में नैकपैक समस्या शब्द का प्रयोग अधिकांशतः विशेष रूप से उपसमुच्चय योग समस्या को संदर्भित करने के लिए किया जाता है और इसे सामान्यतः कार्प की 21 एनपी-पूर्ण समस्याओं में से के रूप में जाना जाता है।

उपसमुच्चय योग समस्या के सामान्यीकरण को बहु उपसमुच्चय सम समस्या कहते हैं, जिसमें समान क्षमता वाले अनेक डिब्बे उपस्थित होते हैं। यह दिखाया गया है कि सामान्यीकरण में एफपीटीएएस नहीं है।

किंग समस्या के समान है। यह बिन पैकिं

ज्यामितीय नैकपैक समस्या

ज्यामितीय नैपसैक समस्या में विभिन्न मानों के साथ आयतों का समूह है और आयताकार नैकपैक है। लक्ष्य सबसे बड़ा संभव मान नैकपैक में पैक करना है।

यह भी देखें

• बिन पैकिंग समस्या
• परिवर्तन करने की समस्या
• मिश्रित नीलामी
• संयुक्त अनुकूलन
• लगातार नैकपैक की समस्या
• स्टॉक की समस्या में कटौती
• बस्ता समस्याओं की सूची
• पैकिंग की समस्या

टिप्पणियाँ

संदर्भ

• Garey, Michael R.; David S. Johnson (1979). Computers and Intractability: A Guide to the Theory of NP-Completeness. W.H. Freeman. ISBN 978-0-7167-1045-5. A6: MP9, pg.247.
• Kellerer, Hans; Pferschy, Ulrich; Pisinger, David (2004). Knapsack Problems. Springer. doi:10.1007/978-3-540-24777-7. ISBN 978-3-540-40286-2. MR 2161720. S2CID 28836720.
• Martello, Silvano; Toth, Paolo (1990). Knapsack problems: Algorithms and computer implementations. Wiley-Interscience. ISBN 978-0-471-92420-3. MR 1086874.

बाहरी संबंध

• Lecture slides on the नैपसैक problem
• PYAsUKP: Yet Another solver for the Unbounded क्नाप्सैक Problem, with code taking advantage of the dominance relations in an hybrid algorithm, benchmarks and downloadable copies of some papers.
• Home page of David Pisinger with downloadable copies of some papers on the publication list (including "Where are the hard नैपसैक problems?")
• क्नाप्सैक Problem solutions in many languages at Rosetta Code
• Dynamic Programming algorithm to 0/1 क्नाप्सैक problem
• क्नाप्सैक Problem solver (online)
• Solving 0-1-नैपसैक with Genetic Algorithms in Ruby Archived 23 May 2011 at the Wayback Machine
• Codes for Quadratic क्नाप्सैक Problem Archived 14 February 2015 at the Wayback Machine

• Optimizing Three-Dimensional Bin Packing
• क्नाप्सैक Integer Programming Solution in Python Gekko (optimization software)