T-J मॉडल: Difference between revisions
(Created page with "{{DISPLAYTITLE:''t''-''J'' model}} File:2D-Hubbard-model.png|thumb|2डी हबर्ड मॉडल। टी-जे मॉडल यू >> टी के लिए ह...") |
No edit summary |
||
| Line 1: | Line 1: | ||
{{DISPLAYTITLE:''t''-''J'' model}} | {{DISPLAYTITLE:''t''-''J'' model}} | ||
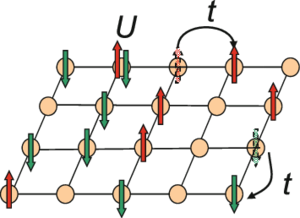
[[File:2D-Hubbard-model.png|thumb|2डी हबर्ड मॉडल। टी-जे मॉडल यू >> टी के लिए हबर्ड मॉडल है]]ठोस-अवस्था भौतिकी में, ''t''-''J'' मॉडल पहली बार 1977 में जोज़ेफ स्पालेक द्वारा [[हबर्ड मॉडल]] से लिया गया | [[File:2D-Hubbard-model.png|thumb|2डी हबर्ड मॉडल। टी-जे मॉडल यू >> टी के लिए हबर्ड मॉडल है]]ठोस-अवस्था भौतिकी में, ''t''-''J'' मॉडल पहली बार 1977 में जोज़ेफ स्पालेक द्वारा [[हबर्ड मॉडल]] से लिया गया मॉडल है।<ref name=":0">{{Cite journal |last1=Chao |first1=K. A. |last2=Spałek |first2=J. |last3=Oleś |first3=A. M. |date=1978-10-01 |title=हबर्ड मॉडल का विहित गड़बड़ी विस्तार|url=https://link.aps.org/doi/10.1103/PhysRevB.18.3453 |journal=Physical Review B |volume=18 |issue=7 |pages=3453–3464 |doi=10.1103/PhysRevB.18.3453|bibcode=1978PhRvB..18.3453C }}</ref> [[मोट इंसुलेटर|मोट इंसुलेटर (अवरोधक)]] के [[एंटीफेरोमैग्नेटिज्म|एंटीफेरोमैग्नेटिज्म (प्रतिलौह चुंबकत्व)]] गुणों की व्याख्या करने के लिए<ref>{{Cite journal |last=Anderson |first=P. W. |date=1959-07-01 |title=सुपरएक्सचेंज इंटरैक्शन के सिद्धांत के लिए नया दृष्टिकोण|url=https://link.aps.org/doi/10.1103/PhysRev.115.2 |journal=Physical Review |volume=115 |issue=1 |pages=2–13 |doi=10.1103/PhysRev.115.2|bibcode=1959PhRv..115....2A }}</ref> और इस सामग्री में इलेक्ट्रॉन-इलेक्ट्रॉन प्रतिकर्षण की बल के बारे में प्रायोगिक परिणामों को ध्यान में रखते हुए।<ref>{{Cite journal |last=Nagaoka |first=Yosuke |date=1966-07-08 |title=फेरोमैग्नेटिज्म इन ए नैरो, ऑलमोस्ट हाफ-फिल्ड एस बैंड|url=https://link.aps.org/doi/10.1103/PhysRev.147.392 |journal=Physical Review |volume=147 |issue=1 |pages=392–405 |doi=10.1103/PhysRev.147.392|bibcode=1966PhRv..147..392N }}</ref> मॉडल [[सामग्री]] को गांठों (साइटों) में परमाणुओं के साथ [[जाली मॉडल (भौतिकी)]] के रूप में मानता है और केवल एक या दो बाहरी [[इलेक्ट्रॉन]] उनके बीच चलते हैं (आंतरिक इलेक्ट्रॉनों पर विचार नहीं किया जाता है), जैसे मूल हबर्ड मॉडल में। यह अंतर यह मानने में है कि इलेक्ट्रॉनों को मजबूत सहसंबद्ध सामग्री होने का अनुमान है | दृढ़ता से सहसंबद्ध, इसका मतलब है कि इलेक्ट्रॉन पारस्परिक कूलम्ब के नियम के लिए बहुत समझदार हैं, और इसलिए दूसरे इलेक्ट्रॉन द्वारा पहले से ही कब्जा कर ली गई जाली की साइटों पर कब्जा करने से बचने के लिए अधिक विवश हैं। बुनियादी हबर्ड मॉडल में, यू के साथ संकेतित प्रतिकर्षण छोटा और अशक्त भी हो सकता है, और इलेक्ट्रॉन एक साइट से दूसरी साइट पर कूदने के लिए स्वतंत्र होते हैं (हॉपिंग, ट्रांसफर या क्वांटम टनलिंग के रूप में टी द्वारा पैरामीट्रिज्ड)। टी-जे मॉडल में, यू के बजाय, पैरामीटर जे है, अनुपात टी/यू का फ़ंक्शन (गणित), इसलिए नाम। | ||
इलेक्ट्रॉनों के बीच मजबूत युग्मन की परिकल्पना में [[डोपिंग (सेमीकंडक्टर)]] एंटीफेरोमैग्नेट्स में उच्च तापमान सुपरकंडक्टिविटी को समझाने के लिए संभावित मॉडल के रूप में इसका उपयोग किया जाता है।<ref>{{cite journal |last=Spalek |first=Jozef |date=2007-06-28 |title=t-J model then and now: A personal perspective from the pioneering times |journal=Acta Physica Polonica A |volume=111 |issue=4 |page=409 |doi=10.12693/APhysPolA.111.409 |arxiv=0706.4236 |bibcode=2007AcPPA.111..409S |s2cid=53117123 }}</ref><ref>{{Cite journal |last1=Rømer |first1=Astrid T. |last2=Maier |first2=Thomas A. |last3=Kreisel |first3=Andreas |last4=Eremin |first4=Ilya |last5=Hirschfeld |first5=P. J. |last6=Andersen |first6=Brian M. |date=2020-01-31 |title=कमजोर से मजबूत युग्मन के लिए द्वि-आयामी हबर्ड मॉडल में बाँधना|url=https://link.aps.org/doi/10.1103/PhysRevResearch.2.013108 |journal=Physical Review Research |volume=2 |issue=1 |pages=013108 |doi=10.1103/PhysRevResearch.2.013108|arxiv=1909.00627 |bibcode=2020PhRvR...2a3108R |s2cid=202540002 }}</ref> | इलेक्ट्रॉनों के बीच मजबूत युग्मन की परिकल्पना में [[डोपिंग (सेमीकंडक्टर)]] एंटीफेरोमैग्नेट्स में उच्च तापमान सुपरकंडक्टिविटी को समझाने के लिए संभावित मॉडल के रूप में इसका उपयोग किया जाता है।<ref>{{cite journal |last=Spalek |first=Jozef |date=2007-06-28 |title=t-J model then and now: A personal perspective from the pioneering times |journal=Acta Physica Polonica A |volume=111 |issue=4 |page=409 |doi=10.12693/APhysPolA.111.409 |arxiv=0706.4236 |bibcode=2007AcPPA.111..409S |s2cid=53117123 }}</ref><ref>{{Cite journal |last1=Rømer |first1=Astrid T. |last2=Maier |first2=Thomas A. |last3=Kreisel |first3=Andreas |last4=Eremin |first4=Ilya |last5=Hirschfeld |first5=P. J. |last6=Andersen |first6=Brian M. |date=2020-01-31 |title=कमजोर से मजबूत युग्मन के लिए द्वि-आयामी हबर्ड मॉडल में बाँधना|url=https://link.aps.org/doi/10.1103/PhysRevResearch.2.013108 |journal=Physical Review Research |volume=2 |issue=1 |pages=013108 |doi=10.1103/PhysRevResearch.2.013108|arxiv=1909.00627 |bibcode=2020PhRvR...2a3108R |s2cid=202540002 }}</ref> | ||
Revision as of 12:15, 14 June 2023
ठोस-अवस्था भौतिकी में, t-J मॉडल पहली बार 1977 में जोज़ेफ स्पालेक द्वारा हबर्ड मॉडल से लिया गया मॉडल है।[1] मोट इंसुलेटर (अवरोधक) के एंटीफेरोमैग्नेटिज्म (प्रतिलौह चुंबकत्व) गुणों की व्याख्या करने के लिए[2] और इस सामग्री में इलेक्ट्रॉन-इलेक्ट्रॉन प्रतिकर्षण की बल के बारे में प्रायोगिक परिणामों को ध्यान में रखते हुए।[3] मॉडल सामग्री को गांठों (साइटों) में परमाणुओं के साथ जाली मॉडल (भौतिकी) के रूप में मानता है और केवल एक या दो बाहरी इलेक्ट्रॉन उनके बीच चलते हैं (आंतरिक इलेक्ट्रॉनों पर विचार नहीं किया जाता है), जैसे मूल हबर्ड मॉडल में। यह अंतर यह मानने में है कि इलेक्ट्रॉनों को मजबूत सहसंबद्ध सामग्री होने का अनुमान है | दृढ़ता से सहसंबद्ध, इसका मतलब है कि इलेक्ट्रॉन पारस्परिक कूलम्ब के नियम के लिए बहुत समझदार हैं, और इसलिए दूसरे इलेक्ट्रॉन द्वारा पहले से ही कब्जा कर ली गई जाली की साइटों पर कब्जा करने से बचने के लिए अधिक विवश हैं। बुनियादी हबर्ड मॉडल में, यू के साथ संकेतित प्रतिकर्षण छोटा और अशक्त भी हो सकता है, और इलेक्ट्रॉन एक साइट से दूसरी साइट पर कूदने के लिए स्वतंत्र होते हैं (हॉपिंग, ट्रांसफर या क्वांटम टनलिंग के रूप में टी द्वारा पैरामीट्रिज्ड)। टी-जे मॉडल में, यू के बजाय, पैरामीटर जे है, अनुपात टी/यू का फ़ंक्शन (गणित), इसलिए नाम।
इलेक्ट्रॉनों के बीच मजबूत युग्मन की परिकल्पना में डोपिंग (सेमीकंडक्टर) एंटीफेरोमैग्नेट्स में उच्च तापमान सुपरकंडक्टिविटी को समझाने के लिए संभावित मॉडल के रूप में इसका उपयोग किया जाता है।[4][5]
हैमिल्टनियन
क्वांटम भौतिकी प्रणाली के मॉडल आमतौर पर हैमिल्टनियन (क्वांटम यांत्रिकी) ऑपरेटर (भौतिकी) पर आधारित होते हैं। , उस प्रणाली की कुल ऊर्जा के अनुरूप, गतिज ऊर्जा और संभावित ऊर्जा दोनों सहित।
टी-जे हैमिल्टनियन से प्राप्त किया जा सकता है Schrieffer–Wolff परिवर्तन का उपयोग करते हुए हबर्ड मॉडल का, परिवर्तन जनरेटर के साथ t/U पर निर्भर करता है और इलेक्ट्रॉनों के लिए जाली की साइट पर दोगुना कब्जा करने की संभावना को छोड़कर,[6] जिसके परिणामस्वरूप:[7]
जहां टी में शब्द गतिज ऊर्जा से मेल खाता है और हबर्ड मॉडल में एक के बराबर है। दूसरा एक दूसरे क्रम में संभावित ऊर्जा का अनुमान है, क्योंकि यह हबर्ड मॉडल का एक अनुमान है जो सीमा U >> t में t की शक्ति में विकसित हुआ है। उच्च क्रम में शर्तें जोड़ी जा सकती हैं।[1]
पैरामीटर हैं:
- निकटतम-पड़ोसी साइटों i और j का योग है, सभी साइटों के लिए, आमतौर पर द्वि-आयामी वर्ग जाली पर,
- सी†
iσ, सी
iσ साइट i पर फ़र्मोनिक निर्माण और विनाश संचालक हैं, - σ स्पिन ध्रुवीकरण है,
- t टाइट बाइंडिंग#दूसरा परिमाणीकरण है,
- जे एंटीफेरोमैग्नेटिक एक्सचेंज इंटरेक्शन है, जे = 4t2/U,
- यू ऑन-साइट कूलम्ब का कानून है, जिसे यू >> टी के लिए शर्त को पूरा करना चाहिए,
- एनi= सी†
iσसी
iσ साइट पर कण संख्या है और अधिकतम 1 हो सकता है, ताकि डबल अधिभोग वर्जित हो (हबर्ड मॉडल में संभव है), - 'एस'i और एसj स्पिन (भौतिकी) हैं # साइटों I और j पर गणितीय सूत्रीकरण,
- एच। सी। हर्मिटियन संलग्न के लिए खड़ा है,
अगर एनi= 1, जब जमीनी अवस्था में, प्रति जाली की साइट (आधा भरने) में सिर्फ एक इलेक्ट्रॉन होता है, तो मॉडल क्वांटम हाइजेनबर्ग मॉडल को कम कर देता है और जमीनी राज्य एक ढांकता हुआ एंटीफेरोमैग्नेट्स (मोट इंसुलेटर) को पुन: पेश करता है।[8] अगले-निकटतम-पड़ोसी साइटों और कणों की कुल संख्या के कार्य में जमीनी स्थिति निर्धारित करने की रासायनिक क्षमता को देखते हुए मॉडल को और बढ़ाया जा सकता है:[9][10]
जहां ⟨...⟩ और ⟨⟨...⟩⟩ होपिंग इंटीग्रल के लिए दो अलग-अलग मानों के साथ क्रमशः निकटतम और अगले-निकटतम पड़ोसियों को दर्शाता है (टी1 और टी2) और μ रासायनिक क्षमता है।
संदर्भ
- ↑ 1.0 1.1 Chao, K. A.; Spałek, J.; Oleś, A. M. (1978-10-01). "हबर्ड मॉडल का विहित गड़बड़ी विस्तार". Physical Review B. 18 (7): 3453–3464. Bibcode:1978PhRvB..18.3453C. doi:10.1103/PhysRevB.18.3453.
- ↑ Anderson, P. W. (1959-07-01). "सुपरएक्सचेंज इंटरैक्शन के सिद्धांत के लिए नया दृष्टिकोण". Physical Review. 115 (1): 2–13. Bibcode:1959PhRv..115....2A. doi:10.1103/PhysRev.115.2.
- ↑ Nagaoka, Yosuke (1966-07-08). "फेरोमैग्नेटिज्म इन ए नैरो, ऑलमोस्ट हाफ-फिल्ड एस बैंड". Physical Review. 147 (1): 392–405. Bibcode:1966PhRv..147..392N. doi:10.1103/PhysRev.147.392.
- ↑ Spalek, Jozef (2007-06-28). "t-J model then and now: A personal perspective from the pioneering times". Acta Physica Polonica A. 111 (4): 409. arXiv:0706.4236. Bibcode:2007AcPPA.111..409S. doi:10.12693/APhysPolA.111.409. S2CID 53117123.
- ↑ Rømer, Astrid T.; Maier, Thomas A.; Kreisel, Andreas; Eremin, Ilya; Hirschfeld, P. J.; Andersen, Brian M. (2020-01-31). "कमजोर से मजबूत युग्मन के लिए द्वि-आयामी हबर्ड मॉडल में बाँधना". Physical Review Research. 2 (1): 013108. arXiv:1909.00627. Bibcode:2020PhRvR...2a3108R. doi:10.1103/PhysRevResearch.2.013108. S2CID 202540002.
- ↑ This is due using a projector quantum operator that project on the subspace where fermionic operators can not add an electron on a site already occupied (see next note)
- ↑ Eckle, Hans-Peter (2019). "8.8.1 From the Hubbard to the t–J model: non-half filled band case" (PDF). क्वांटम पदार्थ के मॉडल. Oxford University Press. ISBN 9780199678839.
- ↑ Izyumov, Yu. A.; Chashchin, N. I. (1998). "टीजे -वैरिएबल डेरिवेटिव के साथ समीकरणों के संदर्भ में मॉडल" (PDF). Condensed Matter Physics. 1 (1): 41–56. Bibcode:1998CMPh....1...41I. doi:10.5488/CMP.1.1.41. S2CID 11254082.
- ↑ Karchev, Naoum (1998). "Generalized CP1 model from the t1-t2-J model". Phys. Rev. B. 57 (17): 10913. arXiv:cond-mat/9706105. Bibcode:1998PhRvB..5710913K. doi:10.1103/PhysRevB.57.10913. S2CID 12865671.
- ↑ Yanagisawa, Takashi (2008-02-12). "Phase diagram of thet–U2Hamiltonian of the weak coupling Hubbard model". New Journal of Physics (in English). 10 (2): 023014. arXiv:0803.1739. Bibcode:2008NJPh...10b3014Y. doi:10.1088/1367-2630/10/2/023014. ISSN 1367-2630. S2CID 55405863.
अग्रिम पठन
- Fazekas, Patrik (1999). Lectures on Correlation and Magnetism. Series in Modern Condensed Matter Physics: Volume 5 (in English). Vol. 5. World Scientific. p. 199. doi:10.1142/2945. ISBN 978-981-4499-62-0.
- Spałek, Józef (2007). "t-J model then and now: A personal perspective from the pioneering times". Acta Phys. Pol. A. 111 (4): 409–424. arXiv:0706.4236. Bibcode:2007AcPPA.111..409S. doi:10.12693/APhysPolA.111.409. S2CID 53117123.
- Dr Mitchell, Electron interactions and the Hubbard model (in English), retrieved 2022-08-29