एकसमान निरंतरता

किसी बिंदु पर का ग्राफ $f(x)={\tfrac {1}{x}}$ ऊंचाई के साथ (यहां नीली) खिड़की के ऊपर और/या नीचे घुस जाएगा $2\varepsilon \in \mathbb {R} _{>0}$ और चौड़ाई $2\delta \in \mathbb {R} _{>0}$ जबकि $(f)$ एक से अधिक लेकर $x$-अंतराल से छोटा $\delta$, क्योंकि उस विंडो का केंद्र ग्राफ़ के ऊपर की दिशा में चलता है $x=0$. यदि कोई ऐसी खिड़की मौजूद है जिसके ऊपर और/या नीचे इस ग्राफ़ द्वारा कभी प्रवेश नहीं किया जाता है क्योंकि खिड़की ग्राफ़ के ऊपर की दिशा में चलती है $x=0$, तो इसकी चौड़ाई असीम रूप से छोटी होगी, अर्थात $f(x)$ समान रूप से सतत नहीं है. कार्यक्रम $g(x)={\sqrt {x}}$दूसरी ओर, समान रूप से निरंतर है।

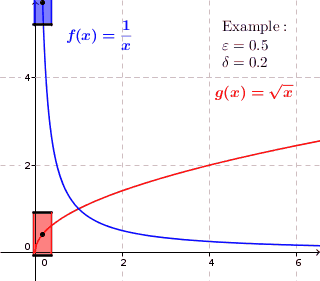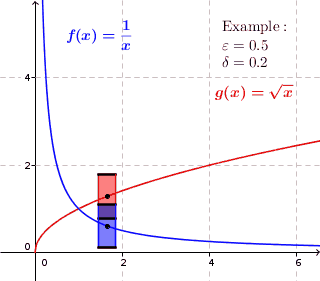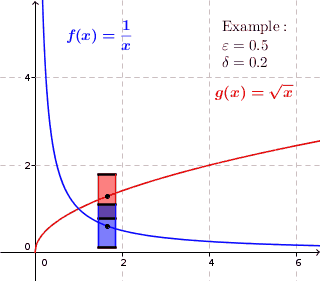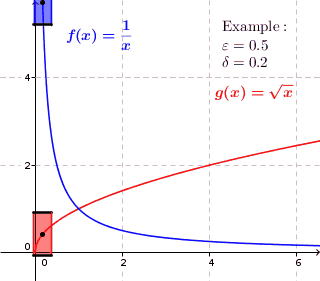
गणित में, एक वास्तविक फलन (गणित) $f$ यदि कोई सकारात्मक वास्तविक संख्या है तो वास्तविक संख्याओं को समान रूप से निरंतर कहा जाता है $\delta$ जैसे कि आकार के किसी भी फ़ंक्शन डोमेन अंतराल पर फ़ंक्शन मान $\delta$ एक-दूसरे के उतने ही करीब हैं जितना हम चाहते हैं। दूसरे शब्दों में, वास्तविक संख्याओं के एक समान रूप से निरंतर वास्तविक फ़ंक्शन के लिए, यदि हम चाहते हैं कि फ़ंक्शन मान अंतर किसी भी सकारात्मक वास्तविक संख्या से कम हो $\epsilon$, तो एक सकारात्मक वास्तविक संख्या है $\delta$ ऐसा है कि $|f(x)-f(y)|<\epsilon$ किसी पर $x$ और $y$ आकार के किसी भी फ़ंक्शन अंतराल में $\delta$.

एकसमान निरंतरता और (साधारण) सतत कार्य के बीच अंतर यह है कि, एकसमान निरंतरता में विश्व स्तर पर लागू होता है $\delta$ (फ़ंक्शन डोमेन अंतराल का आकार जिस पर फ़ंक्शन मान अंतर से कम है $\epsilon$) जो केवल पर निर्भर करता है $\varepsilon$, जबकि (सामान्य) निरंतरता में स्थानीय रूप से लागू होता है $\delta$ यह दोनों पर निर्भर करता है $\varepsilon$ और $x$. अतः एकसमान निरंतरता, निरंतरता की तुलना में अधिक मजबूत निरंतरता की स्थिति है; एक फलन जो एकसमान रूप से सतत है वह सतत है लेकिन एक फलन जो सतत है जरूरी नहीं कि वह एकसमान रूप से सतत हो। समान निरंतरता और निरंतरता की अवधारणाओं को मीट्रिक स्थानों के बीच परिभाषित कार्यों तक विस्तारित किया जा सकता है।

निरंतर कार्य समान रूप से निरंतर होने में विफल हो सकते हैं यदि वे किसी बंधे हुए डोमेन पर असंबद्ध हों, जैसे कि $f(x)={\tfrac {1}{x}}$ पर $(0,1)$, या यदि उनकी ढलानें अनंत डोमेन पर असीमित हो जाती हैं, जैसे $f(x)=x^{2}$ वास्तविक (संख्या) रेखा पर. हालाँकि, मीट्रिक स्थानों के बीच कोई भी लिप्सचिट्ज़ निरंतरता समान रूप से निरंतर है, विशेष रूप से किसी भी आइसोमेट्री (दूरी-संरक्षण मानचित्र) में।

हालाँकि सामान्य टोपोलॉजिकल रिक्त स्थान के बीच कार्यों के लिए निरंतरता को परिभाषित किया जा सकता है, समान निरंतरता को परिभाषित करने के लिए अधिक संरचना की आवश्यकता होती है। यह अवधारणा अलग-अलग बिंदुओं के पड़ोस (गणित) के आकार की तुलना करने पर निर्भर करती है, इसलिए इसके लिए एक मीट्रिक स्थान, या अधिक सामान्यतः एक समान स्थान की आवश्यकता होती है।

मीट्रिक स्पेस पर फ़ंक्शंस की परिभाषा

एक समारोह के लिए $f:X\to Y$ मीट्रिक रिक्त स्थान के साथ $(X,d_{1})$ और $(Y,d_{2})$, एकसमान निरंतरता और (साधारण) निरंतरता की निम्नलिखित परिभाषाएँ मान्य हैं।

एकसमान निरंतरता की परिभाषा

• $f$ प्रत्येक वास्तविक संख्या के लिए समान रूप से निरंतर कहा जाता है $\varepsilon >0$ वहाँ एक वास्तविक संख्या मौजूद है $\delta >0$ ऐसा कि हर किसी के लिए $x,y\in X$ साथ $d_{1}(x,y)<\delta$, अपने पास $d_{2}(f(x),f(y))<\varepsilon$. सेट $\{y\in X:d_{1}(x,y)<\delta \}$ प्रत्येक के लिए $x$ का पड़ोस है $x$ और सेट $\{x\in X:d_{1}(x,y)<\delta \}$ प्रत्येक के लिए $y$ का पड़ोस है $y$ पड़ोस (गणित) द्वारा।
  • अगर $X$ और $Y$ तो, वास्तविक रेखा के उपसमुच्चय हैं $d_{1}$ और $d_{2}$ Real_line#As_a_metric_space|मानक एक-आयामी यूक्लिडियन दूरी हो सकती है, जिससे निम्नलिखित परिभाषा प्राप्त होती है: प्रत्येक वास्तविक संख्या के लिए $\varepsilon >0$ वहाँ एक वास्तविक संख्या मौजूद है $\delta >0$ ऐसा कि हर किसी के लिए $x,y\in X$, $|x-y|<\delta \implies |f(x)-f(y)|<\varepsilon$ (कहाँ $A\implies B$ यह कहते हुए एक भौतिक सशर्त कथन है कि यदि $A$, तब $B$).
• समान रूप से, $f$ यदि समान रूप से सतत कहा जाता है $\forall \varepsilon >0\;\exists \delta >0\;\forall x\in X\;\forall y\in X:\,d_{1}(x,y)<\delta \,\Rightarrow \,d_{2}(f(x),f(y))<\varepsilon$. यहाँ परिमाणीकरण (तर्क) ($\forall \varepsilon >0$, $\exists \delta >0$, $\forall x\in X$, और $\forall y\in X$) उपयोग किया जाता है।
• वैकल्पिक रूप से, $f$ यदि सभी सकारात्मक वास्तविक संख्याओं का एक फलन मौजूद है तो इसे समान रूप से निरंतर कहा जाता है $\varepsilon$, $\delta (\varepsilon )$ अधिकतम सकारात्मक वास्तविक संख्या का प्रतिनिधित्व करना, जैसे कि प्रत्येक के लिए $x,y\in X$ अगर $d_{1}(x,y)<\delta (\varepsilon )$ तब $d_{2}(f(x),f(y))<\varepsilon$. $\delta (\varepsilon )$ एक मोनोटोनिक फ़ंक्शन है | मोनोटोनिक रूप से गैर-घटने वाला फ़ंक्शन।

(सामान्य) निरंतरता की परिभाषा

• $f$ निरंतर कहा जाता है ${\underline {{\text{at }}x}}$ यदि प्रत्येक वास्तविक संख्या के लिए $\varepsilon >0$ वहाँ एक वास्तविक संख्या मौजूद है $\delta >0$ ऐसा कि हर किसी के लिए $y\in X$ साथ $d_{1}(x,y)<\delta$, अपने पास $d_{2}(f(x),f(y))<\varepsilon$. सेट $\{y\in X:d_{1}(x,y)<\delta \}$ का पड़ोस है $x$. इस प्रकार, (सामान्य) निरंतरता बिंदु पर फ़ंक्शन की एक स्थानीय संपत्ति है $x$.
• समान रूप से, एक फ़ंक्शन $f$ यदि निरंतर कहा जाता है $\forall x\in X\;\forall \varepsilon >0\;\exists \delta >0\;\forall y\in X:\,d_{1}(x,y)<\delta \,\Rightarrow \,d_{2}(f(x),f(y))<\varepsilon$.
• वैकल्पिक रूप से, एक फ़ंक्शन $f$ यदि सभी सकारात्मक वास्तविक संख्याओं का कोई फलन हो तो इसे सतत कहा जाता है $\varepsilon$ और $x\in X$, $\delta (\varepsilon ,x)$ अधिकतम सकारात्मक वास्तविक संख्या का प्रतिनिधित्व करना, जैसे कि प्रत्येक पर $x$ अगर $y\in X$ संतुष्ट $d_{1}(x,y)<\delta (\varepsilon ,x)$ तब $d_{2}(f(x),f(y))<\varepsilon$. प्रत्येक पर $x$, $\delta (\varepsilon ,x)$ एक नीरस रूप से गैर-घटता हुआ कार्य है।

स्थानीय निरंतरता बनाम वैश्विक समान निरंतरता

परिभाषाओं में, एकसमान निरंतरता और सतत कार्य के बीच अंतर यह है कि, एकसमान निरंतरता में विश्व स्तर पर लागू होता है $\delta$ (एक पड़ोस का आकार $X$ फ़ंक्शन मानों के लिए मीट्रिक के किन मानों पर $Y$ से कम हैं $\varepsilon$) जो केवल पर निर्भर करता है $\varepsilon$ जबकि निरंतरता में स्थानीय रूप से लागू होता है $\delta$ यह दोनों पर निर्भर करता है $\varepsilon$ और $x$. निरंतरता एक फ़ंक्शन की एक स्थानीय संपत्ति है - अर्थात, एक फ़ंक्शन $f$ किसी विशेष बिंदु पर निरंतर है या नहीं $x$ फ़ंक्शन डोमेन का $X$, और यह केवल उस बिंदु के मनमाने ढंग से छोटे पड़ोस में फ़ंक्शन के मूल्यों को देखकर निर्धारित किया जा सकता है। जब हम किसी फ़ंक्शन के किसी अंतराल (गणित) पर निरंतर होने की बात करते हैं, तो हमारा मतलब है कि फ़ंक्शन अंतराल के प्रत्येक बिंदु पर निरंतर होता है। इसके विपरीत, एकसमान निरंतरता एक वैश्विक संपत्ति है $f$, इस अर्थ में कि एकसमान निरंतरता की मानक परिभाषा प्रत्येक बिंदु को संदर्भित करती है $X$. दूसरी ओर, ऐसी परिभाषा देना संभव है जो प्राकृतिक विस्तार के संदर्भ में स्थानीय हो $f^{*}$(जिनकी विशेषताएं गैरमानक बिंदुओं पर वैश्विक गुणों द्वारा निर्धारित की जाती हैं $f$), हालांकि एक मनमाना हाइपररियल-वैल्यू फ़ंक्शन के लिए एकसमान निरंतरता की स्थानीय परिभाषा देना संभव नहीं है, समान निरंतरता#गैर-मानक विश्लेषण देखें।

एक गणितीय परिभाषा जो एक फलन है $f$ एक अंतराल पर निरंतर है $I$ और एक परिभाषा कि $f$ समान रूप से निरंतर चालू है $I$ संरचनात्मक रूप से समान हैं जैसा कि निम्नलिखित में दिखाया गया है।

किसी फ़ंक्शन की निरंतरता $f:X\to Y$ मीट्रिक रिक्त स्थान के लिए $(X,d_{1})$ और $(Y,d_{2})$ हर बिंदु पर$x$एक अंतराल का $I\subseteq X$ (अर्थात, की निरंतरता $f$ अंतराल पर $I$) परिमाणीकरण (तर्क) से शुरू होने वाले सूत्र द्वारा व्यक्त किया जाता है

$\forall x\in I\;\forall \varepsilon >0\;\exists \delta >0\;\forall y\in I:\,d_{1}(x,y)<\delta \,\Rightarrow \,d_{2}(f(x),f(y))<\varepsilon$,

(मेट्रिक्स $d_{1}(x,y)$ और $d_{2}(f(x),f(y))$ हैं $|x-y|$ और $|f(x)-f(y)|$ के लिए $f:\mathbb {R} \to \mathbb {R}$ वास्तविक संख्या के लिए $\mathbb {R}$).

एक समान निरंतरता के लिए, पहले, दूसरे और तीसरे परिमाणक (तर्क)तर्क) का क्रम ($\forall x\in I$, $\forall \varepsilon >0$, और $\exists \delta >0$) घुमाए गए हैं:

$\forall \varepsilon >0\;\exists \delta >0\;\forall x\in I\;\forall y\in I:\,d_{1}(x,y)<\delta \,\Rightarrow \,d_{2}(f(x),f(y))<\varepsilon$.

इस प्रकार अंतराल पर निरंतरता के लिए, कोई एक मनमाना बिंदु लेता है $x$ अंतराल का, और फिर एक दूरी मौजूद होनी चाहिए $\delta$,

$\cdots \forall x\,\exists \delta \cdots ,$

जबकि एकसमान निरंतरता के लिए, एक $\delta$ सभी बिंदुओं पर समान रूप से कार्य करना चाहिए $x$ अंतराल का,

$\cdots \exists \delta \,\forall x\cdots .$

गुण

प्रत्येक समान रूप से सतत फलन सतत फलन होता है, लेकिन इसका व्युत्क्रम मान्य नहीं होता। उदाहरण के लिए सतत फलन पर विचार करें $f\colon \mathbb {R} \rightarrow \mathbb {R} ,x\mapsto x^{2}$ कहाँ $\mathbb {R}$ वास्तविक संख्या है. एक सकारात्मक वास्तविक संख्या दी गई है $\varepsilon$, एकसमान निरंतरता के लिए एक सकारात्मक वास्तविक संख्या के अस्तित्व की आवश्यकता होती है $\delta$ ऐसा कि सभी के लिए $x_{1},x_{2}\in \mathbb {R}$ साथ $|x_{1}-x_{2}|<\delta$, अपने पास $|f(x_{1})-f(x_{2})|<\varepsilon$. लेकिन

$f\left(x+\delta \right)-f(x)=2x\cdot \delta +\delta ^{2},$

और के रूप में $x$ उच्चतर और उच्चतर मूल्य होता जा रहा है, $\delta$ संतुष्ट करने के लिए निम्न और निम्न होना आवश्यक है $|f(x+\beta )-f(x)|<\varepsilon$ सकारात्मक वास्तविक संख्याओं के लिए $\beta <\delta$ और दिया गया $\varepsilon$. इसका मतलब यह है कि कोई निर्दिष्ट करने योग्य (चाहे वह कितनी भी छोटी क्यों न हो) सकारात्मक वास्तविक संख्या नहीं है $\delta$ के लिए शर्त को पूरा करने के लिए $f$ समान रूप से निरंतर होना $f$ समान रूप से सतत नहीं है.

कोई भी पूर्णतया सतत फलन (संक्षिप्त अंतराल पर) समान रूप से सतत होता है। दूसरी ओर, कैंटर फ़ंक्शन समान रूप से निरंतर है लेकिन पूरी तरह से निरंतर नहीं है।

एक समान रूप से निरंतर फ़ंक्शन के तहत पूरी तरह से घिरे हुए स्थान उपसमुच्चय की छवि पूरी तरह से बंधी हुई है। हालाँकि, एक समान रूप से निरंतर फ़ंक्शन के तहत एक मनमाना मीट्रिक स्थान के एक बंधे हुए उपसमुच्चय की छवि को सीमित करने की आवश्यकता नहीं है: एक प्रतिउदाहरण के रूप में, असतत मीट्रिक के साथ संपन्न पूर्णांकों से सामान्य यूक्लिडियन मीट्रिक के साथ संपन्न पूर्णांकों तक पहचान फ़ंक्शन पर विचार करें।

हेन-कैंटर प्रमेय का दावा है कि एक कॉम्पैक्ट सेट पर प्रत्येक निरंतर कार्य समान रूप से निरंतर होता है। विशेष रूप से, यदि कोई फ़ंक्शन वास्तविक रेखा के अंतराल (गणित) पर निरंतर है, तो यह उस अंतराल पर समान रूप से निरंतर है। निरंतर कार्यों का डार्बौक्स अभिन्न इस प्रमेय से लगभग तुरंत अनुसरण करता है।

यदि एक वास्तविक-मूल्यवान फ़ंक्शन $f$ निरंतर चालू है $[0,\infty )$ और $\lim _{x\to \infty }f(x)$ अस्तित्व में है (और परिमित है), तो $f$ समान रूप से निरंतर है. विशेष रूप से, प्रत्येक तत्व $C_{0}(\mathbb {R} )$, निरंतर कार्यों का स्थान $\mathbb {R}$ जो अनंत पर लुप्त हो जाता है, समान रूप से निरंतर है। यह ऊपर वर्णित हेन-कैंटर प्रमेय का सामान्यीकरण है $C_{c}(\mathbb {R} )\subset C_{0}(\mathbb {R} )$.

उदाहरण और कोई उदाहरण नहीं

उदाहरण

• रैखिक कार्य $x\mapsto ax+b$ समान रूप से निरंतर कार्यों के सबसे सरल उदाहरण हैं।
• अंतराल पर कोई सतत कार्य $[0,1]$ चूँकि, यह भी समान रूप से निरंतर है $[0,1]$ एक कॉम्पैक्ट सेट है.
• यदि कोई फ़ंक्शन किसी खुले अंतराल पर अवकलनीय है और उसका व्युत्पन्न परिबद्ध है, तो फ़ंक्शन उस अंतराल पर समान रूप से निरंतर होता है।
• दो मीट्रिक स्थानों के बीच प्रत्येक लिप्सचिट्ज़ निरंतर मानचित्र समान रूप से निरंतर होता है। अधिक सामान्यतः, प्रत्येक होल्डर सतत फलन समान रूप से सतत होता है।
• पूर्ण मान समान रूप से निरंतर है, भिन्न न होने के बावजूद $x=0$. इससे पता चलता है कि समान रूप से निरंतर कार्य हमेशा भिन्न नहीं होते हैं।
• कहीं भी भिन्न न होने के बावजूद, वीयरस्ट्रैस फ़ंक्शन समान रूप से निरंतर है।
• कार्यों के एकसमान समनिरंतरता सेट का प्रत्येक सदस्य समान रूप से निरंतर होता है।

कोई उदाहरण नहीं

• जो कार्य किसी परिबद्ध डोमेन पर असीमित हैं वे समान रूप से निरंतर नहीं होते हैं। अंतराल पर स्पर्शरेखा फलन सतत है $(-\pi /2,\pi /2)$ लेकिन उस अंतराल पर समान रूप से निरंतर नहीं है, क्योंकि यह अनंत तक जाता है $x\to \pi /2$.
• ऐसे फलन जिनका व्युत्पन्न अनंत की ओर प्रवृत्त होता है $x$ बड़ा होना समान रूप से निरंतर नहीं हो सकता। घातांकीय फलन $x\mapsto e^{x}$ वास्तविक रेखा पर हर जगह निरंतर है, लेकिन रेखा पर समान रूप से निरंतर नहीं है, क्योंकि इसका व्युत्पन्न है $e^{x}$, और $e^{x}\to \infty$ जैसा $x\to \infty$.

विज़ुअलाइज़ेशन

एक समान रूप से सतत फलन के लिए, प्रत्येक सकारात्मक वास्तविक संख्या के लिए $\varepsilon >0$ एक सकारात्मक वास्तविक संख्या है $\delta >0$ जैसे कि दो फ़ंक्शन मान $f(x)$ और $f(y)$ अधिकतम दूरी हो $\varepsilon$ जब कभी भी $x$ और $y$ अधिकतम दूरी के भीतर हैं $\delta$. इस प्रकार प्रत्येक बिंदु पर $(x,f(x))$ यदि हम ग्राफ़ से थोड़ी कम ऊंचाई वाला एक आयत बनाते हैं $2\varepsilon$ और चौड़ाई इससे थोड़ी कम है $2\delta$ उस बिंदु के आसपास, तो ग्राफ़ पूरी तरह से आयत की ऊंचाई के भीतर होता है, यानी, ग्राफ़ आयत के ऊपर या नीचे की ओर से नहीं गुजरता है। ऐसे कार्यों के लिए जो समान रूप से निरंतर नहीं हैं, यह संभव नहीं है; इन कार्यों के लिए, ग्राफ़ ग्राफ़ पर किसी बिंदु पर आयत की ऊंचाई के अंदर स्थित हो सकता है लेकिन ग्राफ़ पर एक बिंदु होता है जहां ग्राफ़ आयत के ऊपर या नीचे स्थित होता है। (ग्राफ़ आयत के ऊपर या नीचे की ओर प्रवेश करता है।)

• 

  समान रूप से निरंतर कार्यों के लिए, प्रत्येक सकारात्मक वास्तविक संख्या के लिए $\varepsilon >0$ एक सकारात्मक वास्तविक संख्या है $\delta >0$ जैसे कि जब हम ग्राफ़ के प्रत्येक बिंदु के चारों ओर एक आयत बनाते हैं जिसकी चौड़ाई थोड़ी कम होती है $2\delta$ और ऊंचाई उससे थोड़ी कम $2\varepsilon$, ग्राफ पूरी तरह से आयत की ऊंचाई के अंदर स्थित है।

• फ़ाइल:निखत ग्लीचमाß
• Ig stetige Funktion.svg

  ऐसे कार्यों के लिए जो समान रूप से निरंतर नहीं हैं, एक सकारात्मक वास्तविक संख्या होती है $\varepsilon >0$ ऐसा कि प्रत्येक सकारात्मक वास्तविक संख्या के लिए $\delta >0$ ग्राफ़ पर एक बिंदु होता है जिससे कि जब हम एक आयत बनाते हैं जिसकी ऊँचाई थोड़ी कम होती है $2\varepsilon$ और चौड़ाई उससे थोड़ी कम $2\delta$ उस बिंदु के आसपास, आयत के सीधे ऊपर या नीचे एक फ़ंक्शन मान होता है। एक ग्राफ़ बिंदु ऐसा हो सकता है जहां ग्राफ़ पूरी तरह से आयत की ऊंचाई के अंदर है लेकिन यह ग्राफ़ के प्रत्येक बिंदु के लिए सत्य नहीं है।

इतिहास

एक समान निरंतरता की पहली प्रकाशित परिभाषा 1870 में एडुआर्ड_हेन द्वारा दी गई थी, और 1872 में उन्होंने एक प्रमाण प्रकाशित किया था कि एक खुले अंतराल पर एक निरंतर कार्य को समान रूप से निरंतर होने की आवश्यकता नहीं है। ये प्रमाण लगभग शब्दशः पीटर गुस्ताव लेज्यून डिरिचलेट द्वारा 1854 में निश्चित अभिन्नों पर अपने व्याख्यान में दिए गए हैं। एक समान निरंतरता की परिभाषा पहले बोलजानो के काम में दिखाई देती है जहां उन्होंने यह भी साबित किया कि एक खुले अंतराल पर निरंतर कार्यों को समान रूप से निरंतर होने की आवश्यकता नहीं है। इसके अलावा वह यह भी कहते हैं कि एक बंद अंतराल पर एक निरंतर कार्य समान रूप से निरंतर होता है, लेकिन वह इसका पूरा प्रमाण नहीं देते हैं।

अन्य लक्षण

गैर-मानक विश्लेषण

गैर-मानक विश्लेषण में, एक वास्तविक-मूल्यवान फ़ंक्शन$f$एक वास्तविक चर का एक बिंदु पर सूक्ष्म निरंतरता है$a$ठीक है अगर अंतर $f^{*}(a+\delta )-f^{*}(a)$ जब भी होता है तो अतिसूक्ष्म होता है$\delta$अतिसूक्ष्म है. इस प्रकार$f$एक सेट पर निरंतर है$A$में $\mathbb {R}$ ठीक है अगर $f^{*}$ प्रत्येक वास्तविक बिंदु पर सूक्ष्म सतत् है $a\in A$. एकसमान निरंतरता को इस स्थिति के रूप में व्यक्त किया जा सकता है कि (प्राकृतिक विस्तार) $f$ न केवल वास्तविक बिंदुओं पर सूक्ष्म-निरंतर है $A$, लेकिन इसके गैर-मानक समकक्ष (प्राकृतिक विस्तार) में सभी बिंदुओं पर $^{*}A$ में $^{*}\mathbb {R}$. ध्यान दें कि ऐसे हाइपररियल-मूल्यवान फ़ंक्शन मौजूद हैं जो इस मानदंड को पूरा करते हैं लेकिन समान रूप से निरंतर नहीं हैं, साथ ही समान रूप से निरंतर हाइपररियल-मूल्यवान फ़ंक्शन भी मौजूद हैं जो इस मानदंड को पूरा नहीं करते हैं, हालांकि, ऐसे कार्यों को फॉर्म में व्यक्त नहीं किया जा सकता है $f^{*}$ किसी भी वास्तविक-मूल्यवान फ़ंक्शन के लिए $f$. (अधिक विवरण और उदाहरणों के लिए गैर-मानक कैलकुलस देखें)।

कॉची निरंतरता

मीट्रिक रिक्त स्थान के बीच एक फ़ंक्शन के लिए, एकसमान निरंतरता का तात्पर्य कॉची निरंतरता से है (Fitzpatrick 2006). अधिक विशेष रूप से, आइए $A$ का एक उपसमुच्चय हो $\mathbb {R} ^{n}$. यदि कोई फ़ंक्शन $f:A\to \mathbb {R} ^{n}$ अनुक्रमों की प्रत्येक जोड़ी के लिए समान रूप से निरंतर है $x_{n}$ और $y_{n}$ ऐसा है कि

$\lim _{n\to \infty }|x_{n}-y_{n}|=0$

अपने पास

$\lim _{n\to \infty }|f(x_{n})-f(y_{n})|=0.$

विस्तार समस्या से संबंध

होने देना $X$ एक मीट्रिक स्थान बनें, $S$ का एक उपसमुच्चय $X$, $R$ एक पूर्ण मीट्रिक स्थान, और $f:S\rightarrow R$ एक सतत कार्य. उत्तर देने के लिए एक प्रश्न: कब कर सकते हैं $f$ सभी पर एक सतत कार्य के लिए विस्तारित किया जाए $X$?

अगर$S$में बंद है $X$, उत्तर टिट्ज़ विस्तार प्रमेय द्वारा दिया गया है। अतः विस्तार करना आवश्यक एवं पर्याप्त है$f$को बंद करने के लिए $S$ में $X$: अर्थात्, हम व्यापकता खोए बिना यह मान सकते हैं$S$में सघन है $X$, और इसका एक और सुखद परिणाम यह है कि यदि विस्तार मौजूद है, तो यह अद्वितीय है। के लिए पर्याप्त शर्त $f$ एक सतत कार्य का विस्तार करना $f:X\rightarrow R$ क्या यह कॉची-निरंतर फ़ंक्शन है | कॉची-निरंतर, यानी, नीचे की छवि$f$कॉची अनुक्रम का कॉची ही रहता है। अगर $X$ पूरा हो गया है (और इस प्रकार पूरा हो गया है$S$), फिर हर निरंतर कार्य से$X$एक मीट्रिक स्थान के लिए$Y$कॉची-निरंतर है। इसलिए जब$X$तैयार है,$f$एक सतत कार्य तक विस्तारित है $f:X\rightarrow R$ अगर और केवल अगर$f$कॉची-निरंतर है।

यह देखना आसान है कि प्रत्येक समान रूप से निरंतर कार्य कॉची-निरंतर है और इस प्रकार इसका विस्तार होता है$X$. फ़ंक्शन के बाद से, बातचीत लागू नहीं होती है $f:R\rightarrow R,x\mapsto x^{2}$ जैसा कि ऊपर देखा गया है, समान रूप से निरंतर नहीं है, लेकिन यह निरंतर है और इस प्रकार कॉची निरंतर है। सामान्य तौर पर, असीमित स्थानों पर परिभाषित कार्यों के लिए$R$, एक समान निरंतरता एक मजबूत स्थिति है। यह वांछनीय है कि एक कमजोर स्थिति हो जिससे विस्तारशीलता का अनुमान लगाया जा सके।

उदाहरण के लिए, मान लीजिए $a>1$ एक वास्तविक संख्या है. प्रीकैलकुलस स्तर पर, फ़ंक्शन $f:x\mapsto a^{x}$ के तर्कसंगत मूल्यों के लिए ही सटीक परिभाषा दी जा सकती है$x$(सकारात्मक वास्तविक संख्याओं की qवीं जड़ों के अस्तित्व को मानते हुए, मध्यवर्ती मूल्य प्रमेय का एक अनुप्रयोग)। कोई बढ़ाना चाहेगा $f$ सभी पर परिभाषित एक फ़ंक्शन के लिए $R$. पहचान

$f(x+\delta )-f(x)=a^{x}\left(a^{\delta }-1\right)$

पता चलता है कि$f$सेट पर समान रूप से निरंतर नहीं है$Q$सभी परिमेय संख्याओं का; हालाँकि किसी भी सीमित अंतराल के लिए$I$का प्रतिबंध$f$को $Q\cap I$ समान रूप से निरंतर है, इसलिए कॉची-निरंतर है, इसलिए $f$ पर एक सतत कार्य तक विस्तारित होता है$I$. लेकिन चूंकि यह हर किसी के लिए लागू है$I$, तो इसका एक अनूठा विस्तार है$f$सभी पर एक सतत कार्य के लिए$R$.

अधिक सामान्यतः, एक सतत कार्य $f:S\rightarrow R$ जिसका प्रत्येक परिबद्ध उपसमुच्चय पर प्रतिबंध है$S$समान रूप से निरंतर विस्तार योग्य है$X$, और व्युत्क्रम यदि धारण करता है$X$स्थानीय रूप से सघन है.

एक समान रूप से निरंतर फ़ंक्शन की विस्तारशीलता का एक विशिष्ट अनुप्रयोग व्युत्क्रम फूरियर परिवर्तन सूत्र का प्रमाण है। हम पहले यह साबित करते हैं कि सूत्र परीक्षण कार्यों के लिए सत्य है, उनमें से बहुत सारे हैं। फिर हम इस तथ्य का उपयोग करके व्युत्क्रम मानचित्र को संपूर्ण स्थान तक विस्तारित करते हैं कि रैखिक मानचित्र निरंतर है; इस प्रकार, समान रूप से निरंतर।

टोपोलॉजिकल वेक्टर रिक्त स्थान का सामान्यीकरण

दो टोपोलॉजिकल वेक्टर रिक्त स्थान के विशेष मामले में $V$ और $W$, मानचित्र की एकसमान निरंतरता की धारणा $f:V\to W$ बन जाता है: किसी भी पड़ोस के लिए $B$ शून्य में $W$, वहाँ एक पड़ोस मौजूद है $A$ शून्य में $V$ ऐसा है कि $v_{1}-v_{2}\in A$ तात्पर्य $f(v_{1})-f(v_{2})\in B.$ रैखिक परिवर्तनों के लिए $f:V\to W$, एकसमान निरंतरता निरंतरता के बराबर है। इस तथ्य का उपयोग बानाच स्थान के घने उपस्थान से एक रेखीय मानचित्र का विस्तार करने के लिए कार्यात्मक विश्लेषण में अक्सर अंतर्निहित रूप से किया जाता है।

समान स्थानों का सामान्यीकरण

जिस तरह निरंतरता के लिए सबसे प्राकृतिक और सामान्य सेटिंग टोपोलॉजिकल स्पेस हैं, उसी तरह एकसमान निरंतरता के अध्ययन के लिए सबसे प्राकृतिक और सामान्य सेटिंग एकसमान स्पेस हैं। एक समारोह $f:X\to Y$ समान स्थानों के बीच को समान रूप से निरंतर कहा जाता है यदि प्रत्येक परिवेश के लिए (टोपोलॉजी)$V$में$Y$वहाँ एक घेरा मौजूद है$U$में$X$ऐसा कि हर किसी के लिए $(x_{1},x_{2})$ में $U$ अपने पास $(f(x_{1}),f(x_{2}))$ में $V$.

इस सेटिंग में, यह भी सच है कि समान रूप से निरंतर मानचित्र कॉची अनुक्रमों को कॉची अनुक्रमों में बदल देते हैं।

प्रत्येक कॉम्पैक्ट हॉसडॉर्फ स्पेस में टोपोलॉजी के साथ संगत बिल्कुल एक समान संरचना होती है। एक परिणाम हेइन-कैंटर प्रमेय का सामान्यीकरण है: एक कॉम्पैक्ट हॉसडॉर्फ स्थान से एक समान स्थान तक प्रत्येक निरंतर कार्य समान रूप से निरंतर होता है।

यह भी देखें

• Contraction mapping
• Uniform isomorphism

अग्रिम पठन

• Bourbaki, Nicolas. General Topology: Chapters 1–4 [Topologie Générale]. ISBN 0-387-19374-X. Chapter II is a comprehensive reference of uniform spaces.
• Dieudonné, Jean (1960). Foundations of Modern Analysis. Academic Press.
• Fitzpatrick, Patrick (2006). Advanced Calculus. Brooks/Cole. ISBN 0-534-92612-6.
• Kelley, John L. (1955). General topology. Graduate Texts in Mathematics. Springer-Verlag. ISBN 0-387-90125-6.
• Kudryavtsev, L.D. (2001) [1994], "Uniform continuity", Encyclopedia of Mathematics, EMS Press
• Rudin, Walter (1976). Principles of Mathematical Analysis. New York: McGraw-Hill. ISBN 978-0-07-054235-8.
• Rusnock, P.; Kerr-Lawson, A. (2005), "Bolzano and uniform continuity", Historia Mathematica, 32 (3): 303–311, doi:10.1016/j.hm.2004.11.003