संक्रामी घटाव (ट्रान्सिटिव रिडक्शन): Difference between revisions
| Line 1: | Line 1: | ||
{{short description|Copy of a directed graph with redundant edges removed}} | {{short description|Copy of a directed graph with redundant edges removed}} | ||
ग्राफ़ सिद्धांत के [[गणितीय]] क्षेत्र में, [[निर्देशित ग्राफ]] {{mvar|D}} का सकर्मक न्यूनीकरण समान [[वर्टेक्स (ग्राफ़ सिद्धांत)|शीर्षों (ग्राफ़ सिद्धांत)]] और यथासंभव अल्प किनारों वाला एक और निर्देशित ग्राफ़ है, जैसे कि शीर्षों के सभी जोड़े {{mvar|v}}, {{mvar|w}} के लिए (निर्देशित) पथ (ग्राफ़ सिद्धांत) से {{mvar|v}} को {{mvar|w}} में {{mvar|D}} मौजूद है यदि और केवल यदि ऐसा पथ न्यूनीकरण में विद्यमान है।{{harvtxt|अहो|गैरी|उल्मैन|1972}} द्वारा सकर्मक न्यूनीकरणपेश किए गए, जिन्होंने उनके निर्माण की | ग्राफ़ सिद्धांत के [[गणितीय]] क्षेत्र में, [[निर्देशित ग्राफ]] {{mvar|D}} का सकर्मक न्यूनीकरण समान [[वर्टेक्स (ग्राफ़ सिद्धांत)|शीर्षों (ग्राफ़ सिद्धांत)]] और यथासंभव अल्प किनारों वाला एक और निर्देशित ग्राफ़ है, जैसे कि शीर्षों के सभी जोड़े {{mvar|v}}, {{mvar|w}} के लिए (निर्देशित) पथ (ग्राफ़ सिद्धांत) से {{mvar|v}} को {{mvar|w}} में {{mvar|D}} मौजूद है यदि और केवल यदि ऐसा पथ न्यूनीकरण में विद्यमान है।{{harvtxt|अहो|गैरी|उल्मैन|1972}} द्वारा सकर्मक न्यूनीकरणपेश किए गए, जिन्होंने उनके निर्माण की अभिकलनात्मक जटिलता पर कड़ी सीमाएं प्रदान कीं है। | ||
तकनीकी रूप से, न्यूनीकरण एक निर्देशित ग्राफ़ है जिसमें समान [[गम्यता|अभिगम्यता]] संबंध {{mvar|D}} होता है समान रूप से, {{mvar|D}} और इसकी सकर्मक न्यूनीकरण में एक दूसरे के समान [[सकर्मक समापन]] और {{mvar|D}} की सकर्मक न्यूनीकरण में उस गुण के साथ सभी ग्राफ़ के बीच जितना संभव हो उतना अल्प किनारा होना चाहिए। | तकनीकी रूप से, न्यूनीकरण एक निर्देशित ग्राफ़ है जिसमें समान [[गम्यता|अभिगम्यता]] संबंध {{mvar|D}} होता है समान रूप से, {{mvar|D}} और इसकी सकर्मक न्यूनीकरण में एक दूसरे के समान [[सकर्मक समापन]] और {{mvar|D}} की सकर्मक न्यूनीकरण में उस गुण के साथ सभी ग्राफ़ के बीच जितना संभव हो उतना अल्प किनारा होना चाहिए। | ||
| Line 7: | Line 7: | ||
परिमित निर्देशित चक्रीय ग्राफ (निर्देशित चक्रों के बिना निर्देशित ग्राफ) की सकर्मक न्यूनीकरण अद्वितीय है और दिए गए ग्राफ का एक प्रेरित सबग्राफ़ है। हालाँकि, (निर्देशित) चक्र वाले ग्राफ़ के लिए विशिष्टता विफल हो जाती है, और अनंत ग्राफ़ के लिए अस्तित्व की भी गारंटी नहीं होती है। | परिमित निर्देशित चक्रीय ग्राफ (निर्देशित चक्रों के बिना निर्देशित ग्राफ) की सकर्मक न्यूनीकरण अद्वितीय है और दिए गए ग्राफ का एक प्रेरित सबग्राफ़ है। हालाँकि, (निर्देशित) चक्र वाले ग्राफ़ के लिए विशिष्टता विफल हो जाती है, और अनंत ग्राफ़ के लिए अस्तित्व की भी गारंटी नहीं होती है। | ||
'''न्यूनतम समतुल्य ग्राफ''' की निकटतम संबंधित अवधारणा {{mvar|D}} का सबग्राफ़ है जिसमें समान पहुंच | '''न्यूनतम समतुल्य ग्राफ''' की निकटतम संबंधित अवधारणा {{mvar|D}} का सबग्राफ़ है जिसमें समान पहुंच अभिगम्यता संबंध और यथासंभव अल्प किनारे होते हैं।{{sfnp|Moyles|Thompson|1969}} अंतर यह है कि सकर्मक न्यूनीकरण के लिए {{mvar|D}} का उपसमूह होना जरूरी नहीं है। परिमित निर्देशित चक्रीय ग्राफ़ के लिए, न्यूनतम समतुल्य ग्राफ़ सकर्मक न्यूनीकरण के समान है। हालाँकि, ऐसे ग्राफ़ के लिए जिनमें चक्र हो सकते हैं, न्यूनतम समतुल्य ग्राफ़ का निर्माण एनपी-कठोरता होता है, जबकि बहुपद समय में सकर्मक न्यूनीकरण का निर्माण किया जा सकता है। | ||
निर्देशित ग्राफ में संबंध के जोड़े को चाप के रूप में व्याख्या करके, [[सेट (गणित)]] पर अमूर्त द्वयी सम्बन्ध के लिए सकर्मक न्यूनीकरण को परिभाषित किया जा सकता है। | निर्देशित ग्राफ में संबंध के जोड़े को चाप के रूप में व्याख्या करके, [[सेट (गणित)|समुच्चय (गणित)]] पर अमूर्त द्वयी सम्बन्ध के लिए सकर्मक न्यूनीकरण को परिभाषित किया जा सकता है। | ||
==निर्देशित चक्रीय ग्राफ़ में== | ==निर्देशित चक्रीय ग्राफ़ में== | ||
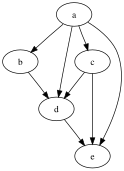
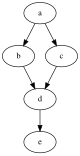
परिमित निर्देशित ग्राफ ''G'' की सकर्मक न्यूनीकरण सबसे अल्प संभव किनारों वाला ग्राफ है जिसमें मूल ग्राफ के समान पहुंच | परिमित निर्देशित ग्राफ ''G'' की सकर्मक न्यूनीकरण सबसे अल्प संभव किनारों वाला ग्राफ है जिसमें मूल ग्राफ के समान पहुंच अभिगम्यता संबंध है। अर्थात्, यदि ग्राफ़ ''G'' में शीर्ष x से शीर्ष y तक कोई पथ है, तो ''G'' की सकर्मक न्यूनीकरण में x से y तक का पथ भी होना चाहिए, और इसके विपरीत भी होना चाहिए। विशेष रूप से, यदि x से y तक कुछ पथ है, और y से z तक कोई अन्य पथ है, जिसमें y शामिल न हो तो x से z तक कोई पथ नहीं हो सकता है। x, y, और z के लिए [[परिवर्तनशीलता (गणित)]] का अर्थ है कि यदि x < y और y < z, तो x < z है। यदि y से z तक किसी पथ के लिए x से y तक कोई पथ है, तो x से z तक कोई पथ है; हालाँकि, यह सच नहीं है कि किसी भी पथ x से y और x से z के लिए पथ y से z है, और इसलिए शीर्ष x और z के बीच के किसी भी किनारे को सकर्मक न्यूनीकरण के तहत बाहर रखा गया है, क्योंकि वे उन पथों का प्रतिनिधित्व करते हैं जो सकर्मक नहीं हैं। निम्नलिखित छवि गैर-संक्रमणीय द्वयी सम्बन्ध (बाईं ओर) और इसकी सकर्मक न्यूनीकरण (दाईं ओर) के अनुरूप ग्राफ़ के चित्र प्रदर्शित करती है। | ||
<div वर्ग= केंद्र > | <div वर्ग= केंद्र > | ||
| Line 23: | Line 23: | ||
परिमित निर्देशित चक्रीय ग्राफ़ ''G'' की सकर्मक न्यूनीकरण अद्वितीय है, और इसमें ''G'' के किनारे शामिल हैं जो उनके समापन बिंदुओं के बीच एकमात्र पथ बनाते हैं। विशेष रूप से, यह हमेशा दिए गए ग्राफ़ का फैला हुआ सबग्राफ होता है। इस कारण से, इस मामले में सकर्मक न्यूनीकरण न्यूनतम समकक्ष ग्राफ के साथ मेल खाती है। | परिमित निर्देशित चक्रीय ग्राफ़ ''G'' की सकर्मक न्यूनीकरण अद्वितीय है, और इसमें ''G'' के किनारे शामिल हैं जो उनके समापन बिंदुओं के बीच एकमात्र पथ बनाते हैं। विशेष रूप से, यह हमेशा दिए गए ग्राफ़ का फैला हुआ सबग्राफ होता है। इस कारण से, इस मामले में सकर्मक न्यूनीकरण न्यूनतम समकक्ष ग्राफ के साथ मेल खाती है। | ||
द्विआधारी संबंधों के गणितीय सिद्धांत में, किसी | द्विआधारी संबंधों के गणितीय सिद्धांत में, समुच्चय ''X'' पर किसी भी संबंध ''R'' को निर्देशित ग्राफ़ के रूप में माना जा सकता है इसके शीर्ष समुच्चय के रूप में समुच्चय ''X'' है और इसमें ''R'' में संबंधित तत्वों के प्रत्येक क्रमित युग्म के लिए चाप ''xy'' है। विशेष रूप से, यह विधि आंशिक रूप से क्रम किए गए सेटों को निर्देशित चक्रीय ग्राफ़ के रूप में दोबारा व्याख्या करने की अनुमति देती है, जिसमें आंशिक क्रम के तत्वों की दी गई जोड़ी के बीच जब भी क्रम संबंध ''x'' < ''y'' होता है तो ग्राफ़ में चाप xy होता है। जब सकर्मक न्यूनीकरण ऑपरेशन को इस तरह से निर्मित निर्देशित चक्रीय ग्राफ़ पर लागू किया जाता है, तो यह आंशिक क्रम के कवरिंग संबंध को उत्पन्न करता है, जिसे अक्सर [[हस्से आरेख]] के माध्यम से दृश्य अभिव्यक्ति दी जाती है। | ||
नेटवर्क पर | नेटवर्क पर सकर्मक न्यूनीकरण का उपयोग किया गया है जिसे नेटवर्क के बीच संरचनात्मक अंतर प्रकट करने के लिए निर्देशित चक्रीय ग्राफ़ (जैसे [[उद्धरण ग्राफ]] या उद्धरण ग्राफ) के रूप में दर्शाया जा सकता है।{{sfnp|Clough|Gollings|Loach|Evans|2015}} | ||
==चक्र वाले ग्राफ़ में== | ==चक्र वाले ग्राफ़ में== | ||
चक्र वाले | चक्र वाले परिमित ग्राफ़ में, सकर्मक न्यूनीकरण अद्वितीय नहीं हो सकती है: एक ही शीर्ष समुच्चय पर एक से अधिक ग्राफ़ हो सकते हैं जिनमें किनारों की न्यूनतम संख्या होती है और दिए गए ग्राफ़ के समान पहुंच अभिगम्यता संबंध होता है। इसके अतिरिक्त, ऐसा भी हो सकता है कि इनमें से कोई भी न्यूनतम ग्राफ़ दिए गए ग्राफ़ का सबग्राफ न हो। फिर भी, दिए गए ग्राफ़ ''G'' के समान अभिगम्यता संबंध के साथ न्यूनतम ग्राफ़ को चिह्नित करना सीधा है।<ref name="agu72">{{harvtxt|Aho|Garey|Ullman|1972}}</ref> यदि ''G'' यादृच्छिक निर्देशित ग्राफ है, और ''H'' किनारों की न्यूनतम संभावित संख्या वाला ग्राफ है जिसमें ''G'' के समान पहुंच अभिगम्यता संबंध है, तो ''H'' में शामिल हैं | ||
* | *''G'' के प्रत्येक दृढता से जुड़े घटक के लिए [[निर्देशित चक्र]], इस घटक में शीर्षों को एक साथ जोड़ता है | ||
*दृढ़ता से जुड़े घटक की सकर्मक न्यूनीकरण के प्रत्येक किनारे XY के लिए | *दृढ़ता से जुड़े घटक की सकर्मक न्यूनीकरण के प्रत्येक किनारे ''XY'' के लिए किनारा xy की परिभाषा, जहां ''X'' और ''Y'', ''G'' के दो दृढता से जुड़े हुए घटक हैं जो संक्षेपण में किनारे से जुड़े हुए हैं, ''x'' घटक ''X'' में कोई शीर्ष है, और ''y'' घटक ''Y'' में कोई शीर्ष है। ''G'' का संघनन निर्देशित चक्रीय ग्राफ है जिसमें ''G'' के प्रत्येक दृढता से जुड़े घटक के लिए शीर्ष होता है और ''G'' में किनारे से जुड़े प्रत्येक दो घटकों के लिए किनारा होता है। विशेष रूप से, क्योंकि यह चक्रीय है, इसकी सकर्मक न्यूनीकरण को पिछले अनुभाग के अनुसार परिभाषित किया जा सकता है। | ||
इस प्रकार की सकर्मक न्यूनीकरण में किनारों की कुल संख्या संक्षेपण की सकर्मक न्यूनीकरण में किनारों की संख्या के बराबर होती है, साथ ही गैर-तुच्छ दृढ़ता से जुड़े घटकों (एक से अधिक शीर्ष वाले घटक) में शीर्षों की संख्या के बराबर होती है। | इस प्रकार की सकर्मक न्यूनीकरण में किनारों की कुल संख्या संक्षेपण की सकर्मक न्यूनीकरण में किनारों की संख्या के बराबर होती है, साथ ही गैर-तुच्छ दृढ़ता से जुड़े घटकों (एक से अधिक शीर्ष वाले घटक) में शीर्षों की संख्या के बराबर होती है। | ||
संक्षेपण किनारों के अनुरूप सकर्मक न्यूनीकरण के किनारों को हमेशा दिए गए ग्राफ़ | संक्षेपण किनारों के अनुरूप सकर्मक न्यूनीकरण के किनारों को हमेशा दिए गए ग्राफ़ ''G'' का सबग्राफ चुना जा सकता है। हालाँकि, प्रत्येक दृढ़ता से जुड़े घटक के भीतर चक्र को केवल ''G'' का सबग्राफ चुना जा सकता है यदि उस घटक में हैमिल्टनियन चक्र हो, कुछ ऐसा जो हमेशा सत्य नहीं होता और जिसे जांचना कठिन होता है। इस कठिनाई के कारण, समान अभिगम्यता (इसका न्यूनतम समतुल्य ग्राफ) के साथ दिए गए ग्राफ ''G'' का सबसे छोटा सबग्राफ ढूंढना एनपी-कठोरता है।<ref name="agu72"/> | ||
==अभिकलनात्मक जटिलता== | |||
अहो एट अल के रूप में दिखाएँ,<ref name="agu72"/>जब ग्राफ़ एल्गोरिदम की समय जटिलता को केवल ग्राफ़ में शीर्षों की संख्या ''n'' के फलन के रूप में मापा जाता है, न कि किनारों की संख्या के फलन के रूप में, निर्देशित चक्रीय ग्राफ़ के सकर्मक समापन और सकर्मक न्यूनीकरण में समान जटिलता होती है। यह पहले ही दिखाया जा चुका है कि आकार ''n × n'' के [[ तार्किक मैट्रिक्स |बूलियन आव्यूह]] के सकर्मक समापन और [[मैट्रिक्स गुणन|आव्यूह गुणन]] में एक दूसरे के समान जटिलता थी,<ref>Aho et al. credit this result to an unpublished 1971 manuscript of Ian Munro, and to a 1970 Russian-language paper by M. E. Furman.</ref> इसलिए इस परिणाम ने सकर्मक न्यूनीकरण को उसी वर्ग में डाल दिया है। 2015 तक, [[मैट्रिक्स गुणन की कम्प्यूटेशनल जटिलता|आव्यूह गुणन की अभिकलनात्मक जटिलता]] में O(''n''<sup>2.3729</sup>) समय लगता है,{{sfnp|Le Gall|2014}} और यह सघन ग्राफ़ में सकर्मक न्यूनीकरण के लिए सबसे तेज़ ज्ञात सबसे खराब स्थिति की समय सीमा देता है। | |||
== | |||
अहो एट अल के रूप | |||
===क्लोजर का उपयोग करके न्यूनीकरण की गणना करना=== | ===क्लोजर का उपयोग करके न्यूनीकरण की गणना करना=== | ||
यह साबित करने के लिए कि सकर्मक | यह साबित करने के लिए कि सकर्मक कमी सकर्मक समापन जितना आसान है, अहो एट अल बूलियन आव्यूह गुणन के साथ पहले से ज्ञात तुल्यता पर भरोसा करें। उन्होंने A को दिए गए निर्देशित एसाइक्लिक ग्राफ का आसन्न मैट्रिक्स होने दिया, और B को इसके सकर्मक समापन का आसन्न मैट्रिक्स होने दिया (किसी भी मानक सकर्मक समापन एल्गोरिदम का उपयोग करके गणना की गई)। तब एक किनारा uv संक्रमणीय कमी से संबंधित होता है यदि और केवल यदि मैट्रिक्स A की पंक्ति u और कॉलम v में एक गैर-शून्य प्रविष्टि है, और मैट्रिक्स उत्पाद एबी की उसी स्थिति में एक शून्य प्रविष्टि है। इस निर्माण में, मैट्रिक्स एबी के गैर-शून्य तत्व दो या अधिक लंबाई के पथों से जुड़े शीर्षों के जोड़े का प्रतिनिधित्व करते हैं।<ref name="agu72"/> | ||
===न्यूनीकरण का उपयोग करके समापन की गणना करना=== | ===न्यूनीकरण का उपयोग करके समापन की गणना करना=== | ||
यह साबित करने के लिए कि सकर्मक न्यूनीकरण सकर्मक समापन जितनी ही कठिन है, अहो एट | यह साबित करने के लिए कि सकर्मक न्यूनीकरण सकर्मक समापन जितनी ही कठिन है, अहो एट अल दिए गए निर्देशित चक्रीय ग्राफ़ ''G'' से एक और ग्राफ ''H'' का निर्माण करें, जिसमें ''G'' के प्रत्येक शीर्ष को तीन शीर्षों के पथ से बदल दिया जाता है, और ''G'' का प्रत्येक किनारा इन पथों के संबंधित मध्य शीर्षों को जोड़ने वाले ''H'' में किनारे से मेल खाता है। इसके अलावा, ग्राफ ''H'', अहो एट अल में प्रत्येक पथ के आरंभ से प्रत्येक पथ के अंत तक किनारा जोड़ें। ''H'' की सकर्मक न्यूनीकरण में, ''u'' के लिए पथ प्रारंभ से ''v'' के लिए पथ के अंत तक किनारा है, यदि और केवल यदि किनारा ''uv'' ''G'' के सकर्मक समापन से संबंधित नहीं है। इसलिए, यदि ''H'' की सकर्मक न्यूनीकरण हो सकती है कुशलतापूर्वक गणना करने पर, ''G'' के सकर्मक समापन को सीधे इससे पढ़ा जा सकता है।<ref name="agu72"/> | ||
===[[विरल ग्राफ]]़ में न्यूनीकरण की गणना करना=== | ===[[विरल ग्राफ]]़ में न्यूनीकरण की गणना करना=== | ||
जब निर्देशित | जब निर्देशित चक्रीय ग्राफ़ में शीर्षों की संख्या n और किनारों की संख्या m दोनों के संदर्भ में मापा जाता है, तो समय O(nm) में सकर्मक न्यूनीकरण भी पाई जा सकती है, एक सीमा जो विरल ग्राफ़ के लिए आव्यूह गुणन विधियों से तेज़ हो सकती है . ऐसा करने के लिए, प्रारंभिक शीर्ष के प्रत्येक संभावित विकल्प के लिए, दिए गए निर्देशित चक्रीय ग्राफ में एक [[रैखिक समय]] सबसे लंबे पथ समस्या को लागू करें। गणना किए गए सबसे लंबे पथों में से, केवल एक लंबाई (एकल किनारे) वाले पथों को ही रखें; दूसरे शब्दों में, उन किनारों (u, v) को रखें जिनके लिए u से v तक कोई अन्य पथ मौजूद नहीं है। यह ओ (एनएम) समयबद्ध [[गहराई-पहली खोज]] या चौड़ाई पहली खोज का उपयोग करके सकर्मक समापन के निर्माण की जटिलता से मेल खाता है। आरंभिक शीर्ष के हर विकल्प से पहुंच योग्य शीर्ष, इसलिए फिर से इन मान्यताओं के साथ सकर्मक समापन और सकर्मक न्यूनीकरण एक ही समय में पाई जा सकती हैं। | ||
==टिप्पणियाँ== | ==टिप्पणियाँ== | ||
Revision as of 12:00, 6 July 2023
ग्राफ़ सिद्धांत के गणितीय क्षेत्र में, निर्देशित ग्राफ D का सकर्मक न्यूनीकरण समान शीर्षों (ग्राफ़ सिद्धांत) और यथासंभव अल्प किनारों वाला एक और निर्देशित ग्राफ़ है, जैसे कि शीर्षों के सभी जोड़े v, w के लिए (निर्देशित) पथ (ग्राफ़ सिद्धांत) से v को w में D मौजूद है यदि और केवल यदि ऐसा पथ न्यूनीकरण में विद्यमान है।अहो, गैरी & उल्मैन (1972) द्वारा सकर्मक न्यूनीकरणपेश किए गए, जिन्होंने उनके निर्माण की अभिकलनात्मक जटिलता पर कड़ी सीमाएं प्रदान कीं है।
तकनीकी रूप से, न्यूनीकरण एक निर्देशित ग्राफ़ है जिसमें समान अभिगम्यता संबंध D होता है समान रूप से, D और इसकी सकर्मक न्यूनीकरण में एक दूसरे के समान सकर्मक समापन और D की सकर्मक न्यूनीकरण में उस गुण के साथ सभी ग्राफ़ के बीच जितना संभव हो उतना अल्प किनारा होना चाहिए।
परिमित निर्देशित चक्रीय ग्राफ (निर्देशित चक्रों के बिना निर्देशित ग्राफ) की सकर्मक न्यूनीकरण अद्वितीय है और दिए गए ग्राफ का एक प्रेरित सबग्राफ़ है। हालाँकि, (निर्देशित) चक्र वाले ग्राफ़ के लिए विशिष्टता विफल हो जाती है, और अनंत ग्राफ़ के लिए अस्तित्व की भी गारंटी नहीं होती है।
न्यूनतम समतुल्य ग्राफ की निकटतम संबंधित अवधारणा D का सबग्राफ़ है जिसमें समान पहुंच अभिगम्यता संबंध और यथासंभव अल्प किनारे होते हैं।[1] अंतर यह है कि सकर्मक न्यूनीकरण के लिए D का उपसमूह होना जरूरी नहीं है। परिमित निर्देशित चक्रीय ग्राफ़ के लिए, न्यूनतम समतुल्य ग्राफ़ सकर्मक न्यूनीकरण के समान है। हालाँकि, ऐसे ग्राफ़ के लिए जिनमें चक्र हो सकते हैं, न्यूनतम समतुल्य ग्राफ़ का निर्माण एनपी-कठोरता होता है, जबकि बहुपद समय में सकर्मक न्यूनीकरण का निर्माण किया जा सकता है।
निर्देशित ग्राफ में संबंध के जोड़े को चाप के रूप में व्याख्या करके, समुच्चय (गणित) पर अमूर्त द्वयी सम्बन्ध के लिए सकर्मक न्यूनीकरण को परिभाषित किया जा सकता है।
निर्देशित चक्रीय ग्राफ़ में
परिमित निर्देशित ग्राफ G की सकर्मक न्यूनीकरण सबसे अल्प संभव किनारों वाला ग्राफ है जिसमें मूल ग्राफ के समान पहुंच अभिगम्यता संबंध है। अर्थात्, यदि ग्राफ़ G में शीर्ष x से शीर्ष y तक कोई पथ है, तो G की सकर्मक न्यूनीकरण में x से y तक का पथ भी होना चाहिए, और इसके विपरीत भी होना चाहिए। विशेष रूप से, यदि x से y तक कुछ पथ है, और y से z तक कोई अन्य पथ है, जिसमें y शामिल न हो तो x से z तक कोई पथ नहीं हो सकता है। x, y, और z के लिए परिवर्तनशीलता (गणित) का अर्थ है कि यदि x < y और y < z, तो x < z है। यदि y से z तक किसी पथ के लिए x से y तक कोई पथ है, तो x से z तक कोई पथ है; हालाँकि, यह सच नहीं है कि किसी भी पथ x से y और x से z के लिए पथ y से z है, और इसलिए शीर्ष x और z के बीच के किसी भी किनारे को सकर्मक न्यूनीकरण के तहत बाहर रखा गया है, क्योंकि वे उन पथों का प्रतिनिधित्व करते हैं जो सकर्मक नहीं हैं। निम्नलिखित छवि गैर-संक्रमणीय द्वयी सम्बन्ध (बाईं ओर) और इसकी सकर्मक न्यूनीकरण (दाईं ओर) के अनुरूप ग्राफ़ के चित्र प्रदर्शित करती है।
परिमित निर्देशित चक्रीय ग्राफ़ G की सकर्मक न्यूनीकरण अद्वितीय है, और इसमें G के किनारे शामिल हैं जो उनके समापन बिंदुओं के बीच एकमात्र पथ बनाते हैं। विशेष रूप से, यह हमेशा दिए गए ग्राफ़ का फैला हुआ सबग्राफ होता है। इस कारण से, इस मामले में सकर्मक न्यूनीकरण न्यूनतम समकक्ष ग्राफ के साथ मेल खाती है।
द्विआधारी संबंधों के गणितीय सिद्धांत में, समुच्चय X पर किसी भी संबंध R को निर्देशित ग्राफ़ के रूप में माना जा सकता है इसके शीर्ष समुच्चय के रूप में समुच्चय X है और इसमें R में संबंधित तत्वों के प्रत्येक क्रमित युग्म के लिए चाप xy है। विशेष रूप से, यह विधि आंशिक रूप से क्रम किए गए सेटों को निर्देशित चक्रीय ग्राफ़ के रूप में दोबारा व्याख्या करने की अनुमति देती है, जिसमें आंशिक क्रम के तत्वों की दी गई जोड़ी के बीच जब भी क्रम संबंध x < y होता है तो ग्राफ़ में चाप xy होता है। जब सकर्मक न्यूनीकरण ऑपरेशन को इस तरह से निर्मित निर्देशित चक्रीय ग्राफ़ पर लागू किया जाता है, तो यह आंशिक क्रम के कवरिंग संबंध को उत्पन्न करता है, जिसे अक्सर हस्से आरेख के माध्यम से दृश्य अभिव्यक्ति दी जाती है।
नेटवर्क पर सकर्मक न्यूनीकरण का उपयोग किया गया है जिसे नेटवर्क के बीच संरचनात्मक अंतर प्रकट करने के लिए निर्देशित चक्रीय ग्राफ़ (जैसे उद्धरण ग्राफ या उद्धरण ग्राफ) के रूप में दर्शाया जा सकता है।[2]
चक्र वाले ग्राफ़ में
चक्र वाले परिमित ग्राफ़ में, सकर्मक न्यूनीकरण अद्वितीय नहीं हो सकती है: एक ही शीर्ष समुच्चय पर एक से अधिक ग्राफ़ हो सकते हैं जिनमें किनारों की न्यूनतम संख्या होती है और दिए गए ग्राफ़ के समान पहुंच अभिगम्यता संबंध होता है। इसके अतिरिक्त, ऐसा भी हो सकता है कि इनमें से कोई भी न्यूनतम ग्राफ़ दिए गए ग्राफ़ का सबग्राफ न हो। फिर भी, दिए गए ग्राफ़ G के समान अभिगम्यता संबंध के साथ न्यूनतम ग्राफ़ को चिह्नित करना सीधा है।[3] यदि G यादृच्छिक निर्देशित ग्राफ है, और H किनारों की न्यूनतम संभावित संख्या वाला ग्राफ है जिसमें G के समान पहुंच अभिगम्यता संबंध है, तो H में शामिल हैं
- G के प्रत्येक दृढता से जुड़े घटक के लिए निर्देशित चक्र, इस घटक में शीर्षों को एक साथ जोड़ता है
- दृढ़ता से जुड़े घटक की सकर्मक न्यूनीकरण के प्रत्येक किनारे XY के लिए किनारा xy की परिभाषा, जहां X और Y, G के दो दृढता से जुड़े हुए घटक हैं जो संक्षेपण में किनारे से जुड़े हुए हैं, x घटक X में कोई शीर्ष है, और y घटक Y में कोई शीर्ष है। G का संघनन निर्देशित चक्रीय ग्राफ है जिसमें G के प्रत्येक दृढता से जुड़े घटक के लिए शीर्ष होता है और G में किनारे से जुड़े प्रत्येक दो घटकों के लिए किनारा होता है। विशेष रूप से, क्योंकि यह चक्रीय है, इसकी सकर्मक न्यूनीकरण को पिछले अनुभाग के अनुसार परिभाषित किया जा सकता है।
इस प्रकार की सकर्मक न्यूनीकरण में किनारों की कुल संख्या संक्षेपण की सकर्मक न्यूनीकरण में किनारों की संख्या के बराबर होती है, साथ ही गैर-तुच्छ दृढ़ता से जुड़े घटकों (एक से अधिक शीर्ष वाले घटक) में शीर्षों की संख्या के बराबर होती है।
संक्षेपण किनारों के अनुरूप सकर्मक न्यूनीकरण के किनारों को हमेशा दिए गए ग्राफ़ G का सबग्राफ चुना जा सकता है। हालाँकि, प्रत्येक दृढ़ता से जुड़े घटक के भीतर चक्र को केवल G का सबग्राफ चुना जा सकता है यदि उस घटक में हैमिल्टनियन चक्र हो, कुछ ऐसा जो हमेशा सत्य नहीं होता और जिसे जांचना कठिन होता है। इस कठिनाई के कारण, समान अभिगम्यता (इसका न्यूनतम समतुल्य ग्राफ) के साथ दिए गए ग्राफ G का सबसे छोटा सबग्राफ ढूंढना एनपी-कठोरता है।[3]
अभिकलनात्मक जटिलता
अहो एट अल के रूप में दिखाएँ,[3]जब ग्राफ़ एल्गोरिदम की समय जटिलता को केवल ग्राफ़ में शीर्षों की संख्या n के फलन के रूप में मापा जाता है, न कि किनारों की संख्या के फलन के रूप में, निर्देशित चक्रीय ग्राफ़ के सकर्मक समापन और सकर्मक न्यूनीकरण में समान जटिलता होती है। यह पहले ही दिखाया जा चुका है कि आकार n × n के बूलियन आव्यूह के सकर्मक समापन और आव्यूह गुणन में एक दूसरे के समान जटिलता थी,[4] इसलिए इस परिणाम ने सकर्मक न्यूनीकरण को उसी वर्ग में डाल दिया है। 2015 तक, आव्यूह गुणन की अभिकलनात्मक जटिलता में O(n2.3729) समय लगता है,[5] और यह सघन ग्राफ़ में सकर्मक न्यूनीकरण के लिए सबसे तेज़ ज्ञात सबसे खराब स्थिति की समय सीमा देता है।
क्लोजर का उपयोग करके न्यूनीकरण की गणना करना
यह साबित करने के लिए कि सकर्मक कमी सकर्मक समापन जितना आसान है, अहो एट अल बूलियन आव्यूह गुणन के साथ पहले से ज्ञात तुल्यता पर भरोसा करें। उन्होंने A को दिए गए निर्देशित एसाइक्लिक ग्राफ का आसन्न मैट्रिक्स होने दिया, और B को इसके सकर्मक समापन का आसन्न मैट्रिक्स होने दिया (किसी भी मानक सकर्मक समापन एल्गोरिदम का उपयोग करके गणना की गई)। तब एक किनारा uv संक्रमणीय कमी से संबंधित होता है यदि और केवल यदि मैट्रिक्स A की पंक्ति u और कॉलम v में एक गैर-शून्य प्रविष्टि है, और मैट्रिक्स उत्पाद एबी की उसी स्थिति में एक शून्य प्रविष्टि है। इस निर्माण में, मैट्रिक्स एबी के गैर-शून्य तत्व दो या अधिक लंबाई के पथों से जुड़े शीर्षों के जोड़े का प्रतिनिधित्व करते हैं।[3]
न्यूनीकरण का उपयोग करके समापन की गणना करना
यह साबित करने के लिए कि सकर्मक न्यूनीकरण सकर्मक समापन जितनी ही कठिन है, अहो एट अल दिए गए निर्देशित चक्रीय ग्राफ़ G से एक और ग्राफ H का निर्माण करें, जिसमें G के प्रत्येक शीर्ष को तीन शीर्षों के पथ से बदल दिया जाता है, और G का प्रत्येक किनारा इन पथों के संबंधित मध्य शीर्षों को जोड़ने वाले H में किनारे से मेल खाता है। इसके अलावा, ग्राफ H, अहो एट अल में प्रत्येक पथ के आरंभ से प्रत्येक पथ के अंत तक किनारा जोड़ें। H की सकर्मक न्यूनीकरण में, u के लिए पथ प्रारंभ से v के लिए पथ के अंत तक किनारा है, यदि और केवल यदि किनारा uv G के सकर्मक समापन से संबंधित नहीं है। इसलिए, यदि H की सकर्मक न्यूनीकरण हो सकती है कुशलतापूर्वक गणना करने पर, G के सकर्मक समापन को सीधे इससे पढ़ा जा सकता है।[3]
विरल ग्राफ़ में न्यूनीकरण की गणना करना
जब निर्देशित चक्रीय ग्राफ़ में शीर्षों की संख्या n और किनारों की संख्या m दोनों के संदर्भ में मापा जाता है, तो समय O(nm) में सकर्मक न्यूनीकरण भी पाई जा सकती है, एक सीमा जो विरल ग्राफ़ के लिए आव्यूह गुणन विधियों से तेज़ हो सकती है . ऐसा करने के लिए, प्रारंभिक शीर्ष के प्रत्येक संभावित विकल्प के लिए, दिए गए निर्देशित चक्रीय ग्राफ में एक रैखिक समय सबसे लंबे पथ समस्या को लागू करें। गणना किए गए सबसे लंबे पथों में से, केवल एक लंबाई (एकल किनारे) वाले पथों को ही रखें; दूसरे शब्दों में, उन किनारों (u, v) को रखें जिनके लिए u से v तक कोई अन्य पथ मौजूद नहीं है। यह ओ (एनएम) समयबद्ध गहराई-पहली खोज या चौड़ाई पहली खोज का उपयोग करके सकर्मक समापन के निर्माण की जटिलता से मेल खाता है। आरंभिक शीर्ष के हर विकल्प से पहुंच योग्य शीर्ष, इसलिए फिर से इन मान्यताओं के साथ सकर्मक समापन और सकर्मक न्यूनीकरण एक ही समय में पाई जा सकती हैं।
टिप्पणियाँ
- ↑ Moyles & Thompson (1969).
- ↑ Clough et al. (2015).
- ↑ 3.0 3.1 3.2 3.3 3.4 Aho, Garey & Ullman (1972)
- ↑ Aho et al. credit this result to an unpublished 1971 manuscript of Ian Munro, and to a 1970 Russian-language paper by M. E. Furman.
- ↑ Le Gall (2014).
संदर्भ
- Aho, A. V.; Garey, M. R.; Ullman, J. D. (1972), "The transitive reduction of a directed graph", SIAM Journal on Computing, 1 (2): 131–137, doi:10.1137/0201008, MR 0306032.
- Clough, J. R.; Gollings, J.; Loach, T. V.; Evans, T. S. (2015), "Transitive reduction of citation networks", Journal of Complex Networks, 3 (2): 189–203, arXiv:1310.8224, doi:10.1093/comnet/cnu039.
- Moyles, Dennis M.; Thompson, Gerald L. (1969), "An Algorithm for Finding a Minimum Equivalent Graph of a Digraph", Journal of the ACM, 16 (3): 455–460, doi:10.1145/321526.321534.
- Le Gall, François (2014), "Powers of Tensors and Fast Matrix Multiplication", Proc. 39th International Symposium on Symbolic and Algebraic Computation (ISSAC '14), pp. 296–303, doi:10.1145/2608628.2608664.